|
RÉPUBLIQUE DU MALI
UN PEUPLE-UN BUT-UNE FOI
ECOLE NORMALE SUPÉRIEURE DE BAMAKO
ANNÉE SCOLAIRE 20006-2007
MÉMOIRE PROFESSIONNEL
PROFESSEUR DE L'ENSEIGNEMENT SECONDAIRE
MATHÉMATIQUES
UNE SÉQUENCE D'ENSEIGNEMENT/APPRENTISSAGE DE LA
GÉOMÉTRIE PLANE DANS L'ENVIRONNEMENT GEOGEBRA
PRÉSENTÉ ET SOUTENU PAR
SALOUM TOURÉ ET SINALY DISSA
SOUS LA DIRECTION DE
DR MAMADOU SANGARÉ
Sommaire :
Introduction................................................................
A. Partie
théorique..................................................................
I. La notion de figure et de dessin en
géométrie..........................................
II. Présentation du logiciel
GeoGebra ......................................................
III. Les apports du logiciel GeoGebra dans
l'appréhension de la notion de figure
géométrique................................................................................
IV.Le rôle de la figure dans
l'argumentation .............................................
B .PARTIE
EXPERIMENTALE................................................
I. Méthodologie :
.............................................................................
II. Description et analyse de la
séquence.................................................
III. Analyse des résultats de
l'expérimentation .........................................
IV.Synthèse des
résultats....................................................................
V.
Discussion.................................................................................
C.
CONCLUSION........................................................................
ANNEXES.........................................................................................
INTRODUCTION
L'informatique et les ordinateurs sont de plus en plus
présents dans les différentes professions et interviennent dans
tout un ensemble de pratiques sociales : optimisation et recherche
opérationnelle, automatisation, consultation des bases de
données, écritures d'articles ou de rapport etc.
Durant ces deux ans, nous entendons parler de T.I.C.E
(Technologie de l'information et de la Communication pour l'Enseignement). Nous
n'en avions pas entendu parler pendant nôtre passage à la
faculté. Mais nous étions convaincu que l'utilisation de ces
« nouvelles » technologies dans l'enseignement semble
être un bon moyen de rendre attractif une séance, de comprendre
une notion mathématique ou en encore de « varier »
un enseignement.
La présence de salles d'informatique dans la plupart
des lycées et l'intérêt que porte les élèves
pour l'ordinateur sont venus renforcer nôtre motivation à vouloir
intégrer les T.I.C (Technologie de l'Information et de la Communication)
dans l'enseignement de mathématiques.
Nous avons découvert que l'ordinateur permet de
rechercher et d'observer des lois expérimentales dans deux champs
naturels d'application interne des mathématiques : les nombres et
les figures du plan et de l'espace. Cette possibilité
d'expérimenter, classiquement plus propre aux autres disciplines, doit
ouvrir largement la dialectique entre l'observation et la démonstration,
et, sans doute à terme, changer profondément la nature de
l'enseignement.
Face à une telle importance accordée à
l'intégration des T.I.C.E dans l'enseignement des mathématiques,
l'analyse de la question suivante devient cruciale.
« Est-ce possible d'engager nos élèves
dans une situation d'enseigement-apprentissage avec
l'ordinateur ? »
Nous avons alors décidé de faire un travail de
réflexion commune sur cette question. En étudiant
précisément l'utilisation d'un logiciel de
géométrie dynamique : GeoGebra. Pour cause, l'enseignement
de la géométrie pause beaucoup de problème dû au
statut de ses objets en environnement papier/crayon. De plus, les instructions
officielles (programmes, savoir faire et découpage de programme) du Mali
n'exigent pas un environnement de travail (papier/crayon ou ordinateur) pour
l'enseignement/apprentissage de la géométrie en
10ème Science.
L'apprentissage par l'enseignant de ces
« nouvelles » technologies est une étape que nous
avons trouvé indispensable, mais il nous semble important d'avoir une
véritable réflexion sur ces outils : Quelles potentialités
de ces outils utiliser en fonction des notions enseignées ? A quel
moment de l'étude les utiliser ? Quels sont les apports de cette
utilisation pour notre enseignement ? Pour nos élèves ?
Nous avons donc cherché des outils théoriques de
la didactique des mathématiques. Ceux qui nous ont aidés à
formuler nôtre problématique. Puis nous avons
élaboré une séquence d'enseignement apprentissage que nous
avons expérimentée et analysée.
Le plan de ce mémoire est le suivant :
- Une première partie qui comprend les outils
théoriques qui ont servis à notre travail de réflexion ;
- Une deuxième partie, qui comprend la description de
l'ensemble des séances que nous avons expérimentées et qui
se termine par une analyse des résultats.
- Dans la troisième partie, nous donnons les
conclusions de notre travail de réflexion ;
- La quatrième et dernière partie de ce
mémoire regroupe les documents annexes dont la bibliographie
utilisée dans notre travail.
A. PARTIE THÉORIQUE :
I. LA NOTION DE FIGURE ET DE DESSIN EN
GÉOMÉTRIE
La géométrie a pour objet la construction et
l'étude raisonnée des figures .On peut naturellement se poser la
question :
I.1. Qu'est-ce qu'une figure géométrique
?
Dans les articles abordant ce sujet, peu d'auteurs se risquent
à donner une définition de l'expression « figure
géométrique » mais il est beaucoup question de la relation
entre figure, dessin, représentation...
Platon évoquait déjà se sujet dans La
République (Livre IV) : « ... tu sais aussi qu'ils se servent de
figures visibles et qu'ils raisonnent sur ces figures, quoique ce ne soit point
à elles qu'ils pensent, mais à d'autres auxquelles celles-ci
ressemblent. Par exemple, c'est du carré en soi, de la diagonale en soi
qu'ils raisonnent, et non de la diagonale telle qu'ils la tracent, et il faut
en dire autant de toutes les autres figures. »
Cette phrase contient deux points essentiels : le fait qu'une
figure sert à raisonner, et que le tracé visible n'est que le
représentant d'un objet abstrait. On retrouve ces idées dans les
textes actuels, avec cependant des nuances. Tous s'accordent pour dire qu'un
dessin géométrique n'est pas une figure, bien que l'expression
« tracer une figure » entretienne l'ambiguïté. Pour
certains, le dessin devient figure dès qu'il est complété
par l'énoncé de ses propriétés. Parzysz1(*) (1989) pense que « la
figure géométrique est l'objet géométrique
décrit par le texte qui la définit, une idée, une
création de l'esprit tandis que le dessin en est une
représentation ».
Laborde et Capponi2(*) précisent cette idée en
définissant la figure géométrique comme « relation
entre un objet géométrique et ses représentations
possibles ».
Dans tous les cas, il y a bien, d'une part un objet
idéal, dont on peut énoncer des propriétés et sur
lequel porte le raisonnement, d'autre part des représentations de cet
objet. Il semble que dans l'usage courant, le même mot, par exemple
carré, serve à désigner à la fois l'objet
idéal et les représentations de cet objet.
Comment un élève, au cours de sa
scolarité, prend-il conscience de ce double statut de la figure
géométrique ? Cette prise de conscience est-elle
nécessaire ?
I.2. La figure est elle d'abord un dessin
?
Dans l'article de Laborde et Capponi (1994) il est
évoqué la complexité des rapports entre dessin et objets
géométriques : le dessin géométrique n'est pas
nécessairement interprété par son lecteur comme renvoyant
à un objet géométrique. De plus un même dessin peut
avoir de multiples interprétations (selon les connaissances du lecteur
mais aussi selon la nature du dessin, le contexte). Parzysz (1986)3(*) souligne aussi ce
problème : « la représentation [d'une figure] se
révèle par nature insuffisante, de l'ordre de la métaphore
en quelque sorte, et l'interprétation nécessaire qu'en fait le
récepteur pour lui donner un sens risque alors d'être abusive
». Pour lui l'interprétation peut se faire grâce à une
certaine connivence entre l'auteur de la représentation et son lecteur
(le récepteur). Cette connivence porte :
- sur la nature des êtres représentés
(basés sur un certain nombre d'archétypes : point, segment,
cercle, etc.) ;
- sur le fait que certaines figures ne sont pas
représentables (droites, plans).
Un dessin peut rendre compte des propriétés d'un
objet géométrique mais il ne peut pas définir
complètement cet objet. La pratique de la géométrie
nécessite donc, comme le dit Arsac (1992)4(*) « un aller retour constant entre le dessin et un texte,
un énoncé ». Par exemple, c'est en revenant à
l'énoncé que l'on décide de la validité d'une
conjecture en prenant en compte ce qui est donné en hypothèse ou
ce qui peut s'en déduire.
Par son caractère figé, on ne peut pas savoir
exactement ce qui est propre à l'objet mathématique ou ce qui
dépend seulement de la configuration. Par exemple, le fait que
l'orthocentre se trouve à l'intérieur d'un triangle est une
propriété qui pourrait sembler vraie sur un grand nombre de
dessins (Arsac, 1992, page 174).
C'est pourquoi les possibilités de modifications
interactives d'un dessin à l'aide d'un logiciel comme GeoGebra parait
intéressantes.
I.3. Le dessin et la figure en
papier/crayon :
Dans l'enseignement/apprentissage de la
géométrie en papier/crayon les figures ne sont pas modifiables.
La validation d'une construction devient très difficile voire même
impossible.
Les instruments de l'environnement papier/crayon (crayon,
équerre, règle, compas etc.) cachent des propriétés
géométriques importantes dans l'appréhension d'une figure.
Puisqu'ils ne mettent pas assez d'outils de validation à la disposition
des élèves lors de la construction.
Cet environnement favorise aussidles évidences
mathématiques implicites (par exemple l'intersection de deux objets
géométriques) qui diminuent la rigueur dans la construction d'une
figure géométrique.
Par contre, lors des situations problèmes, les
élèves ont parfois besoin de se confronter au réel pour
faire interagir les différents sens (vue, toucher...) et les
associations mentales. Dans ces cas, la réalité virtuelle
proposée par un logiciel pourrait tout à fait évacuer des
entrées importantes pour l'élève (la représentation
en trois dimension par exemple).
Ceci implique de ne pas omettre d'enseigner en classe
l'utilisation des outils (crayon, équerre, règle, compas etc.)
qui seraient absente dans le cas d'une utilisation systématique d'un
logiciel de géométrie..
II. PRÉSENTATION DU LOGICIEL
GEOGEBRA :
Que signifie géométrie
dynamique ?
Le terme géométrie dynamique désigne
à la fois l'environnement géométrique et l'ensemble des
outils qui permettent d'explorer de façon interactive les
propriétés des objets géométriques en effectuant
des opérations de nature géométrique : tracé de
courbe, transformation géométrique, projection, etc., tout en
respectant les contraintes du milieu géométrique :
parallélisme et orthogonalité en géométrie
euclidienne, par exemple.
La plupart du temps, ce terme désigne les logiciels qui
offrent un tel environnement de travail. Ils offrent une panoplie d'outils qui
permettent d'explorer de façon étendue différentes
propriétés géométriques.
II.1.Description et historique du
logiciel GeoGebra :
GeoGebra est un logiciel de géométrie dynamique
qui permet de manipuler des objets géométriques du
plan (cercle, droite et angle, par exemple) et de voir
immédiatement le résultat, de plus il admet un ensemble de
fonctions algébriques.
Lorsqu'on compare les figures faites avec GeoGebra au
tracé sur feuille de papier, son intérêt tient à ce
qu'il soit possible d'établir des liens entre les différents
objets (par exemple, parallélisme et bissectrice d'un angle) et le
logiciel maintient ceux-ci après un
« Déplacement ».
Il est principalement utilisé par des enseignants, mais
toute personne souhaitant explorer de façon visuelle les transformations
euclidiennes dans le plan en tirera profit.
Ce logiciel est en théorie, fonctionnel sur tout
système d'exploitation : Windows, Linux, Mac OS, etc. Il suffit de
le lancer via Internet, il vient généralement avec la
distribution récente.
Une fois le logiciel lancé, l'utilisateur peut
manipuler les différents objets géométriques de base dans
un plan : cercle, droite, angle, etc. Il peut aussi s'exécuter depuis un
poste d'ordinateur non connecté à Internet en le
téléchargeant.(Voir le site officiel en annexe).
C'est un logiciel libre et gratuit. Il est distribué
sous la licence GNU, c'est à dire tout le monde peut l'utiliser,
l'étudier le modifier et le redistribuer. Dans tous les cas, certaines
restrictions s'appliquent, mais aucune qui empêche de l'utiliser et de le
répliquer autant que souhaité.
Il a été développé par
Markus Hohenwarter, professeur autrichien travaillant à
l'Université de Salzbourg, qui ne le maintient plus depuis
l'été 2006. Le développement et la maintenance du logiciel
sont effectués par une autre personne.
II.2. Quelques utilisations possibles du logiciel
dans l'enseignement des maths au lycée :
Comme décrit précédemment,
géométrie dynamique, algèbre et calculs s'associent pour
former GeoGebra. C'est un logiciel, qui associe
géométrie et algèbre comme des partenaires d'égale
importance.
De la manière la plus simple, on peut faire des
constructions contenant des points, des vecteurs, des segments, des droites, et
des coniques aussi bien que des fonctions, qui peuvent être
modifiées ensuite dynamiquement à la souris. D'une autre
manière, la saisie telle que : g: 3x + 4y = 7 ou: c: (x - 2)2 + (y - 3)2
= 25 est possible, et une gamme de commandes contenant différentiation
et intégration est à votre disposition.
La caractéristique la plus remarquable de GeoGebra est
la double perception des objets : chaque expression de la
« Fenêtre Algèbre » correspond à un
objet dans « la Feuille de Travail » et vice versa
(voir fenêtre de démarrage en annexe).
Les exploitations pédagogiques possibles sont :
- Le professeur pourra l'utiliser dans le cadre de la
préparation de ses cours pour produire certaines constructions de figure
géométrique du plan difficilement réalisable en papier/
crayon (par exemple l'ellipse) ;
- L'utiliser autour d'un projecteur (ou dans une salle
d'informatique) pour faire voir aux élèves les cas de figures
possibles et les invariants d'une construction géométrique
à l'aide du « déplacement » .
III. LES APPORTS DU LOGICIEL GEOGEBRA DANS
L'APPRÉHENSION DE LA NOTION DE FIGURE
GÉOMÉTRIQUE :
L'utilisation de GeoGebra peut aider les élèves
à comprendre le rôle des propriétés
géométriques dans la définition d'un objet. Il permet de
construire soit des éléments de base (points, droites....) soit
des objets définis par des relations aux éléments
déjà tracés.
Pour obtenir, à partir de deux points A et B, un
parallélogramme ABCD, un élève peut tracer « au
jugé », des droites de base, c'est-à-dire qu'il se fie
à sa perception visuelle : « ça à l'air d'un
parallélogramme ». Bien qu'il n'ait nullement enregistré que
les droites tracées sont parallèles, il pense avoir
réalisé la tâche demandée. Si alors, on lui demande
de déplacer le point A, le parallélogramme se déforme en
un quadrilatère dont les côtés ne sont plus
parallèles, ce qui invalide sa construction. Il peut alors mieux
comprendre la nécessité d'utiliser les propriétés
de la figure pour définir les éléments à
construire. Ceci est particulièrement flagrant pour certaines
constructions comme celle d'une tangente à un cercle passant par un
point donné. En papier/crayon, les élèves ont tendance
à procéder empiriquement en faisant tourner la règle
autour du point, et il est très difficile de disqualifier leur
procédé : pour eux, la droite tracée respecte bien la
caractéristique d'une tangente. Avec un logiciel comme GeoGebra, un tel
procédé au jugé sera immédiatement invalidé
par un déplacement, mais alors, cette sanction ne sera pas perçue
comme une contrainte arbitraire fixée par l'enseignant ; « le
dispositif oblige à la distinction entre tracé et
procédé de tracé . D'autre part, l'enseignant est absent
du processus de communication au dispositif ».
De plus, la possibilité de modifier le dessin en
déplaçant les points de base a le même effet que la
construction en papier/crayon de plusieurs figures correspondant au même
énoncé : elle met en évidence les invariants et est ainsi
source de conjectures et de questionnements.
En effet un GeoGebra-dessin5(*) possède en quelque sorte une mobilité
intelligente qui offre à un objet géométrique une nouvelle
représentation. Un dessin appartient à l'univers des
représentations possibles d'un objet géométrique. A partir
d'un GeoGebra-dessin on peut décrire une large partie de cet univers
avec rapidité et simplicité. Ceci offre ainsi un formidable outil
pour conjecturer.
IV. LE RÔLE DE LA FIGURE DANS LA
DEMONSTRATION :
Au second cycle de l'enseignement fondamentale et encore
souvent au lycée, les élèves ont du mal à se
convaincre du fait qu'un dessin ne suffit pas pour démontrer une
propriété. Mais les élèves font-ils la
différence entre démonstration et argumentation ? En effet, si
pour eux démontrer signifie argumenter, alors un dessin est un bon
argument pour convaincre ses pairs. C'est d'ailleurs un point
développé par (Arsac 1992, page 175) : « On constate donc
que la démonstration en géométrie présente des
difficultés particulières à cause du statut de l'objet sur
lequel elle porte. Ceci constitue une spécificité par rapport
à la démonstration en arithmétique par exemple ».
Comme nous avons pu le constater dans le paragraphe
précédent, l'interprétation d'un dessin pose
problème aux élèves. Or ce dessin a un statut qui
évolue tout au long du cursus de l'élève : jusqu'en
cinquième (7e au Mali), l'accent est mis sur la
précision du tracé, la description, l'utilisation du
matériel de géométrie ; par la suite, le statut de figure
va évoluer et de nouvelles tâches apparaissent ou disparaissent
(Arsac, 1992, page 167). Certains problèmes sont encore des
problèmes de construction. Mais cette construction peut faire appel
à une propriété et nécessite donc un raisonnement,
voire même une démonstration. La tâche peut être aussi
compliquée afin d'obliger l'élève à utiliser une
propriété (par exemple le professeur peut décider
d'interdire l'utilisation de la règle ou de l'équerre).
Avec l'apparition progressive de la démonstration (qui
apparaît dès la 7e sous la forme de « courtes
séquences déductives »), le dessin est un outil, en ce sens
qu'il peut aider l'élève à plusieurs niveaux :
1) Visualiser :
passer du registre du langage naturel au registre graphique (au sens de
Raymond Duval, 1993) aide à avoir une meilleure perception d'une
situation. De plus l'illustration d'un théorème par un dessin
permet de se construire une image mentale à laquelle on peut faire appel
lors de la résolution d'un problème ;
2) Conjecturer : à partir de
plusieurs dessins, on peut voir apparaître un invariant qui peut donner
lieu à une propriété qu'il faudra démontrer ;
3) Démontrer : à
partir d'un énoncé, faire un dessin codé comportant les
données aide à reconnaître des configurations et donne une
idée des propriétés à utiliser. Dans les exercices
de géométrie, la tâche « faire un dessin »
disparaît peu à peu. Cependant elle doit être un geste
automatique pour l'élève ;
4) Se convaincre : un
dessin peut servir à illustrer une propriété mais peut
être aussi un contre-exemple.
Dans chacun de ces actes le dessin a un statut
différent et l'élève ne s'y retrouve pas forcément.
L'élève doit parfois constater des choses sur un dessin
(lorsqu'il conjecture ou qu'il donne un contre-exemple) mais il n'aura pas le
droit de le faire lorsqu'il s'agit de faire une démonstration. Ainsi, un
élève peut être tout à fait convaincu d'une
propriété alors que ce n'est encore qu'une conjecture. Par
exemple en 8e, les élèves doivent conjecturer le
théorème suivant : « Dans un triangle, si une droite passe
par le milieu d'un côté et est parallèle à un
deuxième côté, alors elle passe par le milieu du
troisième côté ». Après avoir fait le dessin,
la plupart des élèves sont persuadés que la droite passe
par le milieu du troisième côté, c'est une évidence.
Ce type de difficulté se retrouve encore en 10e, certains
élèves utilisant en début de démonstration des
évidences visuelles comme si elles étaient des données de
l'énoncé (droites parallèles, vecteurs et angles
égaux).
Par contre, un dessin peut induire en erreur ou donner une
fausse impression et c'est alors la démonstration qui convaincra. C'est
d'ailleurs une des réponse à la question : « pourquoi
démontrer ? ». La démonstration permet de convaincre mais
aussi de comprendre (Arsac, 1992, page 6).
Il faut pourtant noter qu'il est courant et accepté de
prendre certaines informations sur la figure sans justification. Un exemple
simple : sur le segment [AB], placer les points E et F tels que AE = EF = FB.
Tout le monde admettra qu'il y a une seule figure possible, mais ce n'est
jamais démontré et pourtant ce n'est pas un
théorème du cours. De même, pour calculer une mesure
d'angle, on écrira cet angle comme somme d'angles de mesure connue, sans
justifier cette décomposition. C'est la même chose pour un calcul
d'aire. Ainsi, les propriétés d'ordre, de régionalement,
dans certains cas d'intersection, peuvent être généralement
admises directement de la constatation visuelle sur le dessin.
« Le dessin est donc soit superflu soit
indispensable » ( Rolet, 1997)
B. PARTIE EXPÉRIMENTALE :
I. Méthodologie :
Dans cette partie expérimentale les activités
sont définies à partir d'une séquence que nous nommons
« sous séquence3 » (SS3). En fait, c'est lors de
cette sous séquence que nous proposons aux élèves des
activités de constructions géométriques dans
l'environnement du logiciel GeoGebra.
Ainsi nous avons fait ressortir de l'analyse de la
« sous séquence3 » les instructions du logiciel
nécessaire à son exécution. Ce qui fera l'oeuvre d'une
séquence d'enseignement que nous nommons « sous
sequence2 » (SS2).
D'autre part, nous ferons ressortir les instructions du
système d'exploitation de Microsoft Windows (qui est sur les machines
dont nous disposons) et des techniques de manipulation de l'ordinateur
nécessaire à l'exécution de la « sous
séquence2 » par rapport à la « sous
séquence3 ». Nous nommons l'enseignement de ces instructions
du système d'exploitation « sous séquence1 »
(SS1).
Les trois sous séquences définies ci-dessus sont
exécutées en deux séances.
La première séance (Séance1) regroupe les
« sous séquence1 » et « sous
séquence2 ». Et la deuxième séance
(Séance2) pour la « sous séquence3 ».
Par suite Nous analysons pour chaque sous séquence les
comportements des élèves dans l'exécution des
activités. Nous récupérons de plus des productions
d'élèves (qui seront enregistré sur les machines) que nous
analysons par rapport à nôtre problématique.
II. DESCRIPTION ET ANALYSE DE LA SÉQUENCE
Contexte d'étude :
Niveau: 10ème Science
Établissement : Lycée Gandiamory Keïta de
Faso Kanu
Effectif: 10 élèves
Matériels de travail :
Classe : Une salle d'ordinateurs (voir disposition en
annexe)
Logiciel : GeoGebra2.6b pour Windows (le système
d'exploitation le plus fréquent dans les lycées est Windows)
Une fiche élève : La feuille sur laquelle
figure les instructions de la situation.
Le Dossier « GeoGebra »: le dossier dans
lequel se trouve les fichiers qui seront utilisés tout au long de la
séquence.
II.1.SÉANCE1 :
II.1.1.Sous Sequence1 (SS1): (Prise en
main du système d'exploitation).
Les élèves reçoivent
régulièrement des cours d'informatique sous l'environnement
Windows XP.
II.1.1.1. Objectif :
Tester si les élèves ont une maîtrise
suffisante du Système d'Exploitation Windows par rapport à
SS3.
Si le test est concluant nous passons à SS2 sinon nous
faisons une mise en niveau pratique.
II.1.1.2. Liste des instructions du S.E à
utiliser :
- Le fonctionnement de la souris (Pointer, cliquer,
cliquer-glisser, double cliquer et le clic droit) : dans la manipulation de la
barre d'outils de géométrie de GeoGebra les élèves
feront presque toutes les manipulations avec la souris ; ils auront des
dossiers à créer, de même utiliser le
« déplacement ».
- Le clavier (majuscule, minuscule et chiffre) : d'une part
les élèves auront à nommer les dossiers et fichiers qu'ils
vont créer d'autre part ils vont renommer des points sous GeoGebra.
- Gestion de dossiers et Fichiers (création,
ouverture, nomination et copie) : utilisation pratique de la souris et le
clavier, les élèves auront à gérer un
système de dossier pour enregistrer et ouvrir les fichiers dans les
dossiers appropriés.
- La fenêtre de Windows (barre de titre : titre du
document, réduire, maximiser, minimiser et fermer une fenêtre; et
la barre des menus: surtout le menu fichier) : manipulation de la fenêtre
et la gestion du menu fichier pour enregistrer et/ou ouvrir un fichier.
II.1.1.3.SCÉNARIO :
Phase1 : (5 mn)
Phase2 : (15 mn)
a. Objectif:: évaluer le niveau de
maîtrise des élèves sur l'environnement Windows par
rapport à la liste des instructions citées ci-dessus.
b. Test1:
Tâches pour l'élève :
T1). Allumer l'ordinateur.
T2). Retrouver le dossier « GeoGebra »
dans le sous dossier « Logiciel » du sous dossier
« Expérimentation » dans le dossier « Mes
documents » sur le Bureau.
T3). Faire une copie de ce dossier sur le Bureau.
T4).Créer un nouveau dossier sur le Bureau, donner lui
votre prénom en mettant la première lettre du prénom en
majuscule.
T5). Déplacer le dossier
« GeoGebra » dans le dossier précédemment
crée.
T6). Ouvrir le dossier « GeoGebra » pour
voir ce qu'il contient.
Consignes :
Les tâches seront exécutées les unes
après les autres ie pour passer de la tâche Ti à
la tâche Ti+1 il faut avoir les résultats de la
tâche.
c. Eléments d'analyse des
tâches :
T1 : les élèves ne doivent pas
avoir de difficulté dans l'exécution de cette tâche car les
boutons d'allumage de l'ordinateur (ie de l'écran et de l'unité
centrale) ne sont pas cachés et de plus ils sont marqués d'un
symbole qui ne se trouve sur aucun autre bouton .
T2 :
T2.1. La formulation de la question de cette tâche peut
être source de difficulté pour les élèves. Dans les
pratiques de classe, les élèves ont l'habitude de partir toujours
de l'existant (ie ce qu'ils voient) puis chercher et retrouver ce qui est
caché. Dans de tel cas, le professeur peut intervenir en reformulant la
question de cette tâche de la manière suivante :
1. Ouvrir « Mes documents » sur le Bureau
et chercher le dossier « Expérimentation »
2. Ouvrir le dossier »
expérimentation » et retrouver le dossier
« logiciel ».
3. Ouvrir dossier « logiciel » et
retrouver le dossier « GeoGebra ».
T2.2. Retrouver un objet parmi plusieurs et de
différents types peut être difficile si le nombre d'objets est
très élevé.
Le professeur pourrait intervenir en guidant les
élèves par des questions qui suivent :
Quelles sont les couleurs des différents objets que
vous voyez ?
Chercher le dossier
« expérimentation » qui est de couleur jaune.
Utiliser la barre de défilement (à
l'extrême droit de la fenêtre) pour voir tous les dossiers.
T3 : Cette tâche peut avoir deux niveaux de blocage
pour les élèves dans son exécution.
D'une part des élèves peuvent penser que
« faire une copie » correspond à l'instruction
« copier » du menu déroulant de la souris. D'autre
part, « faire une copie sur le bureau » peut faire penser
à une action qui doit se passer sur le Bureau.
Le passage de T2 à T3 peut être aussi difficile
pour des élèves. En effet, en T2 il y a un ensemble de
fenêtres ouvertes et l'élève peut vouloir aller
directement au Bureau.
Dans les deux cas ci-dessus le professeur pourrait reformuler
la question de la manière suivante :
1) « Copier » le dossier «
GeoGebra » ;
2) Fermer toutes les fenêtres ouvertes ;
3) « Coller » alors sur le Bureau
à un espace vide
T4 : Ici le fait de ne pas taper sur la
touche « Entrer » du clavier à la fin de la
saisie peut être une source de difficultés pour les
élèves. Si l'élève touche par inadvertance une
autre touche, le nom est aussitôt modifié. En lisant le mot saisi
à l'écran l'élève pense exécuter la
tâche demandée.
Le professeur pourrait les guider en leur demandant de taper
sur la touche « Entrer » du clavier tout juste à la
fin de la saisie.
T5 : Sur le bureau il n y a que 4
icônes ; donc les élèves ne doivent pas avoir de
difficultés car ils connaissent le langage de la souris. Par contre
Ouvrir le dossier « GeoGebra »peut ne pas être aussi
facile car il n'est plus sur le Bureau (l'élève l'a
déplacer dans le dossier qu'il vient de créer). Le professeur
peut alors orienter les élèves avec les questions
suivantes:
Quelle est la dernière action que tu viens de
faire ?
Ouvres alors le dossier que tu viens de créer.
d. Rôle du professeur :
Le professeur se tient dans une position isolée. Si un
élève se bloque le professeur intervient en donnant des
instructions susceptibles de relancer l'activité (sans donner la
réponse ni la méthode de l'atteindre mais plutôt des
indices) de cet élève sans pour autant déranger ou
arrêter les autres. Au niveau de « 6. »Le dossier
« GeoGebra » est aussi accessible à partir du
dossier Binôme (i) qu'à partir du dossier « Mes
documents ».
Bilan 1.1
a. Éléments
d'évaluation:
L'exécution correcte du test1 se vérifie en
regardant le chemin d'accès du dossier « GeoGebra »
dans la barre d'adresse de la fenêtre. Le professeur donne alors des
indications sur le contenu de ce dossier.
b. Institutionnalisation de
« copier/coller »:
Si on fait la copie d'un dossier, ce dossier devient
accessible à partir de deux emplacements (i.e. l'emplacement d'origine
et là où on a fait la copie).
Phase3:(15 mn)
Dans cette phase les élèves seront
groupés en binômes. Cette réorganisation de la salle nous
permettrait d'avoir des binômes de niveau
« équilibré ». Ceci pour une
régulation interne de la classe. Tous les groupes pourront ainsi avancer
ensemble et le professeur gagne du temps puisque les élèves se
comprennent mieux entre eux.
a. Objectifs:
1) Retrouver et ouvrir un fichier à partir du menu
« Fichier » du logiciel GeoGebra.
2) Lorsque GeoGebra est actif permettre aux
élèves de découvrir la possibilité d'ouvrir
plusieurs fichiers «. ggb » et les manipuler en terme de
multi fenêtrage.
b. Test2 :
Tâches pour l'élève :
T1. Changer le Nom du dossier crée individuellement en
« Binôme (i) » (où i est le numéro du
binôme).
T2. Lancer le logiciel GeoGebra à partir de ce dossier
et réduire cette fenêtre.
T3. Fermer toutes les autres fenêtres ouvertes.
T4. Restaurer la fenêtre du logiciel puis enregistrer-le
sous le nom « Essai » dans le dossier « Binôme
(i) ».
T5. Ouvrir à partir de cette fenêtre le fichier
« Activite1.ggb » se trouvant dans le dossier
« TP1 » de GeoGebra
Consignes : l'exécution des
tâches de ce test nécessite les résultats des tâches
de test1.
c. Élements d'analyse des
tâches :
T1: Cette tâche met en jeu la
manipulation direct du menu déroulant qui est connu au préalable
par les élèves, donc ils ne doivent pas avoir de
difficulté dans l'exécution de cette tâche.
T2: Des élèves pourront
s'arrêtés juste après avoir retrouver la feuille
« GeoGebra » au lieu de l'ouvrir. En effet, lorsque
l'élève retrouve le fichier « GeoGebra »
à l'écran, il peut penser l'avoir ainsi ouvert.
T3: les élèves connaissent les
différentes barres d'une fenêtre Windows et les manipulations
qu'ils peuvent en faire, donc l'exécution de cette tâche ne doit
pas poser de difficultés
T4: la feuille du logiciel étant
réduite à la barre des tâches, ouvrir encore cette feuille
peut faire penser à l'élève de passer dans le
système de fichier pour le retrouver puisqu'il ne le voit à
l'écran.
T5: Sous Windows l'exécution des
instructions « ouvrir » et
« enregistrer » du menu « Fichier »
amène par défaut le dossier « parent » du
fichier déjà ouvert. Ce pendant les fichiers
« Essai.ggb » et
« Activité1.ggb » ne se trouvent pas dans le
même dossier, les élèves peuvent avoir des
difficultés à retrouver le fichier
« Activité1.ggb ».
Le professeur peut alors guider les élèves
à remonter le système d'arborescence des répertoires
jusqu'à retrouver le fichier
« Activité1.ggb ».
d. Rôle du professeur :
Le professeur se tient dans une position isolée, si un
binôme se bloque le professeur intervient en donnant des instructions
susceptibles de relancer l'activité (sans donner la réponse ni la
méthode de l'atteindre mais plutôt des indices) de ce binôme
sans pour autant déranger ou arrêter les autres binômes.
Il existe d'autre moyen d'avoir le « 5. »
i.e. on peut ouvrir le fichier « Activite1.ggb » à
partir du dossier GeoGebra mais notre objectif ici est l'utilisation du menu
« Fichier » de GeoGebra.
Bilan1.2
Éléments d'évaluation :
Vérifier les fichiers
« Activité1.ggb » et
« Essai.ggb » sur la barre des tâches.
a. Institutionnalisation :
« Si le logiciel est ouvert alors on peut ouvrir
plusieurs fichiers « .ggb » qui vont s'afficher sur la
barre des tâches. Le fichier actif est visible sur l'écran tandis
que les autres sont réduites. »
II.1.2. SOUS
SÉQUENCE 2 : SS2
(Prise en main du logiciel GeoGebra)
II.1.2.1. Objectif :
Permettre aux élèves d'avoir une maîtrise
suffisante du logiciel de géométrie dynamique GeoGebra par
rapport aux tâches à exécuter en SS3.
II.1.2.2. Liste des instructions de GeoGebra à
utiliser :
1). « Nouveau point » : Dans le
tracé effectif avec les instructions de GeoGebra, on définit
d'abord les points.
2) « Segment entre deux points » :
Segment délimité pour deux points
3) « Droite passant par deux
points » : Une droite est construite à partir de deux de
ses points.
4) « Droite perpendiculaire » :
Droite perpendiculaire à une autre et passant par un point
quelconque.
6) « Cercle (centre-point) » : Cercle
défini par son centre et passant par un point.
7) « Intersection entre deux
objets » : le point d'intersection de deux objets
géométriques est une instruction à part dans GeoGebra ce
qui est ostensible en papier/crayon
8) « Effacer les objets » : supprime
les figures géométriques avec leurs propriétés
9) « Déplacer » :
déplace un objet (contrôle perceptif et dynamique en temps
réel).
10 )« Afficher/Cacher l'objet » :
rend visible/invisible certains objets géométriques tout en
concernant les propriétés géométriques qui leur
sons liées.
11)« Annuler »,
« Refaire » : retour en arrière dans la
construction.
12).« Ouvrir »,
« Nouveau », « Enregistrer »,
« Enregistrer sous » : quelques instructions du menu
« Fichier » de GeoGebra.
13)« Renommer » : Changer le nom d'un
objet géométrique
14 « Angle »: Angle défini par
trois points.
II.1.2.3.
SCÉNARIO:
Phase1:(15 mn)
a. Objectif: découvrir les commandes
de la barre d'outils de géométrie de GeoGebra par rapport
à la liste des instructions citées ci-dessus.
b. 1 2 3 4 5 6 7 8 9
10 11

Activité1 ;
Tâches pour élève
Écris devant chacune des instructions suivantes le
numéro du menu dans le quel elle se trouve :
1. Nouveau point;
2. Segment entre deux points;
3. Droite passant par deux points;
4. droite perpendiculaire
5. Distance
6. Cercle (centre-objet)
7. intersection entre deux objets
8. Effacer des objets
9. Déplacer
10. Afficher/Cacher l'objet
11. Annuler, Refaire
12. Angle;
Consignes :
Cliquer sur la petite flèche située à
l'extrême gauche et en bas des icônes pour voir les instructions
que l'outil contient.
c. Élements d'analyse des tâches :
La technique de recherche étant déjà
expliquée par le professeur, c'est seulement au niveau de
« 11. » qu'il peut avoir de difficulté puisqu'il
faut cette fois ci pointer sur les icônes pour lire contrairement. Par
contre pour les autres icônes ,il faut cliquer sur la petite
flèche au bout pour voir les instructions qui l'appartiennent.
d. Rôle du professeur :
Le professeur donne la consigne de recherche qui est de
cliquer sur chaque outil pour voir les instructions qu'il contient et
d'écrire devant chaque instruction le numéro de l'icône
dans le quel elle se trouve.
Bilan2.1
Éléments d'évaluation :
Les fiches de travail des élèves seront
récupérées et vérifiées.
Le professeur explique alors le rôle de chacune de ces
instructions aux élèves.
Phase2 :(20 mn)
a. Objectif :
1). Construire des objets géométriques dans
l'environnement de géométrie dynamique GeoGebra.
2). Permettre aux élèves d'effectuer un
contrôle perceptif et dynamique.
b. Activité2 :
Tâches pour élève :
Le fichier « Activite1.ggb » est
ouvert.
1. Construire un segment d'extrémités A et
B ;
2. Construire le milieu de A et B, nommer le O ;
3. Tracer une droite perpendiculaire à [AB] passant
par O ;
4. Comment appelle t-on cette droite par rapport au segment
[AB]?
5. Déplacer les points A ou B. Est-ce que la relation
entre le segment [AB] et la droite tracée reste la même?
6. Construire le cercle de centre O passant A
7. Construire les intersections de ce cercle avec la droite
construite en 3.)
8. Construire les droites (AD) et (BC).
9. Enregistrer ce Fichier Dans TP1.
Consignes:
Utiliser les résultats de l'activité
précédemment faite sur la fiche élève pour faire
l'activité suivante.
Il n'est pas autorisé d'utiliser l'instruction
« médiatrice »
c. Élements d'analyse des tâches :
Les élèves ont à leur disposition le
stock d'instructions nécessaire et de plus ils savent que le
tracé effectif d'un objet géométrique est toujours
défini à partir des points qui l'appartiennent.
Le logiciel affiche au niveau de chaque icône l'image de
la dernière instruction utilisée. Ceci peut être source de
blocage pour les élèves.
Le professeur interviendrais si nécessaire en
demandant aux élèves de refaire une suite de construction et les
dire de regarder à chaque fois l'icône qui s'affiche. Ils
comprendront ainsi que c'est l'icône de la derrière instruction
utilisée qui s'affiche.
d. Rôle du professeur
Le professeur dévient un observateur et quand tous les
élèves auront terminé il identifie ceux qui n'ont pas pus
faire ou qui ont mal fait. Il interroge un des binômes qui a pu faire
pour qu'il explique sa procédure.
Bilan2.2 :
Éléments d'évaluation
Vérification de la construction sur la fenêtre
ouverte.
Phase3 : bilan de la Séance (30
mn)
En classe entière, contrôle de
l'effectivité de la mise en oeuvre de la validation et
institutionnalisation finale des acquis. Le professeur pose des questions,
laisse les élèves discuter entre eux puis donne un cours de fin
qui est en fait une synthèse des bilans.
Durée de la séance : 1 h 40 mn.
Activité :( à chercher
à la maison)
Construis une droite (D) et un point M n'appartenant pas
à (D).
1) Construis le symétrique M' du point M par rapport
à cette (D).
2) Explique les étapes de ta construction.
3) Donne une justification de ta construction.
Justification du choix de cette
activité :
Lors de la séance2 les élèves
travailleront en binômes. Cette activité engagerait donc en avance
chaque élève à une recherche individuelle.
Ainsi au cours du travail en binôme, les
élèves échangeront les connaissances sur leurs
méthodes de construction. Par suite, ils se convaincront sur une
méthode à présenter.
Avec l'objectif de guider les élèves à la
« reconstitution » d'une construction
géométrique, cette activité a sa place dans nôtre
scénario.
FIN SÉANCE1
![]()
II.2. SÉANCE 2 : (sous séquence
3 : SS3) : Mise en oeuvre de la situation expérimentale.
Cette sous séquence s'exécute en deux
étapes :
II.2.1.
Etape1 :
Construction de l'image d'un point par
rapport à une droite en papier/crayon. Rappelons que les
élèves ont suivi des cours sur les transformations du plan.
a. Objectif :
Tester si les élèves sont capables de construire
le symétrique d'un point par rapport à une droite en
papier/crayon.
b. Test :
L'activité donnée à chercher à la
maison à la fin de la séance1.
c. Bilan de l'étape1 :
Si le test est concluant, nous passons à
l'étape2. Sinon nous ferons une
rémédiation avec les instruments de géométrie au
tableau en salle d'informatique.
II.2.2. Etape2 :
Si les élèves savent construire en papier/crayon
et savent utiliser les instructions du logiciel GeoGebra, sauront-ils
reporter leur construction sous GeoGebra ?
a. Objectifs :
Construire le symétrique d'un point par rapport
à une droite (D) sans utiliser l'instruction « Symétrie
axiale (Objet-axe) » de GeoGebra.
Engager les élèves dans une justification
pratique (sur GeoGebra) et théorique de cette construction (en
papier/crayon).
b.Activité1 :
Construis une droite (D) et un point M n'appartenant pas
à (D).
1) Construis le symétrique M' du point M par rapport
à la droite (D) sans utiliser l'instruction
« symétrie axiale » de la barre d'outils de
géométrie de GeoGebra.
2) En faisant déplacer M ou la droite (D), est-ce que
M' reste toujours le symétrique de M par rapport à la droite
(D) ?
c.Activité2 :
Dites pourquoi vôtre construction est juste ? (En
papier/crayon). Expliquez clairement.
II.2. 3.ANALYSE DES SITUATIONS DE LA SÉANCE
2 :
Rappelons que les élèves ont déjà
vu des outils de GeoGebra leur permettant de construire le symétrique
d'un point.
II.2. 3.1.Activité1 :
a. Objectifs ;
Engager les élèves :
Dans la construction du symétrique d'un point par
rapport à une droite (D) sans utiliser l'instruction
« Symétrie axiale (Objet -axe) » ;
Dans une justification par déplacement de cette
construction.
Énoncé :
Construis une droite (D) et un point M n'appartenant pas
à (D).
1) Construis le symétrique M' du point M par rapport
à la droite (D) sans utiliser l'instruction
« symétrie axiale » de la barre d'outils de
géométrie de GeoGebra.
2) En faisant déplacer M ou la droite (D), est-ce que
M' reste toujours le symétrique de M par rapport à la droite
(D)
3) Vous devez expliquer vôtre méthode de
construction à un camarade absent. Écrivez un texte pour
expliquer à ce camarade vôtre méthode de construction
étape par étape.
Consignes :
Inspirez-vous de vôtre construction faite avec les
instruments de géométrie pour reporter la construction en
environnement GeoGebra en utilisant les instructions appropriées.
Enregistrez ce fichier sous le nom
« activite2 » dans le dossier
« GeoGebra ».
b. Difficultés des élèves :
La transposition des étapes de construction du
papier/crayon aux instructions de GeoGebra.
Exemple : pour le report de longueur (utilisation du
cercle avec GeoGebra au lieu d'un arc de cercle).
c. Rôle du professeur dans la phase de
rémédiation :
Le professeur pose des questions pour guider les
élèves dans leur recherche jusqu'à ce qu'ils trouvent
l'instruction appropriée sans leur donne
II.2.
3.2..Activité2 :
a. Objectif :
Permettre aux élèves de passer d'une
construction effective à une justification théorique de la
construction du symétrique d'un point par rapport à une droite.
Énoncé :
Dites pourquoi vôtre construction est juste ? (En
papier/crayon). Expliquez clairement.
Consigne :
Regardez vôtre construction avec GeoGebra en
activité1.
b.Difficultés des élèves :
c. Rôle du professeur dans la phase de
rémédiation :
La justification théorique d'une construction
géométrique n'est pas habituelle dans les pratiques. Le
professeur doit alors :
II.2. 3.3..Justification des
choix :
Si l'instruction « Symétrie axiale
(objet-axe) » n'est pas exclue, les élèves
n'utiliseront pas de connaissances géométriques dans la
construction. En effet, cette instruction de GeoGebra permet de construire le
symétrique d'un objet géométrique en de simples clics.
Cette instruction cache donc aux élèves les connaissances
géométriques liées à cette activité qui
permettra de « reconstituer » une procédure de
construction géométrique.
Les élèves utiliseront l'instruction
« Déplacer » de GeoGebra pour la validation de leur
construction. En effet, cette instruction de GeoGebra permet de déplacer
certain point d'une construction tout en conservant ses
propriétés géométriques.
En activité2 la justification théorique permet
d'institutionnaliser des connaissances mathématiques sur la
transformation symétrie orthogonale (les configurations qui accompagnent
la construction). En effet, l'enseignement de la géométrie ne
pourrait se limiter à de simples constructions qui se réduisent
à des techniques. Les logiciels de géométrie dynamique
constituent un moyen pour l'enseignement des mathématiques et non une
fin.
II.2.
3.4...METHODE1 :
a. Programme de construction en
papier/crayon :
(D)
()
(C1)
b. Justification théorique de la
construction :
- Le triangle MAM' est isocèle en A (car M et M'
appartiennent à l'arc de cercle de centre A) AM=AM'
A appartient à la médiatrice de [MM'] (1).
- Le triangle MBM' est isocèle en B (car M et M'
appartiennent à l'arc de cercle de centre B ) BM=BM'
B de la médiatrice de [MM'] (2).
Les relations (1) et (2) la droite (AB) est la
médiatrice de [MM'](comme ensemble des points équidistants de 2
points M et M').
(AB) est perpendiculaire au segment [MM'] en son milieu.
M' est l'image de M par la symétrie orthogonale d'axe
(D).
c. Configurations utilisées :
|
Figures géométriques :
|
Propriétés :
|
|
Le triangle isocèle
|
les côtés de l'angle au sommet sont
égaux.
|
|
Le cercle
|
les points sur un cercle sont équidistants de son
centre.
|
Questions susceptibles de guider les
élèves dans la justification:
Quand dit-on que M' est l'image de M par rapport à
(D) ?
Quelles sont les natures des figures qu'on retrouve sur la
construction ?
Que représente la droite (AB) pour le segment
[MM'] ?
d. Programme de construction avec
GeoGebra :
Choisis le mode « Droite passant par deux
points » ; clique dans la feuille de travail : A
apparaît ; glisse la souris et clique : B apparaît et la
droite (AB) est construite (GeoGebra le nomme a) ;
Choisis le mode « Nouveau point » ;
clique dans la feuille de travail : un point C apparaît ;
Choisis le mode « Cercle
(centre-point) » ; clique successivement sur A et C : un
cercle de centre A passant par C apparaît( GeoGebra le nomme c) ;
clique de même sur B puis sur C : un cercle de centre B passant par
C apparaît ( GeoGebra le nomme d).
Choisis le mode « Intersection entre deux
objets » ; clique alors sur la seconde intersection des deux
cercles précédemment construis : un point D
apparaît.
Le point D ainsi construit est l'image du point C par la
symétrie orthogonale d'axe (AB).
Il suffit alors de nommer d en (D), C en M et D en M' pour se
conformer aux notations de l'activité.
e. Justification pratique :
Choisis le mode « Symétrie axiale
(objet-axe) ; clique successivement sur le point C puis sur (a) ie
(AB) ;
Clique droit sur D : « Point D, Point
E » s'affiche D=E ; choisis le pont E : GeoGebra
décris alors le point E comme étant l'image du point C par la
symétrie d'axe (a) ie (AB).
Choisis le mode « Déplacer » ;
les propriétés de la figure ne changent pas quelque soit le
déplacement de A, B ou C.
L'image de C est alors D par la symétrie d'axe (D).
NB : D est un objet auxiliaire donc ne
peut être déplacé de façon indépendante.
II.2.
3.5...Methode2 :
a. Programme de construction en
papier/crayon :
(D)
(C)
(D')
b. Justification théorique :
(Le cercle C de rayon [OM] coupe (D') en M') ([MM'] est un
diamètre de C) O est le milieu de [MM'] (1).
(D') est perpendiculaire à (D) en O (D) est
perpendiculaire à [MM'] en O (2).
(1) et (2) (D) est la médiatrice de [MM'] M' est
l'image de M par la symétrie d'axe (D).
c. Configurations utilisées :
|
Figures
géométriques :
Le cercle
|
Propriétés :
- Le centre d'un cercle représente le milieu d'un
diamètre de ce cercle.
|
|
Un segment de l'une contenant leur intersection est
perpendiculaire à l'autre.
|
|
Droites perpendiculaires
|
Questions susceptibles de guider les
élèves dans la justification :
Comment sont la droite (D) et le segment [MM'] ?
Que représente le segment [MM'] pour le cercle
(c) ?
Que représente le point O pour le segment
[MM'] ?
Que représente alors droite (D) pour le segment
[MM'] ?
d. Programme de construction avec
GeoGebra :
Choisis le mode « Droite passant par deux
points » ; clique dans la feuille de travail : A
apparaît ; glisse la souris et clique : B apparaît et la
droite (AB) est construite (GeoGebra le nomme a) ;
Choisis le mode « Nouveau point » ;
clique dans la feuille de travail : un point C apparaît ;
Choisis le mode « Droite perpendiculaire »
clique successivement sur C puis sur (AB) : une droite b apparaît
perpendiculaire à (AB).
Choisis le mode « Intersection entre deux
objets » ; clique alors sur l'intersection la droite (b) avec
(AB) : un point D apparaît.
Choisis le mode « Cercle
(centre-point) » ; clique successivement sur D et C : un
cercle de centre D passant par C apparaît( GeoGebra le nomme c) ;
Choisis le mode « Intersection entre deux
objets » ; clique alors sur la seconde intersection (b) et le
cercle c : un point E apparaît.
Le point E ainsi construis est l'image du point C par la
symétrie orthogonale d'axe (AB).
Il suffit alors de nommer d en (D), C en M et E en M' pour se
conformer aux notations de l'activité.
e. Justification pratique :
Choisis le mode « Symétrie axiale
(objet-axe) ; clique successivement sur C puis sur a ie (AB) ;
Clique droit sur D : « Point E, Point
F » s'affiche E=F ; choisis le pont F : GeoGebra
décris alors le point F comme étant l'image du point C par la
symétrie d'axe (a) ie (AB).
Choisis le mode « Déplacer » ;
les propriétés de la figure ne changent pas quelque soit le
déplacement de A, B ou C.
L'image de C est alors E par la symétrie d'axe (AB).
NB : D, E et F sont des objets auxiliaires donc ne
peuvent être déplacés de façon indépendante.
II.2. 3.6. Comparaison des programmes de
construction en papier/crayon et avec GeoGebra :
Avec GeoGebra, pour construire une droite, les
élèves construisent d'abord deux points par les quels passe la
droite, contrairement aux pratiques des élèves en papier/crayon
(ici les élèves tracent des droites sans penser aux points qui
l'appartiennent).
En papier/crayon très généralement les
élèves tracent le segment puis ses extrémités.
Cette procédure est erronée sous GeoGebra (ici c'est les
extrémités du segment qui sont d'abord construites).
Pour reporter des distances en papier/crayon, les
élèves tracent des arcs de cercles. Sous GeoGebra, ils tracent
des cercles entiers.
En papier/crayon, les intersections d'objets
géométriques son nommées de façon naturelle par les
élèves. Sous GeoGebra, les élèves sont contraints
de construirent ces intersections d'objets comme tout autre objet
géométrique.
Le mode « Déplacer » de GeoGebra
permet aux élèves d'observer les différentes variantes
d'une construction, de conjecturer des propriétés
géométriques. Ce qui est difficile à réaliser en
papier/crayon.
II.2. 3.7.Scénario de la
séance :
Phase1 : (10 mn)
Mise en place des élèves dans la salle et
récupération des tâches effectuées à la
maison.
Rôle du professeur :
Vérifier les productions d'élèves.
Faire une rémédiation si nécessaire.
Phase2: (5 mn)
Explication orale du travail qui sera demandé aux
binômes et distribution de la « fiche
élève » (fiche des activités de la
séance) ;
Rôle du professeur : Expliquer
l'activité et ses cosignes.
Phase3: (15 mn)
Travail de recherche des élèves: sur la
question 1) de l'activité1. (Tâche 1)
Critère d'arrêt: après 15 mn.
Rôle du professeur : Circuler pour
voir les productions des élèves.
Phase4: (15 mn)
Bilan et rémédiation sur la tâche 1.
Rôle du professeur :
Interroger les élèves pour les guider dans leur
recherche jusqu'à se qu'ils trouvent l'instruction appropriée
sans leur donner directement l'instruction.
Faire une synthèse.
Phase5 : (5 mn)
Travail de recherche pour question 2) de l'activité1
(Tâche2)
Critère d'arrêt : quand le maximum de
binômes aura fini.
Rôle du professeur : Circuler pour
voir les productions des élèves.
Phase6 : (10 mn)
Bilan de la tâche2
Rôle du professeur :
Interroger les élèves sur la justification de
leurs réponses.
Institutionnaliser le mode
« Déplacer » du logiciel.
Phase7: (15 mn)
Travail de recherche sur l'activité2 (Tâche3)
Critère d'arrêt: après 15mn.
Rôle du professeur : Neutre
Phase8 (15)
Bilan de la Tâche3.
Rôle du professeur :
Phase9 : (15)
Mise en commun ; Bilan final (bilan de la
séance2).
Rôle du professeur :
Contrôler l'effectivité des acquis.
Faire une synthèse.
Durée:1 heures 45mn.
NB :
la fin de la séance le professeur organise une mise en
commun et fait le bilan.
Pour mettre en oeuvre le scénario de classe, les
fichiers utilisés sont placés dans un sous répertoire T.P.
du répertoire GeoGebra (répertoire où se trouve le
logiciel GeoGebra) sur le Bureau.
III. ANALYSE DES RÉSULTATS
Pour ces analyses, nôtre méthodologie est la
suivante :
Nous décrivons pour chaque activité les
productions des élèves. Nous regardons en particulier leurs
erreurs et les raisons possibles. En suite nous faisons un commentaire de
l'activité et des recommandations si nécessaires.
III.1 SÉANCE1 :
III.1.1 SOUS SEQUENCE1 (SS1) :
a. Test1 :
Nous rappelons que l'objectif de cette activité est
d'évaluer le niveau des élèves sur la manipulation de
l'environnement Windows par rapport à sous séquence2( SS2).
Au cours de cette activité les élèves
vont travailler individuellement.
Les comportements recensés lors de
l'exécution des tâches:
T1 : Cette tâche consistait à appuyer sur
les boutons d'allumages de l'ordinateur.
Tous les élèves ont pu exécuter
correctement cette tâche.
T2 : Cette tâche consistait à ouvrir
« Mes documents » sur le Bureau, retrouver et ouvrir le
dossier « Expérimentation ». Dans le dossier
« Expérimentation » ouvrir le dossier
« Logiciel » et retrouver le dossier
« GeoGebra » :
- Pour ouvrir le dossier « Mes documents »
sur le Bureau, un seul élève n'y arrivait pas ; en effet cet
élève avait des incapacités dans l'exécution du
double clic (il prenait un temps assez long entre les deux clics). Mais elle
est aidée par son voisin.
- Après avoir ouvert le dossier « Mes
documents », certains élèves n'arrivaient pas à
retrouver « expérimentation », car ils ne voyaient
pas directement expérimentation à l'écran. Nous avions
remarqué des réactions comme « Monsieur, je ne vois pas
« Expérimentation » ». Le dossier
« Mes documents » contenait beaucoup de dossiers et de
fichiers. Ces élèves ne savaient pas qu'il faut utiliser la barre
de défilement verticale pour voir le dossier
« Expérimentation ».
T3 : Cette tâche consistait à faire une copie
du dossier « GeoGebra » sur le Bureau :
- Un seul élève a pu exécuter
correctement cette tâche. Certains élèves, en voyant le
seul dossier « GeoGebra » à l'écran, croient
qu'ils n'ont plus besoin de faire le clic droit sur le dossier pour le copier,
ce qui explique le fait de faire le clic droit dans n'importe quel endroit de
la fenêtre ouverte.
- D'autres élèves, après la copie du
dossier, se trouvent dans l'incapacité de revenir sur le Bureau. Ceux-ci
ne savaient pas qu'il faut réduire ou fermer la fenêtre en cours,
on remarque une confusion entre le fait de
« réduire » et « minimiser » une
fenêtre chez certains élèves. Ceci peut être dû
à la formulation de l'énoncé puisqu'il n'est pas
clairement signaler dans l'énoncé de fermer ou réduire les
fenêtres après la copie du dossier. Le professeur donne la
parole à l'élève qui a pu exécuter pour qu'il
explique sa technique, ainsi les autres ont pu exécuter correctement la
tâche.
T4 : Cette tâche consistait à créer et
nommer un dossier vide sur le bureau
- Certains élèves avaient des incapacités
dans l'exécution de cette tâche, ils ne connaissaient pas la
technique. Après qu'ils aient eu la technique par leur camarade,
l'exécution de la tâche n'a plus causée de
problème.
Lors de la saisie au clavier du nom du dossier, nous n'avions
remarqué aucune erreur. De même que dans les tâches
« T5. » (Cette tâche consistait à
déplacer le dossier « GeoGebra » dans le dossier
qu'ils ont crée) et « T6 » (Cette tâche
consistait à ouvrir le dossier « GeoGebra » pour
voir son contenu).
Commentaires :
Ce test nous a permis de savoir d'une part que certains
élèves avaient des difficultés pour manipuler la souris
(précisément le clic et le double clic), les barres de
défilement et les barres d'une fenêtre Windows, d'autre part que
les élèves n'ont pas des problèmes au niveau de la saisi
du texte (dans le cadre des tâches citées ci-dessus) au
clavier.
Lors de la dernière tâche, tous les
élèves ont utilisé le cliquer glisser pour déplacer
le dossier « GeoGebra ». Nous ne leurs avions pas
montrés les instructions « couper »
puis « coller » comme une autre technique pour
déplacer un dossier. Puisque dans nôtre analyse à priori
cette technique n'était pas nécessaire pour l'exécution
des autres sous séquences qui suivront.
b. Test2 :
Les objectifs de cette activité
étaient :
1. Retrouver et ouvrir un fichier à partir du menu
fichier du logiciel GeoGebra
2. Lorsque GeoGebra est actif permettre aux
élèves de découvrir la possibilité d'ouvrir
plusieurs fichiers « .ggb » et les manipuler en terme de
multi fenêtrage prévu dans la phase bilan.
Au cours de l'activité la classe est
réorganisée en binôme de travail.
Les tâches consistaient :
T1 : Renommer un dossier
T2 : Lancer le logiciel GeoGebra à partir de ce
dossier puis réduire la fenêtre du logiciel.
T3 : Fermer un ensemble de fenêtre ouverte.
T4 : Restaurer une fenêtre à partir de la
barre des tâches.
T5 : Ouvrir le
fichier «Activite1.ggb » à partir du menu fichier du
logiciel.
Les comportements recensés lors de
l'exécution des tâches:
Comme prévu dans nôtre analyse à priori,
les échanges entres membres des binômes ont permis à
certains binômes retardataires de rattraper les autres pour
l'exécution des tâches prévues dans cette activité.
Cependant, aucun binôme n'a pu exécuté la dernière
tâche de cette activité c'est-à-dire ouvrir le fichier
« Activité1.ggb » car après le choix de
l'instruction ouvrir du menu « Fichier » le fichier
« Activite1.ggb » n'apparaissent pas dans la boite de
dialogue qui s'affiche. Ils ne savaient pas remonter le système de
fichiers avec la boite de dialogue « Ouvrir » pour
retrouver le fichier.
Cette incapacité peut s'expliquée par le fait
qu'il n'est pas rappeler dans l'énoncé que le fichier
« Activité1.ggb» se trouve dans le dossier
« TP », puisque c'est ce dossier qu'ils verront dans la
boite de dialogue qui s'affiche après l'exécution de
l'instruction « ouvrir » du menu
« Fichier ».
Après la reformulation (correction) de
l'énoncé les élèves ont pu exécuter cette
tâche. Elle a permis aussi de faire gérer le multi fenêtrage
par les élèves dans la phase bilan.
Commentaires :
Lors du lancement de la feuille
« GeoGebra », deux binômes se sont trouvés
avec plusieurs fenêtres ouvertes. En effet, le chargement du logiciel
était très lent sur certaines machines. Il était important
de faire cette remarque aux élèves pour éviter une telle
situation.
III.1.2.SOUS SEQUENCE2 :
a. Activité1 :
Rappelons que l'objectif de cette activité est la
découverte des commandes du logiciel par rapport à la sous
séquence3 ( SS3).
Les élèves travaillent toujours en binôme
sans changer de partenaire.
Cette activité consistait à retrouver les menus
dans les quelles se trouvent les instructions (ces instructions se trouvent
sur la fiche élève) nécessaires à
l'exécution de SS3.
Les comportements recensés lors de
l'exécution des tâches:
- La manière dont le professeur à formuler
l'énoncé a bloqué la plupart des binômes puisqu'ils
pensaient que chaque instruction est propre à un seul menu. Les
consignes données ne faisaient pas voir aux élèves qu'un
menu peut contenir plusieurs instructions. Le professeur après avoir dit
aux élèves que l'importance ici est d'écrire devant chaque
instruction le menu dans lequel il se trouve ; peu importe le nombre
d'instruction disponible dans ce menu. Ceci a permis aux élèves
de continuer l'exécution de la tâche sans problème.
- D'autres n'arrivaient pas à ouvrir les icônes.
La consigne était pourtant de cliquer sur la petite flèche
à droite en bas des icônes.
Mais après un accompagnement oral du professeur sur
l'énoncé et des consignes, les élèves ont
continué sans d'autres questions.
Commentaires :
Avant même la fin du temps donné aux
élèves pour chercher cette activité, tous avaient fini et
bien répondu.
Par inattention lors de la saisie de l'énoncé,
nous avions mis « cercle (centre-objet) » au lieu
de « cercle (centre-point) » et
« effacer des objets » au lieu de
« effacer les objets ». Un des binômes nous
a signalé les erreurs et nous avions rectifié pour toute la
classe.
Nous devons revoir la formulation de l'énoncé de
cette activité pour nos séances à venir.
b. Activié2 :
Rappelons que les objectifs de cette activité sont les
suivants :
1. Construire des objets géométriques dans
l'environnement de géométrie dynamique GeoGebra
2. Permettre aux élèves d'effectuer un
contrôle perceptif et dynamique.
Pendant l'exécution de cette activité, les
élèves avaient toutes les instructions nécessaires
à utiliser sur la fiche (Corrigée et redistribuée aux
binômes) de l'activité1.
Les comportements recensés lors de
l'exécution des tâches :
- Pour construire un objet, certains faisaient des doubles
cliques. Ils étaient surpris de ne pas avoir le résultat attendu.
Il fallait leur faire comprendre que chaque clic dans la feuille de travail
est une commande qui dans GeoGebra exécute la dernière
instruction choisie.
- Certains n'arrivaient pas facilement à pointer les
objets sur la feuille de travail lors de leurs clics. Nous avions
remarqué des réactions comme « Monsieur, ça
ne marche pas », « Monsieur, ça ne fait
rien »
- Incompréhension de certaines syntaxes de
GeoGebra : « Cercle (Centre-point), « intersection
entre les objets ».
Commentaires :
Cette activité a permis de faire découvrir aux
élèves, un environnement nouveau pour faire de la
géométrie. Ils étaient tous enthousiastes de construire
des points, des segments, des droites, des cercles..., en de simples clics et
de pouvoir les modifier en toute autonomie.
Nous avions aussi remarqué une prompte acquisition des
techniques à chaque fois que le mode opératoire des instructions
était expliqué.
II.2 SÉANCE2 : Sous sequence3
(SS3)
a. Activité1 (Exercice chercher à la
maison) :
Rappelons que l'objectif de cette activité est de
tester si les élèves sont capables de construire le
symétrique d'un point par rapport à une droite en
papier/crayon.
L'activité avait été donnée aux
élèves à la fin de la première séance
à faire dans l'environnement papier/crayon.
Les comportements recensés lors de
l'exécution des tâches:
Dans la construction du point image, les élèves
n'avaient pas eu de difficulté. Par contre, pour expliquer leur
méthode de construction et pour justifier leur construction, nous avions
remarqué beaucoup de difficultés. Seulement deux
élèves ont pu donné une justification. Les autres avaient
soient des difficultés dans la formulation des propriétés
soient des problèmes de vocabulaire lors de la rédaction.
Commentaires :
Nôtre analyse à priori a été
vraiment concluant pour cette activité. En effet, après le
dépouillement des productions d'élèves, il n'est ressorti
que les deux méthodes de construction décrites dans nôtre
analyse à priori (voir page ..).
Dans nos analyses de pratiques de classe, la justification
d'une construction n'est pas une activité habituelle pour les
élèves de 10èmeSciences. Etant conscient de
cette situation, nous dévions alors insister sur la justification lors
de notre phase bilan, puisque l'enseignement de la géométrie ne
doit pas se limiter à des techniques de construction.
b. Activité2 :
En rappel, l'objectif de cette activité est de
construire le symétrique d'un point par rapport à une droite (D)
sans utiliser l'instruction « Symétrie axiale (Objet-axe) » de
GeoGebra.
Les élèves travaillent en binômes. Dans
cette réorganisation de la classe, les partenaires ont utilisés
la même méthode de construction en papier/crayon.
Cette activité consistait à reprendre la
construction effectuée à la maison dans l'environnement de
géométrie dynamique GeoGebra.
Les comportements recensés lors de
l'exécution des tâches:
- Un seul (Binôme1) des deux binômes
(Binôme3 et Binôme1) qui avaient fait la première
méthode de construction en papier/crayon avaient des incapacités
dans l'exécution de l'instruction « Cercle
(Centre-point) ». Ce binôme n'arrivait pas à bien
utiliser l'instruction. Mais après plusieurs tentatives ils y sont
parvenus.
- Les deux autres binômes (Binôme2 et
Binôme4) avaient fait la seconde méthode de construction en
papier/crayon. L'un (Binôme2) des binômes n'arrivait pas à
faire le report de longueur. Ils n'y sont pas parvenus car ils utilisaient
l'instruction « arc défini par 3 points ». Quand
à l'autre binôme (Binôme4), l'un des élèves
avait effacé leur construction par inadvertance avant nôtre
passage pour la vérification.
(Voir les productions des binômes en Annexe)
Commentaires :
Le Binôme2 ne pouvait pas utiliser l'instruction
« arc de cercle (Centre-2points) » pour reporter la
distance. En effet, sous GeoGebra, trois points définissent un arc de
cercle lorsque l'un des trois points est sur la médiatrice des deux
autres.
Après la phase de rémediation, la construction
du Binôme4 (Voir Fig.4 et Fig.4' en annexe) était toujours au
jugé donc fausse sous GeoGebra. On pouvait remarquer sur leur
construction que le point image est fixé lorsqu'on déplace le
point objet. Nous avions institutionnalisé l'instruction
« Déplacer » de GeoGebra. Les autres binômes
ont alors déplacé les points de leur construction pour
vérifier si elle était correcte (Par exemple Fig.1 et Fig.1' voir
annexe).
Lors de la phase bilan de cette activité, nous avions
aussi utilisé la fenêtre algèbre de GeoGebra (Non
prévu dans nôtre scénario). Ceci pour que les
élèves puisse vérifier par des mesures que la droite de
symétrie est bien la médiatrice du segment formé par le
point objet et son image(résistance de la perpendicularité (ie
l'angle 90°) et que le milieu reste toujours le milieu).
c. Activité3 :
L'objectif de cette activité était d'engager les
élèves dans une justification par déplacement (sur
GeoGebra) et théorique (en papier/crayon) de cette construction.
Les comportements recensés lors de
l'exécution des tâches:
Certains élèves n'arrivaient pas à
caractériser les figures géométriques des constructions.
Notamment, le triangle isocèle, le cercle, la médiatrice d'un
segment.
Commentaires :
La phase bilan de cette activité n'a pas
été facile à mener. Elle a pris trop de temps que
prévu (presque le double).
L'activité nous a permis de voir réellement que
le logiciel pouvait faire écran aux connaissances mathématiques
des élèves. En effet, sauf deux élèves, tous
avaient donné comme justification la résistance des
propriétés de la figure lors du déplacement.
IV. SYNTHÈSE
IV.1. Les points positifs de la séquence :
D'après nos analyses, la séquence a fait
ressortir que :
- Les élèves sont beaucoup plus
concentrés, et mettent plus d'énergie dans la résolution
des tâches.
- Chacun peut progresser à son rythme, ce qui n'est
pas possible durant une séance « traditionnelle » (en
salle de classe).
- Le logiciel GeoGebra facilite un rôle actif de
l'élève. On remarque également que la salle d'informatique
permet un climat d'entraide au sein du groupe-élève, qui
constitue un stimulant supplémentaire dans l'apprentissage.
- De plus l'acquisition des connaissances par les
élèves est plus rapide. On pouvait entendre lors des phases bilan
« Monsieur, c'est facile... ».
- Nous avons aussi noté que GeoGebra incite les
élèves à être plus rigoureux dans leurs
constructions que lors des séances classiques en papier/crayon. Les
difficultés des élèves lors de l'utilisation des
instructions comme « Intersection des objets », « Cercle
(Centre-Point) », « Droites perpendiculaires » en
sont des preuves.
- Les constructions sont également
exécutées plus rapidement, et les élèves se
corrigent eux-mêmes. Ils sont d'ailleurs assez fiers d'eux ! et insistent
pour nous montrer leurs constructions.
IV.2. Les « leçons
pédagogiques » tirées de la
séquence :
Les séances en salle d'informatique nous ont toutefois
causés beaucoup de problème mais elles nous ont permis d'en tirer
beaucoup de « leçons » d'ordre
pédagogique :
- Lors de nôtre première activité, deux
machines sont tombées en panne. Nous étions obligés de
réorganiser la classe (on avait prévu pour cette activité
un élève par machine). De plus le jour de la seconde
séance, nous avions eu une panne d'électricité. Nous
pensons qu'il est nécessaire de bien connaître le fonctionnement
de l'ordinateur et leur alimentation en électricité pour que les
séances en environnement informatique se déroulent du mieux
possible.
- Un second point à souligner est le changement de nos
rôles dans cet environnement. En effet, au lieu de mener le jeu comme
lors des séances « traditionnelles », en salle
d'informatique nous faisons des suggestions et nous relançons
l'activité.
- Nous avions eu beaucoup de difficultés à avoir
l'attention des élèves lorsqu'on donne des consignes ou lors des
phases bilan. Nous pensons qu'il serait utile de mettre les machines en mode
veille pendant de telle phase.
- Beaucoup d'élèves se rattachent aux
réponses du logiciel comme si elles avaient un statut de preuve. Nous
pensons que cela explique le fait que peu d'élèves n'aient pas
donné une justification. Pour eux, GeoGebra ne fait pas d'erreur (Voir
leurs réactions en annexe par rapport à la séance). Nous
pensons que cette impression peut être rectifiée après
plusieurs séances sur ordinateurs.
- Nous avions remarqué aussi que les
élèves construisaient des cas particuliers de figure (par exemple
dans le tracé des figures la plus part des binômes tracent des
segments (ou des droites) parallèles comme en papier/crayon ce qui
explique la difficulté de détacher les élèves du
papier/crayon.
V. DISCUSSION :
On pourrait enrichir les compétences des
élèves au niveau de certain pré requis :
- Un dossier copié reste accessible à partir de
son nouvel emplacement qu'à partir de l'ancien.
- La copie d'un dossier ou fichier dans un autre dossier
s'exécute de deux manières différentes : soit avec le
clic glisser soit avec le « couper coller » ou le
« copier coller » (si on veut garder une autre copie sur le
bureau).
Aussi, une fois le logiciel GeoGebra lancé on peut ouvrir
à partir de cette fenêtre les fichiers de type
« .ggb » dans l'ordinateur ou dans un autre
périphérique connecté à l'ordinateur.
De plus, on doit insister sur le fait que, dans
l'environnement de géométrie dynamique, on peut toujours
vérifier la validité d'une construction
géométrique en faisant déplacer certains points de la
figure à l'aide de la souris. Si la construction est juste les
propriétés mises en jeu résistent au
déplacement.
La géométrie ne peut se construire qu'en acte,
à travers de multiples expériences personnelles qui vont
permettre de dégager des invariants. En utilisant le mode
« Déplacer » du logiciel sur les figures,
l'élève percevra ce qui varie et ce qui subsiste. Il
émettra ainsi des conjectures et, peu à peu, sentira la
nécessité de faire appel à des méthodes abstraites
pour prouver certaines propriétés plus subtiles dans des cas
où un seul dessin ne suffit pas à emporter la conviction. Il
pourra ainsi prouver plus de plaisir et de motivation chercher puis
démontrer.
D'autre part il sera parfois intéressant de formuler
les activités de telle sorte que l'élève en explorant la
situation, en déformant la figure, en étudiant des cas
particuliers, observe des configurations remarquables, des invariants. Il sera
poussé à formuler des hypothèses, des questions et se
trouvera dans une situation plus proche d'une situation de recherche que d'une
situation scolaire.
C. CONCLUSION :
L'élaboration de cette séquence d'enseignement
nous a permis d'entamer un travail de réflexion sur l'utilisation de
l'ordinateur dans nôtre enseignement de la géométrie, nous
avons fait des choix et nous nous sommes confrontés à des
difficultés.
Dans nos activités, nous n'avions exploité dans
l'ensemble que les fonctionnalités de géométrie du
logiciel GeoGebra. On pourra étudier les mêmes activités
selon un point de vu analytique ou numérique en utilisant la
fenêtre algèbre et les axes de la « feuille de
travail » du logiciel. D'autre part, l'utilisation de GeoGebra
demande à insister sur les consignes des énoncés puis
qu'il ne permet pas d'avoir un menu contextuel sur les instructions. Mais ce
logiciel reste quand même un bon logiciel de géométrie
dynamique pour l'enseignement de la géométrie.
Nous pensons qu'il est bien possible et même plus
intéressant d'engager des élèves de
10èmeS dans la recherche d'un problème de
géométrie dans un environnement de géométrie
dynamique. Mais il faudrait que l'enseignant se pose ces questions : à
qu'elle moment utiliser le logiciel ? Pour illustrer quelle notion ?
De quelle manière ?
Les élèves ont beaucoup apprécié
les séances sur ordinateur (voir des questionnaires remplis par les
élèves en annexe). Mais, l'utilisation de l'ordinateur ne doit
pas avoir pour objet de faire de l'élève un expert dans
l'utilisation de tel ou tel logiciel. Qu'il sache reconnaître certaines
questions susceptibles d'être illustrées ou résolues
grâce à l'ordinateur et qu'il sache interpréter les
réponses que l'ordinateur fournit ; l'élève doit apprendre
à situer et intégrer l'usage des outils informatiques dans une
démarche scientifique.
Quant à l'intégration effective des outils
informatiques dans notre enseignement, beaucoup d'efforts devront être
fournis. En effet, Il n'est pas toujours aisé pour l'enseignant d'avoir
du matériel (Assez d'ordinateurs dans les salles) à sa
disposition ou encore de bien connaître les logiciels (l'apprentissage
des T.I.C.E n'est pas dans le programme de l'ENSup).
De plus :
- Il faudrait des manuels avec des activités utilisant
les T.I.C.E à la disposition des enseignants.
- Intégrer l'enseignement de ces logiciels dans les
programmes et dans les évaluations. Puis que les élèves
peuvent voir les T.I.C. comme un divertissement et non comme une aide à
la compréhension.
On pourra alors se demander : S'il est possible
d'intégrer le T.I.C dans l'enseignement des mathématiques au
Mali. Faudrait-il changer les programmes des mathématiques ?
ANNEXES
Annexe1 ;
Fenêtre de démarrage de GeoGebra.
Barre d'outils
Feuille de
Travail
Fenêtre
Algèbre
Annexe2 :
Disposition des ordinateurs dans la salle
d'informatique
Tableau noir
P1
P2
P3
P4
P7
P5
P6
P9
P10
P8
Poarte
Porte
![]()
NB : P : poste sur un ordinateur.
Annexe3 : Tableau synoptique de la sous
séquence3
|
Phases
|
Objectifs
|
Environnement de travail
|
Rôle de l'élève
|
Rôle du professeur
|
|
1
|
Mise en place des élèves
|
|
S'installer et sortir ses effets.
|
- Veiller à l'installation du calme
- Installer les binômes de travail
|
|
2
|
Explication des attentes du professeur
|
|
Écouter,
Comprendre les consignes.
|
Expliquer les attentes ; s'assurer que tout le monde ait
compris
|
|
3
|
Recherche d'activité
|
-Travail par binôme
avec GeoGebra
|
Faire la construction de la question 1 (l'activité1 )
|
Stimuler le travail ; ou expliquer l'activité
|
|
4
|
Faire un bilan
|
Classe entière
|
- Suivre les explications du professeur ou d'un camarade.
- Poser des questions si nécessaire
|
- Interroger les binômes ;
- Donner des explications ;
- Établir un bilan.
|
|
5
|
Recherche d'activité
|
-Travail par binôme
avec GeoGebra
|
Rechercher la question 2 de l'activité1
|
Stimuler le travail ; ou expliquer l'activité
|
|
6
|
Faire un bilan
|
Classe entière
|
- Suivre les explications du professeur ou d'un
camarade :
- Poser des questions si nécessaire
|
- Interroger les élèves ;
- Donner des explications ;
- Établir un bilan.
|
|
7
|
Recherche d'activité
|
Travail par binôme sur feuille de papier
|
Rechercher l'activité2
|
Stimuler le travail ; ou expliquer l'activité
|
|
8
|
Faire un bilan
|
Classe entière
|
- Suivre les explications du professeur ou d'un camarade
- Poser des questions si nécessaire.
|
- Interroger les binômes.
- Donner des explications
- Établir un bilan
|
|
9
|
Faire un bilan et institutionnaliser les acquis
|
Classe entière
|
- Suivre les explications du professeur ou d'un camarade
- Poser des questions si nécessaire.
|
- Interroger les binômes.
- Donner des explications
- Institutionnaliser les acquis
|
Annexe4 :
Questionnaire donné aux élèves
à la fin de la séquence
1. As-tu apprécié les séances ?
...............................................................................................................
2. Quelles sont les parties que tu as
préférées ? Pourquoi ?
................................................................................................................
.................................................................................................................
3. Quelles difficultés as-tu rencontrées dans
l'utilisation
De l'ordinateur ?
......................................................................................................
Du logiciel ?
......................................................................................................
Dans la compréhension des consignes ?
......................................................................................................
4. Préfères-tu une séance d'exercice en
salle d'informatique ou en classe ?
Explique ta réponse.
...................................................................................................................................................................................................................
5. Qu'est-ce que le logiciel t'a apporté de plus qu'une
séance en classe ?
......................................................................................................
......................................................................................................
6. Quels changements proposes-tu afin d'améliorer une
telle séance ?
......................................................................................................
......................................................................................................
7. Coche ta réponse dans le tableau suivant :
|
Tout à fait
d'accord
|
Plutôt
d'accord
|
Plutôt pas
d'accord
|
Pas
d'accord
du tout
|
|
Le logiciel GeoGebra aide à comprendre la
géométrie.
|
|
|
|
|
|
Le logiciel GeoGebra ne fait jamais d'erreurs.
|
|
|
|
|
|
Si on constate une propriété avec le logiciel
GeoGebra, alors on peut affirmer qu'elle est vraie.
|
|
|
|
|
|
Si on constate une propriété sur un dessin, alors
on peut affirmer qu'elle est vraie.
|
|
|
|
|
Annexe5 :
Les productions des binômes sur
l'activité1 de la seconde séance :
Binôme1
Fig.1
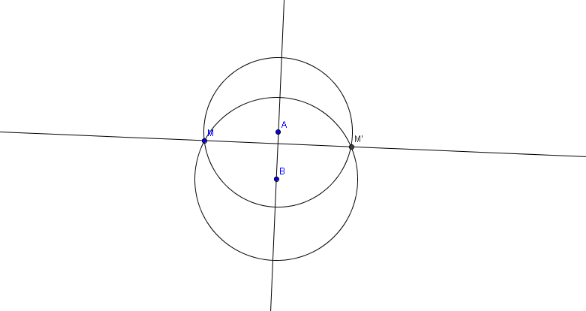
Binôme1
Fig.1'
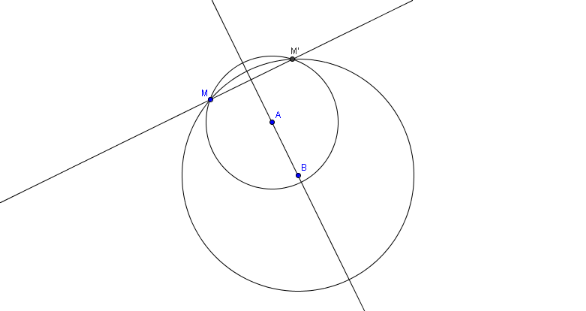
Binôme2
Fig.2
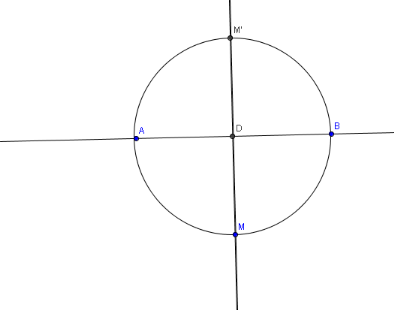
Binôme3
Fig.3
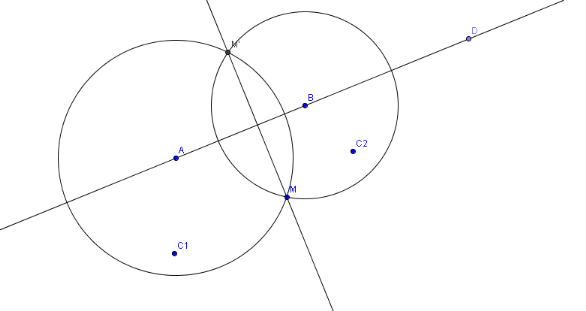
Annexe6 :Annexe7 :
Binôme4
Fig.4
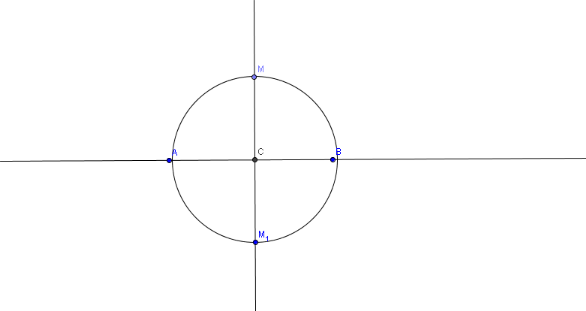
Fig.4'
Binôme4
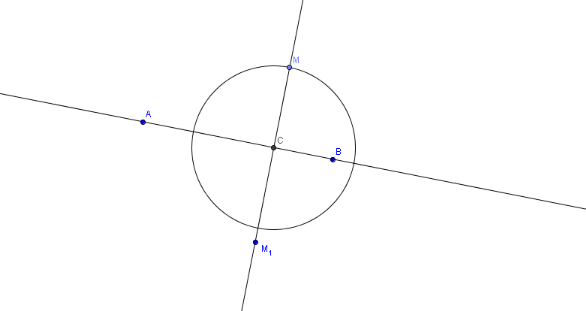
* 1 Bernard Parzysz,
Représentations planes et enseignement de la géométrie
de l'espace au lycée. Contribution à l'étude de la
relation voir-savoir, Thèse, Université de Paris VII,
1989
* 2 Colette Laborde et
Bernard Capponi, Cabri-géomètre constituant d'un milieu pour
l'apprentissage de la notion de figure géométrique,
Recherche en didactique des mathématiques vol. 14/1-2, La pensée
sauvage, 1994.
* 3 PARZYSZ Bernard. Voir et
savoir, la représentation du « perçu » et du « su
» dans les dessins de la géométrie dans l'espace.
Bulletin de l'APMEP n° 364. 1986.
* 4 ARSAC Gilbert et al.
Initiation au raisonnement déductif au collège. Presse
universitaire de Lyon. 1992
* 5 Représentation
graphique sur l'écran de GeoGebra.
| 


