1.3 Méthodes traditionnelles de délimitation
des zones de chalandise
Deux classes de méthodes de
délimitation, l'une subjective et l'autre normative, sont
employées pour déterminer les frontières de zones
de chalandise. Alors que la première catégorie de
méthodes reste théorique, les méthodes normatives au
contraire sont caractérisées
par leurs observations du monde réel. Elles sont donc plus
précises et plus commodes à mettre
en oeuvre et peuvent même aller jusqu'à
décrire les variations dynamiques des frontières des
392 INGENE C. et YU (1981) Determinants of
Retail Location in SMSAs, Regional Science and Urban
Economics 11, p.529-547.
393 HALL M. et KNAPP J. et WINSTEN C. (1961)
Distribution in Great Britain and North America, Oxford
University Press, London.
394 INGENE C. et LUSCH R. (1980) Market Selection
Decisions for Department Stores, Journal of Retailing, 56, p.21-40.
395 INGENE C. et YU (1981) Determinants of
Retail Location in SMSAs, Regional Science and Urban
Economics 11, p.529-547.
396 APPLEBAUM W. et COHEN S.B. (mars 1961)
The Dynamics of Store Trading Areas and Market
Equilibrium, Annals of the Association of American
Geographers, N°51/1.
397 CLIQUET G. (1995) Implementing a Subjective
MCI Model: An Application to the Furniture Market,
European Journal of Operational Research 84, pp
279-291.
zones de chalandise. Nous allons d'abord passer en
revue les principales méthodes subjectives.
1.3.1 Approches subjectives : la méthode du temps de
conduite
Cette méthode employée par beaucoup de
professionnels suppose que les clients sont disposés
à fréquenter un magasin seulement selon
des critères de proximité mesurés en termes de
distance ou de temps de conduite. En pratique, on trace des courbes
isochrones autour du point de vente ou de son implantation envisagée.
Les courbes indiquent les temps de trajet en général automobile
qui les séparent du point de vente en tenant compte des voies
de circulation et des obstacles (feux tricolores, croisements et
inter-parties, limitations de vitesse,...). La zone de chalandise
équivaut à la surface géographique intérieure
à l'une de ces courbes en se fixant un temps de conduite limite
au-delà duquel on pense qu'une faible
proportion de consommateurs potentiels sera prête à
se déplacer jusqu'au point de vente 398.
Parmi différents paramètres déterminant les
habitudes des consommateurs comme la densité
de population, le pouvoir d'achat, l'importance des
réseaux de communication, on a montré en effet
numériquement que les temps de conduite requis pour atteindre
un ensemble de magasins a une influence forte sur le choix d'un
centre commercial 399. Certaines études comportementales
avaient montré en leur temps qu'à partir d'un temps de conduite
supérieur à
20 minutes, les consommateurs hésitaient à se
rendre dans un centre commercial 400.
Actuellement, certains clients, particulièrement dans
les zones rurales, n'hésitent pas à parcourir 50
kilomètres pour faire leurs courses dans les hypermarchés qui
remplacent de plus
en plus les petits commerces traditionnels de plus en plus
rares401. Mais, dans les zones de
398 BRUNNER J. A. et MASON J. L. (1968) The Influence
of Driving Time Upon Shopping Center Preference,
Journal of Marketing Vol. 32, p.57.
399 BRUNNER J. A. et MASON J. L. (1968) The Influence
of Driving Time Upon Shopping Center Preference,
Journal of Marketing Vol. 32, p.57.
400 NELSON R.L. (1958) The Selection of Retail
Locations, F.W. Dodge Corp, p.153, New York.
401 BOVET P. (2001) L'hypermarché, le Caddie
et le congélateur, Le Monde Diplomatique, Mars 2001, p.32.
périphérie urbaine où les
services commerciaux sont plus denses, les consommateurs deviennent
plus exigeants quant à la proximité des centres commerciaux. Aux
Etats-Unis, au début des années 90, on était
prêt, selon Madame Yecko, une spécialiste renommée
de la distribution et la présidente du groupe d'immobilier
commercial Capital Realty Group, à parcourir 50 miles pour se
rendre dans un hypermarché Wal-Mart402. De nos jours,
une distance de 20 à 30 miles (30 à 50 kilomètres
environ) semble être la limite que les gens peuvent supporter
pour accéder à un tel centre commercial.
Brunner et Mason ont avancé, quant à eux,
que les limites de zone de chalandise se ramenaient à un temps
de conduite de 15 minutes autour du centre commercial et que ce sont
l'importance de la population, le nombre de ménages et les revenus au
sein de cette zone qui conditionnent les performances du centre. D'autres
auteurs ont énoncé que les consommateurs sont prêts
à parcourir en moyenne une distance correspondant à un temps
moyen de conduite
de 10 minutes403. Même si la méthode ne
prétend pas être parfaite puisqu'elle ne prend pas en
considération la puissance d'attractivité du
magasin, on constate donc qu'il n'y a pas dans la littérature un temps
de conduite bien défini pour mesurer les limites de la zone de
chalandise. Sans doute, l'effort que les consommateurs sont prêts
à fournir pour atteindre un centre commercial dépend-il
d'autres facteurs que le simple temps de conduite ou que des facteurs
d'attractivité. Les conditions météorologiques,
l'âge, le sexe, les quartiers traversés, les
facilités de parking, le pouvoir d'achat plus généralement
peuvent conduire à ce que l'effort fourni ou évalué soit
ressenti comme étant plus ou moins élevé par
l'individu.
402 SCHOOLEY T. (2001) For some retailers,
drive-time is more important than location, Pittsburgh Business
Times, American City Business Journals, march 9, 2001, p.10.
403 APPLEBAUM W. et GREEN H.L. (1974)
Determining Store Trade Areas, Handbook of Marketing
Research, edited by R. Ferber NY Mac Graw Hill, pp
4.313-4.323.
1.3.2 Approches normatives
L'approche subjective de la méthode du temps de
conduite décrite précédemment est facile à mettre
en application et fournit des données assez fiables mais avec
un degré de précision inconnue. Elle est
préconisée dans le cas où les données marketing sur
la clientèle ne sont pas accessibles ou lorsque cette méthode est
trop longue ou trop coûteuse à mettre en oeuvre. En revanche, les
méthodes normatives prennent en considération l'information
sur la clientèle et/ou les performances passées du point
de vente. Ces données d'observation obtenues par enquêtes
s'avèrent indispensables pour évaluer une zone de
chalandise existante avec une précision accrue par rapport aux
méthodes subjectives qui n'utilisaient que des données
environnementales.
Les méthodes normatives les plus populaires fondées
sur l'expérience passée pour déterminer
les frontières de zone de chalandise sont:
- la méthode analogique
- la méthode par le modèle de régression
- la méthode par les surfaces enveloppantes
- la méthode des nuées dynamiques
Détaillons ces différentes approches dans leurs
principes et leurs inconvénients.
1.3.2.1 La méthode analogique
La méthode analogique sous-tend que la géographie
se répète: si un point de vente est placé à
un emplacement similaire à un autre, ou alors on
s'attend à ce que la performance des deux points de vente soit
identique. Supposons qu'un magasin connaisse les adresses de ses clients.
Celles-ci peuvent alors être représentées sur une carte par
des points dont la densité indique
grâce à un examen visuel, la taille, la
forme et les caractéristiques générales de la zone
de chalandise de ce magasin 404.
La délimitation des zones de chalandise s'apprécie
traditionnellement en prenant des paliers
en matière de niveau de clientèle en progression
linéaire 405. En première approximation, la zone de
chalandise est supposée à frontière circulaire irradiant
à partir du point de vente sur
un rayon r. Ainsi, on considère en
général la zone de chalandise comme le disque dont le
rayon a une dimension telle qu'il concentre au minimum X % de la
clientèle (X=80 % par exemple). Le problème est que la zone de
chalandise est loin d'avoir la géométrie parfaite d'un disque. En
outre, ce mode de procédure s'avère peu précis, car il
présuppose une diminution régulière du taux de
pénétration selon l'éloignement au point de vente ou bien
une certaine homogénéité et une bonne
répartition de la clientèle sur la surface
géographique compacte déterminée par cette
méthode.
Fig 1.1 - Exemple de détermination d'une zone de
chalandise par un logiciel commercial utilisant la méthode analogique
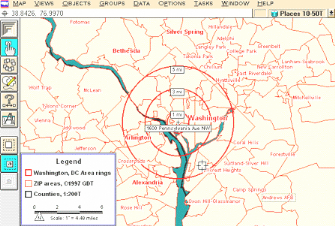
Or, les irrégularités
socio-économiques de la population dans l'espace, les
frontières géographiques, les caractéristiques de la
concurrence et la politique commerciale du magasin
404 APPLEBAUM W. et GREEN H.L. (1974)
Determining Store Trade Areas, Handbook of Marketing
Research, edited by R. Ferber NY Mac Graw Hill, pp
4.313-4.323.
405 APPLEBAUM W. (1968) The Analog Method for
Estimating Potential Store Sales, Guide to Store Location
Research, Addison-Wesley, Reading, Mass.
font que très souvent les zones de chalandise ne sont pas
totalement compactes. Les "trous"
ou discontinuités de la clientèle au sein de
cette surface sont donc négligés dans la méthode
précédente. On ne pense pas également à
considérer la rupture pouvant être assez brusque qui
s'opère entre une zone à forte densité de clients et une
zone à faible densité.
1.3.2.2 La méthode par les modèles de
régression
La méthode par le modèle régression
cherche à mesurer un paramètre de performance en le
corrélant avec diverses variables socio-économiques,
environnementales et marketing. Il suppose ainsi d'avoir pour base un
certain nombre de magasins ou des études commerciales antérieures
à partir desquelles, on mesurera les coefficients d'une droite de
régression du type:
Y = b0 + b1X1 + b2X2 + ... + bnXn
où Y est le paramètre de performance ; X1, X2, ...
, Xn les variables explicatives et b0, b1, b2,
..., bn les coefficients de la droite de régression.
Les modèles de régression sont fondés sur
deux hypothèses: premièrement, la performance du point de vente
est fonction des caractéristiques de localisation de son
emplacement, de l'environnement socio-économique, du niveau de la
concurrence et des caractéristiques du magasin. Deuxièmement,
les facteurs fondamentaux de performance peuvent être isolés
grâce
à une analyse statistique des données.
La méthode est en particulier employée pour
prévoir la performance globale projetée Y d'un magasin qui est
évaluée par cette formule et l'emploi de données locales
406. Mais elle peut également être utilisée pour
estimer la part du marché des zones entourant un nouveau point
de vente et délimiter alors la zone de chalandise.
Il suffit pour cela de parcourir l'espace
entourant le point de vente à la recherche des populations
tendant à accroître le paramètre de
406 LORD J.D. et OLSEN L.M. (1979) Market Area
Characteristics and Branch Bank Performance, Journal of
Bank Research 10, p. 102-110.
performance Y du fait de leurs caractéristiques
démographiques et socio-économiques entrant
en tant que variables dans le modèle de
régression. On pourra considérer qu'au-dessus ou qu'en
dessous d'un certain niveau de contribution à la
performance, les populations considérées appartiendront ou
n'appartiendront pas à la zone de chalandise.
Des difficultés peuvent cependant
apparaître dans l'utilisation de la méthode lorsque
apparaissent des corrélations entre des variables supposées
indépendantes dans le modèle de régression. Un test
simple préalable consiste à mesurer le taux de
corrélation entre les données. Un taux supérieur
à 0,5 ou plus est significatif d'une certaine
multicolinéarité entre des variables redondantes 407
408.
On peut également utiliser le test de Fisher (ou test
d'égalité des variances) qui a pour but de
comparer deux distributions de valeurs X et Y supposées
suivre chacune une loi normale. Si
n1 et (S1)² respectivement la taille et la variance non
biaisée du premier échantillon et n2 et (S2)² sont la
taille et la variance non biaisée du second échantillon (S1 et
S2 sont les écarts- types), alors le calcul de la quantité F
définie par :
F = [ n1 * (S1)² / (n1 - 1) ] / [ n2 * (S2)² / (n2 -
1) ]
(dans le cas où F<1, on inverse le numérateur et
le dénominateur)
permettra de savoir si les distributions sont de
même nature en se fondant sur la règle de décision
suivante : si F est supérieure au quantile d'une loi de Fisher de
paramètres n1 et n2 au risque 0,05, les variances ne sont pas
homogènes et les distributions sont de natures différentes.
Dans le cas contraire, les variances sont
considérées équivalentes et les distributions de
même nature.
Un autre moyen pour détecter la
multicolinéarité est de séparer les données en deux
groupes
et de calculer pour chaque groupe un modèle de
régression. L'absence de multicolinéarité se
révèlera par une certaine similitude des résultats
en ce qui concerne les coefficients de
407 JOHNSTON J. (1972) Econometric Methods,
McGraw-Hill, New York.
408 MALINVAUD E. (1980) Statistical Methods of
Econometrics, North Holland, New York.
régression et la qualité d'ajustement. Dans
le cas contraire, il est souhaitable d'éliminer certaines
variables parmi celles corrélées entre elles soit en examinant
les variables prises 2
par 2, en pratiquant une analyse factorielle, ou
mieux une régression ridge qui considère un estimateur
légèrement biaisé des paramètres pour
améliorer la variance des estimations (coûteux en temps de
calcul) ou une régression pas à pas (stepwise) qui
consiste à introduire
les variables l'une après l'autre dans le modèle
(selon leur contribution partielle) et, à chaque étape, à
vérifier si l'ensemble des variables déjà
introduites sont encore significatives (une variable qui ne le serait plus
serait rejetée).
Un autre problème pouvant surgir dans
l'élaboration d'un modèle de régression est
l'intégration de données difficilement quantifiables comme celles
relatives à la perception du consommateur ou bien concernant
l'évaluation de la concurrence ou bien l'image de marque malgré
que cette difficulté ait été surmontée dans
certains modèles comme le MIC subjectif409
que nous verrons plus tard (§ 2.1.5). L'objectif de
ce modèle est en effet avant tout de se
fonder sur l'expérience d'un site commercial pour
approcher par calcul la performance future d'un nouvel emplacement et
accessoirement d'identifier ce que pourra être sa zone de
chalandise.
1.3.2.3 La méthode par les surfaces
enveloppantes
Les surfaces enveloppantes ont été mises en
application par Peterson 410 dans la continuation
des travaux de Bucklin 411 et de McKay
412. Cette méthode consiste à représenter les
taux de pénétration sur une carte quadrillée en zones de
manière à obtenir un relief. La surface de ce relief
épousant les variations spatiales du taux de pénétration
est approximée par des courbes
409 CLIQUET G. (1995) Implementing a Subjective
MCI Model: An Application to the Furniture Market,
European Journal of Operational Research 84, 279-291.
410 PETERSON R.A. (1974) Trade Area Analysis
Using Trend Surface Mapping, Journal of Marketing
Research, Vol. XI, 338-42.
411 BUCKLIN L.P. (1971) Trade Areas Boundaries:
Some Issues in Theory and Methodology, Journal of
Marketing Research, 30-7.
412 MCKAY D.B. (1973) Spatial Measurement of Retail
Store Demand, Journal of Marketing Research, 10, 4, p.
447-453.
ou des plans et en particulier par des équations dont les
coefficients sont déterminés grâce à
un modèle de régression. Ces surfaces peuvent
être modélisées par des séries de Fourier
surtout si elles présentent une certaine périodicité.
Mais, comme cette régularité de l'espace
est plutôt rare dans le monde réel, on
préfère décrire le taux de pénétration
spatiale par des polynômes orthogonaux qui sont plus aptes à
rendre compte de la concurrence et des irrégularités
spatiales telles que les barrières naturelles (rivières,
espaces verts protégés, autoroutes,...).
Il serait théoriquement possible, même si
les auteurs n'effectuent pas la démonstration, de délimiter
la zone de chalandise en déterminant les minima de cette courbe
polynomiale par l'annulation de sa dérivée seconde.
Cependant, la méthode des surfaces enveloppantes comporte des
limitations notamment l'impossibilité de trouver des polynômes
orthogonaux ou d'autres fonctions pas trop élaborées qui puissent
suffisamment bien modéliser le relief des taux de
pénétration. Peterson l'a bien compris dans son étude en
faisant remarquer qu'il y avait une faible corrélation entre
certains paramètres spatiaux du type socio-économique et
les variations de taux de pénétration
modélisé: la raison en était sans doute en
particulier la présence de termes résiduels,
différences entre les courbes du modèle et les taux de
pénétration constatés.
1.3.2.4 La méthode des nuées dynamiques
La méthode de délimitation par les nuées
dynamiques repose sur une famille d'algorithmes
dus à Diday 413. Son principe est de construire
itérativement une classification d'un nuage de points.
- chaque classe étiquetée i est
représentée par son noyau Ni (souvent le barycentre de
la
classe, mais pas nécessairement), calculable en
utilisant une fonction à partir des
413 CELLEUX G. et DIDAY E. (1980) L'analyse
des Données, Bulletin de liaison de la recherche en
informatique et automatique, INRIA.
représentants de la classe.
- on dispose d'une mesure de similarité d entre
un point et un noyau de classe. (d est par exemple la distance
euclidienne au noyau lorsque ce dernier est un point).
L'algorithme est alors le suivant:
i,
· On initialise les noyaux Ni, 1 i k à leur valeur
de départ N
1 i k, la variable
booléenne STABLE à FAUX et le compteur
d'itérations t à 1.
· Tant que (STABLE - FAUX) et
(t < tmax), on effectue :
Î Début
i
· On affecte chacun des points à la classe dont le
noyau N(t) est le plus proche au
sens de la mesure de similarité d.
i
· Pour chacune des classes, on calcule le nouveau noyau
N(t+1)
avec .
· Si l'un des noyaux a été modifié,
alors STABLE vaut FAUX sinon il vaut VRAI.
Î Fin
(les instructions principales de l'algorithme sont en
gras).
Cette méthode consiste donc à incorporer des
zones autour de centres mobiles ou centres de gravité: une
nécessité est de définir au préalable le
nombre k de zones. Puis, k centres de gravité supposés
sont alors tirés au hasard et chaque point géographique
appartenant à l'espace géographique est assigné au plus
proche des k centres de gravité engendrant ainsi k cellules
géographiques. Le vrai centre de gravité de chacune des
k zones est calculé et le processus qui consiste à assigner
chaque point géographique à l'un des nouveaux centres de
gravité recommence. Cet algorithme fonctionne en boucle jusqu'à
ce que les k zones et les k centres de gravité soient invariables. Un
calcul de la variance à l'intérieur de chaque zone peut
être effectué pour vérifier si les moyennes sont
sensiblement différentes d'une classe à une autre et si le
nombre de classes est exact.
La méthode a été employée pour
indiquer les limites de zones de chalandise de centres commerciaux
414 avec l'exécution de fonctions spline qui consiste
à réduire au minimum le
rayon de courbe de la fonction représentant les limites de
la zone de chalandise f(x) pour la
rendre plus régulière (
[f(x)' ' ]² dx
minimisé). Ainsi, lors de l'application de cette
méthode à
la délimitation des zones de chalandise, l'aire
géographique est initialement découpée en
secteurs caractérisés par une plus ou
moins forte fréquentation du point de vente considéré
(l'étude de Roger415 comporte par exemple 50 secteurs). Les
fréquentations obtenues auprès d'un échantillon de
clients sont chacune affectées au secteur géographique de
leur lieu de domicile, l'ensemble desdites fréquentations
étant ensuite moyenné. Ces secteurs sont alors
agglomérés en zones de fréquentation homogènes
(les classes mentionnées précédemment)
par l'algorithme des nuées dynamiques ce qui permettra
ultérieurement de tracer les lignes de niveau de fréquentation
entourant le point de vente considéré grâce en
particulier aux fonctions splines qui joignent harmonieusement les
centres de gravité des secteurs. On constate que la zone de
chalandise est finalement délimitée de façon assez
imprécise puisqu'en général le nombre de secteurs pour
définir sa frontière est faible. Ces secteurs ne correspondent
d'autre part qu'à un découpage artificiel pas forcément
logique le plus souvent
en quartiers ou en arrondissements dans les grandes
villes. De plus, les secteurs peuvent rassembler des populations et des
fréquentations inhomogènes ce qui risque de conduire à des
erreurs puisqu'en considérant une fréquentation moyenne au
sein de ces secteurs, on fait abstraction de cette
hétérogénéité de clientèle. D'autre
part, la transition de fréquentation de la clientèle entre les
secteurs voisins est supposée s'effectuer de manière progressive
ce qui n'est pas forcément le cas. La lourdeur de la méthode et
son manque de côté pratique la rendent très
difficilement accessibles aux professionnels.
414 ROGER P. (1983) Description du Comportement
Spatial du Consommateur, Thèse de Doctorat, Lille.
415 ROGER P. (1983) Description du Comportement
Spatial du Consommateur, Thèse de Doctorat, Lille.
La méthode des nuées dynamiques est
cependant susceptible en fait de résoudre la
problématique de l'analyse typologique qui vise à chercher les
principales représentants d'un nuage de points. Nous verrons au
paragraphe 2.2.3 que ce type de méthode peut simplifier la recherche de
localisations commerciales en particulier lors de l'utilisation du
modèle p- médian. En bref, le modèle p-médian
(voir § 2.2) pose le problème de positionner et d'allouer
p centres (p points de vente pour l'application
à la localisation commerciale) à chacun des points d'un
nuage de points (les clients) de telle manière que la somme des
distances de ces points au centre correspondant atteigne un minimum, ce
qui permet effectivement de rassembler les points en un certain
nombre de cellules (ou clusters en anglais) de
caractéristiques (souvent le niveau moyen de fréquentation)
homogènes.
| 


