Chapitre 2 :

«J'espère prouver que la nature possède
les moyens et les facultés qui lui sont nécessaires pour produire
elle-même ce que nous admirons en elle.»
Jean Baptiste de Monet, chevalier de LAMARCK.
1. Chapitre 02 Métaheuristique
d'optimisation
24
Introduction
L'Optimisation est l'une des branches les plus importantes
des mathématiques appliquées modernes, et de nombreuses
recherches. La résolution de problèmes d'optimisation est devenue
un sujet central en recherches opérationnelles. Il existe deux classes
de base des méthodes d'optimisation : exactes et approchées.
Les méthodes exactes sont des méthodes
permettant de trouver une solution optimale en temps fini mais elles sont
incapables de résoudre les problèmes trop complexes parmi les
méthodes exactes on distingue : la programmation dynamique, la
programmation linéaire et les algorithmes avec retour arrière
[Layeb, 2010]. Contrairement aux méthodes exactes, les méthodes
approchées ne procurent pas forcément une solution optimale, mais
seulement une bonne solution (de qualité raisonnable) en un temps de
calcul aussi faible que possible [Troudi, 2006], il existe une partie
importante de méthodes approchées connues sous le nom de
métaheuristiques.
Les métaheuristiques sont des méthodes
approchées d'optimisation basées sur la bio-inspiration.
Plusieurs classifications des métaheuristiques sont été
proposées. La plupart distinguent globalement deux catégories :
les métaheuristiques à base de population et les
métaheuristiques à base de voisinage.
2. Définitions
2.1. Problèmes d'optimisation
Un problème d'optimisation se définit comme un
problème de minimisation ou de maximisation, c'est à dire on
cherche une solution de valeur optimale, minimale, si on minimise la fonction
objectif, ou maximale, si on la maximise [Troudi, 2006].
Il existe plusieurs problèmes d'optimisations :
problème mono ou multi objectif, problème combinatoire ou a
variables continues, problèmes statistiques ou dynamiques, etc.
[Boudieb, 2008].
2.2. Optimum local
Une solution s S est un optimum local si et seulement
si' il n'existe pas de solution 0 voisinage v(s) de s, dont
l'évaluation est de meilleure qualité que s, soit
[Devarenne, 2007 ; Layeb, 2010]:
Chapitre 02 Métaheuristique d'optimisation
25
|
s0 ( )
|
s0 Dans le cas problème de minimisation
s0 Dans le cas d un probleme de maximisation
avec l ensembledes solution voisines de
|
2.3. Optimum global
Une solution est un optimum global à un problème
d'optimisation s'il n'existe pas d'autres solutions de meilleure
qualité. La solution s* S est un optimum global si et seulement
si :
s ?S Dans le cas d'un problème de minimisation
Dans le cas d'un probleme de maximisation
La figure 1.3 schématise la courbe d'une fonction
d'évaluation en faisant apparaître l'optimum global et local
[Devarenne, 2007 ; Layeb, 2010].
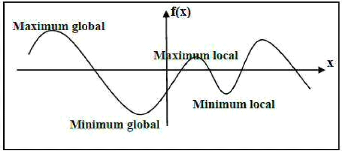
Figure 2.1 Optima locaux et optima globaux
d'une fonction a une variable.
3. Métaheuristiques
Les métaheuristiques sont des algorithmes stochastiques
itératifs qui progressent vers un optimum global. Il existe de
nombreuses métaheuristiques allant de la simple recherche locale
à des algorithmes plus complexes de recherche globale [Layeb, 2010].
Donc on peut distinguer deux catégories des méthodes heuristiques
: les méthodes locales et les méthodes globales.
Les méthodes locales celles qui convergent vers un
minimum local. Ces méthodes, appelées aussi méthodes de
recherche par voisinages [Layeb, 2010]. On trouve plusieurs méthodes
locales parmi elles on peut citer : le recuit simulé, la recherche
tabou, etc.
Chapitre 02 Métaheuristique d'optimisation
26
Les méthodes globales sont des méthodes qui
permettent d'atteindre un ou plusieurs optima globaux. Ces méthodes sont
appelées aussi méthodes à base de population [Layeb,
2010]. Parmi elles on peut distinguer : les algorithmes
génétiques, les algorithmes à évolution
différentielle, les colonies de fourmis, etc.
4. Classification des métaheuristiques
On distingue plusieurs classifications des
métaheuristiques dans ce chapitre nous présentons une
classification mono objectif des métaheuristiques d'optimisation. La
figure 2.2 résume cette classification.
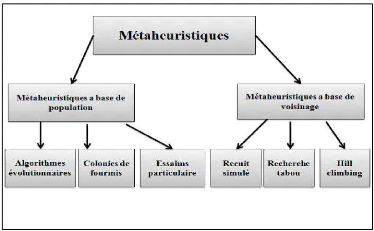
Figure 2.2 Classification des
métaheuristiques [Collette, 2002 ; Troudi, 2006].
4.1. Métaheuristique a base de
population
Les méthodes à base de population utilisent la
population comme un facteur de diversité. Parmi ces méthodes on
distingue les algorithmes évolutionnaires (algorithmes
génétiques, algorithme a évolution differentielle), les
colonies de fourmis, les algorithmes basés sur l'essaim de particule,
etc .
4.1.1. Algorithmes evolutionnaires
Les Algorithmes Evolutionnaires (AEs), sont des algorithmes
basés sur le concept de la selection naturelle élaborée
par Charles Darwin [Koza, 1999]. On distingue quatre types d'AEs : les
algorithmes genetiques(AG), les strategies d'évolution (SE), la
programmation
Chapitre 02 Métaheuristique d'optimisation
27
évolutionnaire (PE) et la programmation
génétique (PG) [Benlahrache, 2007]. Dans ce qui suit, nous
présentons les algoritmes génetiques et les algorithmes a
évolution différantielle.
A. Algorithmes génétiques
Les algorithmes génétiques sont une abstraction
de la théorie de l'évolution. Ce sont des algorithmes
d'optimisation stochastique (aléatoire) fondés sur les
mécanismes de la sélection naturelle de Darwin et sur
les méthodes de combinaison des gènes introduites par Mendel
pour traiter des problèmes d'optimisation.
Les algorithmes génétiques sont appliques dans
des différents domaines comme : L'optimisation de fonctions
numériques difficiles (discontinues, etc.), traitement d'images
(alignement de photos satellites, reconnaissance de suspects, etc.),
optimisation d'emplois du temps, apprentissage des réseaux de neurones,
etc.
A .1.Éléments des algorithmes
génétiques
Gène: Un gène est le
plus petit élément dans l'AG. Généralement, il
correspond à un seul symbole (0 ou 1 dans le cas de codage binaire).
Chromosome : Un chromosome est
constitué d'une suite finis de gènes.
Individu : un individu est une forme
qui est le produit de l'activité des gènes. Pour un AG, il est
réduit à un chromosome et on l'appelle donc chromosome ou
individu pour désigner un même objet [Laboudi, 2009].
Population : une population est un
ensemble d'individus.
Génération: une
génération est un ensemble des opérations qui permettent
de passer d'une population à une autre. Ces opérations sont :
sélection des individus de la population courante, croisement, mutation
et enfin l'évaluation des individus de la nouvelle population.
A.2. Fonctionnement générale d'un
algorithme génétique
Le principe général du fonctionnement d'un
algorithme génétique standard est présenté par
l'algorithme suivant [Souquet et Radet, 2004]:
Chapitre 02 Métaheuristique d'optimisation
28
Algorithme 2.1 : Algorithme
évolutionnaire génétique
Début
Initialiser la population initiale P.
Évaluer P.
Tant Que(Pas Convergence) faire
P ' = Sélection des Parents dans P
P ' = Appliquer Opérateur de Croisement sur P '
P ' = Appliquer Opérateur de Mutation sur P '
P = Remplacer les Anciens de P par leurs Descendants de P '
Évaluer P
Fin Tant Que
Fin
| 


