Chapitre 1 :
« Si l'esprit d'un homme s'égare, faites-lui
étudier les mathématiques car dans les démonstrations,
pour peu qu'il s'écarte, il sera obligé de recommencer
»
Francis Bacon.
1. Chapitre 1 Recalage d'images médicales
3
Introduction
A l'évolution des nouvelles techniques occupées
à l'interprétation des images par ordinateur, le traitement
d'image joue un rôle très important dans plusieurs domaines tels
que l'imagerie satellitaire, médicale, industrielle, etc. L'imagerie
médicale a connu des techniques efficaces qui permettent
d'acquérir et de traiter des images internes du corps humain et
d'établir un diagnostic ou même la mise en oeuvre d'une
thérapeutique en temps réel comme échographie, IRM, TEP et
scanner [Larousse médicale, 2006]. Selon la technique utilisée,
on peut distinguer deux types d'images médicales. Les images anatomiques
médicales permettant d'obtenir des informations
géométriques sur la structure des organes (taille, volume,
localisation, etc.). Et les images fonctionnelles permettant d'obtenir une
vision sur la fonctionnalité des organes, par exemple le TEP.
Malgré l'efficacité de la vision par ordinateur
dans plusieurs domaines, elle reste incapable de visualiser certains objets
correctement. Parmi les vieilles problématiques de la vision par
ordinateur, on trouve le recalage. Le recalage d'images est un processus qui
permet de faire une transformation spatial entre deux ou plusieurs images.
Dans ce chapitre, nous présentons le problème
de recalage en imagerie médicale. Nous commençons par une
introduction sur l'imagerie médicale. Puis, nous présentons les
fondamentaux théoriques du recalage des images : définitions,
types, méthodes de recalage les plus pertinentes, mesure de
similarités entre images (en se concentrant sur l'information mutuelle).
En fin, nous pressentons les différentes applications de recalage en
imagerie médicale.
2. Imagerie médicale
De la trépanation à la robotique chirurgicale,
la pratique médicale a connu une véritable révolution
(Figure 1.1). De nos jours, grâce aux nouvelles techniques d'imagerie,
les procédés de traitement se sont modernisés, le
diagnostic est devenu plus précis et la qualité des soins est
désormais meilleure. Loin des pratiques traditionnelles, où
«voir» passait par «ouvrir», aujourd'hui, les radiologues,
à l'aide des techniques tomographiques, peuvent diagnostiquer et traiter
de façon quasiment non-invasive. Le recours à la chirurgie
invasive est devenu la solution de dernier recours [Atif, 2004].
Chapitre 1 Recalage d'images médicales

4
Une trépanation exercée XVIième
siècle Un chirurgien opérant à l'aide d'un
microscope
Figure 1.1 Évolution de la pratique
chirurgicale : de la trépanation à la chirurgie microscopique.
Parmi les modalités d'acquisition, on distingue celles
qui fournissent des propriétés structurelles (morphologiques) de
la zone étudiée (IRM, TDM, X-Ray, etc.), de celles qui restituent
des aspects fonctionnels (TEP, TEMP, IRMf, MEG, etc.) [Atif, 2004] (Figure
1.2). Donc, selon la technique utilisée on peut distinguer deux types
d'images médicales. Les images anatomiques permettant d'obtenir des
informations géométriques sur la structure des organes (taille,
volume, localisation, etc.), et les images fonctionnelles permettant d'obtenir
une vision sur la fonctionnalité des organes.
2.1. Quelques types de modalité
? L'imagerie par résonance magnétique
(IRM) : On distingue deux types d'IRM anatomique et fonctionnelle.
L'IRM anatomique permet de visualiser la structure anatomique de tout volume du
corps. L''IRM fonctionnelle permet de suivre l'activité d'un organe,
à travers l'afflux de sang oxygéné dans certaines de ses
zones [Frija et Mazoyer, 2002].
? la Radiologie : La radiologie repose sur
l'utilisation des rayons X. Elle s'applique au diagnostic et au traitement des
maladies selon différents modalités techniques : La radiographie
(Standard), La radioscopie et La tomodensitométrie (scan RX, TDM)
[Larousse médicale, 2006].
? la tomographie par émission de positions
(TEP) : La TEP renseigne sur la biochimie des organes. Elle fournit
des informations sur le fonctionnement des tissus normaux et pathologiques
[Frija et Mazoyer, 2002].
? Tomographie d'Émission Mono Photonique (TEMP)
: Le principe de la TEMP est de suivre l'évolution dans le
corps humain d'un radioélément, qui est dans ce cas un
Chapitre 1 Recalage d'images médicales
5
émetteur naturel de simples photons ã. La
TEMP constitue ainsi une technique d'exploration de la perfusion
cérébrale [Grova, 2005].
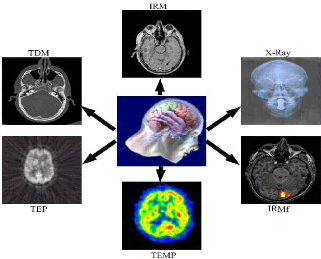
Figure 1.2 Multi modalité fonctionnelle
et structurelle pour la compréhension Du cerveau humain
[Atif, 2004].
2.2. Fusion et Recalage
Plusieurs modalités sont parfois utilisées pour
effectuer un seul diagnostic. Pour certaines anomalies, le radiologue doit
à la fois étudier l'aspect structurel et fonctionnel d'une zone
d'intérêt. Or, ces modalités sont en général
utilisées avec un décalage dans le temps. Les informations
recueillies doivent être alors fusionnées dans un même
repère pour permettre d'effectuer les différentes analyses et
comparaisons, nécessaires à l'établissent d'un diagnostic
précis et efficace [Atif ,2004].
Le développent parallèle des sciences
informatiques a fait naître l'idée que des logiciels pourraient
aider le praticien dans ce travail. Parmi les besoins les plus courants du
praticien se trouvent une variété de tâches de comparaison
: comparer des images d'un même patient acquises à des instants
différents ou selon des modalités différentes comparer des
images de patients différents ou encore comparer une image avec un atlas
anatomique ou fonctionnel.
Chapitre 1 Recalage d'images médicales
6
Ces tâches de comparaison relèvent toutes d'une
même problématique : le recalage [Roche, 2011].
3. Recalage d'image 3.1. Définitions
? Définition 01 : Le recalage (en
Anglais registration) est la tâche qui cherche la meilleure
transformation qui permet de superposer la plus grande partie commune possible
des images à apparier compte tenu des variations de la scène
[Talbi, 2009 ; Brown, 1992].
? Définition 02 : Le recalage d'image
est la tâche qui permet d'aligner deux images.
Si on considère ces deux images comme deux matrices
notées I1 et I2 où I1 (x, y)
et I2 (x, y) sont les intensités des pixels au
point dont les cordonnées sont x et y, Alors, le
recalage est l'opération qui permet d'estimer les fonctions f
et g qui vérifient la relation suivante [Talbi, 2009 ;
Brown, 1992] :
I2(x, y)=g (I2 (f(x, y))) (1.1)
Où : f est une fonction à deux dimensions
représentant la transformation géométrique et g
est une fonction à une dimension représentant la
transformation photométrique.
? Définition 03 : Le recalage est la mise
en correspondance des images ayant la formule générale [Bloch]
:
min f (I1, t(I2)), t C T (1.1)
Où :
I1 et I2 sont les images à recaler
(ou informations extraites de ces images), t : transformation, T
: ensemble des transformations possibles / admissibles, f :
critère de dissimilarité (min) ou de similarité (max).

Chapitre 1 Recalage d'images médicales
7
Figure 1.3 Recalage d'image.
3.2. Types de recalage
On distingue généralement quatre types de recalage
[Mashoul, 2004] :
a) Recalage multi-modalité : Traite
les problèmes où les images de la même scène sont
prises par des capteurs différents.
- Exemple d'application :
Intégration d'information de deux images, l'une prise par un
radar et l'autre par un système optique.
b) Recalage de gabarit : Recherche une forme de
référence dans une image. - Exemple d'application
: Localisation d'une cible par un missile.
c) Recalage d'image prises de différents
points de vue : Ce type de recalage requiert souvent des
transformations locales afin d'éliminer les distorsions perspectives.
- Exemple d'application : Vision
stéréoscopique.
d) Recalage temporel : La mise en
correspondances entre deux images prises à des moments
différents, ce type de recalage doit accepter les divergences entre les
deux images dues aux changements réels dans la scène.
- Exemple d'application : Suivre
l'évolution d'une pathologie.
Chapitre 1 Recalage d'images médicales
3.3. Classification des transformations
géométriques
3.3.1. Transformation linéaire
Transformations linéaires définie par : X -
A?X + b? où n est la dimension,
An est une application linéaire de dimension
nxn, et bn est un vecteur de translation de
dimension nx1. Il existe plusieurs types de transformations
géométriques linéaires.
a) Transformations rigides
La transformation rigide est la composition d'une rotation et
d'une translation. L'hypothèse de rigidité convient au cas
où l'on cherche à compenser la différence de
positionnement d'un objet par rapport aux capteurs sans tenir compte
d'éventuelles déformation des tissus imagés ou de
distorsions géométriques créées par les
procèdes d'imagerie [Roche, 2011].
La formulation de transformations rigides d'une image 2D est la
suivante :
T(x) = Rx + t (1.2)
Où : t est un vecteur 2×1 qui
représente la translation, et R est une matrice orthogonale
directe 2x2.

8
Figure 1.4 Transformation rigide.
b) Similitudes
Consiste en l'estimation d'un facteur d'échelle isotrope
en plus des translations et des rotations. Ce type de recalage conserve les
angles et le rapport entre les distances :
T(x)=sRx+t, s>0 (1.3)
s c'est le facteur d'échelle [Brown, 1992].

Chapitre 1 Recalage d'images médicales
Figure 1.5 Transformation de similitude.
c) Transformations affines
Ces transformations autorisent, en plus des rotations et des
translations, de prendre en compte un facteur d'échelle anisotrope et de
modéliser des cisaillements, elles conservent le parallélisme.
T(x)=A(x)+t (1.4)
Sachant que A est une matrice 2×2 quelconque
[Roche, 2011].

Figure 1.6 Transformation affine.
d) Transformations projectives
Les transformations projectives sont utilisées dans le
cas où des images 3D sont recalées avec des images 2D acquises au
moyen d'une camera, par exemple les images radiologique et les images
vidéo [Talbi, 2009].

9
Figure 1.7 Transformation projective.
3.3.2. Transformations non linéaires (non
rigides)
Contrairement aux transformations linéaires, les
déformations non-rigides sont appliquées localement, c'est
à dire que la transformation appliquée en un point peut
effectivement être
Chapitre 1 Recalage d'images médicales
différente de celle appliquée à ses
voisins. L'amplitude des déformations recherchées est
généralement plus faible et localisée. Un nombre important
de modèles de déformation non-rigide ont été
proposés dans la littérature du recalage. Parmi ceux-ci, on fait
la distinction entre les transformations locales non paramétriques et
les transformations locales paramétriques [Rubeaux, 2011].
a) Transformations locales
non-paramétriques
Dans ce type, la transformation est définie en chaque
pixel de l'image. Ces modèles nécessitent l'utilisation d'un
terme de régularisation pour contraindre la solution, car le
modèle de déformation est totalement libre [Rubeaux, 2011].
b) Transformations locales
paramétriques
Des transformations d'ordre plus général
pourront être obtenues en perturbant localement la composante globale du
mouvement. Les coordonnés de la déformation résiduelle
peuvent être modélisées comme des combinaisons
linéaires de fonctions élémentaires [Roche 2001].

10
Figure 1.8 Transformation local.
3.4. Méthodes de recalage
On peut distinguer deux approches de recalages :
géométrique et iconique. La première est basée sur
l'extraction des primitives, et la deuxième est basée sur la
mesure de similarité.
3.4.1. Méthodes
géométriques
Les méthodes géométriques sont peut
être les plus naturelles car elles procèdent de façon
analogue à l'esprit humain conscient. Elles sont basées sur
l'extraction dans les images de sous-ensembles de points homologues
(primitives) qui peuvent être des points, des lignes, des surfaces, des
volumes, etc., qu'il s'agit ensuite de mettre en correspondance [Roche,
2011].
Le choix des primitives doit être guidé par un
certain nombre de propriétés : détection facile et
précise, répartition sur l'ensemble de l'image, robustesse au
bruit, aux artefacts et aux
Chapitre 1 Recalage d'images médicales
11
différents changements liés à
l'acquisition [Noblet, 2006]. Cependant, la majorité des approches se
basent soit sur une sélection manuelle, soit sur une détection
semi-automatique des amers (ou primitives géométriques) communs
aux deux images, ce qui impose un prétraitement des données pour
extraire ces points, lignes ou surfaces d'intérêt [Rubeaux,
2011].
En effet ces méthodes reposent sur deux étapes
bien distinctes, qui sont d'ailleurs généralement menés de
façons complètement indépendantes : La première
étape, dite de segmentation est souvent la plus problématique
dès lors que l'on souhaite la réaliser automatiquement. Elle
requiert d'extraire des primitives qui soient significatives ce qui peut
s'avérer difficile si les images sont fortement bruitées (par
exemple, des images ultrasonores). Après la segmentation des primitives
la deuxième étape est celle du recalage proprement dit, C'est
à dire le calcul d'une transformation spatiale "optimale". Il convient
de distinguer le cas où les correspondances entre primitives sont
connues à l'avance (primitives labélisées) du cas
contraire (primitives non labélisées), très
fréquent lorsque la segmentation est automatique [Roche, 2011].
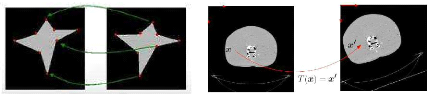
Figure 1.9 Transformation
géométrique : A gauche les primitives sont des points. A droite
la primitive est une surface.
Avantages et Limites des méthodes
géométriques
a) Avantages
On peut résumer les avantages des méthodes
géométriques dans les points suivants :
~? Optimisation de la charge calculatoire par la gestion de
zones d'images plutôt que de détails sur l'image c'est à
dire temps de traitement très réduit, par contre aux
méthodes iconiques où le temps de traitement est très
élevé [Gardeux, 2008].
~? Utilisation de données déjà issues de
l'image et donc plus pertinentes [Gardeux, 2008].
Chapitre 1 Recalage d'images médicales
12
~? Pallier aux problèmes d'artefacts dans les images
initiales et des Différences d'intensité entre les 2 images
à recaler [Gardeux, 2008].
~? Primitives très informatives [Rubeaux, 2011].
b) Limites
On peut résumer les limites des méthodes
géométriques dans les points suivants :
~? Sélection manuelle ou semi-annuelle des primitives,
même si plusieurs équipes travaillent sur la conception de
méthodes d'identification automatiques [Rubeaux, 2011 ; Noblet,
2006].
~? Le choix des primitives est très arbitraire. Il est
difficile de trouver les primitives optimales [Gardeux, 2008].
~? Généralement réservé au recalage
monomodal [Rubeaux, 2011].
~? Prétraitement (segmentation) nécessaire
[Rubeaux, 2011].
3.4.2. Méthodes iconiques (denses)
Les méthodes iconiques sont des approches bas-niveau.
Contrairement aux premières, celles-ci ne nécessitent pas la
segmentation préalable des images. Elles consistent essentiellement
à optimiser une mesure de similarité fondée uniquement sur
des comparaisons locales d'une intensité. Dans ce cas, les primitives
guidant le recalage sont des vecteurs 3D contenant la position et
l'intensité des pixels (voxels).
On reconnait une méthode iconique à deux
propriétés essentielles : D'une part le choix des primitives est
complètement arbitraire : tous les voxels sont a priori des candidats
valables. D'autre part, les primitives ne sont pas des entités
géométriques, elles appartiennent à un espace figuratif
différent du monde réel. Ainsi, le critère utilisé
pour comparer ces primitives est une mesure de similarité
reflétant indirectement une distance géométrique [Talbi,
2009 ; Roche, 2011].
3.4.2.1 Mesure de similarité
Il existe plusieurs mesures de similarité dans la
littérature du recalage d'images. La plupart des mesures existantes
peuvent être définies à partir d'un histogramme conjoint.
D'autres peuvent être appréhendées indépendamment de
la notion d'histogramme conjoint [Roche, 2011].
Chapitre 1 Recalage d'images médicales
13
a) Concept d'histogramme conjoint ?
Histogramme
La première question posée avant d'expliquer
brièvement le concept d'histogramme conjoint : c'est quoi un histogramme
d'une image ? L'histogramme des niveaux de gris ou des couleurs d'une image est
une fonction qui donne la fréquence d'apparition de chaque niveau de
gris (couleur) dans l'image. Il permet de donner une bonne quantité
d'information sur la distribution des niveaux de gris (couleur).

Figure 1.10 Une image et son histogramme.
? Histogramme conjoint
Maintenant, nous allons expliquer la notion d'histogramme
conjoint : L'histogramme conjoint de deux images I et J est
calculé à partir du calcul des fréquences d'apparitions de
l'intensité de chaque couple de pixels de même rang de deux
matrices de pixels. La figure 1.11 démontre ce processus [Bendaib,
2003].
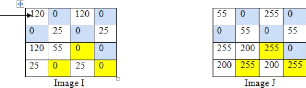
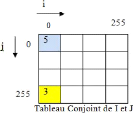
Figure 1.11 Représentation graphique
d'histogramme conjoint.

Chapitre 1 Recalage d'images médicales
Figure 1.12 Exemple d'histogrammes conjoints
obtenus pour (a) des images non recalées et(b) des
images recalées.
b) Classification des mesures de
similarité
Une mesure de similarité est une fonction à
valeurs réelles dont l'argument est l'histogramme conjoint,
lui-même fonction de la transformation spatiale. Le fondement commun aux
nombreuses mesures proposées dans la littérature est
l'idée que les intensités de deux images manifestent une
cohérence d'autant plus forte que les images sont bien alignées.
Le rôle de la mesure de similarité est précisément
de donner une signification quantitative à cette notion de
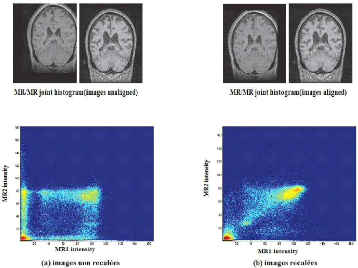
cohérence (figures 1.13 et 1.14) [Roche, 2011].
14
Figure 1.13 Histogramme conjoint de deux IRM
cérébrales (coupes coronales représentés)
calculé
pour deux transformations différentes [Roche,
2011].
Chapitre 1 Recalage d'images médicales
Dans la première situation (a) les couples
d'intensité sont répartis dans le plan de façon
relativement désordonné. La cohérence est manifestement
plus forte dans la deuxième situation (b) où on a la très
nette impression que les intensités sont regroupées le long d'une
droite.
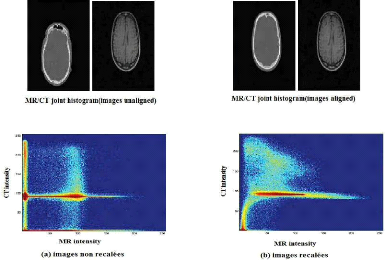
15
Figure 1.14 Histogramme conjoint d'un couple
IRM/scanner (coupes axiales représentés) calcule
pour deux
transformations différentes.
La situation de recalage (b) donne l'impression visuelle d'un
gain de cohérence. Mais la relation entre les intensités n'est
clairement plus de type affine lorsque les images sont recalées. La
majorité des couples d'intensités est regroupé autour
d'une courbe d'allure parabolique. On observe un amas secondaire nettement plus
dispersé autour de l'intensité 50 dans l'IRM et 150c dans le
scanner. Il n'est pas évident de caractériser une telle
relation.
Les mesures de similarités font une hypothèse
sur la relation liant les niveaux de gris des deux images à recaler. En
général, la nature de cette relation permet de faire une
classification des différentes mesures de similarité. Le tableau
1.1 résume les principales mesures de similarité.
Chapitre 1 Recalage d'images médicales
16
3.4.2.2. Avantages et Inconvénients de la
méthode iconique
a) Avantages
On peut résumer les avantages des méthodes
géométriques dans les points suivants [Gardeux, 2008] :
· On travaille avec toutes les informations portée
par l'image. Celle-ci ne subit pas de prétraitement.
· Adapté au recalage multimodal [Rubeaux, 2011].
· Méthode totalement automatique.
c) limites
On peut résumer les limites des méthodes
géométriques dans les points suivants :
· Difficulté de lier deux images ayant des niveaux
d'intensité différents.
· le problème d'optimisation est bien plus
difficile à résoudre que dans le cas des méthodes
géométriques à cause de la présence de nombreux
minima locaux d'énergie [Noblet, 2006].
· Très grand coût calculatoire de par la
nécessité de calculer l'intensité de tous les voxels de
l'image [Gardeux, 2008], c'est à dire cette méthode
nécessite un temps de traitement important. Pour diminuer le temps de
calcule il existe des approches hiérarchiques par construction de
pyramides d'images [Noblet, 2006].
· Primitives peu informatives (de bas niveau) [Rubeaux,
2011].
3.4.3. Méthodes hybride
Les méthodes hybrides combinent plusieurs types de
caractéristiques extraites des images à Recaler. Le but est
d'améliorer la robustesse du recalage en combinant les avantages
liés aux caractéristiques utilisées. Trois cas sont
envisagés [Rubeaux, 2011] :
a) La combinaison de primitives géométriques de
nature différente comme la combinaison de points et de courbe ou la
combinaison de courbes et de surfaces.
b) La combinaison de différentes informations issues
des niveaux de gris : c'est le cas où le gradient de l'image et
l'information des niveaux de gris sont utilisés conjointement.
c) La combinaison des approches géométriques et
iconiques.
Chapitre 1 Recalage d'images médicales
17
|
Nature de la dépendance
|
Mesure
|
|
Formule
|
|
Conservation de l'intensité
|
SDC*
|
|
? ??,? (? - ?)2 ?,?
|
|
SDA*
|
|
???,? ~? - ?~ ?,?
|
|
Linéaire
|
|
Inter-corrélation normalisé
|
|
??
|
|
???,?
????
?,?
|
|
Critère d'Albert*
|
|
J
? ??,? (?? ? - ?)2
?,?
|
|
Affine
|
|
Coefficient de corrélation
|
|
?? - ???(? - ??)
?
|
|
??,? ????
?,?
|
|
Fonctionnelle
|
|
Critère de Woods*
|
|
??
? ?? ???
|
|
Rapport de corrélation*
|
|
?
?
?
|
|
?? ??2
- ??2
?
|
|
Statistique
|
|
Entropie conjointe *
|
|
-? ??,? ??? ??,??,?
|
|
Information mutuelle
|
|
??,?
?
|
|
???
??,?
????
?,?
|
|
Notations
|
?? = ? ??,?
?
?? = ???,? ? = ?,?
?? = ???,? ?
?,?
?? = ? ????
?
|
??,?
?
|
?=
|
? ?? ?? = ??
??? = ??? - ???
??? = ??? - ???
|
|
?? = ??,? ???? =
? ??
?
? ?? ? ??? = ? ??,? ?
? ?,?
?
= ??? ? ??? = ? ??,? ?
? ?,?
? ??? = ? ???? ? 2 - ??2
?
|
Tableau 1.1 Quelques mesures de
similarité utiles. Les mesures marqués d'un astérisque *
sont à
minimiser. Tandis que les autres sont à maximiser
[Roche, 2011].
Chapitre 1 Recalage d'images médicales
18
3.5. Information mutuelle et recalage d'image
L'Information Mutuelle (IM) est née du fruit de travail
de Claude Elwood Shannon en1949. En recalage
d'images, l'IM fut utilisée pour la première fois et à la
même année par deux équipes de recherche. Depuis 1995, la
liste des publications qui traitent de cette mesure en recalage ne cesse de
s'allonger, et elle est devenue la mesure de référence en
recalage d'images médicales multimodales d'intensités
inversées [Rubeaux, 2011].
Avant de parler de l'information mutuelle, la notion
d'entropie sera d'abord introduite.
3.5.1 Entropie
L'entropie est la quantité d'information contenue dans
une série d'événements. Une image A est par exemple
constituée d'une série d'événements, des pixels,
ayant tous une probabilité pi d'avoir une intensité
i. Plus une image n'est complexe, plus son entropie 11(A) est grande.
Shannon propose une définition de l'entropie telle que [Lombaert et
Thériault, 2005] :
? = ? ?? log 1 = - ? ? ?? ??? ?? (1.5)
? ??
La première expression montre bien que plus un
élément est rare, plus il a de signification. Si une image est
constituée de pixels de plusieurs tons de gris, l'image transporte une
information plus importante qu'une image d'un ton unique. La définition
de Shannon de l'entropie indique l'information moyenne que l'on peut s'attendre
de chaque élément de l'image [Lombaert et Thériault,
2005].
3.5.2 Entropie conjointe
Si on considère les deux images à recaler comme
deux variables aléatoires X et Y, avec ??,? la
distribution conjointe correspondante. L'entropie conjointe est formulée
comme suit :
???, ?? = ? ?,???,??x, y? log ??,?(x, y) (1.6)
??,?(x, y) est la densité de
probabilité conjointe des 2 images.
En effet l'aspect de l'histogramme conjoint reflète
directement l'entropie conjointe. L'entropie conjointe est une mesure de
dispersion de la distribution conjointe présentée par
l'histogramme conjoint. Plus ce dernier est inhomogène, plus l'entropie
conjointe est élevée, plus l'alignement est médiocre
[Saidonai, 2010].
Chapitre 1 Recalage d'images médicales
19
3.5.3. Information mutuelle
L'information mutuelle MI (A, B) de deux images A, B,
possède 3 définitions équivalentes. Chacune d'elles permet
d'expliquer différemment l'information mutuelle. La première
utilise la différence de l'entropie d'une image A et de l'entropie de la
même image A sachant une autre image B [Lombaert et Thériault,
2005] :
MI (A, B) = H (A) - H (AIB) (1.7)
= H (B) - H (BIA)
Ici, H(A) mesure l'information contenu dans l'image A, tandis
que H(AIB) mesure la quantité d'information contenu dans l'image A
lorsque l'image B est connue. L'information mutuelle correspond donc à
la quantité d'information que l'image B possède sur l'image A, ou
similairement, la quantité d'information que l'image A possède
sur l'image B.
La seconde définition évoque la distance de
Kullback-Leibler [Lombaert et Thériault, 2005] :
MI(A, B) = Ea,b pab log
pab (1.8)
apb
p
Soit la mesure entre la distribution pab des images A
et B et la distribution papb où les images A et B sont
indépendantes. Cette définition de l'information mutuelle mesure
donc la dépendance des images A et B. Il y aura recalage lorsque les
images A et B sont le plus semblables.
La troisième définition de l'information
mutuelle est une combinaison des entropies de deux images,
s'éparées et jointes [Lombaert et Thériault, 2005] :
MI (A, B) = H (A) + H (B) - H (A, B) (1.9)
Les entropies séparées H(A) et H(B)
mesurent la complexité des images A et B. L'entropie jointe H (A,
B) mesure la quantité d'information que les images A et B apportent en
même temps. Si les images A et B sont proches, une image explique bien la
seconde, et l'entropie jointe est minimale.
Studholme a introduit une autre formule
normalisée de l'IM pour éliminer l'effet lié à la
superposition des images sur la mesure [Lombaert et Thériault ,2005]
:
Chapitre 1 Recalage d'images médicales
H(A)+H(B)
MI(X,Y) = (1.10)
H(A, B)
La recherche de la transformation T recalant les images
A(x) et B(T (x)) correspond au maximum de la fonction de coût J(T) = MI
(A, B) [Lombaert et Thériault, 2005].

20
Figure 1.15 L'entropie, l'entropie conjointe et
l'information mutuelle pour deux images A et B
[Saidonai, 2010]
3.5.4. Avantages et limites de l'utilisation de
l'IM
a) Avantages
On peut résumer les avantages de l'utilisation de l'IM
dans les points suivants [Roche, 2011] :
? Elle est mieux adaptée au problème de recalage
multimodal
? Parce qu'elle repose sur des hypothèses faibles
concernant la relation entre les intensités des images, l'information
mutuelle à toutes les apparences d'une mesure de similarité
universelle.
? L'information mutuelle traite les intensités comme
des variables purement qualitatives
c'est à dire sans faire intervenir une relation d'ordre
dans l'espace des intensités.
b) Limites
On peut résumer les avantages de l'utilisation de l'IM
dans les points suivants [Rubeaux, 2011] :
? L'inconvénient majeur de MI, à côté
de la charge calculatoire importante, est le risque de tomber sur des optimums
locaux lors de la phase d'optimisation itérative et les
difficultés confrontées lors de cette phase [Saidonai ,2010].
? Quoique l'information mutuelle soit le critère le plus
généraliste, il est déconseillé de l'utiliser dans
les cas où des mesures plus restrictives peuvent être
utilisées.
Chapitre 1 Recalage d'images médicales
21
? L'IM est reconnue pour être sensible à la zone
de recouvrement partiel des données. En effet, lorsque l'on recale des
images de modalités différentes, par exemple, il arrive qu'une
structure, ou plus généralement qu'une partie des données
présente dans une des images ne le soit pas dans l'autre. C'est la
notion de recouvrement partiel. Plusieurs critères ont été
développés pour répondre à cette
problématique. Le plus connu est sans doute l'Information Mutuelle
Normalisée (IMN).
? Un désagrément reconnu de l'IM est qu'elle ne
fait aucune supposition sur l'information spatiale contenue dans les images
à recaler. Traitant les pixels/voxels des images comme des
réalisations d'une VA, la localisation spatiale de ces pixels n'entre
pas du tout en compte dans l'estimation de l'IM.
? Incorporer une information supplémentaire directement
dans l'IM n'est pas simple, car dans la plupart des cas, cela se traduit par la
définition d'une IM d'un couple de deux vecteurs aléatoires de
dimension 2.
? IM se prémunissant du calcul de l'histogramme
conjoint
4. Recalage et l'imagerie médicale
En imagerie médicale, le mot recalage est apparu dans
le courant des années soixante-dix. Le recalage est le processus qui
vise à apparier des données provenant de sources
différentes. Au début, son utilisation se limitait à la
seule comparaison des examens acquis avec un décalage temporel. Ces
examens provenaient d'une même modalité, en l'occurrence la
tomodensitométrie. Ce type de recalage dit monomodal avait pour but une
évaluation post-traitement.
Les cliniciens peuvent ainsi évaluer la pertinence d'un
traitement en comparant les variations du volume des lésions
traitées. Par contre, le besoin de représenter conjointement des
informations provenant de plusieurs modalités d'acquisition n'est apparu
que vers la fin des années 70, avec l'arrivée de l'IRM. Ce sont
à la fois les propriétés physiques et le rendu de ces
types de modalités qui ont poussé les chercheurs à
combiner les informations fournies par ces techniques, pour pallier le manque
d'imageur couvrant tous les aspects d'une forme étudiée. Ce
recalage est dit structurel multimodal, puisque les modalités
sollicitées ne mettent en exergue que la structure anatomique des zones
étudiées (Figure. 1.16). Il intervient davantage dans
l'évaluation pré et post-opératoire que dans les
comparaisons diachroniques [Atif, 2004].
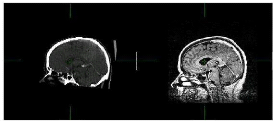
Chapitre 1 Recalage d'images médicales
22
Figure 1.16 Recalage Multimodal Structurel :
alignement d'une image TDM sur une image IRM.
Récemment, les chercheurs se sont
intéressés à un nouveau type de recalage dit structurel/
fonctionnel, qui fait appel à la fois à des modalités
structurelles et fonctionnelles comme son nom l'indique (Figure. 1.17).
L'imagerie cérébrale a été et reste le domaine le
plus consommateur de ce type de recalage. Par exemple, pour traiter un patient
épileptique, aussi bien le CT-scanner, l'IRMf où la scintigraphie
est utilisée [Atif, 2004].
La compréhension des processus physiologiques
cérébraux passe aussi par le recalage structurel/fonctionnel. On
peut alors associer une activation cérébrale à une
structure.
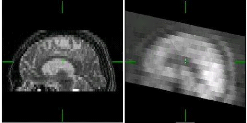
Figure 1.17 Recalage Multimodal
Structurel-Fonctionnel : alignement d'une image TEP
(fonctionnelle) sur une
image IRM-T2 (structurelle).
Il existe aussi la classe de recalage dite recalage
données/atlas. Pour des besoins plus liés à la
détection d'anomalies, les données provenant soit d'un seul
imageur, soit d'une fusion multimodale, sont recalées avec un atlas
numérique préalablement établi. L'utilisation de l'atlas
peut aussi servir de critère de recalage comme c'est le cas pour l'atlas
de Talairach/Tournoux (figure 1.18).
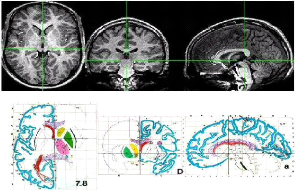
Chapitre 1 Recalage d'images médicales
23
Figure 1.18 Recalage multimodal
données/atlas : alignement d'un volume TDM sur l'atlas
anatomique de
Talairach-Tournoux.
Finalement, On peut évoquer le recalage multi-sujet. La
fusion de données provenant de sujets différents est utile pour
la construction d'atlas anatomiques et pour d'éventuelles études
statistiques sur une population. Ce type de recalage est d'autant plus
intéressant qu'il constitue la brique de base de la détection
automatique des anomalies [Atif, 2004].
5. conclusion
Dans ce chapitre on a présenté le
problème de recalage dans l'imagerie médicale : ses principes,
ses types et ses méthodes. Aussi, on a expliqué la notion de
mesure de similarité en donnant à l'information mutuelle plus
d'importance parce qu'on l'a choisi comme mesure de similarité dans
notre travail.
Le problème de recalage peut être formulé
sous forme de problème d'optimisation. La recherche de la solution
optimale est une tâche très couteuse voire impossible à
affecter par les méthodes exhaustives. Ceci a favorisé le
développement des méthodes approchées dont le principe est
de trouver une solution acceptable, qui n'est pas forcement l'optimale mais en
un temps raisonnable, en utilisant des processus stochastiques. Nous allons
utiliser un algorithme d'évolution différentielle pour le
recalage multimodal des images médicales en maximisant l'information
mutuelle. Dans le prochain chapitre nous allons présenter les
problèmes d'optimisation et les métaheuristiques destinées
à la résolution de ces problèmes.
| 


