Incidence du climat politique sur les activités socioéconomiques des cultivateurs de mayangose.

CHAPITRE TROISIEME : PRESENTATION DES DONNEES, ANALYSE ET INTERPRETATION DES RESULTATS

Dans ce chapitre, nous présentons et analysons les données relatives à notre thème de recherche. En titre de rappel, nous analysons ici les données relatives à l'incidence du climat politique sur les activités socioéconomiques des cultivateurs de MAYANGOSE.

Pour une observation plus poussée des phénomènes que nous voulons étudier, nous avons prélevé un échantillon de 374 ménages sur une population d'étude de 5000 ménages.

En vue d'une concision, nous présentons nos données dans des tableaux puis sur graphiques. Une fois dans le tableau et sur graphique, nos données font l'objet d'une analyse.

Tableau N° 01 : Accroissement de la population⁴³

ANNEE	INDIVIDUS	MENAGES
2010	4800	600
2011	7552	921
2012	12054	1470
2013	18730	2650
2014	31160	3800
2015	57399	7000
2016	49199	6000
2017	41000	5000

Source : Rapport de l'UEPCO/Beni, 2017

Commentaire : Ce tableau nous montre l'évolution de la population cultivatrice de MAYANGOSE depuis 2010 à 2017. Cette population a évolué d'une manière croissante. Cette évolution a été de 600 ménages soit 4800 individu à2010 et de 5000 ménages soit 41000 individus à 2017.

43 Bureau de l'IAPCO/BENI

49

- Taux d'accroissement de la population

En considérant la population de l'année de base (Po), la population de fin de période (Pn), et le nombre d'années de la période considérée, nous pouvons donc apprécier le taux d'accroissement de la population cultivatrice dans cette zone cible.

Nous allons déterminer l'accroissement de la population à partir de la formule suivante :

(1+a)ⁿ =

Pn

o

a= Pn 1l

C n Po /

=

(V41000 -- 1

4800

= (v ,5 1

-- 1) X 100

= ( 1,3074907 -- 1) X 100

0,3074907 x 100

a= 30, 749%

Ce résultat nous montre de quel degré la population cultivatrice augmentait chaque année. De par les données recueillies sur terrain, il en résulte que chaque année, cette population augmentait de 30,8% c'est-à-dire à moyenne chaque année de 2010 à 2017, plus au moins 1478 nouveaux cultivateurs étaient constatés chaque année.

50

Graphique n° 02 : Accroissement de la population

40000

70000

60000

50000

30000

20000

10000

Série1

Série2

0

4800

2010

1

2011

7552

2

12054

2012

3

18730

2013

4

31160

2014

5

57399

2015

6

49199

2016

7

41000

2017

8

Source : Nos recherches

Commentaire : De ce graphique, nous constatons une évolution linéaire de la population depuis le début de la nouvelle MAYANGOSE jusqu'à 2015. Le désintéressement de la population se manifeste à partir de 2015 jusqu'à 2017 suite à l'aggravation des cas de tuerie dans le milieu.

=

51

- Détermination de l'âge moyen des cultivateurs

Dans ce point, il s'agit d'analyser l'âge moyen des cultivateurs de MAYANGOSE. Pour se rassurer de leur tranche d'âge, il importe de retenir que le cultivateur le moins âgé a 18 ans et les plus âgés 68 ans.

A partir des formules ci-après, nous pouvons ainsi déterminer l'intervalle dans lequel varie l'âge de la plupart des cultivateurs. Ainsi, nous avons :

a) K= 1+ logn

b) d= Xmax-Xmin

c) a=

d) L1= Xin-

e) L2= L1+ a

k= est le nombre des classes

d= l'étendue de la variation
Xmax= âge élevé

Xmin= âge inferieur

a= amplitude
L1= Limite inférieure L2= Limite supérieure n= taille de l'échantillon

Concrètement nous avons :

a) k= 1+ log374

= 1+ x 2,57

= 1 + (3,33 x 2,57)

= 1+8,55

= 9,5 classes 9 classes

b) Nous savons que l'étendue de variation « d )) est déterminée pard= Xmax-Xmin

= 68-18

= 50 ans

L'amplitude « a )) est aussi déterminée par la formule suivante :

c) a=

52

=

= 6,25 6

d) L1= Xmin-= 18 - =

=

= 15

e) L2= L1+ a = 15 + 6 = 21

Tableau n° 02 : Age moyen des cultivateurs

Classes	ni	%	xi	nxi	xi-	(x- )2	ni(x- )2
[15-21[	11	2,94	18	198	-19	-361	-3971
[21-27[	72	19,25	24	1728	-13	-169	-12168
[27-33[	80	21,39	30	2400	-7	-49	-62720
[33-39[	70	18,71	36	2520	-1	-1	-70
[39-45[	66	17,64	42	2772	5	25	1650
[45-51[	25	6,68	48	1200	11	121	3025
[51-57[	24	6,41	54	1296	17	289	6936
[57-63[	16	4,27	60	960	23	529	8464
[63-69[	10	2,67	66	660	29	841	8410
?	374			13734			107414
				37

Source : Nos calculs Nous savons que : = ?

2= ? ( )

53

2= =287,2 287

v

v = 16,9 17
n= 374

= 37

z. = 1,96

Intervalle de confiance å ( #177; z. . v )

å (37 #177; 1,96. )

å (37 #177;1,72)

å( )

Interprétation : Le tableau ci-haut nous présente 9 classes reprenant les tranches d'âges en rapport avec les 374 individus soumis à notre enquête. L'âge de nos enquêtés se situe entre 35 ans et 39 ans.

Ainsi, l'espérance mathématique en moyenne est de 37 ans. En termes d'intervalle de confiance, cette espérance mathématique de 37 ans est comprise entre 35 ans et 39 ans.

=

54

- Ancienneté des cultivateurs de Mayangose

Il s'agit ici d'apprécier la moyenne d'ancienneté des cultivateurs de

Mayangose.
= ?		= 4ans

k= 1+ logn

d= Xmax-Xmin a=

L1= Xin-L2= L1+ a

k= est le nombre des classes

d= l'étendue de la variation
Xmax= âge élevé

Xmin= âge inferieur

a= amplitude

L1= Limite inférieure L2= Limite supérieure n= taille de l'échantillon

Concrètement nous avons :

f) k= 1+ log374

= 1+ x 2,57

= 1 + (3,33 x 2,57)

= 1+8,55

= 9,5 classes 9 classes

g) Nous savons que d= Xmax-Xmin d= 8-1

= 7 ans

h) a=

55

=

= 0,875 1

i) L1= Xmin-

= 1 -

= 0,5

j) L2= L1+ a = 0,5 + 1

= 1,5

Tableau N° 03 : Ancienneté des cultivateurs de MAYANGOSE

classes	ni	%	xi	nxi	xi-	(x- )2	n(x- )2
[0,5-1,5[	10		1	10	-4	16	160
[1,5-2,5[	18		2	36	-3	9	162
[2,5-3,5[	40		3	120	-2	4	160
[3,5-4,5[	82		4	328	-1	1	82
[4,5-5,5[	90		5	450	0	0	0
[5,5-6,5[	98		6	588	1	1	98
[6,5-7,5[	25		7	175	2	4	100
[7,5-8,5[	7		8	56	3	9	63
[8,5-9,5[	4		9	36	4	16	64
?	374			1799			889
				5

Nous savons que :

=	?

A partir des formules ci-après, nous pouvons ainsi déterminer l'intervalle dans lequel varie l'ancienneté de la plupart des cultivateurs de Mayangose.

56

Ainsi, nous avons :

2= ? ( )

2= =2,377

v

v = 1,54 2
n= 374

= 5

2

Nous constatons que l'ancienneté moyenne des cultivateurs de MAYANGOSE est égale à 5 ans. Ainsi, nous étudions l'intervalle de confiance à partir de la formule suivante :

z. = 1,96

Intervalle de confiance å ( #177; z. . v )

å (5 #177; 1,96. )

å (5#177;0,2)

å = (4,8#177; 5,2)

Commentaire : Nous sommes confiants à 95% partant des résultats ci-haut que l'ancienneté de cultivateurs est comprise entre 4,8 et 5,2 ans. Nous estimons que cette moyenne de l'ancienneté est consécutive à la situation vécue dans ce milieu, c'est-à-dire ce milieu est fréquenté essentiellement par la population ayant encore une force physique et courageuse.

57

Tableau n° 04: Répartition de la population selon les principales cultures.

N°	Principales cultures	Effectifs
01	Manioc	335 ménages
02	Riz	255 ménages
03	Haricot	325 ménages
04	Maïs	278 ménages
05	Banane	223 ménages
06	Cacao	60 ménages
07	Café	20 ménages

Sources : Nos recherches

Commentaire : De ce tableau, nous trouvons que 335 ménages soit 89,57% font la culture de manioc, 255 ménages soit 68,18% cultivent le riz, 325 ménages soit 86,89% cultivent les haricots.

Ainsi, Nous constatons qu'un ménage cultive plus d'une variété à la fois, ce qui ne lui permet pas de se spécialiser et se concentrer dans une seule culture.

Tableau n° 05 : Estimation de la production agricole

ANNEE PRODUITS	2010	2011	2012	2013	2014	2015	2016	2017
Cossette de Manioc	8007kg	17510kg	282220kg	338350kg	579600kg	482300kg	11000kg	530kg
Riz	20100kg	132000kg	240000kg	781760kg	953350kg	506900kg	1000kg	0 kg
Haricot	1325kg	31000 kg	75600kg	120575kg	193540kg	136212kg	1233 kg	329kg
Maïs	1223 kg	2910 kg	10880 kg	171804kg	199503 kg	9870 kg	798 kg	225 kg
Banane	0	1320 reg	121000 Re	392604 reg	396200reg	223400	1620 reg	187 regim

Source : Nos recherches

Commentaire : Ce tableau nous présente l'évolution de quelques produits agricoles pendant la période allant 2010 à 2017. Ces produits ont évolué d'une manière croissante jusqu'à 2014 pour la plupart.

58

De par ces éléments, nous comprenons que la production moyenne annuelle de ces produits agricoles est de 530 kg /par an pour les cossettes de manioc, 0 kg/ans pour le riz, 329 kg/an pour le haricot et 225 kg/an pour le maïs. Nous pouvons visualiser cela sur graphique.

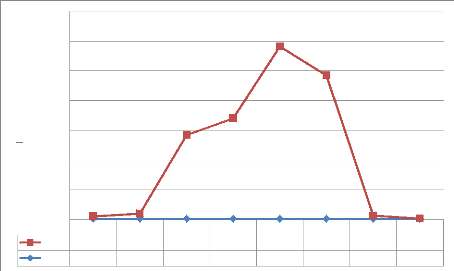
Graphique N° 03 : Evolution de la production de cossette de manioc

la production

400000

700000

600000

500000

300000

200000

100000

Série2

Série1

0

8007

2010

1

17510

2011

2

282220

2012

3

338350

2013

4

579600

2014

5

482300

2015

6

11000

2016

7

2017

530

8

Source : Nos recherches

Commentaire : De ce graphique, nous constatons que la production de cossettes de manioc a progressivement augmenté au fur et à mesure que la population cultivatrice évoluait. Cet accroissement a sensiblement chuté voir même dépasser la ligne d'abscisses suite à la peur qui a gagné les cultivateurs et qui n'accédaient plus facilement à leurs champs.

59

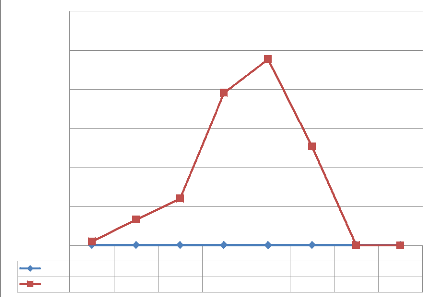
Graphique n° 04 : Evolution de la production du riz

1200000

1000000

400000

800000

600000

200000

Série1

Série2

0

20100

2010

1

132000

2011

2

240000

2012

3

781760

2013

4

953350

2014

5

506900

2015

6

2016

1000

7

2017

8

0

Commentaire : De ce graphique ci-haut, l'évolution de la production du riz a été fonction de l'accroissement de la population et de la sécurité. En 2014, la production a été d'à peu près de 953 tonne. Cette production en échelle a directement joué positivement sur les conditions de vie des cultivateurs. En 2017, nous avons constaté une production nul (0) suite à l'insécurité dans la région.

60

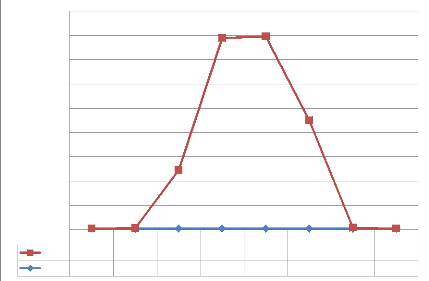
Graphique n° 05 : Evolution de la production de régime des bananes

Titre de l'axe

450000

400000

350000

300000

250000

200000

150000

100000

50000

Série2

Série1

0

2010

0

1

2011

1320

2

121000

2012

3

392604

2013

4

396200

2014

5

223400

2015

6

2016

1620

7

2017

187

8

Commentaire : Ce graphique nous montre une évolution croissante de la production des bananes à partir de 2011 jusqu'à 2015. Cette production revient encore à la case de départ à partir de 2016 jusqu'aujourd'hui où on enregistre quelques régimes de bananes en provenance de MAYANGOSE.

61

Tableau n° 06 : Estimation de l'évolution du prix

ANNEE PRODUITS	2010	2011	2012	2013	2014	2015	2016	2017
Cossette de Manioc	300 fc	250 fc	200 fc	150 fc	170 fc	250 fc	500 fc	600 fc
Riz	850 fc	800 fc	700 fc	450 fc	500 fc	550 fc	1000 fc	1600 fc
Haricot	300 fc	250 fc	200 fc	200 fc	350 fc	450 fc	600 fc	1500 fc
Maïs	350 fc	250 fc	200 fc	250 fc	350 fc	500 fc	600 fc	750 fc
Banane	800 fc	800 fc	1000 fc	1000 fc	1500 fc	4000 fc	6500 fc	8000 fc

Source : Nos enquêtes

Commentaire : De ce tableau ci-haut, nous constatons que le prix de la quasi-totalité de produits agricoles a sensiblement augmenté après la période de 2013 suite à l'inaccessibilité des champs.

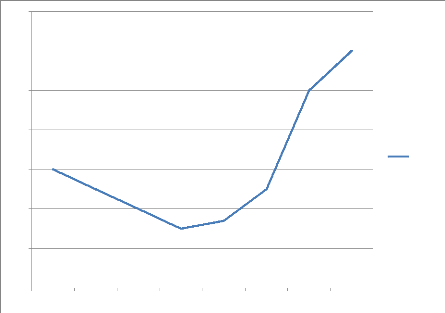
Ceci nous pousse à représenter graphiquement nos données. Graphique n° 06 : Evolution du prix de cossettes de manioc

400

700

600

500

300

200

100

0

1 2 3 4 5 6 7 8

Série1

Source : Nos recherches

62

Commentaire : De ce graphique, nous constatons que le prix de cossettes de manioc a augmenté suite à la quantité insuffisante produite.

La farine de manioc constituent l'aliment de base de la population du milieu, l'accroissement du prix a sensiblement influencé le budgte et le revenu. Cette situation a aussi influencé le revenu des autres secteurs dans la région et plus particulièrement en ville de Beni.

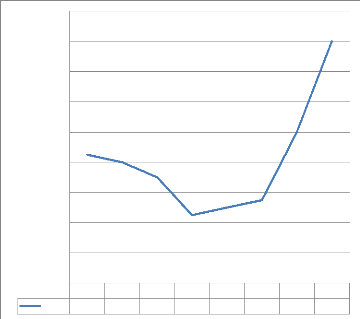
Graphique n° 07 : Evolution du prix du riz

1600

1400

1200

Titre de l'axe

1000

800

600

1800

400

200

0

Série1

1	2	3	4	5	6	7	8
850	800	700	450	500	550	1000	1600

Source : Nos enquêtes

Commentaire : Le prix du riz a été de 850fc à 2010, de 800 fc à 2011, de 450 fc à 2013 et de 1600 fc à 2017.

Cette variation du prix s'est manifestée au cours des années 2013 et 2014, où il y a eu croissance production suite au bon fonctionnement de l'appareil sécuritaire. La situation d'insécurité s'est beaucoup dégradée à partir de 2016 jusqu'aujourd'hui et par conséquent la rareté de produit sur le marché de négoce fait que le prix augmente sensiblement.

63

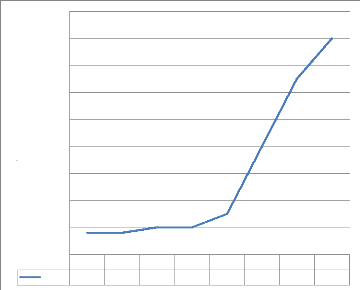
Graphique n° 08 : Evolution du prix des régimes de banane

Titre de l'axe

4000

9000

8000

7000

6000

5000

3000

2000

1000

Série1

0

800

1

800

2

1000

3

1000

4

1500

5

4000

6

6500

7

8000

8

Source : Nos enquêtes Commentaire :

A ce stade, le prix de produits agricoles au cours de l'année 2017, n'est plus abordable c'est-à-dire les quantités offertes sur le marché soit insuffisantes données ne correspondent. Un régime de banane qui se vendait à 800 fc à 2010, ce même régime se vend à 8000 fc même plus au cours des années 2017, 2018..

Ces différentes fluctuations de prix sur le marché, ont des effets sur le revenu et le budget des ménages. Nous pouvons donc apprécier cet effet sur le budget d'un ménage moyen à travers les calculs de l'inflation.

III. 4. L'INFLATION

L'inflation désigne une hausse durable des prix. Lorsque le prix d'un seul bien ou de quelques biens augmente, il n'y a pas forcement d'inflation car les prix de tous les autres biens peuvent ne pas bouger, voir

64

diminuer. L'inflation correspond alors à une hausse du prix moyen de tous les biens et services⁴⁴.

En période d'inflation, certains prix augmentent plus vite que d'autres ; l'inflation s'accompagne donc d'une modification des prix relatifs c'est-à-dire des rapports de prix entre les biens considérés deux à deux. L'inflation peut prendre des formes extrêmes, c'est l'hyperinflation. Si l'inflation caractérise la hausse des prix, le contraire de ce phénomène est donc la baisse de prix. Il s'agit de la déflation ; qu'on ne doit pas confondre avec la désinflation qui désigne la baisse du taux d'inflation. Quand les prix augmentent toujours, mais à un rythme moins important qu'auparavant, il s'agit de la désinflation.

Mesure de l'inflation

a) Indices simples

Un indice simple est un rapport ente deux grandeurs dont la première appelée base, est adoptée comme valeur de référence et à laquelle on donne par convention la valeur 100⁴⁵. Cet indice se caractérise par le fait qu'il fait la moyenne de tous les indices simples de plusieurs produits.

On parle d'indices statistiques chaque fois que l'on a à comparer deux grandeurs soit dans le temps soit dans l'espace et qu'on en effectue le rapport. Il est souvent utile de comparer les indices entre eux, ou simplement de connaitre la croissance des indices de deux années ou de deux périodes.⁴⁶

44 Philippe le BOLLOCH, Economie générale, Paris, 1998, P., 61

45 Philippe le Bolloch, OpCit, P., 63

46 Ct. Kanduki Mbusa, Population et Environnement, Cours Inédit, L1 UNIC Beni, 2017

65

Tableau n° 07: Indice de prix

N°	produits	Prix 2017	Indice de prix des produits en 2013
01	Farine de Manioc	600fc/kg	600fc= 4
			1 5 0 f c
02	Riz	1600fc/kg	1600fc=
			5 300fc
03	Haricot	1500fc/kg	1500f c= 6
			250fc
04	Maïs	700fc/kg	700fc=
			4 180fc
05	Banane	8000fc/kg	8000fc = 8
			1000fc

Source : Nos calculs

Commentaire : Les indices obtenus sont calculés en considérant la période de 2010 jusqu'à 2017.

Ainsi, nous avons compris que :

- Pour les cossettes de manioc, le prix d'un kilogramme a varié de 150fc à 600 fc. Ce qui nous a donné un indice de 4. En d'autres termes, le prix d'un kilogramme de cossettes de manioc a été multiplié par quatre. Donc un seau de 10 kg qui coutait 1500fc, est vendu à 6000 fc ;

- Pour le riz, l'indice est de 5 ;

- Pour le haricot, l'indice est de 6 ;

- Pour les bananes, l'indice est de 8.

Ces variations de prix ont sans doute de conséquences sur le budget des ménages. Ceci nous pousse donc à apprécier le taux d'inflation qui a perturbé le budget du ménage dont nous avons estimé le revenu moyen à 160 000fc soit aujourd'hui l'équivalant de 100$.

66