III.2.2. STATIONNARITE DES
VARIABLES
La modélisation des séries temporelles
nécessite que ces dernières soient stationnaires. Autrement dit,
la série ne doit comporter ni tendance, ni cycle et ni
saisonnalité. Cette notion de stationnarité représente un
point crucial dans l'économétrie des séries temporelles,
où l'estimation des séries non stationnaires conduit à des
régressions fallacieuses ou illusoires. Pour éviter ces
estimations fallacieuses, les économètres procèdent
à la stationnarisation des séries chronologiques.Nous avons donc
effectué de test de racine unitaire de Dickey Fuller Augmenté
(ADF) sur chacune des variables en logarithme.
Une série temporelle est dite stationnaire au sens
faible si ses propriétés statistiques, à savoir
l'espérance mathématique, la variance et l'auto-covariance, ne
varient pas dans le temps. Il est à noter que la variance doit
être finie. Si l'une de ces conditions n'est pas remplie, on parle alors
de non stationnarité. Une série temporelle non stationnaire peut
alors de ce fait, soit du type DS, soit du type TS.
Un processus TS (Trend Stationary) représente
une non-stationnarité de type déterministe. En d'autres termes,
la série comporte une tendance qui est significative. Dans ce type de
modélisation, l'effet produit par un choc (ou par plusieurs chocs
aléatoires) à un instant t est transitoire.Le
modèle étant déterministe, la chronique retrouve son
mouvement delong terme qui est ici la droite de tendance.
Un processus DS (Differency Stationary) est dit des
processus non stationnairesaléatoires. Ces derniers sont des processus
que l'on peut rendre stationnaires par l'utilisationd'un filtre aux
différences. Dans les processus de type DS, un choc à un instant
donné se répercute à l'infini sur les valeurs futures de
la série ; l'effet du choc est donc permanent etva en
décroissant.
Pour savoir si une série temporelle est stationnaire ou
pas, il existe plusieurs tests. Mais dans le cadre de ce travail pratique, nous
allons appliquer seulement le test de Dickey Fuller augmenté. Ce test
s'effectue suivant 3 modèles, à savoir :
- Modèle 1 : Modèle sans la constante, ni
la tendance ;
- Modèle 2 : Modèle avec la
constante ;
- Modèle 3 : Modèle avec la constante et la
tendance.
Dans la procédure du test, l'on commence toujours par
le modèle 3.
L'hypothèse nulle de ce test est que la série
comporte une racine unitaire, c'est-à-dire que la série est non
stationnaire. Et l'hypothèse alternative est que la série ne
comporte pas une racine unitaire, c'est-à-dire que la série est
stationnaire. Au seuil de significativité choisi, l'on rejette
l'hypothèse nulle si la statistique du test de Dickey Fuller est
strictement supérieure à la valeur critique de Mackinnon. Il est
à noter que dans le cadre de notre étude, le nombre des lags dans
le test ADF est choisi en minimisant le SIC (Schwarz Information Criterion).
Les résultats du test ADF sur les variables de notre
analyse montrent que lesvariables 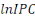 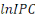 et et 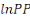 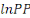 sont intégrées d'ordre 1 (c'est-à-dire
stationnaires en différence première), alors que la variable sont intégrées d'ordre 1 (c'est-à-dire
stationnaires en différence première), alors que la variable 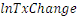 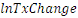 est stationnaire en niveau sur la période 2007-2017. De ce fait,
l'équation (2) devient : est stationnaire en niveau sur la période 2007-2017. De ce fait,
l'équation (2) devient :
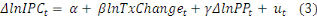
Dans le modèle (3) toutes les variables incluses sont
stationnaires. La différence première de la variable 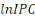 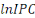 notée notée 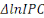 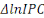 représente le taux d'inflation. Celle du prix du pétrole
traduit le taux de croissance du prix du pétrole sur le marché
international. représente le taux d'inflation. Celle du prix du pétrole
traduit le taux de croissance du prix du pétrole sur le marché
international.
| 


