Le taux de dé-confinement du terrain s'écrit :
? = ????-?? (I.3)
????
??0 : Contrainte initiale isotrope dans le terrain
P : pression du soutènement correspondant au point
considéré de la courbe caractéristique du terrain.
Si et seulement si le comportement du terrain est
élastique, le déplacement de la paroi est lié au taux de
déconfinement par la relation ?? = ?. ????, Ue étant le
déplacement élastique de la paroi pour P=0.
A.2 Domaine élastique
linéaire
Si ???? < ??? ??? avec ???? = ????-?????? ??
résistance à la compression simple du terrain
??-?????? ??
La courbe caractéristique est une droite qui coupe l'axe
de déplacement en un point
A.3 Zone en état limite de
rupture
Si ó0 > ???2? à partir d'une
certaine valeur de la pression (p=Pa), il se développe autour de
la cavité une zone circulaire en état limite de
rupture plastique de rayon (rp). Lorsque p diminue, rp augmente. En
considérant le critère de rupteur de Mohr-Coulomb, nous avons
:
Pa = ????(1-?????? ??) -
(?? × ?????? ??) (I.4)
Le déplacement de la
paroi à l'apparition de la rupture :
U0= ???. ???? (I.5)
17
Chapitre I- Revue bibliographique
??+??
????= ?? .R.???? (I.6)
A.4 Domaine élastoplastique
parfait
Plusieurs formules ont été données pour
tracer la courbe caractéristique du terrain après qu'une zone en
état limite de rupture se formée autour de l'excavation.
??(??) = ??+??
?? .????. ????. ??
??+?? . [??. (????(??)
?? )??+?? - ?? + ??] . ?? (I.7)
Avec :
(????(??))
=
( ?? (????-??).????+???? )??p??
(I.8)
?? ????+?? . (??-??).(????-??).????+????
.ô
Le taux de déconfinement à une distance `x' du
front de taille est donné par la formule (Panet, 1995) :
?? (x)= 1-0.75× [ ??
(I.9)
??+(??? ?)*(?? ??)]??
La détermination de cette convergence permettra la
définition de la position relative des courbes caractéristiques
du soutènement et du terrain dont dépendra l'équilibre
final. Tracé de la courbe de confinement du
soutènement
Le soutènement aura pour Rôle d'appliquer la
contrainte de confinement sur les parois de l'excavation. Cette pression de
confinement s'établira au fur et à mesure que la convergence
s'effectuera et que les terrains prendront appui sur le soutènement.
???? = ???? . ?? (I.10)
??
U : déplacement radial du soutènement ; Ks : rayon
de l'excavation ;
P : pression sur le soutènement.
Tableau I-7 : Expression de la raideur et de la
pression maximale pour chaque type
de soutènement (Bouvard et al,
1995).

18
Chapitre I- Revue bibliographique
Évaluation des charges agissant sur le
tunnel
Il existe de nombreuses formules théorico-empiriques
pour évaluer quantitativement la poussée verticale sur la calotte
et les poussées latérales sur les piédroits, qui souvent
sont notablement différentes selon les diverses hypothèses
adoptées et les paramètres mis en évidence. Étant
donné que le tunnel objet du présent projet se trouve
relativement en surface (rameau de connexion d'un tunnel de métro), la
méthode la plus adéquate pour évaluer les charges est
celle de Terzaghi (Terzaghi, 1943). Cette méthode sera
présentée dans ce qui suit.
Calcul des charges verticales
Selon les effets, on distingue les classes suivantes :
? Terrains non cohésifs ;
? Terrains cohésifs.
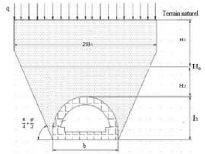
Figure I-2 : pression verticale sur la calotte
(Terzaghi, 1943).
Terrains non cohésifs
Le matériau est considéré en
équilibre plastique. En se basant sur une série
d'expériences, Terzaghi (1946) fournit deux expressions
différentes de la pression au sommet du tunnel selon la hauteur de la
couverture.
? Pour H0 = 5. ??1 l'effet de voute
s'entend jusqu'à la surface (Fig. I.14) et la pression verticale est
:
???? = ??.????
??.?????? (?? - ??(-??.??.??????
???? )) (I.11)
Avec K: le coefficient
expérimental pris 1 selon Terzaghi.
Et ????= ??+ ??. ??.??????(?? ?? - ?? ??)
(I.12)
? Pour H0 > 5. ??1 l'effet de
voute ne se fait pas ressentir jusqu'à la surface (Fig. II.1). la
hauteur totale sera par conséquent composée de deux hauteurs, une
hauteur



