22
Chapitre I- Revue bibliographique
confinement. Cette analyse 2D est rapide par rapport à
l'analyse tridimensionnelle et permet donc d'utiliser des modèles de
comportements plus complexes si les données de terrain sont suffisantes.
La modélisation transversale ne permet cependant pas d'analyser la
stabilité du front de taille.
Pour effectuer cette étude, on peut envisager une
modélisation longitudinale parallèlement à l'axe du
tunnel, mais les résultats obtenus sont toujours insatisfaisants. En
effet l'excavation est considérée comme une bande de longueur
infinie alors que le tunnel est circulaire, ce qui conduit à
négliger l'effet de voûte se produisant autour du tunnel.
La modélisation tridimensionnelle
C'est le type qui permettant de traiter le problème
rencontré dans toute sa complexité car il peut prendre en compte
:
? La géométrie tridimensionnelle du projet (tunnel
en forme de fer à cheval, tunnel incliné, écaille de sol,
etc....).
? L'état de contraintes initial (coefficient des terres
au repos). Le phasage souvent complexe de la technologie d'excavation retenue
(radier décalé).
? L'ensemble des phénomènes mis en jeu (effet de
voûte au front de taille, mise en place du soutènement,
etc....).
C'est aussi l'approche la plus exigeante en taille du
système, en temps de calcul et en temps d'exploitation des
résultats. Compte tenu de sa lourdeur, ce type de calcul reste encore du
domaine de recherche et de projets importants afin de valider des approches
simplifiées
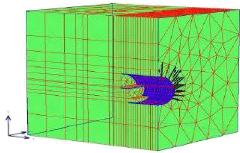
Figure I-5 : Exemple de maillage
3D.
La méthode des éléments finis
(M.E.F)
La méthode des éléments finis est une
méthode de calcul approchée qui consiste à transformer les
équations différentielles de la mécanique des milieux
continus en un système linéaire fini d'équations
algébriques, que l'on résout par des techniques
numériques
23
Chapitre I- Revue bibliographique
traditionnelles. Pour ce faire, le milieu réel est
remplacé par un milieu équivalent contenu dans un contour
polygonal, le plus proche possible du contour réel. Ce milieu
équivalent est ensuite divisé en sous-domaines réguliers,
appelés éléments finis (triangles et quadrilatères
pour un problème plan ; hexaèdres et pentaèdres pour un
problème tridimensionnel). Le champ de déplacement à
l'intérieur et sur le contour de chaque élément fini est
déterminé par une interpolation polynomiale entre des valeurs du
champ en certains points de l'élément, appelés noeuds.
L'ensemble forme par les éléments finis est appelé
maillage. [6]

Figure I-6 : Exemple d'un maillage.
[3]
L'objectif de la méthode des
éléments finis
· Apprendre la méthode des éléments
finis (MEF)
· Maîtriser les concepts de base de la
modélisation numérique ;
· Être capable de résoudre des
problèmes mécaniques et physiques. Domaines
d'application de la MEF
· Analyse linéaire (statique et dynamique) ;
· Analyse non linéaire (grands
déplacements, grandes déformations, contact et frottement,
flambage, ...)
· Mise en forme des matériaux thermique (en
régime permanent et transitoire, ...) ;
· Mécanique des fluides ;
· Électromagnétisme ;
| 


