3.3 Analyse Multicritère Hiérarchique
Les données d'entrées et le choix du poids des
critères influencent le résultat final [Aly et al.,
2017]. Dans les faits, les facteurs n'ont pas le même coefficient
d'importance. Afin de distinguer la potentialité des sites, nous
attribuons un poids aux facteurs, pour qu'ils se hiérarchisent du moins
favorable au plus favorable.
L'Analyse Multicritère Hiérarchique ou bien
« Analytic Hierarchy Process » (AHP), est une méthode
acceptée par la communauté scientifique internationale comme un
outil de décision multicritère pour résoudre la question
de décision et de pondération [Sánchez-Lozano et
al., 2013]. C'est une méthode mathématique simple
développée par Saaty [Lee et al., 2009 ;
Sánchez-Lozano et al., 2016] qui permet de produire un poids
à chaque critère. Elle repose sur les concepts suivants :
- décomposer le problème en n
critères
n1 n2 n3
n?? n???? n??2 n??3
A= {
n2 n21 n22 n23
n3 n31 n32 n33
- comparer, à l'aide d'une matrice, les critères
selon une échelle de Saaty allant de 1 à 9 (Tableau 5) en
fonction de l'importance relative par paire de critères [Pechanec et
Machar, 2013], c'est-à-dire les critères sont comparés
deux par deux. Si la valeur du critère de la ligne horizontale par
rapport au critère de la colonne verticale est k,
réciproquement la valeur sera
1/k [Höfer et
al., 2016].
Tableau 5 : Échelle de comparaison selon Saarty pour
appliquer la méthode de l'AHP
Degrés d'importance de chaque
Définition Explication
caractéristique
1 Importance égale Deux
caractéristiques contribuent
de la même façon à l'objectif.
L'expérience et l'appréciation
personnelles
favorisent légèrement
une caractéristique par rapport
à
une autre.
L'expérience et l'appréciation
favorisent
fortement une
caractéristique par rapport à une
autre.
Une caractéristique est fortement
favorisée et
sa dominance est
attestée dans la pratique.
Les preuves favorisant une
caractéristique par
rapport à une
autre sont aussi convaincantes que
possible.
5 Importance forte
7 Importance très forte
9 Importance absolue
Faible importance d'une
caractéristique par rapport
à une
autre
3
Lorsqu'un compromis est
2, 4, 6, 8 Valeurs intermédiaires
nécessaire.
Source : Höfer et al., 2016
AHP : Analyse Multicritère
Hiérarchique
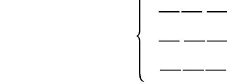
- synthétiser le poids de chaque critère
à partir de la matrice A, dans une nouvelle matrice
B et diviser chaque valeur (nx) par la somme de la colonne
(Nx). Le poids est la moyenne des lignes de la matrice B
n1 n2 n3
n1 n2 n3
n1 n11 n12 n13 A = n2 n21 n22 n23 n3 n31 n32 n33 {N1 N2
N3
n11
n1
n12
N2
N1
n13
N3
n11
B=
n2
n12
N2
N1
n13
N3
n11
n12
n3
n13
N2
N1
N3
40
- vérifier la cohérence des résultats.
Saaty [1987] propose deux paramètres : l'indice de cohérence (IC)
et le ratio de cohérence (RC). Tant que RC est inférieur à
0,1 le résultat est bon
IC CA
41
???????? - ??
IC = ?? - ??et ??C =
X max : est la moyenne de la valeur propre de la matrice
n : est le nombre de critères
CA : est l'indice de cohérence aléatoire, cet
indice est standard, il dépend de la taille
de la matrice (Tableau 6).
Tableau 6 : Tableau d'indice aléatoire
|
n
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
|
CA
|
0
|
0
|
0,58
|
0,90
|
1,12
|
1.24
|
1,32
|
1,41
|
1,45
|
1,49
|
1,51
|
Source : Saaty, 1987
42
| 


