II.1.1. Définition d'un
système cryptographique
Soit  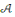 un ensemble fini, appelé l'alphabet de
définition. un ensemble fini, appelé l'alphabet de
définition.
Soit   un ensemble appelé l'espace des messages clairs. un ensemble appelé l'espace des messages clairs.
Soit   un ensemble appelé l'espace des messages
chiffrés. un ensemble appelé l'espace des messages
chiffrés.
Soit   un ensemble appelé l'espace des clés. un ensemble appelé l'espace des clés.
Chaque  , détermine une injection , détermine une injection   de de   vers vers  , appelée fonction de chiffrement, , appelée fonction de chiffrement,   est appelé clé de chiffrement. est appelé clé de chiffrement.
A chaque   est associé un est associé un  , tel que , tel que   dénote une injection de dénote une injection de   vers vers   , appelée fonction de déchiffrement, , appelée fonction de déchiffrement,   est appelé clé de déchiffrement. est appelé clé de déchiffrement.
Un système cryptographique (cryptosystème)
est un quintuple   tel que tel que
 
II.2 Cryptosystème
symétrique et asymétrique
II.2.1 Cryptosystème
symétrique
Les algorithmes de cryptographie
symétrique utilisent les mêmes clés lors du chiffrement et
du déchiffrement.
Considérons un ensemble fini de fonctions de
chiffrement   et un autre ensemble fini de fonctions de déchiffrement et un autre ensemble fini de fonctions de déchiffrement   , nous avons: , nous avons: 
Dans un système symétrique, la
sécurité repose sur la clé. La clé doit rester
inconnue aux tierces personnes. La génération des clés est
choisie d'une manière aléatoire dans l'espace des clés.
L'avantage du cryptosystème symétrique est
basé sur sa rapidité et son désavantage réside dans
la distribution des clés. Pour un système à   utilisateurs, il y aura utilisateurs, il y aura   paires des clés. paires des clés.
II. 2.1.1 Exemples des chiffrements symétriques
II.2.1.1.1 Chiffrement symétriques
classiques
Identifions l'alphabet usuel avec   par par   et les opérations sont réalisées dans et les opérations sont réalisées dans  
1. Chiffrement par décalage
Soit  
Soit  
Et soit   et et  
  et et  
Ainsi pour   nous avons le chiffrement de César. nous avons le chiffrement de César.
Exemple: Avec  , le texte clair '' politique'', nous obtenons le texte
chiffré '' srolwltxh'' , le texte clair '' politique'', nous obtenons le texte
chiffré '' srolwltxh''
Ce système de chiffrement est facilement cassable
puisque l'espace des clés ne contient que 26 éléments (26
clés possibles).
2. Chiffrement par substitution
Soit  
L'espace des clés est l'ensemble des permutations
de  . .
Chacune des lettres est remplacée par une autre lettre
de l'alphabet.
Pour 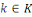  , nous avons : , nous avons :
  et et  
où   et et   est la permutation inverse de est la permutation inverse de  
Le nombre de clés possibles est  , une recherche exhaustive n'est pas possible. Cette méthode est
facilement cassable suite à la fréquence des lettres. , une recherche exhaustive n'est pas possible. Cette méthode est
facilement cassable suite à la fréquence des lettres.
Exemple:
|
a
|
b
|
c
|
d
|
e
|
f
|
g
|
h
|
i
|
j
|
k
|
l
|
m
|
n
|
o
|
p
|
q
|
r
|
s
|
t
|
u
|
v
|
w
|
x
|
y
|
z
|
|
f
|
l
|
h
|
j
|
a
|
r
|
c
|
p
|
u
|
x
|
d
|
i
|
q
|
y
|
m
|
k
|
b
|
t
|
g
|
w
|
n
|
z
|
s
|
v
|
o
|
e
|
Soit la permutation suivante :
Le texte clair ''symétrique'' est chiffré en ''
goqawtubna'
3. Chiffrement du Vigenère
Soit  
Soit  
Soit 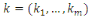 
Alors 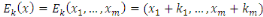 
et  
où  
Le nombre de mots-clés possibles de longueur   est est   , une recherche exhaustive est impossible. , une recherche exhaustive est impossible.
Exemple:
Soit le mot en clair '' Faculté '' et la clé ''
Ornela ''
|
Texte
claire
|
f
|
a
|
c
|
u
|
l
|
t
|
e
|
|
5
|
0
|
2
|
20
|
11
|
19
|
4
|
|
Clé
|
o
|
r
|
n
|
e
|
l
|
a
|
o
|
|
14
|
17
|
13
|
4
|
11
|
0
|
14
|
|
Texte
chiffré
|
19
|
17
|
15
|
24
|
22
|
19
|
18
|
|
t
|
r
|
p
|
y
|
w
|
t
|
s
|
4. Chiffrement par permutation
Soit  
Soit  
Soit   l'ensemble des permutations de l'ensemble des permutations de  
Pour   nous avons : nous avons :
  et et
 
où   et et   est la permutation inverse de est la permutation inverse de  
Exemple :
Si   et et   est la permutation qui envoie ( est la permutation qui envoie (  sur sur   alors le texte clair `' cryptographie '' est chiffré en `'
prctoyprghea `'. alors le texte clair `' cryptographie '' est chiffré en `'
prctoyprghea `'.
5. Chiffrement de Verman
Le chiffrement de Verman est aussi appelé Masque
jetable, en Anglais One- time pad est définit sur les bits,  
Ainsi pour un message binaire   est modifié par une clé est modifié par une clé   binaire de même taille, comme suit: binaire de même taille, comme suit:
 
 
Le chiffrement est incassable si la clé est choisie
aléatoirement, et si cette même clé n'est plus jamais
utilisée.
Exemple:
Soit le message clair `' 101001101110101 `' et la clé
`' 100111101110110 ''
On a :


I.2.1.1.2 Chiffrement par bloc
Un chiffrement par bloc   est une fonction prenant en paramètre une clé est une fonction prenant en paramètre une clé   et un texte clair et un texte clair   d'une longueur finie. Alors d'une longueur finie. Alors   génère un texte chiffré de longueur finie à
partir d'un message clair et d'une clé. génère un texte chiffré de longueur finie à
partir d'un message clair et d'une clé.
Principe:
1. Remplacer les caractères du message par des bits
2. Segmenter cette chaine en blocs de chacun n bits
3. Chiffré successivement chaque bloc:
- Appliquer l'opération logique bit par bit avec une
clé
- Déplacer certains bits du bloc
- Recommencer un certain nombre de fois l'opération
3.
4. Passer au bloc suivant et retourner au point 3
jusqu'à ce que tout le message soit chiffré.
Il existe trois catégories de chiffrement par bloc:
- Chiffrement par substitution
- Chiffrement par transposition
- Chiffrement par produit
1. Chiffrement par substitution
Le chiffrement par substitution consiste à remplacer
les symboles par d'autres symboles.
Exemple:

Fig.1.Exemple de chiffrement par substitution
2. Chiffrement par transposition
Le chiffrement par transposition est un chiffrement dans
lequel est réalisé une permutation sur les symboles de chaque
bloc à chiffré.

Fig.2.Exemple de chiffrement par transposition
Exemple:
3. Chiffrement par produit
Le chiffrement par produit est la combinaison
du chiffrement par substitution et du chiffrement par transposition.
Le chiffrement par substitution ou par transposition ne
garantie pas un niveau de sécurité élevée, on
obtient en combinant ces deux transformations, un chiffrement ayant un niveau
de sécurité élevée.
Les algorithmes les plus utilisés sont: DES, 3DES, AES,
RC5.
Exemple

Fig.3.Exemple de chiffrement par produit
II. 2.1.1.2 Chiffrement par flot
Le chiffrement par flot est un chiffrement par
bloc de longueur égale à un. Cette opération s'effectue
sur chaque caractère, bits. La structure d'un chiffrement par flot
réside sur un générateur de clés qui produit une
séquence des clés   (voir chapitre 3). C'est la qualité du générateur
qui détermine la sécurité du chiffrement par flot. Si la
séquence des clés est infinie et aléatoire, on a un
One-time pad. (voir chapitre 3). C'est la qualité du générateur
qui détermine la sécurité du chiffrement par flot. Si la
séquence des clés est infinie et aléatoire, on a un
One-time pad.
Texte
Clair
Texte
Clair
 
Clé k
Chiffrement
Texte
Chiffré
 
Clé k
Déchiffrement
Fig.3. Schéma du chiffrement à flot
Une erreur dans   n'affecte qu'un bit de n'affecte qu'un bit de   . La perte ou l'ajout d'un bit de . La perte ou l'ajout d'un bit de   affecte tous les bits suivants de affecte tous les bits suivants de   après déchiffrement. après déchiffrement.
| 


