I.6. Résidus
quadratiques
Soit   un entier positif , et un entier positif , et   tel que tel que  
On dit que   est un résidu quadratique est un résidu quadratique   si si 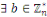  tel que tel que   . .
Si un tel   n'existe pas, n'existe pas,   est un non-résidu quadratique est un non-résidu quadratique   . .
Avec  
- Si   et et  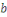 sont des résidus quadratique sont des résidus quadratique   ,alors leur produit est ,alors leur produit est  
- Si   est un résidu quadratique est un résidu quadratique   , et , et   un non-résidu quadratique un non-résidu quadratique   , alors , alors   est un non-résidu quadratique est un non-résidu quadratique  
- Le produit de deux résidus quadratiques   n'est pas nécessairement un résidu quadratique n'est pas nécessairement un résidu quadratique   . .
Théorème 1
Soit   un nombre premier impair. Exactement la moitie des
éléments de un nombre premier impair. Exactement la moitie des
éléments de   sont des résidus quadratiques. sont des résidus quadratiques.
Preuve
Chaque résidu quadratique modulo   est congru à un des est congru à un des  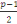 résidus suivants : résidus suivants :

On montre que ces classes des résidus sont tous
distincts. Pour   , ,   si et seulement si si et seulement si   est divisible par est divisible par   , ceci est impossible puisque chacun de , ceci est impossible puisque chacun de   et et   est petit que est petit que   . .
Corollaire 1
Soit   un nombre premier impair, le produit de deux non résidus
est un résidu quadratique. un nombre premier impair, le produit de deux non résidus
est un résidu quadratique.
Théorème 2
Soit   un nombre premier impair. un nombre premier impair.   est un résidu quadratique est un résidu quadratique   si et seulement si si et seulement si   . .
Preuve
Si   , alors par le petit théoreme de Fermat : , alors par le petit théoreme de Fermat :
  . Ceci signifie que . Ceci signifie que   est pair, et est pair, et   . Inversement si . Inversement si   , l'entier , l'entier   est pair. Par le théorème de Wilson, est pair. Par le théorème de Wilson,

Les solutions de   sont donc sont donc   . .
Voici les racines carrés de   pour les 20 premiers nombres premiers de la forme pour les 20 premiers nombres premiers de la forme   : :
|
5
|
13
|
17
|
29
|
37
|
41
|
53
|
61
|
73
|
89
|
97
|
101
|
109
|
113
|
137
|
149
|
157
|
173
|
181
|
193
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Théorème 3
Il y a une infinité des nombres premiers de la
forme  
Preuve
Supposons qu'il y a une finité des nombres premiers
  de la forme de la forme  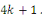 Considérons le produit Considérons le produit  
Notons que   . Puisque . Puisque   est grand que chaque est grand que chaque   , il ne peut pas être premier, ainsi il doit y avoir un facteur
premier , il ne peut pas être premier, ainsi il doit y avoir un facteur
premier   différent de différent de  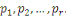 Mais alors modulo ,-1 est une racine. Par le théorème
précédent, Mais alors modulo ,-1 est une racine. Par le théorème
précédent,   doit être de la forme doit être de la forme   , une contradiction. , une contradiction.
Dans la table ci-dessus nous montrons pour les nombres
premiers 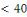  , les résidus quadratiques ainsi que leurs racines
carrés. Il est à noter que les racines carrées entrent en
pairs. Par exemple, l'entrée (2,7) pour le nombre premier 47 serait
interpréter comme disant que les deux solutions de la congruence , les résidus quadratiques ainsi que leurs racines
carrés. Il est à noter que les racines carrées entrent en
pairs. Par exemple, l'entrée (2,7) pour le nombre premier 47 serait
interpréter comme disant que les deux solutions de la congruence  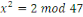 sont sont   Aussi, pour les nombres premiers de la forme Aussi, pour les nombres premiers de la forme   , puisque -1 est un résidu quadratique modulo , puisque -1 est un résidu quadratique modulo   , on liste seulement les résidus quadratiques plus petit que , on liste seulement les résidus quadratiques plus petit que
  . Ceux qui sont plus grands que . Ceux qui sont plus grands que   peuvent être trouvé avec l'aide des racines carrés
de -1. peuvent être trouvé avec l'aide des racines carrés
de -1.
|
3
|
(1,1)
|
|
7
|
(-1,2) (1,1) (2,3) (4,2)
|
|
11
|
(1,1) (3,5) (4,2) (5,4) (9,3)
|
|
13
|
(-1,5) (1,1) (3,4) (4,2)
|
|
17
|
(-1,13) (1,1) (2,6) (4,2) (8,5)
|
|
19
|
(1,1) (4,2) (5,9) (6,5) (7,8) (9,3) (11,7) (16,4)
(17,6)
|
|
23
|
(1,1) (2,5) (3,7) (4,2) (6,11) (8,10) (9,3)
(12,9) (13,6) (16,4) (18,8)
|
|
29
|
(-1, 12) (1,1) (4,2) (5,11) (6,8) (7,6) (9,3) (13,10)
|
|
31
|
(1,1) (2,8) (4,2) (5,6) (7,10) (8,15) (9,3)
(10,14) (14,13) (16,4) (18,7)
(19,9) (20,12) (25,5) (28,11)
|
|
37
|
(-1, 6) (1,1) (3,15) (4,2) (7,9) (9,3) (10,11) (11,14) (12,7)
(16,4)
|
|
|



