Génération des clés pour cryptosystèmes symétriques basée sur les bits pseudo-aléatoires

CHAPITRE I : ELEMENTS DE LA THEORIE DES NOMBRES

I.1.Quelques notions de base

Définition

Un entier est dit premier s'il est différent de et s'il n'admet aucun diviseur positif différent de et .

Un nombre qui n'est pas premier est appelé nombre composé.

Proposition

Il existe une infinité de nombres premiers

Preuve

Montrons par l'absurde. Supposons qu'il n'existe qu'un nombre fini

d'entiers premiers, soit . On peut alors montrer un entier qui n'est divisible par aucun de ces nombres premiers, ce qui est contradictoire compte tenu du fait que cet entier possède un diviseur premier. En effet, considérons : si divisait , alors diviserait , ce qui est absurde.

Lemme de Gauss.

Si des entiers et sont tels que divise et premier avec

alors divise .

Preuve

Comme est premier avec , on peut écrire pour des entiers . Ainsi et comme divise (car il divise ) et (car il divise ), il divise la somme qui vaut .

Théorème (Décomposition en facteurs premiers)

Ce théorème est appelé théorème fondamental de l'arithmétique.

Soit un entier se décompose d'une et d'une seule manière en un produit de nombres premiers. Autrement dit, pour tout entier , il existe des nombres premiers deux à deux distincts et des

entiers strictement positifs , uniquement déterminés à l'ordre près, tels que :

Preuve

Le théorème reste bien vrai pour : il faut choisir , le produit d'aucun entier étant par convention égal à 1.

Commençons par l'existence de la décomposition. On raisonne par récurrence sur . Pour alors ça s'écrit comme un produit de nombres premiers, étant lui-même premier.

Soit un entier. Supposons que tous les entiers strictement inferieurs à s'écrivent comme le précise le théorème et montrons que la conclusion subsiste pour l'entier . Il y a deux cas : soit est premier, soit il ne l'est pas. Le premier cas est vite réglé : premier s'écrit bien comme un produit de nombres premiers. Supposons donc que soit composé.

Ainsi, il s'écrit avec et . Les entiers et relèvent de l'hypothèse de récurrence et on peut écrire :

pour des nombres premiers et Il ne reste plus qu'à effectuer le produit pour conclure.

Montrons l'unicité :

Supposons que Pour certains nombres premiers et .

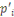On veut montrer que et que les sont égaux aux à l'ordre près.

Raisonnons ensuite par l'absurde. Le nombre premier divise le produit donc par le lemme précédent, il divise .

Or, les diviseurs de (qui est premier) ne sont que 1 et . Comme il ne reste plus que la possibilité On peut alors simplifier l'égalité :

en divisant par ,on obtiens une contradiction et l'unicité est prouvé.