EPIGRAPHE
Si les mathématiques offraient mille exemples
différents d'une même règle, la preuve d'un seul de ces
exemples démontrerait l'exactitude de tous les autres.
« MARY BAKER
Eddy»
DEDICACE
A l'Eternel, Père-Mère Dieu ;
A toute ma famille ;
A ma future épouse.
Je dédie ce travail.
REMERCIEMENTS
Nos sincèrement remerciements au Professeur Dr. MANYA
NDJADI Léonard, qui a bien voulu assurer la direction de ce travail
malgré ses multiples occupations.
Nous pensons également à tous les Professeurs,
Chefs des travaux et Assistants de la Faculté des Sciences en
Générale et du Département de Mathématiques et
Informatique en particulier, pour la formation qu'ils ont assurée durant
toutes ces années d'études.
Nous pensons aussi à tous nos compagnons de lutte.
Enfin, nous remercions très sincèrement toutes
les personnes qui ont contribué d'une manière où d'une
autre pour la réussite de nos études.
INTRODUCTION
Les nombres aléatoires jouent un rôle
important en cryptographie. Ils sont utilisés pour générer
des clés, à chiffrer les messages ou à masquer les
contenus de certains protocoles en les associant avec une séquence
aléatoire. Claude Shannon a montré que dans un système
cryptographique, si la clé est générée de
manière aléatoire et que cette clé n'est plus
utilisée, alors ce système est parfaitement sûr.
On distingue deux types des
générateurs de nombres : les générateurs de
nombres aléatoires non déterministes et les
générateurs de nombres aléatoires déterministes.
Les générateurs de nombres aléatoires non
déterministes sont basés sur des mécanismes physiques tels
que le lancer des dés, roulette, le bruit thermique dans les
résistances de circuits électroniques, etc. La reproduction d'une
séquence du générateur non déterministe est
impossible. Tandis que les générateurs de nombres
aléatoires déterministes sont basés sur des moyens
mathématiques, la séquence est initialisée par une valeur
appelée germe ou graine. La reproduction de la séquence est
possible.
Dans ce travail, nous étudions comment
produire une séquence binaire aléatoire cryptographiquement
sûr, indépendante, imprédictible et équiprobable
à utiliser pour clés au chiffrement par flot ou au chiffrement
de Verman.
Notre travail est subdivisé en quatre
chapitres. Dans le premier chapitre, nous parlons des quelques
éléments de la théorie des nombres. Nous avons beaucoup
plus détaillé la notion des résidus quadratiques qui
constitue l'outil de base du générateur utilisé. Dans le
second chapitre, nous présentons les généralités
sur la cryptographie et ensuite nous présentons l'aspect d'un
système cryptographique parfaitement sûr. Le troisième
chapitre concerne les générateurs pseudo-aléatoires. Nous
avons présenté quelques générateurs
pseudo-aléatoires ; ensuite nous nous sommes concentrés sur
le générateur utilisé : Blum-Blum-Shub. Et enfin, au
quatrième chapitre, nous présentons l'implémentation du
générateur Blum-Blum-Shub et l'interprétation des
résultats obtenus.
[1], [2], [3], [13], [14], [15], [16]
CHAPITRE I : ELEMENTS
DE LA THEORIE DES NOMBRES
I.1.Quelques notions de base
Définition
Un entier 
est dit premier s'il est différent de 
et s'il n'admet aucun diviseur positif différent de
et 
.
Un nombre qui n'est pas premier est appelé nombre
composé.
Proposition
Il existe une infinité de nombres premiers
Preuve
Montrons par l'absurde. Supposons qu'il n'existe qu'un nombre
fini
d'entiers premiers, soit 
. On peut alors montrer un entier qui n'est divisible par aucun de ces
nombres premiers, ce qui est contradictoire compte tenu du fait que cet entier
possède un diviseur premier. En effet, considérons 
: si 
divisait 
, alors 
diviserait 
, ce qui est absurde.
Lemme de Gauss.
Si des entiers 
et 
sont tels que 
divise 
et 
premier avec 
alors 
divise 
.
Preuve
Comme 
est premier avec 
, on peut écrire 
pour des entiers 
. Ainsi 
et comme 
divise 
(car il divise 
) et 
(car il divise 
), il divise la somme qui vaut 
.
Théorème (Décomposition en
facteurs premiers)
Ce théorème est appelé
théorème fondamental de l'arithmétique.
Soit un entier 
se décompose d'une et d'une seule manière en un
produit de nombres premiers. Autrement dit, pour tout entier 
, il existe des nombres premiers deux à deux distincts
et des
entiers strictement positifs 
, uniquement déterminés à l'ordre près,
tels que :
Preuve
Le théorème reste bien vrai pour 
: il faut choisir 
, le produit d'aucun entier étant par convention égal
à 1.
Commençons par l'existence de la décomposition.
On raisonne par récurrence sur 
. Pour 
alors ça s'écrit comme un produit de nombres premiers,
étant lui-même premier.
Soit
un entier. Supposons que tous les entiers strictement inferieurs
à 
s'écrivent comme le précise le théorème et
montrons que la conclusion subsiste pour l'entier 
. Il y a deux cas : soit 
est premier, soit il ne l'est pas. Le premier cas est vite
réglé : 
premier s'écrit bien comme un produit de nombres premiers.
Supposons donc que 
soit composé.
Ainsi, il s'écrit 
avec 
et
. Les entiers 
et 
relèvent de l'hypothèse de récurrence et on peut
écrire :
pour des nombres premiers 
et 
Il ne reste plus qu'à effectuer le produit pour conclure.
Montrons l'unicité :
Supposons que 
Pour certains nombres premiers 
et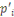 
.
On veut montrer que 
et que les 
sont égaux aux 
à l'ordre près.
Raisonnons ensuite par l'absurde. Le nombre premier 
divise le produit 
donc par le lemme précédent, il divise 
.
Or, les diviseurs de 
(qui est premier) ne sont que 1 et 
. Comme 
il ne reste plus que la possibilité 
On peut alors simplifier l'égalité :
en divisant par 
,on obtiens une contradiction et l'unicité est prouvé.
I.2. La congruence
Définition
Soient 
et 
des entiers, alors on dit que 
est congru à 
modulo
, ce qui s'écrit 
si 
; 
est le module de la congruence.
Propriétés de la congruence
- 
et 
ont le même reste dans la division par 
- 
(réflexivité).
- 
(symétrie).
- 
et 
(transitivité).
- 
et 
I.3. Classes des
résidus
Soit 
Pour chaque entier 
on définit 
, en d'autres termes 
est l'ensemble de tous les entiers qui sont congrus à 
modulo 
. Les autres auteurs appellent 
la classe congruence ou la classe d'équivalence de 
modulo 
Théorème.
Pour
on a : 
.
Preuve
Supposons
pour tout 
. Notons que 
dépends de 
On a deux façons d'écrire l'équation
ci-haut :
ou 
Tout élément 
est une représentation de la classe de résidu 
.
I.4. Ensemble réduit des
résidus
Définition
On défini 
, alors 
est l'ensemble de toutes les classes modulo 
. Nous appelons 
l'anneau des entiers 
.
Addition et multiplication dans 
Pour 
, on a :
et 
Exemple
Pour 
et 
Notons que puisque 
et 
,nous avons 
et 
. Nous pouvons aussi écrire 
et 
I.5. La fonction d'Euler ou
fonction totient
Définition
Pour 
,soit 
le nombre d'entiers premiers avec 
dans l'intervalle 
. La fonction 
est la fonction d'Euler.
Exemple
Pour 
, il y a 
différentes classes de résidu modulo 
; les classes 
et 
ne sont pas premiers avec 
; ainsi seules les classes 
et 
sont premiers avec 
:alors 
.
Si 
est un premier, toutes les 
classes 
sont premiers avec , alors 
Exemple :
|
2
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
12
|
15
|
|
2
|
2
|
4
|
2
|
6
|
4
|
6
|
4
|
4
|
8
|
Théorème (Euler)
Soit 
, alors 
Ceci permet de calculer l'inverse modulaire définit
par :
Exemple
Quel est l'inverse de 
on sait que 
On a 
d'où 
Théorème (Petit théorème
de Fermat)
Soit 
un premier et 
un entier tel que 
alors 
Preuve
Considérons les 
entiers suivants :
ainsi que leurs restes dans la division euclidienne par 
notés :
Ces restes sont compris entre 
En effet, d'après le même de Gauss, si 
divisait un des ces produits 
diviserait 
puisque 
et 
sont premiers entre eux, mais ceci est impossible puisque 
De plus les restes de division de 
par 
sont tous différents. Si on trouvait des restes identiques pour
et 
alors le reste de 
par 
serait nul, ce qui est impossible d'après ce qui
précède.
Notons que ces restes sont donc des entiers compris entre 
et 
.
En multipliant membre à membre les
congruences :
Alors nous obtenons :
Par définition de la congruence, cette
égalité signifie que 
divise 
Or 
ne divise aucun des entiers 
il est également premier avec leur produit 
Ainsi d'après le lemme de Gauss 
divise 
c'est-à-dire 
.
Théorème de Wilson
Si 
est un premier, alors 
Preuve
Considérons la congruence 
Alors 
, ainsi les seules solutions sont 
et 
Donc, pour chaque 
, il existe qu'un inverse unique 
de 
,
. Ainsi lorsque nous groupons des inverses en pairs, nous
obtenons :
Théorème du reste Chinois
Soit 
des entiers et 
des entiers relativement premiers entre eux, alors le
système des congruences
,
admet une unique solution modulo 
Preuve
Soit 
,et considérons 
.Ceci est relativement premier à 
ainsi il existe un entier 
tel que
.
En conséquence, soit 
. Alors 
et 
D'une manière similaire, 
il existe un 
tel que 
et 
,
Alors 
est une solution du système ci-haut.
Soit 
une autre solution, alors 
pour tout 
I.6. Résidus
quadratiques
Soit 
un entier positif , et 
tel que 
On dit que 
est un résidu quadratique 
si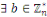 
tel que 
.
Si un tel 
n'existe pas, 
est un non-résidu quadratique 
.
Avec 
- Si 
et 
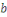sont des résidus quadratique 
,alors leur produit est 
- Si 
est un résidu quadratique 
, et 
un non-résidu quadratique 
, alors 
est un non-résidu quadratique 
- Le produit de deux résidus quadratiques 
n'est pas nécessairement un résidu quadratique 
.
Théorème 1
Soit 
un nombre premier impair. Exactement la moitie des
éléments de 
sont des résidus quadratiques.
Preuve
Chaque résidu quadratique modulo 
est congru à un des 
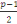résidus suivants :
On montre que ces classes des résidus sont tous
distincts. Pour 
, 
si et seulement si 
est divisible par 
, ceci est impossible puisque chacun de 
et 
est petit que 
.
Corollaire 1
Soit 
un nombre premier impair, le produit de deux non résidus
est un résidu quadratique.
Théorème 2
Soit 
un nombre premier impair. 
est un résidu quadratique 
si et seulement si 
.
Preuve
Si 
, alors par le petit théoreme de Fermat :
. Ceci signifie que 
est pair, et 
. Inversement si 
, l'entier 
est pair. Par le théorème de Wilson,
Les solutions de 
sont donc 
.
Voici les racines carrés de 
pour les 20 premiers nombres premiers de la forme 
:
|
5
|
13
|
17
|
29
|
37
|
41
|
53
|
61
|
73
|
89
|
97
|
101
|
109
|
113
|
137
|
149
|
157
|
173
|
181
|
193
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Théorème 3
Il y a une infinité des nombres premiers de la
forme 
Preuve
Supposons qu'il y a une finité des nombres premiers
de la forme 
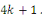Considérons le produit 
Notons que 
. Puisque 
est grand que chaque 
, il ne peut pas être premier, ainsi il doit y avoir un facteur
premier 
différent de 
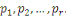Mais alors modulo ,-1 est une racine. Par le théorème
précédent, 
doit être de la forme 
, une contradiction.
Dans la table ci-dessus nous montrons pour les nombres
premiers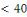 
, les résidus quadratiques ainsi que leurs racines
carrés. Il est à noter que les racines carrées entrent en
pairs. Par exemple, l'entrée (2,7) pour le nombre premier 47 serait
interpréter comme disant que les deux solutions de la congruence 
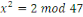sont 
Aussi, pour les nombres premiers de la forme 
, puisque -1 est un résidu quadratique modulo 
, on liste seulement les résidus quadratiques plus petit que
. Ceux qui sont plus grands que 
peuvent être trouvé avec l'aide des racines carrés
de -1.
|
3
|
(1,1)
|
|
7
|
(-1,2) (1,1) (2,3) (4,2)
|
|
11
|
(1,1) (3,5) (4,2) (5,4) (9,3)
|
|
13
|
(-1,5) (1,1) (3,4) (4,2)
|
|
17
|
(-1,13) (1,1) (2,6) (4,2) (8,5)
|
|
19
|
(1,1) (4,2) (5,9) (6,5) (7,8) (9,3) (11,7) (16,4)
(17,6)
|
|
23
|
(1,1) (2,5) (3,7) (4,2) (6,11) (8,10) (9,3)
(12,9) (13,6) (16,4) (18,8)
|
|
29
|
(-1, 12) (1,1) (4,2) (5,11) (6,8) (7,6) (9,3) (13,10)
|
|
31
|
(1,1) (2,8) (4,2) (5,6) (7,10) (8,15) (9,3)
(10,14) (14,13) (16,4) (18,7)
(19,9) (20,12) (25,5) (28,11)
|
|
37
|
(-1, 6) (1,1) (3,15) (4,2) (7,9) (9,3) (10,11) (11,14) (12,7)
(16,4)
|
I.6.1.Le symbole de Legendre
Soit 
un premier. Pour un entier 
, on définit le symbole de Legendre
Lemme 1
Preuve
Ceci est équivalent de dire que, le produit de deux
résidus quadratiques 
(respectivement non-résidu 
) est un résidu quadratique 
, et le produit d'un résidu quadratique 
et un non-résidu quadratique 
est un non résidu quadratique
.
Pour un premier impair 
, 
. Ceci est une répétition du théorème 2 que
-1 est un résidu quadratique 
si et seulement si 
Théorème (Euler)
Soit 
un premier impair. Pour chaque entier 
non divisible par 
Preuve
Supposons que 
est un non-résidu quadratique 
. Les résidus quadratique 
sont partitionnés en pairs en satisfaisant l'équation
. Dans ce cas, 
Cas l'autre sens, si 
est un résidu quadratique, avec 
à part 0, 
, le reste de 
éléments de 
peut être partitionné en pairs satisfaisant 
En résumant, on obtient
Notons qu'en mettant 
on obtient le théorème de Wilson : 
Par comparaison, on obtient une formule pour 
:
I.6.2.Le symbole de Jacobi
Définition
Le symbole de Jacobi est une généralisation du
symbole de Legendre utilisant la décomposition en produit de facteurs
premiers du nombre du dessous. Sa définition est la suivante :
Soit
un entier impair supérieur à 2 et 
la décomposition de n en facteurs
premiers.
Alors, pour tout entier 
, le symbole de Jacobi 
vaut :
Propriétés du symbole de
Jacobi
Le symbole de Jacobi possède de très nombreuses
propriétés :
1. Si 
est premier, le symbole de Jacobi et le symbole de Legendre
sont équivalents.
2. 
3. 
si et seulement si 
et 
ne sont pas premiers entre eux.
4. 
si 
est impair.
5. Si 
alors 
si 
est impair.
6. 
7. 
vaut 1 si 
et -1 si 
8. 
vaut 1 si 
ou 
et -1 si 
ou 
si 
et 
sont impairs, autrement dit 
sauf si 
et 
sont tous deux congrus à 
auquel cas
Les énoncés généraux sur les
résidus quadratiques faisant intervenir le symbole de Legendre ne
s'étendent pas au symbole de Jacobi. Cependant, si 
alors 
n'est pas un résidu quadratique de 
puisque 
n'est pas le résidu quadratique d'un des 
divisant 
.
Dans le cas où 
, il est impossible de dire si 
est un résidu quadratique de 
. Puisque le symbole de Jacobi est un produit de symboles de Legendre,
il y a des cas ou deux symboles de Legendre sont égaux à -1 et le
symbole de Jacobi est égal à 1.
[5], [12], [13], [14], [15], [17], [18], [20]
CHAPITRE II : GENERALITES SUR LA
CRYPTOGRAPHIE
II.1 Définitions
Cryptologie: Science des messages secrets, elle est
composée en deux disciplines: la Cryptographie et la cryptanalyse.
Cryptographie: Art de transformer un message clair en un
message inintelligible par celui qui ne possède pas les clés de
chiffrement.
Cryptanalyse: Art d'analyser un message chiffré afin de
le décrypter.
Chiffrement: Procédé qui consiste à
transformer une donnée (généralement un message texte)
afin de la rendre incompréhensible à toute personne qui ne
connait pas la clé.
Déchiffrement: Procédé qui consiste
à retrouver le texte clair à partir du texte chiffré.
Cryptogramme: Texte chiffré ou message
chiffré.
Clé: Séquence sécrète en bits qui
permettent de chiffrer ou de déchiffrer un message donné.
II.1.1. Définition d'un
système cryptographique
Soit 
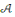un ensemble fini, appelé l'alphabet de
définition.
Soit 
un ensemble appelé l'espace des messages clairs.
Soit 
un ensemble appelé l'espace des messages
chiffrés.
Soit 
un ensemble appelé l'espace des clés.
Chaque
, détermine une injection 
de 
vers
, appelée fonction de chiffrement, 
est appelé clé de chiffrement.
A chaque 
est associé un
, tel que 
dénote une injection de 
vers 
, appelée fonction de déchiffrement, 
est appelé clé de déchiffrement.
Un système cryptographique (cryptosystème)
est un quintuple 
tel que
II.2 Cryptosystème
symétrique et asymétrique
II.2.1 Cryptosystème
symétrique
Les algorithmes de cryptographie
symétrique utilisent les mêmes clés lors du chiffrement et
du déchiffrement.
Considérons un ensemble fini de fonctions de
chiffrement 
et un autre ensemble fini de fonctions de déchiffrement 
, nous avons:
Dans un système symétrique, la
sécurité repose sur la clé. La clé doit rester
inconnue aux tierces personnes. La génération des clés est
choisie d'une manière aléatoire dans l'espace des clés.
L'avantage du cryptosystème symétrique est
basé sur sa rapidité et son désavantage réside dans
la distribution des clés. Pour un système à 
utilisateurs, il y aura 
paires des clés.
II. 2.1.1 Exemples des chiffrements symétriques
II.2.1.1.1 Chiffrement symétriques
classiques
Identifions l'alphabet usuel avec 
par 
et les opérations sont réalisées dans 
1. Chiffrement par décalage
Soit 
Soit 
Et soit 
et 
et 
Ainsi pour 
nous avons le chiffrement de César.
Exemple: Avec
, le texte clair '' politique'', nous obtenons le texte
chiffré '' srolwltxh''
Ce système de chiffrement est facilement cassable
puisque l'espace des clés ne contient que 26 éléments (26
clés possibles).
2. Chiffrement par substitution
Soit 
L'espace des clés est l'ensemble des permutations
de
.
Chacune des lettres est remplacée par une autre lettre
de l'alphabet.
Pour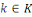 
, nous avons :
et 
où 
et 
est la permutation inverse de 
Le nombre de clés possibles est
, une recherche exhaustive n'est pas possible. Cette méthode est
facilement cassable suite à la fréquence des lettres.
Exemple:
|
a
|
b
|
c
|
d
|
e
|
f
|
g
|
h
|
i
|
j
|
k
|
l
|
m
|
n
|
o
|
p
|
q
|
r
|
s
|
t
|
u
|
v
|
w
|
x
|
y
|
z
|
|
f
|
l
|
h
|
j
|
a
|
r
|
c
|
p
|
u
|
x
|
d
|
i
|
q
|
y
|
m
|
k
|
b
|
t
|
g
|
w
|
n
|
z
|
s
|
v
|
o
|
e
|
Soit la permutation suivante :
Le texte clair ''symétrique'' est chiffré en ''
goqawtubna'
3. Chiffrement du Vigenère
Soit 
Soit 
Soit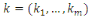 
Alors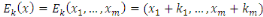 
et 
où 
Le nombre de mots-clés possibles de longueur 
est 
, une recherche exhaustive est impossible.
Exemple:
Soit le mot en clair '' Faculté '' et la clé ''
Ornela ''
|
Texte
claire
|
f
|
a
|
c
|
u
|
l
|
t
|
e
|
|
5
|
0
|
2
|
20
|
11
|
19
|
4
|
|
Clé
|
o
|
r
|
n
|
e
|
l
|
a
|
o
|
|
14
|
17
|
13
|
4
|
11
|
0
|
14
|
|
Texte
chiffré
|
19
|
17
|
15
|
24
|
22
|
19
|
18
|
|
t
|
r
|
p
|
y
|
w
|
t
|
s
|
4. Chiffrement par permutation
Soit 
Soit 
Soit 
l'ensemble des permutations de 
Pour 
nous avons :
et
où 
et 
est la permutation inverse de 
Exemple :
Si 
et 
est la permutation qui envoie (
sur 
alors le texte clair `' cryptographie '' est chiffré en `'
prctoyprghea `'.
5. Chiffrement de Verman
Le chiffrement de Verman est aussi appelé Masque
jetable, en Anglais One- time pad est définit sur les bits, 
Ainsi pour un message binaire 
est modifié par une clé 
binaire de même taille, comme suit:
Le chiffrement est incassable si la clé est choisie
aléatoirement, et si cette même clé n'est plus jamais
utilisée.
Exemple:
Soit le message clair `' 101001101110101 `' et la clé
`' 100111101110110 ''
On a :
I.2.1.1.2 Chiffrement par bloc
Un chiffrement par bloc 
est une fonction prenant en paramètre une clé 
et un texte clair 
d'une longueur finie. Alors 
génère un texte chiffré de longueur finie à
partir d'un message clair et d'une clé.
Principe:
1. Remplacer les caractères du message par des bits
2. Segmenter cette chaine en blocs de chacun n bits
3. Chiffré successivement chaque bloc:
- Appliquer l'opération logique bit par bit avec une
clé
- Déplacer certains bits du bloc
- Recommencer un certain nombre de fois l'opération
3.
4. Passer au bloc suivant et retourner au point 3
jusqu'à ce que tout le message soit chiffré.
Il existe trois catégories de chiffrement par bloc:
- Chiffrement par substitution
- Chiffrement par transposition
- Chiffrement par produit
1. Chiffrement par substitution
Le chiffrement par substitution consiste à remplacer
les symboles par d'autres symboles.
Exemple:
Fig.1.Exemple de chiffrement par substitution
2. Chiffrement par transposition
Le chiffrement par transposition est un chiffrement dans
lequel est réalisé une permutation sur les symboles de chaque
bloc à chiffré.
Fig.2.Exemple de chiffrement par transposition
Exemple:
3. Chiffrement par produit
Le chiffrement par produit est la combinaison
du chiffrement par substitution et du chiffrement par transposition.
Le chiffrement par substitution ou par transposition ne
garantie pas un niveau de sécurité élevée, on
obtient en combinant ces deux transformations, un chiffrement ayant un niveau
de sécurité élevée.
Les algorithmes les plus utilisés sont: DES, 3DES, AES,
RC5.
Exemple
Fig.3.Exemple de chiffrement par produit
II. 2.1.1.2 Chiffrement par flot
Le chiffrement par flot est un chiffrement par
bloc de longueur égale à un. Cette opération s'effectue
sur chaque caractère, bits. La structure d'un chiffrement par flot
réside sur un générateur de clés qui produit une
séquence des clés 
(voir chapitre 3). C'est la qualité du générateur
qui détermine la sécurité du chiffrement par flot. Si la
séquence des clés est infinie et aléatoire, on a un
One-time pad.
Texte
Clair
Texte
Clair
Clé k
Chiffrement
Texte
Chiffré
Clé k
Déchiffrement
Fig.3. Schéma du chiffrement à flot
Une erreur dans 
n'affecte qu'un bit de 
. La perte ou l'ajout d'un bit de 
affecte tous les bits suivants de 
après déchiffrement.
II.2.2 Cryptosystème
asymétrique
Dans un Cryptosystème asymétrique,
chaque interlocuteur possède deux clés, l'une étant
privée (secrète) et l'autre publique, elles sont
mathématiquement liées avec impossibilité de
déduire la clé privée à partir de la clé
publique. La clé privée doit rester secrète tandis que la
clé publique sera distribuer; la clé publique permet de
chiffré un message et la clé privée permet de
déchiffré un message.
Soit un ensemble fini de fonctions de chiffrement
et de déchiffrement 
, pour toutes paires de transformation
, il est impossible (ou très difficile) de trouver le message
clair 
tel que 
Considérons deux interlocuteurs Alice et
Bob qui désirent communiquer ensemble, Bob sélectionne une paire
de clés 
et envoie 
à Alice. Alice après avoir reçu
, envoie un message 
à Bob. Alice calcule 
puis le fait parvenir à Bob. A la réception, Bob calcule
la transformation inverse 
.
II.2.2.1 Exemples de chiffrement asymétrique
Nous distinguons plusieurs méthodes de
chiffrements asymétrique tels que : RSA, CCE, Rabin, El Gamal, Mc
Eliece, Merkle-Hellman, Gold wasser-Micali, etc.
- Méthode RSA
RSA est basé sur le calcul exponentiel; sa
sécurité repose sur la fonction unidirectionnelle et la
difficulté de factoriser un grand nombre en deux facteurs premiers.
a. Génération des
clés
- choisir aléatoirement deux grands premiers distincts
et 
approximativement de la même taille
- calculer 
et 
- choisir un entier 
aléatoire dans 
tel que 
- calculer l'unique 
tel que 
- La clé publique est 
et la clé privée est 
b. Chiffrement
Soit le message 
à chiffrer,
Calculer 
c. Déchiffrement
est déchiffré en calculant : 
Exemple :
Considérons 
et 
très petits, 
et 
Nous avons :
On peut choisir 
(7 est premier avec 40)
On calcule 
tel que :
On obtient :
Clé publique : 
Clé privée : 
Soit le texte clair à chiffrer `' IMAGE `'
1. Chiffrement
- I : 
- M : 
- A : 
- G : 
- E : 
2. Déchiffrement
- 14 : 
- 52 : 
- 1 : 
- 13 : 
- 15 : 
La distribution des clés ne pose pas problème,
chaque utilisateur possède une paire de clés. L'utilisateur
après avoir chiffré le message du destinataire ne sera plus
capable de déchiffrer son propre message, seul le détenteur de la
clé gardée secrète pourra déchiffrer le message. On
utilise le chiffrement asymétrique aussi pour chiffrer les nombres
aléatoires qui servent de clés secrètes pour les
algorithmes de chiffrement symétrique; on l'utilise également
pour assurer l'authenticité d'un message.
II.3. Sécurité
d'un système cryptographique
On distingue deux approches fondamentales dans l'étude
de la sécurité d'un cryptosystème : la
sécurité parfaite de Shannon et la sécurité
calculatoire.
II.3.1. Notions
élémentaires de probabilité
Définition classique de
probabilité
Considérons une expérience aléatoire 
possédant la symétrie mutuelle et 
un événement quelconque relatif à 
La probabilité de l'événement 
est le nombre 
, où 
est le nombre de cas favorables à 
et 
le nombre total des éventualités rattaché à
l'épreuve.
Définition axiomatique de
probabilité
Une mesure de 
définie sur un espace probabilisable 
, l'application 
qui vérifie les 3 axiomes suivants :
1. 
2. Si 
pour 
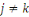
alors 
;
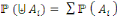3. 
Le triplet 
est appelé espace probabilisé.
Probabilité conditionnelle
Soient 
et 
deux événement telque 
On appelle probabilité conditionnelle de
l'événement 
par rapport à l'événement 
, ou encore la probabilité de A étant donné
B :
La probabilité conditionnelle nous permet de calculer
la probabilité de l'intersection :
Indépendance stochastique des
événements
Deux événements 
et 
sont indépendant si
si 
et 
et que les événement 
et 
sont indépendants alors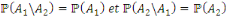 
Les événements 
sont indépendants si
Théorème de Bayes
Si 
est un système complet d'événements et 
est un événement quelconque.
Supposons que 
puisse se produire qu'en combinaison avec l'un des
événements de 
, c'est-à-dire 
.
, alors on a la formule de Bayes
Preuve. Voir [12]
II.3.2. La
sécurité calculatoire
La sécurité calculatoire est basée sur la
mesure de la quantité de calcul nécessaire pour casser un
système. On dit qu'un procédé est sûr au sens de la
théorie de la complexité si le meilleur algorithme pour le casser
nécessite 
opérations où 
est un nombre beaucoup trop grand pour que cet algorithme soit
applicable en pratique. Dans la pratique, on dit souvent qu'un système
est sûr si la meilleure attaque connue ne peut se faire avec une
quantité raisonnable de temps de calcul. Le problème de cette
approche c'est qu'un cryptosystème peut être sûr pendant un
moment puis ne plus l'être lorsque l'on découvre un algorithme
plus efficace.
II.3.3 La
sécurité parfaite de Shannon
Claude Shannon en 1949 dans son article
intitulé « Communication Theory of Secrecy
System » introduit la notion des systèmes cryptographiquement
sûrs, qui eut une influence considérable sur l'étude de la
cryptographie.
Considérons l'ensemble fini 
de textes clairs, l'ensemble fini 
de textes chiffrés, l'ensemble fini 
de clés.
Supposons qu'une clé 
est utilisée une et une seule fois.
Notons que l'ensemble des textes clairs 
est muni d'une probabilité 
ainsi que l'ensemble des clés 
muni d'une probabilité 
Supposons que les clés sont choisies
indépendamment des textes clairs.
Ainsi les deux probabilités 
et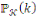 
induisent une probabilité sur l'ensemble des textes
chiffrés 
Nous pouvons calculer la probabilité 
que le texte chiffré 
soit transmis.
Pour une clé 
, notons que 
représente l'ensemble des textes chiffrés avec la
clé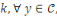 
nous définissons
, qui est l'ensemble de toutes les clés possibles qui permettent
d'obtenir le chiffré 
Nous avons alors la probabilité de 
donnée par :
L'événement « le texte chiffré
est 
» n'est possible que si 
ou 
.
La probabilité d'avoir le « texte
chiffré 
» est la somme de toutes les probabilités mutuelles
les événements « le texte clair est 
» et « la clé est 
» sont supposés indépendants, alors cette
probabilité est égale à 
.
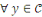
et 
,nous pouvons calculer la probabilité conditionnelle 
(la probabilité que
soit le texte chiffré en sachant que 
est la texte clair) par 
où 
.
En utilisant le théorème de Bayes, nous
avons :
II.3.4. Système
cryptographique parfaitement sûr
Un système cryptographique parfaitement sûr si on
a :
En d'autres termes : la probabilité que le texte clair soit
sachant que le texte chiffré est 
est égale à la probabilité que le texte clair soit
Dans ce cas le texte chiffré n'apporte aucune information sur le
texte clair.
Lemme 1
Un système cryptographique vérifiant la
propriété de sécurité parfaite et tel que 
alors :
Démonstration
Fixons 
tel que 
, on a :
, d'après le théorème de Bayes :
donc 
ceci signifie qu'il exite au moins une clé 
telle que 
.
Par suite 
, comme 
est injective on a :
Théorème
Un système cryptographique vérifiant 
ainsi que 
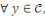
il est à la sécurité parfaite si et seulement si
les deux conditions suivantes sont réalisées :
a. Toutes les clés sont équiprobables,
b. Pour chaque 
et chaque 
existe une unique clé 
vérifiant 
.
Démonstration
Supposons les conditions vérifiées. Alors
, on a successivement :
= 
,
= 
D'autre part pour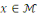 
et 
, puisqu'il n'y a qu'une clé 
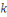qui vérifie 
on a :
En appliquant le théorème de Bayes :
La sécurité est donc parfaite.
Réciproquement, supposons que la sécurité
est parfaite. Comme dans le lemme précédent, on montre que pour
chaque couple 
, il existe une clé 
telle que
.
Pour 
fixé on a donc 
ce qui montre que pour 
fixé l'ensemble des 
est de cardinal
. Ces 
sont donc distincts deux à deux et pour chaque 
la clé 
vérifiant 
est unique.
Pour deux clés 
et 
, comparons 
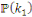et 
. Pour cela fixons 
et désignons 
et 
les uniques éléments de 
vérifiant 
et 
(chaque 
est injective et donc ici bijective.
Par le théorème de Bayes, et à la
sécurité parfaite on obtient :
Le même calcul peut être fait avec 
Ce qui prouve que 
Les clés sont donc équiprobables.
Exemple
Le chiffrement de Verman ou le one-time-pad ou encore le
masque jetable vérifie les conditions du théorème
précédent. C'est un système parfaitement sûr. Il
utilise une clé secrète très longue (séquence
aléatoire binaire) où chaque bit est indépendant des
autres et une probabilité 
d'être 
ou 
. Une nouvelle clé est utilisée à chaque
chiffrement, la clé est aussi longue que le texte clair. La construction
de cette clé aussi longue sera l'objet de notre chapitre suivant.
[4], [6], [7], [8], [9], [10], [11], [14] , [17],
[19],[20], [21], [22], [23], [24],[25], [26],
[27]
CHAPITRE III :
GENERATEURS PSEUDO-ALEATOIRES
Définition
Soit 
un ensemble fini appelé espace d'états, un
générateur pseudo-aléatoires est défini
par :
,
et l'état s'évolue selon : 
, 
l'état initial 
s'appelle germe ou graine.
Autrement dit un générateur
pseudo-aléatoire est un procédé qui, à partir d'une
initialisation de taille fixée appelée germe ou graine, engendre
de manière déterministe une séquence de très grande
longueur.
Cette séquence consiste à imiter une
séquence de variables aléatoires.
Définition
Une séquence binaire 
constituée de 
bits est dite aléatoire lorsque les 
bits sont indépendants, imprédictibles et
équiprobables.
Un générateur de nombres
pseudo-aléatoires et un générateur de bits
aléatoires ont pour buts de générer une séquence
de mots aléatoires. Les mots appartiennent à l'alphabet fini 
Dans le cas d'un générateur de bits aléatoires,
l'alphabet est de dimension 2 c'est.-à-dire. 
On distingue plusieurs générateurs
pseudo-aléatoires tels que Générateur à congruence
linéaire, Générateur
carré-médian, Générateur à
congruence additive, Générateur de type «
multiplication avec retenue », Générateur de Blum-Blum-Shub
ou Générateur quadratique etc....
III.1. Exemples de quelques
générateurs pseudo-aléatoires
1. Générateur à congruence
linéaire
Le générateur à congruence
linéaire est un algorithme inventé par Lehmer en 1948. C'est une
suite définie par la relation suivante :
où 
est appelé multiplicateur, 
est l'incrément, et 
est le module (le maximum plus un des nombres de la suite). La suite
est initialisée par le germe 
. Tous ces nombres sont positifs.
Pours avoir une période maximale, les paramètres
suivants doivent être respecté avec 
non nul :
- 
et 
doivent être premiers entre eux
- 
doit être multiple de 
, 
nombre premier diviseur de 
Exemple : 
Avec
, la suite est :
2. Générateur
carré-médian
Le générateur carre-médian
est construit de la manière suivante : on
élève au carré un nombre de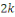 
-chiffres et on prend les
-chiffres du milieu du produit (de 
chiffres). Il fut historiquement l'un des premiers
générateurs utilisés mais c'est un très mauvais
générateur ; si l'on tombe sur zéro tous les autres termes
de la suite seront nuls et de manière générale sa
période est trop courte.
Exemple :
|
12
|
14
|
19
|
36
|
29
|
84
|
5
|
2
|
0
|
0
|
|
0144
|
0196
|
0361
|
1296
|
0841
|
7056
|
0025
|
0004
|
0
|
0
|
3. Générateur à congruence
additive
Le générateur à congruence additive est
défini de la manière suivante :
Soient 
des entiers naturels, pour 
Pour 
on obtient la suite de Fibonacci.
Cette méthode a deux inconvénients :
1. Il nécessite de stocker 
nombres.
2. Si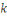 
est petit les nombres présentent une forte
corrélation.
4. Générateur Blum-Blum-Shub
Définition
L'ensemble des résidus quadratiques 
est noté par 
et l'ensemble des non-résidus quadratiques 
est noté par 
Définition
Un entier de Blum est un produit de deux premiers distincts
dont tous deux congrus à 3 modulo 4.
Proposition
Soit 
un entier de Blum et soit 
un carrée de 
alors 
possède quatre racines carrées dont une (et une
seule) est un carrée de 
. Cette racine est appelée racine principale de 
Preuve
Comme le nombre de racines carrées de 
est quatre, on peut écrire que ces racines carrées
sont : 
dans 
(qui s'identifie à 
grâce au théorème des restes chinois), seul le
couple formé par les deux racines principales de 
modulo 
et modulo 
est un carré modulo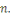 
Définition
Le générateur Blum-Blum-Shub est définit
de la manière suivant :
Soit 
un entier de Blum tel que 
et 
On choisit un nombre 
d'une manière aléatoire tel que 
, alors le germe de la suite est calculé par : 
. Et les autres termes de la suite sont définis par :
Exemple
Soit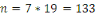 
et 
. Alors 
. Les autres termes sont : 
. La sortie en bit : 1, 0, 0,1, avec 
.
III.2.
Générateurs cryptographiquement sûrs
Du point de vue de la formalisation de la
sécurité d'un générateur pseudo-aléatoire,
il faut d'une part définir le problème de sécurité,
d'autre part il faut définir ce qu'est l'attaque. Un attaquant est
considéré comme un algorithme réalisable qui sort un
résultat relatif au problème de sécurité
posé. La notion d'algorithme réalisable est extrêmement
importante car comme on travaille souvent sur des situations finies on peut
décrire théoriquement des algorithmes qui cassent la
sécurité des systèmes. Mais ces algorithmes ne sont pas
réalisables en pratique à cause de la durée des calculs.
On cherche donc à assurer la sécurité calculatoire.
Nous allons utiliser le générateur de
Blum-Blum-Shub qui est cryptographiquement sûr.
Définition
Soit 
un paramètre, appelé paramètre de
sécurité.
Définition
Soit 
une fonction en 
telle que 
Un générateur pseudo-aléatoire est une fonction
calculable en temps polynomial en 
de 
dans
.
Lorsque nous composons la distribution uniforme sur 
avec 
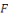, nous obtenons une distribution sur 
appelée la distribution induite par
.
Définition
Soit 
un générateur pseudo-aléatoire et 
. Un 
-distingueur pour 
est un algorithme 
probabiliste polynomial 
tel que
où 
signifie que les bits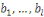 
sont choisis selon la distribution induite par 
et 
qu'ils sont choisis selon la distribution uniforme.
Définition
Un générateur pseudo-aléatoire 
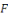est dit cryptographiquement sûr s'il n'existe d' 
-distingueur pour 
que pour des fonctions 
négligeables (par rapport au paramètre 
III.3. Extrapoleurs
Définition
Soit 
un générateur pseudo-aléatoire,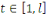 
un entier, et 
. On note 
des bits choisis suivant la distribution induite par 
sur 
. Un extrapoleur d'ordre 
pour 
d'avantage 
est un algorithme probabiliste polynomial calculant le bit 
en fonction des précédents 
avec probabilité 
.
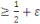
Ainsi à partir d'un extrapoleur 
d'ordre 
et d'avantage 
pour 
, nous obtenons un 
-distingueur 
pour 
comme suit :
La probabilité que 
soit égal à 
vaut au moins 
lorsque 
est choisi selon la distribution induite par 
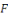et vaut 
lorsque 
est choisi selon la distribution uniforme.
Théorème de Yao
Un générateur pseudo-aléatoire 
est sûr si et seulement si, pour chaque 
entier, il n'existe pas d'extrapoleur pour 
autres que d'avantage négligeable.
Preuve
D'après la construction de distingueur à partir
d'un extrapoleur, 
ne peut être sûr que si tout extrapoleur n'est que
d'avantage négligeable.
Inversement, supposons que 
ne soit pas sûr. Pour
, notons 
la distribution sur 
selon laquelle les 
premiers bits 
sont produits par 
et les autres 
sont choisis uniformément au hasard. Ainsi,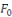 
est la distribution uniforme et 
celle induite par
. Par hypothèse, il existe un 
-distingueur 
pour 
telle que 
ne soit pas négligeable, c'est-à -dire
Donc il existe un 
et une fonction 
pas négligeable tels que
Considérons l'algorithme 
suivant :
Nous allons montrer que 
est un extrapoleur d'avantage 
pour 
On a tout d'abord 
et
.
On a aussi 
donc
Pour alléger les notations, nous posons 
et 
. La probabilité que 
prévoie le bit 
correctement est donnée par
III.4 Sécurité du
générateur Blum-Blum-Shub
III.4.1 Problème de la
résiduosité quadratique
Le problème de la résiduosité quadratique
est comme suit : étant donné un nombre 
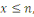il faut déterminer si 
est un carré modulo 
ou non.
Lorsque 
un premier, le problème sera résolu en temps polynomial
en la taille de 
par le calcule du symbole de Legendre 
Puisqu'on sait que 
est un résidu quadratique modulo 
si et seulement si son symbole de Legendre est 1.
Lorsque 
est un nombre composé dont on ne connait pas la factorisation,
aucun algorithme polynomial en la taille de 
sera disponible pour résoudre le problème de la
résiduosité quadratique.
Supposons que 
où 
et 
deux premiers distincts. Si la factorisation de 
est connue alors le problème de la résiduosité
quadratique se résout en temps polynomial en cherchant tout simplement
si 
et 
sont des résidus quadratiques par le calcul de leurs symboles de
Legendre. Mais lorsqu'on ne connait pas la factorisation de 
,il sera impossible de résoudre le problème en temps
polynomial.
Un autre problème s'oppose à savoir
l'extraction d'une racine carrée modulaire : sachant qu'un nombre
est un résidu quadratique 
, comment déterminer un nombre 
tel que 
Nota
Soit 
un entier de Blum, 
un élément de symbole de Jacobi 1 et 
son carré modulo 
On sait que 
, et possède 4 racines carrées dont deux ont pour symbole
de Jacobi 1 : 
et 
. Une et une des deux valeurs 
et 
est dans 
En outre 
et 
ont des parités différentes. Autrement dit, si on
disposait d'un algorithme capable de déterminer avec une
probabilité de succès non négligeable, à partir de
quelle est la parité de la racine carrée qui est
elle-même un carré, on pourrait déterminer avec la
même probabilité de succès si 
est un carré ou non.
III.4.2 Détails sur la
sécurité du générateur Blum-Blum-Shub
On va noter 
l'ensemble des entiers 
de symbole de Jacobi 
valant 1.
Les nombres d'éléments de 
est donné par :
Et aussi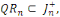 
alors 
Comme 
est un entier de Blum, par conséquent l'application 
de 
dans lui-même définie par 
est une bijection.
Soit 
la taille de l'entier 
qui servira de paramètre de sécurité. On dispose
d'un algorithme probabiliste polynomial en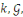 
qui étant donné en entrée le paramètre de
sécurité 
construit au hasard un environnement de travail, c'est-à-dire
un entier de Blum 
de taille 
(pour notre cas). Soit la fonction 
d'élévation au carrée modulo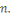 
On note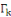 
l'ensemble des environnements possibles.
Soit 
un algorithme probabiliste polynomial en 
dont l'entrée est le paramètre de sécurité
le nombre 
et un élément 
de 
et la sortie un bit 
dont on souhaite qu'il détermine avec succès si 
est un élément de 
ou non.
Considérons les expériences :
L'avantage de l'attaquant 
est définie par :
Le problème de la résiduosité quadratique
est sûr par l'hypothèse de la difficulté de la
résiduosité quadratique, c'est-à-dire que pour tout
attaquant polynomial 
et pour tout entier 
Autrement dit tout attaquant polynomial a un avantage qui est une
fonction négligeable du paramètre de sécurité
.
Les algorithmes d'extrapolation
Soit 
le paramètre de sécurité, 
un entier de Blum de taille 
et 
le générateur des nombres pseudo-aléatoire
définie par :
, où pour tout 
le calcul de 
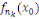se fait de la façon suivante :
1. La bijection 
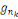de 
dans lui-même définie par 
permet de calculer 
2. Chaque 
donne un bit 
3. 
Lemme
Soit 
et 
un algorithme probabiliste polynomial qui étant donnés
les bits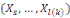 
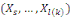prédit le bit 
avec un avantage non négligeable. Alors on fournit en
entrée de cet algorithme probabiliste polynomial, les 
bits 
d'un 
, il prédit le bit 
avec le même avantage non négligeable.
Preuve
Du fait 
est une bijection, la loi de probabilité du terme calculé
est la même que la loi de probabilité du terme tiré
au sort dans 
qui sert de germe 
Pour prouver que le générateur BBS est
sûr, on montrera que s'il existe un extrapoleur probabiliste polynomial
qui prédit le bit 
avec un avantage non négligeable, alors, il existe un algorithme
probabiliste polynomial qui possède un avantage non négligeable
pour résoudre le problème de la résiduosité
quadratique.
Soit 
un algorithme polynomial probabiliste, dont les entrées sont
et dont l'avantage de prédiction du bit 
n'est pas une fonction négligeable de 
. Construisons l'algorithme 
dont les entrées sont (
où 
et sort un bit.
Par le nota précédent, on voit que l'algorithme
ainsi construit, a un avantage 
non négligeable pour le problème de la
résiduosité quadratique. En tenant compte de la difficulté
de la résiduosité quadratique, on conclut que le
générateur Blum-Blum-Shub est sûr.
CHAPITRE IV :
IMPLEMENTATION ET INTERPRETATION DES RESULTATS
Dans ce chapitre nous présentons
l'implémentation de l'algorithme de Blum-Blum-Shub et
l'interprétation des résultats obtenus.
Voici l'algorithme de Blum-Blum-Shub :
Générer 
et 
Faire 
Choisir 
Calculer le germe : 
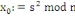
La séquence est 
Sortie est : 
Nous avons implémenté l'algorithme de
Blum-Blum-Shub en c++ à partir du compilateur DEV-C++.
Voici les codes du programme :
#include <iostream>
#include<conio.h>
using namespace std;
int main()
{
int i,B;
unsigned long long int X,n,p,q,s;
cout<<endl<<"Entrer la valeur de p:";// p un
entier congru à 3 modulo 4
cin>>p;
cout<<endl<<"Entrer la valeur de q:";//q un
entier congru à 3 modulo 4
cin>>q;
n=p*q;//ceci calcule l'entier de blum
cout<<endl<<" L'entier de Blum
est:"<<n;
cout<<endl<<"Entrer la valeur pour calculer
le germe:";//Le germe,un entier premier avec n
cin>>s;
X=(s*s);
X=X%n;//calcule du germe
for(int i=1;i<=10000;i++)
{
X=(X*X)%n;//
B=X%2;//calcule les bits de la séquence
cout<<B;
}
getch ();
}
Nous savons que l'entier de Blum est défini par 
, où 
et 
sont tous deux congrus à 3 modulo 4. En d'autres termes 
et 
. Nous prenons 
et
petits, avec 
et 
.
Alors 
et 
, alors 
,prenons 
, puisque 
,la séquence comportera 10.000 bits.
La séquence était produite en 1,20 secondes dans
un ordinateur dont les caractéristiques sont :
Ø Dual Core , Processeur AMD Sempron (tm) 2.10 GHz
Ø 3.00 Go de RAM
Voici la sequence :
011100001010110011000110100111000001011000001000000101010101110101101111110111110100011110100100100011000100100010010010000001111100010111010101111110100001010101101011101100001111111001101100100000110111000000101010011101010101111100100010111110111111101010111111001110100101111010000001101110001101100010111101000100110000010000101001110110110101000011010011100000001111110110100110110101010100100110100111011010100101001001111011001111010001000101000111110100011000110110000110010110001000000101101010111001110101010001100100110111100110110111011101101000100110011000011100101001000101011010010011011101000001100001111111010000001010101001000110100010111101000100111001010101011010001100011101011111010000011000110101111011001010001110111100101101101111101110110100101000011001111010000011110100001000111100000010011111111100010111011111100010001001001110010111010101001111000101010011001010000111010000000011011010110101011000111100011111100100110110000010101100101111000111000111111110100001110100000101110100011110001001011100100001111001101100101100001101011100010111011000001011100000101010111000100111001010100110101111011111001111001101000000000101111111101000000001001110011010010011011110110110011111100001001010000111000111000110100111001010100011111100011010100111110001110010011000101001110101111111100011110001111001010001011011000001110001111110000010011011001000011101000001110001101101010010010000011101111111101100101100110000000011100011110100101101010010010000100010110010010101010101011000110100100111111111010001010101000011001010111100111111000011000001110011010011111011000111100000101101011010011000010000000111011100011100110011011011010001100101001011010001011101110111101100100010100000001100111011111000100011000100110000110001110010000000011000101100000100110100101010101011010011001011010111111100011001011011011110000110101111101011111000000000101000000100011100100000111110010100111010110101101011011000010001001111011100100010001010010000000010010010000001001111011010101101011111000001111110000010100011101011011110011011000111011011111100011011001000101001001010110011010011110101111101011111010110111101011011110011100011001100101010011010010111100101100111010001000100000011100100110010001111000010010010100110001001100000110010100011010001101000010111000100100001000010001000001010111010110001100010001101100000001010011100101000011011000001011001001011011111000100101010010011111101101110010110100010110101111101100111010010101111110110111011111100110100010011111010010011010010000011110000001110000011100000010011010000101000101110001001001101100000000001001110110100110001000101100011000110010000100100010001001000101100110001010010100111011100010001110100111100011101100001011110100001110100001100000110010011110001100000010000000111000001001000111010001011101010110000010011010000100010101001001100111011100010011011010000100001001110111111000100011100111010011000000110000101001111111101111100001010111000100000101111000111101010011000110111010010100110101010110110001010011001101000001101001100111101101110001101011111101011100100000101101101010010111001110011001111110011110000110111000100111010100001111111101110011000110110000101110111101000001110100100010101101110101011101100101001111100110100100011100110111001010011010110010100111100010010011010111000111101010110011100010101111101011111111111101101010100011010000000110101101101001100000010111001101100010100100001001110001000101000001100110010010011011000000011011000100001100110111110111111111000100101100000011001111110110110110110011010111001000010100100110000111100101011100111011001100110000110000111000101100111000100010111011101001110110101011001111010101111001000101000110111000011000111110111100011000010010101101100001111100100111001100110101000001011010000000010110101000111011110111011001101001011010110111111000000001110000011110001110011010101100101001000001111100011111101010000010101101001010100100101110011001000111101111100011100010011100001011001101001101100100111110111001011111001001011011111010111000100011000110000100000000100000110001110011010111001111101101000001101111000100101111000111010001110000001111101110100011100101101010010010000000110010101110011001011101010011000010101000100001111101001110111010010010000011011100000001110000001110110010101000101010101001001001011001111001111001011110000001100010010110001100111101110011000111001000010011000111111010100110101101101001101111000001100100010110110110001010010010101101100101100000000101001000001111110001110001101100000100101110000101001001010111110000110110101000111111011110010000101011111010110100110101011011110100101110110001100100100000000010011001100000110011111011010000001111011101001100111001010000100001000000000011101101001011110011100000010000011001001010111111010011100000010010111101110001111110011010011010000001000111100000100010001101111011100110011000010011001010011001000011001010101110110010001100001011000010011100101101111111110011010000101010000111001100000111110101011011011001000101011011001010100110101110110100001111111
001111101111001001111111001110110011110101001010010100111010010100111110011001100000001000010010101000111000111111100000110100111001010110101101110111110110111110111001010101011101011010101101010011000000010011000101100110011010111110110011011000111111011000110000111111100110100111010110011100111100001001111010000100101000111010111000101100110000100000111010001000010100000000000111000110101011100011110000111100111010001001100001110100001011111010010100011011111000110011010110001110101000011100000101011110011001100010000011110010101011001111011100110011001001100000110000101110101001110110010111101011100011011001001010010111010111100110000011101100010010010010111111011011101111111110101111110100000010110110100111111001111001001111000110111111100101011111111111010001000100011100101011100000001101111101100001001001010001101110010101001110100111001110110101001111110011101111101110111010110001000101001010101100001111101101100000001110010000000000000001011100001010011101110110001100101101111011101110111101101001110100010010111110101101110011001011000000001011011101100100101011010111111111100001101000100010110110000000011010000110010011000111010011010000111110001000100110111010110000111011001101010111001010001110001111000100100001110110011101111101010000000010000001110000100010001111001000101110111111010110011010101100000101101111111010010100000011010100100101000001010110100111100000100010010000111001011001111010110111010110101011011010111011000101011011000000101111110011001101111010100110010101001000101101101001101000000000110101011111001101110101101000101111010100010000001110100100111110111010110110101010111101000111101010101100100110011010000011111000011011100100111001111111001101000110111010100110011110100100001010111100111100001101010010000001010011010010110011000010100000001111000101100111010000000000001000011111000100001111001111001010011110001001000010101000000001011101010110111100110001100010011110111001111100000111100100100010100010001111100100001100011100111011011101011001010010101101001001011100111000110011000011010011101101110111000011000000010000110001100110100111010001011111100000011001000110111110001110010010101111011111010111110101010111111100111001100100000010010011000011111000000010011100000101111010111111110000001010010110011110111110110101101001000111011011000110010011110110101110011010011100111000000011110000001010001101001001010000001111110000010111100110000011100111011001111101010011111110011110101110010010001001111110011000100001010010101101111110010010111100011011100001001110011000110001001010111011100100110110110001110001001000000100101111110101111000011000001111100100001110111001111010111110010101100101011110101111010000011011000001000111101011000101100100001011000001100011110010101010111000101001000111010000100011000010001101110001010111001111101011010101010000000000101100100010110011000100100000000101011001111001100100000010101000001010010101100000111111000001001010000000000010111100100001010110101100101100101101100001011101001011101110001110110000000010101101101101110000010101011100001000100001100110010101011100101111011111001101110111001011101111000001101011110110001101100010110001111110111010101110011101011111101101101111000001000111011000011011010011110101110100100001101100110001110000011101000011010010111001001101100110110011011010101100000110001111010110001110111011110011100110000111000110000011010011110100101100101111010001101111100111111111100110111111110001010001111101110010101100110101001111101001111010110011110001001010100101101110100111010001100001110111001011010010100111101110001011010000110101010000001010010011001010111010111111110110010101011000101000000101101010100001010010111101000110111000010000001010010110101010000101001101011100010010011100111000011110010001110101100001101001111111100011011000010111011001101010110010101011110010011101101001000101110100001000100010001011101001100101010001110011000011001101010101010110011010111000110001101011011100000111100111001100010111001011101011001100111011000011000001111001100000110000011101001010000010110010110000000101111000101100010111000010111110100000100001010100010111001110001001010011101010100100011011010110110001000100111111111110011000111001100011010011100111111010011011001101011101111010011011010011001100010000001111100110110111111000100001010110011100111011111110101110000101000111011010101011000001100010010110000111011100010110101010100101111110001111101110100011010111011010001110010011011111101010011011011100111101011100000001010100110111010110001011101110101011000100101110111100011010000110000111110110010111111000011111010101111100001110111011110010011100010100101101101011001101001110001101111110110001100001010100100011000111110110010011100110101111011100110011010010011111011110100101101010100011010000100100011011001110011101000011010000100111010101111000000100010011100100110001101100111010111010011001100101011110111010010101101011111101001010110000101100000100101111011000000
La séquence binaire aléatoire produite peut
être utilisée pour clés au chiffrement par flot ou au
chiffrement de verman enfin de répondre aux conditions du
théorème de Claude Shannon sur la sécurité parfaite
: une nouvelle clé est tirée à chaque chiffrement, la
clé est aussi longue que le texte clair, toutes les clés sont
équiprobables.
Si nous avons un message 
de 
bits à chiffrer, on considère les 
premiers bits de la séquence aléatoire
générée qui constituent un mot 
et on fait l'opération « ou exclusif bit à
bit » entre le message et la partie de la séquence
aléatoire considérée comme clé. C'est-à-dire
Il est à noter que l'expéditeur et le
destinateur ont le même générateur. A la réception,
le destinateur extrait de la même façon les 
premiers bits de la séquence aléatoire et calcule ensuite
. Les deux interlocuteurs jettent la partie 
utilisée et peuvent effectuer une nouvelle transaction en
procédant de même avec le reste de la clé.
Voici le schéma illustrant l'utilisation de la
séquence binaire générée avec un message quelconque
binaire 
Fig.4. Schéma illustrant l'utilisation de la
séquence binaire produite
Clé
Partie utilisée K
Nouvelle clé
Message clair 
Message chiffré 
1
0
0
0
1
0
0
1
0
0
1
0
1
0
1
1
0
0
.
.
.
.
1
1
1
0
0
0
0
1
0
.
1
1
1
1
0
0
0
1
0
1
1
CONCLUSION
Il existe plusieurs générateurs
pseudo-aléatoires mais tous ne sont pas utiliser pour l'usage
cryptographique, la plupart sont utilisés en simulation. Nous avons
étudié dans le présent travail la façon dont un
générateur produit une séquence complètement
déterministe à partir d'une valeur initiale appelé germe.
Nous avons montré que le générateur
Blum-Blum-Shub est cryptographiquement sûr suite au problème de
la résiduosité quadratique et à la difficulté de
décomposer un grand nombre en deux facteurs premiers. Même si le
générateur Blum-Blum-Shub est cryptographiquement sûr, il
faudra respecter les paramètres de base pour générer une
bonne séquence sinon la séquence à produite serait un
échec du point de vue cryptographique.
Enfin, la génération des séquences
aléatoires cryptographiquement sûres est un défi chez les
cryptographes, mathématiciens, informaticiens et ingénieurs.
BIBLIOGRAPHIE
I. Ouvrages
[1] Hans Delfs, Helmut Knebl,
Introduction to Cryptography-Principles and Applications, 2nd ed,
(Springer, 2007) WW
[2] Johannes Buchmann, Introduction
à la cryptographie, Dunod, Paris, 2006
[3] J.S. Milne, Algebraic Number
Theory, version 3.02, April 30,2009
II. Articles
[4] Lenore Blum, Manual Blum, and Michael
Shub. A Simple Unpredict
able PseudoRandom Number Generator. SIAM Journal on
Computing,
15(2):364.383, May 1986.
[5] C.E. Shannon. Communication theory of
secrecy systems. Bell Systems Technical journal, 28 : 656-715, 1949.
[6] Pascal Junod. Cryptographic Secure
Pseudo-Random Bits Generation : The Blum-Blum-Shub Generator. August
1999
[7] Andrey Sidorenko and Berry Schoenmakers.
Concrete Security of the Blum-Blum-Shub
[8] Pseudorandom Generator, Lecture
Notes in Computer Science 3796 (2005) 355-375. Springer-Verlag.
[9] Robert Rolland,
Sécurité des générateurs
pseudo-aléatoires
[10] Kaustubh Gawande and Maithily Mundle,
Various implementations of Blum Blum Shub pseudo-random sequence
generator
[11] Robert Rolland,
Sécurité des générateur de Blum Blum Shub,
partie I, 22 mars 2008
III. Cours
[12] MANYA NDJADI L.,
Probabilité, Note de cours, deuxième graduat
Mathématiques, Université de Kinshasa, 2006-2007.
[13] Olivier MARKOVITCH ,
sécurité informatique , note de cours en format
imprimable,UNIVERSITÉ LIBRE DE BRUXELLES
[14] Francois ARNAULT, Théorie des
nombres et cryptographie, Note de cours de D.E.A en format imprimable,
Univérsité de Limoges, France, 2002
[15] Renaud Dumont, Cryptographie et
Sécurité informatique, note de cours en format imprimable,
Université de Liège, Faculté des Sciences
Appliquées, 2009 - 2010
[16] W. Edwin Clark, Elementary Number
Theory, Note de cours en format imprimable, University of South Florida,
Departement of Mathmatics, revised December 17, 2002,
IV.Thèses
[17] Renaud SANTORO, Vers des
générateurs de nombres aléatoires uniformes et gaussiens
à très haut débit, Thèse en Traitement du
signal et télécommunications, école doctorale Matisse ,
Université de rennes 1,soutenue jeudi 17 décembre 2009.
[18] Duong Hi?u PHAN,
Sécurité et efficacité des schémas
cryptographiques, École normale supérieure,
Département d'informatique, présentée et soutenue
publiquement le 16 septembre 2005
[19] Andrea Röck, Quantifying
Studies of (Pseudo) Random
Number Generation for Cryptography, Thèse de
Doctorat présentée à L'ÉCOLE POLYTECHNIQUE pour
obtenir le titre de DOCTEUR EN SCIENCES Spécialité Informatique
soutenue le 18 mai 2009
V. Sites internet
[20] http://www.acrypta.fr
[21]
http://en.wikipedia.org/wiki/Random_number_generation#cite_ref-0
[22]
http://en.wikipedia.org/wiki/Hardware_random_number_generator
[23] http://www.random.org/randomness/
[24]
http://en.wikipedia.org/wiki/Pseudorandom_number_generator#cite_note-0
[25]
http://fr.wikipedia.org/wiki/Blum_Blum_Shub
[26]
http://en.wikipedia.org/wiki/Lagged_Fibonacci_generator
[27]
http://fr.wikipedia.org/wiki/Linear_congruential_generator
TABLE DES
MATIERES
EPIGRAPHE
Erreur ! Signet non
défini.
DEDICACE
ii
REMERCIEMENTS
iii
INTRODUCTION
1
CHAPITRE I : ELEMENTS DE LA
THEORIE DES NOMBRES
3
I.1.Quelques notions de base
3
I.2. La congruence
5
I.3. Classes des résidus
5
I.4. Ensemble réduit des résidus
6
I.5. La fonction d'Euler ou fonction totient
6
I.6. Résidus quadratiques
9
I.6.1.Le symbole de Legendre
12
I.6.2.Le symbole de Jacobi
13
II.1 Définitions
15
II.1.1. Définition d'un système
cryptographique
15
II.2 Cryptosystème symétrique et
asymétrique
16
II.2.1 Cryptosystème symétrique
16
II.2.2 Cryptosystème asymétrique
22
II.3. Sécurité d'un système
cryptographique
25
II.3.1. Notions élémentaires de
probabilité
25
II.3.2. La sécurité calculatoire
27
II.3.3 La sécurité parfaite de
Shannon
27
II.3.4. Système cryptographique parfaitement
sûr
28
CHAPITRE III : GENERATEURS
PSEUDO-ALEATOIRES
31
III.1. Exemples de quelques
générateurs pseudo-aléatoires
32
III.2. Générateurs
cryptographiquement sûrs
34
III.3. Extrapoleurs
35
III.4 Sécurité du
générateur Blum-Blum-Shub
38
III.4.1 Problème de la
résiduosité quadratique
38
III.4.2 Détails sur la
sécurité du générateur Blum-Blum-Shub
39
CHAPITRE IV : IMPLEMENTATION
ET INTERPRETATION DES RESULTATS
43
CONCLUSION
50
BIBLIOGRAPHIE
51
TABLE DES MATIERES
54
