Planification et gestion du parc de transport au niveau de la SARL Ibrahim et fils

2

Rappels théoriques

2.1 Introduction

Pour des besoins dans les chapitres ult'erieurs, nous rappelons quelques notions de fonctions et d'ensembles convexes ensuite nous pr'esenterons les 'el'ements essentiels et quelques r'esultats classiques concernant les systèmes de files d'attente, de r'egression et on terminera par des notion de simulation.

2.2 Optimisation des fonctions convexes[7]

D'efinition 2.1. Un ensemble non vide X c Rⁿ est dit convexe, si V A E [0, 1] et V x, x0 E X on a :

(1--A)x0+Ax E X. (2.1)

D'une facon 'equivalente, on peut dire que X est convexe si pour deux points quelconques x0 et x pris dans X, le segment [x0, x] tout entier est contenu dans X.

Exemple 1. La figure ci-dessous représente un ensemble convexe et un ensemble non convexe :

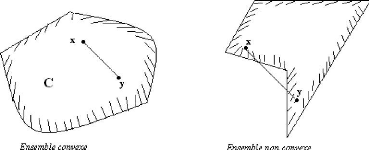
FIG 2.1

Exemple 2. Soit H={x E Rⁿ | cx=d} un hyperplan de Rⁿ avec c E Rⁿ, d E R. si y E H et z E H, on vérifie que x=Ay + (1 - A)z satisfait cx=d pour tout A E [0, 1]. Ainsi H est convexe; sa dimension est n-1 si c =6 0.

Exemple 3. Soit H={x E Rⁿ | cx = d} un demi espace de Rⁿ avec c E Rⁿ, d E R. On vérifie de même que H est convexe; sa dimension est n.

D'efinition 2.2. Soit X c Rⁿ un sous-ensemble convexe. Une fonction f : X ? R est convexe, si V A E [0, 1] et V x, x0 E X on a :

Af(x) + (1 - A)f(x0) = f((1 - A)x0 + Ax). (2.2)

Si nous avons une inégalitéstricte pour x =6 x0 et A E ]0, 1[, nous dirons que f est strictement convexe.

La figure suivante représente le schéma classique d'une fonction convexe.

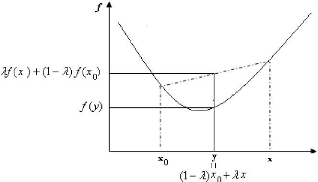
FIG 2.2

D'efinition 2.3. Soit f : X -* R une fonction différentiable sur un ensemble ouvert convexe X c Rⁿ. Alors, f est convexe si et seulement si V x, x0 E X, l'une des deux conditions suivantes est vérifiée :

(i) f(x) - f(x0) ~ [Vf(x0)]^t (x - x0),

(ii) (x - x0)^t [Vf(x) - Vf(x0)] ~ 0,

o`u Vf(x) désigne le gradient de f en x0.

D'efinition 2.4. Soit X c Rⁿ ; f :X -* R. On dit que x^* est un minimum local de f sur X s'il existe un c > 0 tel que f(x) ~ f(x^*) pour tout x appartenant a` B(x^*, c).

x* est un minimum global de f sur X si f(x) ~ f(x^*) pour tout x dans X.

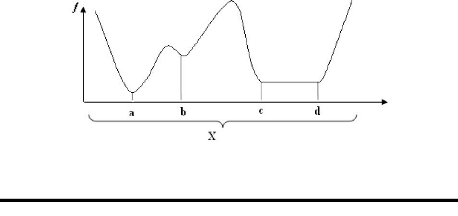
FIG 2.3

23

Sur la figure 2.3, a, b et les points de [c, d] sont des minima locaux de f sur X. Seul a est un minimum global de f sur X.

Remarque 2.1. Notons qu'on peut toujours ramener un problème de minimisation a` un

problème de maximisation et inversement en utilisant l'égalité: maxf(x) = --min

_x?X(--f(x)).

x?X

Theorème 2.1. [13] Soit X c Rⁿ un ensemble convexe et f : X ? R convexe sur X ; l'ensemble M des points o`u f atteint son minimum est convexe; de plus, tout minimum local est un minimum global.

Preuve. S'il n'y a pas de minimum, M est vide et donc convexe. Soit x0 = min

x?Xf(x) ;

M = {x | f(x) -- x0 < 0} est convexe car f(x) -- x0 est encore une fonction convexe.

Soit x^* un minimum local de f et supposons qu'il existe un y E X avec f(y) < f(x^*). Sur la droite d'efinie par {z | z = Ay + (1 -- A)x^*, 0 < A < 1}, voir la figure 2.4, on a :

f(Ay + (1 -- A)x^*) < Af(y) + (1 -- A)f(x^*) < f(x^*)

Ceci contredit le fait que x^* est un minimum local (car on peut trouver un point z voisin de x^* avec f(z)< f(x^*)). Donc, il existe pas de tel y et x^* est bien un minimum global.

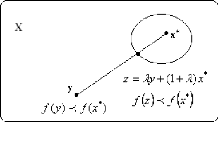
FIG 2.4

Definition 2.5. Soit X c Rⁿ un sous-ensemble convexe. Une fonction f : X ? R est concave, si V A E [0, 1] et V x, x0 E X on a :

Af(x) + (1 -- A)f(x0) < f((1 -- A)x0 + Ax). (2.3)

Si nous avons une inégalitéstricte pour x =6 x0 et A E ]0, 1[, nous dirons que f est strictement concave.

Remarque 2.2. Tout les résultats vus dans cette section peuvent aussi être formulés en termes de fonctions concaves, il suffit alors de changer les sens des inégalités et de remplacer les minima par des maxima.