4.4 Approche par minimisation d'une fonction convexe
[8]
4.4.1 Introduction
Quand les décisions doivent être prises de
manière séquentielle, les conséquences de chaque
décision n'étant pas toujours parfaitement
maàýtrisées mais pouvant être anticipées
jusqu'àun certain point avant que la prochaine décision ne soit
prise. Le but recherchéest la minimisation d'un coàut (ou la
maximisation d'un profit) associéa` la suite de décisions
retenues et a` leurs conséquences.
En effet, le désir d'un coàut immédiat aussi
faible que possible doit généralement être
évaluéa` la lumière du danger de coàuts futurs
élevés[9].
Cette approche consiste a optimiser la taille m de
véhicule que doit avoir l'entreprise et elle nous permettra d'atteindre
le meilleur compromis possible entre les coàuts engendrés par la
flotte ( un coàut fixe pour chaque véhicule
possédéy compris les coàuts d'amortissement et d'assurance
et un coàut variable pour l'utilisation de chaque camion) et les
coàuts engendrés par le manque de camions (coàuts de
location de camions ). On considère ce problème comme un
problème de gestion de stock d'un parc de camions.
4.4.2 Le coàut fixe, coàut variable et
coàut de location
L'entreprise supporte un coàut fixe de Cf DA par jour pour
chaque véhicule possédé(ceci, qu'il roule ou
qu'il reste au parc), il inclut entre autre l'amortissement et l'assu
rance.
D'autre part l'utilisation de chaque véhicule de l'entreprise
crée un coàut dit variable journalier de Cv DA.
Le coàut variable journalier d'un camion peut
être déterminer en incluant la consommation en gasoil durant
l'opération de livraison, la marge sur les salaires des chauffeurs, les
frais de mission, une marge pour les pièces de rechange qui est
fixée par l'entreprise. Pour un camion loué, le coàut Cl
inclut le coàut fixe et le coàut variable.
4.4.3 Coàut total journalier d'un parc de m
camions
Le coàut journalier C est une fonction de la demande
aléatoire en camions D. Une statistique faite sur un historique
récent a permis d'évaluer la probabilitép(w) d'avoir
besoin de w camions pour un jour donné.
la probabilitép(w) d'avoir besoin de w camions pour un
jour donnésuit une loi de poisson.
w P(ë = 48.66);
-ëëk
k! .
e
p(w = k) =
Exprimons C lorsque la taille de la flotte, n, est connue .
- Si D > m C=(Cf + Cv)m + (D - m)Cl
- Si D < m C=Cfm + CvD
Le calcul de
l'espérance mathématique du coàut total, soit C(m), est
alors :
|
E(C) = C(m) =
|
m
E
ù=0
|
(Cfm + Cvù)p(ù) +
|
8
E
ù=m+1
|
[(Cf + Cv)m + (ù - m)Cl]p(ù).
|
On va calculer la variation des coàuts A(m) = C(m) - C(m -
1) (m=1)
|
A(m) = C(m) - C(m - 1) =
|
m
E
ù=0
|
(Cfm + Cvù)p(ù) +
|
8
E
ù=m+1
|
[(Cf + Cv)m + (ù - m)Cl]p(ù)
|
-
|
m-1E
ù=0
|
(Cf(m - 1) + Cvù)p(ù) -
|
8
E
ù=m
|
[(Cf + Cv)(m - 1) + (ù - m +
1)Cl]p(ù);
|
|
=
m-1E
ù=0
(Cfm + Cvù)p(ù) + (Cfm +
Cvm)p(m)
8
+ E
ù=m+1
|
[(Cf + Cv)m + (ù - m)Cl]p(ù) + Cf
|
m-1E
ù=0
|
p(ù) -
|
m-1E
ù=0
|
(Cfm + Cvù)p(ù)
|
|
-
|
8
E
ù=m
|
[(Cf + Cv)m + (ù - m)Cl]p(ù) +
(Cv + Cf - Cl)
|
8
E
ù=m
|
p(ù);
|
|
= (Cf + Cv)mp(m) +
|
8
E
ù=m+1
|
[(Cf + Cv)m + (ù - m)Cl]p(ù)
|
|
+Cf
|
m-1E
ù=0
|
p(ù) -
|
8
E
ù=m+1
|
[(Cf + Cv)m + (ù - m)Cl]p(ù) - (Cf +
Cv)mp(m)
|
|
+(Cv + Cf - Cl)
|
8
E
ù=m
|
p(ù);
|
|
A(m) = C(m) - C(m - 1) = Cf + (Cv - Cl)
|
8
E
ù=m
|
p(ù).
|
A(m) représente la différence de l'espérance
du coàut total journalier pour un parc de m et m - 1 camions.
Si on calcule A(m + 1) - A(m), on aura :
A(m + 1) - A(m) = C(m + 1) - C(m) - C(m) + C(m - 1)
|
A(m+1) - A(m) = Cf + (Cv - Cl)
|
8
E
ù=m+1
|
p(ù) - Cf - (Cv - Cl)
|
8
E
ù=m
|
p(ù) = (Cl - Cv)p(m).
|
La fonction de variation A(m) est croissante puisque dans les
conditions normales de rentabilitede l'entreprise, on a : Cl > Cv
+ Cf. Si les p(ù) sont strictement positifs pour tout ù, elle
sera màeme strictement croissante.

On a V m e N, A(m + 1) - A(m) > 0, et donc elle peut s'ecrire
sous la forme : C(m + 1) - C(m) - C(m) + C(m - 1) > 0 soit : C(m) <
C(m + 1) + C(m - 1)
Ceci entraine la convexitede C(m), et on peut l'expliquer par
le schema classique d'une fonction convexe. L'axe d'abscisses correspond au
nombre de camions et les ordonnees a` l'esperance du coàut total
journalier.
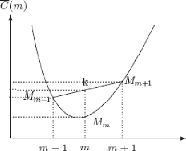
FIG. 4.7 - Schema classique d'une fonction convexe
Sur le schema ci-dessus on constate que l'ordonnee du milieu k de
la corde Mm-1Mm+1 est au dessus du point Mm d'abscisse m et
d'ordonnee C(m). Tel que :
(m, C(m2 +1)+ Cm-1) ).
(
- k correspond au point de coordonnees
- Les ordonnees des points respectivement Mm-1,
Mm et Mm+1 correspond au esperances mathematiques des
coàuts totaux journalier pour respectivement un parc de m - 1, m, et m +
1 camions.
L'objectif de ce qu'on a fait jusqu'àpresent est la
minimisation de C(m) qui est une fonction convexe. Donc la fonction objectif a`
minimiser est :
|
min C(m) =
|
m
E
ù=0
|
(Cfm + Cvù)p(ù) +
|
8
E
ù=m+1
|
[(Cf + Cv)m + (ù - m)Cl]p(ù).
|
Pour determiner le minimum de la fonction C(m), on partant de
l'etat que l'entreprise poss`ede un seul camion et on calcule la variation des
coàuts A(m) avec un
pas d'un camion. La procedure continue jusqu'`a ce que le signe
change et on arràete.
L'abscisse correspondante au dernier point o`u
la variation est negative est le point optimal.
Le point minimum de la fonction coàut total journalier
sera le point d'ordonnee C(m*) correspondante a` l'abscisse
m* qui verifie les deux conditions :
1. A(m*) = 0
2. A(m* + 1) = 0
Calculons m* qui satisfait ces conditions :
|
A(m*) = 0 ? A(m*) = C(m*) -
C(m* - 1) = Cf + (Cv - Cl)
|
8
E
ù=m*
|
p(ù) = 0.
|
|
1 -
|
m*-1E
ù=0
|
p(ù) =
|
m*-1
Cf X
?
Cl -
Cv
ù=0
|
p(ù) =
Cl - (Cv + Cf) .
Cl - Cv
|
Pour la deuxième condition :
|
A(m* + 1) = 0 ? A(m* + 1) =
C(m* + 1) - C(m*) = Cf + (Cv - Cl)
|
8
E
ù=m*+1
|
p(ù) = 0.
|
1 -
m*
E
ù=0
C
m*
%-"N
f '
p(ù) = ?
Cl - Cv
ù=0
p(ù) = Cl - (Cv + Cf)
l - Cv .
C
Pour trouver m*, il suffit de cumuler les
probabilites p(ù) et dès que le cumul d'epasse la
C/-(Ct, #177;C f )
valeur le m correspondant n'est autre que la valeur optimale
m*.
| 


