3.5.1.2 Ajustement des données avec le test de
Kolmogorov-Smirnov
Soit un 11324-échantillon constituédes
données concernant les temps de service chaque jour durant les dix
derniers mois (Aoàut jusqu'au mois de Mai), on veut tester si la loi de
Y est une loi exponentielle, donc on va tester :
H0 » La loi exponentielle est la loi de Y» Contre
H1 »La loi exponentielle n'est pas la loi de Y».
On partitionne le domaine des valeurs de Y en 7 classes, le
tableau suivant nous donne l'effectif empirique de chaque classe, les
probabilités théoriques rattachées, l'effectif
théorique, le pourcentage cumuléthéorique et
observé.
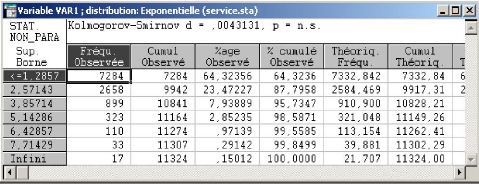
FIG. 3.7 - Tableau représentant les paramètres
calculés
Le plus grand écart entre la distribution empirique et la
distribution théorique (loi exponentielle) est :
D = max |Fn(x) - F0(x)| = 0.0043,
tel que F0 est la fonction de répartition de la loi
exponentielle. Dans la table de Kolmogorov-Smirnov on a :
1.30
d(N, a) = d(11324, 0.05) = v11324 = 0.0122,
avec N représente la taille de l'échantillon et a
le niveau de signification.
1.30
D = max |Fn(x) - F0(x)| = 0.0043 < d(N, a) =
d(11324, 0.05) = v11324 = 0.0122.
On accepte que que la loi régissant les durées de
service est exponentielle de paramètre u = 0.8111.
Le schéma suivant nous montre le graphe d'ajustement par
la loi exponentielle. En rouge l'histogramme de la loi exponentielle, en bleu
l'histogramme des données observées.
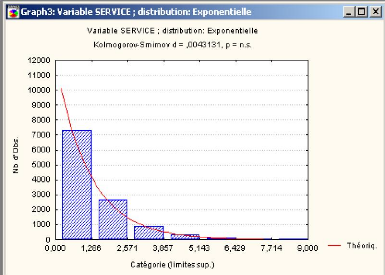
FIG. 3.8 - Graphe d'ajustement par la loi exponentielle
Conclusion
Le test de Kolmogorov-Smirnov nous confirme que la loi
régissant les durées de service est exponentielle. Donc on peut
affirmer que la loi de Y est une loi exponentielle de paramètre u =
0.8111.
| 


