Planification et gestion du parc de transport au niveau de la SARL Ibrahim et fils

République Algérienne Démocratique et Populaire

Ministère de l'Enseignement Supérieur et de la Recherche Scientifique

UniversitéA/Mira de Béja·ýa

Facultédes Sciences et des Sciences de l'Ingéniorat

Département de Recherche Opérationnelle

M'EMOIRE DE FIN D''ETUDES

En vue de l'obtention du diplôme

d'Ingénieur d''Etat en Recherche Opérationnelle

TH`EME

OPTIMISATION ET GESTION DU PARC DE

TRANSPORT AU NIVEAU DE LA SARL

ifri



Présentépar : Devant le jury :

Mr Karim MEGHAR Président : Mme F. AOUDIA

Mr Karim MEKHNECHE Promoteurs : Mr H. SLIMANI

: Mlle Z. AOUDIA

Examinateurs : Mme K. ADEL

: Mme N. HALIMI Invité: Mr A. BELKADI

Remerciments

Nous remercions vivement nos promoteurs Mr H. SLIMANI et Mlle Z. AOUDIA et nous tenons a` leur exprimer notre gratitude pour avoir acceptéde nous encadrer et pour l'honneur qu'ils nous ont fait en assurant le suivi scientifique et technique du présent mémoire. Nous les remercions pour leur grande contribution a` l'aboutissement de ce travail, et pour s'être montrés disponibles.

Nous remercions aussi Mr A. BELKADI d'abord, d'avoir acceptéde nous encadrer au sein de l'entreprise IBRAHIM & Fils ifri et puis pour sa disponibilitéet ses conseils tout au long de notre stage, sans oublier de remercier toute l'équipe du département transport plus particulièrement Kamel et Ami Rachid.

Nos remerciements vont aussi a` Mme F. AOUDIA pour l'honneur qu'elle nous fait en acceptant de présider le jury de ce mémoire.

Nos remerciements s'adresse également a` Mme N. HALIMI et Mme K. ADEL pour l'honneur qu'elles nous font en acceptant d'examiner ce mémoire.

Nous remercions tous ceux qui ont contribuéde prés ou de loin a` l'élaboration de ce travail.

* Mes três chêres parents;

* Mes três chêres frêres : Fatah, Zahir et Tarik;

* Mes grands parents;

* Va Amirouche et sa famille;

* Mes oncles et tantes Da Rachid, Da Kacem, Da Kamal, Na Houria et toutes leurs familles;

* Vadda, Na Nouara, Da Hamid et toute la grande famille;

* Ma promotion; * Mes amis (es); * T ous ceux qui m'ont aiméet qui ne méritent pas d'être oubliés.

Karim MEKHNECHE.

* La mémoire de mon pêre que la miséricorde et la gràace de dieu lui soient attribuées; * DADA Ameur mon oncle que j'ai toujours considérécomme pêre;

* Ma três chêre mêre;

* Ma soeur Ouarda;

* Mon frêre Youcef;

* Ma petite copine Souhila;

* Mes amis (es).

Karim MEGHAR.

Table des matières Introduction Générale 1 Présentation de la sarl ifri			1 6 8
1.1	Présentation de l'entreprise		8
	1.1.1	Introduction	8
	1.1.2	Organigramme de l'entreprise	10
	1.1.3	Les différents services et directions et leurs ràoles	11
		1.1.3.1 La direction	11
		1.1.3.2 Service qualité	11
		1.1.3.3 Secrétariat	11
		1.1.3.4 Service informatique	11
		1.1.3.5 Direction commerciale	11
		1.1.3.6 Direction finance et comptabilité	12
		1.1.3.7 Direction des ressources humaines	12
		1.1.3.8 Service sécurité	12
		1.1.3.9 Direction technique	12
		1.1.3.10 Direction de production	12
		1.1.3.11 Direction des achats	13
		1.1.3.12 Direction des moyens généraux	13
		1.1.3.13 Direction logistique	13
1.2	Récolte des données		13
	1.2.1	Données récoltées auprès du service commercial	13
	1.2.2	Données récoltées auprès du service production	14
	1.2.3	Données récoltées auprès du service parc :	14
	1.2.4	Données concernant les coàuts de transport	15
1.3	Réseau de distribution		16

1.3.1 Système de distribution 16

1.3.2 Système de distribution de la sarl ifri 18

1.4 Gestion des chauffeurs 20

1.5 Position du problème 20

2 Rappels théoriques 21

2.1 Introduction 21

2.2 Optimisation des fonctions convexes 21

2.3 Le formalisme des flles d'attente 25

2.4 Analyse mathématique des systèmes des flles d'attente 27

2.4.1 Modélisation des systèmes de flles d'attente 27

2.4.1.1 Modèles markoviens 28

2.4.1.2 Processus de naissance et de mort 28

2.4.1.3 Processus de naissance pur 28

2.4.1.4 Processus de mort pur 28

2.4.1.5 Modèles non markoviens 29

2.4.2 Analyse opérationnelle des systèmes de flles d'attente 29

2.4.2.1 Les caractéristiques de performance 30

2.4.2.2 La formule de Little 30

2.5 Quelques systèmes de flles d'attente 31

2.5.1 Le système M/M/1 31

2.5.1.1 Régime transitoire 31

2.5.1.2 Régime stationnaire 31

2.5.1.3 Quelques caractéristiques 32

2.5.2 Le système M/M/m 33

2.5.2.1 Régime stationnaire 33

2.5.2.2 Quelques caractéristiques 34

2.6 La régression 34

2.6.1 La régression linéaire 34

2.6.1.1 Test sur les paramètres du modèle 35

2.6.1.2 Test sur la validitédu modèle 35

2.6.2 La régression non linéaire 36

2.6.2.1 Estimation des paramètres du modèle 36

2.6.2.2 Validation du modèle 37

2.7 Notions de simulation 37

2.7.1 Déflnition de la simulation 37

2.7.2 Les 'etapes de la simulation 37

2.7.3 Problème du temps en simulation 38

2.7.3.1 M'ethode synchrone ou simulation par horloge 38

2.7.3.2 M'ethode asynchrone ou simulation par 'ev'enements . . . 38

2.7.3.3 Avantages et inconv'enients de la simulation 38

2.7.4 G'en'eration de variables al'eatoires 39

2.7.4.1 La m'ethode d'inversion 39

2.7.4.2 La m'ethode de rejet 39

2.7.4.3 La m'ethode de composition 40

2.8 Conclusion 40

3 Tests et ajustements 41

3.1 Introduction 41

3.2 Tests d'ajustement 41

3.2.1 Test de Khi-deux 41

3.2.2 Test de Kolmogorov-Smirnov 42

3.3 Estimation par intervalle de confiance 43

3.4 Loi r'egissant le besoin journalier en camions 43

3.4.1 Application au cas d'Ifri 43

3.4.1.1 Ajustement des donn'ees avec le test de Khi-deux 44

3.4.1.2 Ajustement des donn'ees avec le test de Kolmogorov-Smirnov 45

3.4.2 Intervalle de confiance du besoin en camions 47

3.4.3 Conclusion 49

3.5 La distribution du temps al'eatoire de service des camions 49

3.5.1 Application au cas d'Ifri 50

3.5.1.1 Ajustement des donn'ees avec le test de Khi-deux 50

3.5.1.2 Ajustement des donn'ees avec le test de Kolmogorov-Smirnov 52 3.6 Conclusion 54

4 D'etermination du nombre de camions 55

4.1 Introduction 55

4.2 Probl'ematique 55

4.3 Approche par files d'attente 55

4.3.1 Modèle avec file 55

4.3.1.1 Interpr'etation des r'esultats 58

4.3.1.2 Conclusion 59

	4.4	4.3.2 Modèle sans file (avec d'ecouragement) 4.3.2.1 Interpr'etation des r'esultats 4.3.2.2 Conclusion Approche par minimisation d'une fonction convexe	59 63 63 64
		4.4.1 Introduction	64
		4.4.2 Le coàut fixe, coàut variable et coàut de location	64
		4.4.3 Coàut total journalier d'un parc de m camions	64
		4.4.4 Application au cas d'ifri	67
		4.4.5 Conclusion	68
5	Estimation du nombre de chauffeurs		69
	5.1	Introduction	69
	5.2	Analyse du système	69
	5.3	Repr'esentation du système	70
	5.4	Pr'esentation du modèle de simulation	71
		5.4.1 Description du simulateur	71
		5.4.2 Entr'ees du programme	72
		5.4.2.1 Les donn'ees en entr'ee	72
		5.4.2.2 Entr'ees g'en'er'ees	72
	5.5	G'en'eration de nombre al'eatoires	72
		5.5.1 G'en'eration de la demande suivant une loi de poisson	72
		5.5.2 G'en'eration de la loi de service exponentielle	76
	5.6	Pr'esentation de l'organigramme de simulation	78
		5.6.1 Les variables caract'eristiques du simulateur	78
		5.6.2 Modèle avec file	80
		5.6.3 Modèle sans file	81
		5.6.4 D'eroulement de l'algorithme de simulation (modèle avec file) . . . .	82
	5.7	V'erification et validation du modèle de simulation	84
	5.8	Mise en oeuvre du simulateur	86
		5.8.1 Modèle avec file	86
		5.8.1.1 Interpr'etation des r'esultats	88
		5.8.1.2 Variation du nombre de camions	90
		5.8.2 Modèle sans file	93
		5.8.2.1 Interpr'etation des r'esultats	95
		5.8.2.2 Variation du nombre de camions	96
	5.9	Conclusion	103

Conclusion Générale 104

Bibliographie 106

A Données récoltées 108

B Présentation de l'application 115

C Modèles de régression 118

La raison primaire de d'evelopper une architecture d'entreprise est de soutenir les affaires en fournissant les moyens, la technologie fondamentale et la structure des processus pour une strat'egie optimale. Ce qui fait une strat'egie commerciale moderne et r'eussie.

Les responsables d'entreprises d'aujourd'hui savent que la gestion efficace et l'exploitation d'information sont la cl'e du succès des affaires et sont un moyen indispensable pour cr'eer un avantage concurrentiel.

En ce qui concerne la SARL ifri, et plus exactement le d'epartement transport, les g'erants de l'entreprise ont fait appel a` leur exp'erience et ont opt'e pour une strat'egie bien pr'ecise pour le système de transport qui consiste a` donner un d'elai forfaitaire, suivant la distance a` parcourir, aux chauffeurs de camions pour desservir leurs clients.

Les moyens de transport actuels ne r'epondent pas a` l'attente des usagers. Les besoins de transport sont d'etermin'es principalement par le style de fonctionnement d'une soci'et'e, et le mode de fonctionnement contemporain exige une modification des moyens de transport existants. Cela explique que des problèmes toujours croissants se posent dans ce domaine. Par cons'equent il faut intensifier les recherches pour une am'elioration et une innovation dans le domaine des transports.

Lors de notre pr'esentation a` l'entreprise ifri en tant que «sp'ecialistes» d'aide a` la d'ecision, la première chose qui nous a 'et'e propos'e est de d'eterminer le nombre de camions que devra avoir l'entreprise, vu qu'elle pr'evoyait d'en acheter d'autres. Puisque les camions sont neufs, l'entreprise veut les exploiter au maximum contrairement aux chauffeurs qui se reposent 2 jours après avoir cumul'e 5 jours de travail. Alors le problème de d'eterminer le nombre de chauffeurs a 'et'e soulever puisque se sont deux problèmes qui se complètent. Donc si l'entreprise prend la d'ecision d'avoir un nombre pr'ecis de camions, combien de chauffeurs, compte tenu de la demande al'eatoire et de la strat'egie adopt'ee par l'entreprise,

devrait elle avoir?

La mod'elisation de l'architecture des processus de fonctionnement permet d'am'eliorer les performances de l'entreprise et de d'efinir la strat'egie optimale afin de l'aligner sur la strat'egie commerciale. Mod'eliser les processus de fonctionnement permet de comprendre comment fonctionne une organisation et de concevoir des modifications sur sa future architecture.

L'objectif principal de cette 'etude et de d'eterminer les moyens a` employer pour que l'entreprise puisse les exploiter au maximum de façon a` couvrir la demande de sa clientèle d'une part et de minimiser les coàuts engendr'es d'une autre part. Pour chaque problème pos'e, nous avons 'elaborer une ou plusieurs approches pour aboutir aux r'esultats recherch'es. Nous avons 'egalement inclus le calcul de quelques caract'eristiques du système notamment le nombre de camions inoccup'es par unit'e de temps et le nombre de chauffeurs inoccup'es par unit'e de temps et d'autres comme le nombre de clients et le temps d'attente dans le système pour donner une aide a` la d'ecision aux g'erants de l'entreprise.

Dans le but de r'ealiser ces objectifs, cinq chapitres lui sont consacr'es et sont r'epartis comme suit :

Nous avons commenc'e, dans le premier chapitre, par une pr'esentation de l'entreprise ifri avec un bref historique et un aperçu sur ses diff'erents d'epartements et services puis on l'a clôtur'e avec une position du problème.

Le deuxième chapitre est consacr'e aux rappels th'eoriques sur les outils math'ematiques n'ecessaires pour la mod'elisation et la r'esolution du problème.

Le troisième chapitre comprend les ajustements statistiques et leurs applications au cas d'ifri pour d'eterminer les paramètres des modèles utilis'es dans les chapitres quatre et cinq.

Le quatrième chapitre a pour principal objectif de pr'esenter la mod'elisation du système avec les camions seuls et de le r'esoudre.

Le cinquième chapitre sera consacr'e a` l''elaboration d'un programme de simulation pour la mod'elisation et la r'esolution du problème de chauffeurs avec interpr'etation des r'esultats. Et nous terminerons par une conclusion g'en'erale, une bibliographie et des annexes.

1

Pr'esentation de la sarl ifri

1.1 Pr'esentation de l'entreprise

1.1.1 Introduction

L'entrée de l'Algérie en économie de marchéa incitéla création des entreprises privés. Ifri, une sociétéa` responsabilitélimitée, sise a` la zone industrielle dite Ahrik dans la commune d'Ouzellaguen wilaya de Béjaia, est parmi l'une des plus importantes sociétés industrielles Algériennes dans le domaine de l'agro-alimentaire.

A l'origine, il y avait la limonaderie IBRAHIM Laid, créée en 1986 par des fonds privés, ayant pour activités la production d'eaux gazeuses (LIMONADES) et sirops. Et ce n'est que dix ans plus tard, en 1996 que l'entreprise hérite d'un statut juridique de SNC (Societeau Nom Collectif ) puis de SARL (SocieteA` ResponsabiliteLimitee), composée de plusieurs associés.

La SARL IBRAHIM & Fils -ifri- investi ses efforts dans le but d'élargir sa gamme de produits, d'accroitre sa capacitéde production et d'optimiser son systeme de distribution. Cela permettra d'élargir son champ d'action d'une part et de subvenir au besoin sans cesse croissant en consommation d'autre part.

Auparavant, l'entreprise disposait d'une capacitéde production tres limitée et avait

souvent fait recours a` la location de camions pour desservir ces clients qui demandaient de petites quantit'es, jusqu'àce qu'elle cr'ee sa propre flotte de v'ehicules en 2002.

Jusque-là, le système de distribution se faisait sous forme de tourn'ees, et une 'etude a 'et'e faite en 2000 pour l'optimiser.

Actuellement, l'entreprise produit plus de 3 millions de bouteilles par jour et dispose d'une flotte de 75 v'ehicules de type semi-remorque. Vu le nombre important de ses clients ainsi que les grandes quantit'es demand'ees, l'entreprise a modifi'e son système de distribution, en alimentant chaque client directement du d'epôt central avec des quantit'es multiples de camions sans faire de tourn'ees.

Comme perspectives, la SARL ifri envisage de cr'eer sa propre entreprise de transport, pour 'eviter les coàut engendr'es par l'inutilisation de ces v'ehicules surtout dans la p'eriode hivernale, et avoir le droit de les louer.

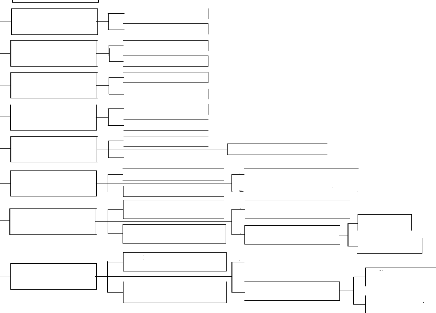
1.1.2 Organigramme de l'entreprise

La structure organisationnelle de la SARL IBRAHIM & Fils repose sur un modèle hiérarchique classique. L'organigramme suivant schématise les différentes directions et services de l'entreprise :



Direction Générale



			? V ? ? V ' ? Secrétariat ? Service Informatique
				Qualité? ?

' V '

Service

? ?

V

? ?



?

Gardiennage

?

Service sécurité

? Laboratoire ?



?

?

Contrôle de production

Nettoyage et désinfection

?

?

?

?

?

Réception
expéditions et
gestion des stocks

			?
?	Direction technique			Maintenance
			?
				Laboratoire
			?
	Direction finance et ^comptabilité			^Comptabilité
			?
?				Finance achats locaux
			?
?	Direction des achats
			?
				achats étrangers
?	Direction commerciale			Recouvrement
			? ?
				Facturation Paie ?
			?
?	Direction ressources humaines
			?	Social Production
			?
?	Direction de production
			?	Traitement des eaux
				Administration des patrimoines
?	Direction des moyens généraux		?
			?	Gestion des archives

?

Département
transport

Suivi des carrieres

Magasin des moyens
généraux

Gestion des infrastructures

Hygiene

Entretien

et réparation

Gestion des
produits finis

Gestion des
déchets

Direction
logistique

?

?

?

?

Gestion des matieres
premieres

?

Gestion des
emballages

FIG 1.1 Structure organisationnelle de la SARL ifri

1.1.3 Les différents services et directions et leurs ràoles[14]

La SARL ifri est constitu'ee d'une direction g'en'erale, un secr'etariat,trois services et huit directions contenant chacune une ou plusieurs sections repr'esent'es dans l'organigramme de la Figure 1.1.

1.1.3.1 La direction

Dirig'e par un directeur g'en'eral qui assure et applique les d'ecisions prises lors des diff'erents conseils d'administration. A l'instar de tout autre centre de d'ecision, la direction g'en'erale d'ifri est le poumon de l'ensemble de la soci'et'e o`u tout se coordonne et ce d'ecide pour tout ce qui a trait au quotidien et a` la politique de gestion de l'entreprise.

1.1.3.2 Service qualité

Son ràole principal est :

/ La mise en place des proc'edures de travail de chaque structure;

/ Assurer l''etablissement, la mise en oeuvre et l'entretien des processus n'ecessaires au système de la qualit'e;

/ Repr'esenter l'organigramme auprès des parties externes relatif au système de management de qualit'e.

1.1.3.3 Secrétariat

C'est l'organe de r'eception, il s'occupe de la saisie et classement des dossiers importants et confidentiels, charg'e aussi des courriers d'epart et arriv'e, r'eception et enregistrement des appels t'el'ephoniques.

1.1.3.4 Service informatique

Son ràole est :

/ D'eveloppement et r'ealisation des projets informatiques; / Introduction de nouvelles technologies;

( Maintenance du système informatique;

( Administration du r'eseau;

/ Formation du personnel dans les techniques informatiques; / Archivage et sauvegarde des donn'ees de l'entreprise.

1.1.3.5 Direction commerciale

Subdivis'e en deux sections a` savoir section facturation et section recouvrement, cette direction s'occupe de :

/ Recevoir les bons des commandes des clients;

/ 'Etablir les factures pro-formats et les ordres de versement pour les clients; / 'Etablir et viser les facturations et les bons de livraison;

/ Répondre a` toutes demande de la clientèle sur les plans de la qualitéet de la quantité;

/ Rapprocher le plus possible le produit du consommateur (Marketing);

/ ^àEtre a` la disposition du consommateur pour toute réclamation ou suggestion; / On y trouve la section vente qui s'occupe de toutes les ventes.

1.1.3.6 Direction finance et comptabilité

Elle comprend la section comptabilitégénérale et la section finance, son ràole est :

/ Assurer la conformitédes opérations comptables; / 'Etablir les situations financières;

/ Planifier les financements et les investissements; / Gérer les recettes et les dépenses.

1.1.3.7 Direction des ressources humaines

Ses sections sont : paie, social, suivi des carrières. Cette direction en plus du règlement des problèmes sociaux du personnel, de la bonne tenue de ses dossiers et du suivi de ses mouvements et carrière, élabore également les paies.

1.1.3.8 Service sécurité

Il est composéd'une seule section, son ràole principal est : / Veiller a` la prévention en matière de sécurité;

/ Intervention en cas d'incendie ou d'accident;

/ Effectuer des visites quotidiennes des lieux de travail;

/ Assurer le port de l'équipement de protection individuelle.

1.1.3.9 Direction technique

Dotéde tous les moyens d'intervention et des deux sections : maintenance et le laboratoire d'analyse et préparation des sirops, elle a pour ràole la maintenance des équipements de production en :

( Veillant au bon fonctionnement des équipements de production;

( Réglant des machines;

/ Assurant la maintenance et l'entretien des machines et tous les véhicules.

1.1.3.10 Direction de production

Elle est responsable du personnel et des trois ateliers de production, son ràole est : ( La gestion du carnet de bord de la production;

/ Le contràole et le suivi des statistiques de production;

/ La production de l'équivalent en quantités demandées par le service commercial et en normes exigées par les laboratoires internes.

1.1.3.11 Direction des achats

Cette direction est muni de la section achats locaux et la section achats étrangers, o`u il prend en charge la gestion des achats et assure le suivi des commandes jusqu'àleurs satisfaction en assurant les délais comptables avec l'urgence des besoins et a` moindre coàut.

1.1.3.12 Direction des moyens généraux

Son ràole principal est :

/ Administration des patrimoines; / Gestion des archives;

/ Gestion des infrastructures.

1.1.3.13 Direction logistique

Elle comporte trois services qui sont :

- Réception expéditions et gestion des stocks. - Gestion des matieres premieres.

- Gestion des emballages.

Les principales activités de ces services sont :

/ Coordonner les activités des magasiniers;

/ Veiller a` la bonne tenue des stocks;

/ Contràoler les différents documents relatifs aux entrées et sorties de marchandise dans les divers magasins.

Et un département :

Département transport : C'est lào`u on a effectuéla plus grande partie de notre stage. Il a pour ràole :

V La coordination entre le service commercial et le service parc.

V La gestion des camions.

V La gestion des chauffeurs.

1.2 Récolte des données

1.2.1 Données récoltées auprès du service commercial

En ce qui concerne la récolte des données, et pour identifier et analyser d'une facon plus précise les variations des coàuts de commercialisation des produits, on a eu recours au service commercial, pour voir comment fonctionne les opérations de demande et livraison

des clients, et le mode d''etablissement des factures ainsi l'encaissement des paiements. Les donn'ees qu'on a r'ecolt'e dans ce service sont :

/ La liste des clients et leurs adresses.

/ Les demandes journalières pour chaque client et le type des produits demand'es.

1.2.2 Données récoltées auprès du service production

On a aussi eu recours au service production, cela dans le but d''evaluer la capacit'e de production de l'entreprise et d''enum'erer la gamme de produits (voir aussi le processus de production et conditionnement des produits). Durant cette visite on a pu :

/ Calculer la capacit'e de production journalière de l'entreprise.

/ Le nombre de type de produits fabriqu'es.

/ Le nombre de bouteilles dans une palette pour chaque produit.

1.2.3 Données récoltées auprès du service parc :

Et comme nous nous int'eressons au problème de transport, les donn'ees les plus int'eressantes sont r'ecolt'ees au service parc o`u on a effectu'e notre stage. D'abord on a pr'elev'e la composition de la flotte (V'ehicules de transport des produits), ainsi leurs caract'eristiques comme : la r'ef'erence de chaque camion, date de mise en circulation, le tonnage, la marque, le type d''energie et la consommation par 100Km.

R'ef'erence	Mise en circulation	Tonnage	Marque	'Energie	Consommation
001201	21/04/2002	20	YV2A4DMAA32A	G.O	45 L
. .
001665	23/07/2006	32	FH13	G.O	43 L

TAB. 1.1 - Exemple d'information concernant la flotte

L'entreprise a un champ d'action qui s''etale sur tout le territoire national, elle a subdivis'e le territoire en plusieurs r'egions et cela en fonction de la distance qui s'epare l'entreprise d'un client ou d'un groupe de clients. Les informations qu'on a r'ecolt'e en ce qui concerne ceci sont : Les destinations (r'egions), le client (ou les clients sis a` cette destination), la distance qui s'epare l'entreprise de cette r'egion, le temps n'ecessaire pour faire un Aller-Retour, les frais de mission, la quantit'e de gasoil n'ecessaire pour faire un Aller-Retour, comme le montre le tableau suivant :

Destination	Client (s)	Distance	Période	F de mission	Consommation
Adrar	N.Client	2945km	5jours	4500DA	1178 L
. .
Tougourt	N.Client	1138km	2jours	1500DA	485 L

TAB. 1.2 - Destination, clients, temps et consommation pour un Aller-Retour

On a aussi récoltéles données concernant l'état détaillédes frais de missions dont on a dégagédes données intéressantes comme :

( Le nombre de camions utilisés chaque jour pendant la période Aoàut-Mai. / Les rotations effectuées par chaque camions pendant la période Aoàut-Mai.

L'état détaillédes frais de missions est présentédans le tableau suivant :

Numéro	Chauffeur	Date	Ville de destination	Frais de mission
1	Ci	02/08/2006	Alger	500DA
.	.	.	.	.
120	Ck	09/02/2007	Tamenrast	8500DA
.	.	.	.	.
11324	Cj	24/05/2007	Oran	1500DA

TAB. 1.3 - 'Etat détaillédes frais de missions

1.2.4 Données concernant les coàuts de transport

Parmi les objectifs de toute entreprise, on trouve celui de minimisation de ses coàuts. La s.A.R.L IBRAHIM & FILs a toujours essayéd'appliquer de nouvelles techniques pour minimiser ses coàuts. Durant notre stage, on a vu la méthode utilisée par l'entreprise dans ce but pour l'opération de distribution.

L'entreprise a considérépour une livraison, les coàuts suivants :

( La consommation en gasoil durant l'opération de livraison.

/ La marge sur les salaires des chauffeurs et convoyeurs, et cela lorsqu'il s'agit d'un trajet qui nécessite un convoyeur.

/ Les frais de mission pour le chauffeur ainsi que son convoyeur, et cela lorsqu'il s'agit d'un trajet qui nécessite un convoyeur.

/ Une marge pour les pièces de rechange (elle est fixée par l'entreprise). / Une taxe sur la valeur a` ajoutée (TVA) (aussi fixée par l'entreprise). Pour plus de détails concernant les données récoltées, voir annexe A.

Remarque 1.1. Durant notre stage, on a pas pu obtenir quelques informations (coàuts de
production, coàuts de stockage, les quantités livrées d'un produit quelconque par unitéde

temps,...) soit parce qu'elles sont tenues confidentielles, soit inexistantes. Dans le chapitre 4, on a voulu ajuster le gain moyen d'un camion par unitéde temps (jour), qui se calcule a` base de ce genre d'informations, et pour remédier on a considéréplusieurs valeurs du gain pour délimiter la valeur exacte.

1.3 Réseau de distribution

1.3.1 Système de distribution [2]

Transporter sur de grandes et moyennes distances des quantités très importantes de produits engendre des coàuts de transport pouvant représenter plus de 30% du prix de revient du produit. Toute réduction de ces coàuts, même minime, a une importance économique considérable.

La distribution regroupe toutes les activités de transport de l'entreprise, qu'il s'agisse de l'acheminement des matières premières aux sites de production, du transport des produits finis des usines aux entrepôts ou aux dépôts et enfin de ceux-ci aux clients.

Concevoir un système de distribution pour des produits est un problème stratégique de planification qui est dàu a` plusieurs facteurs parmi eux, la concentration de la production, l'ouverture des marchés d'échange et la croissance de la tendance d'utilisation des services de transport externe.

Un système de transport généralement peut être représentépar un diagramme a` trois niveaux :

- Le premier niveau constituépar les usines.

- Les dépôts forment le second niveau.

- Les clients sont au troisième niveau.

Une entreprise industrielle qui englobe l'usine et les dépôts dans le système de distribution, occupe en quelque sorte une position intermédiaire entre les sources et le marché. Elle est concernée par la conversion de toutes ces entrées en bien et services qui devront être disponibles aux points de vente. L'entreprise doit planifier l'exécution effective de toutes les opérations.

Le réseau de distribution comprend l'écoulement du produit fini d'une compagnie industrielle a` partir des usines jusqu'aux consommateurs. Le réseau de distribution contient les noeuds suivants :

1. Les usines : Elles représentent un noeud additionnel appelé»Source».

2. Les dépôts centraux : Les différents produits des usines doivent être disponibles dans un ou plusieurs dépôts dans le but de centraliser les produits.

3. Les dépôts régionaux : Il servent de destination du transport de produits des usines ou des dépôts centraux et comme point de départ de livraison des clients. L'implementation de tels dépôts permet un gain en mati`ere de coàut de transport et temps de livraison.

4. Les points de transport : Il ont le même rôle que les dépôts régionaux. Cependant, il sont ravitaillés quotidiennement et destinés pour la livraison des demandes quotidiennes.

5. Les clients : Ce sont les revendeurs en détail, les aires de stockage, les supermarchés et les consommateurs directs.

Les chemins de distribution sont les relations de transport mentionnées sur la Figure 1.2 :

- Des Usines aux dépôts centraux,

- Des dépôts centraux aux dépôts régionaux ou aux points de transport,

- Des dépôts régionaux ou des points de transport aux consommateurs, mais d'autres relations peuvent exister comme :

- Des usines aux dépôts régionaux ou au points de transport.

- Des dépôts centraux aux clients.

- Des usines aux clients, ce transport réf`ere a` une livraison directe, généralement pour des clients ayant une demande importante.

Le schéma ci-dessous représente un réseau de distribution d'une mani`ere générale :



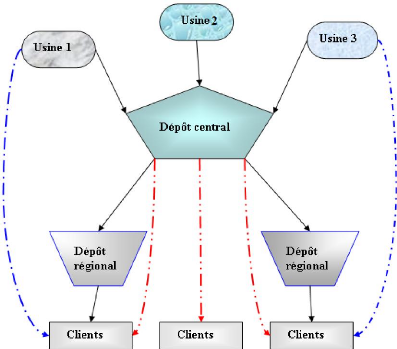
FIG 1.2 Sch'ema g'en'eral d'un r'eseau de distribution

1.3.2 Système de distribution de la sarl ifri

Actuellement, le champ d'action de la S.A.R.L IBRAHIM & FILS s''etend sur tout le territoire national et la forte demande a` chang'e le système de distribution. Auparavant l'entreprise effectuait des livraisons sous forme de tourn'ees et elle pouvait livrer a` plusieurs clients avec un seul camion.

Le r'eseau de distribution de l'entreprise forme un r'eseau 'etoile, dont la source est un d'epôt central auprès de l'entreprise. Les clients de l'entreprise sont dispers'es sur tout le territoire national. Comme le montre le sch'ema suivant :



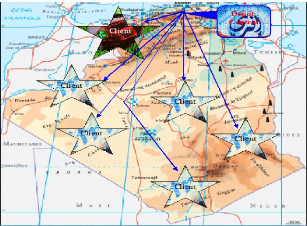
FIG 1.3 Réseau de distribution de la S.A.R.L IBRAHIM & FILS

Le réseau de distribution adoptépar l'entreprise est représentépar le schéma suivant :



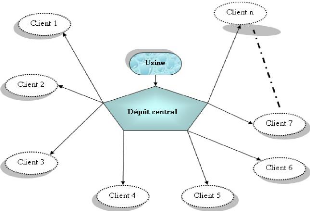
FIG 1.4 Système de distribution de la S.A.R.L IBRAHIM & FILS

1.4 Gestion des chauffeurs

La sarl -ifri- a attribuéa` chaque camion un chauffeur permanent qui travail 5 jours sur 7, et puisque la durée des trajets varie et peut atteindre jusqu'a 9 jours, le surplus qui dépasse les jours de travail est considérécomme heures supplémentaires.

Comme les camions sont neufs, l'entreprise veut les exploiter au maximum, et pour cela elle a recrutédes chauffeurs remplaçants pour remplacer les chauffeurs titulaires durant leurs jours de repos. En ce qui concerne les longs trajets (plus de 3 jours), le chauffeur est accompagnépar un convoyeur.

1.5 Position du problème

La recherche opérationnelle peut remédier a` une large gamme de problème concernant la gestion organisationnelle optimale des ressources, il est généralement nécessaire de cerner et de bien comprendre le problème en question et de le modéliser sous forme mathématique.

A l'heure actuelle le maintien en compétitivitéde la S.A.R.L IBRAHIM & FILS dépend de sa rentabilité. Cette dernière se traduit par l'utilisation rationnelle des biens et moyens dont elle dispose, comme par exemple la conception d'un système de commercialisation intelligent de ses produits, puisque d'autre solutions comme l'augmentation du prix de vente des produits ou du prix de transport aide beaucoup plus la concurrence. En plus, généralement ces alternatives sont fixées par le marché.

Dans le cadre de la planification et de la gestion de la fonction de distribution, les responsables du service parc de l'entreprise IBRAHIM & FILS désirent appuyer leurs décisions en matière de transport par des méthodes et outils scientifiques, qui permettront d'améliorer leur efficacitéafin de satisfaire la demande de la clientèle, surtout qu'ils ont envisagéde créer leur propre entreprise de transport.

Partant du principe qu'il existe toujours une façon optimale d'accomplir chaque tâche, le principal objectif de ce travail est de proposer un modèle d'optimisation qui représente au mieux le fonctionnement du système de distribution permettant une gestion scientifique, et cela en fonction des moyens dont dispose l'entreprise. En d'autre termes,

NOTRE TRAVAIL CONSISTE A` :

1. Déterminer les lois qui régissent les demandes journalière en camions et les durées des trajets parcourus.

2. Déterminer le nombre de camions qu'il faudra mettre a` la disposition du service parc.

3. Déterminer le nombre de chauffeurs remplaçants nécessaire pour une utilisation optimale des camions.

2

Rappels théoriques

2.1 Introduction

Pour des besoins dans les chapitres ult'erieurs, nous rappelons quelques notions de fonctions et d'ensembles convexes ensuite nous pr'esenterons les 'el'ements essentiels et quelques r'esultats classiques concernant les systèmes de files d'attente, de r'egression et on terminera par des notion de simulation.

2.2 Optimisation des fonctions convexes[7]

D'efinition 2.1. Un ensemble non vide X c Rⁿ est dit convexe, si V A E [0, 1] et V x, x0 E X on a :

(1--A)x0+Ax E X. (2.1)

D'une facon 'equivalente, on peut dire que X est convexe si pour deux points quelconques x0 et x pris dans X, le segment [x0, x] tout entier est contenu dans X.

Exemple 1. La figure ci-dessous représente un ensemble convexe et un ensemble non convexe :



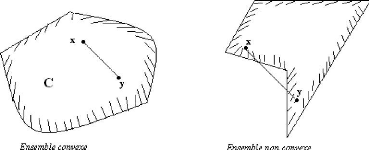
FIG 2.1

Exemple 2. Soit H={x E Rⁿ | cx=d} un hyperplan de Rⁿ avec c E Rⁿ, d E R. si y E H et z E H, on vérifie que x=Ay + (1 - A)z satisfait cx=d pour tout A E [0, 1]. Ainsi H est convexe; sa dimension est n-1 si c =6 0.

Exemple 3. Soit H={x E Rⁿ | cx = d} un demi espace de Rⁿ avec c E Rⁿ, d E R. On vérifie de même que H est convexe; sa dimension est n.

D'efinition 2.2. Soit X c Rⁿ un sous-ensemble convexe. Une fonction f : X ? R est convexe, si V A E [0, 1] et V x, x0 E X on a :

Af(x) + (1 - A)f(x0) = f((1 - A)x0 + Ax). (2.2)

Si nous avons une inégalitéstricte pour x =6 x0 et A E ]0, 1[, nous dirons que f est strictement convexe.

La figure suivante représente le schéma classique d'une fonction convexe.



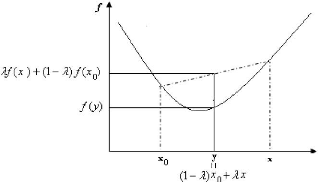
FIG 2.2

D'efinition 2.3. Soit f : X -* R une fonction différentiable sur un ensemble ouvert convexe X c Rⁿ. Alors, f est convexe si et seulement si V x, x0 E X, l'une des deux conditions suivantes est vérifiée :

(i) f(x) - f(x0) ~ [Vf(x0)]^t (x - x0),

(ii) (x - x0)^t [Vf(x) - Vf(x0)] ~ 0,

o`u Vf(x) désigne le gradient de f en x0.

D'efinition 2.4. Soit X c Rⁿ ; f :X -* R. On dit que x^* est un minimum local de f sur X s'il existe un c > 0 tel que f(x) ~ f(x^*) pour tout x appartenant a` B(x^*, c).

x* est un minimum global de f sur X si f(x) ~ f(x^*) pour tout x dans X.



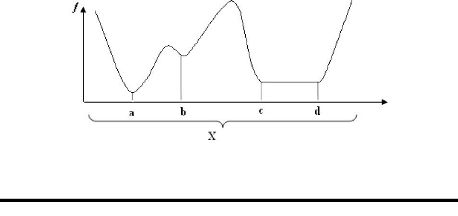
FIG 2.3

23

Sur la figure 2.3, a, b et les points de [c, d] sont des minima locaux de f sur X. Seul a est un minimum global de f sur X.

Remarque 2.1. Notons qu'on peut toujours ramener un problème de minimisation a` un

problème de maximisation et inversement en utilisant l'égalité: maxf(x) = --min

_x?X(--f(x)).

x?X

Theorème 2.1. [13] Soit X c Rⁿ un ensemble convexe et f : X ? R convexe sur X ; l'ensemble M des points o`u f atteint son minimum est convexe; de plus, tout minimum local est un minimum global.

Preuve. S'il n'y a pas de minimum, M est vide et donc convexe. Soit x0 = min

x?Xf(x) ;

M = {x | f(x) -- x0 < 0} est convexe car f(x) -- x0 est encore une fonction convexe.

Soit x^* un minimum local de f et supposons qu'il existe un y E X avec f(y) < f(x^*). Sur la droite d'efinie par {z | z = Ay + (1 -- A)x^*, 0 < A < 1}, voir la figure 2.4, on a :

f(Ay + (1 -- A)x^*) < Af(y) + (1 -- A)f(x^*) < f(x^*)

Ceci contredit le fait que x^* est un minimum local (car on peut trouver un point z voisin de x^* avec f(z)< f(x^*)). Donc, il existe pas de tel y et x^* est bien un minimum global.



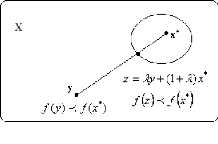
FIG 2.4

Definition 2.5. Soit X c Rⁿ un sous-ensemble convexe. Une fonction f : X ? R est concave, si V A E [0, 1] et V x, x0 E X on a :

Af(x) + (1 -- A)f(x0) < f((1 -- A)x0 + Ax). (2.3)

Si nous avons une inégalitéstricte pour x =6 x0 et A E ]0, 1[, nous dirons que f est strictement concave.

Remarque 2.2. Tout les résultats vus dans cette section peuvent aussi être formulés en termes de fonctions concaves, il suffit alors de changer les sens des inégalités et de remplacer les minima par des maxima.

2.3 Le formalisme des files d'attente[15]

La th'eorie des files d'attente s'attache a` mod'eliser et a` analyser de nombreuses situations diff'erentes en apparences, mais qui relèvent n'eanmoins du sch'ema descriptif g'en'eral suivant. Des clients arrivent a` intervalles al'eatoires dans un système comportant plusieurs serveurs auxquels ils vont adresser une requête. La dur'ee du service auprès de chaque serveur est elle-même al'eatoire. Après avoir 'et'e servis, les clients quittent le système. Illustrons cette description g'en'erale par des exemples sp'ecifiques.

· Arrivee des voitures vers une station service

Ici, les serveurs sont des places de parking, les clients sont les voitures qui arrivent. Typiquement, toutes les places du parking offrent le même service, et chaque client ne devra donc stationner que dans une seule place.

· Reparation des machines

Les clients sont les machines qui tombent en panne, et les serveurs sont les m'ecaniciens qui s'occupent de la r'eparation.

Un système de files d'attente g'en'eral peut être vu comme une boàýte noire dans laquelle les clients arrivent suivant un processus quelconque, s'ejournent pour recevoir un ou plusieurs services et finalement quittent le système. Ce système pourra être compos'e d'une file simple ou d'un ensemble de files appel'e réseau de files d'attente.

Definition. On appelle système de files d'attente l'abstraction math'ematique d'un sujet qu'on peut d'ecrire par les 'el'ements suivants :

1. Le flot des arriv'ees des clients.

2. La source des clients

3. Le comportement du client.

4. La loi de la dur'ee de service de chaque client.

5. La discipline de service

6. Le nombre de serveurs.

7. La capacit'e de la file.

· Le flot des arrivées des clients.

D'habitude, on suppose que les temps des inter arriv'ees sont ind'ependants et identiquement distribu'es. En g'en'eral, le flot des arriv'ees des clients est poissonnien, ce qui revient a` dire que la distribution du temps des inter arriv'ees est exponentiel. Les clients peuvent arriver individuellement ou par groupes. Un exemple d'arriv'ee par groupes est un poste de police au niveau d'une frontière o`u les passagers ainsi que leurs bagages sont soumis au contrôle.

· La source des clients.

Dans la plupart des cas, cette source est suppos'ee infinie. Cependant, pour les modèles de fiabilit'e, la source des clients est limit'ee (par exemple le cas d'un r'eparateur au sein d'une usine).

· Le comportement du client.

Certains clients peuvent être patients et vouloir attendre pendant longtemps. Par contre d'autres s'impatientent et quittent après un bout de temps. C'est le cas par exemple d'une centrale t'el'ephonique o`u les clients raccrochent quand ils ont a` attendre longtemps avant qu'une ligne ne soit disponible pour rappeler ult'erieurement.

· La durée de service.

En g'en'eral, on suppose que les dur'ees de service sont ind'ependantes, identiquement distribu'ees et ind'ependantes des temps des inter arriv'ees. Ce qui n'est toujours pas le cas. Par exemple, le temps de traitement des machines au niveau d'un système de production peut s''elever une fois le nombre de tâches a` ex'ecuter devient trop grand.

· La discipline de service.

Les clients peuvent être servis individuellement ou par groupe. Cependant, plusieurs possibilit'es existent quant a` l'ordre selon lequel ils seront servis. Les principales disciplines de service sont :

* FIFO(First In First Out) : les entit'es sortent dans l'ordre suivant lequel elles sont entr'ees. Cette discipline est la plus utilis'ee.

* LIFO(Last In First Out) : la dernière entit'e dans la file est la première a` être servie. C'est le cas de la pile au niveau des ordinateurs.

* Random : toutes les entit'es ont la même probabilit'e d'être servies en premier.

* Prioritaire : les entit'es sont servies suivant un attribut qui leur est associ'e. Par exemple l'entit'e ayant le plus court temps de traitement d'abord.

· Le nombre de serveur.

Il peut être 'egale a` l'unit'e ou plus selon la nature du service a` fournir.

· La capacitéde la file.

Dans pas mal de cas, la file est suppos'ee infinie. Cependant, il n'est pas rare de rencontrer des situations dans lesquelles elle est finie (par exemple le cas d'une salle d'attente).

Pour la classification des systèmes d'attente, on a recours a` la notation symbolique introduite par Kendall au d'ebut des ann'ees cinquante. Cette notation comprend quatre symboles rang'es dans l'ordre

A/B/s/N

o`u

A = distribution des temps entre deux arriv'ees successives,

B = distribution des dur'ees de service,

s = nombre de postes de service en parallèle,

N = capacit'e du système

On peut toutefois faire abstraction du dernier symbole lorsque N = 8. Pour sp'ecifier les distributions A et B, les symboles suivants sont utilis'es :

M = distribution exponentielle,

Ek = distribution d'Erlang d'ordre k,

Hk = distribution hyperexponentielle,

C = distribution g'en'erale,

D = cas d'eterministe

Notion de classes de clients

Une file d'attente peut être parcourue par diff'erentes classes de clients. Ces diff'erentes classes se distinguent par :

- des processus d'arriv'ee diff'erents;

- des temps de service diff'erents;

- un ordonnancement dans la file d'attente en fonction de leur classe.

Pour d'efinir une file multiclasse, il y a lieu de pr'eciser pour chaque classe de clients le processus d'arriv'ee et la distribution du temps de service associ'es ainsi que la manière dont les clients des diff'erentes classes s'ordonnent dans la file.

2.4 Analyse mathématique des systèmes des files d'attente

L''etude math'ematique d'un système d'attente se fait le plus souvent par l'introduction d'un processus stochastique d'efini de façon appropri'ee. En g'en'eral, on s'int'eresse au nombre X(t) de clients se trouvant dans le système a` l'instant t (t = 0). En fonction des quantit'es qui d'efinissent la structure du système, on cherche a` calculer

* les probabilités d'état p_n(t) = P(X(t) = m) qui d'efinissent le régime transitoire du processus {X(t)}t>0 ; les probabilit'es p_n(t) doivent 'evidemment d'ependre de l''etat initial ou de la distribution initiale du processus.

* le régime stationnaire du processus stochastique, d'efini par

p_n = lim p_n(t) = P(X(+8) = m), m = 0,1,2,...

t--+oo

A partir de la distribution stationnaire du processus {X(t)}t>0, il est possible d'obtenir d'autres caractéristiques d'exploitation du système.

2.4.1 Modélisation des systèmes de files d'attente

Plusieurs variantes existent pour la mod'elisation selon la nature et le comportement du système. On distingue deux cat'egories de modèles en files d'attente : les modèles markoviens et les modèles non markoviens. Si pour les premiers, la propri'et'e d'absence de m'emoire permet une grande facilit'e dans l''etude, il n'en est pas de même pour les modèles non markoviens. Cependant, on dispose de plusieurs m'ethodes, qui permettent de rendre ces derniers markoviens moyennant certaines transformations.

2.4.1.1 Modèles markoviens

Ils caractérisent les systèmes dans lesquels les deux quantités stochastiques principales le temps des inter arrivées et la durée de service sont des variables aléatoires indépendantes exponentiellement distribuées. La propriétéd'absence de mémoire de la loi exponentielle facilite l'étude de ces modèles. L'étude mathématique de tels systèmes se fait par l'introduction d'un processus stochastique approprié. Ce processus est souvent le processus de naissance et de mort {X(t)}t=0 défini par le nombre de clients dans le système a` l'instant t. L'évolution temporelle du processus markovien {X(t)}t=0 est complètement définie gràace a` la propriétéd'absence de mémoire.

2.4.1.2 Processus de naissance et de mort

Le processus d'état stochastique {n(t) : t = 0} est un processus de naissance et de mort si, pour chaque n = 0, 1, 2
·
·
· , il existe des paramètres ë_n et u_n (avec u0 = 0) tels que, lorsque le système est dans l'état n, le processus d'arrivée est poissonnien de taux ë_n et le processus de sortie est poissonnien de taux u_n.

2.4.1.3 Processus de naissance pur

Dans un processus de naissance pur, ë_n = ë et u_n = 0 pour n = 0, 1, 2
·
·
· . Donc, les arrivées ont lieu a` taux constant et il y a pas de départs. Pour un tel processus, le nombre de clients dans le système est évidement égal au nombre d'arrivées enregistrées pour un processus de poisson classique, si bien que :

P_n(t) = probabilitéque l'état du système a` l'époque t soit égale a` n

= e--ët(ët)n

n! , n = 0,1,
·
·
·

2.4.1.4 Processus de mort pur

Dans un processus de mort pur, l'ensemble des états possibles est {0, 1, 2
·
·
· } et ë_n = 0 pour n = 0, 1,
·
·
·

f0, si n = 0, u, si n = 1,
·

u_n =


·
·N.

Intuitivement l'état initial d'un tel système vaut N, il n'y pas d'arrivées et les départs se produisent a` taux (moyen)constant jusqu'àce que le système soit vide. En interprétant les départs comme des »arrivées a` l'extérieur du système», on conclut facilement que :

P_n(t) = probabilitéque (N-n) départs se produisent dans l'intervalle [0,t)

= e

et

--pt (ut)N--n (N - n)! ,

^àP_n(t) = probabilitéque N départs au moins se produisent dans l'intervalle [0,t)

P8 = j=N			e_ut (it)j j!		=1 -- =1 --
N_1 P j=0 PN n=1		e_ut (it)j j! Pn(t).

2.4.1.5 Modèles non markoviens

En l'absence de l'exponentialitéou plutôt lorsque l'on s'écarte de l'hypothèse d'exponentialitéde l'une des deux quantités stochastiques le temps des inter arrivées et la durée de service, ou en prenant en compte certaines spécificités des problèmes par introduction des paramètres supplémentaires, on aboutit a` un modèle non markovien. La combinaison de tous ces facteurs rend l'étude mathématique du modèle très délicate, voire impossible. On essaye alors de se ramener a` un processus de Markov judicieusement choisi a` l'aide de l'une des méthodes d'analyse suivantes :

- Méthode de la chaàýne de Markov induite

Cette méthode, élaborée par Kendall, est souvent utilisée. Elle consiste a` choisir une séquence d'instants 1, 2, . . . , m (déterministes ou aléatoires) telle que la chaàýne induite {X<sub>n</sub>, m = 0}, o`u X_n = X(m), soit markovienne et homogène.

- Méthode des variables auxiliaires

Elle consiste a` compléter l'information sur le processus {Xt}t=0 de telle manière a` lui donner le caractère markovien. Ainsi, on se ramène a` l'étude du processus {X(t), A(t1), A(t2), . . . , A(t_n)}. Les variables A(tk), k E {1, 2,. . . , m} sont des variables aléatoires supplémentaires.

- Méthode des événements fictifs

Le principe de cette méthode est d'introduire des événements fictifs qui permettent de donner une interprétation probabiliste aux transformées de Laplace et aux variables aléatoires décrivant le système étudié.

- Simulation

C'est un procédéd'imitation artificielle d'un processus réel donné. Comme résultat de cette imitation, on obtient des approximations des caractéristiques du système étudié, permettant ainsi de mesurer ses performances.

2.4.2 Analyse opérationnelle des systèmes de files d'attente

Cette analyse, plus connue sous le nom de l'évaluation de performances, consiste au calcul des caractéristiques de performances d'un système. Cette opération s'impose dès lors o`u l'on souhaite connaàýtre les performances d'un système réel et que l'on ne peut effectuer de mesure directe sur celui-ci. Les paramètres de performances que l'on souhaite obtenir sont de différents ordres en fonction des systèmes considérés. C'est ainsi dans les systèmes de production, un paramètre de performances important est le débit en produits finis. Tandis que pour le cas d'un guichet, le paramètre de performances qui intéresse

l'usager est le temps d'attente alors que la direction quant a` elle s'intéresse au nombre de clients en attente au guichet.

2.4.2.1 Les caractéristiques de performance

Les caract'eristiques d'exploitation du système auxquels on s'intéresse le plus souvent sont :

· le nombre moyen de clients dans le système,

· la durée de séjour d'un client dans le système,

· la durée d'attente d'un client,

· le taux d'occupation des postes de service. 2.4.2.2 La formule de Little

La formule de Little est l'un des résultats les plus beaux et les plus utiles de la théorie des files d'attente. De par sa grande simplicitéet sa généralité, ce théorème possède une multitude d'application.

Comme la plupart des résultats présentés dans ce chapitre, la formule de Little n'est valable que pour les systèmes stable, dans lesquels un équilibre s'est établi et tournant » donc en régime stationnaire[9].

Théorème 2.2. (Formule de Little)[9] Soit un système en r'egime stationnaire, alors

N = AT, (2.4)

o`u

1) N est le nombre moyen de clients dans le système,

2) A est le taux moyen d'arriv'ee des clients dans le système,

3) T est le temps moyen de s'ejour d'un client dans le système.

Exemple 4. Les g'erant d'un supermarch'e ont fait une 'etude statistique montrant que, pendant la semaine, il y a en moyenne 80 clients dans le magasin et que la fr'equence d'arriv'ee des clients est de 120 personnes a` l'heure.

Sur la base de ces statistiques, il est facile de calculer le temps moyen qu'un client passe dans le magasin. En effet, isolant T dans la formule de Little, on obtient

N T = A

80 2 = 120 = 3[h] = 40[min].

2.5 Quelques systèmes de files d'attente

2.5.1 Le système M/M/1

Une file M/M/1 compte un seul serveur offrant un service dont la durée est une variable exponentielle de taux u indépendant de l'état du système et recevant des clients selon un processus de poisson de taux constant A . Il s'agit làdu plus simple parmi les modèles de files d'attente. Il permet, cependant, d'illustrer les principaux phénomènes observés dans ce systèmes.

Représentant l'état d'un tel système a` un instant quelconque par le nombre de clients présents, le graphe des transitions possible entre ses différents états correspond a` la figure ci-dessous. Pour étudier une telle file, nous pouvons nous rabattre directement sur la théorie des processus de naissance et de mort. Un système M/M/1 en constitue, en effet, un cas très particulier, chaque arrivée d'un client pouvant être assimilée a` une naissance et chaque départ a` une mort. Le taux d'arrivée qui correspond au taux de naissance est constant et égal a` A. Tout comme le taux de service, correspondant au taux de mort, qui vaut u, tout au moins tant qu'il y a des clients dans le système[9].



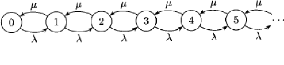
FIG 2.5

2.5.1.1 Régime transitoire

Vu les propriétés fondamentales du processus de poisson et de la loi exponentielle, le processus (X(t))t~0 : »nombre de clients dans le système a` l'instant t», est markovien. Les équations différentielles de Kolmogorov de ce processus sont de la forme :

~P ⁰ ₀(t) = --AP0(t) + uP1(t), (2.5)
P ⁰ _n(t) = --(A + u)P_n(t) + _APn--1(t) + _uPn+1(t), m = 1, 2,
·
·
· . Ce système d'équations permet de calculer les probabilités d'états P_n(t) en faisant appel

aux équations de Bessel et si l'on connaàýt les conditions initiales (X(0)).

2.5.1.2 Régime stationnaire

lim

t'--+oo

Lorsque t tend vers l'infini dans le système (2.5), on peut montrer que les limites p_n(t) = ð_n existent et sont indépendantes de l'état initial du processus et que :

lim t'--+oo

0 pn(t) = 0, V m = 0,1, · · ·

Ainsi, a` la place d'un systeme d'equations differentielles, on obtient un systeme d'equations {

lineaires et homogenes :

uð1 = kr0,

ëðn-1 + uðn+1 = (ë + u)ð_n, n = 1, 2
·
·
· .

00

De plus, nous avons la condition E ð_n = 1 car _(ðn)n est une distribution de pro-

n=0

babilite.

La solution de ces equations est donn'ee par :

ðn = ð0 (ë u

n ë ) = (1 -- u)(u^ë)^n , n = 0, 1, · · ·

a` condition que ë < u (condition d'ergodicitegeometrique du systeme). On montre que le regime stationnaire du systeme M/M/1 est gouvernepar la loi geometrique.

2.5.1.3 Quelques caract'eristiques

· Le nombre de clients dans le systeme : Si on note cette caracteristique par N, alors :

N = E(X) =

00 E n=0

nðn = (1 -- ñ)

00 E n=0

nñ^n = ñ = ë . 1 -- ñ u -- ë (2.6)

ñ= ë est la charge du systeme. u

· Le nombre de clients dans la file : Notons cette caracteristique par Q. Soit X_q le nombre de clients se trouvant dans la file d'attente, on a :

X_q = { 0, si X = 0

X -- 1, siX > 1.

Alors :

Q = E(Xq) =

00 E n=1

ë2 (n -- 1)ðn = (2.7) u(u -- 1)^.

T =^N ë

=

ñ

1/u

1 -- A' (2.8) u

ë(1 -- ñ)

1 -- ñ

W = Q ë

=

ñ2

ñ

ñ (2.9) u -- ë.

ë(1 -- ñ)

u(1 -- ñ)

D'autres caracteristiques comme le temps moyen de sejour T et d'attente W d'un client dans le systeme peuvent àetre calculees a` l'aide de la formule de Little.

2.5.2 Le système M/M/m [9]

Une file M/M/m poss`ede m serveurs identiques partageant les mêmes places d'attente et servant chacun un client a` la fois. La dur'ee d'un service est une variable al'eatoire distribu'ee d'apr`es une loi exponentielle de param`etre u et les clients arrivent dans le syst`eme d'apr`es un processus de Poisson de taux ë. Comme pour le cas pr'ec`edent, le processus d'ecrivant l''evolution du nombre de clients dans le syst`eme est un processus de naissance et de mort. On peut donc d'eriver les 'equations d''equilibre a` partir de son graphe repr'esentatif (fig.2.6.)



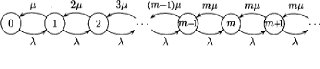
FIG 2.6

2.5.2.1 Régime stationnaire

Le syst`eme pouvant traiter m clients en parall`ele, un maximum de mu clients quittent la file par unit'e de temps. Le taux d'arriv'ee des clients 'etant de ë par unit'e de temps, l'intensit'e du trafic d'une file M/M/m est ñ = ë/mu et une telle file est stable si et

seulement si

ë

ñ = < 1 . (2.10)

mu

Sous cette condition, la r'esolution des 'equations de bilan fournit les probabilit'es stationnaires

I (mñ)k

k! ð0, k=1,. . .,m-1

ðk = (2.11)

ñ^km^m

m! ð0, k=m,m+1,...

Ainsi

^m-1X^ð0( k=0

ñk k! +

X8 k=m

m! mm ( ^ñ m)^k) = 1,

Il en r'esulte

"m-1X ñk k! + ñm ð0 = m!(1 - ^ñ m) k=0

I-1

.

(2.12)

ñk-m = ð0 m!(1 - ñ). (2.13)

æ =

X8 k=m

ðk = ð0

(mñ)^m m!

X8 k=m

(mñ)^m

Pour les syst`emes a` plusieurs serveurs, il est utile de calculer la probabilit'e æ qu'un client qui arrive doit attendre, c'est-à-dire la probabilit'e que tous les serveurs soient occup'es. Cette probabilit'e est connue sous le nom de formule C d'Erlang, est 'egale a`

2.5.2.2 Quelques caractéristiques

Utilisant les r'esultats pr'ec'edents, le calcul des performances de la file n'est pas diff'erent du cas de la file M/M/1. Le nombre moyen N de clients pr'esents dans le système et le nombre moyen Q de clients en attente sont

N= _X8

k=1

kðk = mñ + ñæ

1 - _ñ, (2.14)

Q =

X8 k=m+1

(k - m)ðk = ñæ 1 - ñ. (2.15)

Une simple application de la formule de Little permet d'obtenir les expressions des temps moyens de s'ejour T et d'attente W :

N T = ë	1 æ = + mu(1 - ñ), (2.16) u
Q W = ë		æ = mu(1 - ñ). (2.17)

Pour calculer le taux d'utilisation de chaque serveur, remarquons que, pendant un intervalle de temps suffisamment long ô, un nombre moyen de ëô clients entreront dans le système. Le traitement de ces clients demandera, en moyenne, un temps total 'egal a` ëô u . Le taux d'utilisation de chaque serveur s'obtient en r'epartissant ce temps sur les m serveurs et en divisant par le temps d'observation :

ëô/u U = mô

ë = = ñ. (2.18) mu

Théorème 2.3. (théorème de Burke[6])

Pour les systêmes M/M/m, si ë < um alors le flot des departs est poissonnien de paramêtre ë > 0.

P(ç < t) = 1 - e^-ët,

ç : duree d'intervalle entre deux departs successifs.

2.6 La régression

2.6.1 La régression linéaire[17]

La r'egression est une technique qui s'applique a` une population dont les caractères peuvent être class'es en deux cat'egories :

Les variables indépendantes : qui sont des caractères maàýtris'es par l'exp'erimentateur et qui peuvent prendre des valeurs choisies.

Les variables d'ependantes : qui sont aleatoires et constituent des resultats des experiences par des valeurs fixees des variables independantes.

Si on note par Xk les variables independantes avec k = 1, n et Y la variable dependante, la regression permet de voir s'il existe un lien stochastique lineaire entre Y et X1, X2, , Xk. Une fois le modele choisi il peut servir a` plusieurs fins :

ü Trouver la meilleure equation de regression (modele) et en evaluer la precision et la signification.

ü Estimer la contribution relative de deux ou plusieurs variables explicatives sur la variation d'une variable a` expliquer.

ü Juger l'importance relative de plusieurs variables explicatives sur la variable dependante.

Remarque 2.3. Dans ce qui suit on considere la regression lineaire simple. C'est a` dire l'equation de regression va s'ecrire sous la forme :

yi = a + bxi + e.

2.6.1.1 Test sur les param`etres du mod`ele

Apres l'estimation des parametres du modele par la methode des moindres carres (minimisation de la somme des carres des erreurs d'estimation de la variable dependante), on teste l'eventualites qu'il sont egaux a` zero, c-`a-d, on teste :

H0 »a = 0» Contre H1 »a =6 0» et H⁰₀ »b = 0» Contre H⁰₁ »b =6 0».

On obtient les deux statistiques de decision :			? ? ?	Ta = vn(àa-a) ó \/1#177;nx x Tb = vnS Sxàb .
variation de la regression	Xn i=0	(àyi - y)^2 est tres grande (àyi = aà +^àbxi et y = 1n			Xn i=0	yi).

aà : Estimateur de a,

bà : Estimateur de b.

R`egle de d'ecision

Soit c un parametre du modele, alors :

{

Si |T_c| > t(n-2,^á₂ ) On rejette l'hypothese que c = 0; Si |T_c| < t(n-2,^á₂ ) On accepte l'hypothese que c = 0; t(n-2,^á₂ ) : Le quantile sur la table de Student a` n-2 degrede liberte, et d'ordre (1 - á)

(á niveau de signification).

2.6.1.2 Test sur la validit'e du mod`ele

Soit le modele de regression yi = a + bxi + e, i = 1, n. Le modele est validesi la

C'est-`a-dire :					Xn i=1		(àyi -- y)^2 > K la statistique de d'ecision sera alors :
Xn i=0					(àyi - y)^2
F=				1		f(1,n-2, ).
			Xn i=0
				(yi - àyi)^2

n-2

f

Si F > Al,n-2,`J) le mod`ele est valid'e ; Si F < f(1,n-2,^á₂ ) le mod`ele est rejett'e ; f(1,n-2,<sup>á</sup><sub>2</sub> ) : Le quantile sur la table de Fisher a` deux degr'es de libert'e d'ordre (1 -- á).

2.6.2 La r'egression non lin'eaire

La r'egression non lin'eaire demeure aujourd'huit une m'ethode mystique. Plusieurs raisons pourraient expliquer cet 'etat de fait. D'une part, la mise en oeuvre des calculs r'eclame l'intervention directe de l'utilisateur, et les aspects algorithmiques, auxquels il est confront'e en premier lieu, ont longtemps estomp'e la v'eritable nature statistique du probl`eme. D'autre part, la th'eorie statistique sous-jacente n'est pas tr`es simple, et tous les probl`emes concrets qui r'ev`elent de cette m'ethode ne sont pas encore r'esolus.

Le mod`ele de r'egression le plus g'en'eral est d'ecrit math'ematiquement par l''equation suivante :

Yi = f(xi, è) + ci i = 1, . . . , n.

La loi de probabilit'e des ci est une loi sur ,centr'ee et de variance ó²_i finie. Les ci sont ind'ependants entre eux.

f est une fonction de forme bien d'efinie, d'ependante d'une variable r'eelle x et d'un vecteur de param`etres è. On note par p le nombre de ces param`etres. Donc on cherchera è dans l'ensemble È, partie de l'ensemblep.

2.6.2.1 Estimation des param`etres du mod`ele

Pour effectuer ce genre de r'egressions, on utilise toujours les moindres carr'es, mais on se retrouve avec un syst`eme non lin'eaire, que l'on r'esout de mani`ere approch'ee (par exemple, par la m'ethode de Newton-Raphson). Le calcul effectif de ces estimateurs passe donc par la r'esolution num'erique. On entre alors dans le domaine de l'optimisation d'une fonction avec toute les difficult'es que cela peut impliquer (non convergence, convergence vers des optimums locaux, calculs importants, . . . ). Ces probl`emes augmentes avec le nombre de param`etres a` estimer, une autre m'ethode courante consiste a` utiliser l'expansion en s'erie de Taylor de la fonction et d'appliquer la r'egression a` la partie lin'eaire 'evalu'ee en un point initial pas trop 'eloign'e de la solution cherch'ee, on trouve alors un deuxi`eme point o`u l'on 'evalue a` nouveau l'expansion de Taylor et ainsi de suite jusqu'`a l'optimum.

2.6.2.2 Validation du modèle

La première chose a` faire est 'evidement de juger a` »l'oeil» la quantit'e d'ajustement du modèle au donn'ees. Un tel examen peut r'ev'eler un mauvais choix du modèle de r'egression, ou une erreur dans les contraintes impos'ees aux paramètres.

Enfin, pour revenir a` la validation du modèle, c'est sans doute l'examen de diverses
repr'esentations graphiques des r'esidus qui fournit le moyen de validation le plus int'eressant.

2.7 Notions de simulation

2.7.1 Définition de la simulation

La simulation est une technique qui consiste a` construire un modèle d'une situation r'eelle, puis a` faire des exp'eriences sur ce modèle. Cette d'efinition est toutefois très vaste, et dans notre travail on considère la simulation telle que d'efinie par Naylor et al : » La simulation est une technique num'erique pour 'elaborer des exp'eriences sur l'ordinateur. Elle implique l'utilisation de modèles logiques et math'ematiques qui d'ecrivent le comportement de systèmes administratifs ou 'economiques (ou de leurs sous-systèmes) durant une p'eriode de temps prolong'ee»[3].

2.7.2 Les étapes de la simulation

Les diff'erentes 'etapes a` suivre pour faire une simulation d'un système sont :

1. Formulation du modèle : cette 'etape consiste a` identifier et analyser le problème, en d'eterminant ses composantes, leurs relations et les frontières entre le système et son environnement.

2. 'Elaboration du modèle : cette 'etape consiste a` extraire un modèle aussi fidèle que possible du système r'eel.

3. Identification du modèle et collecte de donn'ees : la collecte de donn'ees est indispensable pour l'estimation des paramètres du modèle. Ceci requiert une connaissance des m'ethodes statistiques et des tests d'hypothèses.

4. Validation du modèle : cette 'etape consiste a` 'evaluer les performances du modèle puis les comparer a` celles du système r'eel.

5. Ex'ecution de la simulation : pour mettre a` l''epreuve le modèle. Le concepteur doit effectuer plusieurs ex'ecutions et recueillir les r'esultats.

6. Analyse et interpr'etation des r'esultats : une fois les r'esultats obtenus, le concepteur passe a` l'analyse et l'interpr'etation de ces r'esultats pour donner des recommandations et des propositions.

7. Conclusion : cette dernière 'etape consiste a` 'evaluer les perspectives d'exploitation du modèle pour d'autres pr'eoccupations.

2.7.3 Problème du temps en simulation [11]

Consid'erons le problème d'une file d'attente : un client arrive au système, rejoint soit la file soit le serveur, il est servi pendant un certain temps et enfin il libère le serveur et quitte le système.

On voit que ses temps d'arriv'ee, d'attente, de service et de lib'eration du serveur, doivent être synchronis'es par le modèle. Pour r'epondre a` cette exigence, on peut agir de deux manières :

2.7.3.1 Méthode synchrone ou simulation par horloge

Dans ce type de simulation, le temps du modèle est avanc'e par une unit'e de temps choisie 'egale a` Lt. La mise a` jour du système est assur'e par l'ensemble des 'ev'enements qui se r'ealisent durant cet intervalle de temps. Si Lt est choisi assez petit, un nombre presque n'egligeable d''ev'enements peuvent se r'ealiser dans cet intervalle; par cons'equent si Lt est suffisamment grand, on peut rater beaucoup de ces 'ev'enements.

On voit que la robustesse du modèle repose donc sur le choix de Lt.

2.7.3.2 Méthode asynchrone ou simulation par événements

Elle diffère de la première par le fait que le temps est avanc'e par une quantit'e variable d'eterminant l'instant de r'ealisation d'un 'ev'enement.

Dans ce genre de simulation, il faut noter que chaque 'ev'enement provoque un changement dans l''etat du système; donc il faut prendre en consid'eration ce changement au niveau du programme qui d'ecrit le modèle.

Dans le cas des files d'attente, et a` titre d'indication, on peut pr'evoir une liste d''ev'enements a` deux dimensions : l'une des colonnes donne le temps de r'ealisation d''ev'enement et l'autre donne le num'ero du sous programme qu'il faudrait ex'ecuter pour sch'ematiser le changement de l''etat du système que provoque cet 'ev'enement.

2.7.3.3 Avantages et inconvénients de la simulation

Comme toute approche scientifique, la simulation pr'esente des avantages et des inconv'enients.

Avantages

- Seule alternative technologique quand le système a` 'etudier est physiquement difficile a` d'eployer.

- R'ep'etitions d'exp'eriences.

- Permet de r'epondre a` des questions de type, qu'est-ce qui se passe si . . . Moins d'hypothèses simplificatrices.

- Permet d'adresser des systèmes très complexes.

Inconv'enients

Quant a` ses inconvénients, on cite :

- Très gourmand en ressources (cpu, disks, . . . ).

- Coàuteux en terme de temps de calcul.

- Résultats orientés pire-cas généralement sans validité.

- Elle ne fournit que des estimations de ce que l'on cherche.

2.7.4 G'en'eration de variables al'eatoires [5]

Il s'agit d'engendrer une variable aléatoire X suivant une certaine loi a` partir des lois plus simples (loi uniforme [0, 1]) en se basant sur des techniques connues dont les principales sont citées ci-dessous.

2.7.4.1 La m'ethode d'inversion

La méthode de l'inverse n'est utilisée que si la fonction densitéest connue analytiquement, continue et peut être intégrer facilement, elle est définit comme suit : pour générer une variable aléatoire X ayant une fonction densitéf(x) et une fonction de répartition F(x), il suffit de générer des nombres aléatoires ui de variable aléatoire U[0, 1] et déduire :

x = F -1

x (u), ?x.

G'en'eration de variables al'eatoires suivant une loi exponentielle

Pour simuler une variable aléatoire qui suit une loi exponentielle, il suffit de générer des nombres aléatoires uniformes sur [0, 1] et déduire les réalisations xi, telles que :

xi = -1 ë log(ui).

G'en'eration de variables al'eatoires suivant une loi Uniforme

Pour simuler une variable aléatoire uniforme sur [a, b], il suffit de générer des nombres aléatoires ui de variable aléatoire uniforme sur l'intervalle [0, 1] et déduire les réalisations xi, telles que :

xi = a + (b - a)ui .

2.7.4.2 La m'ethode de rejet [1]

La méthode de rejet peut être utiliser si la fonction densitéf(x) est bornée et la variable aléatoire X appartient a` un domaine borné, c'est-à-dire : a = X = b. Elle se résume en quatre étapes :

1. Normaliser le domaine de f(x) a` l'aide d'une échelle c, de sorte que :

g(x) = c[f(x)] = 1, a = X = b.

2. Définir X comme fonction linéaire de r :

X = a + (b - a)r .

3. Générer une paire de nombres aléatoires (r1, r2) de loi uniforme sur [0,1].

4. Chaque fois que l'on rencontre une paire de nombres aléatoires satisfaisants : r2 c[f(a + (b - a)r1)],

on accepte X = a + (b - a)r1 comme variable aléatoire suivant f(x). 2.7.4.3 La méthode de composition [3]

La méthode de composition consiste a` remplacer f(x) par un mélange probabiliste de fonctions de densités gj(x) judicieusement choisies. Autrement dit, elle exploite une relation du type:

f(x) = _Xn gj(x)pj.

j=1

2.8 Conclusion

Dans ce chapitre, nous avons rappeléquelques notions de base concernant la convexité, les systèmes d'attente, la régression et la simulation qui seront utilisées dans les chapitres quatre et cinq.

3

Tests et ajustements

3.1 Introduction

Dans ce chapitre, nous rappelons quelques notions sur les tests d'ajustement et l'estimation par intervalle de confiance pour les utiliser ensuite dans la détermination de la loi régissant le besoin journalier en camions, le calcul de l'intervalle de confiance de ce dernier et dans la détermination de la distribution du temps aléatoire de service des camions.

3.2 Tests d'ajustement

Les tests d'ajustement ont pour but de vérifier si un échantillon provient ou pas d'une variable aléatoire de distribution connue F0(x).

Soit F_n(x), la fonction de répartition de la variable échantillonnée. Il s'agit de tester :

H0 » F_n(x) = F0(x) » contre H1 » F_n(x) =6 F0(x) » Les tests les plus classiques sont :

3.2.1 Test de Khi-deux [12]

Soit X1, X2, .. . , X_nun n-échantillon issu d'une variable aléatoire X.

On partage le domaine D de la variable aléatoire X, partie de l' ensemble des réels R, en r classes c1, c2, .. . , c_r. Généralement, on prend r ' vn.

Soit :

* ni : l'effectif de la classe ci.

Xr i=1

(Ni - npi) npi

suit asymptotique-

* pi : la probabilitéde se trouver dans la classe ci. Elle est déduite a` partir de la loi de probabilitéa` tester.

* nipi : effectif théorique de la classe ci

Pearson a démontréque la variable aléatoire K2 fl =

ment un Khi-deux a` (r - 1) degrés de liberté.

Ni étant la variable aléatoire représentant l'effectif de la classe ci et dont la réalisation est ni.

Soit k2 fl la réalisation de la variable aléatoire K2 fl. La règle de décision est alors :

· Si k2 fl < ÷2 (r-1,á), on accepte l'ajustement de la variable aléatoire X par la loi choisie avec un niveau de signification a.

· Si k2 fl > ÷2 (r-1,á), on rejette l'ajustement de la variable aléatoire X par la loi choisie avec un niveau de signification a.

Lorsque les paramètres de la loi a` valider sont estimés a` partir de l'échantillon, le degréde libertédu Khi-deux est alors égale a` (r -l-1), l étant le nombre de paramètres estimés. L'application du test du Khi-deux doit satisfaire les conditions suivantes :

1. Le nombre de classes doit être supérieur ou égale a` 7.

2. L'effectif théorique npi de chaque classe doit être supérieur ou égale a` 8.

Remarque 3.1. Si le nombre de degréde libertéest supérieur a` 30, on peut assimiler la

/ fl - v2r ? ?(0, 1).

loi de Khi-deux par une loi normale. On montre que 2K²

3.2.2 Test de Kolmogorov-Smirnov[16]

Soit X1, X2, . . . , _Xflun n-échantillon issu d'une variable aléatoire X que l'on veut ajuster par une loi théorique F0(x). Soit F_fl(x) sa fonction de répartition empirique.

Kolmogorov a démontréque la variable aléatoire Dfl = max F_fl(x) - F0(x) avec x E R suit asymptotiquement une loi indépendante de F0, Telle que :

lim P(vnD_fl < t) = ~(x),

fl?8

avec

? ??

??

h(t) =

(-1)^ke^-2k2x2, pour x > 0.

0, pour x = 0

Cette fonction est tabulée (table de Kolmogorov).

Soit d(a) la valeur tabulée, telle que p(D_n > d(a)) = a, avec a un seuil de signification fixéa` l'avance. La règle de décision est alors :

· Si Dfl > d(a), on rejette l'ajustement de la variable aléatoire X par la loi choisie.

· Si D_n < d(a), on accepte l'ajustement de la variable aléatoire X par la loi choisie.

3.3 Estimation par intervalle de confiance[16]

On appelle intervalle de confiance au niveau (1 - á) pour un param`etre è, l'intervalle [T1(x1, x2, .., x_n),T2(x1, x2, .., _xn)] tel que :

P(T1(x1, x2, .., x_n) = è = T2(x1, x2, .., x_n)) = 1 - á,

avec á donne, T1(x1, x2, .., x_n) et T2(x1, x2, ..,x_n) sont appeles limites de confiance de è au niveau (1 - á).

Soit è^à un estimateur ponctuel de è. Pour determiner les bornes de confiance, on doit determiner les deux constantes î1 et î2 telles que :

á1 = P(T < è - î1) et á2 = P(T > è + î2) ,

á1 = á2 = ^á₂, avec á donneet T=^àè.

On a P(è - î1 < T < è + î2) = 1 - á, par transformation on aura :

f T < è + î2 f è > T - î2

T > è - î1 lè < T + î1

Ce qui donne P(T - î2 < è < T + î1) = 1 - á , Alors les deux statistiques sont :

ü T1(x1, x2, .., x_n)=T-î2,

ü T2(x1, x2, ..,x_n)=T+î1.

3.4 Loi r'egissant le besoin journalier en camions

Pour determiner le nombre moyen ainsi que le nombre minimum et maximum de camions utilises, on a eu recours aux donnees concernant le nombre journalier de camions utilises dans les dix mois derniers (Aoàut jusqu'au mois de Mai), comme le montre le tableau suivant :

Date i		Nombre de camions utilises a` la date i	19/08/2006
48		. .
. .		24/05/2007
51

TAB. 3.1 - Nombre journalier de camions utilises

3.4.1 Application au cas d'Ifri

Soit X » Le nombre de camions utilises en un jour donne»

3.4.1.1 Ajustement des données avec le test de Khi-deux :

Soit un 234-échantillon constituédes données concernant le nombre journalier de camions utilisés dans les dix mois derniers (Aoàut jusqu'au mois de Mai). On veut tester si la loi de X est une loi de poisson, donc on va tester:

H0 »Poisson est la loi de X» Contre H1 »Poisson n'est pas la loi de X»

En partitionnant le domaine des valeurs de X en 7 classes, le tableau suivant nous donne l'effectif empirique de chaque classe, les probabilités théoriques rattachées, l'effectif théorique, le pourcentage cumuléthéorique et observé.



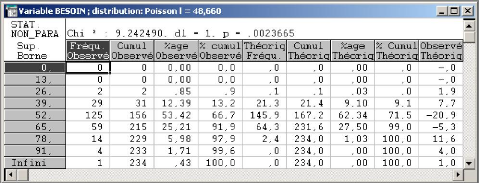
FIG. 3.1 - Tableau représentant les paramètres calculés La réalisation de la statistique de décision nous a donné:

K2 n

=

Xn i=1

(Ni - npi)^2 npi

= 9.24.

Dans la table de Khi-deux, on a :

÷2 (r-1-1,á) = ÷2 (5,0.05) = 11.07,

tel que r représente le nombre de classes et á le niveau de signification.

K2 n =

Xn i=1

(Ni - npi)^2 npi

= 9.24 < ÷^2(r-1-1,á) = ÷2 (5,0.05) = 11.07,

d'o`u on accepte que le nombre de camions utilisés a` une date donnésuit une loi de poisson de paramètre ë=48.66.

X P(ë = 48.66).

Le schéma suivant nous montre le graphe d'ajustement par la loi de poisson. En rouge l'histogramme de la loi de poisson, en bleu l'histogramme des données observées.



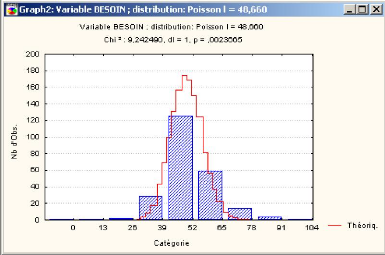
FIG. 3.2 - Graphe d'ajustement par la loi de poisson

Conclusion :

Avec les données récoltées, le test de Khi-deux révèle que la loi régissant le besoin journalier en camions est poissonnienne de paramètre A = 48.66.

Pour confirmer et justifier l'acceptation du processus poissonnien comme processus qui régis le nombre de camions utilisés, on va refaire le test d'ajustement par une loi de poisson et cela par le test d'ajustement de Kolmogorov-Smirnov.

3.4.1.2 Ajustement des données avec le test de Kolmogorov-Smirnov

Soit un 234-échantillon constituédes données concernant le nombre journalier de camions utilisés dans les dix mois derniers (Aoàut jusqu'au mois de Mai) de fonction de répartition F, on veut tester si la loi de X est une loi de poisson, donc on va tester :

H0 »Poisson est la loi de X» Contre H1 »Poisson n'est pas la loi de X»

En partitionnant le domaine des valeurs de X en 7 classes, le tableau suivant nous donne l'effectif empirique de chaque classe, les probabilités théoriques rattachées, l'effectif théorique, le pourcentage cumuléthéorique et observé.



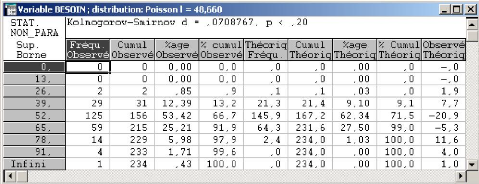
FIG. 3.3 - Tableau représentant les paramètres calculés

Le plus grand écart entre la distribution empirique et la distribution théorique (loi de poisson) est :

D = max |F_n(x) - F0(x)| = 0.070,

tel que F0 est la fonction de répartition de la loi de poisson. Dans la table de Kolmogorov-Smirnov on a :

1.30

d(N, a) = d(234, 0.05) = _v234 = 0.085,

avec N représente la taille de l'échantillon et a le niveau de signification. D = max |F_n(x) - F0(x)| = 0.070 < d(N, a) = 0.085,

d'o`u on accepte que le nombre de camions utilisés a` une date donnésuit une loi de poisson de paramètre A estiméa` 48.66.

Le schéma suivant nous montre le graphe d'ajustement par la loi de poisson. En rouge l'histogramme de la loi de poisson, en bleu l'histogramme des données observées.



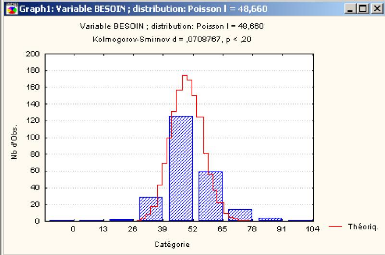
FIG. 3.4 - Graphe d'ajustement par la loi de poisson

Conclusion :

Le test de Kolmogorov-Smirnov nous confirme que le processus r'egissant le besoin journalier en camions est poissonnien. Donc on peut affirmer que la loi de X est une loi de poisson de paramètre A = 48.66.

3.4.2 Intervalle de confiance du besoin en camions

Jusqu'àpr'esent, nous n'avons d'etermin'e que l'estimation ponctuelle de A, not'e ^àA. On sait seulement que si la taille de l''echantillon est grande l'estimateur A^à se rapproche de plus en plus de A.

Une telle situation est souvent peu satisfaisante surtout dans notre cas, pour cela nous allons d'eterminer deux statistiques T1(x1, x2, .., x_n) et T2(x1, x2, .., x_n) telles que : l'intervalle [T1(x1, x2, .., x_n), T2(x1, x2, .., x_n)] contienne la valeur exacte mais inconnue de A.

Intervalle de confiance de A :

Soit le 234-'echantillon issu de X P(A = 48.66). Le but est de trouver un intervalle

de confiance au niveau (1-a) pour le paramètre A.

On a estim'e A par la statistique T =X = 1 n _Xn Xi = 48.66.

i=1

ü T1(x1, x2, .., x_n)= X-î2

ü T2(x1, x2, .., x_n)= X+î1

P( X < ë - î1) = á2 et P( X > ë + î2) = á 2 .

Calcul de î1 :

X P(ë), donc X = 1 Pn i=1 Xi P(ë)

n

On a ë=48.66>10, donc on peut approcher la loi de poisson par une loi normale, alors ^X ?(ë, ë).

P( X < ë - î1) = á2 = P(	X - ë v< ë		ë - î1- ë) = P( vë	X - ë < v ë	-î1) vë
d^ro`u ö(		-î1á = vë ) 2 .

î1ë 2 á î1 á

On a : 1 - ö( ) = alors = (1 - ₂),
v

et donc î1 = 1^àëö^-1(1 - 2).

Calcul de î2 :

P( X > ë + î2) = á2 = P(	X - ë > vë		ë + î2 - ë) = P( vë	X - ë 2 > vë
d^ro`u P(		X - ë î2 vë v ë < ) = 1 - 2.



î2 á

î2 á

On a : ö( _vë) = 1

2 -1

alors = ö (1 - ₂),

et donc î2 = ^-0,ö^-1(1 - ₂).

Ce qui donne :

î1 = î2 = - Vàëö-1( ^á2 ),

alors

X - V^àëö^-1(1 - á2 ) = ë = X + V^àëö^-1(1 - á2 )

L'intervalle de confiance sera donc :

- V^àëö^-1(1 - á2 ), X+ V^àëö^-1(1 - á2 )] Pour un niveau de confiance 1-á =95%, on aura :

ö^-1(1 - á2 ) = ö^-1(1 - 0.025) = ö^-1(0.975) = 1.96.

L'intervalle de confiance sera:

\/ \/

[ ^X - 1.96 ^àë, ^X + 1.96 ^àë].

On a X = ë^à = 48.66. On remplace ^X _et ë^à par leurs valeurs, l'intervalle de confiance devient :

[34.98,62.33]

3.4.3 Conclusion

Cette 'etude nous a permis de d'eterminer la loi r'egissant le besoin journalier en camions et cela grace a` l'ajustement par une loi de poisson des donn'ees concernant le nombre de camions utilis'es durant la p'eriode entre septembre 2006 et mai 2007.

L'ajustement par la loi de poisson nous a permis aussi, a` un niveau de confiance de 95%, de d'eterminer l'intervalle de confiance du paramètre ë consid'erer comme la moyenne de la loi de poisson et comme esp'erance de la variable X. En effet, dans ce cas ë repr'esente le besoin moyen journalier en camions.

Durant la p'eriode 'etudi'ee, le nombre moyen de camions utilis'es est de 48.66. On est confiant a` 95% que le besoin journalier en camions est compris entre 34 et 63 camions.

3.5 La distribution du temps aléatoire de service des camions

Actuellement, le champ d'action de la SARL IBRAHIM & Fils s''etend sur tout le territoire national. Le temps n'ecessaire pour servir un client varie en fonction de la distance qui s'epare ce dernier de l'entreprise, les clients les plus proches sont servis en une seule journ'ee et les plus loin n'ecessitent neuf jours de route et cela pour un Aller-retour.

Vu la variation des temps de service entre 1 et 9 jours en fonction des trajets et pour d'eterminer le temps moyen de service, on a eu recours aux donn'ees concernant les trajets effectu'es et cela pour chaque jour (Aoàut jusqu'au mois de Mai) et chaque camion.

Le tableau suivant nous donne les donn'ees utilis'es pour l'ajustement des dur'ees de services.

Date i	camion N^°	temps de service (jour)
19/08/2006	1	1
19/08/2006	2	1
19/08/2006	3	2
19/08/2006	4	7
19/08/2006	5	9
. .	. .	. .
01/02/2007	1	1
01/02/2007	2	4
01/02/2007	3	4
01/02/2007	4	2
01/02/2007	5	3
01/02/2007	6	7
. .	. .	. .
24/05/2007	1	3
24/05/2007	2	1
24/05/2007	3	9

TAB. 3.2 - Durée de service

3.5.1 Application au cas d'Ifri

Soit Y » Le temps nécessaire pour servir un client»

3.5.1.1 Ajustement des données avec le test de Khi-deux

Soit un 11324-échantillon constituédes données concernant les temps de service chaque jour durant les dix derniers mois (Aoàut jusqu'au mois de Mai). On veut tester si la loi de Y est une loi exponentielle, donc on va tester :

H0 » La loi exponentielle est la loi de Y» Contre

H1 »La loi exponentielle n'est pas la loi de Y».

On partitionne le domaine des valeurs de Y en 7 classes, le tableau suivant nous donne l'effectif empirique de chaque classe, les probabilités théoriques rattachées, l'effectif théorique, le pourcentage cumuléthéorique et observé.



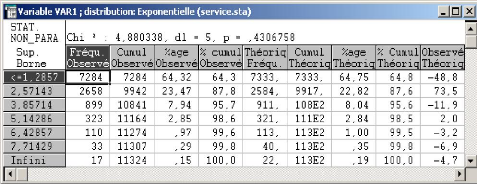
FIG. 3.5 - Tableau représentant les paramètres calculés La réalisation de la statistique de décision nous a donné:

K2 n Dans la table de Khi-deux on a :

=

Xn i=1

(Ni - npi)^2 npi

= 4.88.

÷2 (r-1-1,á) = ÷2 (5,0.05) = 11.07.

Tel que r représente le nombre de classes et a le niveau de signification

K2 n =

Xn i=1

(Ni - npi)^2 npi

= 4.88 < ÷2 (r-1-1,á) = ÷^2(5,0.05) = 11.07.

On accepte que la durée de service suit une loi exponentielle de paramètre ,i=0.8111.

Y Exp(,i = 0.8111).

Le schéma suivant nous montre le graphe d'ajustement par la loi exponentielle. En rouge l'histogramme de la loi exponentielle, en bleu l'histogramme des données observées.



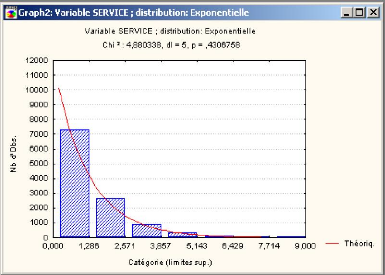
FIG. 3.6 - Graphe d'ajustement par la loi exponentielle

Conclusion :

Avec les données récoltées, le test de Khi-deux révèle que la loi régissant les durées de service est exponentielle de paramètre u = 0.8111.

Pour confirmer et justifier l'acceptation de la loi exponentielle comme loi qui régis la durée de service, on va refaire le test d'ajustement par une loi exponentielle et cela par le test d'ajustement de Kolmogorov-Smirnov.

3.5.1.2 Ajustement des données avec le test de Kolmogorov-Smirnov

Soit un 11324-échantillon constituédes données concernant les temps de service chaque jour durant les dix derniers mois (Aoàut jusqu'au mois de Mai), on veut tester si la loi de Y est une loi exponentielle, donc on va tester :

H0 » La loi exponentielle est la loi de Y» Contre

H1 »La loi exponentielle n'est pas la loi de Y».

On partitionne le domaine des valeurs de Y en 7 classes, le tableau suivant nous donne l'effectif empirique de chaque classe, les probabilités théoriques rattachées, l'effectif théorique, le pourcentage cumuléthéorique et observé.



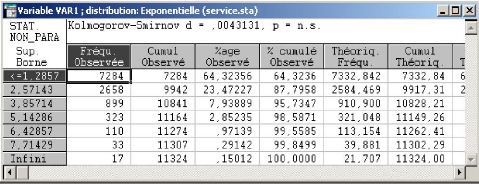
FIG. 3.7 - Tableau représentant les paramètres calculés

Le plus grand écart entre la distribution empirique et la distribution théorique (loi exponentielle) est :

D = max |F_n(x) - F0(x)| = 0.0043,

tel que F0 est la fonction de répartition de la loi exponentielle. Dans la table de Kolmogorov-Smirnov on a :

1.30

d(N, a) = d(11324, 0.05) = v11324 = 0.0122,

avec N représente la taille de l'échantillon et a le niveau de signification.

1.30

D = max |F_n(x) - F0(x)| = 0.0043 < d(N, a) = d(11324, 0.05) = v11324 = 0.0122.

On accepte que que la loi régissant les durées de service est exponentielle de paramètre u = 0.8111.

Le schéma suivant nous montre le graphe d'ajustement par la loi exponentielle. En rouge l'histogramme de la loi exponentielle, en bleu l'histogramme des données observées.



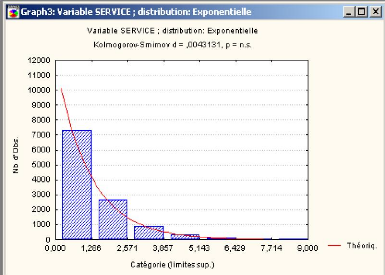
FIG. 3.8 - Graphe d'ajustement par la loi exponentielle

Conclusion

Le test de Kolmogorov-Smirnov nous confirme que la loi régissant les durées de service est exponentielle. Donc on peut affirmer que la loi de Y est une loi exponentielle de paramètre u = 0.8111.

3.6 Conclusion

Dans ce chapitre, nous avons effectuédes ajustements sur la loi régissant le besoin journalier en camions et la distribution du temps aléatoire de service des camions pour les utiliser dans les chapitres quatre et cinq.

4

D'etermination du nombre de camions

4.1 Introduction

La mod'elisation est sans doute l''etape la plus importante dans une 'etude quelle qu'elle soit. Avant de d'eterminer un modèle math'ematique utilis'e en recherche op'erationnelle et d'expliquer les m'ethodes qui sont g'en'eralement mises en oeuvre a` partir de ces modèles pour obtenir des conclusions int'eressantes, nous nous efforcons de faire apparaàýtre la nature propre du sujet et le domaine a` l'int'erieur duquel vont se placer nos pr'eoccupations.

Dans ce chapitre, nous allons nous efforcer de se rapprocher le plus possible de la r'ealit'e, en pr'esentant pour chaque problème son modèle math'ematique correspondant, et avec plusieurs approches si c'est possible.

4.2 Problématique

On veut d'eterminer le nombre de v'ehicules qui r'epond le mieux aux exigences de l'entreprise compte tenu de la demande journalière, des diff'erentes destinations et leurs distance (dur'ee de services) respectives, la capacit'e de production et le profit r'ealis'e ou coàut engendr'e par v'ehicule.

4.3 Approche par files d'attente

4.3.1 Modèle avec file

On considère un parking de camions o`u les clients arrivent selon un processus de poisson de taux ë, le service correspondant a` une livraison par un camion, et les dur'ees de



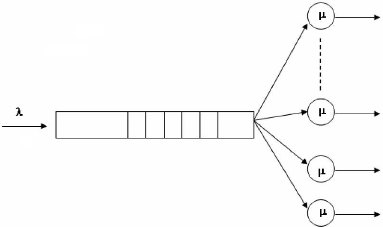
service sont indépendantes et suivent toutes une loi exponentielle de moyenne 1/u. Dans cette approche, nous allons représenter chaque véhicule par un serveur et les demandes journalières par des clients. Dans le chapitre trois (tests et ajustements), nous avons pu ajuster la loi qui régisse la demande journalière et cela pour déterminer le processus d'arrivée des clients qui est un processus poissonnien de taux A = 48.66 camions/jour. Quand a` la loi de service, pour chaque camion, elle est exponentielle de taux u = 0.8111.

En résumé:

- Le nombre de serveurs est m, a` déterminer, et sont tous identiques avec la même loi de service qui est exponentielle de moyenne1 u (le temps nécessaire pour livrer et revenir a` l'usine).

- Les clients arrivent selon un processus de Poisson de taux A et sont servis selon leur ordre d'arrivée suivant la discipline (FIFO).

- La capacitéde la file est infinie.

Donc le modèle a` étudier est un modèle M/M/m (FIFO,8) comme représentédans le schéma suivant :

FIG. 4.1 -

Avec cette approche, pour déterminer le nombre de serveurs, on va utiliser les caractéristiques du système et ensuite faire le chemin inverse. Le but de l'entreprise est de satisfaire la demande de sa clientèle et de réaliser le maximum de profit possible, et pour cela, soit on fixe le nombre de clients, soit le temps d'attente dans la file puis déterminer le nombre de serveurs correspondant.

Comme mentionnedans le chapitre deux (Rappels theoriques), le temps d'attente W et le nombre de clients dans la file Q se calculent comme suit :

La longueur moyenne de la file Q est :

Q =

8 E k=m+1

m^m (k - m)ðk = ð0 m!

8 E k=m+1

(k - m)( r n ^ñn)^k = 7ro^ñr^m!^cE^° k=1

k( ^ñ )k, m

ñ

_ñm+1

soit _ñm 1 m \

Q = 7ro m! (1-- _m)² ) = ⁷⁰ (m--1)!(m--ñ)2 .

On a aussi Q =

8 E k=m+1

8 kðk - m V z_., k=m+1

ðk = N - (

m E k=1

kðk +

8 E k=m+1

mðk) = N - ñ.

ñ =

m-1E k=1

kðk -

m-1 E k=0

mðk + m (car

8 E k=0

ðk = 1),

Avec



k=0

₁-1

.

Fm-1 _ñk _ñm

ð0 = [E+

k! m!(1 - mñ )

Pour eviter l'engorgement, il faut que la condition d'ergodicitesoit verifiee : mñ < 1 soit ë < mu.

Avec les param`etre du syst`eme ë = 48.66 et u = 0.8111, on aura : m > ë/u = 59.99 donc il faut avoir au moins 60 camions.



Le nombre moyen de clients dans le syst`eme N est : N = Q + ñ .

Le temps moyen d'attente dans la file est : W = Që .

Le temps moyen d'attente dans le syst`eme est : T = Në = W + ^1u .

Le nombre moyen de camions inoccupes, d'apr`es l'equation des debits on a :



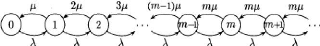
FIG. 4.2 -

8 m-1 8

_E ëðk = _E kuðk + _E muðk,

k=0 k=1 k=m

8 m-1 8

ë E ðk = u( _E kðk + _E mðk),

k=0 k=1 k=m

d'o`u m-1_X (m - k)ðk = m - p.

k=0

Si on note par g le gain moyen d'un camion et par Cf le coàut fixe engendrépar un camion par unitéde temps (jour), alors le gain moyen journalier G pour un parc de m camions est :

D'apres le théoreme de Burke, le nombre moyen de clients servis par unitéde temps est A. Ce qui donne

G(m) = gA - mCf.

Donc pour différentes valeurs de m, on obtient le tableau suivant :

Nbr de serveurs		60			61			62			63			64			65			66			67		68			69
Q/(jours)		8100,61			50,70			21,54			12,09			7,57			5,02			3,44			2,40		1,70			1,21
N/(jours)		8160,60			110,69			81,53			72,08			67,56			65,01			63,43			62,40		61,69			61,20
W(jours)		166,47			1,04			0,44			0,24			0,15			0,10			0,07			0,04		0,03			0,02
T(jours)		167,70			2,27			1,67			1,48			1,38			1,33			1,30			1,28		1,26			1,25
Nbr de serveurs		70		71			72			73			74		75			76			77			78			79
Q/(jours)		0,87		0,62			0,44			0,31			0,22		0,16			0,11			0,07			0,05			0,03
N/(jours)		60,86		60,61			60,43			60,31			60,21		60,15			60,10			60,07			60,04			60,03
W(jours)		0,01		0,01			0,009			0,006			0,004		0,003			0,002			0,001			0,001			7,83E-04
T(jours)		1,25		1,24			1,24			1,23			1,23		1,23			1,23			1,23			1,23			1,23
Nbr de serveurs	80		81			82			83			84				85			86			87				88			. . .
Q/(jours)	0,02		0,01			0,01			0,008			0,005				0,003			0,002			0,001				E-04			~
N/(jours)	60,01		60,01			60,00			60,00			59,99				59,99			59,99			59,99				59,99			~
W(jours)	E-04		E-04			E-04			E-04			E-04				E-05			E-05			E-05				E-05			~
T(jours)	1,23		1,23			1,23			1,23			1,23				1,23			1,23			1,23				1,23			~

4.3.1.1 Interprétation des résultats

Pour minimiser le nombre de clients ou le temps d'attente dans la file et par conséquent répondre au mieux aux exigences de la clientele, on doit disposer du maximum de camions possible a` la limite de la capacitéde production, c'est un objectif qui est directement proportionnel a` la taille de la flotte. Par contre, réaliser le plus grand profit tout en évitant l'engorgement impose de limiter la taille de la flotte a` 60 véhicules. Des que le nombre de camions dépasse les 60, le gain moyen journalier G décroàýt et cela est dàu aux coàuts fixes engendrés par l'inactivitédes camions par unitéde temps, donc c'est un objectif qui est inversement proportionnel a` la taille de la flotte.



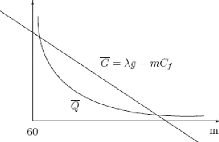
FIG. 4.3 -

4.3.1.2 Conclusion

Avec ce modèle, trouver un compromis entre le gain moyen journalier et le nombre moyen de clients dans la file n'est pas 'evident. Car lorsqu'on opte pour le gain, et par cons'equent r'eduire la taille de la flotte, ceci engendre un nombre de clients avec un temps d'attente dans la file consid'erable, dans ce cas, si on est confront'e a` un march'e concurrentiel il y aurait des d'ecouragement de certains clients pour s'adresser a` un concurrent. Pour prendre en consid'eration ces pertes, on va consid'erer un modèle avec d'ecouragement puis trouver un compromis entre les gains et les pertes.

4.3.2 Modèle sans file (avec découragement)

On considère a` nouveau le modèle pr'ec'edent avec les mêmes paramètres, mais cette fois ci sans file. Chaque camion joue le ràole d'un serveur et le modèle 'etudi'e est M/M/m( ,m) (il est a` noter que la discipline de service n'a pas de sens car il n'y a pas d'attente dans la file). Comme repr'esent'e dans le sch'ema suivant :



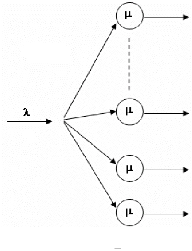
FIG. 4.4

On a

Q = 0 et W = 0 (pas de file).

T = W + 1 = 1 et N = ë(1 - ð_m)T = ñ(1 - ð_m) o`u ñ = ë/u,

u u



ð_m = ñm m! ð0 avec ð0 = 1 m _X

k=0

_ñk , k!

de plus, le nombre moyen de places occupées, par unitéde temps, est N.
Ce qui donne le nombre de places inoccupées par unitéde temps m - N.

Le bénéfice moyen journalier est donnépar:

G(m) = gN - mCf = gñ(1 - ð_m) - mCf, et ð_m est obtenu comme suit :



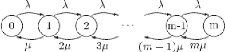
FIG. 4.5

ou encore	ðm =	1
		, ñm + m! m! ñm-1 + · · · +m(mñ2 ^-1) +^mñ + 1
ceci pour tout ñ.

Dans le modèle M/M/m+1 ( ,m+1)

1

,

(m+1)! _ñm+1 + (m+1)!

_ñm + · · · + (m+1)m

_ñ2 + m+1

ñ + 1

_ñm+1

=

(m+1)!

_ñk

ðm+1 =

k!

m+1
k=0

ce dernier dénominateur étant supérieur a` celui de ð_m, et pour tout ñ on a :

ðm+1 < ð_m.

Pour calculer _ðm+1 (probabilitéd'avoir m+1 serveurs occupés dans un système M/M/m+1 ( ,m+1)) en fonction de ð_m (probabilitéd'avoir m serveurs occupés dans un système M/M/m ( ,m)), on cherche une forme récurrente :

ðm+1 =	ñm+1 (m + 1)!^ð0						ñk ñ LJm k=0 k!
	ñm										1
=
	ñk m! Pm k=0 k!						(m + 1)				v.m+1 ñk k=0 k!
= ðm		ñ			Pm ñk k=0 k!
		m + 1			Pm+1 ñk k=0 k!
= ðm		~ Pm ~ ñk ñ k=0 k! m + 1(1 - ðm+1) car Pm+1 = 1 - ðm+1 ñk k=0 k!
d'o`u ðm+1 =			ñ m+1						et pour m = 0, on a évidement ð0 = 1.
			1 + ñm+1ðm

On calcule la variation Ä(m) = G(m) - G(m - 1) (m = 1).

Ä(m) = G(m) - G(m - 1)

= gñ(1 - ð_m) - mCf - gñ(1 - ðm-1) + (m - 1)Cf Ä(m) = gñ(ðm-1 - ð_m) - Cf

On calcule Ä(m + 1) - Ä(m) :

Ä(m + 1) - Ä(m) = gñ(ð_m - ðm+1 - ðm-1 + ð_m) = gñ(2ð_m - ðm+1 - ðm-1)

Le signe de Ä(m + 1) - Ä(m) est de même signe que (2ð_m - ðm+1 - ðm-1) car gñ est toujours positif.

On accepte sans démontrer que Ä(m + 1) - Ä(m) = 0 car les calculs s'avèrent très longs. Pour des différentes valeurs de m on calcule (2ð_m - ðm+1 - ðm-1), comme le montre le tableau suivant :

m	1	2	...	81	82	...	139	140
(2ðm - ðm+1 - ðm-1)	-8.81	-9.23	...	-0.00013	-0.00010	...	-9.785	-4.269

TAB. 4.1 - Variation de la fonction (2ð_m - ðm+1 - ðm-1).

On a Ä(m + 1) - Ä(m) = 0 donc Ä(m) est décroissante pour tout m, ce qui entraàýne la concavitéde G. Et Ä(m + 1) - Ä(m) = 0 s'écrit sous la forme :



G(m + 1) - G(m) - G(m) + G(m - 1) = 0 soit : G(m) = G(m+1)+G(m-1) .

2

Et on peut l'expliquer par le schéma classique d'une fonction concave. l'axe d'abscisses correspond au nombre de camions et les ordonnées au gain moyen journalier.



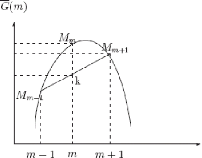
FIG. 4.6 - Schéma classique d'une fonction concave

Sur le schéma ci-dessus, on constate que l'ordonnée du milieu k de la corde Mm-1Mm+1 est au dessous du point M_m d'abscisse m et d'ordonnée G(m). Tel que :

- k correspond au point de coordonnées (m,G(m+1)+G(m-1)

₂ ).

- Les ordonnées des points respectivement _Mm-1, M_m et _Mm+1 correspondent aux
gains moyens journaliers pour respectivement un parc de m-1, m, et m+1 camions.
La valeur de m^* qui maximise la fonction gain G et celle qui satisfasse Ä(m^*) = 0
et Ä(m^* + 1) = 0. C'est a` dire que pour trouver m^*, il suffit de calculer les Ä(m) et
dès qu'on ait une valeur négative, le m correspondant n'est autre que la valeur optimale m^*.

Pour différentes valeurs du gain moyen journalier, on aura le tableau suivant :

g = 40000DA
m	...	74	75	76	77	78	79	80	81	. . .
Ä(m)	+	1436,18	435,55	-459,19	-	-	-	-	-	-
g = 50000DA
m	...	74	75	76	77	78	79	80	81	. . .
Ä(m)	+	2985,86	1735,06	616,63	-367,21	-	-	-	-	-
g = 60000DA
m	...	74	75	76	77	78	79	80	81	. . .
Ä(m)	+	4535,54	3034,58	1692,46	511,84	-509,67	-	-	-	-
g = 70000DA
m	...	74	75	76	77	78	79	80	81	. . .
Ä(m)	+	6085,22	4334,10	2768,29	1390,90	199,13	-815,05	-	-	-

TAB. 4.2 - Variation de la fonction Ä(m).

4.3.2.1 Interprétation des résultats

Avec les conditions normales de rentabilité(c-à-d le gain moyen journalier dépasse les coàuts fixes) et la demande considérée, on remarque qu'en partant d'une flotte de taille 0 et en augmentant a` chaque fois cette dernière d'un camion, le gain augmente car il n y aura pas de coàuts engendrés par des camions inutilisés. Mais dès que le nombre de camions dépasse une certaine limite, le surplus de camions inutilisés qui dépasse le besoins considéré, induit la décroissance de la fonction gain.

Pour les différentes valeurs du gain considérées, on obtient les dimensions de la flotte suivantes :

Valeur du gain	40000	50000	60000	70000
Dimension de la flotte	75	76	77	78

4.3.2.2 Conclusion

Avec ce modèle, on a pu trouver un compromis entre le gain journalier et les coàuts fixes engendrés par les camions.

Alors si l'entreprise décide d'augmenter la taille de sa flotte, elle aurait recours a` dépenser beaucoup d'argent car un camion coàute cher. La question qui ce pose est : est ce que l'entreprise n'aurait pas intérêt a` louer des camions au lieu d'en acheter?

L'approche suivante va nous aider a` répondre a` cette question.

4.4 Approche par minimisation d'une fonction convexe [8]

4.4.1 Introduction

Quand les décisions doivent être prises de manière séquentielle, les conséquences de chaque décision n'étant pas toujours parfaitement maàýtrisées mais pouvant être anticipées jusqu'àun certain point avant que la prochaine décision ne soit prise. Le but recherchéest la minimisation d'un coàut (ou la maximisation d'un profit) associéa` la suite de décisions retenues et a` leurs conséquences.

En effet, le désir d'un coàut immédiat aussi faible que possible doit généralement être évaluéa` la lumière du danger de coàuts futurs élevés[9].

Cette approche consiste a optimiser la taille m de véhicule que doit avoir l'entreprise et elle nous permettra d'atteindre le meilleur compromis possible entre les coàuts engendrés par la flotte ( un coàut fixe pour chaque véhicule possédéy compris les coàuts d'amortissement et d'assurance et un coàut variable pour l'utilisation de chaque camion) et les coàuts engendrés par le manque de camions (coàuts de location de camions ). On considère ce problème comme un problème de gestion de stock d'un parc de camions.

4.4.2 Le coàut fixe, coàut variable et coàut de location

L'entreprise supporte un coàut fixe de Cf DA par jour pour chaque véhicule ^possédé(ceci, qu'il roule ou qu'il reste au parc), il inclut entre autre l'amortissement et l'assu
rance. D'autre part l'utilisation de chaque véhicule de l'entreprise crée un coàut dit variable journalier de C_v DA.

Le coàut variable journalier d'un camion peut être déterminer en incluant la consommation en gasoil durant l'opération de livraison, la marge sur les salaires des chauffeurs, les frais de mission, une marge pour les pièces de rechange qui est fixée par l'entreprise. Pour un camion loué, le coàut Cl inclut le coàut fixe et le coàut variable.

4.4.3 Coàut total journalier d'un parc de m camions

Le coàut journalier C est une fonction de la demande aléatoire en camions D. Une statistique faite sur un historique récent a permis d'évaluer la probabilitép(w) d'avoir besoin de w camions pour un jour donné.

la probabilitép(w) d'avoir besoin de w camions pour un jour donnésuit une loi de poisson.
w P(ë = 48.66);

-ë_ëk

k! .

e

p(w = k) =

Exprimons C lorsque la taille de la flotte, n, est connue .

- Si D > m C=(Cf + Cv)m + (D - m)Cl

- Si D < m C=Cfm + C_vD
Le calcul de l'espérance mathématique du coàut total, soit C(m), est alors :

E(C) = C(m) =

m E ù=0

(Cfm + Cvù)p(ù) +

8 E ù=m+1

[(Cf + Cv)m + (ù - m)Cl]p(ù).

On va calculer la variation des coàuts A(m) = C(m) - C(m - 1) (m=1)

A(m) = C(m) - C(m - 1) =			m E ù=0	(Cfm + Cvù)p(ù) +			8 E ù=m+1	[(Cf + Cv)m + (ù - m)Cl]p(ù)
-	m-1E ù=0	(Cf(m - 1) + Cvù)p(ù) -			8 E ù=m	[(Cf + Cv)(m - 1) + (ù - m + 1)Cl]p(ù);

=

m-1_E
ù=0

(Cfm + C_vù)p(ù) + (Cfm + C_vm)p(m)

8 + E ù=m+1

[(Cf + Cv)m + (ù - m)Cl]p(ù) + Cf

m-1E ù=0

p(ù) -

m-1E ù=0

(Cfm + Cvù)p(ù)

-

8 E ù=m

[(Cf + Cv)m + (ù - m)Cl]p(ù) +^(Cv + Cf - Cl)

8 E ù=m

p(ù);

= (Cf + Cv)mp(m) +

8 E ù=m+1

[(Cf + Cv)m + (ù - m)Cl]p(ù)

+Cf

m-1E ù=0

p(ù) -

8 E ù=m+1

[(Cf + Cv)m + (ù - m)Cl]p(ù) - (Cf + Cv)mp(m)

+(Cv + Cf - Cl)

8 E ù=m

p(ù);

A(m) = C(m) - C(m - 1) = Cf + (Cv - Cl)

8 E ù=m

p(ù).

A(m) représente la différence de l'espérance du coàut total journalier pour un parc de m et m - 1 camions.

Si on calcule A(m + 1) - A(m), on aura :

A(m + 1) - A(m) = C(m + 1) - C(m) - C(m) + C(m - 1)

A(m+1) - A(m) = Cf + (Cv - Cl)

8 E ù=m+1

p(ù) - Cf - (Cv - Cl)

8 E ù=m

p(ù) = (Cl - Cv)p(m).

La fonction de variation A(m) est croissante puisque dans les conditions normales de rentabilitede l'entreprise, on a : Cl > C_v + Cf. Si les p(ù) sont strictement positifs pour tout ù, elle sera màeme strictement croissante.



2

.

On a V m e N, A(m + 1) - A(m) > 0, et donc elle peut s'ecrire sous la forme : C(m + 1) - C(m) - C(m) + C(m - 1) > 0 soit : C(m) < C(m + 1) + C(m - 1)

Ceci entraine la convexitede C(m), et on peut l'expliquer par le schema classique d'une fonction convexe. L'axe d'abscisses correspond au nombre de camions et les ordonnees a` l'esperance du coàut total journalier.



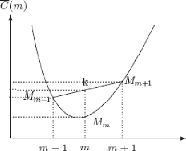
FIG. 4.7 - Schema classique d'une fonction convexe

Sur le schema ci-dessus on constate que l'ordonnee du milieu k de la corde Mm-1Mm+1 est au dessus du point M_m d'abscisse m et d'ordonnee C(m). Tel que :

(m, C(m₂ +1)+ Cm-1) ).

(

- k correspond au point de coordonnees

- Les ordonnees des points respectivement _Mm-1, M_m et _Mm+1 correspond au esperances mathematiques des coàuts totaux journalier pour respectivement un parc de m - 1, m, et m + 1 camions.

L'objectif de ce qu'on a fait jusqu'àpresent est la minimisation de C(m) qui est une fonction convexe. Donc la fonction objectif a` minimiser est :

min C(m) =

m E ù=0

(Cfm + Cvù)p(ù) +

8 E ù=m+1

[(Cf + Cv)m + (ù - m)Cl]p(ù).

Pour determiner le minimum de la fonction C(m), on partant de l'etat que l'entreprise poss`ede un seul camion et on calcule la variation des coàuts A(m) avec un

pas d'un camion. La procedure continue jusqu'`a ce que le signe change et on arràete.
L'abscisse correspondante au dernier point o`u la variation est negative est le point optimal.

Le point minimum de la fonction coàut total journalier sera le point d'ordonnee C(m^*) correspondante a` l'abscisse m^* qui verifie les deux conditions :

1. A(m^*) = 0

2. A(m^* + 1) = 0

Calculons m^* qui satisfait ces conditions :

A(m^*) = 0 ? A(m^*) = C(m^*) - C(m^* - 1) = Cf + (Cv - Cl)					8 E ù=m^*	p(ù) = 0.
1 -	m^*-1E ù=0	p(ù) =	m^*-1 Cf X ? Cl - Cv ù=0	p(ù) = Cl - (Cv + Cf) . Cl - Cv

Pour la deuxième condition :

A(m^* + 1) = 0 ? A(m^* + 1) = C(m^* + 1) - C(m^*) = Cf + (Cv - Cl)

8 E ù=m^*+1

p(ù) = 0.

1 -

_m*

E

ù=0

C

_m*

%-"N

^f '

p(ù) = ?

Cl - C_v

ù=0

p(ù) = Cl - (Cv + Cf)

l - Cv .

C

Pour trouver m^*, il suffit de cumuler les probabilites p(ù) et dès que le cumul d'epasse la

C/^-(Ct, #177;C f )

valeur le m correspondant n'est autre que la valeur optimale m^*.

4.4.4 Application au cas d'ifri

Pour les coilts fixes, variables et coilts de locations, que l'entreprise nous a communique :

Cf =4762,52 DA /camion/jour

C_v=3996 DA /camion/jour

Cl=30000 DA /camion/jour

On a :

Cl - (Cv + Cf )		21241,48	= 0.816.
Cl - Cv		26004

Pour depasser 0.816 en cumulant les probabilites, on trouve m^* = 55 camions.

4.4.5 Conclusion

Si l'entreprise opte pour la location, en cas de manque en camions dans son parc, le nombre qu'elle doit avoir est de 55 camions, car elle est limitépar le taux d'arrivées de sa client`ele. De plus, si elle dépasse ce nombre, les coàuts engendrés par l'inactivitédu surplus seront supérieurs au coàuts de location durant la période de leurs activités, par conséquent il est plus raisonnable de louer des camions que de les avoir et payer leurs charges.

Estimation du nombre de chauffeurs

5.1 Introduction

Ce chapitre est consacrer a` la modélisation et la résolution d'un tout autre problème qui s'impose et qui concerne le nombre de chauffeurs que devra disposer l'entreprise ifri pour une gestion optimale de ses camions. En premier lieu, nous allons cerner le problème en passant par une description physique du système, puis nous allons élaborer un modèle de simulation le représentant : C'est un programme informatique qui aura pour but principal d'estimer ce nombre de chauffeurs.

5.2 Analyse du système (description physique)

Après avoir déterminer le nombre de camions dont devra disposer l'entreprise (suivant chaque approche utilisée) dans le chapitre précédant, le nombre de chauffeurs correspondant pour une gestion optimale de ses camions pose problème. En effet, les normes imposées

par l'entreprise et le droit de travail créent une grande perturbation du système ^modéliséavec les camions seuls. Logiquement il faut avoir au minimum un nombre de chauffeurs

correspondant exactement au nombre de camions et au maximum a` deux fois ce nombre. Pour des raisons de sécuritéet pour un contrôle plus rigoureux, l'entreprise a affectépour chaque camion un chauffeur titulaire, puis pour couvrir leurs jours de repos l'entreprise a recrutédes chauffeurs remplacants.

Parfois, lors des livraisons, un chauffeur titulaire peut devenir remplacant, car en revenant de son repos et trouve son camion occupé, il sera affectéa` un autre. Donc chauffeur titulaire ou remplacant n'est qu'une formalitéet lors de la modélisation on ne considérera que le nombre de chauffeurs dans l'ensemble.



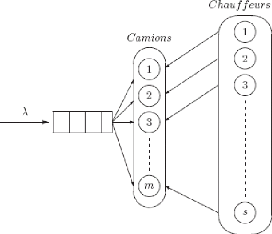
FIG. 5.1 - Représentation des chauffeurs

Vu la nouveautédes camions (de l'année 2006), l'entreprise veut les exploiter au maximum (pas de jours de repos pour les camions) et ce qui n'est pas le cas pour les chauffeurs a` qui on impose de travailler 5 jours sur 7. Et puisque la durée des trajets qui est aléatoire et varie entre 1 et 9 jours, on ne peut pas déterminer exactement le nombre de jours de travail par semaine pour un chauffeur. Ainsi, la politique adoptée par l'entreprise est qu'un chauffeur prend 2 jours de repos a` son retour d'une livraison dès qu'il atteigne ou dépasse 5 jours successifs de travail et tout se qui dépasse ses 5 jours sera considérécomme heures supplémentaires.

5.3 Repr'esentation du système

On étudie le système pour chaque unitéde temps qui représente 1 jour :

· La demande journalière (qui est un multiple de camions) arrive au début de chaque unitéde temps suivant une loi de poisson de paramètre ë = 48.66 et passe directement en file d'attente.

· Soit au début de chaque unitéde temps:

Nbrf : le nombre de clients présents dans la file. Nbrc : le nombre de camions disponibles.

- Nbrch : le nombre de chauffeurs disponibles.

Si on d'esigne par s le nombre de clients a` servir durant une unit'e de temps, alors : s=min{Nbrf, Nbrc, Nbrch}.

· Pour les s clients a` servir, la dur'ee de service est une variable al'eatoire exponentielle de paramètre u = 0.8111.

· Pour les chauffeurs, la dur'ee de service est la même que celle des camions puisque c'est eux qui conduisent, mais a` chaque fin de service, si un chauffeur cumule une dur'ee de service qui atteint ou d'epasse les 5 jours depuis son dernier repos, il prend a` nouveau un repos de 2 jours. Et c'est se qui pose problème dans la mod'elisation.

Si on note par :

* Di : la ^i`eme dur'ee de service depuis le dernier repos,

* R : dur'ee de repos.

Le sch'ema suivant nous montre la facon avec laquelle les chauffeurs travaillent :



FIG. 5.2 - Dur'ees de services des chauffeurs

En effet, prendre de nouveau son repos d'epend du cumul des dur'ees de service après son dernier repos. De plus, le cumul des dur'ees de service est une somme ind'etermin'ee de r'ealisations d'une variable al'eatoire exponentielle de paramètre u = 0.8111, car il se peut que la somme soit constitu'ee d'une seule r'ealisation, comme elle peut être constitu'ee de plusieurs. Ce qui veut dire que cet 'ev'enement ne d'epend pas seulement de l''etat pr'ec'edent, mais peut d'ependre de plusieurs 'etats ant'erieurs.

5.4 Pr'esentation du modèle de simulation

5.4.1 Description du simulateur

Avec une mod'elisation de notre problème par la simulation, on aura l'avantage de repr'esenter fidèlement notre système sans restriction sur les hypothèses. En effet, la simulation permet de consid'erer tous ou presque tous les paramètres composant notre système.

Dans cette mod'elisation, on a opt'e pour une approche temps car les ajustements ont 'et'e faits par rapport a` une journ'ee qui repr'esente l'unit'e de temps.

Le principe est de faire varier le nombre de chauffeurs, qui est un paramètre d'entr'ee, jusqu'àl'obtention d'un nombre de chauffeurs qui r'epond a` nos exigences.

5.4.2 Entr'ees du programme

5.4.2.1 Les donn'ees en entr'ee

Elles comportent les donn'ees suivantes :

· En premier lieu, nous fixons l'horizon qui est le temps de la simulation en jours

· On introduit le taux d'entr'ee ë=48.66

· Le paramètre de la loi exponentielle u=0.8111

· Le nombre de camions

· Le nombre de chauffeurs remplacants, ce qui veut dire que le nombre total de chauffeurs

serait 'egal au nombre de camions plus le nombre de chauffeurs remplacants

· La dur'ee de service cumul'ee d'un chauffeur avant de prendre son repos

· La dur'ee de repos d'un chauffeur

· Le modèle utilis'e : avec ou sans file.

5.4.2.2 Entr'ees g'en'er'ees

Elles comportes les donn'ees g'en'er'ees selon des lois de probabilit'e effectu'ees par des

g'en'erateurs de nombres al'eatoires comme :

· Les demandes journalières suivant une loi de poisson de paramètre ë.

· Les dur'ees de services suivant une loi exponentielle de paramètre u.

5.5 G'en'eration de nombre al'eatoires

Dans une simulation d'un ph'enomène stochastique, la g'en'eration de nombres al'eatoires est primordiale, car elle sera incluse dans le modèle et fournira, au fur et a` mesure, les 'echantillons artificiels d'entr'ee au simulateur. Pour que ce dernier reproduise fidèlement le ph'enomène r'eel, il est absolument n'ecessaire que ces 'echantillons d'entr'ee suivent la même loi de probabilit'e qu'un 'echantillon construit d'observations faites sur le ph'enomène r'eel [10].

5.5.1 G'en'eration de la demande suivant une loi de poisson [5]

La loi de poisson mod'elise le nombre d''ev'enements ind'ependants qui se produisent dans un intervalle de temps donn'e.

X P(ë) et on aura sa densit'e de probabilit'e :

P(X = x) = ëxe-ë

x! avec x un entier naturel et ë un r'eel positif

Sa fonction de r'epartition :

? Xx

?? ëk

e-ë k! , x = 0 ;

FX(x) = ? ?k=0

0, Sinon;

d'espérance E(X) = A et de variance V (X) = A.

Soit :

- X P(At)

- T Exp(A) o`u Exp représente la loi exponentielle On peut montrer que :

P(X > 0) = P(T < t),

f(t) = Ae^-ët _T[[t>0] (T[ est le symbole de la fonction indicatrice) F(t) = P(T < t) = 1 - e-ët

P(X > 0) = 1 - P(X = 0) = 1 - e-ët

Considérons une variable aléatoire suivant une loi de poisson de paramètre A :

A^xe^-ë

P (X = x) = x! ,

- x représente le nombre d'occurrences dans [0,1]

- Les durées entre les occurrences successives suivent une loi exponentielle de paramètre A

Si on considère _(Ti)i=1 une suite de variables aléatoires suivant une loi exponentielle Exp(A) :

x = _X8 nT[[T1+T2+···+T_n=1<T1+T2+···+T_n+1]. n=1

Donc x suit une loi de poisson de paramètre A tel que :

P(x = n) = P(T1 + T2 + ··· + T_n = 1 < T1 + T2 + ··· + Tn+1) Aⁿe^-ë

=

n!

_Xn ti = 1 < _Xn+ 1 ti.

i=1 i=1

'Etant donné(ui)i uniformes sur [0,1]; ti = -1 ë ln(ui).

Xn i=1

-1 A ln(ui) = 1 <

Xn+ 1 i=1

-1A ln(ui)

_Xn+ 1 ln(ui) < -A = _Xn ln(ui)

i=1 i=1

ln n+1_Y (ui) < -A = ln _Yn (ui)

i=1 i=1

n+1_Y (ui) < e^-ë = _Yn (ui).

i=1 i=1

Donc pour générer un nombre suivant une loi de poisson de paramètre A : - On génère des nombres aléatoires _(ui)i suivant une loi uniforme sur [0,1].

- On cherche alors le premier instant m tel que n+1_Y (ui) < e-ë.

i=1

- On pose alors x = m - 1.



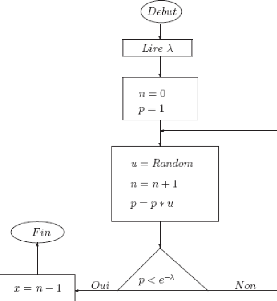
FIG. 5.3 - Organigramme pour générer un nombre suivant une loi de poisson

Algorithme 5.1. (G'en'eration de nombre al'eatoire suivant une loi de poisson)

D'ebut

Lire(A);

m :=0;

p :=1;

R'ep'eter

u := Random¹ ;

m := m + 1;

p := p*u;

Jusqu'àp < e^-ë ;

x := m - 1;

Fin

Un modèle de simulation ne peut être d'eclar'e repr'esentatif du système r'eel sans avoir v'erifier que les 'echantillons g'en'er'es qu'il produise suivent bien les même lois de probabilit'e que les 'echantillons tir'es a` partir des donn'ees r'ecolt'ees sur le terrain.

On g'enère 100 nombres al'eatoire suivant la loi de poisson de paramètre A = 48.66 repr'esent'es dans le tableau suivant :

24	49	43	53	47	52	36	52	51		49	53
55	50	54	41	48	43	47	50	43		46
41	50	44	45	50	50	45	50	42		54
53	46	48	57	52	45	55	61	51		46
45	58	53	46	51	41	51	57	46		43
59	33	40	45	41	44	62	37	50		54
55	43	51	43	43	44	62	54	53		39
44	55	47	39	48	51	51	47	45		44
57	50	36	49	60	47	46	41	50		58
47	44	44	53	55	44	44	57	64

TAB. 5.1 - Nombres al'eatoires poissonniens de paramètre A = 48.66

L'application des tests de ÷² et de Kolmogorov-Smirnov pour valider le g'en'erateur de nombre al'eatoires suivant une loi de poisson de paramètre A = 48.66 donne les r'esultats suivants :

'Random : fonction de g'en'eration d'un nombre al'eatoire uniforme sur [0,1].

	Test ÷^2		Test Kolmogorov-Smirnov
	Valeur		Valeur calculée
1.26 5	0.024		Valeur tabulée
11.07 5	0.13

TAB. 5.2 - Tests d'ajustement du générateur de nombres aléatoires poissonniens

On constate que pour a = 0.05, la valeur calculée est largement inférieure a` la valeur tabulée pour les deux tests : l'ajustement est acceptéet donc on peut affirmer que l'échantillon d'entrée de notre simulateur suit bien une loi de poisson.

5.5.2 G'en'eration de la loi de service exponentielle [16]

On rencontre souvent la loi exponentielle lorsqu'il s'agit de représenter le temps d'attente avant l'arrivée d'un événement spécifique. Elle est souvent utilisée lorsque le nombre de données ne permet pas de choisir efficacement entre plusieurs distributions.

On dit qu'une variable aléatoire X suit une loi exponentielle de paramètre u et on note X Exp(u), si sa distribution s'écrit sous la forme :

{ ue^-u^x, x = 0 ; f(x) = 0, Sinon.

Sa fonction de répartition :

{ 1 -- e^-u^x, x = 0 ;

FX(x) = 0, Sinon ;

d'espérance E(X) = 1 u et de variance V (X) = u2 1 .

A` l'aide de la méthode de la transformation inverse, on génère une variable aléatoire suivant une loi exponentielle comme suit :

X = F ^-1(U) = -- 1 ln(1 -- U),

u

o`u U est une variable aléatoire uniforme sur [0,1].

Algorithme 5.2. (G'en'eration de nombres al'eatoires suivant une loi exponentielle)

D'ebut

Lire(u);

u := Random;

x := -- 1 ln(1 -- u);

u

Fin

Dans le programme de simulation, on veut g'en'erer que des dur'ees de service entières et non nulles car l'approche utilis'ee est une approche temps. Pour ce faire, on utilise l'algorithme suivant :

Algorithme 5.3. (G'en'eration de nombres al'eatoires arrondis suivant une loi exponentielle)

D'ebut

Lire(u);

u := Random;

k := --¹ln(1 -- u);

u

x :=round²(k); Si x=0 alors x=1;

Fin

Avec cette proc'edure et en utilisant le paramètre u = 0.8111, la moyenne de l''echantillon g'en'er'e varie autour de 1.52 et ce qui ne repr'esente pas le système r'eel (avec une dur'ee moyenne de service 'egale a` 1.23) et ne donne pas de bons r'esultats de simulation.

Pour rem'edier a` ce problème, on fait varier u jusqu'àavoir un 'echantillon de moyenne autour de 1.23 et accepter par les tests d'ajustement (c-à-d : qu'il est issu d'une variable al'eatoire suivant une loi exponentielle de paramètre u = 0.8111.

Après avoir g'en'erer plusieurs 'echantillons en variant u, on constate que la valeur qui repr'esente au mieux le système r'eel est u = 1.21.

On g'enère 100 nombres al'eatoires en utilisant la proc'edure de g'en'eration de nombres al'eatoires arrondis suivant la loi exponentielle cit'ee ci-dessus avec u = 1.21. Les r'esultats obtenus sont repr'esent'es dans le tableau suivant :

²Round : fonction qui arrondie une valeur réelle.

1	1	2	1	1	1	1	1	1		1	1
1	1	2	1	1	3	1	2	1		1
2	2	1	1	1	1	1	2	1		1
1	3	1	2	5	1	3	2	1		1
1	1	1	1	1	2	1	2	2		1
1	1	1	4	1	8	1	1	1		1
2	1	3	1	1	4	1	1	1		2
6	2	2	1	1	3	2	1	2		1
1	1	1	1	3	1	1	1	4		1
1	1	1	1	1	1	1	1	2

TAB. 5.3 - Nombres aléatoires de loi exponentielle de paramètre ,t = 1.21

L'application des tests de x² et de Kolmogorov-Smirnov pour valider le générateur de nombres aléatoires suivant une loi exponentielle de paramètre ,t = 0.8111 donne les résultats suivants :

	Test x^2		Test Kolmogorov-Smirnov
	Valeur		Valeur calculée
2.52 5	0.055		Valeur tabulée
11.07 5	0.13

TAB. 5.4 - Tests d'ajustement du générateur de nombres aléatoires de loi exponentielle

On constate que pour a = 0.05, la valeur calculée est largement inférieure a` la valeur tabulée pour les deux tests : l'ajustement est acceptéet donc on peut affirmer que l'échantillon d'entrée de notre simulateur suit bien une loi exponentielle de paramètre ,t = 0.8111.

5.6 Présentation de l'organigramme de simulation

Dans cette section, nous donnerons les variables et caractéristiques du simulateur en-suite les deux organigrammes des modèles avec et sans file et enfin l'application des algorithmes de simulation pour les deux modèles.

5.6.1 Les variables caractéristiques du simulateur

t : Représente l'état de l'horloge.

Nbrc : Représente le nombre de camions. Nbrch : Représente le nombre de chauffeurs.

Dserv : Représente la durée de service cumulée exigée par l'entreprise pour qu'un chauffeur prenne son repos.

Drep : Représente la durée de repos exigée par l'entreprise.

Camion : Représente un tableau dynamique a` une dimension correspondant a` l'état des camions

- Camion[i]=0 : le camion i est disponible.

- Camion[i]=k : il reste k jours au camion i pour rentrer.

Chauffeur : Représente un tableau dynamique a` deux dimensions comportant 3 colonnes et correspondant a` l'état des chauffeurs.

la première colonne correspond au reste de jours de repos avant de reprendre son service, la deuxième correspond au reste de jours pour rentrer de la livraison, quand a` la troisième elle correspond au cumule de jours de service après son dernier repos. - Chauffeur[i]=(0,0,k) : le chauffeur i est disponible et cumule k jour de service après

son dernier repos.

- Chauffeur[i]=(0,j,k) : il reste j jours au chauffeur i pour rentrer.

- Chauffeur[i]=(k,0,0) : il reste k jours de repos au chauffeur i avant de reprendre son service.

Etatfile : Représente un tableau dynamique a` deux dimensions comportant deux colonnes et correspondant a` l'état de la file.

la première colonne correspond a` des demandes non servies classées selon leur ordre d'arrivées, quand a` la deuxième colonne elle correspond au temps de séjours dans la file.

- Etatfile[i]=(j,k) : j clients ont séjournék jours dans la file jusqu'àprésent.

D : Correspond a` la demande journalière générée.

Nbrf : Correspond au nombre de clients dans la file au début de journée. NbrcD : Correspond au nombre de camions disponibles au début de journée. NbrchD : Correspond au nombre de chauffeurs disponibles au début de journée. S : Correspond au nombre de clients a` servir durant une journée donnée.

DS : Correspond a` la durée de service générée pour un client donné.

Ctf : Correspond au cumule des temps d'attente dans la file de tous les clients servis jusqu'àprésent.

Cts : Correspond au cumule des temps d'attente dans le système de tous les clients servis jusqu'àprésent.

Tf : Correspond au temps moyen d'attente dans la file.

Ts : Correspond au temps d'attente moyen dans le système.

Nbrs : Correspond au nombre total de clients servis jusqu'àprésent.

CNf : Correspond au cumul du nombre de clients dans la file jusqu'àprésent. CNs : Correspond au cumul du nombre de clients dans le système jusqu'àprésent. Nf : Correspond au nombre moyen de clients dans la file.

Ns : Correspond au nombre moyen de clients dans le système.

CNbrcI : Correspond au cumul du nombre de camions inoccupes jusqu'àpresent. CNbrchI : Correspond au cumul du nombre de chauffeurs inoccupes jusqu'àpresent. NbrcI : Correspond au nombre moyen de camions inoccupes par unitede temps. NbrchI : Correspond au nombre moyen de chauffeurs inoccupes par unitede temps.

5.6.2 Modèle avec file



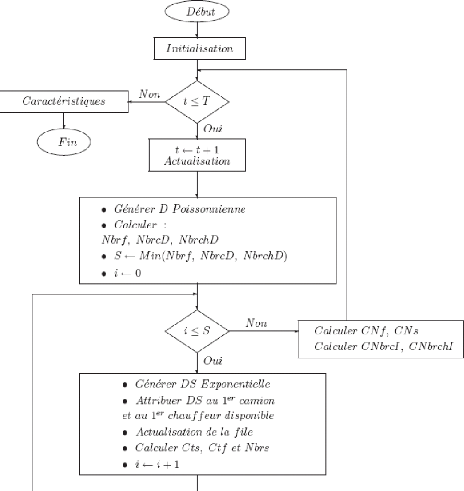
5.6.3 Modèle sans file



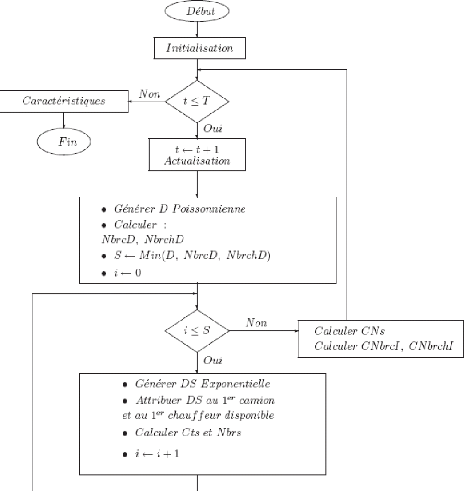
5.6.4 Déroulement de l'algorithme de simulation (modèle avec file)

Notre modèle de simulation repr'esent'e par l'organigramme pr'ec'edent, r'esume les principales tâches et proc'edures suivantes :

1) Initialisation : C'est une 'etape n'ecessaire a` tout programme informatique. Les variables les plus importantes a` initialiser dans notre simulateur sont :

· Pour i allant de 0 a` Nbrc-1 faire: Camion[i] :=0.

· Pour i allant de 0 a` Nbrch-1 faire : Chauffeur[i] :=(0,0,0).

· Initialiser la taille du tableau Etatfile a` 0.

· Initialiser le compteur temps : t :=0.

· Initialiser le nombre de clients servis : Nbrs :=0.

· Initialiser le cumule des temps d'attente dans la file et dans le système :

- Ctf :=0;
- Cts :=0.

· Initialiser le cumule des nombres de clients dans la file et dans le système :

- CNf :=0;
- CNs :=0.

· Initialiser le cumule des nombres de camions et de chauffeurs inoccup'es par unit'e de temps : - CNbrcI :=0;

- CNbrchI :=0.

2) Pour t allant de 0 a` T ex'ecuter les 'etapes 3 a` 6.

3) Actualisation : c'est une proc'edure qui serve a` actualiser les tableaux Camion, Chauffeur et Etatfile a` chaque d'ebut de journ'ee comme suit :

a) Pour les camions non pas encore rentr'es : Camion[i]6=0, faire d'ecr'ementer la dur'ee restante de leurs trajets d'une unit'e de temps Camion[i] :=Camion[i]-1.

b) Pour les chauffeurs:

· qui sont encore au repos : Chauffeur[i,0]6=0, faire d'ecr'ementer la dur'ee restante de leurs repos d'une unit'e de temps Chauffeur[i,0] :=Chauffeur[i,0]-1.

· qui sont en service : Chauffeur[i,1]6=0 :

- faire d'ecr'ementer la dur'ee restante de leurs services d'une unit'e de temps Chauffeur[i,1] :=Chauffeur[i,1]-1.

- faire inc'ementer la dur'ee de service cumul'ee après leurs dernier repos d'une unit'e de temps Chauffeur[i,2] :=Chauffeur[i,2]+1.

· qui sont rentr'es et ont cumul'e une dur'ee de service sup'erieure ou 'egale a` la dur'ee de service exig'ee : Chauffeur[i,1]=0 et Chauffeur[i,2]= Dserv :

- leurs donner une dur'ee de repos 'egale a` Drep : Chauffeur[i,0] := Drep.

- mettre a` z'ero leurs dur'ees de service cumul'ees : Chauffeur[i,2] := 0.

c) Pour la file on incr'emente la dur'ee de s'ejour des clients dans la file d'une unit'e de temps : Etatfile[i,1] := Etatfile[i,1] + 1;

4) Générer D poissonnienne : Avec l'algorithme 5.1, on génère une demande poissonnienne D et la mettre en fin du tableau Etafile avec un temps de séjour égale a` 0.

5) Calculer les disponibilités :

· en camions NbrcD =	Nbrc--1 >2 i=0			I[Camion[i]=0].		· en chauffeurs NbrchD =
Nbrch--1 >2 i=0			I[Chauffeur[i,0]=0 et Chauffeur[i,1]=0].

Long Etatfile--1

· nombre de clients dans la file Nbrf =

Etafile[i, 0].

i=0

· calculer le nombre de clients a` servir S :=min(NbrcD,NbrchD,Nbrf).

6) Servir les clients : Pour i allant de 1 a` S, exécuter les étapes suivantes :

· générer DS exponentielle : Avec l'algorithme 5.3, on génère une durée de service exponentielle DS.

· attribuer DS au premier camion disponible (Camion[i]=0) : Camion[i] :=DS.

· attribuer DS au premier chauffeur disponible (Chauffeur[i,0]=0 et Chauffeur[i,1]=0) : Chauffeur[i,1] :=DS.

· actualiser la file :

- si Etatfile[0,0]=0 alors pour i allant de 0 a` long(Etatfile)-1 faire Etatfile[i] :=Etatfile[i+1].

- on soustrait un client de la file : Etatfile[0,0] :=Etatfile[0,0]-1.

· actualiser le cumul du temps dans la file : Ctf :=Ctf+Etafile[0,1].

· actualiser le cumul du temps dans le système : Cts :=Cts+Etafile[0,1]+DS.

· actualiser le nombre de clients servis : NbrS :=NbrS+1.

7) Cumuls des caractéristiques : Actualisation des cumuls suivants :

· CNf :=CNf+Nbrf-S.

· CNs :=CNs+Nbrc-NbrcD+Nbrf.

· CNbrcI :=CNbrcI+NbrcD-S.

· CNbrchI :=CNbrchI+NbrchD-S.

8) Sortie des caractéristiques : En utilisant les cumuls calculés, on aura les paramètres caractéristiques de notre simulateur :

V Tf :=CTf/NbrS.

V Ts :=CTs/NbrS.

V Nf :=CNf/T.

V Ns :=CNs/T.

V NbrcI :=CNbrcI/T.

V NbrchI :=CNbrchI/T.

5.7 Vérification et validation du modèle de simulation

Pour la v'erification et la validation du simulateur, on va se r'ef'erer au fonctionnement du modèle th'eorique avec les camions seuls. En effet, le modèle simul'e n'est qu'une perturbation, avec des chauffeurs, du système mod'elis'e avec les camions seuls. Pour se ramener a` ce système, il suffit de fixer la dur'ee de repos des chauffeurs a` 0 pour avoir des camions qui travaillent sans arrêt, puis comparer les r'esultats simul'es avec les r'esultats th'eoriques.

Remarque 5.1. Si la dur'ee de repos est nulle, alors un nombre de chauffeurs qui d'epasse le nombre de camions n'a pas de sens. Par cons'equent, on fixe le nombre de chauffeurs au nombre de camions.

On fixe le nombre de camions a` 75 qui correspond au nombre de camions dont dispose l'entreprise, et avec un horizon de 5000 jours (14 ans), on ex'ecute notre simulateur 10 fois et on obtient les r'esultats suivants :

	1	2	3	4	5	6	7	8	9	10
Nf	0,0886	0,084	0,1178	0,1098	0,1184	0,1166	0,1342	0,128	0,1166	0,1186
Ns	59,89	59,89	60,13	60,16	60,08	60,12	60,14	60,27	60,26	60,04
Tf	0,0018	0,0017	0,0024	0,0022	0,0024	0,0023	0,0027	0,0026	0,0023	0,0024
Ts	1,2341	1,2318	1,2353	1,2356	1,2338	1,2348	1,2331	1,2355	1,2350	1,2341
NbrcI/j	15,21	15,20	15,00	14,96	15,04	15,00	15,00	14,86	14,86	15,09

TAB. 5.5 - R'esultats de la simulation pour Nbrc=75

On utilisant les formules cit'ees dans le chapitre 4 dans l'approche avec file, on obtient les r'esultats analytiques suivants :

Paramètres de performance	Formules th'eoriques	r'esultats analytiques
Nf	ñm+1	0,1606
	ð0 (m-1)!(m-ñ)^2
Ns	Nf + p	60,1533
Tf	Nf	0,0033
	A
Ts	Ns	1,2361
	A
NbrcI	Pm-1 k=0 (in - k)ðk = in - p.	15,0073

TAB. 5.6 - R'esultats th'eoriques pour Nbrc=75 Comparaison des résultats

Pour les dix r'eplications, on constate qu'il y a une diff'erence minime au niveau des paramètres de performances calcul'es. En effet, on a ex'ecut'e plusieurs fois notre simulateur avec diff'erents paramètres d'entr'ee et a` chaque fois, les r'esultats simul'es sont aussi repr'esentatifs des r'esultats analytiques que le sont les dix premières r'eplications, comme

le montre les tableaux suivants :

	1	2	3	4	5	6	7	8	9	10
Nbrc=76
Nf	0,068	0,0638	0,0898	0,0804	0,0836	0,0856	0,092	0,0974	0,0786	0,0826
Ns	59,85	59,88	60,07	60,14	60,06	60,13	60,09	60,20	60,15	59,95
Tf	0,0014	0,0013	0,0018	0,0016	0,0017	0,0017	0,0018	0,0019	0,0016	0,0016
Ts	1,232	1,231	1,234	1,235	1,233	1,234	1,232	1,235	1,234	1,232
NbrcI/j	16,22	16,19	16,03	15,95	16,03	15,96	16,01	15,90	15,94	16,14
Nbrc=77
Nf	0,0482	0,0426	0,062	0,0646	0,0562	0,0614	0,0648	0,0828	0,0608	0,0542
Ns	59,86	59,84	60,02	60,17	59,99	60,01	60,06	60,19	60,15	59,93
Tf	0,0009	0,0008	0,0012	0,0013	0,0011	0,0012	0,0013	0,0016	0,0012	0,0011
Ts	1,232	1,231	1,233	1,234	1,232	1,233	1,231	1,234	1,233	1,232
NbrcI/j	17,19	17,20	17,05	16,90	17,07	17,06	17,01	16,89	16,92	17,13

TAB. 5.7 - Résultats de la simulation pour Nbrc=76 et Nbrc=77 Résultats analytiques :

Paramètres de performance	Nbrc=76	Nbrc=77
Nf	0,1132	0,0792
Ns	60,10	60,07
Tf	0,0023	0,0016
Ts	1,235	1,234
NbrcI	16,0073	17,0073

TAB. 5.8 - Résultats théoriques pour Nbrc=76 et Nbrc=77

Conclusion :

Après avoir vérifier que les générateurs de nombres aléatoires suivent bien les lois de

poisson et exponentielle comme les échantillons tirés du système réel, puis vérifier l'intégritédu programme de simulation en comparant les résultats simulés avec les résultats analytiques, on peut affirmer que notre simulateur représente fidèlement le système réel.

5.8 Mise en oeuvre du simulateur

Pour déterminer le nombre de chauffeurs correspondant a` un nombre de camions précis, l'idée est de faire varier le nombre de chauffeurs partant du nombre de camions jusqu'àdeux fois ce nombre, puis trouver un compromis entre le nombre de camions inoccupés par unitéde temps (NbrcI) et le nombre de chauffeurs inoccupés par unitéde temps (NbrchI).

Pour définir ce compromis, on définit une fonction qui va lier le nombre de camions et le nombre de chauffeurs inoccupés par unitéde temps en introduisant leurs pertes respectives qu'ils engendrent a` l'entreprise.

Lors d'une livraison, l'entreprise considère que le client paye un prix de transport de sa marchandise estiméa` Pc = 30000 DA par unitéde temps. Alors si un camion reste inoccupé, cette somme est considérée comme un manque a` gagner (perte).

De plus un chauffeur est payéPch = 560 DA par unitéde temps que se soit qu'il travaille ou qu'il reste inoccupé, par conséquent ses jours d'inoccupation en dehors des jours de repos sont considérés comme pertes pour l'entreprise.

La fonction perte s'écrit alors sous la forme :

f(Nbrch) = Pc * NbrcI + Pch * NbrchI -? min. 5.8.1 Modèle avec file

On fixe le nombre de camions a` 75 et avec un horizon de 5000 jours, on exécute notre simulateur avec un nombre de chauffeurs allant de 75 a` 150 et on obtient les résultats suivants :



466863,7

450332,9

470981,6

478053,6

463070,2

462564,5

487569,2

15,2564

15,0764

14,8884

36,0924

15,0068

18,3438

15,0882

45,3708

15,2338

0,2302

15,186

27,503

54,563

9,604

137

110

119

128

101

83

92

467950,7

480772,4

454097,2

460858,6

476310,5

474235,6

15,5974

14,9836

15,1948

26,0868

15,2136

14,9826

15,0308

53,3008

15,3866

17,5072

35,5402

465648

496752

0,0514

14,875

62,775

8,195

44,21

127

100

109

118

136

145

82

91

460646,7

460963,7

478184,7

480028,7

488208,7

489384,3

464929,6

TAB. 5.9 - Resultats de la simulation pour le modele avec file

473831,1

25,6914

52,2834

61,4264

15,2142

16,3102

15,3148

14,8622

34,0422

43,4192

15,127

0,0434

16,312

15,129

15,025

15,061

7,537

117

108

126

144

135

90

99

81

476041,7

473126,7

483809,7

510406,3

456543,9

459132,8

476341,6

463619,1

15,0994

15,0196

15,2586

24,2556

15,2414

42,2084

14,9234

15,0024

17,0132

15,0012

51,1422

0,0184

6,3606

14,983

60,246

33,571

107

134

116

125

143

80

89

98

451517,824

463219,872

532187,4

470088,5

478454,5

482469,2

486307,2

470269,1

23,5734

17,7392

14,9538

14,4462

15,2356

15,0662

15,1742

41,4796

15,1408

15,1016

59,3916

0,0204

5,1854

32,326

50,438

15,171

124

106

115

133

142

97

79

88

456767,7

457607,0

554300,8

469857,2

481931,2

487765,9

463748,1

488171,1

18,4764

49,7234

15,3696

14,9788

14,8422

22,0376

15,0768

15,3052

15,3442

58,4928

15,167

0,0158

4,7502

31,345

13,221

40,67

114

123

105

132

141

87

78

96

473902,7

464955,4

575843,2

445434,8

487772,8

470199,1

19,1944

14,8338

12,0358

15,0996

21,3704

30,3914

15,1856

57,5086

14,7922

15,0232

451754

477726

15,106

15,062

39,362

48,268

0,02

2,98

104

113

122

140

131

77

95

86

482211,7

466702,4

597532,3

457911,9

456854,9

469740,2

472728,8

481731,2

19,9174

15,2164

15,0184

15,1744

29,4004

15,0424

15,1714

11,2552

15,1092

38,3158

47,4808

15,0228

56,2996

0,0184

2,5356

20,483

103

130

139

112

121

94

76

85

476423,7

619850,4

456965,6

454440,3

461860,5

469812,3

472855,5

483900,9

15,2036

10,1684

19,2938

15,1298

28,4256

15,0646

37,3528

15,2596

55,0496

20,6612

14,9582

15,0352

46,6302

14,8532

0,0258

1,5316

102

120

129

138

111

84

93

75

f(Nbrch)

f(Nbrch)

f(Nbrch)

f(Nbrch)

f(Nbrch)

f(Nbrch)

f(Nbrch)

f(Nbrch)

Nbrchl

Nbrchl

Nbrchl

Nbrchl

Nbrchl

Nbrchl

Nbrchl

Nbrchl

Nbrch

Nbrch

Nbrch

Nbrch

Nbrch

Nbrch

Nbrch

Nbrch

Nbrcl

Nbrcl

Nbrcl

Nbrcl

Nbrcl

Nbrcl

Nbrcl

Nbrcl

Le graphe de la fonction f(Nbrch) est représentédans la figure suivante :



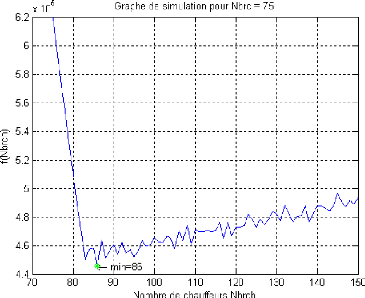
FIG. 5.4 - Graphe de la fonction perte pour Nbrc = 75.

5.8.1.1 Interprétation des résultats

On constate que lorsqu'on augmente le nombre de chauffeurs, le nombre de camions inoccupés par unitéde temps diminue, contrairement au nombre de chauffeurs inoccupés par unitéde temps qui augmente, par conséquent, la courbe de f a tendance a` décroàýtre très rapidement au début et cela est dàu a` la perte engendrée par un camion inoccupé(30000 DA) qui est largement supérieur a` celle engendrée par l'inoccupation d'un chauffeur (560 DA).

Après que le nombre de chauffeurs atteigne une certaine limite, le nombre de camions
inoccupés par unitéde temps a` tendance a` se stabiliser autour de 15,0073 qui représente

le nombre de camions inoccupés par unitéde temps (m - ñ) dans le système ^modéliséavec les camions seuls et dès que le nombre de chauffeurs dépasse cette limite, la courbe

a tendance a` croàýtre. Alors, cette limite représente le nombre total de chauffeurs que doit avoir l'entreprise.

Pour cette exécution, le nombre total de chauffeurs qui minimise la fonction perte est Nbrch=86 chauffeurs.

Remarque 5.2. Lors de la simulation avec un horizon très petit, on constate qu'il peut y avoir, sur le graphe de la fonction perte, des pics non significatifs comme on le voit sur la figure ci-dessous qui represente une simulation avec un horizon T=1000 unites de temps :



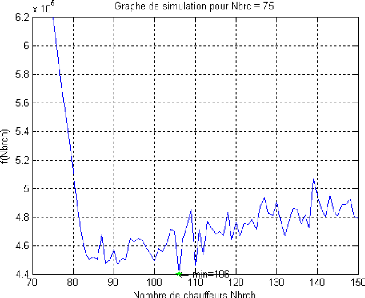
FIG. 5.5 - Graphe de la fonction perte avec des pics non significatifs.

Pour faire face a` ce problème, on fixe l'horizon de simulation a` 10000 (soit 27 ans), et on remarque que le graphe de la fonction f a tendance a` se lisser comme le montre le graphe suivant :



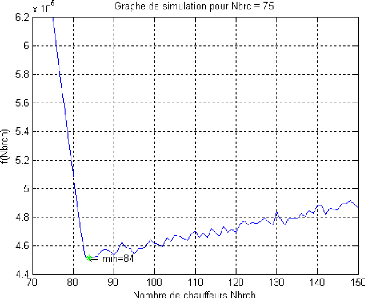
FIG. 5.6 - Graphe de la fonction perte lissé.

Dans ce qui suit, la simulation se fera avec un horizon de 10000 unités de temps. 5.8.1.2 Variation du nombre de camions

Pour différentes valeurs du nombre de camions (Nbrc), on simule 5 réplications pour un nombre de chauffeurs variant entre Nbrc et deux fois Nbrc avec un horizon de 10000 unitéde temps et on obtient les résultats suivant :

Nombre de camions	Réplications					Moyenne
	1	2	3	4	5
60	90	90	92	90	90	90.4
61	86	85	87	88	86	86.4
62	85	84	84	86	85	84.8
63	85	85	87	86	85	85.6
64	87	85	84	84	84	84.8
65	85	83	83	85	88	84.8
66	85	86	85	85	84	85
67	86	86	84	87	84	85.4
68	85	85	84	84	84	84.4
69	83	83	85	84	83	83.6
70	85	87	83	85	89	85.8
71	84	87	86	84	90	86.2
72	83	89	83	83	87	85
73	83	83	83	84	88	84.2
74	84	90	83	87	85	85.8
75	85	87	88	83	84	85.8
76	85	84	83	85	84	84.2
77	88	87	84	84	85	85.6
78	83	90	85	85	83	85.2
79	85	84	84	83	84	84
80	83	85	84	85	86	84.6

TAB. 5.10 - Nombre de chauffeurs correspondant au nombre de camions par la simulation

Du tableau ci-dessus, on constate que la moyenne du nombre de chauffeurs n'a pas de tendance et varie autour de 85 indépendamment du nombre de camions comme le montre la figure ci-après, a` l'exception de la première valeur qui est une valeur non significative car elle représente la condition d'ergodicité, par conséquent les caractéristiques correspondantes du système sont très difficile a` atteindre par le simulateur.



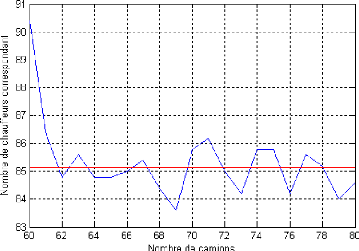
FIG. 5.7 - Ajustement du nombre de chauffeurs.

Pour trancher sur la valeur du nombre de chauffeurs Nbrch a` prendre, on va effectuer un ajustement par une droite, puis tester la validitédu modèle.

A` l'aide du logiciel de statistique »R», on a effectuéune régression linéaire simple sur les moyennes calculées et on a aboutit aux résultats suivants :



L''equation de r'egression lin'eaire s''ecrit alors sous la forme :

y= aà + ^àbx = 85.32 -- 0.02737x

Tests sur les param`etres

t_a = 805.3.32 2 = 266, 62.

Au niveau de á = 0.05, sur la table de Student t(_n-2_; 2) = t(18;0.025) = 2.101.

t_a = 266, 62 > t(18;0.025) = 2.101. Par cons'equent, on rejette l'hypoth`ese »a = 0».

tb = |-0%02297639 7| = 0.92.

Au niveau de á = 0.05, sur la table de Student t(n-2; 2) = t(18;0.025) = 2.101. tb = 0.92 < t(18;0.025) = 2.101.

Par cons'equent, on accepte l'hypoth`ese »b = 0» ce qui veut dire que le nombre de chauffeurs et le nombre de camions ne sont pas li'es et que y est une constante.

Le mod`ele sera alors y=85.32 ce qui veut dire que l'entreprise doit avoir 86 chauffeurs ind'ependamment du nombre de camions.

5.8.2 Mod`ele sans file

Contrairement au mod`ele pr'ec`edent, ce mod`ele n'a pas de condition d'ergodicit'e (il existe toujours un r'egime stationnaire), par cons'equent on peut simuler pour un nombre de camions Nbrc > 1.

On fixe le nombre de camions a` 75 et avec un horizon de 10000 jours, on ex'ecute notre simulateur avec un nombre de chauffeurs allant de 75 a` 150 et on obtient les r'esultats suivants :



481512,7

486939,7

482591,4

462967,9

473569,5

544135,1

18,0547

45,5157

15,8912

15,0896

27,6242

15,1122

36,3875

15,2008

15,2136

10,4561

18,3571

473743

4,4539

54,521

15,27

137

110

119

128

101

83

92

463109,4

485838,8

473110,6

475816,2

477358,2

494264,2

17,3937

53,1894

18,3966

16,0149

15,1123

26,5905

15,1978

14,9613

62,6505

35,5041

478625

554091

9,6283

15,274

15,084

44,354

15,306

3,9161

127

100

109

118

136

145

82

91

TAB. 5.11 - Resultats de la simulation pour le modele sans file

476715,7

463055,4

490438,5

486442,1

472705,1

477018,1

15,2787

34,5807

61,5027

15,0814

15,2704

18,9092

16,0526

16,3973

25,6146

52,6083

15,1999

15,1291

15,2551

569308

487572

3,6286

8,6859

43,346

117

144

108

126

135

90

99

81

584277,8

495308,8

473407,2

477997,5

480305,6

485363,2

467896,1

42,4367

60,3094

15,5698

15,1406

24,4252

15,1558

33,4523

15,0523

51,3155

16,3591

15,2371

15,1411

465832

8,0997

19,414

3,3176

15,053

107

134

116

125

143

80

89

98

594604,4

501081,4

479862,9

486537,6

483400,3

467394,5

471331,5

469896,1

32,3867

15,1424

15,0074

16,5652

15,3878

14,7538

23,4332

15,1065

15,2202

41,5302

50,6155

15,2731

2,7937

59,247

19,768

7,3669

124

106

115

133

142

97

79

88

610261,4

512815,2

471598,9

465935,3

470358,8

478385,2

477253,6

488254,6

13,8677

14,9897

15,1834

20,2948

16,9645

15,0932

31,3623

58,4868

15,4611

15,1131

22,3971

15,1901

40,5041

49,219

2,5311

6,9291

114

105

123

132

141

87

78

96

469737,7

625430,3

517552,6

480619,4

464077,3

478098,8

480981,2

487460,5

39,5104

20,8059

17,1366

15,7723

13,3043

21,3346

15,0912

30,3602

15,1289

48,4183

15,1758

57,4759

15,1991

2,2382

6,1691

15,071

104

113

122

140

131

77

86

95

640866,7

525574,6

474366,5

469332,8

484679,5

487560,2

480982,1

21,3256

15,5873

29,5269

38,6646

15,2673

56,5076

17,4152

12,0492

47,6082

15,1972

15,2601

15,2241

473258

20,589

5,5691

15,311

1,962

103

112

130

139

121

94

76

85

656542,8

539057,8

464964,4

471168,6

477024,6

484445,6

487528,4

474354,5

55,5347

21,8533

11,0796

15,1363

19,4205

28,4743

15,2006

37,5118

15,2778

46,6279

15,2143

15,1741

5,1747

1,6854

17,872

15,605

102

120

129

138

111

84

75

93

f(Nbrch)

f(Nbrch)

f(Nbrch)

f(Nbrch)

f(Nbrch)

f(Nbrch)

f(Nbrch)

f(Nbrch)

Nbrchl

Nbrchl

Nbrchl

Nbrchl

Nbrchl

Nbrchl

Nbrchl

Nbrchl

Nbrch

Nbrch

Nbrch

Nbrch

Nbrch

Nbrch

Nbrch

Nbrch

Nbrcl

Nbrcl

Nbrcl

Nbrcl

Nbrcl

Nbrcl

Nbrcl

Nbrcl

Le graphe de la fonction f(Nbrch) est représentédans la figure suivante :



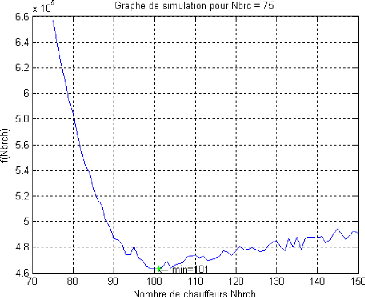
FIG. 5.8 - Graphe de la fonction perte pour Nbrc = 75.

5.8.2.1 Interprétation des résultats

Même chose que pour le mod`ele préc`edent, la courbe a la même allure, sauf que ici le nombre de camions inoccupés par unitéde temps correspondant a` un nombre de chauffeurs précis est plus important et diminue faiblement a` l'augmentation du nombre de chauffeurs, ce qui justifie l'augmentation du besoin en chauffeurs.

Apr`es une certaine limite du nombre de chauffeurs, le nombre de camions inoccupés par unitéde temps se stabilise autour de 15.506 qui représente le nombre de camions inoccupés par unitéde temps (m - N) dans le syst`eme modéliséavec les camions seuls et d`es que le nombre de chauffeurs dépasse cette limite, la courbe a tendance a` croàýtre. Alors, cette limite représente le nombre total de chauffeurs que doit avoir l'entreprise.

Pour cette exécution, le nombre total de chauffeurs qui minimise la fonction perte est Nbrch=101 chauffeurs.

5.8.2.2 Variation du nombre de camions

Pour différentes valeurs du nombre de camions (Nbrc), on simule 5 réplications pour un nombre de chauffeurs variant entre Nbrc et deux fois Nbrc avec un horizon de 10000 unitéde temps et on obtient les résultats suivant :

Nombre de camions	R'eplications					Moyenne	Nombre de camions	R'eplications					Moyenne
	1 2 3 4 5							1 2 3 4 5
1	2	2	2	2	2	2	2	4	4	4	4	4	4
3	6	6	6	6	6	6	4	8	8	8	8	8	8
5	9	9	9	9	9	9	6	11	11	11	11	11	11
7	13	13	12	13	12	12.6	8	14	14	14	14	14	14
9	16	16	16	15	16	15.8	10	17	17	17	17	17	17
11	19	19	19	19	18	18.8	12	20	20	20	20	21	20.2
13	22	22	22	22	22	22	14	23	23	23	23	23	23
15	25	25	25	25	25	25	16	27	27	27	27	26	26.8
17	27	28	28	28	27	27.6	18	29	30	29	29	30	29.4
19	31	31	31	31	30	30.8	20	32	32	32	32	32	32
21	33	33	34	34	33	33.4	22	35	35	35	35	35	35
23	36	37	37	37	37	36.8	24	39	38	38	38	38	38.2
25	40	40	40	40	40	40	26	41	42	41	41	41	41.2
27	43	42	43	43	42	42.6	28	44	44	45	44	45	44.4
29	46	45	46	46	45	45.6	30	47	48	47	47	47	47.2
31	48	48	49	49	48	48.4	32	50	50	50	50	50	50
33	52	51	52	52	52	51.8	34	53	53	52	53	54	53
35	54	54	54	55	55	54.4	36	56	56	55	56	55	55.6
37	57	58	57	57	57	57.2	38	59	58	60	58	59	58.8
39	60	60	61	60	60	60.2	40	61	62	63	62	62	62
41	62	63	63	63	62	62.6	42	64	65	65	64	65	64.6
43	65	66	66	66	66	65.8	44	67	68	67	68	67	67.4
45	71	68	69	69	70	69.4	46	69	72	70	70	70	70.2
47	72	72	72	71	73	72	48	73	74	73	74	73	73.4
49	74	74	73	75	75	74.2	50	77	76	77	75	75	76
51	78	76	78	78	78	77.6	52	77	80	78	80	79	78.8
53	80	81	82	79	83	81	54	80	82	84	81	82	81.8
55	87	83	84	84	83	84.2	56	83	85	86	86	85	85
57	86	89	84	86	85	86	58	87	85	88	88	87	87
59	88	88	90	92	87	89	60	88	92	93	89	88	90
61	91	90	88	93	92	90.8	62	91	90	90	93	91	91
63	91	93	93	91	98	93.2	64	96	95	96	99	95	96.2
65	92	95	93	94	98	94.4	66	99	96	95	99	95	96.8
67	97	95	96	98	97	96.6	68	93	98	96	96	95	95.6
69	99	98	96	102	99	98.8	70	96	98	95	104	98	98.2
71	100	101	99	97	97	98.8	72	101	97	100	101	100	99.8
73	105	105	97	99	105	102.2	74	106	102	102	101	101	102.4
75	104	103	106	100	103	103.2	76	102	101	104	105	103	103
77	107	101	104	101	105	103.6	78	101	104	102	100	102	101.8
79	102	103	107	104	106	104.4	80	102	104	106	104	106	104.4
81	103	104	97	102	106	102.4	82	106	101	102	102	100	102.2
83	100	104	102	105	103	102.8	84	106	105	108	109	103	106.2
85	101	103	107	102	104	103.4	86	104	104	102	102	103	103
87	102	102	105	104	106	103.8	88	101	103	107	99	102	102.4
89	106	104	102	107	102	104.2	90	100	104	102	102	106	102.8
91	102	101	102	103	108	103.2	92	103	102	101	102	104	102.4
93	108	100	103	106	106	104.6	94	108	102	100	103	100	102.6
95	103	104	100	103	105	103	96	102	103	102	105	102	102.8

TAB. 5.12 - Nombre de chauffeurs correspondant au nombre de camions par la simulation

Du tableau ci-dessus, on remarque que le nombre de chauffeurs augmente linéairement en fonction du nombre de camions, mais après une certaine limite, on constate qu'il a tendance a` se stabiliser comme le montre la figure suivante :



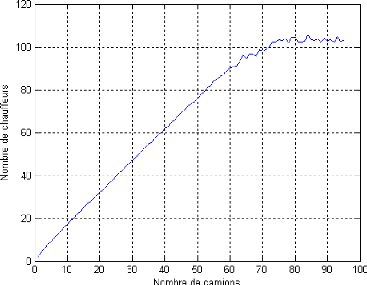
FIG. 5.9 - Nombre de chauffeurs en fonction du nombre de camions.

Pour trancher sur la valeur du nombre de chauffeurs Nbrch, correspondant a` un nombre précis de camions a` prendre, on va effectuer un ajustement par un modèle de régression, puis tester sa validité.

On remarque que l'allure du graphe n'est pas linéaire, par conséquent il faudra chercher un modèle de régression correspondant. En effet, on a proposéplusieurs modèles de régression qui ont la même allure que le graphe (voir annexe C) et a` l'aide du logiciel de statistique »R», on a effectuéune régression non linéaire sur les résultats obtenus et on a choisit celui qui correspond le mieux.

L'équation du modèle choisit s'écrit comme suit :

a

Y = + bruit

1 + ce^-bx

C'est un modèle qui représente une croissance sinuso·ýdale symétrique et a` l'aide du logiciel R on a estiméses paramètres et on a obtenu les résultats suivants :



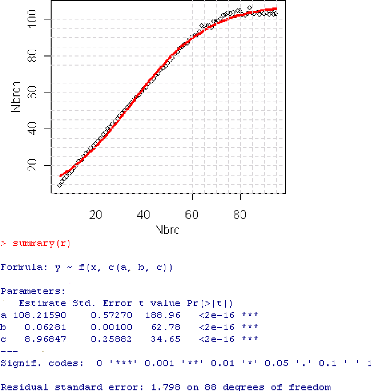
FIG. 5.10 - Ajustement par une croissance sinuso·ýdale.

Comme on l'a mentionnéprécédemment, jusqu'àune certaine limite du nombre de camions, le graphe a une tendance linéaire, alors il vaut mieux de diviser nos données en deux ensembles puis ajuster le premier avec un modèle linéaire et le deuxième avec avec le modèle précédant.

Pour le premier ensemble (Nbrc < 60), on effectue une régression linéaire et on obtient les résultats suivants :



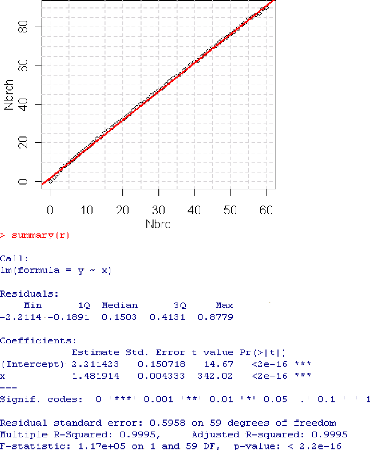
FIG. 5.11 Ajustement par une droite.

L'équation de régression linéaire s'écrit alors sous la forme :

y= aà + ^àbx = 2.21 + 1.48x

Tests sur les paramètres

t_a = 2.21

0.15 = 14.73.

Au niveau de á = 0.05, sur la table de Student t(n_2; ' 2 ) = t(59;0.025) = 1.67.

t_a = 14.73 > t(59;0.025) = 1.67. Par consequent, on rejette l'hypothèse »a = 0».

tb = 1.48

0.0043 = 34.41.

Au niveau de á = 0.05, sur la table de Student t(n_2;' ₂ ) = t(59;0.025) = 1.67. tb = 34.41 < t(59;0.025) = 1.67.

Par consequent, on rejette l'hypothèse »b = 0».

Tests sur la validation du modèle

Pour valider le modèle on teste H0 »a = b = 0» contre H1 »a =6 0 ou b =6 0» F = 1.17 10⁺⁵. Au niveau á = 0.05, sur la table de Ficher, f(1,59,0.05) = 4.0

F = 1.17 10⁺⁵ > 4.0. Par consequent on valide ce modèle de regression.

Pour le deuxième ensemble (Nbrc = 60), on effectue une regression non lineaire et on obtient les resultats suivants :



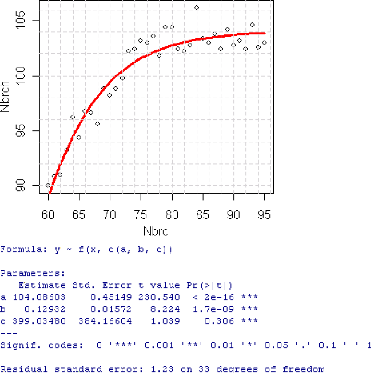
FIG. 5.12 - Ajustement par une croissance sinuso·ýdale.

L'équation de régression non linéaire s'écrit alors sous la forme :

aà

y= 1 + àce_^àbx =

Validation du modèle

104.08
1 + 399.03.e_^0.129x

Pour la validation du modèle, on utilisera la méthode graphique en montrant que les résidus suivent bien un processus Bruit Blanc³

A` l'aide du logiciel STATISTICA, on effectue un ajustement des résidus et on obtient les résultats suivants :



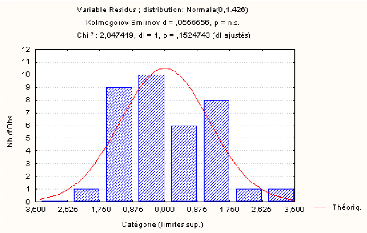
FIG. 5.13 - Ajustement des résidus par une loi normale.

	Test x^2	Test Kolmogorov-Smirnov
	Valeur ddl	Valeur
Valeur calculée	2.047 5	0.055
Valeur tabulée	11.07 5	0.216

TAB. 5.13 - Tests d'ajustement des résidus

On constate que pour á = 0.05 la valeur calculée est largement inférieur a` la valeur tabulée pour les deux tests : l'ajustement est accepté, donc on peut affirmer que les résidus suivent bien une loi Normale de moyenne u = 0 et de variance ó² = 1.42.

³Bruit Blanc: suite de variables aléatoires indépendantes de même loi, de même moyenne 0 et de même variance ó² finie.

De ce fait, on peut affirmer que les résidus forment un processus Bruit Blanc et par conséquent on valide notre modèle.

Pour déterminer le nombre de chauffeurs, correspondant a` un nombre de camions précis, que devra avoir l'entreprise on utilisera les modelés de régression définis précédemment.

Pour Nbrc < 60 :

En ce qui concerne les dix premières valeurs on prendra celles données par le simulateur car elle sont plus représentatives puis on utilise le modèle de régression linéaire et on obtient le tableau suivant :

Nombre de camions	Nombre de chauffeurs	Nombre de camions	Nombre de chauffeurs	Nombre de camions	Nombre de chauffeurs
0	0	20	32	40	62
1	2	21	34	41	63
2	4	22	35	42	65
3	6	23	37	43	66
4	8	24	38	44	68
5	9	25	40	45	69
6	11	26	41	46	71
7	13	27	43	47	72
8	14	28	44	48	74
9	16	29	46	49	75
10	17	30	47	50	77
11	19	31	49	51	78
12	20	32	50	52	80
13	22	33	52	53	81
14	23	34	53	54	83
15	25	35	55	55	84
16	26	36	56	56	86
17	28	37	58	57	87
18	29	38	59	58	89
19	31	39	61	59	90

TAB. 5.14 Nombre de chauffeurs correspondant au nombre de camions par la régression

Pour Nbrc = 60 :

Pour déterminer le nombre de chauffeurs correspondant, on utilise le modèle de régression non linéaire et on obtient le tableau suivant :

Nombre de camions	Nombre de chauffeurs	Nombre de camions	Nombre de chauffeurs
60	90	78	103
61	91	79	103
62	92	80	103
63	94	81	103
64	95	82	104
65	96	83	104
66	97	84	104
67	98	85	104
68	99	86	104
69	99	87	104
70	100	88	104
71	100	89	104
72	101	90	104
73	101	91	104
74	102	92	104
75	102	93	104
76	102	94	104
77	103	95	104

TAB. 5.15 - Nombre de chauffeurs correspondant au nombre de camions par la régression

Remarque 5.3. Le nombre maximum de chauffeurs, d'après le modèle de régression non linéaire, que devra avoir l'entreprise est :

~

lim

x--+8 1 + 399.03.e_^0.129x

104.08 ) = 104.08 105

5.9 Conclusion

L'objectif principal de notre simulateur est de déterminer un recouvrement optimal des camions par les chauffeurs compte tenu de leurs repos est de la demande journalière. Avec le modèle avec file, on a pu déterminer qu'il fallait un nombre de chauffeurs précis indépendamment du nombre de camions, car d'après le théorème de Burke, le taux de sortie des clients est le même que celui de leurs arrivées si la condition d'ergodicitéest vérifiée. Donc il faudra avoir un nombre de chauffeurs de telle sorte qu'ils se couvrent mutuellement durant leurs jours de repos pour satisfaire la demande.

Avec le modèle sans file, on a trouvéque le nombre de chauffeurs dépend du nombre de camions, car contrairement au modèle avec file, l'entreprise perd des clients qui ne trouvent pas de serveurs libres, donc a` chaque fois qu'on augmente le nombre de camions, il faudra avoir un nombre de chauffeurs plus important pour se couvrir mutuellement d'une part, et éviter au maximum les découragements des clients d'une autre part.

Le problème de transport est un problème complexe et sa r'esolution a fait l'objet de plusieurs 'etudes. Les responsables de l'entreprise savaient bien que les moyens investis et le système de fonctionnement du service transport posaient problème, mais le plus difficile, dans ce genre d''etude, est de bien cerner le problème pour pouvoir le d'evelopper.

A` priori, le problème paraissait comme un problème de transport qui consiste a` livrer des quantit'es du d'epôt central appel'e origine aux diff'erents clients appel'es destinataires. Puis le problème est apparu sous forme de problème de tourn'ee o`u l'on est confront'e a` un ensemble d'itin'eraires, pour une flotte de v'ehicules, bas'e sur un ou plusieurs d'epôts et qui doit être d'etermin'e pour un certain nombre de villes ou de clients g'eographiquement dispers'es. Une 'etude a 'et'e faite en 2000 a` ce sujet (voir [2]).

Finalement, les responsables de l'entreprise ont opt'e pour une politique de transport inspir'ee de l'exp'erience de ces g'erants, consid'er'ee comme un système forfaitaire qu'ils ont jug'e plus ad'equat et cela pour des raisons bien pr'ecises.

L'objectif de cette 'etude est l'optimisation et la gestion du parc de transport de l'entreprise tout en respectant le système de distribution impos'e par les g'erants.

Après avoir compris le fonctionnement du système, nous avons d'abord 'etudi'e les arriv'ees des demandes puis les dur'ees de service des camions. On a constat'e que le système peut être mod'eliser sous forme de file d'attente. Faute de manque de donn'ees, on a pas pu d'eterminer si le système sera mod'elis'e avec ou sans file, alors on a mod'elis'e avec les deux approches et on a laiss'e la prise de d'ecision aux d'ecideurs.

Avec le modèle avec file, on est arriv'e a` d'eterminer le nombre de camions que devra avoir l'entreprise selon les caract'eristiques du système. Donc c'est une d'ecision a` prendre par l'entreprise.

Avec le modèle sans file, on a pris en compte les pertes engendr'ees par le d'ecouragement des clients, alors on a pu trouver un compromis entre ces pertes et le nombre de camions qu'il faut mettre a` la disposition de l'entreprise.

On a aussi prit en compte l'alternative qu'au lieu d'acheter des camions, l'entreprise ait recours a` la location de ces derniers.

Après avoir d'eterminer le nombre de camions, le nombre de chauffeurs qu'il faut mettre en service pour une gestion optimale de ses camions pose problème. Pour rem'edier a` ca, un modèle de simulation a 'et'e 'elabor'e et valid'e. C'est un programme informatique r'ealis'e avec Delphi⁴ (voir annexe B) pour la d'etermination des paramètres li'es au modèle.

Avec ce simulateur, on est arriv'e a` des r'esultats bien int'eressants. Si l'on considère le système avec file, alors on a aboutit que l'entreprise devra avoir un nombre de chauffeurs bien pr'ecis, ind'ependamment du nombre de camions et r'egit seulement par le flux des arriv'ees. Et cela est interpr'et'e par le fait qu'il n'y a pas de perte de clients. Par contre, si on considère le modèle sans file, le nombre de chauffeurs est directement proportionnel avec le nombre de camions et cela est dàu aux d'ecouragements des clients qui engendrent des pertes consid'erables a` l'entreprise.

Comme perspective, il est très int'eressant après avoir d'eterminer le nombre de camions et le nombre de chauffeurs, de d'evelopper une application pour une affectation des chauffeurs aux camions, de facon a` minimiser les heures suppl'ementaires et par cons'equent infliger moins de pertes a` l'entreprise.

⁴Delphi : Environnement de programmation permettant de développer des applications pour les systèmes d'exploitation des familles MS-Windows et Linux.

Bibliographie

[1] A. A·ýssani. Eléments de simulation statistique. USTHB Alger, 1998.

[2] A. Belkadi, Z. Beddar. Optimisation de la distribution au niveau de la sarl Ibrahim & Fils ifri. Mémoire d'ingéniorat en Rø. Département de Recherche Opérationnelle, universitéde Béja·ýa, 2000.

[3] A. Martel. Techniques et applications de la recherche opérationnelle. Gaëtan morin Ed, ^2`eme edition, 1979.

[4] A. Ruegg. Processus stochastiques. Presses polytechniques romandes edition, Suisse, 1989.

[5] B. Rabta. Cours de simulation, ^4`eme année Recherche Opérationnelle. Département de Recherche Opérationnelle, universitéde Béja·ýa, 2005/2006.

[6] D. Aissani. Cours de Processus aléatoires appliqués et prévisions, ^4`eme année Recherche Opérationnelle. Département de Recherche Opérationnelle, universitéde Béja·ýa, 2005/2006.

[7] D. de Werra. Eléments de programmation linéaire avec application aux graphes. Presses polytechniques et universitaires romandes edition, 1990.

[8] Groupe Roseaux. Phénomênes aléatoires en recherche opérationelle. Masson edition, tome2, Paris, 1983.

[9] J-F. Hêche, T. M. Liebling, D. de Werra. Recherche Opérationnelle pour ingénieur II. Presses polytechniques et universitaires romandes edition, tome2, 2003.

[10] J-M. Hélary, R. Pédrono. Recherche Opérationnelle Travaux dirigés. Hermann edition, Paris, 1983.

[11] M. Babes. Statistiques, files d'attente et simulation. Office des publications universitaires edition, 1995.

[12] M. R. Spigel. Schaum's outline of theory and problems of statistics. Dunod edition, Paris, 2002.

[13] M. S. Radjef. Cours de Programmation mathématique, ^4`eme année Recherche Opérationnelle. Département de Recherche Opérationnelle, universitéde Béja·ýa, 2005/2006.

[14] N. Bernine, E. Guechari. Planification multicritêre de la production au niveau de la sarl Ibrahim & Fils ifri. Mémoire d'ingéniorat en Rø. Département de Recherche Opérationnelle, universitéde Béja·ýa, 2004.

R'ef'erences bibliographiques

[15] N. Hamadouche.Approximation dans les systêmes prioritaires. Mémoire de magister. Département de Recherche Opérationnelle, universitéde Béja·ýa, 2004.

[16] S. Adjabi. Cours de Statistique, ^3`eme année Recherche Opérationnelle. Département de Recherche Opérationnelle, universitéde Béja·ýa, 2003/2004.

[17] S. Adjabi. Cours de Méthodes statistiques de la prévision, ^5`eme année Recherche Opérationnelle. Département de Recherche Opérationnelle, universitéde Béja·ýa, 2006/2007.

Donne' es récoltées

TAB. A.1: Liste des véhicules

Num MAT Km ACTUEL CONSOMMATION/100 Km MISE EN CIRCULA TONNAGE CODE MARQUE

1201	00181-502-06	666680	45	21/04/2002	30	T/R 4X2	YV2A4DMA32A
1202	00182-502-06	3164243	45	20020421	25	T/R	YV2A4DMA12A
1203	00183-502-06	970092	45	20020421	25	T/R	YV2A4DMA92A
1204	00184-502-06	481887	45	20020421	25	T/R	YV2A4DMA52A
1205	00185-502-06	682882	45	20020421	25	T/R	YV2A4DMA72A
1206	00186-502-06	7044317	45	20020421	25	T/R	YV2A4DMA82A
1207	00187-502-06	489400	45	20020421	25	T/R	YV2A4DMA52A
1208	00188-502-06	607039	45	20020421	25	T/R	YV2A4DMAX2A
1209	00189-502-06	477041	45	20020421	25	T/R	YV2A4DMA72A
1210	00190-502-06	586857	43	20020421	25	T/R	YV2A4DMA42A
1211	00529-202-06	2261989	43	20020731	20	CAM	YV2E4CCA1
1601	01676-506-06	761086	43	20060710	30	TR 4X2	FH13
1602	01709-506-06	55613	43	20060723	30	TR	YV2ASO2A66A
1603	01731-506-06	57165	43	20060723	56	TR	YV2ASO2A16A
1604	01733-506-06	72302	43	20060814	30	TR	/
1605	01713-506-06	62687	43	20060723	56	TR 4X2	FH13
1606	01712-506-06	39074	43	20060823	56	TR	YV2ASO2A46A
1607	01717-506-06	77083	43	20060723	56	TR	YV2ASO2AX6A
1608	01729-506-06	75696	43	20060712	30	TR 4X2	FH13
1609	01705-506-06	82131	43	20060712	30	TR 4X2	FH13
1610	01686-506-06	86024	43	20060712	30	TR 4X2	FH13
1611	01688-506-06	637708	43	20060723	56	TR	YV2ASO2A36A
1612	01693-506-06	691948	43	20060814	30	T.R
1613	01694-506-06	702759	43	20060723	56	TR	YV2ASO2A36A
1614	01707-506-06	68635	43	20060810	32	T.R	/
1615	01700-506-06	81388	43	20060718	30	TR 4X2	FH13
1616	01698-506-06	736593	43	20060712	30	TR 4X2	FH13
1617	01692-506-06	55286	43	20060814	30	T.R
1618	01702-506-06	79236	43	20060718	30	TR 4X2	FH13
1619	01690-506-06	70107	43	20060723	32	TR	TV2ASO2A06A
1620	01332-506-06	85190	43	20060719	30	TR 4X2	FH13
1621	01695-506-06	68768	43	20060723	56	TR	YV2ASO2A76A
1622	01667-506-06	799462	43	20060718	30	TR 4X2	FH13
1623	01680-506-06	872460	43	20060712	30	TR 4X2	FH13
1624	01696-506-06	86019	43	20060723	56	TR	YV2AOS2A56A
1625	01691-506-06	70436	43	20060806	30	TR	FH13
1626	01697-506-06	58006	43	20060723	56	TR	YV2ASO2A06A
1627	01681-506-06	31088	43	20060723	56	TR	YV2ASO2A36A
1628	01687-506-06	84283	43	20060712	30	TR 4X2	FH13
1629	01684-506-06	814367	43	20060710	30	TR 4X2	FH13
1630	92099-00-16	69913	43	20060814	30	TR	/
1631	01683-506-06	786545	43	20060723	32	TR	YV2ASO256A
1632	01682-506-06	57993	43	/	30	/	/
1633	01704-506-06	63781	43	20060723	32	TR	YV2ASO2A06A

TAB. A.1: suite

1634	01735-506-06	71346	43	20060723	56	TR	YV2ASO2A96A
1635	01674-506-06	59034	43	20060723	56	TR	YV2ASO2AX6A
1636	01671-506-06	64919	43	20060723	56	TR	YV2ASO2A06A
1637	01672-506-06	63316	43	20060814	30	T.R	/
1638	01689-506-06	696623	43	20060723	30	TR	YV2ASO2A56A
1639	1706-506-06	609069	43	20060814	30	TR	/
1640	01679-506-06	458009	0	20060723	32	TR	YV2ASO2AX6A
1641	01736-506-06	74769	43	20060814	30	T.R	YV2ASO2A26A
1642	1685-506-06	50497	43	20060813	30	TR	/
1643	1678-506-06	62267	43	20060813	32	TR	/
1644	01726-506-06	70564	43	20060723	30	TR6X4	YV2ASO2A46A
1645	01725-506-06	64658	43	20060814	30	T.R
1646	1739-506-06	21076	43	20060813	20	TR	/
1647	1741-506-06	144507	43	20060813	32	TR	/
1648	1737-506-06	133473	43	20060815	30	TR	/
1649	01740-506-06	155601	43	/	40	/	/
1650	01722-506-06	80757	43	20060718	30	TR 4X2	FH13
1651	01675-506-06	86743	43	20060718	30	TR 4X2	FH13
1652	1723-506-06	/	43	20060814	30	TR	/
1653	01677-506-06	57322	43	20060723	56	TR	YV2ASO2A86A
1654	01727-506-06	77167	43	20060723	32	TR	YV2ASO2A26A
1655	01670-506-06	82849	43	20060712	30	TR 4X2	FH13
1656	1720-506-06	713199	43	20060814	30	TR	/
1657	01728-506-06	79459	43	20060718	30	TR 4X2	FH13
1658	1718-506-06	65429	43	20060814	30	TR	/
1659	01714-506-06	585004	43	20060723	56	TR	YV2AOS2A36A
1660	01716-506-06	619016	43	20060723	32	TR	YV2ASO2A26A
1661	01669-506-06	81792	43	20060718	30	TR 4X2	FH13
1662	1738-506-06	245925	43	20060723	56	TR	YV2ASO2A66A
1663	01673/506/06	565290	43	20060723	56	TR	YV2ASO2A56A
1664	01730-506-06	78889	43	20060718	32	TR 4X2	FH13
1665	01732-506-06	51710	43	20060723	56	TR	YV2ASO2A56A

TAB. A.2: Liste des destinations

DESTINATION CLIENT DISTANCE PERIODE FRAIS DE MISSION GASOILS NBRE BON RETOUR-L

ADRAR	KHELIL	2945 KM	5 JOURS	4500 DA	1178 L	23 BONS	187 L
AIN AMINAS	CNA	3126KM	6 JOURS	5500 DA	1320L	25 BONS	100 L
AIN TIMOCHENT	ALOUL	1361KM	3 JOURS	2000 DA	600L	4 BONS	153 L
ALGER	MOKRANE ALI	396KM	1 JOUR	500 DA	170L	0 BON	420 L
ALGER	KHELIL	432KM	1 JOUR	500 DA	190L	0 BON	400 L
ALGER	PEROQUET	400KM	1 JOUR	500 DA	180L	0 BON	410 L
ANADARCO	MULTICATERING	1881 KM	4 JOURS	3000 DA	790 L	10 BONS	132 L
ANNABA	BADREDINE	940KM	2 JOURS	1500 DA	400L	0 BON	190 L
BATNA	MERAOUCH	678KM	2 JOUR	1000 DA	290L	0 BON	400 L
BECHAR	CRAI 3EME REGION	2134KM	4 JOURS	3500 DA	900L	13 BONS	100 L
BEJAIA	IBRAHIM FARID	106KM	1 JOUR	500 DA	50L	0 BON	550 L
BEJAIA	IDJOUADIEN	108KM	1 JOUR	500 DA	50L	0 BON	550 L
BLIDA	MAHI BRAHIM	464KM	1 JOUR	500 DA	200L	0 BON	400 L
BORDJ	SNC IBRAHIM YOUNES	154KM	1 JOUR	500 DA	65L	0 BON	535 L
BOUDOUAOU	CASCADES	346KM	1 JOUR	500 DA	150L	0 BON	450 L
BOUIRA	FERKAL	172KM	1 JOUR	500 DA	80L	0 BON	520 L
BOUSSAADA	SAIGH ALI	432KM	1 JOUR	500 DA	190L	0 BON	410 L
BRN	MULTICATERING	2147KM	4 JOURS	3500 DA	910L	13 BONS	124 L
CEPSA HMD	CEPSA	2146 KM	4 JOURS	3500 DA	902 L	13 BONS	128 L
CHERAGA	HAMADACHE	420KM	1 JOUR	500 DA	190L	0 BON	410 L
CHLEF	MELOUK	786KM	2 JOURS	1000 DA	340L	0 BON	260 L
CONSTANTINE	ZERMANE	614KM	1 JOUR	500 DA	260L	0 BON	340 L
DJELFA	MAHDJOUB	668KM	1 JOUR	500 DA	285L	0 BON	315 L
EL TAREF	BOUDJA SAMIR	1098 KM	2 JOURS	1500 DA	440 L	0 BONS	150 L
GHARDAIA	KOUMNIE	1254KM	3JOURS	2000 DA	530L	2 BONS	128 L
HASSI BARKINE	MULTICATERING	2126 KM	4 JOURS	3500 DA	900 L	13 BONS	100 L
HMD	ALMAFRIQUE	1501KM	3 JOURS	2500 DA	640 L	6 BONS	134 L
I/AMOKRANE	MOUSSAOUI	7KM	1 JOUR	0 DA	4L	0 BON	580 L
JIJEL	KEDJA AICHA	292KM	1 JOUR	500 DA	130L	0 BON	460 L
KHENCHLA	CHOUAKRIA	939KM	2 JOURS	1500 DA	400L	0 BON	190 L
MASCARA	BOUCIF	1114KM	2 JOURS	1500 DA	480L	1 BONS	144 L
MEDEA	BAHA NADJIA	438KM	1 JOUR	500 DA	190L	0 BON	400 L
MILA	SAIGHI ALI	680KM	1 JOUR	1000 DA	290L	0 BON	310 L
MOSTAGUANEM	RAHMANI	1034KM	2 JOURS	1500 DA	440L	0 BONS	150 L
M'SILA	LAIFA	292KM	1 JOUR	500 DA	130L	0 BON	470 L
NABORS 288	ACS	2080 KM	4 JOURS	3500 DA	875 L	13 BONS	160 L
NABORS 810	ACS	2180 KM	4 JOURS	3500 DA	873 L	14 BONS	192 L
NABORS F22	ACS	1513 KM	3 JOURS	2500 DA	640 L	6 BONS	152 L
OHANET	BHP BILITON	2800 KM	5 JOURS	4500 DA	1180 L	22 BONS	135 L
ORAN	GUERBOUKHA	1176KM	2 JOURS	1500 DA	500L	1 BONS	124 L
OUARGLA	BENCHILA DJAMEL	1485KM	3 JOURS	2500 DA	630L	6 BONS	135 L
OUM ELBOUAGUI	AGUEMOUNE	968KM	2 JOURS	1500 DA	415L	0 BON	185 L
OURHOUD FILD	ACS	2126KM	4 JOURS	3500 DA	900L	14 BONS	135 L

TAB. A.2: suite

RELIZANE	AIT KHEDACHE	946KM	2 JOURS	1500 DA	400L	0 BON	200 L
RIG	MULTICATERING	2001 KM	4 JOURS	3500 DA	840 L	12 BONS	135 L
SAIDA	/	1286KM	3 JOURS	2000 DA	540 L	2 BONS	138 L
SARPI EL-GASSI	MULTICATERING	1813 KM	4 JOURS	3000 DA	765 L	8 BONS	140 L
SETIF	BABOURI	394KM	1 JOUR	500 DA	170L	0 BON	430 L
SETIF	SAOUDI SABER	394KM	1 JOUR	500 DA	170L	0 BON	430 L
SIDI BELABBES	SOULEH	1254KM	3 JOURS	2000 DA	530L	2 BONS	128 L
SKIKDA	DJERROUD	816KM	2 JOURS	1500 DA	350L	0 BON	250 L
SKIKDA	SARL AKOUAS	834KM	2 JOURS	1500 DA	360L	0 BON	240 L
SONARCO	MULTICATRING	1687KM	3JOURS	2500 DA	671L	8 BONS	197 L
SOUK AHRAS	/	1104KM	2JOURS	1500 DA	480 L	0 BON	144 L
TAMENRASET	BB MD/AMEZIANE	4213 KM	9 JOURS	8500 DA	1806 L	42 BONS	201 L
TEBBESSA	MENANI	1036KM	2 JOURS	1500 DA	450L	0 BONS	140 L
TIARET	IBALIDEN AZEDINE	888KM	2 JOURS	1500 DA	380L	0 BON	220 L
TINDOUF	CRAI 3EME REGION	3761KM	7 JOURS	6500 DA	1590 L	35 BONS	170 L
TINFOUY TFT	MULTICATERING	2150KM	4 JOURS	3500 DA	900 L	12 BONS	100 L
TIPAZA	IBRAHIM HAMID	486KM	1 JOUR	500 DA	210L	0 BON	390 L
TIZIOU OUZOU	AMERI CHERIF	400KM	1 JOUR	500 DA	170L	0 BON	430 L
TLEMCEN	RAJA AZEDINE	1520KM	3 JOURS	2500 DA	650L	6 BONS	151 L
TOUGOURT	SARL NORTH	1138KM	2 JOURS	1500 DA	485L	0 BONS	105 L

TAB. A.3: Demandes par jours

DATE	Nbr de camions	DATE	Nbr de camions	DATE	Nbr de camions
02/08/2006	1	09/11/2006	49	16/02/2007	10
04/08/2006	6	10/11/2006	42	17/02/2007	52
05/08/2006	36	11/11/2006	46	18/02/2007	40
06/08/2006	3	12/11/2006	53	19/02/2007	42
07/08/2006	3	13/11/2006	49	20/02/2007	42
08/08/2006	24	14/11/2006	53	21/02/2007	51
09/08/2006	11	15/11/2006	45	22/02/2007	44
10/08/2006	20	16/11/2006	46	23/02/2007	11
11/08/2006	10	17/11/2006	31	24/02/2007	48
12/08/2006	11	18/11/2006	46	25/02/2007	41
13/08/2006	6	19/11/2006	48	26/02/2007	40
14/08/2006	9	20/11/2006	48	27/02/2007	42
15/08/2006	4	21/11/2006	55	28/02/2007	41
16/08/2006	46	22/11/2006	49	01/03/2007	83
17/08/2006	17	23/11/2006	41	02/03/2007	1
18/08/2006	1	24/11/2006	20	03/03/2007	64
19/08/2006	48	25/11/2006	44	04/03/2007	62
20/08/2006	44	26/11/2006	53	05/03/2007	55
21/08/2006	44	27/11/2006	45	06/03/2007	57
22/08/2006	49	28/11/2006	41	07/03/2007	51
23/08/2006	49	29/11/2006	47	08/03/2007	63
24/08/2006	25	30/11/2006	39	09/03/2007	2
26/08/2006	5	01/12/2006	17	10/03/2007	66
27/08/2006	53	02/12/2006	41	11/03/2007	41
28/08/2006	47	03/12/2006	44	12/03/2007	34
29/08/2006	51	04/12/2006	42	13/03/2007	55

TAB. A.3: suite

30/08/2006	44	05/12/2006	44	14/03/2007	65
31/08/2006	74	06/12/2006	47	15/03/2007	59
01/09/2006	3	07/12/2006	32	16/03/2007	6
02/09/2006	6	08/12/2006	17	17/03/2007	66
03/09/2006	41	09/12/2006	37	18/03/2007	62
04/09/2006	49	10/12/2006	46	19/03/2007	57
05/09/2006	52	11/12/2006	45	20/03/2007	66
06/09/2006	38	12/12/2006	42	21/03/2007	51
07/09/2006	76	13/12/2006	45	22/03/2007	40
08/09/2006	3	14/12/2006	42	23/03/2007	25
09/09/2006	52	15/12/2006	14	24/03/2007	46
10/09/2006	57	16/12/2006	32	25/03/2007	70
11/09/2006	50	17/12/2006	42	26/03/2007	55
12/09/2006	48	18/12/2006	39	27/03/2007	52
13/09/2006	55	19/12/2006	37	28/03/2007	63
14/09/2006	82	20/12/2006	38	29/03/2007	44
16/09/2006	47	21/12/2006	33	31/03/2007	53
17/09/2006	58	22/12/2006	6	01/04/2007	53
18/09/2006	49	23/12/2006	38	02/04/2007	61
19/09/2006	45	24/12/2006	27	03/04/2007	54
20/09/2006	44	25/12/2006	34	04/04/2007	55
21/09/2006	33	26/12/2006	33	05/04/2007	50
22/09/2006	42	27/12/2006	29	06/04/2007	9
23/09/2006	44	28/12/2006	24	07/04/2007	50
24/09/2006	44	02/01/2007	37	08/04/2007	64
25/09/2006	48	03/01/2007	47	09/04/2007	58
26/09/2006	45	04/01/2007	41	10/04/2007	64
27/09/2006	48	05/01/2007	15	11/04/2007	82
28/09/2006	19	06/01/2007	38	12/04/2007	59
29/09/2006	38	07/01/2007	44	13/04/2007	7
30/09/2006	2	08/01/2007	41	14/04/2007	62
01/10/2006	82	09/01/2007	41	15/04/2007	72
02/10/2006	40	10/01/2007	40	16/04/2007	45
03/10/2006	54	11/01/2007	48	17/04/2007	56
04/10/2006	60	12/01/2007	11	18/04/2007	58
05/10/2006	27	13/01/2007	36	19/04/2007	60
06/10/2006	2	14/01/2007	46	20/04/2007	8
07/10/2006	46	15/01/2007	46	21/04/2007	52
08/10/2006	94	16/01/2007	41	22/04/2007	57

TAB. A.3: suite

09/10/2006	5	17/01/2007	42	23/04/2007	52
10/10/2006	54	18/01/2007	43	24/04/2007	52
11/10/2006	59	19/01/2007	15	25/04/2007	60
12/10/2006	43	20/01/2007	41	26/04/2007	59
13/10/2006	27	21/01/2007	46	27/04/2007	2
14/10/2006	40	22/01/2007	42	28/04/2007	71
15/10/2006	50	23/01/2007	51	29/04/2007	66
16/10/2006	51	24/01/2007	56	30/04/2007	61
17/10/2006	49	25/01/2007	42	01/05/2007	52
18/10/2006	52	26/01/2007	22	02/05/2007	48
19/10/2006	46	27/01/2007	30	03/05/2007	54
20/10/2006	25	28/01/2007	43	04/05/2007	5
21/10/2006	42	29/01/2007	30	05/05/2007	74
22/10/2006	41	30/01/2007	25	06/05/2007	57
23/10/2006	2	31/01/2007	33	07/05/2007	51
25/10/2006	27	01/02/2007	33	08/05/2007	59
26/10/2006	75	02/02/2007	1	09/05/2007	56
27/10/2006	19	03/02/2007	48	10/05/2007	55
28/10/2006	56	04/02/2007	50	11/05/2007	8
29/10/2006	58	05/02/2007	45	12/05/2007	71
30/10/2006	54	06/02/2007	41	13/05/2007	60
31/10/2006	58	07/02/2007	45	14/05/2007	63
01/11/2006	56	08/02/2007	33	15/05/2007	60
02/11/2006	43	09/02/2007	1	16/05/2007	7
03/11/2006	46	10/02/2007	46	18/05/2007	45
04/11/2006	47	11/02/2007	40	19/05/2007	57
05/11/2006	46	12/02/2007	47	20/05/2007	69
06/11/2006	48	13/02/2007	42	21/05/2007	61
07/11/2006	54	14/02/2007	41	22/05/2007	67
08/11/2006	49	15/02/2007	45	23/05/2007	58

TAB. A.4: Durées de services pour les journées 05/09/2006 et 06/09/2006

DATE	DUR'EE DU TRAJET	DATE	DUR'EE DU TRAJET
05/09/2006	3	06/09/2006	1
05/09/2006	1	06/09/2006	1
05/09/2006	1	06/09/2006	1
05/09/2006	1	06/09/2006	1

TAB. A.4: suite

05/09/2006	1	06/09/2006	1
05/09/2006	1	06/09/2006	1
05/09/2006	1	06/09/2006	1
05/09/2006	1	06/09/2006	1
05/09/2006	1	06/09/2006	1
05/09/2006	1	06/09/2006	1
05/09/2006	1	06/09/2006	1
05/09/2006	1	06/09/2006	1
05/09/2006	1	06/09/2006	1
05/09/2006	1	06/09/2006	2
05/09/2006	1	06/09/2006	1
05/09/2006	1	06/09/2006	1
05/09/2006	1	06/09/2006	1
05/09/2006	2	06/09/2006	1
05/09/2006	2	06/09/2006	1
05/09/2006	1	06/09/2006	1
05/09/2006	1	06/09/2006	1
05/09/2006	1	06/09/2006	1
05/09/2006	1	06/09/2006	1
05/09/2006	1	06/09/2006	1
05/09/2006	1	06/09/2006	1
05/09/2006	1	06/09/2006	2
05/09/2006	2	06/09/2006	2
05/09/2006	2	06/09/2006	2
05/09/2006	2	06/09/2006	2
05/09/2006	1	06/09/2006	2
05/09/2006	1	06/09/2006	2
05/09/2006	3	06/09/2006	2
05/09/2006	3	06/09/2006	1
05/09/2006	3	06/09/2006	1
05/09/2006	2	06/09/2006	3
05/09/2006	2	06/09/2006	1
05/09/2006	2	06/09/2006	1
05/09/2006	2	06/09/2006	1
05/09/2006	2
05/09/2006	2
05/09/2006	2
05/09/2006	2
05/09/2006	1

TAB. A.4: suite

05/09/2006	1
05/09/2006	2
05/09/2006	1
05/09/2006	1
05/09/2006	1
05/09/2006	1
05/09/2006	1
05/09/2006	1
05/09/2006	3

B

Pr'esentation de l'application

Comme nous l'avons citéauparavant, notre application est réalisée avec Delphi7. On présente dans ce qui suit cette application avec le mode de son fonctionnement.

Pour cela, on commence par la représentation de l'interface utilisateur dans la figure suivante :



FIG. B.1 - Interface du simulateur.
115

Après avoir fixer les entrées, on simule en cliquant sur le bouton »Simuler» et on aura les résultats dans le tableau avec indication du nombre de chauffeurs qui minimise la fonction perte comme le montre la figure suivante :



FIG. B.2 - Exécution du simulateur.

On peut visualiser le graphe de la fonction perte en cliquant sur le bouton »Graphe» :



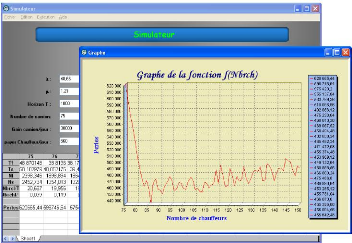
Avec possibilitéde copier et de déplacer les résultats pour pouvoir les traiter ailleurs,

fonctionnant comme un tableur Excel:



Ou bien de les enregistrer sous forme d'un fichier et de le rouvrir plus tard :



C

Modèles de r'egression



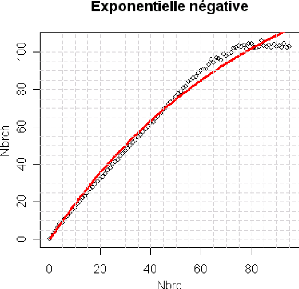
FIG. C.1 - Exponentielle n'egative : y = a(1 - ^e(-bx)) + bruit.



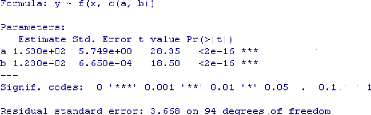
FIG. C.2 - Estimation et validation des paramètres du modèle avec R.



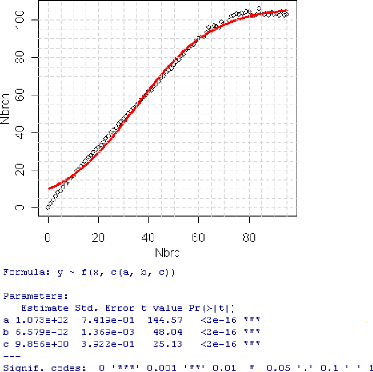
FIG. C.3 - Croissance sigmo·ýde : y = a

1+Ce(_vx) + bruit.





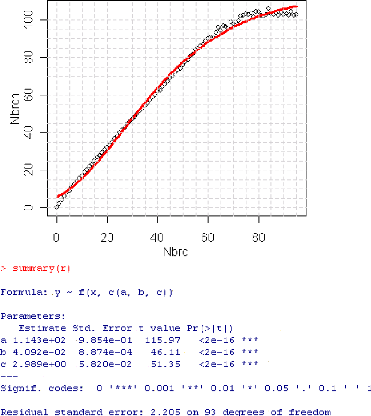
FIG. C.4 - Croissance sigmo·ýde moins symétrique : y = ae(-ce(-bx))+ bruit.

R'esum'e

Le but de ce travail est l'optimisation et la gestion du parc de transport au niveau de la sarl ifri tout en respectant le système de distribution impos'e par les g'erants.

Après avoir compris le fonctionnement du système, nous avons d'abord d'etermin'e les lois r'egissant les arriv'ees des demandes ainsi que les dur'ees de service des camions. On a constat'e que le système peut être mod'eliser sous forme de file d'attente. On n'a pas pu d'eterminer si le système sera mod'elis'e avec ou sans file, alors on a mod'elis'e avec les deux modèles et on a laiss'e la prise de d'ecision sur le choix du modèle aux d'ecideurs.

Avec le modèle avec file, on est arriv'e a` d'eterminer le nombre de camions que devra avoir l'entreprise selon les caract'eristiques du système. Par contre, avec le modèle sans file, on a pu trouver un compromis entre les pertes engendr'ees par le d'ecouragement des clients et le nombre de camions qu'il faut mettre a` la disposition de l'entreprise. On a aussi d'etermin'e le nombre de camions, si l'entreprise opte pour la location de ces derniers.

Après avoir d'eterminer le nombre de camions, le nombre de chauffeurs qu'il faut mettre en service pour une gestion optimale de ses camions pose problème. Pour rem'edier, un modèle de simulation a 'et'e 'elabor'e et valid'e, et cela pour les deux modèles avec et sans file.

Mots dl'es : Test, Ajustement, R'egression, Files d'attente, Optimisation, Convexit'e, Simulation.