0. INTRODUCTION
0. 1. Problématique
Les divers nombres sont apparus pour faire face à
diverses nécessités notamment pour trouver des solutions à
certaines équations jugées impossibles. Leur usage s'est
généralisé en même temps que les règles
qu'ils nécessitent se trouvaient mieux connues.
Ainsi a-t-on vu apparaître les nombres relatifs, les
nombres fractionnaires (rationnels), les nombres irrationnels. Chaque type de
ces nombres répondait à un problème nouveau.
Les nombres complexes, eux aussi, sont d'une grande importance
dans la résolution des problèmes non pas seulement en
mathématique pure mais aussi et surtout dans les mathématiques
appliquées et les sciences physiques. Introduits dans les fonctions
élémentaires usuelles, ces nombres confèrent auxdites
fonctions de nouvelles propriétés.
Par exemple, « la fonction exponentielle
à variable complexe ez devient périodique, les
fonctions sin z et cos z cessent d'être bornées, le logarithme des
nombres négatifs (et, en général, de tout nombre complexe
non nul) prend un sens ». (1(*))
La grande question à se poser est la suivante :
« Quels sont les algorithmes (opérations)
à utiliser pour chaque type de fonctions pour en calculer la valeur
numérique lorsque la variable principale est
complexe ? »
Toutefois, quoique ces algorithmes trouvés, se posera
le problème de lenteur et aussi ne serons-nous pas à l'abri des
erreurs. Ainsi, posons-nous la question :
« Comment procéder ou que faire pour pallier
aux difficultés liées à la lenteur et aux erreurs de
calcul ? »
Les réponses à ces deux questions feront l'objet
de notre étude.
0. 2. Hypothèses
L'étude des fonctions multiformes dans le domaine
complexe est d'une importance particulière car seule une telle
étude permet d'expliquer la nature de leur multiformité. En
effet, il y a possibilité de dégager sur certains exemples de
fonctions multiformes des branches uniformes qui s'avèrent des fonctions
analytiques.
En outre, grâce au théorème de Gauss sur
la nature du Corps C des nombres complexes,
l'évaluation des fonctions numériques usuelles sur des valeurs
complexes est rendue possible. Les opérations fondamentales
définies sur des réels sont aussi valables pour des complexes.
Ceci est une généralisation de la notion de
fonctions à variables réelles aux variables complexes. Les
nouvelles fonctions enrichies en propriétés (fonctions à
variables complexes) sont un prolongement naturel des fonctions
élémentaires usuelles en analyse au domaine complexe. Certes,
comme l'avons-nous souligné plus haut, par un tel prolongement ces
fonctions s'enrichissent parfois de nouvelles propriétés.
Dans ce travail, nous allons proposer des algorithmes pour
chaque type de fonctions afin d'en calculer la (les) valeur(s) lorsque la
variable prend des valeurs complexes. (2(*))
Ces algorithmes, bien entendu, donneront les résultats
connus dans IR lorsque appliqués aux nombres complexes
particuliers qui sont les réels.
Enfin, en vue d'éviter la lenteur et les erreurs dans
ces genres de calcul, nous avons pensé nécessaire qu'une fois les
algorithmes trouvés, il faille automatiser le travail de calcul en
concevant des programmes informatiques en langage Visual Basic.
0. 3. Choix et Intérêt du sujet
Face aux difficultés rencontrées dans
l'évaluation des fonctions réelles sur des valeurs prises hors de
leurs domaines de définition, nous avions pensé dans un premier
temps que produire des algorithmes permettant d'évaluer des fonctions
numériques usuelles sur des valeurs complexes allègerait bon
nombre desdites difficultés. De plus, si la notion et l'essentiel sur
les nombres complexes nous sont connus, il ne nous sera pas difficile de
comprendre la démarche utilisée pour obtenir ces algorithmes.
Vu la pertinence du problème et la contribution d'une
telle étude dans la palliation des difficultés
précitées, nous avons été tentés de traiter
du sujet :
« Evaluation de fonctions usuelles
sur des variables complexes : Algorithmisation des calculs et
programmation »
Loin de nous l'idée de prétendre faire une
étude systématique sur les fonctions et les nombres complexes -
ce qui rendrait plus lourd et plus coûteux notre étude - nous
osons croire que nos lecteurs trouveront à travers notre exposé
des bases leur permettant de se familiariser à la recherche, à
l'usage des algorithmes, aux méthodes de résolution et aux
différents types de raisonnement.
0. 4. Délimitation du sujet
Comme l'a soutenu Makiadi Nzumba : «
l'étude des fonctions est une matière assez vaste ; elle
recouvre plusieurs types de fonctions » (3(*))
Nous n'allons pas étudier toutes les fonctions
numériques mais allons nous limiter, moins que MAKIADI d'ailleurs, aux
fonctions suivantes :
Fonctions trigonométriques
Fonctions trigonométriques réciproques
Fonctions logarithmiques
Fonctions exponentielles
Fonctions hyperboliques
Fonctions hyperboliques réciproques
Pour des raisons de beauté et d'esthétique dans
la présentation des résultats générés
automatiquement, nous avons choisi de programmer nos algorithmes dans un
langage orienté objet, ce qui nous a conduit au choix du langage Visual
Basic.
Par ailleurs, les algorithmes de certaines fonctions ne seront
pas programmés parce que découlant de la composition des
fonctions dont on a déjà l'algorithme et le code en Visual Basic.
Cette restriction trouve sa justification par le fait qu'il faille limiter le
volume du travail déjà très lourd au lieu de le surcharger
avec des codes déductibles à partir des précédents.
Les algorithmes de programmation ne tiendront compte que des arguments
principaux des nombres complexes considérés. Ainsi au lieu
d'avoir une infinité de résultats qui fera que notre programme ne
s'arrête jamais nous n'aurons qu'un seul résultat mais sachant
qu'il y en a plusieurs.
0. 5. Méthodes et techniques utilisées
Comme le souligne Badaga (2003), « les
méthodes et techniques sont des procédés
opératoires rigoureux bien définis, transmissibles, susceptibles
d'être appliqués à nouveau dans les mêmes conditions
et adaptés au genre de problème et des phénomènes
en cause ». (4(*))
Dans notre étude, nous avons opté pour deux
méthodes :
- La méthode normative (dite
aussi descriptive) : Il nous sera donné de décrire
les faits suivant un certain nombre de normes.
- La méthode
déductive : Il nous arrivera quelques fois de tirer
une conclusion particulière à partir d'une situation
générale.
Quant aux techniques, nous nous sommes contenté de la
documentation (technique documentaire) : nous avons tiré certaines
notions et informations dans les bouquins et manuels en notre possession ou
dans des bibliothèques.
0. 6. Subdivision du travail
Les connaissances scientifiques, si véridiques
soient-elles, ne sont que très peu convaincantes si elles sont mal
présentées. Pour éviter de tomber dans ce vice, nous avons
jugé bon de présenter notre travail en trois chapitres qui sont
les suivants :
Le premier chapitre consacré à l'ensemble
C des nombres complexes donne une ébauche de notre
travail. En effet, dans le souci de rendre plus clair et plus
compréhensible le présent travail, nous nous sommes donné
la peine de définir et expliquer certaines notions liées aux
nombres complexes.
le deuxième chapitre quant à lui traite des
fonctions à variables complexes. Ici, nous abordons déjà
le vif du sujet de notre étude. Nous y avons utilisé les
règles usuelles de calcul sur les nombres complexes pour définir
des fonctions, connues à variables réelles, sur des nombres
complexes.
Le troisième chapitre intitulé
« Algorithmes et programmation » est le plus important de
notre travail. Il met en oeuvre les résultats trouvés dans les
chapitres précédents et sera donc la clé de
validité de notre étude. C'est dans ce chapitre que le lecteur
pourra se rendre compte de l'extension des réels aux complexes
après viendra l'automatisation des calculs (programmation).
Chapitre I : Le Corps C des nombres complexes
I. 1. Historique des nombres complexes
I. 1. 1. Formule de Cardan
Au 16ème siècle, des
mathématiciens italiens de la Renaissance travaillèrent sur la
résolution des équations du troisième degré. Afin
de calculer des solutions, réelles pour certaines, ils furent
amenés à introduire des nombres non réels. (5(*))
En 1545, Jérôme Cardan (6(*)) publie l'Ars Magna
dans lequel il fournit des formules de résolution d'une équation
de la forme  avec p et q des entiers strictement positifs. Il
développe et complète des méthodes empruntées
à Nicolo Tartaglia et découvre que :
avec p et q des entiers strictement positifs. Il
développe et complète des méthodes empruntées
à Nicolo Tartaglia et découvre que :
Si  alors le réel positif
alors le réel positif  est solution de l'équation.
est solution de l'équation.
Dans cette formule, le nombre noté  , pour
, pour  dans [0, +8[, est le nombre positif qui, élevé au cube,
donne
dans [0, +8[, est le nombre positif qui, élevé au cube,
donne  . On l'appelle « racine cubique de
. On l'appelle « racine cubique de  »
»
I. 1. 2. L'audace de Bombelli
Imposant à l'équation  de CARDAN les conditions p=15 et q=4, Bombelli montre
que la solution
de CARDAN les conditions p=15 et q=4, Bombelli montre
que la solution  de l'équation
de l'équation  peut s'écrire :
peut s'écrire :
 ,
,
mettant en évidence le fait que des nombres
réels peuvent être désignés par des expressions
« imaginaires ». Prendre la racine carrée
d'un négatif, il fallait oser !
Mais comme cette audace permet d'obtenir des résultats,
les imaginaires sont de plus en plus utilisés avec confiance.
I. 1. 3. Apport des autres mathématiciens
Au milieu du 18ème siècle, Euler
propose de remplacer  par i, donc i2 = -1, et d'Alembert montre
que tous les imaginaires inventés, que GAUSS appellera plus tard
nombres complexes, sont de la forme
par i, donc i2 = -1, et d'Alembert montre
que tous les imaginaires inventés, que GAUSS appellera plus tard
nombres complexes, sont de la forme  avec x et y des réels.
avec x et y des réels.
C'est par l'intermédiaire de ces nombres que
Raphaël Bombelli retrouva une des solutions réelles de
l'équation  . L'introduction du nombre i semble alors justifiée
algébriquement. Conjointement, il énonce les règles de
calcul sur ces nombres. L'apparition au 16ème siècle
de ces nouveaux nombres entraîna de vives polémiques.
. L'introduction du nombre i semble alors justifiée
algébriquement. Conjointement, il énonce les règles de
calcul sur ces nombres. L'apparition au 16ème siècle
de ces nouveaux nombres entraîna de vives polémiques.
En 1637, Descartes leur donna le nom d'imaginaires.
Il fallut attendre deux siècles pour qu'ils obtiennent de la
communauté mathématique un réel statut.
I. 2. Définition de C
I. 2. 1. Définition : On munit l'ensemble IR2
des deux lois suivantes :
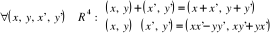
Proposition
Muni de ces deux lois, IR2
possède une structure de Corps. Plus précisément :
Le neutre pour la loi + est 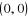
L'opposé de  est
est 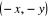
Le neutre pour la loi  (le produit) est
(le produit) est 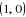
Pour tout  non nul, l'inverse de z est
non nul, l'inverse de z est 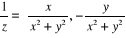
Définition : On note C
l'ensemble IR2 muni des deux lois
précédentes. Ses éléments  sont appelés nombres complexes.
sont appelés nombres complexes.
Proposition :
L'ensemble  est un sous - corps de C. L'application
est un sous - corps de C. L'application  est un isomorphisme de corps IR sur
IK.
est un isomorphisme de corps IR sur
IK.
Conséquence
De cette manière  apparaît comme un sous - corps de
apparaît comme un sous - corps de . Cet isomorphisme permet d'identifier le complexe
. Cet isomorphisme permet d'identifier le complexe  avec le réel
avec le réel .
.
I. 2. 2. Notation cartésienne
Dans le corps , on note i =
, on note i = . Pour tout
. Pour tout  de C, on constate que
de C, on constate que . Avec l'identification de IR avec un Sous - Corps de
C, on peut écrire
. Avec l'identification de IR avec un Sous - Corps de
C, on peut écrire  . On a ainsi obtenu la notation cartésienne (ou
algébrique) des nombres complexes.
. On a ainsi obtenu la notation cartésienne (ou
algébrique) des nombres complexes.
Définitions : Pour tout z de
C, il existe un couple unique  de IR2 tel que
de IR2 tel que . Le réel x est appelé partie réelle de z
et est noté Re(z), le réel y est appelé partie
imaginaire de z et est noté Im(z).
. Le réel x est appelé partie réelle de z
et est noté Re(z), le réel y est appelé partie
imaginaire de z et est noté Im(z).
Un nombre complexe est dit réel si Im(z) = 0,
z est dit imaginaire pur si Re(z) = 0, c'est-à-dire si z = i y,
avec y réel.
Remarques
· Soient  et
et  deux nombres complexes, avec
deux nombres complexes, avec . Les lois de C s'écrivent maintenant :
. Les lois de C s'écrivent maintenant :
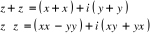
 · (On identifie les parties réelles et les parties
imaginaires)
· (On identifie les parties réelles et les parties
imaginaires)
En particulier :  (attention à vérifier que x et y sont réels)
(attention à vérifier que x et y sont réels)
Puissance du nombre i
On constate que i2= -1. Donc . En fait,
. En fait,  . Plus généralement i3= - i
et i4= 1. Le Sous - Groupe
. Plus généralement i3= - i
et i4= 1. Le Sous - Groupe  engendré par i est cyclique d'ordre 4 :
engendré par i est cyclique d'ordre 4 : 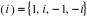
Remarque
Si  est un complexe non réel, alors on peut encore effectuer
l'identification suivante :
est un complexe non réel, alors on peut encore effectuer
l'identification suivante :
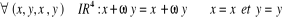
I. 2. 3. Conjugaison
Définition : Soit  (x et y réels) un nombre complexe quelconque. Le nombre complexe
(x et y réels) un nombre complexe quelconque. Le nombre complexe
 est appelé le conjugué de z. On nomme
conjugaison l'application de C dans
C définie par
est appelé le conjugué de z. On nomme
conjugaison l'application de C dans
C définie par .
.
Proposition : La conjugaison est un automorphisme
involutif du corps (C,+,?). Cela signifie que :
· 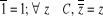
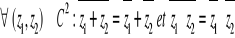
· Propriétés
· Pour tous complexes  ,
,
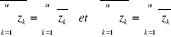
· Pour tout z complexe : 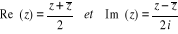
· z est réel 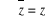
· z est imaginaire pur 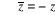
I. 2. 4. Module
Définition : Soit  un nombre complexe quelconque. On appelle module de z
la quantité notée
un nombre complexe quelconque. On appelle module de z
la quantité notée  égale à
égale à  .
.
Remarques :
On constate que  (utile pour se « débarrasser » du module).
(utile pour se « débarrasser » du module).
En particulier, si z est non nul, l'inverse de z est .
.
Si z est réel, le module de z est égal à
sa valeur absolue. Les notations  (valeur absolue ou module) sont donc compatibles.
(valeur absolue ou module) sont donc compatibles.
Propriétés :
L'application « module » vérifie
les propriétés suivantes :
Pour tous  de C2 :
de C2 :
 · . Si z est non nul,
· . Si z est non nul, 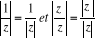
 · . Il y a égalité
· . Il y a égalité 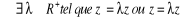
 · . Si
· . Si 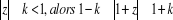
Conséquence : (C, ) est un espace normé.
) est un espace normé.
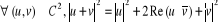
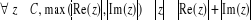
· · Généralisation :
Pour tous complexes 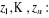
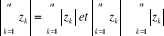
En particulier, 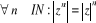
On a  les zk sont produits de l'un d'entre eux par des réels
positifs.
les zk sont produits de l'un d'entre eux par des réels
positifs.
Proposition
L'ensemble U des nombres complexes de module
1 est un sous-groupe de  Pour tout z de U,
Pour tout z de U, 
Proposition (Distance dans C)
Soit d l'application C x C
vers IR, définie par :
 d est une distance sur C, ce qui signifie
qu'elle vérifie les propriétés suivantes :
d est une distance sur C, ce qui signifie
qu'elle vérifie les propriétés suivantes :
Pour tous nombres complexes u, v et w :
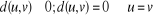
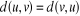
 · · · (Inégalité triangulaire)
· · · (Inégalité triangulaire)
I.2.5. Fonctions à valeurs complexes
Soit X un ensemble quelconque non vide.
F(X, C) désigne
l'ensemble des applications définies sur X et à
valeurs complexes. Le plus souvent X désignera un
intervalle de IR, ou l'ensemble IN (dans ce
cas, on obtient l'ensemble des suites à valeurs complexes)
On sait que F(X,
C) est un anneau commutatif pour les lois déduites de
C, et définies par :
 F(X,C),
F(X,C), 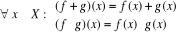
Le neutre de
F(X,C) pour la loi +
(respectivement la loi .) est l'application constante 0 (respectivement 1)
Si f appartient à
F(X, C), on définit
les éléments  de F(X, C) :
de F(X, C) :
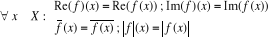
On a pour les opérations « partie
réelle », « partie imaginaire »,
« conjugaison » et « module », des
propriétés dans
F(X,C) analogues
à celles qui ont été rencontrées dans
C.
I.3. Argument, Exponentielle complexe
I.3.1. Notation eiè
Définition :
Une des fonctions principales pour l'analyse des
équations différentielles et pour d'autres idées
mathématiques non citées est l'exponentielle : le familier
ex.
Que vaut cette fonction pour des valeurs complexes en
exposant ?
Pour 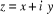
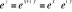
Ceci signifie que tout ce que nous avons à faire est de
rechercher la valeur de l'exponentielle purement imaginaire et le cas
général n'est alors juste qu'un produit.
Il y a plusieurs manières de le calculer telles que
celle que nous proposons ci-dessous :(7(*))
Quelle que soit la valeur de eiy, elle a une partie
réelle et une partie imaginaire.
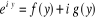
Maintenant en vue de trouver les fonctions  et
et , trouvons une équation différentielle qui les satisfait.
Dérivons cette équation par rapport à y.
, trouvons une équation différentielle qui les satisfait.
Dérivons cette équation par rapport à y.
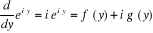
Or  (1)
(1)
D'où 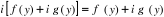
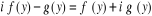
Identifions les parties réelles et imaginaires,
 et
et  (2)
(2)
Nous pouvons résoudre les équations
différentielles simultanées de plusieurs manières, et ici
la manière la plus simple est d'éliminer une des fonctions
inconnues entre elles. Dérivons la première équation et
éliminons .
.
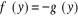
Alors  (3)
(3)
L'équation (3) est l'équation standard
d'oscillateur harmonique. Ainsi, la solution est la combinaison de sinus et
cosinus.
 (4)
(4)
Trouvons les constantes inconnues A et B en utilisant les
conditions initiales sur  et ces valeurs proviennent de la valeur de eiy à
zéro.
et ces valeurs proviennent de la valeur de eiy à
zéro.
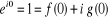
Ainsi, 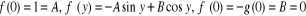
Ceci détermine que et alors l'équation (2) détermine que
et alors l'équation (2) détermine que . Mettons-les ensembles et obtenons la formule d'Euler.
. Mettons-les ensembles et obtenons la formule d'Euler.
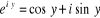
Quelques cas spéciaux donnent :
 et
et 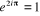
En effet, . Ainsi la fonction exponentielle est une fonction périodique
dans la direction imaginaire.
. Ainsi la fonction exponentielle est une fonction périodique
dans la direction imaginaire.
Calculons . Exprimons
. Exprimons  dans la forme polaire, ou mieux
dans la forme polaire, ou mieux  . Ce qui vaut :
. Ce qui vaut :
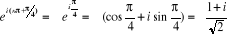
Théorème :
L'application  est un morphisme surjectif du groupe (IR, +) dans le
groupe (U, .) des nombres complexes de module 1, de noyau
est un morphisme surjectif du groupe (IR, +) dans le
groupe (U, .) des nombres complexes de module 1, de noyau
 :
:
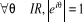
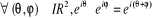
 · · · U (c'est-à-dire
· · · U (c'est-à-dire  ),
), 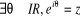
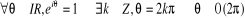
· Propriétés
· L'application  est 2ð-périodique :
est 2ð-périodique :
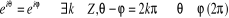
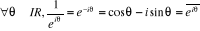
· · Valeurs particulières :
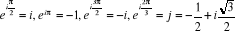
I.3.2. Formules de Moivre et d'Euler
Proposition (Formule de Moivre)
Pour tout réel è, et pour tout entier n
 .
.
Autrement dit : 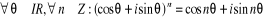
Proposition (Formule d'Euler)
Pour tout réel è :
 (1)
(1)
 (2)
(2)
(1) + (2) :  et
et 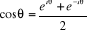
(1) - (2) :  et
et 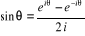
Utilisation
· « Moivre » permet, en
développant  et en identifiant les parties réelles et imaginaires, d'exprimer
et en identifiant les parties réelles et imaginaires, d'exprimer
 et/ou
et/ou 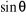
· Les formules d'Euler permettent, par utilisation de la
formule du binôme et regroupement des termes équidistants des
extrémités, de linéariser  et
et , pour
, pour  c'est-à-dire de les exprimer en fonction de quantités du
type
c'est-à-dire de les exprimer en fonction de quantités du
type  et/ou
et/ou .
.
I.3.3. Forme trigonométrique
Définition
Soit  . Il existe une unique classe des réels
. Il existe une unique classe des réels  définies modulo 2ð, telle que
définies modulo 2ð, telle que . Cette classe de réels modulo 2ð est appelée
l'argument de z.
. Cette classe de réels modulo 2ð est appelée
l'argument de z.
Chacun des réels è de cette classe est
appelé une détermination de l'argument de z (ou, par
abus de langage, un argument de z), et on note : arg z =
è (2ð).
Remarque
L'argument d'un nombre complexe non nul z possède une
unique détermination dans tout intervalle , et en particulier dans les intervalles
, et en particulier dans les intervalles  et
et .
.
Proposition
Tout nombre complexe non nul s'écrit de manière
unique , avec
, avec  et
et .
.  est le module de z et è est une
détermination de l'argument de z. On dit que
est le module de z et è est une
détermination de l'argument de z. On dit que  est écrit sous forme trigonométrique.
est écrit sous forme trigonométrique.
Remarques
 · , avec
· , avec  et è réel quelconque. Parler de l'argument
de 0 n'a donc pas aucun sens.
et è réel quelconque. Parler de l'argument
de 0 n'a donc pas aucun sens.
· Soit . Alors :
. Alors :
 et
et 
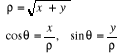
Si  (ce qui détermine è modulo ð)
(ce qui détermine è modulo ð)
Si  (ce qui détermine è modulo 2ð)
(ce qui détermine è modulo 2ð)
· Si  , mais si on n'est pas certain du signe du réel
, mais si on n'est pas certain du signe du réel  :
: 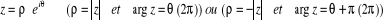
Argument et opérations dans
C
Soient u et v, no nuls :  et
et 
 .
.
 . En particulier :
. En particulier : 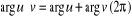
 . En particulier :
. En particulier : 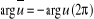
 . En particulier :
. En particulier : 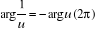
 . En particulier :
. En particulier : 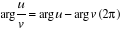
 . En particulier :
. En particulier : 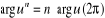
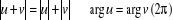
Argument et cas particuliers
Soit  un nombre complexe non nul :
un nombre complexe non nul :
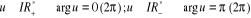
 est réel
est réel 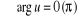
 est imaginaire pur
est imaginaire pur 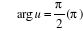
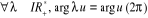
I.3.4. Fonction exponentielle complexe
Définition
Soit  (avec
(avec  IR) un nombre complexe. On pose
IR) un nombre complexe. On pose  , encore noté exp z. On définit ainsi une application de
C dans C, appelée exponentielle
complexe.
, encore noté exp z. On définit ainsi une application de
C dans C, appelée exponentielle
complexe.
Remarques
La restriction à IR de la fonction
 est l'exponentielle réelle déjà connue. Sa
restriction aux imaginaires purs est :
est l'exponentielle réelle déjà connue. Sa
restriction aux imaginaires purs est :  définie précédemment.
définie précédemment.
Pour tout nombre complexe  (avec
(avec  IR) :
IR) :  . Ainsi
. Ainsi 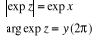
Propriétés
Pour tous nombres complexes z et z' :
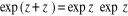
 tel que
tel que  (en particulier exp 0 = 1)
(en particulier exp 0 = 1)
 et
et 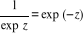
 tel que
tel que 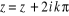
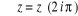
L'application exponentielle est donc périodique de
période  .
.
Résolution de l'équation exp z = a
Soit  un nombre complexe non nul (
un nombre complexe non nul ( est le module de a). Pour tout nombre complexe
est le module de a). Pour tout nombre complexe  (avec
(avec  IR)
IR)
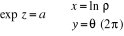
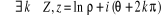
L'équation exp z = a possède donc une
infinité de solutions. Toutes se déduisent de l'une d'entre elles
par ajout d'un multiple entier de  .
.
Remarques
D'après les résultats précédents,
l'application exponentielle est un morphisme surjectif du groupe
(C,+) sur le groupe (C,? ) dont le noyau est
 Z
Z
L'équation exp z = a (a non nul, cherché sous
la forme  ) possède une solution unique si on se limite à
) possède une solution unique si on se limite à  (par exemple
(par exemple  , ou
, ou  ).
).
I.4. Equations polynomiales dans C
I.4.1. Théorème de d'Alembert
Théorème
Tout polynôme non constant (c'est - à - dire de
degré supérieur à 0) à coefficients complexes,
admet au moins une solution dans C.
Conséquence
Tout polynôme P non constant à coefficients dans
C se factorise en un produit de polynôme du
1er degré. Le nombre de racines de P est donc n, chacun
étant compté autant de fois que sa multiplicité.
Racines complexes d'un polynôme à coefficients
réels
Soit P = anxn +
an-1xn-1 + ... + a1x + a0 un
polynôme à coefficients réels. Soit  une racine non réelle de P, avec la multiplicité m. Alors
une racine non réelle de P, avec la multiplicité m. Alors
 est une racine de P avec la même multiplicité.
est une racine de P avec la même multiplicité.
I.4.2. Racines carrées d'un complexe non nul
Proposition
Tout nombre complexe non nul z admet exactement 2 racines
carrées, qui sont opposées. La méthode est la suivante, en
posant  et en cherchant
et en cherchant  sous la forme
sous la forme 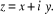
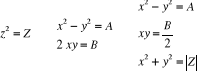
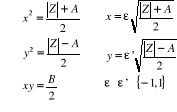
 du signe de
du signe de 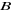
Alors 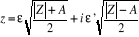
I.4.3. Racines n-ièmes d'un nombre complexe non
nul
Définition
Soit z un nombre complexe non nul, et n un entier naturel non
nul. On appelle racine n-ième de Z tout nombre complexe z tel que
zn=Z.
Proposition
Soit  la forme trigonométrique de
la forme trigonométrique de  (avec
(avec  ),
),  possède exactement n racines n-ièmes données
par :
possède exactement n racines n-ièmes données
par :
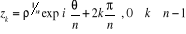
La méthode est la suivante, en cherchant z sous la
forme  .
.
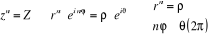
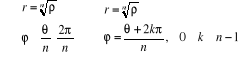
Remarques
Les points images Mk de ces n racines
n-ièmes sont les sommets d'un polygone régulier convexe inscrit
dans le cercle de centre 0 et de rayon 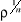
Les n racines n-ièmes  de
de  apparaissent dans la factorisation
apparaissent dans la factorisation 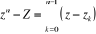
En particulier, par identification des termes de degré
n-1 et des termes constants :
· La somme des n racines n-ièmes  de
de  est nulle (si n >1)
est nulle (si n >1)
· Leur produit vaut 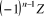
I.4.4. Racines n-ièmes de l'unité
On appelle racines n - ièmes de l'unité les
racines n - ièmes dans C du nombre 1. Elles sont
données par  avec
avec  . Si on note
. Si on note  alors pour tout
alors pour tout  (en particulier
(en particulier  ).
).
Chapitre 2 : Fonctions à variables
complexes
Nous traiterons dans ce chapitre des fonctions que nous
connaissons déjà, définies sur des variables
réelles. Dans notre nouvelle démarche, nous recherchons des
algorithmes pour définir lesdites fonctions sur des nombres complexes.
Notons que les algorithmes que nous proposerons doivent produire des
résultats aussi vrais pour des complexes en général que
pour des réels (qui sont des cas particuliers des nombres complexes).
Les fonctions que nous traiterons sont les suivantes :
1. Fonctions exponentielles
2. Fonctions logarithmiques
3. Fonctions trigonométriques
4. Fonctions trigonométriques réciproques
5. Fonctions hyperboliques
6. Fonctions hyperboliques réciproques
2.1. Fonctions exponentielles
On appelle fonction exponentielle de base a la fonction y
= ax où a est un nombre positif différent de 1 et x la
variable indépendante.
André Antibi et Raymond Barra définissent la
fonction exponentielle comme « La fonction définie sur
IR qui à chaque réel x associe le nombre
ex, dont le logarithme népérien est
x »(8(*))
Il est clair que Antibi et Barra appellent
« fonction exponentielle » seule la fonction y = ax
où a = e avec
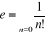
Plusieurs autres auteurs des livres surtout utilisés au
cycle secondaire ont épousé cette définition à
l'instar de Jean - Paul Beltramone(9(*)), Joël Malaval, Denise Courbon. (10(*))
D'autres auteurs par contre préfèrent
l'expression « fonction exponentielle de base a » pour
éviter toute confusion. C'est le cas de Lucien Chambadal (1968) et
Nicolas Schons.
Pour la simple raison que l'expression « fonction
exponentielle de base a » englobe l'autre expression qui sous-entend
la base e, nous adopterons l'expression « fonction
exponentielle » pour exprimer les fonctions :
f
{
} avec a > 0
1
:
+
-
IR
a
avec
a
x
IR
IR
x
a

Pour étendre cette notion aux nombre complexes, on
s'appuiera sur l'égalité adoptée plus haut dans les pages
précédentes  (2.1) où
(2.1) où  est donné en radian. L'équation (2.1) est la forme
exponentielle du nombre complexe
est donné en radian. L'équation (2.1) est la forme
exponentielle du nombre complexe  où
où
Ainsi, pour définir
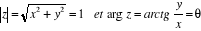
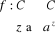
avec  , On fera des transformations suivantes :
, On fera des transformations suivantes :
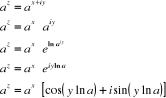
Exemples :
1. 23+i = 23 . [cos(ln 2) + i sin(ln
2)]
2. 45+0i = 45 = 45 . [cos(0
ln 4) + I sin(0 ln 4)] = 45 [cos 0 + I sin 0] = 45 =
1024
2.2. Fonctions Logarithmiques
Ici, nous ne nous limiterons qu'à l'étude des
logarithmes népériens (naturels). L'expression d'autres
logarithmes se fera facilement en appliquant la formule de changement de
base :
En effet,  avec a > 1, b > 1
avec a > 1, b > 1
2.2.1. Définition de la fonction logarithmique
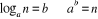
Soit a > 1 et n  IR_*. On appelle logarithme à base a du
réel n le nombre réel b tel que ab = n.
IR_*. On appelle logarithme à base a du
réel n le nombre réel b tel que ab = n.
Lorsque la base a = 10, on dit qu'il s'agit du logarithme
décimal ou logarithme vulgaire ou encore logarithme briggsien que l'on
note simplement log n.
Lorsque la base a = e, on dit qu'il s'agit du logarithme
népérien que l'on note ln n au lieu de loge n.
e est le nombre de Néper (11(*)) obtenu comme somme de la
série 
2.2.2. La fonction logarithme népérien
La fonction logarithme (ici à base e) n'est
définie que pour des réels strictement positifs. Essayons d'abord
de l'évaluer pour des réels strictement négatifs.
a. Logarithmes des nombres négatifs
Soit a > 0, calculons ln (-a).
En effet, ln (-a) = ln (-1. a) = ln (-1) + ln a = ln
eip + ln a = ip + ln a
Exemple : ln (-2) = ln 2 + ip
b. Logarithmes des nombres complexes
Soit  un nombre complexe. Déterminons son logarithme naturel.
un nombre complexe. Déterminons son logarithme naturel.
 où
où  et
et 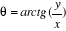
Ainsi
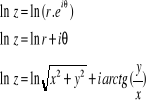
Exemple : 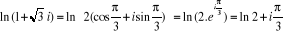
2.3. Fonctions trigonométriques
Parmi les fonctions trigonométriques, nous
n'étudierons que les fonctions sinus et cosinus, les autres étant
facilement déductibles à partir des deux premières.
2.3.1. Fonction sinus
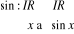
Le domaine de valeurs de la fonction sinus est [-1, 1] et son
domaine de définition est IR.
Pour étendre cette notion et exprimer les sinus des
nombres complexes on se servira de la formule :
 et
et 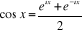
Nous voulons donc avoir les fonctions de la forme
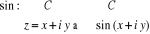
En effet,
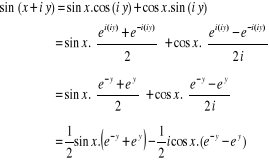
2.3.2. Fonction cosinus
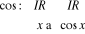
Comme la fonction sinus, la fonction cosinus est
définie pour tout réel et son domaine de valeurs est [-1, 1].
Pour la définir sur des complexes, on procède
comme suit :
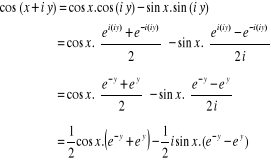
2.4. Fonctions trigonométriques
réciproques
Vu que nous n'avons étudié que deux fonctions
trigonométriques dans le paragraphe précédent, nous ne
nous limiterons ici qu'aux seules fonctions réciproques de sinus et
cosinus, c'est-à-dire les fonctions arcsin et arccos.
2.4.1. Fonction arc sinus
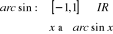
Son domaine de définition est [-1, 1]. Essayons
d'évaluer cette fonction pour n'importe quelle valeur réelle. On
obtiendrait une fonction de la forme :
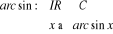
Voici comment nous pourrons procéder :
0
2
1
2
2
sin
sin
=
-
-
=
-
=
-
=
=
-
-
x
i
e
e
x
i
e
e
x
i
e
e
x
y
y
x
arc
iy
iy
iy
iy
iy
iy
Multiplions les deux membres par eiy. On a
donc :
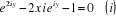
Posons eiy = z, l'équation  devient :
devient :
 qui est une équation du second degré à constantes
complexes.
qui est une équation du second degré à constantes
complexes.
Exemple : Calculer arc sin 2
Soit
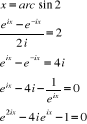
Posons eix = z
z2 - 4z - 1 = 0
3
2
12
)
1
(
)
1
(
4
)
4
(
2
i
i
=
-
=
-
-
-
=

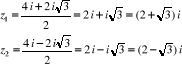
Pour  , on a :
, on a :
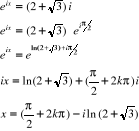
Avec 
Pour  , on a :
, on a :
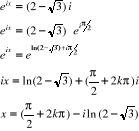
Avec 
Ainsi,
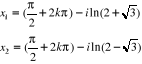
Prolongement de la fonction arc sin aux nombres
complexes
Nous voulons avoir une fonction de la forme :
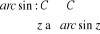
avec 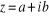
Soit  un nombre complexe,
un nombre complexe,
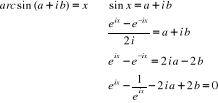
Multiplions les deux membres par 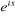
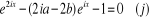
Posons  , l'équation
, l'équation  devient :
devient :
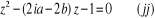
L'équation  ci - dessus est une équation du second degré à
coefficients complexes.
ci - dessus est une équation du second degré à
coefficients complexes.
2.4.2. Fonction arc cos
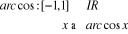
Le domaine de définition de cette fonction est [-1,
1]
Evaluation de la fonction arc cos sur toute valeur
réelle
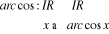
Soit  , déterminons
, déterminons 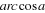
Posons  , on a
, on a 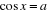
Ainsi,
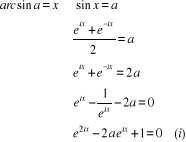
Pour  , l'équation
, l'équation  devient :
devient :
 qui est une équation du second degré à coefficients
réels.
qui est une équation du second degré à coefficients
réels.
Exemple : Calculons arc cos 2
L'équation résolvante est 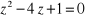
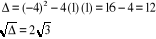
 et
et 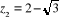
Pour  on a :
on a :
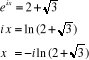
Pour  on a :
on a :
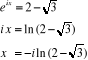
Prolongement de la fonction arc cos aux nombres
complexes
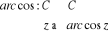
Soit  un nombre complexe,
un nombre complexe,
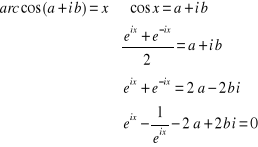
Multiplions les deux membres par 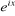
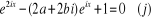
Posons  , l'équation
, l'équation  devient :
devient :
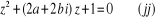
L'équation  ci - dessus est une équation du second degré à
coefficients complexes.
ci - dessus est une équation du second degré à
coefficients complexes.
2.5. Fonctions hyperboliques
Comme pour des fonctions trigonométriques et
trigonométriques réciproques, ici aussi nous n'étudierons
que les fonctions sh et cosh (sinus hyperbolique et cosinus
hyperbolique)
2.5.1. Fonction sh
Nous voulons avoir une fonction de la forme :
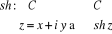
Par définition, 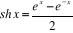
Par extension aux nombres complexes, on a :
)
1
(
sin
2
iz
i
e
e
z
sh
z
z
-
=
-
=
-

Posons 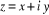
 devient
devient
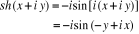
Appliquons la formule de sinus :
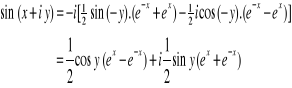
2.5.2. Fonction ch
Procédons de la même manière pour avoir
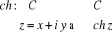
Par définition, 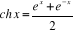
Par extension aux nombres complexes, on a :
iz
e
e
z
ch
z
z
cos
2
=
+
=
-

Posons  . On obtient
. On obtient
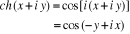
Appliquons la formule de cosinus.
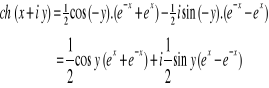
2.6. Fonctions hyperboliques réciproques
Les lignes qui suivent présentent une étude des
fonctions arch (arc cosinus hyperbolique) et arsh (arc sinus hyperbolique).
2.6.1. Fonction arsh
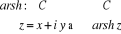
Voici comment nous pourrons procéder pour calculer
arsh(a+ bi) :
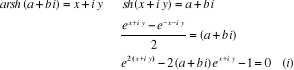
Il suffit de poser  .
.
L'équation  devient
devient  .
.
2.6.2. Fonction arch
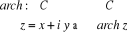
Calculons arch (a+b i):
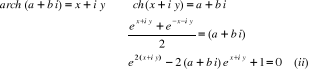
Posons 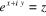
L'équation devient
devient  .
.
Chapitre 3 : Algorithmes et programmation
3.1. Algorithme
Les mathématiciens définissent un algorithme
comme une méthode de résolution d'un problème suivant un
enchaînement déterminé de règles opératoires
(12(*))
En informatique, nous le définissons comme un
procédé mis en oeuvre sur un ordinateur, et qui,
répété autant de fois qu'il est nécessaire, permet
d'obtenir le résultat cherché.
Le mot algorithme n'est pas dérivé d'un mot
latin ou grec, mais d'une contraction et d'une dérivation du nom du
mathématicien arabe Al - Khwarizmi qui publia deux livres
importants : l'un sur l'arithmétique et l'autre sur
« l'action de faire passer et d'agencer les parties d'un
tout » (13(*))
Trois siècles plus tard, le livre, traduit en latin,
porta le nom « Algorismus ».
La première définition du mot algorithme dans
son sens actuel a été donnée par le mathématicien
russe Markov : « Tout ensemble de règles
précises destiné à obtenir un résultat
déterminé à partir de certaines données
initiales »
Les algorithmes sont constitués d'un ensemble de
règles précises et compréhensibles par tous. Ils
s'appliquent à des données qui peuvent changer, élaborent
des résultats en fonction des données initiales.
La réalisation d'un algorithme est un acte
créatif : Il n'existe pas de méthode pour découvrir
un algorithme.
Dans ce travail, nous présenterons un nombre
d'algorithmes en langage humain permettant d'évaluer quelques fonctions
usuelles sur des valeurs complexes puis nous allons plus tard traduire ces
algorithmes en langage de programmation Visual BASIC.
3.1.1. Calcul de l'exponentielle d'un nombre complexe
Soit à calculer 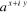
0. Début
1. Initialisation
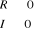
2. Lire a, x, y
3. Calculer
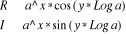
4. Ecrire R, `+ `, I, ` i `
5. Fin
3.1.2. Calcul de logarithmes des nombres complexes
Soit à calculer Log (a + b i)
0. Début
1. Initialisation

2. Lire a, b
3. Calculer
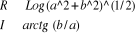
4. Ecrire R, `+ `, I, ` i `
5. Fin
3.1.3. Calcul de Sinus de nombres complexes
Soit à calculer Sin (a + b i)
0. Début
1. Initialisation
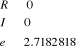
2. Lire a, b
3. Calculer
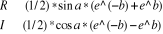
4. Ecrire R, `+ `, I, ` i `
5. Fin
3.1.4. Calcul de Cosinus de nombres complexes
Soit à calculer Cos (a + b i)
0. Début
1. Initialisation
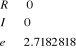
2. Lire a, b
3. Calculer
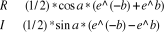
4. Ecrire R, `+ `, I, ` i `
5. Fin
3.1.5. Calcul de l'Arc sinus de nombres complexes
Soit à calculer Arcsin (a + b i)
0. Début
1. Lire a, b
2. Poser 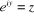
3. Résoudre l'équation 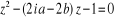
4. Résoudre les équations
x
i
e
z
=

5. Fin
3.1.6. Calcul de l'Arc cosinus de nombres complexes
Soit à calculer Arcos (a + b i)
0. Début
1. Lire a, b
2. Poser 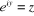
3. Résoudre l'équation 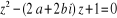
4. Résoudre les équations
x
i
e
z
=
5. Fin
3.1.7. Calcul de Sinus hyperbolique de nombres
complexes
Soit à calculer Sh(a + b i)
0. Début
1. Initialisation
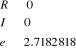
2. Lire a, b
3. Calculer
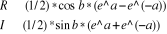
4. Ecrire R, `+ `, I, ` i `
5. Fin
3.1.8. Calcul de Cosinus hyperbolique de nombres
complexes
Soit à calculer Cosh(a + b i)
0. Début
1. Initialisation
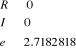
2. Lire a, b
3. Calculer
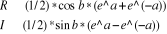
4. Ecrire R, `+ `, I, ` i `
5. Fin
3.1.9. Calcul de l'Arc sinus hyperbolique de nombres
complexes
Soit à calculer Arsh (a + b i)
0. Début
1. Lire a, b
2. Poser 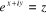
3. Résoudre l'équation 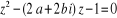
4. Résoudre l'équation 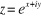
5. Fin
3.1.10. Calcul de l'Arc cosinus hyperbolique de nombres
complexes
Soit à calculer Arch (a + b i)
0. Début
1. Lire a, b
2. Poser 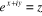
3. Résoudre l'équation 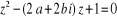
4. Résoudre l'équation 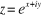
5. Fin
3.2. Les principaux concepts de Visual Basic
3.2.1. Présentation générale
Visual Basic est un langage de programmation «
orienté objet » de Microsoft qui permet de
programmer des applications indépendantes sous l'environnement
Windows.
Il est intégré dans tous les logiciels de
Bureautique de MicroSoft (Word, Excel, Access) sous le nom de :
VBA (Visual Basic Application). Visual Basic est un
langage interprété.
Pour comprendre le processus de développement d'une
application, il est utile d'assimiler certains concepts sur lesquels est
fondé Visual Basic. Comme il s'agit d'un langage de développement
Windows, il convient également de s'être familiarisé avec
l'environnement Windows. Le fonctionnement de Windows s'articule autour de
trois concepts essentiels. A savoir :
· les fenêtres ;
· les événements ;
· les messages.
Considérons qu'une fenêtre est une zone
rectangulaire dotée de ses propres limites. Nous connaissons tous une
fenêtre de document dans un programme de traitement de texte ou une
fenêtre de boite de dialogue quelconque. S'il s'agit là des
exemples les plus courants, il existe bien d'autres types de fenêtres. Un
bouton de commande, les icônes, les zones de texte, les boutons
d'options, les barres de menus constituent tous des fenêtres.
Windows gèrent ces nombreuses fenêtres en
affectant à chacune d'elles un numéro d'identification unique
(« hWnd »). Le système surveille en
permanence chacune de ces fenêtres de façon à
déceler le moindre événement. Les événements
peuvent être engendrés par des actions de l'utilisateur, par un
contrôle programmé, voire par des actions d'une autre
fenêtre.
Chaque fois qu'un événement survient, un message
est envoyé au système d'exploitation, qui traite le message et le
diffuse aux fenêtres concernées.
La plupart de ces messages de bas niveau sont
gérés par Visual Basic tandis que d'autres sont mis à
votre disposition sous forme de procédures
événementiels.
Dans une application « événementielle
», le code ne suit pas un chemin prédéterminé.
Différentes sections du code sont exécutées en fonction
des événements qui se produisent. Nous ne pouvons donc pas
prévoir l'ordre des événements, en revanche nous devons
prévoir les événements qui peuvent se produire et votre
code doit être en mesure de les traiter.
3.2.3. La notion d'objet
Un objet
représente un élément d'une application. Une
feuille de calcul, une cellule, un graphique pour Excel, un formulaire, une
table ou un état pour Access sont des objets. Dans un code Visual Basic,
nous devons identifier un objet avant de pouvoir appliquer l'une des
méthodes de l'objet ou modifier la valeur de
l'une de ses propriétés.
Une collection est
un objet contenant plusieurs autres objets, généralement, mais
pas toujours, du même type. Dans Microsoft Excel, par exemple, l'objet
Workbooks contient tous les objets Workbook.
Dans Visual Basic, la collection Forms contient tous
les objets Form d'une application. Les
éléments d'une collection peuvent être identifiés
par numéro ou par nom. Nous pouvons également manipuler toute une
collection d'objets si les objets partagent des méthodes communes.
3.2.4. Les notions de méthode et de
propriété
Une méthode est une action
qu'un objet peut exécuter. Par exemple, Add est une méthode de
l'objet ComboBox qui ajoute une nouvelle entrée à une liste
modifiable.
Une propriété est un
attribut d'un objet définissant l'une des
caractéristiques de l'objet telle que la
taille, la couleur ou la position à l'écran, ou un aspect de son
comportement, par exemple s'il est activé ou visible. Pour changer les
caractéristiques d'un objet il faut changer les valeurs de ses
propriétés.
Pour définir la valeur d'une propriété,
nous faisons suivre la référence d'un objet d'un point, du nom de
la propriété, d'un signe égal (=) et de la nouvelle valeur
de propriété.
Certaines propriétés ne peuvent pas être
définies. La rubrique d'aide de chaque propriété indique
si vous pouvez la définir (lecture - écriture), seulement la lire
(lecture seule) ou seulement y écrire (écriture seule). Nous
pouvons extraire des informations sur un objet en renvoyant la valeur de l'une
de ses propriétés.
3.2.5. La syntaxe de Visual Basic
Un programme écrit en Visual Basic est un ensemble de
fichiers textes documentés (appelés sources) respectant
une syntaxe précise.
Les commentaires
sont des caractères, de préférence non
accentués, ignorés par l'interpréteur et ne servant
qu'à documenter le programme. Les lignes de commentaires débutent
par une apostrophe (') ou par le mot Rem suivi d'un
espace et peuvent être insérées n'importe où dans
une procédure. Les commentaires peuvent expliquer une procédure
ou une instruction particulière au lecteur du code. Par défaut,
les commentaires s'affichent en vert.
Règles d'affectation des noms
Nous utilisons les règles suivantes pour nommer des
procédures, des constantes, des variables et des arguments dans un
module Visual Basic :
· Utiliser une lettre comme premier caractère ;
· Ne pas utiliser d'espace, de point (.), de point
d'exclamation (!) ou les caractères @, &, $, # dans le nom ;
· Un nom ne peut compter plus de 255 caractères
;
· Généralement, on ne devrait pas utiliser
des noms identiques aux noms de fonction, d'instruction et de méthode de
Visual Basic. Nous ferions,dans ce cas, double emploi des mots clés du
langage. Pour utiliser une fonction, une instruction ou une méthode du
langage intrinsèque en conflit avec un nom attribué, nous devons
l'identifier explicitement. Faire précéder la fonction,
l'instruction ou la méthode intrinsèque du nom de la
bibliothèque de types associée.
Par exemple, si nous avons une variable nommée
Left, pour invoquer la fonction Left, nous devons employer
VBA.Left ;
Nous ne pouvons pas employer deux fois le même nom au
même niveau de portée. Par exemple, nous ne pouvons pas
déclarer deux variables nommées age
dans la même procédure.
Cependant, nous pouvons déclarer une variable
privée nommée age et une variable de
niveau procédure nommée age dans le
même module.
Note : Visual Basic ne différencie pas
les majuscules des minuscules, mais conserve la casse dans l'instruction de
déclaration du nom.
3.2.6. Les types de données
Les types
prédéfinis
Boolean
Les variables de type « Boolean » sont
stockées sous la forme de nombres de 16 bits (2 octets), mais elles ne
peuvent avoir pour valeur que True ou False.
Elles s'affichent sous la forme True et False (avec l'instruction
Print) ou #TRUE# et #FALSE# (avec l'instruction Write #). On utilise
les mots clés True et False pour faire passer d'un
état à l'autre des variables de type « Boolean
».
Lorsque d'autres types de données numériques
sont convertis en valeurs de type Boolean, 0 devient False et
toutes les autres valeurs deviennent True. Lorsque des valeurs de type
Boolean sont converties en d'autres types de données,
False devient 0 et True devient -1.
Byte
Les variables de type « Byte » sont
stockées sous la forme d'un nombre de 8 bits (1 octet unique), non
signé, compris entre 0 et 255. Le type de données « Byte
» est utile pour le stockage d' entiers de petite taille.
Currency
Les variables de type « Currency » sont
stockées sous la forme de nombres de 64 bits (8 octets) au format
entier, avec un décalage de 10 000 afin d'obtenir un nombre à
virgule fixe comprenant 15 chiffres à gauche du séparateur
décimal et 4 chiffres à droite.
Cette représentation offre une plage comprise entre
-922 337 203 685 477,5808 et 922 337 203 685 477,5807. Le caractère de
déclaration de type pour les variables de type « Currency
» est le signe @. Le type de données « Currency
» est utile pour les calculs monétaires et pour les calculs
à virgule fixe dans lesquels la précision revêt une
importance particulière.
Date
Les variables de type « Date » sont
stockées sous la forme de nombres à virgule flottante de 64 bits
(8 octets) IEEE représentant des dates comprises entre le 1er janvier
100 et le 31 décembre 9999, et des heures allant de 0:00:00 à
23:59:59. Toute valeur de littéral de date peut être
attribuée à une variable de type « Date ». Les
littéraux date doivent être délimités par le signe
#, par exemple #January 1, 1993# ou #1 Jan 93#.
Les variables de type « Date » affichent
les dates au format de date abrégé reconnu par un ordinateur. Les
heures s'affichent au format horaire (plage de 12 ou 24 heures) défini
dans un ordinateur.
Lorsque d'autres types de données numériques
sont convertis en données de type « Date », les valeurs
situées à gauche du séparateur décimal
représentent la date, tandis que celles situées à droite
correspondent à l'heure. Minuit est représenté par 0 et
midi par 0,5. Les nombres entiers négatifs représentent des dates
antérieures au 30 décembre 1899.
Decimal
Les variables de type « Decimal » sont
stockées sous la forme d'entiers de 96 bits (12 octets), non
signés, décalés d'une puissance de 10 variable. Le facteur
de décalage (puissance de 10), qui définit le nombre de chiffres
situés à droite du séparateur décimal, est compris
entre 0 et 28. Avec un décalage de 0 (pas de décimales), la
valeur maximale est +/- 79 228 162 514 264 337 593 543 950 335. Avec 28
décimales, la valeur maximale est +/- 7,9228162514264337593543950335 et
la valeur minimale différente de zéro est +/-
0,0000000000000000000000000001.
Pour le moment, le type de données «
Decimal » ne peut être utilisé qu'avec une
donnée de type « Variant ». En d'autres termes, il est
impossible d'attribuer à une variable le type « Decimal
». Nous pouvons en revanche créer une variable de type «
Variant » dont le sous-type est « Decimal » à
l'aide de la fonction CDec.
Double
Les variables de type « Double » (à
virgule flottante en double précision) sont stockées sous la
forme de nombres à virgule flottante de 64 bits (8 octets) IEEE dont la
valeur est comprise entre -1,79769313486232E308 et -4,94065645841247E-324 pour
les nombres négatifs et entre 4,94065645841247E-324 et
1,79769313486232E308 pour les positifs. Le caractère de
déclaration de type pour une variable de type « Double
» est le signe #.
Integer
Les variables de type « Integer » sont
stockées sous la forme de nombres de 16 bits (2 octets) dont la valeur
est comprise entre -32 768 et 32 767. Le caractère de déclaration
de type pour les variables de type « Integer » est le signe
%.
Les variables de type « Integer »
permettent également de représenter des valeurs
énumérées. Celles-ci peuvent contenir un ensemble fini
d'entiers uniques possédant tous une signification particulière
dans le contexte où ils sont utilisés. Elles permettent
d'opérer facilement une sélection parmi un nombre connu de choix,
du type noir = 0, blanc = 1, etc. Il est conseillé de définir des
constantes pour chaque valeur énumérée via l'instruction
Const.
Long
Les variables de type « Long » (entier
long) sont stockées sous la forme de nombres signés de 32 bits (4
octets) dont la valeur est comprise entre -2 147 483 648 et 2 147 483 647. Le
caractère de déclaration de type pour les variables de type
« Long » est le signe &.
Object
Les variables de type « Object » sont
stockées sous la forme d'adresses 32 bits (4 octets) qui font
référence à des objets. L'instruction Set
permet d'affecter une référence d'objet à une
variable déclarée comme « Object ».
Une variable déclarée comme «
Object » est suffisamment flexible pour contenir une
référence à n'importe quel type d'objet, mais la liaison
à l'objet désigné par la variable est effectuée au
moment de l'exécution. Pour obtenir une liaison au moment de la
compilation, on attribue la référence d'objet à une
variable déclarée avec un nom de classe spécifique.
Single
Les variables de type « Single » (à
virgule flottante en simple précision) sont stockées sous la
forme de nombres à virgule flottante de 32 bits (4 octets) IEEE dont la
valeur est comprise entre -3,402823E38 et -1,401298E-45 pour les nombres
négatifs et entre 1,401298E-45 et 3,402823E38 pour les positifs. Le
caractère de déclaration de type pour les variables de type
« Single » est le point d'exclamation
(!).
String
Il existe deux types de chaînes : les chaînes de
longueur variable et les chaînes de longueur fixe. Les chaînes de
longueur variable peuvent contenir environ 2 milliards (2^31) de
caractères.
Les chaînes de longueur fixe peuvent contenir de 1
à environ 64 Ko (2^16) de caractères.
Une chaîne de longueur fixe déclarée comme
Public ne peut être utilisée dans les
modules de classe. Les codes de caractères de type « String »
sont compris entre 0 et 255. Les 128 premiers caractères (0 à
127) du jeu de caractères correspondent aux lettres et symboles d'un
clavier américain standard. Ces 128 caractères sont identiques
à ceux du jeu de caractères ASCII.
Les 128 caractères suivants (128 à 255)
représentent des caractères spéciaux, comme les lettres de
certains alphabets, les accents, les symboles monétaires et les
fractions. Le caractère de déclaration de type pour les variables
de type String est le signe $.
Variant
« Variant » est le type de données
attribué à toutes les variables qui ne sont pas explicitement
déclarées comme étant d'un autre type (à l'aide
d'instructions telles que Dim, Private,
Public ou Static). Le type de données
« Variant » ne possède aucun caractère de
déclaration de type.
Variant est un type de données spécial
pouvant contenir des données de toutes sortes, à l'exception des
données de type « String » de longueur fixe et de
types définis par l'utilisateur. Une variable de type «
Variant » peut également contenir les valeurs
Empty, Error, Nothing et
Null. Nous pouvons déterminer la procédure de traitement
d'une donnée de type « Variant » à l'aide des
fonctions VarType et TypeName.
Les données numériques correspondent à
n'importe quel nombre entier ou réel dont la valeur est comprise entre
-1,797693134862315E308 et -4,94066E-324 pour les négatifs et entre
4,94066E- 324 et 1,797693134862315E308 pour les positifs. En
général, les données numériques de type «
Variant » conservent leur type de données original au sein de la
valeur de type « Variant ».
Par exemple, si nous attribuons une valeur de type «
Integer » à une donnée de type « Variant
», cette dernière sera ultérieurement traitée comme
une valeur de type « Integer ».
Cependant, si une opération arithmétique est
exécutée sur une donnée de type « Variant »
contenant une valeur de type « Byte », « Integer
», « Long » ou « Single » et si le résultat
excède la plage de valeurs du type de données, le résultat
se voit automatiquement affecté le type de données « Variant
» immédiatement supérieur. Une donnée de type «
Byte » est transformée en « Integer », une
donnée de type « Integer » est transformée en
« Long » et une donnée de type « Long » ou «
Single » en « Double ».
Une erreur se produit lorsque des variables de type «
Variant » contenant des données de type « Currency
», « Decimal » ou « Double » dépassent
leur plage de valeurs respective.
Le type de données « Variant » peut
remplacer un autre type de données lorsque vous recherchez plus de
souplesse dans le traitement de celles-ci. Si une variable de type «
Variant » contient des chiffres, il peut s'agir, selon le
contexte, de leur valeur réelle ou de leur représentation sous
forme de chaîne.
Exemple :
Dim MyVar As Variant
MyVar = 98052
Dans l'exemple précédent, MyVar
contient une représentation numérique,
c'est-à-dire la valeur réelle 98052.
Les opérateurs arithmétiques peuvent être
utilisés avec des variables de type « Variant » contenant des
valeurs numériques ou des chaînes de caractères pouvant
être interprétées comme des nombres. Si nous utilisons
l'opérateur + pour ajouter MyVar
à une autre donnée de type « Variant »
contenant un nombre ou à une variable de type numérique, nous
obtiendrons comme résultat une somme arithmétique.
La valeur Empty désigne une
variable de type « Variant » qui n'a pas été
initialisée. Une variable de type « Variant »
contenant la valeur Empty équivaut à
0 si elle est utilisée dans un contexte
numérique et à une chaîne de longueur nulle ("") dans un
contexte de chaînes.
Ne pas confondre Empty et
Null. La valeur Null indique que la variable
de type « Variant » ne contient intentionnellement aucune
donnée valide.
Dans une donnée de type « Variant », la
valeur Error permet d'indiquer qu'une condition
d'erreur s'est produite dans une procédure. Cependant, aucune gestion
d'erreur normale de niveau application n'a lieu dans ce cas. Le programmeur ou
l'application peuvent donc appliquer un certain traitement en fonction de la
valeur d'erreur. Les valeurs de type Error sont
créées par conversion de nombres réels à l'aide de
la fonction CVErr.
Les types définis par le
programmeur
Ces types de données sont définis à
l'aide de l'instruction Type. Les types de données
définis par l'utilisateur peuvent contenir un ou plusieurs
éléments d'un type de données, un tableau ou un type de
données précédemment défini par l'utilisateur.
Exemple :
Type MyType
MyName As String ' La variable de type
String contient un nom
MyBirthDate As Date ' La variable de
type Date contient une date
de
naissance
MySex As Integer ' La variable de type
Integer contient le sexe (0 féminin, 1 masculin)
End Type
3.2.7. Les instructions
Les instructions Visual Basic sont complètes. Elles
contiennent des mots clés, des opérateurs, des variables, des
constantes et des expressions. Chaque instruction appartient à l'une des
trois catégories suivantes : déclaration,
affectation, exécution.
La déclaration
Les instructions de déclaration nomment une variable,
une constante ou une procédure et peuvent également
spécifier un type de données (Const, Dim, Private, Public, New,
Static).
Private myVar As String
Ici on déclare une variable « privée »
de type « String » et de nom « myVar ».
L'affectation
Les instructions d'affectation attribuent une valeur ou une
expression à une variable ou à une constante (=, Let).
Title = "Zone d'accueil"
Les instructions exécutables
Ces instructions exécutent des lignes de codes
(structures alternatives, structures répétitives,
débranchements, appels de modules, ...).
Les structures alternatives
Comme dans la plupart des langages, les mots clés
correspondant à ces structures sont If, Then, Else, End
If.
Private answer As String
If answer = Empty
Then
MsgBox "Vous n'avez pas entré de nom"
Else
MsgBox "Votre nom est " & answer
End If
Les « If multilignes »
On utilise les mots clés « Else If
» autant de fois que nécessaire.
If answer = Empty
Then
MsgBox "Vous n'avez pas entré de nom"
Else If answer = "Toto"
MsgBox "Votre nom est Toto"
Else
MsgBox "Votre nom est Toto" & answer
End If
Le « case »
Select Case answer
Case "Toto"
Nom = "Toto"
Case "Titi"
Nom = "Titi"
Case Else
MsgBox "Nom incohérent"
End Select
Les structures répétitives
Visual Basic utilise les mots clés For, To
et Next pour les boucles « Pour »,
Do While et Loop pour la boucle « Tant
que » (il existe également While et
Wend), Do et Loop Until pour
la boucle « Jusqu'à ce que ». Quelques exemple d'utilisation
de ces boucles.
Private T(10) As
Integer
Private I As
Integer
For I=0 To 9
T[I] = I
Next
I = 0
Do While I < 10
T[I] = I
I = I + 1
Loop
I = 0
Do
T[I] = I
I = I + 1
Loop Until I = 10
Déclaration de l'indice de boucle I et
d'un tableau de 10 entiers T Il est impératif
d'initialiser I
Vérification des erreurs de syntaxe
Si une ligne s'affiche en rouge (avec un éventuel
message d'erreur) après sa saisie et la frappe de la touche
ENTRÉE, l'instruction correspondante comporte une erreur. Il convient de
l'identifier et la corriger.
Attention : Par défaut Visual
basic ne nous oblige pas à déclarer les variables, ce qui est une
source d'erreur importante. Afin de remédier à cet
inconvénient, il est fortement conseillé d'utiliser au
début de chaque module l'instruction « Option
Explicit » de façon à obliger VBA
à détecter les variables non déclarées.
Les instructions sur plusieurs lignes
Une instruction tient généralement sur une
ligne, mais il est possible de la continuer sur la ligne suivante à
l'aide du caractère de continuité de ligne « _ » (blanc
+ blanc souligné).
Dim myVar As String
myVar = "John"
MsgBox Prompt:="Bonjour" & myVar, _
Title:="Zone d'accueil", _
Buttons:=vbExclamation
3.2.8. Les modules
Ecriture d'une procédure
Une procédure est une série d'instructions
délimitée par les instructions Sub et
End Sub exécutant des actions mais ne renvoyant pas de
valeurs. Une procédure prend des arguments tels que des constantes, des
variables ou des expressions passées par un module appelant. Si une
procédure n'a pas d'argument, l'instruction Sub doit
comporter des parenthèses vides.
Sub GetInfo()
Dim answer As String
answer = InputBox("Quel est votre nom?")
If answer = Empty
Then
MsgBox "Vous n'avez pas entré de
nom."
Else
MsgBox "Votre nom est " &
answer
End If
End Sub
Ecriture d'une fonction
Une fonction est une série d'instructions
délimitée par les instructions Function
et End Function. Une fonction est
similaire à une procédure mais peut également renvoyer une
valeur. Une fonction peut prendre des arguments, tels que les constantes, les
variables ou les expressions qui lui sont passées par un module
appelant. Si une fonction n'a aucun argument, son instruction
Function doit comporter des parenthèses vides.
Une fonction renvoie une valeur en affectant une valeur à son nom dans
une ou plusieurs instructions de la procédure. Dans l'exemple suivant,
la fonction Celsius convertit des degrés Fahrenheit en degrés
Celsius.
Lorsque la fonction est appelée depuis la
procédure Main, une variable contenant la valeur de l'argument est
passée à la fonction. Le résultat du calcul est
renvoyé à la procédure appelante et affiché dans un
message.
Function Celsius(fDegrees As
Integer) As Decimal
Celsius = (fDegrees - 32) * 5 / 9
End Function
Sub Main()
temp = InputBox("Veuillez entrer la température en
degrés F.")
MsgBox "La température équivaut à " &
Celsius(temp) & " degrés C."
End Sub
3.3. Implémentation des algorithmes
Les algorithmes présentés dans ce travail sont
implémentés dans une application que nous avons appelé
CPLXE Nombres complexes. CPLXE est un outil qui nous permet
d'évaluer les fonctions usuelles sur des valeurs complexes,
problème que ne résout pas nos calculettes scientifiques.
Toutefois, les opérations arithmétiques ordinaires ne sont pas
reprises dans cette application vu qu'il existe déjà plusieurs
outils permettant de les réaliser. Les arguments des nombres complexes
considérés sont des déterminations principales des
arguments (c'est-à-dire pour k = 0)
3.3.1. Présentation de CPLXE
Propriété du formulaire d'accueil
|
Propriété
|
valeur
|
|
Name
|
Accueil
|
|
Caption
|
CPLXE NOMBRES COMPLEXES
|
|
Back color
|
&H00FFC0C0&
|
|
StartUpPosition
|
CenterScreen
|
Codes
Private Sub Cmdok_Click()
Unload Me
End
End Sub
Private Sub Cmdquit_Click()
If optexp.Value = True Then
Unload Me
Expcplx.Show
End If
If optasincom.Value = True Then
Unload Me
Arcsincplx.Show
End If
If optachcom.Value = True Then
Unload Me
Archcplx.Show
End If
If optasincom.Value = True Then
Unload Me
Arshcplx.Show
End If
If optchcom.Value = True Then
Unload Me
Coshcplx.Show
End If
If optcoscom.Value = True Then
Unload Me
Coscplx.Show
End If
If optlogcom.Value = True Then
Unload Me
Logcplx.Show
End If
If optlogneg.Value = True Then
Unload Me
Logneg.Show
End If
If optshcom.Value = True Then
Unload Me
Shcplx.Show
End If
If optsincom.Value = True Then
Unload Me
Sincplx.Show
End If
If optashcom.Value = True Then
Unload Me
Arshcplx.Show
End If
If Optarcoscom.Value = True Then
Unload Me
Arcoscplx.Show
End If
If Optappli.Value = True Then
Unload Me
Frmlogi.Show
End If
End Sub
Private Sub Command1_Click()
Unload Me
Logneg.Show
End Sub
Private Sub Command11_Click()
Unload Me
Archcplx.Show
End Sub
Private Sub Command12_Click()
End
End Sub
Private Sub Command5_Click()
Unload Me
Coscplx.Show
End Sub
Private Sub Command6_Click()
Unload Me
Arcsincplx.Show
End Sub
Private Sub Command7_Click()
Unload Me
Arcoscplx.Show
End Sub
Private Sub Command8_Click()
Unload Me
Shcplx.Show
End Sub
Private Sub Timer1_Timer()
If Lbtexte.Left >= 120 Then
Lbtexte.Left = Lbtexte.Left - 20
Else
Lbtexte.Left = 9120
End If
End Sub
Private Sub Vcmdok_Click()
End Sub
3.3.2. Fonction exponentielle
Interface visuelle
Propriétés
|
Propriété
|
valeur
|
|
Name
|
Expcplx
|
|
Caption
|
Exponentielle
|
|
Back color
|
&H00FFC0C0&
|
|
StartUpPosition
|
CenterScreen
|
codes
Private Sub A_KeyPress(KeyAscii As Integer)
If KeyAscii = 13 Then
B.SetFocus
End If
End Sub
Private Sub B_KeyPress(KeyAscii As Integer)
If KeyAscii = 13 Then
C.SetFocus
End If
End Sub
Private Sub Command1_Click()
A = ""
B = ""
C = ""
D = ""
E = ""
A.SetFocus
End Sub
Private Sub Command2_Click()
If A = "" Or B = "" Or C = "" Then
MsgBox "Vous avez laissé au moins un champ vide!",
vbExclamation, "Attention"
Else
If A > 0 Then
D = A ^ B * Cos(C * Log(A))
E = A ^ B * Sin(C * Log(A))
Else
If A = 0 Then
If B <> 0 Then
D = 0
E = 0
Else
MsgBox "Ceci est une forme indéterminée",
vbInformation, "Forme indéterminée"
End If
Else
F = 0.043213918264
D = A ^ B * (F ^ C) * Cos(C * Log(-1 * A))
E = A ^ B * (F ^ C) * Sin(C * Log(-1 * A))
End If
End If
End If
End Sub
Private Sub Command3_Click()
Unload Me
accueil1.Show
End Sub
Private Sub Command4_Click()
End
End Sub
3.3.3. Fonction logarithmique
Interface visuelle
Propriétés
|
Propriété
|
valeur
|
|
Name
|
Logcplx
|
|
Caption
|
Logarithmes des nombres complexes
|
|
Back color
|
&H00FFC0C0&
|
|
StartUpPosition
|
CenterScreen
|
Codes
Private Sub A_KeyPress(KeyAscii As Integer)
If KeyAscii = 13 Then
B.SetFocus
End If
End Sub
Private Sub Command1_Click()
A = ""
B = ""
C = ""
D = ""
A.SetFocus
End Sub
Private Sub Command2_Click()
If A = "" Or B = "" Then
MsgBox "Entrer des valeurs numériques svp!",
vbInformation, "Information"
A = ""
B = ""
C = ""
D = ""
A.SetFocus
End If
If A = 0 Then
If B = 0 Then
MsgBox "Le logarithme de zéro est moins l'infini",
vbInformation, "Information"
A = ""
B = ""
C = ""
D = ""
A.SetFocus
Else
C = Log(Sqr(B * B))
If B > 0 Then
D = 1.57079632679
Else
D = -1.57079632679
End If
End If
Else
If A < 0 Then
If B < 0 Then
C = Log(Sqr(A * A + B * B))
E = 3.14159265359
D = Atn(B / A) - E
Else
C = Log(Sqr(A * A + B * B))
E = 3.14159265359
D = E + Atn(B / A)
End If
Else
C = Log(Sqr(A * A + B * B))
D = Atn(B / A)
End If
End If
End Sub
Private Sub Command3_Click()
Unload Me
accueil1.Show
End Sub
Private Sub Command4_Click()
End
End Sub
3.3.4. Fonction sinus
Interface visuelle
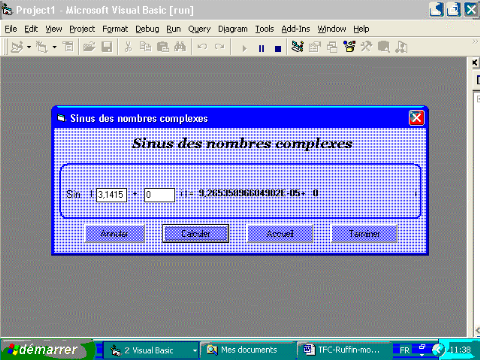
Propriétés
|
Propriété
|
valeur
|
|
Name
|
Sincplx
|
|
Caption
|
Sinuss des nombres complexes
|
|
Back color
|
&H00FFC0C0&
|
|
StartUpPosition
|
CenterScreen
|
codes
Private Sub A_KeyPress(KeyAscii As Integer)
If KeyAscii = 13 Then
B.SetFocus
End If
End Sub
Private Sub Command1_Click()
A = ""
B = ""
C = ""
D = ""
A.SetFocus
End Sub
Private Sub Command2_Click()
If A = "" Or B = "" Then
MsgBox "Verifiez que vous avez rempli tous les champs",
vbInformation, "Information"
A = ""
B = ""
A.SetFocus
Else
C = (1 / 2) * Sin(A) * (2.71828182845924 ^ (-1 * B) +
2.71828182845924 ^ B)
D = -(1 / 2) * Cos(A) * (2.71828182845924 ^ (-1 * B) -
2.71828182845924 ^ B)
End If
End Sub
Private Sub Command3_Click()
Unload Me
accueil1.Show
End Sub
Private Sub Command4_Click()
End
End Sub
3.3.5. Fonction cosinus
Interface visuelle
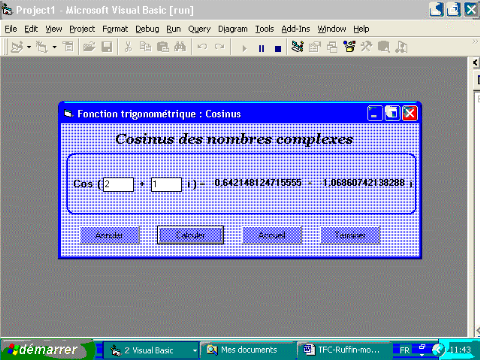
Propriétés
|
Propriété
|
valeur
|
|
Name
|
Coscplx
|
|
Caption
|
Cosinus des nombres complexes
|
|
Back color
|
&H00FFC0C0&
|
|
StartUpPosition
|
CenterScreen
|
Codes
Private Sub A_KeyPress(KeyAscii As Integer)
If KeyAscii = 13 Then
B.SetFocus
End If
End Sub
Private Sub Command1_Click()
A = ""
B = ""
C = ""
D = ""
A.SetFocus
End Sub
Private Sub Command2_Click()
If A = "" Or B = "" Then
MsgBox "Verifiez que vous avez rempli tous les champs",
vbInformation, "Information"
A = ""
B = ""
A.SetFocus
Else
C = (1 / 2) * Cos(A) * (2.71828182845924 ^ (-1 * B) +
2.71828182845924 ^ B)
D = (1 / 2) * Sin(A) * (2.71828182845924 ^ (-1 * B) -
2.71828182845924 ^ B)
End If
End Sub
Private Sub Command3_Click()
Unload Me
accueil1.Show
End Sub
Private Sub Command4_Click()
End
End Sub
3.3.6. Fonction arc sinus
Interface visuelle
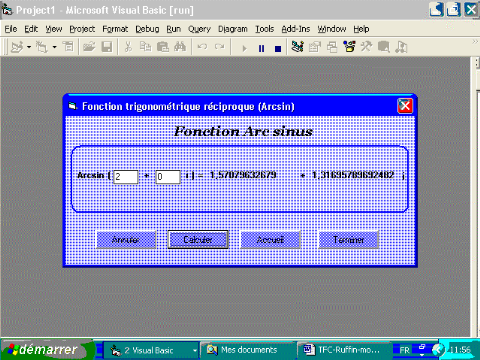
Propriétés
|
Propriété
|
valeur
|
|
Name
|
Arcsincplx
|
|
Caption
|
Fonction trigonométrique réciproque (Arc sin)
|
|
Back color
|
&H00FFC0C0&
|
|
StartUpPosition
|
CenterScreen
|
Codes
Dim A, B, k, l As Long
Private Sub Cmdcal_Click()
If (Txta = "" Or Txtb = "") Then
MsgBox "Verifiez que vous avez rempli tous les champs",
vbInformation, "Information"
Txta = ""
Txtb = ""
Lbla = ""
Lblb = ""
Txta.SetFocus
Else
A = Val(Txta)
B = Val(Txtb)
k = Sqr((Sqr(A ^ 4 + B ^ 4 + 2 * A ^ 2 * B ^ 2 - 2 * A ^ 2 +
2 * B ^ 2 + 1) + A ^ 2 - B ^ 2 - 1) / 2)
l = Sqr((Sqr(A ^ 4 + B ^ 4 + 2 * A ^ 2 * B ^ 2 - 2 * A ^ 2 +
2 * B ^ 2 + 1) - A ^ 2 + B ^ 2 + 1) / 2)
If (A > -1 And A < 1 And A <> 0) And B = 0
Then
Lbla = Atn(Sqr((A ^ 2) / (1 - A ^ 2)))
Lblb = 0
ElseIf A = 1 And B = 0 Then
Lbla = 1.57079632679
Lblb = 0
ElseIf A = 0 And B = 0 Then
Lbla = 0
Lblb = 0
ElseIf (A * B) >= 0 Then
Lbla = 1.57079632679 - (Atn((B + l) / (A + k)))
Lblb = Log(Sqr((A + k) ^ 2 + (B + l) ^ 2))
ElseIf (A * B) < 0 Then
Lbla = 1.57079632679 + Atn((B + l) / (A + k))
Lblb = Log(Sqr((A + k) ^ 2 + (B + l) ^ 2))
End If
End If
End Sub
Private Sub Command1_Click()
Txta = ""
Txtb = ""
Lbla = ""
Lblb = ""
Txta.SetFocus
End Sub
Private Sub Command3_Click()
Unload Me
accueil1.Show
End Sub
Private Sub Command4_Click()
End
End Sub
Private Sub Txta_KeyPress(KeyAscii As Integer)
If KeyAscii = 13 Then
Txtb.SetFocus
End If
End Sub
Private Sub Txtb_KeyPress(KeyAscii As Integer)
If KeyAscii = 13 Then
Cmdcal.SetFocus
End If
End Sub
3.3.7. Fonction arc cosinus
Interface visuelle
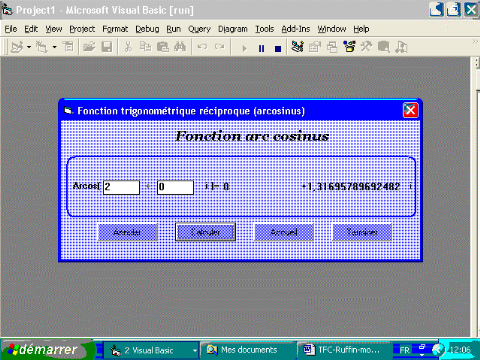
Propriétés
|
Propriété
|
valeur
|
|
Name
|
Arcoscplx
|
|
Caption
|
Fonction trigonométrique réciproque (Arc cos)
|
|
Back color
|
&H00FFC0C0&
|
|
StartUpPosition
|
CenterScreen
|
Codes
Dim A, B, k, l As Long
Private Sub Cmdcal_Click()
If (Txta = "" Or Txtb = "") Then
MsgBox "Verifiez que vous avez rempli tous les champs",
vbInformation, "Information"
Txta = ""
Txtb = ""
Lbla = ""
Lblb = ""
Txta.SetFocus
Else
A = Val(Txta)
B = Val(Txtb)
k = Sqr((Sqr(A ^ 4 + B ^ 4 + 2 * A ^ 2 * B ^ 2 - 2 * A ^ 2 +
2 * B ^ 2 + 1) + A ^ 2 - B ^ 2 - 1) / 2)
l = Sqr((Sqr(A ^ 4 + B ^ 4 + 2 * A ^ 2 * B ^ 2 - 2 * A ^ 2 +
2 * B ^ 2 + 1) - A ^ 2 + B ^ 2 + 1) / 2)
If A = 0 And B = 0 Then
Lbla = 1
Lblb = 0
ElseIf (A > -1 And A < 1 And A <> 0) And B = 0
Then
Lbla = Atn(Sqr((1 - A ^ 2) / (A ^ 2)))
Lblb = 0
ElseIf (A * B) > 0 Then
Lbla = Atn((B + l) / (A + k))
Lblb = Log(Sqr((A + k) ^ 2 + (B + l) ^ 2))
ElseIf (A * B) <= 0 Then
Lbla = -1 * Atn((B + l) / (A + k))
Lblb = Log(Sqr((A + k) ^ 2 + (B + l) ^ 2))
End If
End If
End Sub
Private Sub Command1_Click()
Txta = ""
Txtb = ""
Lbla = ""
Lblb = ""
Txta.SetFocus
End Sub
Private Sub Command3_Click()
Unload Me
accueil1.Show
End Sub
Private Sub Command4_Click()
End
End Sub
Private Sub Txta_KeyPress(KeyAscii As Integer)
If KeyAscii = 13 Then
Txtb.SetFocus
End If
End Sub
Private Sub Txtb_KeyPress(KeyAscii As Integer)
If KeyAscii = 13 Then
Cmdcal.SetFocus
End If
End Sub
3.3.8. Fonction sinus hyperbolique
Interface visuelle
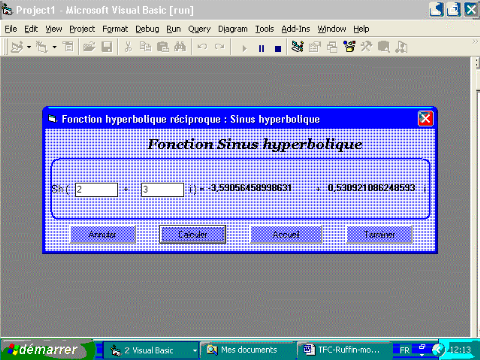
Propriétés
|
Propriété
|
valeur
|
|
Name
|
shcplx
|
|
Caption
|
Fonction hyperbolique : sinus hyperbolique
|
|
Back color
|
&H00FFC0C0&
|
|
StartUpPosition
|
CenterScreen
|
codes
Private Sub Cmdcal_Click()
If (Txta = "" Or Txtb = "") Then
MsgBox "Verifiez que vous avez rempli tous les champs",
vbInformation, "Information"
Txta = ""
Txtb = ""
Lbla = ""
Lblb = ""
Txta.SetFocus
Else
A = Val(Txta)
B = Val(Txtb)
Lbla = (1 / 2) * Cos(B) * (2.71828182845924 ^ A -
2.71828182845924 ^ (-A))
Lblb = (1 / 2) * Sin(B) * (2.71828182845924 ^ A +
2.71828182845924 ^ (-A))
End If
End Sub
Private Sub Command1_Click()
Txta = ""
Txtb = ""
Lbla = ""
Lblb = ""
Txta.SetFocus
End Sub
Private Sub Command3_Click()
Unload Me
accueil1.Show
End Sub
Private Sub Command4_Click()
End
End Sub
Private Sub Txta_KeyPress(KeyAscii As Integer)
If KeyAscii = 13 Then
Txtb.SetFocus
End If
End Sub
3.3.9. Fonction Cosinus hyperbolique
Interface visuelle
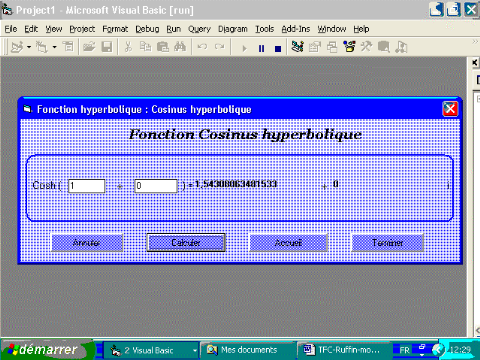
Propriétés
|
Propriété
|
valeur
|
|
Name
|
chcplx
|
|
Caption
|
Fonction hyperbolique : cosinus hyperbolique
|
|
Back color
|
&H00FFC0C0&
|
|
StartUpPosition
|
CenterScreen
|
Codes
Private Sub Cmdcal_Click()
If (Txta = "" Or Txtb = "") Then
MsgBox "Verifiez que vous avez rempli tous les champs",
vbInformation, "Information"
Txta = ""
Txtb = ""
Lbla = ""
Lblb = ""
Txta.SetFocus
Else
A = Val(Txta)
B = Val(Txtb)
Lbla = (1 / 2) * Cos(B) * (2.71828182845924 ^ A +
2.71828182845924 ^ (-A))
Lblb = (1 / 2) * Sin(B) * (2.71828182845924 ^ A -
2.71828182845924 ^ (-A))
End If
End Sub
Private Sub Command1_Click()
Txta = ""
Txtb = ""
Lbla = ""
Lblb = ""
Txta.SetFocus
End Sub
Private Sub Command3_Click()
Unload Me
accueil1.Show
End Sub
Private Sub Command4_Click()
End
End Sub
Private Sub Txta_KeyPress(KeyAscii As Integer)
If KeyAscii = 13 Then
Txtb.SetFocus
End If
End Sub
3.3.10. Fonction arc sinus hyperbolique
Interface visuelle
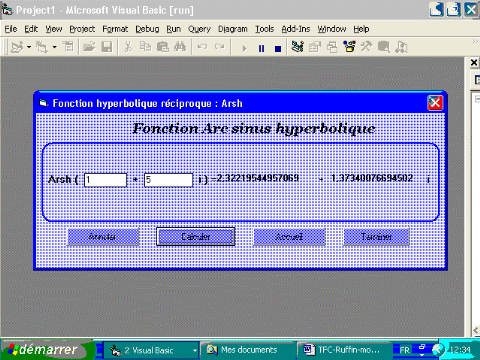
Propriétés
|
Propriété
|
valeur
|
|
Name
|
shcplx
|
|
Caption
|
Fonction hyperbolique réciproque : Arsh
|
|
Back color
|
&H00FFC0C0&
|
|
StartUpPosition
|
CenterScreen
|
Codes
Dim A, B, k, l As Long
Private Sub Cmdcal_Click()
A = Val(Txta)
B = Val(Txtb)
If (Txta = "" Or Txtb = "") Then
MsgBox "Verifiez que vous avez rempli tous les champs",
vbInformation, "Information"
Txta = ""
Txtb = ""
Lbla = ""
Lblb = ""
Txta.SetFocus
Else
A = Val(Txta)
B = Val(Txtb)
k = Sqr((Sqr(A ^ 4 + B ^ 4 + 2 * A ^ 2 * B ^ 2 - 2 * A ^ 2 -
2 * B ^ 2 + 1) + A ^ 2 - B ^ 2 + 1) / 2)
l = Sqr((Sqr(A ^ 4 + B ^ 4 + 2 * A ^ 2 * B ^ 2 - 2 * A ^ 2 -
2 * B ^ 2 + 1) - A ^ 2 + B ^ 2 + 1) / 2)
If (A + k) = 0 Then
Lblb = -1.57079632679
Lbla = Log(Sqr((A + k) ^ 2 + (B + l) ^ 2))
ElseIf (A * B) > 0 Then
Lblb = Atn((B + l) / (A + k))
Lbla = Log(Sqr((A + k) ^ 2 + (B + l) ^ 2))
ElseIf (A * B) <= 0 Then
Lblb = -1 * Atn((B + l) / (A + k))
Lbla = Log(Sqr((A + k) ^ 2 + (B + l) ^ 2))
End If
End If
End Sub
Private Sub Command1_Click()
Txta = ""
Txtb = ""
Lbla = ""
Lblb = ""
Txta.SetFocus
End Sub
Private Sub Command3_Click()
Unload Me
accueil1.Show
End Sub
Private Sub Command4_Click()
End
End Sub
Private Sub Txta_KeyPress(KeyAscii As Integer)
If KeyAscii = 13 Then
Txtb.SetFocus
End If
End Sub
Private Sub Txtb_KeyPress(KeyAscii As Integer)
If KeyAscii = 13 Then
Cmdcal.SetFocus
End If
End Sub
3.3.11. Fonction arc cosinus hyperbolique
Interface visuelle
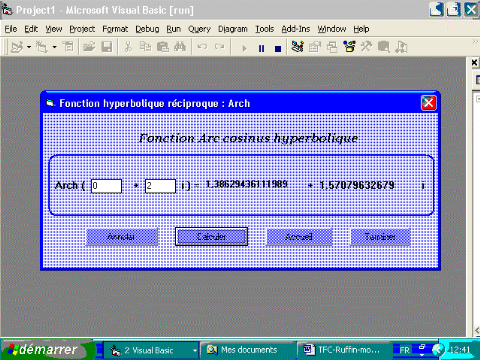
Propriété
|
Propriété
|
valeur
|
|
Name
|
chcplx
|
|
Caption
|
Fonction hyperbolique réciproque : Ch
|
|
Back color
|
&H00FFC0C0&
|
|
StartUpPosition
|
CenterScreen
|
Codes
Dim A, B, k, l As Long
Private Sub Cmdcal_Click()
If (Txta = "" Or Txtb = "") Then
MsgBox "Verifiez que vous avez rempli tous les champs",
vbInformation, "Information"
Txta = ""
Txtb = ""
Lbla = ""
Lblb = ""
Txta.SetFocus
Else
A = Val(Txta)
B = Val(Txtb)
k = Sqr((Sqr(A ^ 4 + B ^ 4 + 2 * A ^ 2 * B ^ 2 - 2 * A ^ 2 +
2 * B ^ 2 + 1) + A ^ 2 - B ^ 2 - 1) / 2)
l = Sqr((Sqr(A ^ 4 + B ^ 4 + 2 * A ^ 2 * B ^ 2 - 2 * A ^ 2 +
2 * B ^ 2 + 1) - A ^ 2 + B ^ 2 + 1) / 2)
If (A > -1 And A < 1 And A <> 0) And B = 0
Then
Lblb = Atn(Sqr((1 - A ^ 2) / A ^ 2))
Lbla = 0
ElseIf A = 0 And B = 0 Then
Lblb = 1.57079632679
Lbla = 0
ElseIf (A + k) = 0 Then
Lbla = Log(Sqr((A + k) ^ 2 + (B + l) ^ 2))
Lblb = 1.57079632679
ElseIf (A * B) >= 0 Then
Lblb = Atn((B + l) / (A + k))
Lbla = Log(Sqr((A + k) ^ 2 + (B + l) ^ 2))
ElseIf (A * B) < 0 Then
Lblb = -1 * Atn((B + l) / (A + k))
Lbla = Log(Sqr((A + k) ^ 2 + (B + l) ^ 2))
End If
End If
End Sub
Private Sub Command1_Click()
Txta = ""
Txtb = ""
Lbla = ""
Lblb = ""
Txta.SetFocus
End Sub
Private Sub Command2_Click()
End Sub
Private Sub Command3_Click()
Unload Me
accueil1.Show
End Sub
Private Sub Command4_Click()
End
End Sub
Private Sub Txta_KeyPress(KeyAscii As Integer)
If KeyAscii = 13 Then
Txtb.SetFocus
End If
End Sub
Private Sub Txtb_KeyPress(KeyAscii As Integer)
If KeyAscii = 13 Then
Cmdcal.SetFocus
End If
End Sub
CONCLUSION
Dans ce travail, nous avons étudié les
prolongements des fonctions réelles dans le corps C des
nombres complexes, c'est-à-dire que les résultats que donnent nos
algorithmes pour des valeurs complexes doivent être une
généralisation des solutions pour des cas particuliers des
réels (noter que les réels sont des complexes particuliers).
Comme nous l'avons soutenu tout au long de ce travail, les
prolongements naturels des fonctions élémentaires usuelles en
Analyse au domaine complexe enrichissent parfois ces fonctions en nouvelles
propriétés qui peuvent être exploitées dans d'autres
domaines de la Mathématique et Sciences physiques. A titre d'exemple,
nous avons vu comment les fonctions sinus et cosinus prolongées dans le
domaine complexe ont cessé d'être bornées et par ailleurs,
les fonctions exponentielles et logarithmiques se sont enrichies des
propriétés intéressantes : prolongée dans le
domaine complexe, la fonction exponentielle ez devient
périodique tandis que la fonction logarithmique devient multiforme.
En vue de rendre disponibles les résultats en temps
record, nous avons implémenté les algorithmes des calculs pour
chaque type de fonction dans un logiciel que nous avons dénommé
CPLXE nombres complexes. Ce dernier est un utilitaire de calcul qui ne
remplace pas une calculette scientifique mais la complète dans les
calculs sur des nombres complexes.
Signalons par ailleurs que CPLXE Nombres complexes
est un produit du département de Mathématique et Informatique de
l'Université Pédagogique Nationale car réalisé aux
moyens des ressources de ce dernier (principalement les ressources humaines).
Toute exploitation dudit logiciel doit être motivée par une
permission préalable du département de Mathématique et
Informatique.
Enfin, nous remercions les membres du département pour
leur soutien dans la réalisation de notre travail.
A tous nos lecteurs, nous restons ouverts à leurs
suggestions et présentons d'avance nos excuses pour d'éventuelles
erreurs dans ce travail.
BIBLIOGRAPHIE
|
"The American Heritage" (1976), Review Ed. New
College Edition
|
|
Antibi, A et Barra, R. (1998) : "Math
TermS, Obligatoire", Ed. Nathan, Paris
|
|
Badaga O'gale, A, (2003): "Méthodes des
recherches scientifiques", EIFI, Kinshasa
|
|
Beltramone, J.P. et al (2002) : "DECLIC Maths,
Terminal S/Enseignement obligatoire", Ed. Hachette, Paris
|
|
Bouteloup, D. (2003) : "Eléments de
Géométrie différentielle", ENSG, Paris
|
|
Canevet, D. (2005) : "L'Algorithmique et le
Pascal", Ed. Delagrave, Paris
|
|
Chambadal, L. (1968) : "Dictionnaire des
mathématiques modernes", Librairie Larousse, Paris
|
|
Chambert, A. (2005 - 2006) : "Algèbre
Commutative", Cours, Université de Rennes
|
|
Cougnard, J. (2004 -2005) : "Compléments
d'Algèbre", Master de Mathématique, Seconde année,
Université de Caen, 2004 - 2005
|
|
CPR Informatique (2002) : "Visual Basic
v.6.0", Cours, Ecole nationale des sciences géographiques
|
|
Engombe Wedi Shamba, B. (2007 - 2008),
"Compléments d'Algèbre", Cours Inédit, UPN,
Kinshasa
|
|
Ferrard, J. M., "Nombres complexes,
trigonométrie", Presse universitaire, ac Lyon
|
|
Granville, W. A, Smith, P. F. et Longley, W.
R (1966) : "Eléments du calcul différentiel et
intégral", Vuibert, 2è édition française,
Paris
|
|
Lavrentiev, M et Chabat,
B,(1972):"Méthodes de la théorie des fonctions d'une variable
complexe", Mir, moscou
|
|
Makiadi Nzumba, J.M., (1994):"Etude des
fonctions" Tome I, CRP, Kinshasa
|
|
Nearing, J. (2006) : "Mathematicals tools for
Physics", Reviewed Ed, University of Miami
|
|
Thiel, E. :"Algorithmes et programmation en
Pascal", DEUG 1, Cours, Luming, 2004
|
|
Van Loo, R. (1985) : "Les grandes
règles de programmation en BASIC", Ed. Marabout, Alleur,
Belgique
|
Sites Web
www.les-mathematiques.net
www.wikipedia.net
http://name.math.univ-rennes.fr
http://www.inc.imag.fr
Autres Sources
Microsoft Encarta 2007.
TABLE DE MATIERES
Epigraphe
DEDICACE
...................................................................................................
I
AVANT - PROPOS
.....................................................................................
II
0. Introduction
..........................................................................................
1
0.1. Problématique
...................................................................... 1
0.2. Hypothèse
..............................................................................
2
0.3. Choix et intérêt du sujet
...................................................... 3
0.4. Délimitation du sujet
........................................................... 3
0.5. Méthodes et techniques
utilisées...................................... 4
0.6. Subdivision du
travail.......................................................... 5
Chap. 1. Le corps C des nombres complexes
....................................... 6
1.1. Historique des nombres complexes
................................. 6
1.1.1. Formule de Cardan
................................................ 6
1.1.2. Audace de Bombelli
............................................... 6
1.1.3. Apport des autres mathématiciens
..................... 7
1.2. Définition de C
...................................................................... 7
1.2.1. Définition
................................................................ 7
1.2.2. Notation cartésienne
............................................ 8
1.2.3. Conjugaison
............................................................. 9
1.2.4. Module
.................................................................... 10
1.2.5. Fonctions à valeurs complexes
............................ 11
1.3. Argument, exponentielle complexe
.................................. 12
1.3.1. Notation eiè
............................................................. 12
1.3.2. Formules de Moivre et d'Euler
............................. 14
1.3.3. Forme trigonométrique
....................................... 15
1.3.4. Fonction exponentielle complexe
........................17
1.4. Equations polynomiales
...................................................... 18
1.4.1. Théorème de d'Alembert
...................................... 18
1.4.2. Racines carrées d'un nombres complexes
......... 19
1.4.4. Racines nième de l'unité
....................................... 21
Chap. 2. Fonctions à variables
complexes ........................................... 22
2.1. Fonctions exponentielles
................................................... 22
2.2. Fonctions logarithmiques
................................................... 24
2.2.1. Définition de la fonction logarithmique
.............. 24
2.2.2. La fonction logarithme népérien
......................... 25
2.3. Fonctions trigonométriques
............................................... 26
2.3.1. Fonction sinus
......................................................... 26
2.3.2. Fonction cosinus
..................................................... 27
2.4. Fonctions trigonométriques
réciproques ........................ 27
2.4.1. Fonction arc sin
...................................................... 27
2.4.2. Fonction arc cosinus
.............................................. 30
2.5. Fonctions hyperboliques
.................................................... 33
2.5.1. Fonction sh
.............................................................. 33
2.5.2. fonction ch
.............................................................. 34
2.6. Fonctions hyperboliques
réciproques .............................. 34
2.6.1. Fonction arsh
.......................................................... 34
2.6.2. Fonction arch
.......................................................... 35
Chap. 3. Algorithme et programmation
............................................... 36
3.1. Algorithme
.............................................................................
36
3.1.1. Calcul de l'exponentielle d'un complexe............
37
3.1.2. Calcul du logarithme d'un nombre complexe ... 37
3.1.3. Calcul de sinus d'un nombre complexe ..............
38
3.1.4. Calcul de cosinus d'un nombre complexe..........
38
3.1.5. Calcul de l'arc sinus d'un nombre complexe ......
39
3.1.6.Calcul de l'arc cosinus d'un nombre complexe ... 39
3.1.7. Calcul de sinus hyperbolique d'un complexe .... 40
3.1.8. Calcul de cos hyperbolique d'un complexe.......
40
3.1.9. Calcul de l'arc sin hyperbolique d'un complexe 41
3.1.10. Calcul d'arc cos hyperbolique d'un complexe 41
3.2. Les principaux concepts de Visual Basic
......................... 42
3.2.1. Présentation générale
........................................... 42
3.2.2. Le modèle événementiel
...................................... 43
3.2.3. La notion d'objet
................................................... 43
3.2.4. La notion de méthode et de
propriété ............... 43
3.2.5. La syntaxe de Visual Basic
..................................... 44
3.2.6. Les types de données
............................................ 45
3.2.7. Les instructions
....................................................... 51
3.2.8. Les modèles
............................................................ 53
3.3. Implémentation des algorithmes
...................................... 55
3.3.1. Présentation de CPLXE
.......................................... 55
3.3.2. Fonction exponentielle
.......................................... 58
3.3.3. Fonction logarithmique
......................................... 61
3.3.4. Fonction sinus
......................................................... 63
3.3.5. Fonction cosinus
..................................................... 65
3.3.6. Fonction arc sinus
.................................................. 66
3.3.7. Fonction arc cosinus
.............................................. 69
3.3.8. Fonction sinus hyperbolique
................................ 71
3.3.9. Fonction cosinus hyperbolique
............................ 73
3.3.10. Fonction arc sinus hyperbolique
........................ 74
3.3.11. Fonction arc cosinus hyperbolique
................... 76
CONCLUSION
.............................................................................................
79
BIBLIOGRAPHIE
.........................................................................................
80
TABLE DE MATIERES
................................................................................
81
* 1 Lavrentiev, M. et Chabat,
B. (1972), « Méthodes de la théorie des fonctions
d'une variable complexe », Mir, Moscou
* 2 Certaines parmi ces
fonctions seront multiformes.
* 3 MAKIADI NZUMBA, J. M.,
Etude des fonctions, Tome I, Ed. CRP, page 2
* 4 Aphy Badaga O'gale Mabagwa
(2003),, Méthodes des recherches scientifiques, EIFI,
Kinshasa
* 5 BELTRAMONE, J. P. et al,
DECLIC Maths, Terminal S/Enseignement obligatoire, Ed.
Hachette, Paris, 2002
* 6 Jérôme
CARDAN de l'Italien Hieronimo CARDAN : médecin, astrologue,
poète et mathématicien italien (Pavie 1501 - Rome 1576)
* 7 On peut faire le
développement en série de Mac-Laurin de la fonction
eiy
* 8 Antibi, A. et Barra, R
(1998)., « Math TermS, Obligatoire », page 139,
Ed. NATHAN, Paris
* 9 Beltramone, J.P. et
al.(2002), « Declic, Maths terminale S/Enseignement
Obligatoire », Ed. Hachette, Paris
* 10 Malaval, J. , Courbon,
D.(2002), « Math Term ES/ Obligatoire et
Spécialité », page 134, Ed. Nathan, Paris
* 11 John Néper (en
Français Jean NAPIER) : Baron de Merchiston, mathématicien
écossais (1550 - 1617).
* 12 Microsoft Encarta 2007
* 13 Le titre original de cet
ouvrage est « Kital Al-jabr wal muqabala »



