IV-2-2-2-Le calcul par le code PLAXIS :
+ Etat vierge :
Présentation du modèle
géométrique :
[Tapez un texte]
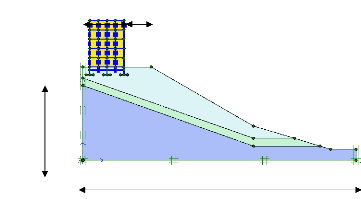
La figure suivante présente le modèle
géométrique (modèle de référence) retenu
pour le calcul. Le nombre des éléments choisi est de 6 noeuds ce
qui est fiable avec le problème traité. Les conditions aux
limites imposées sont définies par des déplacements
horizontaux sur les bords latéraux et par des déplacements
verticaux sur la base inférieure du modèle (substratum) nuls.
20 m 30 m 30 m
6
5
7
10
30 m
4
y
3
2
0 x 1
8 9
11 12
80 m
Figure V-6 L èle
géométrique.
Le code PLAXIS offre la possibilité de faire une
exploitation détaillée des calculs sous forme des tableaux et
courbes. La figure V.7 représente le maillage déformé du
talus, les contraintes de cisaillement (figure V.8), les déplacements
totaux (figure V.9) :
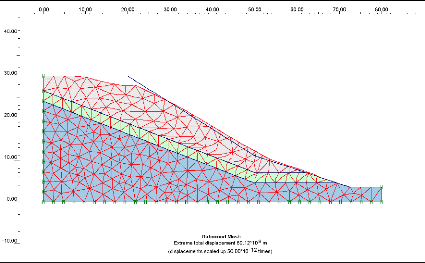
Figure V-7: Le maillage déformé du
talus.
[Tapez un texte]
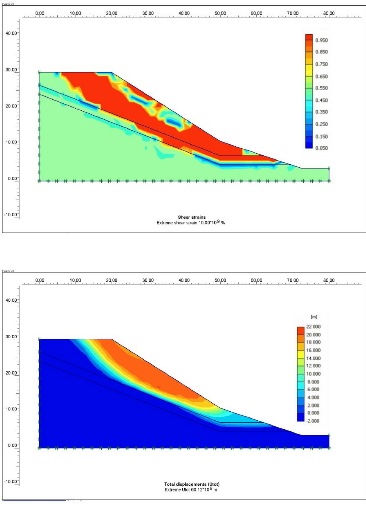
Figure V-8: Les contraintes maximales de
cisaillement
Figure V-9: Les déplacements totaux.
Ainsi le PLAXIS offre des informations sur l'étape des
calculs, et le coefficient de sécurité Fs (Tableau V.9) :
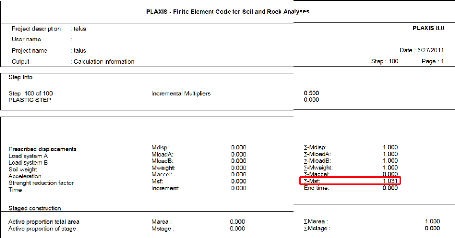
Tableau V-9: Présentation des
informations de calcul. Prise en compte des surcharges :
Le modèle géométrique est semblable au
modèle de référence avec la présence d'une
construction éloignée de 8m de la tête du talus, pour la
prise en compte du poids des bâtiments
10 m 8 m
03613501 1 381243 0 3
935135411421247834
733135311411246732
6
30135111401248631
1245528
5
11
39
1352
29
6 13 4 49 18 4 44 14 25 27 26
24223 211920
7
171516
5
10
Figu
30 m re V10 : Le mod èle
y
0 x 1
4
8 9
11 12
3
2
géométrique avec la
80sm mpte des surcharges.
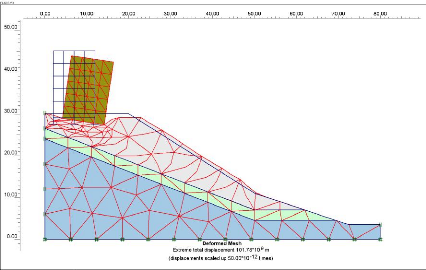
Figure V-11: le maillage déformé
du talus et bâtiment.
Figure V-12: Les contraintes
maximales de cisaillement.
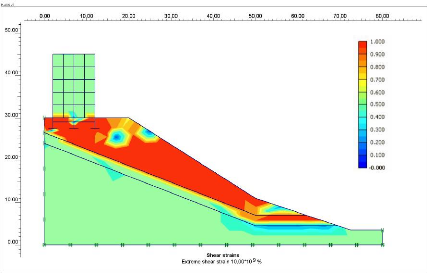
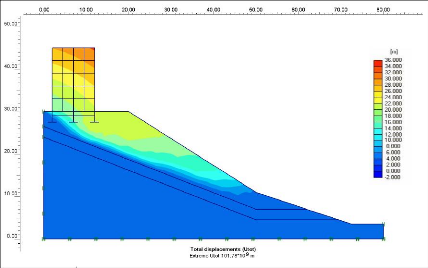
Figure V-13: Les déplacements
totaux.
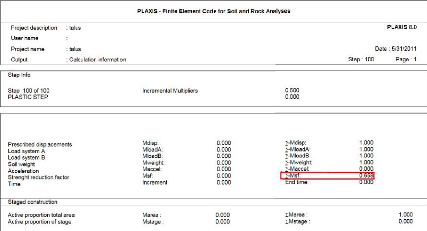
Tableau V-10: Présentation des
informations de calcul.
+ La prise en compte des infiltrations des eaux :
Le modèle géométrique est le même,
sauf qu'on détermine le niveau de la nappe en surface.
Figure V-14: Le maillage déformé
du talus.
Figure V-15: Les pressions interstitielles.
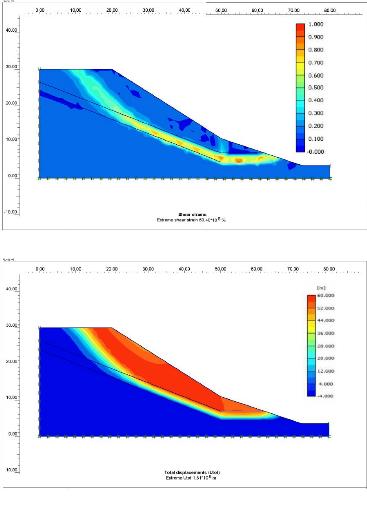
Figure V-16: Les contraintes maximales de
cisaillement.
Figure V-17: Les déplacements totaux.

Tableau V-11 : Présentation des
informations de calcul. + Couplage hydromécanique :
Ce modèle est le plus proche de la réalité,
dont le double effet des surcharges et d'eau s'impose.
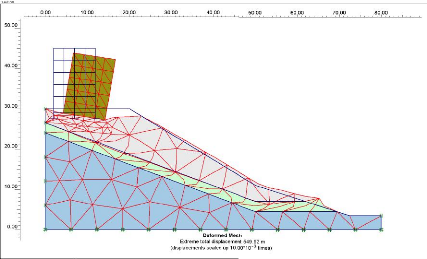
Figure IV-18: Le maillage déformé
du talus et bâtiment.
Figure V-19: Les contraintes maximales de
cisaillement.
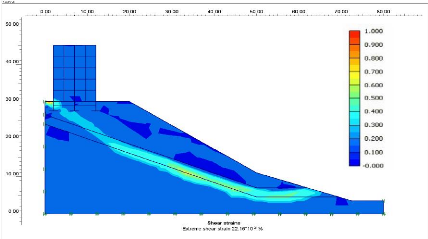
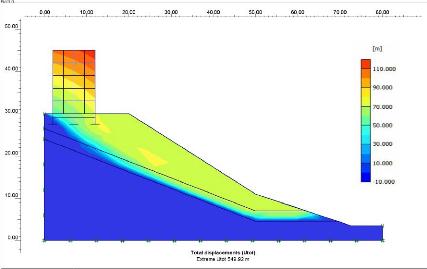
Figure V-20: Les déplacements totaux.
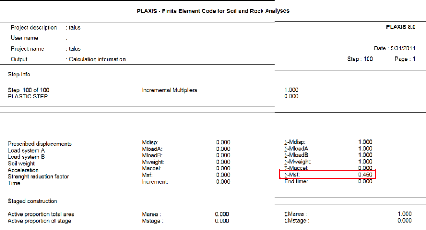
Tableau V-12: Présentation des
informations de calcul. + Récapitulatif des résultats de
code PLAXIS :
|
Variante N°01
|
Variante N°02
|
Variante N°03
|
Variante N°04
|
|
Coefficient de
sécurité Fs
|
1,031
|
0,658
|
0,519
|
0,450
|
|
Modèle
|
Mohr-Coulomb
|
Mohr-Coulomb
|
Mohr-Coulomb
|
Mohr-Coulomb
|
|
Comportement
|
Non drainé
|
Non drainé
|
Non drainé
|
Non drainé
|
Tableau V-13 : Récapitulatif des
résultats de calcul du code PLAXIS. Interprétation des
résultats :
Variante N°01 :
> L'analyse des résultats confirme les calculs
précédents, et que le talus a été instable
avant la construction des bâtiments.
> Les déplacements du talus sont très
importants, et les contraintes de cisaillement sont très importantes au
niveau de la deuxième couche (de 3 à 5.5m), ce qui explique que
la couche d'argile schisteuse constitue un plan favorable au processus de
glissement.
Variante N°02 :
> Le coefficient de sécurité Fs = 0,658, donc
l'influence de la structure suite aux
mouvements du versant.
> Un déplacement important est observé au niveau
de la structure, ce qui traduit que la construction est elle aussi
affectée par les mouvements du versant.
Variante N°03 :
> Le coefficient de sécurité Fs subit une
diminution considérable de 1,031 à 0,519, ce
qui explique l'importance de l'eau dans le
phénomène du glissement de terrain. [Tapez un
texte]
> Le volume de terrain déplacé est plus
important qu'en état vierge, avec une concentration des contraintes de
cisaillement maximales au niveau de la deuxième couche.
Variante N°04 :
> L'effet mixte de l'eau et des surcharges
génère une diminution du coefficient de sécurité
(Fs = 0,450).
> Les déplacements et les contraintes de
cisaillement deviennent importants au niveau de la première et la
deuxième couche ce qui se traduit par un déplacement d'un grand
volume.
> Les désordres observés au niveau des
constructions sont plus important.
| 


