Analyse et modélisation d'un glissement de terrain. Cas de Sidi Youcef (Béni Messous, Alger )

Chapitre V :

Calculs et vérifications

V- 1-INTRODUCTION :

Dans cette partie, en vue d'analyser et de modéliser le glissement, deux logiciels de calcul ont été utilisé : le GEOSLOPE et le PLAXIS, avec la détermination du coefficient de sécurité.

V- 2- DETERMINATION DU COEFFICIENT DE SECURITE FS :

La série des calculs effectuée vise à déterminer les valeurs du coefficient de sécurité par la méthode de Fellenius et par les logiciel ; GEOSLOPE et PLAXIS (Phi-c reduction).

Quatre combinaisons de calcul ont été envisagées :

Un premier calcul (variante N°01) dans lequel le talus est analysé sous l'action de son poids propre ou bien en état vierge.

Un second calcul (variante N°02), on prend en compte les surcharges des bâtiments situés en amont du talus.

Un troisième calcul (variante N°03), dont le niveau d'eau est supposé atteindre le terrain naturel (talus entièrement saturé) pour simuler les infiltrations et les fuites d'eau en surface.

Un quatrième calcul (variante N°04), dans lequel les effets combinés des eaux et les surcharges.

Le tableau suivant regroupe les caractéristiques des différentes couches du terrain :

	ãd (kN/m^3)	ãh (kN/m^3)	ãsat (kN/m^3)	C (kN/m^2)	ö °	E (kN/m^2)	í
Remblai	15,37	17,00	19,51	20	10	4800	0,33
Argile schisteuse	16,20	18,50	20,03	4	28,5	10000	0,33
Schiste	18,90	21,00	21,73	237	33,55	33450	0,30

Tableau V-1 : Caractéristiques des couches de terrain. V- 2-1-Calcul de facteur de sécurité manuellement :

D

nd = H

Avec :

D=30m

H=26.75m

30

nd = 26. ~5 = iE. iE2

Donc le nd <2 ; alors la ligne de glissement passe par le pied.

D'après l'abaque XI-17 (abaque de détermination du cercle de rupture) on a : á0= 37°.

â0=26°

Le calcul manuel se fait avec la méthode de Fellenius, dont la figure en annexe montre la localisation du cercle et du rayon de glissement, ainsi les différentes tranches.

Les résultats de calcul sont indiqués dans les deux tableaux suivants :

N i	?i	Wi	Wicos^2?i	Ub	(Wicos^2?i-Ub) tgö	[Cb + (Wicos^2?i-Ub) tg ö1/cos?i	Wisin?i
1	62°	843,61	185,93	0	31,04	145,35	744,86
2	53°	2039,62	738,71	0	289,01	541,51	1628,91
3	39°	2186,1	1380,31	0	604,8	821,76	1378,76
4	27°	1942,2	1541,9	0	725,11	853,79	881,74
5	21°	675,18	588,47	0	248,79	306,01	241,96
6	- 9°	259,515	253,16	0	111,35	150,04	- 40,6

Tableau V-2 : Les résultats de calcul en état vierge.

v Etat vierge: v Avec surcharges:

Fs3524[38 = 4832,63 3524, 38

=0,73

Fs =			= 0, 69

Avec les surcharges Q = 220kN/m²

Ni	?i	Wi	Wicos^2?i	Ub	(Wicos^2?i-Ub) tg ö	[Cb + (Wicos^2?i-Ub)tg ö]1/cos?i		Wisin?i	1
62°	843,61	185,93	128.76	100,95	294,26	744,86		2
53°	2039,6 2	738,71	206.41	401,08	727,54	1628,91		3
39°	2186,1	1380,31	206.41	716,87	965,21	1375,76		4
27°	1942,2	1541,9	206.41	837,18	979,30	881,74		5
21°	675,18	588,47	130.26	319,51	381,68	241,96		6
-9°	259,51 5	253,16	48.7	137,45	176,39	-40,6

Tableau V-3 : Les résultats de calcul en état entièrement saturé.

v Prise en compte des infiltrations :

2818,46

Fs =			= 0. 58

v Couplage hydromécanique :

2818, 46

Fs =			= 0.55

V-2-2-Calcul a l'aide des logiciels :

V-2-2-1-Calcul par GEOSLOPE :

Le calcul s'effectue par les variantes précédentes avec les différentes méthodes de calcul (Fellenius, Bishop, Jambu,.....etc). La position de cercle de glissement est choisie automatiquement (AUTO LOCATE).

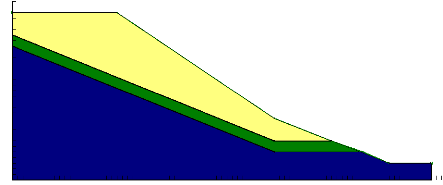
La position des cercles de glissement et les résultats de calcul de chaque variante sont présentés ci-après :

32

31

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 ²⁶ ₂₇ ²⁸ ₂₉ ³⁰ 31 32 33 34 35 ³⁶ ₃₇ ³⁸ 39 40 ⁴¹ 42 43 ⁴⁴ ₄₅ ⁴⁶ 47 48 49 50 51 52 53 ⁵⁴ ₅₅ ⁵⁶ 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 ⁷⁶ 77 78 79 80 81 82

hauteur

30

29

28

27

26

25

24

23

22

21

20

19

18

17

16

15

14

13

12

11

10

9

8

7

6

5

4

3

2

0

1

longueur

Figure V-1 : Le modèle géométrique adopté.

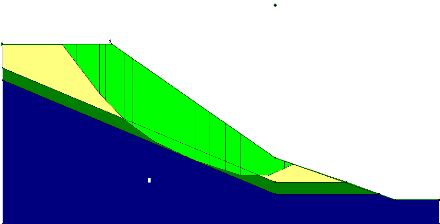
v Etat vierge :

1

6

7

3

4

3

5

8 9

¹0 11

3

12

0.844

Figure V-2 : La position du centre et du cercle de glissement dans le modèle géométrique.

	Fellenius	Bishop	Morgenstern & Price		Jambu	Fs
0,79523	0,84338	0,84426	0,79533

Tableau V-4 : Valeur de coefficient de sécurité avec les différentes méthodes.

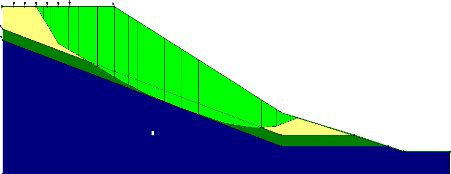
v Prise en compte des surcharges :

[Tapez un texte]

0.683

3

1 14 15 16 17 18 19

3

3

5

8 9

4

10 11

12

Figure V-3 : La position du centre et du cercle de glissement dans le modèle géométrique.

	Fellenius	Bishop	Morgenstern & Price	Jambu
Fs	0,62393	0,64929	0,64977	0,60586

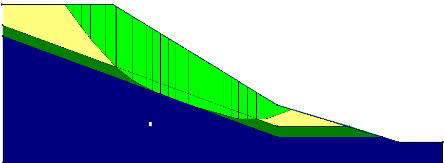
Tableau V-5 : Valeur de coefficient de sécurité avec les différentes méthodes. + La prise en compte des infiltrations des eaux :

0.510

1 2

6

7

3

4

3

5

8 9

10 11

3

12

Figure V-4 : La position du centre et du cercle de glissement dans le modèle géométrique.

	Fellenius	Bishop	Morgenstern & Price	Jambu
Fs	0,50997	0,56053	0,56333	0,5243

Tableau V-6 : Valeur du coefficient de sécurité avec les différentes méthodes. + Couplage hydromécanique :

[Tapez un texte]

0.447

1 14 15 16 17 18 19 2

6

7

3

4

3

5

8 9

10 11

3

12

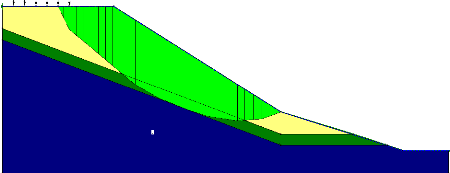
Figure V-5 : La position du centre et du cercle de glissement dans le modèle géométrique.

	Fellenius	Bishop	Morgenstern & Price	Jambu
Fs	0,42388	0,44507	0,44992	0,41749

Tableau V-7 : Valeur de coefficient de sécurité avec les différentes méthodes. + Récapitulatif des résultats de GEOSLOPE :

	Méthode	Variante N°01	Variante N°02	Variante N°03	Variante N°04
GEOSLOP	Fellenius	0,79523	0,62393	0,50997	0,42388
	Bishop	0,84338	0,64929	0,56053	0,44507
	Morgenstern &Price	0,84426	0,64977	0,56333	0,44992
	Jambu	0,79533	0,60586	0,5243	0,41749

Tableau V. 8 : Récapitulatif des données de calcul.

Commentaires et interprétation :

> On remarque que tous les coefficients de sécurité sont inférieurs à 1, donc le talus est

considéré comme instable et que les facteurs extérieurs : les infiltrations et les surcharges accentue le problème ce qui se traduit dans les calculs par une diminution du facteur de sécurité

> Le facteur de l'eau joue un rôle très important dans le processus de glissement par rapport aux surcharges; a titre d'exemple Fs = 0,50 avec la nappe, et Fs = 0,62 avec les surcharges par la méthode de Fellenius.

La comparaison entre les calculs manuels et les calculs par le GEOSLOPE génère un écart n'excède pas 0,1 dans tous les cas.