
 |
Implantation d'algorithme de filtrage numérique sur FPGA(réseau de portes programmables)( Télécharger le fichier original )par Mohamed Bendada Université Ferhat Abbas de Sétif Algérie - Master électronique 2010 |
» I.6- Le langage VHDL dans le flot de conception ~~~~~~ ~~~~~~~~.~~~ 1 I.6.1- Le logiciel de Modelsim dans le flot de synthèse«~«~«~«~«~«~ «~«~«~«~«~. 1 I.7- Modélisation des FP 1 I.7.1- Les circ 1 FPGA«~«~«~«~«~«~«~«~«~«~«~..«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~..«~«~«~ I.7.2- Structure des FP 1 I.7.3- Les ressources de FP 1 a- Cellules d'entrées sor 1
I.8- Conclusion ~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~ 1 Chapitre II : Les filtres numériquesII.1- 1 Introduction«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~..«~«~«~«~«~«~«~«~«~«~«~«~ II.2-Définition 1 filtre«~«~«~«~«~«~«~«~«~«~..«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~.«~«~«~«~.
numériques«~«~«~«~«~«~. «~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~ «~«~«~ a- 2 Linéarité«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~«~
causalite
numerique II.6.1- Les filtre á réponse
impulsionnelle finie (RIF)
II.6.2-L'équation aux differences du filtre
RIF
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Library ieee ; Use ieee.std_logic_1164.all; Use ieee.numeric_std.all ; Use ieee.std_logic_unsigned .all; |
La déclaration d'entité décrit l'interface entre le monde extérieur et une unité de conception. C'est a dire principalement ses signaux d'entrée et de sortie. Une même entité peut être associée à plusieurs architectures différentes. Elle décrit alors une classe d'unités de conception qui présente au monde extérieur le même aspect, avec des fonctionnements internes éventuellement différents. [5]
La déclaration d'entité : La syntaxe générale d'une entité
|
ENTITY Nom de l'ejité IS GENERIC (le nom du signal : type :=la valeur); Port (nom du signal : direction type) ; END Non de l'ejité ; |
+ On spécifie ici le nom de l'entité créée. Ce nom est choisi par le programmeur. Les mots entity et is sont des mots clés du langage VHDL. Ils indiquent le début de la description d'un nouveau design en VHDL.
+ L'instruction GENERIC permet de spécifier certains paramètres de l'entité, comme par exemple la largeur d'un bus. Le paramètre peut être initialisé directement dans l'entité à une certaine valeur, puis modifié ultérieurement lors le son utilisation. De cette manière la description peut rester très générale.
+ l'instruction port permet de décrire les entrées sorties.
? Nom du signal : Il est composée de caractères, le premier caractère doit être une lettre, sa langueur est quelconque, mais ne doit pas dépasser une ligne de code.
· La direction du signal
> In : pour un signal d'entrée.
> Out : pour un signal de sortie. Une sortie ne peut être reliée à l'intérieur de l'architecture associée à l'entité
> Inout : pour un signal en entrée sortie, la connexion peut alors être reliée et réutilisée à l'intérieur de l'architecture associée.
· Le type
La notion de type est très importante en VHDL, chaque entrée, sortie, signal, variable ou constante, est associé à un type. Sans artifice particulier, il n'est pas question d'effectuer une opération entre deux grandeurs de type différent.
> Bit : Il s'agit là, évidemment, du type de base le plus utilisé en électronique numérique. Un objet de type bit peut prendre deux valeurs : '0' et '1', il s'agit, en fait, d'un type énuméré prédéfini.
> Bit_vector : un vecteur de bits est un bus déclaré par exemple pour une largeur de N bits par bit_vector (N downto 0) ou bien bit_ vector (0 to N)
La fin de la déclaration de l'entité est indiquée avec le mot réservé end. Il est facultatif de placer ensuite le nom de l'entité, mais c'est une bonne habitude de le faire pour que les programmes soient plus clairs et faciles à lire.
Exemple du multiplexeur de la figure I.2 :
La déclaration de l'entité du multiplexeur 2 voies vers 1 ENTITY multiplexeur IS
PORT (a, b: in bit ;
S: out bit);
End multiplexeur;
Où:
Le fonctionnement interne d'un module-son corps- est précisé par une architecture que l'on associe a l'entité qui décrit l'aspect extérieur. Une architecture porte un nom, ce qui autorise la création de plusieurs architectures différentes pour la même déclaration d'entité. Définition de l'architecture :
Une définition d'architecture commence par un en-tête où son précisés le nom de l'architecture et celui de l'entité dont elle décrit le comportement. L'architecture est divisée en deux parties : une zone déclarative, placée entre un en-tête et le mot-clé BEGIN, et une zone d'instruction comprise entre les mots clés BEGIN et END [3].
1. Description structurelle
Souvent ce mode de description est utilisé au niveau le plus élevé de la hiérarchie, chaque composant étant lui-même défini par un programme VHDL (entité et architecture).
2. Description comportementale
Une description comportementale (behavioral) se présente comme des blocs d'algorithmes séquentiels exécutés par des processus indépendants. Elle peut traduire un fonctionnement séquentiel ou combinatoire du circuit modélisé.
3. La description flot de données (fonctionnelle)
Ce mode de description permet de reproduire l'architecture logique en décrivant la fonction du circuit par des équations booléennes.
La syntaxe générale d'une architecture comporte une partie de déclaration et un corps de programme :
|
ARCHITECTURE Nom de l'architecture OF Nom de l'entité IS Zone de déclaration. BEGIN Description de la structure logique. |
Le nom de l'architecture est arbitraire, mais il est important d'en donner un, car pour une même entité plusieurs modélisations sont possibles. Ainsi, à une entité peuvent appartenir plusieurs architectures. Architecture of et is sont des mots clés du langage VHDL. Noter aussi qu'il est nécessaire de spécifier à quelle entité se réfère notre architecture.
· La partie déclarative contient la déclaration des sous éléments, les signaux internes et les constantes nécessaires pour la description du circuit.
· Le mot clé Begin indique le début de la partie de la description.
· Tout comme pour l'énoncé entity, end signale la fin de la description de l'architecture. Il est Optionnel de placer à la suite de l'end le nom de l'architecture, mais on le fait pour avoir un code plus facile à maintenir.
Exemple : architecture du multiplexeur (figure I.) définit le fonctionnement interne du multiplexeur
Architecture arch_multiplexeur of multiplexeur is
Begin
S<= a when (sel='0') else
b when ( sel ='1')else
`0';
End arch_multiplexeur ;
Pour sel=0, la sortie s vaut l'entrée a et pour sel=1, elle vaut l'entrée b.
Les instructions qui décrivent une architecture sont des processus indépendants, qui communiquent entre eux par les signaux.
Les principales instructions concurrentes sont : + les affectations concurrentes des signaux, + les « processus >
+ les instructions « generate >
1) Affectations concurrentes de signaux
a) Affectation simple
L'instruction concurrente la plus élémentaire, du point de vue syntaxique, est l'affectation d'une valeur a un signal.
Le symbole réservé a l'affectation a un signal est «<= », par exemple un simple opérateur « OU » s'écrit de la manière suivante :
S <= E1 OR E2 ;
Dans notre exemple : multiplexeur 2 voies vers 1 :
S<= (not (sel) and a) or (sel and b);
b) Affectation conditionnelle du type »WHEN condition ELSE »
Cette instruction permet d'affecter un signal a une expression (expression = signal, équation ou valeur) pour certaines conditions (conditions sur les signaux de type IN ou INOUT).
|
S <= Source_1 when condition_1 else Source_2 when condition_2 else ... `0' when others; |
Exemple (multiplexeur):
S<= a when (sel='0') else
b when (sel='1')else
`0' when others;
c) Affectation sélective de type « WHITH signal SELECT » :
Cette instruction est semblable à la précédente avec en plus une précision préalable du signal sur lequel vont se porter les conditions.
Syntaxe
With expression select
Cible <= source_1 when valeur_1
Source_2 when valeur_2 ..., ... source_n when others ;
A partir de l'exemple du multiplexeur: With sel select:
S<=a when `0',
b when `1',
`0'when others;
2) Processus
L'instruction concurrente de base en VHDL est le processus (process). Tout modèle VHDL peut se décrire de manière équivalente comme un ensemble de processus communiquant par l'intermédiaire de signaux. Un processus encapsule une séquence d'instructions exécutées dans un ordre donné. L'exécution des instructions d'un processus est conditionnée par des événements (event) sur des signaux.
|
Nom : process (liste de sensibilité) Partie déclarative : variables begin Corps du processus. Instructions séquentielles End process [Non] ; |
Notons que la déclaration d'un process débute par le mot clé «process», suivie d'une liste de noms de signaux. Cette liste est appelée «liste de sensibilité», elle contient le nom des signaux, Cette liste peut être remplacée par une instruction « wait » dans le corps du processus.
Lorsqu'il y a plusieurs processus dans la même architecture, il est utile de leur donner un nom
. L'instruction wait
Cette instruction indique au processus que son déroulement doit être suspendu dans l'attente d'un événement sur un signal (un signal change de valeur), et tant qu'une condition n'est pas réalisée.
Sa syntaxe générale est :
wait [on liste_de_signaux ] [until condition ] ;
La liste des signaux dont l'instruction attend le changement de valeur joue exactement le même rôle que la liste de sensibilité du processus, mais l'instruction wait ne peut pas être utilisée en même temps qu'une liste de sensibilité. La tendance, pour les évolutions futures du langage, semble être à la suppression des listes de sensibilités, pour n'utiliser que les instructions d'attente.
L'instruction concurrente generate permet de dupliquer des instructions concurrentes de manière itérative ou conditionnelle.
Syntaxe
|
Nom : for variable in debut to fin generate Instructions concurrentes End generate [Nom] ; ou Nom : if condition generate Instructions concurrentes End generate [Nom] ; |
Comme tout langage de programmation, VHDL possède des instructions séquentielles de contrôle. Elles sont au coeur des descriptions comportementales des circuits plus que jamais, dans ce type de description, il est essentiel de toujours avoir présente a l'esprit l'architecture du circuit que l'on décrit : ses signaux d'horloge, ses registres, ses blocs combinatoire.
Les principales instructions séquentielles sont :
L'affectation séquentielle d'un signal, qui utilise l'opérateur « <= ~, a une syntaxe qui est identique a celle de l'affectation concurrente simple. Seule la place, dans ou hors d'un module de programme séquentiel, distingue les deux types d'affectation ; cette différence, qui peut sembler mineure, cache des comportements différents : alors que les affectations concurrentes peuvent être écrites dans un ordre quelconque, pour leurs correspondantes séquentielles, rarement utilisées hors d'une structure de contrôle, l'ordre d'écriture n'est pas indifférent.
· L'affectation d'une variable, qui utilise l'opérateur « := > est toujours une instruction séquentielle.
· Les tests << if > et << case >.
· Les instructions de contrôle des boucles << loop >, << for >.
1) Les instructions de test
Les instructions de test permettent de sélectionner une ou des instructions à exécuter, en fonction des valeurs prises par une ou des expressions. On notera que, dans un processus, si toutes les branches possibles des tests ne sont pas explicitées, une cellule mémoire est générée pour chaque affectation de signal.
2) L'instruction « if....then....else....end if » :
L'instruction if permet de sélectionner une ou des instructions a exécuter, en fonction des valeurs prises par une ou des conditions.
Syntaxe :
If expression_1 then
Instructions séquentielles [Elsif expression_2 then]
Instructions_séquentielles [else] Instructions_séquentielles; End if ;
3) L'instruction « case....when....end case >>
L'instruction case permet de sélectionner une ou des instructions a exécuter, en fonction des valeurs prises par une expression.
Syntaxe :
|
||
Il faut toujours mettre un « when others ». Cela permet de couvrir tous les cas de figure, et donc de ne pas avoir des états indéterminés.
Exemple du multiplexeur (fig I.2)
Case sel is When `0' =>
S<= a;
When `1' =>
S<= b;
End case;
4) Boucle « for »
Les boucles permettent de répéter une séquence d'instructions. Syntaxe : FOR parametre IN intervalle LOOP
Instructions séquentielles ;
END LOOP ;
Les différentes étapes de la conception d'un circuit intégré sont illustrées par le diagramme de la figure I.3
L'ensemble du processus qui permet de passer de la vision fonctionnelle au circuit constitue la synthèse.
Le premier outil utilisé dans les étapes de synthèse automatique est un éditeur de texte avec lequel on décrit le comportement du circuit logique en langage VHDL. Ensuite, la description VHDL est traduite par l'outil de synthèse. Cette étape est très importante, il s'agit de convertir la description de haut niveau (VHDL) en fonction logique. Le synthétiseur génère en sortie une liste d'interconnexion de composants logiques de base existant dans la technologie cible choisie. Finalement l'intégration physique dr descrription est effectuée dans le circuit programmable.
Nous spécifions trois étapes de simulation soit : > Simulation VHDL.
> Simulation fonctionnelle.
> Simulation temporelle.
La simulation VHDL est rapidement réalisée car elle ne nécessite par de synthèse de la description. Elle sera toujours exécutée. Cette simulation est très utile si le fonctionnement de la description VHDL n'est pas modifié par l'étape de synthèse. L'objectif principal de cette simulation est de donner au lecteur la maitrise de cette description en vue de la synthèse automatique.
La simulation a été effectuée avec le logiciel ModelSim de la société Model Technology. L'utilisation d'un autre simulateur ne pose pas de problème particulier si celui-ci supporte la norme VHDL-93 et dispose des paquetages Std_Logic_1164 et Numeric_Std.
Finalement, il sera nécessaire d'exécuter une simulation après synthèse. La simulation fonctionnelle ne sera pas réalisée. Nous ferons uniquement la simulation temporelle qui utilise le résultat après placement et routage .Cela nous permettra de valider que toute la chaine s'est correctement déroulée. [6]

Technologie cible
Simulation VHDL
(MODELSIM )
Vision fonctionnelle
Description
(Modèle structurel)
Traduction (Modèle VHDL)
Circuit cible
Compilateur
Simulation
Simulation fonctionnelle
Figure : I.3- Flot de conception basé sur VHDL
ModelSim est un environnement de simulation de description de circuits numériques. Il intègre un gestionnaire de projet, un éditeur de texte et un visualiseur de chronogrammes qui permet de visualiser le résultat de simulation. Le coeur du logiciel, le simulateur logique, consomme une description VHDL multi-fichiers et un vecteur de test. Il produit un résultat de simulation qui est automatiquement affiché à l'écran par le visualiseur de chronogrammes. [7]
+ Les étapes de la simulation sous ModelSim sont les suivantes : o Créer et configurer un projet ;
o Compiler le projet ;
o Lancer le simulateur et construire le vecteur de test ; o Simuler ;
o Visualiser et analyser les résultats.
L'environnement de simulation ModelSim est composé de 4 zones (fig. I.4) :

> la zone des barres de menus et d'outils qui rassemble toutes les commandes du logiciel ; > le gestionnaire de projet ;
> la fenêtre d'édition/visualisation qui permet d'éditer les vecteurs de test et de visualiser les chronogrammes de simulation ;
> la console qui renvoie des informations sur le déroulement de la compilation ou de la simulation
4
5
2
3
3- Console
4- Barre d'outils
5- Barre de menus
1
Voici un aperçu de la barre d'outils de ModelSim :

Les FPGA, sigle anglais qui signifie « Field Programmable Gates Arrays » traduit en français par réseau de portes programmables, sont des circuits intégrés reprogrammables. Ils offrent la possibilité de réaliser des fonctions numériques plus ou moins complexes.
Un circuit FPGA contient un très grand nombre de macro cellules avec une très grande souplesse d'interconnexion entre eux. Dans le FPGA, le temps de propagation dans les couches logiques du circuit dépend de l'organisation et de la distance entre les macros cellules interconnectées (InterConnect resources).

La structure du FPGA présentée sur la figure I.5 est composée [9] : a. cellules d'entrées sorties
Qui servent d'interfaces entre les broches du circuit et le coeur du FPGA pour adapter les signaux suivants
· Alimentation
· Signaux d'horloge
· Signaux de configuration du FPGA
· Signaux de test
Contenant les fonctions logiques combinatoires et séquentielles.
· La partie combinatoire permet de réaliser des fonctions de complexité moyenne avec des portes classiques ET, OU et NON de deux à une dizaine d'entrées.
· La partie séquentielle comporte une ou deux bascules généralement de type D. Compte tenu du nombre d'éléments logiques et de leur structure, leur association permet de réaliser tous les types de bascules. L'intérêt est de créer des mémoires élémentaires à un bit.
Ces réseaux relient entre eux les blocs logiques et les blocs d'entrées/sorties. Ces connections peuvent directement relier :
· Des éléments internes dans un bloc grâce à un système de tables logiques appelées LUT. C'est une matrice de connections où les points de routage déterminent le niveau des entrées soit haut soit bas des portes logiques.
· Des éléments proches : on parle de liaisons directes entre les blocs.
· Plusieurs blocs présents sur toute la surface : on parle de liaisons à distance ou générales. [8]
Le langage de description de fonctions logiques, VHDL est un outil indispensable pour la conception des circuits intégrés spécifiques. Il conduit à la synthèse automatique d'une description VHDL d'un circuit en un schéma logique intégrable dans un ASIC ou un FPGA.
I.9. Introduction
Dans ce chapitre nous allons présenter les filtres numériques, leurs types, caractéristiques et structures. On développera d'avantage les filtres numériques a réponse impulsionnelle finie (RIF), les différent paramètre et fonctions de ces filtres seront présentés ainsi que les structures que peuvent avoir lors de leur construction. La synthèse de ces filtres dans des composants numériques va être démontrée pour introduire leur conception dans les FPGA.
I.10. Définition du filtre
Dans sa définition la plus générale, un filtre peut être défini comme tout procédé qui altère la nature d'un signal d'une façon ou d'une autre.
Les filtres sont utilisés dans tous les média et sont une composante essentielle de toute chaîne de communication. Ils constituent la base d'une discipline d'ingénierie, le traitement du signal, qui s'applique à des signaux de tout type (sons, images, vidéo, vibrations sismiques, ...)
I.11. Les différents types de filtres
On peut classer les filtres à partir de la forme de leur fonction de transfert ou par le comportement des éléments qui composent le filtre. Les filtres les plus courants sont de l'un des quatre types suivants : passe-bas, passe-haut, passe-bande et coupe-bande. Sur la figure suivante, ces quatre types de filtres sont représentés par leur réponse en fréquence ou spectre d'amplitude. [9]

Figure II.1- les différents types de filtre
> Un filtre passe-bas ne laisse passer que les fréquences au-dessous de sa fréquence de coupure. C'est un atténuateur d'aigües pour un signal audio. On pourrait l'appeler coupehaut.
> Un filtre passe-haut ne laisse passer que les fréquences au-dessus d'une fréquence déterminée, appelée fréquence de coupure. Il atténue les autres (basses fréquences). Autrement dit, il « laisse passer ce qui est haut ». C'est un atténuateur de graves pour un signal audio. On pourrait aussi l'appeler coupe-bas.
> Un filtre passe-bande ne laisse passer qu'une certaine bande de fréquences (et atténue tout ce qui est au-dessus ou en dessous). Il est très utilisé dans les récepteurs radio, TV... pour isoler le signal que l'on désire capter.
> Un filtre coupe-bande est le complémentaire du passe-bande. Il atténue une plage de fréquences. Cela peut être utile pour diminuer certains parasites par exemple.
I.12. Les filtres numériques
En électronique, un filtre numérique est un élément qui effectue un filtrage à l'aide d'une succession d'opérations mathématiques sur un signal discret. C'est-à-dire qu'il modifie le contenu spectral du signal d'entrée en atténuant ou éliminant certaines composantes spectrales non désirées. Contrairement aux filtres analogiques, qui sont réalisés à l'aide d'un agencement de composantes physiques (résistance, condensateur, inductance, transistor , etc.), les filtres numériques sont réalisés soit par des circuits intégrés dédiés, des processeurs programmables (FPGA, microprocesseur, DSP, microcontrôleur, etc.), soit par logiciel dans un ordinateur.
Le filtrage numérique est une technique essentielle pour le traitement du signal, et les domaines d'application sont chaque jour plus nombreux (télécommunication, musique, radar, traitement d'image ... )[10]
Donc, un filtre numérique H est un algorithme de calcul par lequel une séquence de nombres ,x(n)-, dite séquence d'entrée, est transformée en une autre séquence de nombres {y(n)}, dite la séquence de sortie, Il est invariant dans le temps si la suite x (n - n0) est convertie en la suite y (n - n0) quel que soit n0 entier. Où : [11]
|
(II.1) |
Pour cela, l'unité de calcul est munie des opérateurs : :[12] Addition, Multiplication, Retard. (Figure II.2)
|
Filtre H |
Y(n) |
Figure II.2 Un filtre numérique
+
|
) |
|||||
|
Y(n) |
|||||

Y (n) = Xi(n) + Xz(n)
)

)
A
)
) = A. X(n)
|
) |
R |
Y(n) ) = X(n - 1) |
||||
Figure II.3- les opérateurs dont dispose l'unité de calcul et leur symbole La relation entre la sortie et l'entrée s'écrit :
Dans le domaine temporel :

(II.2)
C'est le produit de convolution numérique .on peut écrit :
|
(II3) |
Dans le domaine fréquentiel:
|
(II.4) |
Notre étude sera limitée aux filtres possédant les trois propriétés suivantes :
> Linéarité.
> Invariance temporelle.
> Causalité.
a. Linéarité

Soient les séquences de sortie correspondant a deux séquences d'entrée
et . Le filtre h est linéaire si a la séquence d'entée :

(II.5)
Il fait correspondre la séquence de sortie : (II.6)
b. Invariance temporelle


est la séquence de sortie correspondant à la séquence d'entrée . Le filtre h est
invariant dans le temps, si la séquence , séquence retardée de k périodes



|
(II.8) |
d'horloge, il fait correspondre la séquence de sortie . [11]
c. Principe de causalité
Le filtre de réponse impulsionnelle h(n) est causal quant la sortie y(n) reste nulle tant que l'entrée x(n) est nulle (système linéaire invariant dans le temps est causal si et seulement si sa sortie pour tout l'instant n ,y(n)-, dépend uniquement du présent et du passé de l'entrée,x(n),x(n-1)...-. [11]
Etant donné la relation (II.7), la réponse impulsionnelle satisfait alors la condition suivante :

(II.7)
Un filtre numérique peut être caractérisé par :


Si l'entrée d'un système est l'impulsion la sortie est appelée répense impilsionnelle
du système Mathématiquement, cette impulsion est modélisée par une impulsion de
Dirac.
Un système linéaire et invariant dans le temps (LTI) est stable si à toute entrée d'amplitude bornée correspond une sortie bornée. Une condition nécessaire et suffisante de stabilité est donnée par l'inégalité :
|
X(n) |
+1 si h(n) =0

-1 si h(n) <0
Il convient alors pour n = 0 : (II.9)
Si l'inégalité (II.8) n'est pas vérifiée, y (0) n'est pas bornée et le système n'est pas stable.[11]
Un filtre analogique peut être défini par une équation différentielle, de même manière un filtre numérique est défini par une équation de récurrence ou de différence (algorithme permettant de calculer la sortie y(n)). D'une façon générale, l'algorithme d'un filtre numérique d'ordre N linéaire causal a une relation de récurrence du type :
|
(II.10) |

Donc :

(II.11)
Avec b(0)=1, nous obtenons :
|
(II.12) |

· sont des coefficients dépendant du type de filtre numérique réalisé.
· représente l'échantillon de l'entrée.
· représente l'échantillon de la sortie.
Les filtres numériques travaillent avec des suites de nombres. A partir d'une suite d'entrée x(n) ils délivrent une suite de sortie y(n) .A chacune de ces suites on peut associer une transformée en z et nous montrerons qu'il existe une fonction de transfert H(z), donc, un filtre est caractérisé par sa fonction de transfert en Z, désignée généralement par H (z), et qui fait intervenir les coefficients par l'équation suivante : [12]
(II.13)
|
(II.14) |
? transformée en Z
A l'image de la Transformée de Laplace en analogique de variable p, il existe aussi une transformée en numérique appelée Transformée en Z de variable z
Soit une séquence x(n) de nombre réels.la transformée en z ,Xz(Z) ,de la séquence x(n) est définie comme suit :
|
(II.15) |
Donc :

Et :

(II.16)
(II.17)

En appliquant la transformation en Z aux deux membres de l'équation (II.12), et en désignant par et les transformés des suites y (n) et x (n), on obtient :
|
(II.18) |
|||
|
Donc la fonction de transfert H(Z) : |
|||
|
(II.20) |
|||
Avec :

(II.21)
|
(II.22) |
Cette fonction de transfert peut encore se mettre sous la forme :

Le terme est un facteur d'échelle qui définit le gain du filtre. La condition de stabilité

du filtre s'exprime très simplement par la contrainte suivante : tous les pôles doivent

être a l'intérieur du cercle unité. La position des pôles et des zéros par rapport au cercle
unité, permet une appréciation très simple et très utilisée des caractéristiques du filtre.
Pour obtenir la réponse en fréquence du filtre, il suffit de remplacer dans H (Z) la variable Z par l'expression suivante oü f désigne la variable fréquence et T la période d'échantillonnage des signaux :
|
(II.23) |
Le fonctionnement de base d'un filtre numérique est relativement simple. On distingue en fait deux types de fonctionnement, illustrés sur les figures ci-dessous :

Délai
Entrée
Sortie
Figure II.4- principe d'un filtre non-récursif
On retarde légèrement une copie du signal d'entrée (d'une ou plusieurs périodes d'échantillonnage) et on combine le signal d'entrée retardé avec le nouveau signal d'entrée. Les filtres numériques basés sur ce fonctionnement sont dit à "RIF - Réponse Impulsionnelle Finie" ou FIR (pour Finite-Impulse-Response). On les qualifie également de filtres nonrécursifs.
Délai


Entrée
Sortie
Figure II.5- principe d'un filtre récursif
On retarde une copie du signal de sortie que l'on combine au nouveau signal d'entrée. Les filtres numériques basés sur ce fonctionnement sont dit à "réponse impulsionnelle infinie" ou IIR (pour Infinite Impulse Response). On les qualifie également de filtres récursifs
Les filtres numériques à réponse impulsionnelle finie (RIF) sont des systèmes linéaires discrets invariants dans le temps définis par une équation selon laquelle un nombre de sortie, représentant un échantillon du signal filtré, est obtenu par sommation pondérée d'un ensemble fini de nombres d'entrée, représentant les échantillons du signal a filtrer. Les coefficients de la sommation pondérée constituent la réponse impulsionnelle du filtre et un ensemble fini d'entre eux seulement prennent des valeurs non nulles. Ce filtre est du type « a mémoire finie ~, c'est-à-dire qu'il détermine sa sortie en fonction d'informations d'entrée d'ancienneté limitée. Il est fréquemment désigné par filtre non récursif, en raison de sa structure, car il ne nécessite pas de boucle de réaction dans sa réalisation, comme c'est le cas pour une autre catégorie de filtres, celle des filtres à réponse impulsionnelle infinie. [13]
A partir de l'équation de forme générale (l'équation II.10 ) , les coefficients b(k) sont tous égaux a zéro pour k=1 donc pour les filtres a réponse impulsionnelle finie, l'équation (II. ) vérifie :

(II.24)
La suite d'entrée et la suite de sortie sont reliées par une équation du type
suivant qui constitue la relation de définition :
|
(II.25) |
Le filtre ainsi défini comporte un nombre N fini de coefficients ak ; considéré comme un système discret, il a pour réponse à la suite unitaire, la suite h( k ) tel que :
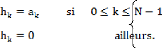
C'est-à-dire que la réponse impulsionnelle est simplement la suite des coefficients.
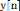
À partir de la transformée en z de l'équation (II.25), on déduit aisément la fonction de transfert du filtre, c'est-à-dire le rapport entre la transformée en z de la sortie et celle
|
de l'entrée |
||
|
(II.26) |
||
Donc :
|
(II.27) |
Elle ne présente pas de pôle mais seulement des zéros, le filtre RIF sera par conséquent toujours stable.
|
(II.28) |
Avec :
|
(II.29) |
L'équation représentée la réponse fréquentielle de filtre. Avec Les coefficients
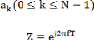
Constituent le développement en série de Fourier de cette fonction Ainsi,
pour la transformée en Z de la suite x(n) coïncide avec sa transformée de Fourier.
C'est-à-dire que l'analyse d'un filtre numérique se faire avec la transformée en Z et, pour connaître la réponse en fréquence, il suffit de remplacer Z par .
La somme de convolution peut être utilisée, en principe, pour mettre en application un filtre numérique avec une réponse impulsionnelle connue, et la réalisation comporte l'addition, la multiplication et le retard, qui sont des opérations basiques. Pour un système LTI avec une réponse impulsionnelle finie (RIF), la relation d'entrée-sortie implique une somme de produits finie, et une exécution directe basée sur cette équation est tout à fait pratique. [14]
X (n- X (n- X (n-

)
a 1 a 2 a3 a
Y(n)
Figure II.6 - Structure directe
Cette structure nécessite N-1 cases mémoire et a une complexité de calcul de N multiplications et N- 1 additions par échantillons de sortie.
La transposition de la structure de forme directe est présentée sur la figure II.7

Y( )
a
a
a
a
X(n)
Figure II.7- Structure transposée
L'implantation d'un filtre numérique dont le comportement est décrit par l'équation aux différences (II.25) se fait en implantant les éléments de calculs décrits par cette équation. Pour ce faire nous avons besoin d'une chaîne de N-1 registres qui permetent de conserver en mémoire les N-1 valeurs de x(n) précédent à l'instant courant n. Cela est réalisé a l'aide d'une cascade de case mémoire (figure II.8. a).
|
) |
(a) Chaîne de retards

X (n- X (n- X (n-
)
a
a 0 a
(b) Produit terme à terme

)
a 0 a 1 a 2 a
X (ni) X (n-2) X (n-N+1)
Y(n)

(c) Somme des produit terme à
terme
Figure II.8 - Étape de réalisation d'un
filtre à réponse impulsionnelle finie
Chaque case mémoire est représentée par un symbole qui est la transformée en Z
d'un filtre ayant comme réponse impulsionnelle ä (n-1) c'est a dire un filtre correspondant a un retard pur d'une période d'échantillonnage.

Il faut ensuite réaliser le produit scalaire entre la suite de coefficients et la suite de

donnée contenue dans la chaîne de retards x(n). Cela
se fait en deux étapes, on effectue les
produits terme à terme
entre la suite de coefficients et la suite de donnée : pour
échantillon x*n+ en entrée, l'ensemble de ces opérations est réalisé afin de fournir un nouvel échantillon y[n] en sortie.
Il est également possible d'établir d'autres structures pour simplifier le calcul et minimiser sa durée en limitant le nombre d'opérations.
Les filtres FIR sont souvent caractérisés par une
phase linéaire, propriété qui se traduit
par une
symétrie ou une antisymétrie des coefficients qu'il est possible
d'exploiter pour
réduire le coût en nombre d'opérations.
Cette propriété s'exprime par :
Le produit de convolution
s'écrit alors dans le cas d'un nombre

pair :
|
(II.32) |
Ce qui conduit à la structure représentée ci-dessous (figure II.8) :

X(n)
a
~
a
~
a ~ 2
Y(n) Figure II.9- Structure symétrique pour un nombre pair de coefficients.



Cette implantation nécessite toujours cases mémoire mais la complexité de calcul est réduite à multiplications et N additions. De plus la longueur du chemin critique est

divisée par 2. Le gain est donc proportionnel à la longueur du filtre qui est souvent importante dans le cas des filtres FIR.
Comme dans le cas de filtre analogique, soit la réponse en amplitude ou la réponse de phase (retard) qui est spécifiée pour la conception d'un filtre numérique. Dans la plupart des applications pratiques, le problème est le développement d'une approximation réalisable selon les spécifications données de la réponse en amplitude.
Il y a quatre types de base de filtres idéaux, dont les réponses en amplitude sont montrées dans la figure II.10. Comme la réponse impulsionnelle correspondante à chacun de ces filtres idéaux est non-causale et de longueur infinie, ces filtres ne sont pas réalisables. Dans la pratique, les caractéristiques de la réponse en amplitude d'un filtre numérique dans la bande passante et dans la bande de coupure (atténuée) sont données avec quelques tolérances acceptables. En outre, une bande de transition est spécifiée entre la bande passante et la bande de coupure [10]
Il y a quatre types de base de filtres idéaux dont les réponses impulsionnelles sont: (a) Filtre passe-bas :
sin ? sin ? ?
? n ? n
|
(II.34) |
|||||
|
|
|
|
||
(II.36)
(g) Filtre coupe-bande :

|
(II.37) |
Et leurs réponses en amplitude sont montrées dans la figure II.9 :

)
1
~
~ 0
)
1

d

-- -- -
-- ~ 0
b)
)
1


c ~

|
1 ~ |
||||
|
~ ~ |
(c
Figure II.10 : Les réponses en amplitude des filtres idéaux
~
)

Par exemple, la réponse en amplitude = d'un filtre numérique passe-

Figure II.11 : Caractéristiques typiques d'amplitude pour un filtre passe-bas numérique
bas peut être donnée par le gabarit illustré dans la figure II.11. Comme il est indiqué dans la figure II.11 :


- Dans la bande passante, définie pour , on a besoin que avec

une erreur c'est-à-dire :


(II. 38)
- Dans la bande de coupure, définie pour , on exige avec une

erreur c'est-à-dire :

(II.39)
Avec :
· : la fréquence maximale de la bande passante.
· : la fréquence minimale de la bande de coupure.
· : l'amplitude maximale des ondulations dans la bande passante.
· : l'amplitude maximale des ondulations dans la bande de coupure.
La réponse en fréquence est une fonction périodique de , et la réponse en
amplitude d'un filtre numérique à coefficients réels est une fonction paire de . En
conséquence, les caractéristiques de filtre sont données uniquement à l'intervalle
Les calculateurs réalisant les filtres numériques sont généralement : > Des microprocesseurs;
> Des microcontrôleurs;
> Des DSP (Digital Signal Processor).
Les DSP sont des processeurs spécialisés dans le traitement des signaux. Ils possèdent des instructions spécifiques (FFT, multiplication, ...) intégrées qui s'exécute dans un temps très court (quelques cycles d'horloges).
L'ensemble des coefficients du filtre numérique est stocké dans la mémoire de ces composants.
La présentation faite dans ce chapitre nous donne un large aperçu sur les filtres numérique notamment les filtres à réponse impulsionnelle fini (RIF), aussi cela nous a permis de mettre en avant les différents structure de ces filtre, ainsi qu'un aperçu sur leur implémentation physique.
Parce que L'objectif de notre projet est la conception d'un filtre FIR, nous avons introduit dans les chapitres précédents une étude générale sur ces filtres, ainsi que les moyens mis en oeuvre pour l'aboutissement de notre travaille.
Dans ce chapitre nous allons présenter les solutions adoptées pour répondre aux objectifs de ce mémoire, nous exposerons dans les paragraphes suivants la conception détaillée de chaque étape de développement. Nous présenterons alors, les différentes techniques de programmation que nous avons utilisées pour réaliser le filtre que selon plusieurs configurations. Aussi nous détaillerons les testes et simulations à chaque étape pour valider notre travaille.
Nous utiliserons dans cette démarche le logiciel ModelSim SE 6.3f pour la simulation comportementale, et ISE Xilinx 8.1 pour la synthèse et l'implémentation.
Pour développer toute application à l'aide de ModelSim, il faut suivre la démarche cidessous :
v' Créer un projet ModelSim ;
v' Créer des fichiers d'édition pour écrire la description du circuit ; v' Compiler les fichiers et corriger les erreurs ;
v' Créer des testbenchs si nécessaire (les compilés et les vérifiés) ;
v' Lancer la simulation à partir du fichier principal sinon du testbench ;
v' Dans la fenêtre du visualiser, il faut ajouter les signaux pour affichage ;
+ Si aucun testbench n'est réalisé, il faut donner à chaque entrée du circuit les
stimuli appropriés ;
1' Exécuter la simulation pour le temps nécessaire à la vérification.
Selon la topologie utilisée du Filtre FIR, nous pouvons réaliser plusieurs descriptions, dans les paragraphes suivants nous exposerons certaines d'entre elles.
La structure commune d'un filtre numérique RIF est constituée généralement des éléments suivants :
· Un ou plusieurs organes de retard (se sont des registres à décalage ou des mémoires temporelles pilotés par une horloge) correspondant à une sortie égale à l'entrée retardée de k périodes d'échantillonnage.
· Des registres fournissent les coefficients du filtre.
· Des opérateurs arithmétiques (additionneurs et multiplieurs).
Pour accélérer le temps de conception, on peut utiliser des fonctions spécifiques de la bibliothèque du logiciel de simulation ModelSim, comme l'addition, la multiplication qui permettent de faire ces opérations pendant un cycle d'horloge. La sortie y[n] est la somme de l'échantillon d'entrée présent x[n] multiplié par le coefficient a0 et de l'échantillon précédent
x[n-1] multiplié par le coefficient a1 et tous les échantillons d'entrée précedents jusqu'au temps [n-N+1] multipliés par leur facteur respectif. (Figure III.1).
Entrée x(n)
a0 a1 a2 a3 a4
Reg
Reg
Reg
Reg
aN+1
Reg
La sortie y(n)
Figure III.1 : structure général d'un filtre RIF
La structure d'un filtre RIF du 1ére ordre est illustrée dans la figure III.2 avec k la largeur de bus d'entrée et de la sortie mais aussi celui des coefficients, ce filtre est composé de deux coefficients et un élément mémoire (figure III.2).
Xin(n)[k]
Process
CLK
X_int[k]
[k] [k]
Yout(n) [k]
[2*k]
Reg_0[2*k]
Regy[2*k+1]
DIV
Figure III.2 : bloc digramme d'un filtre RIF 1 ère La sortie de ce type de filtre est donnée par :
Y'n)=a0x(n) +a1x (n-1)
Le 1ére échantillon xin multiplier par le coefficient a0 donne un bus de largeur [2*k], la propagation de l'entré sur le registre permet de temporiser l'entrée x(n) se qui permet de créer la valeur x(n-1) soit xint (figure III.2). Cette valeur est multipliée par a1 ce qui donne un bus de méme largeur comme l'opération précédente, la somme des deux résultats de multiplication intermédiaire s'exprime en sortie avec des données de largeur [2*k+1], et pour
avoir une sortie avec une largeur [k], il faut diviser la sortie sur [2*k+1] par 2k ou bien supprimer les k dernier bits à droite, tel que :
_
Le programme ci-dessous permet décrit le fonctionnement d'un filtre RIF du premier o
y
ordre.
|
||
Au début du code nous trouvons la déclaration de la bibliothèque, qui contient des définitions des types de signaux et des fonctions arithmétiques. Juste après, la déclaration l'entité est faite pour définir les entrées, les coefficients du filtre et la sortie, L'instruction GENERIC permet de spécifié les paramètres du code, dans notre exemple nous déclarons la
largeur des bus d'entrée/sortie comme générique pour permettre leur modification. L'architecture contient les instructions qui décrivent le fonctionnement du filtre, l'instruction « clk' event and clk ='1' » synchronise l'exécution des instructions sur le front montant, le process permet entre autre la mémorisation de la donnée x(n-1).
La figure suivante montre la structure du code VHDL sous le logiciel Active-HDL 8.1, elle montre la décomposition du code dans ces différentes déclarations.
Figure III.3 : Décomposition fonctionnelle d'un filtre RIF 1 ère ordre sous Active-HDL
On souhaite établir la fonction de transfert H(z) du filtre qui effectue la moyenne glissante sur les 2 derniers échantillons arrivés sur l'entrée.
Son algorithme s'écrit :
avec : a0 = a1 = 0.5
En utilisant la règle de passage au domaine des «z», l'algorithme se transforme en : Y(Z)=0.5 * ( x(z) + x(z) . z-1 )
Ce qui donne la fonction de transfert en z du filtre = 0.5 (1+z-1)
On tirera les réponses en amplitude et en phase :
La réponse fréquentielle sera donc :
Dans un filtre passe bas, la fréquence de coupure est la fréquence où l'amplitude sera diminue par -3db, donc à partir de la figure de la réponse en amplitude (figureIII.4), l'atténuation de 3db correspond à la fréquence de coupure de 2.5 Mhz .
Figure III.4 : Réponse fréquentiel en amplitude
Pour vérifier le bon fonctionnement du filtre, nous allons lui transmettre une série d'échantillon sur x(n), ce test va valider le fonctionnement théorique fait dans les paragraphes précédents, nous allons fournir au filtre une impulsion sur x, est nous devrions avoir une réponse impulsionnelle comme celle décrite dans le tableau suivant.
Tableau III.1 : Réponse impulsionnelle théorique du filtre FIR 1er ordre.
|
|
|
||||
|
|
|
|
|||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
Le résultat de simulation de cet exemple sous le logiciel de simulation ModelSim est représenté sur le chronogramme de la figure suivant.
Figure III.5 Le résultat de la simulation de filtre du1 ère ordre
À l'instant t = 150 ns l'entrée est une impulsion de x='1111' c'est-à-dire la valeur maximal de l'entrée coder sur 4 bits (k=4 x=15) ce qui représente 1 dans le modèle théorique soit x(n) = 1, de ce fait la sortie doit être divisé sur 15 pour avoir les résultats attendus, ceci est réaliser en éliminant les 4 premiers bits à droite (pour éviter d'ajouter un algorithme de division). Alors la valeur résultante sur reg_y doit être justifiée en éliminant les 4 bits de droite.
À 250 ns => x = 15 (1111)b et a0=7 (0111)b Et on à y(n)= a0 * x(n) = 7 * 15 / 16 = 6.5625
Sur le chronogramme de simulation on récupère 6 (0110)b, et en élimine les 0.5625 qui correspond à `1001' en binaire.
Ce filtre permet d'interpoler deux échantillons successifs en calculant leur moyenne. Utile pour augmenter artificiellement la fréquence d'échantillonnage d'un signal en doublant le nombre d'échantillons.
· On constate dans cet exemple que la réponse impulsionnelle est limitée à deux échantillons.
·

Les coefficients d'un filtre non récursif sont donc égaux aux échantillons de sa réponse impulsionnelle.
Tiré de la structure du filtre de 1er ordre, le filtre FIR de 2ème ordre illustré sur la figure III.6 possède trois coefficients et 2 registres de sauvegarde, et pour la description VHDL elle réunit deus process qui assurent la mémorisation des états de l'entrée, en les transmettant d'un process à l'autre pour les multiplier par les coefficients.

x-int1[k]
X_int2[k]
X_in(n)[k]
Process
CLK
Process
CLK
[k]
a [k]
a [k]
Reg_2[2*k]
[2*k+1]
DIV
Reg_y[2*k+2]
Y_out [k]
[2*k]
Reg_1[2*k]
Figure III.6 : bloc digramme d'un filtre FIR 2ème ordre

Figure III.7 : Décomposition fonctionnelle d'un filtre RIF 1 ère ordre sous Active-HDL
Sur la figure III. 7 une reconstitution de la décomposition fonctionnelle du code VHDL faite avec le logiciel Active-HDL, elle permet de bien identifier les grands lignes de notre code et les différents signaux d'interface et ceux utilisé en interne.
Cette reconstitution représente la description VHDL suivante du filtre RIF 2ème ordre.
library ieee;
Use ieee.std_logic _1164.all;
Use ieee.numeric_std.all;
entity FIRFilter is
generic( word_size : integer := 4 );
port( clk : in std_logic;
a_0, a_1, a_2 : in unsigned(word_size-1 downto 0);
x_in : in unsigned(word_size-1 downto 0);
y_out : out unsigned(word_size-1 downto 0)); end entity;
Architecture FIRFilter of FIRFilter is
signal reg_2 : unsigned(2*word_size-1 downto 0):="00000000";
signal reg_ 1 : unsigned(2*word_size-1 downto 0):="00000000";
signal reg y : unsigned(2*word_size-1 downto 0):="00000000";
signal x_int1,x_int2 : unsigned(word_size-1 downto 0):="0000";
begin
process (clk)
begin
x_int1 <= x_in;
end process;
process (clk)
begin
x_int2 <= x_int1;
end process;
reg_y <= (x_in * a_0) + reg_1 + reg_2;
y_out <= reg_y(2*word_size-3 downto word_size-2); end architecture;
On peut tester ce filtre RIF de 2ème comme nous avons testé celui du 1er ordre, et on aura les mêmes résultats et commentaires. Dans ce cas, nous avons testé le filtre décrit avec un signal x(n) périodique de forme triangulaire de période T = 3000ns à l'aide d'un compteur/décompteur tiré des outils intégrées du logiciel de simulation ModelSim. On donne des valeurs codées en 4 bits de 0000 à 1111 et de 1111 à 0000 avec des changements dans quelques états pour simuler le bruit.

Figure III.8 : Résultats de la simulation de filtre du 2ème ordre
Ce filtre est l'extension du filtre de 1er ordre, selon cette configuration il calcule la
moyenne de trois échantillons successifs. La sortie y(n) écrit par :


Avec les coefficients sont égaux = =

Donc se filtre effectue la moyenne glissante sur les 3 derniers échantillons arrivées sur l'entrée x(n) en éliminant les parasites et les valeurs aberrantes, ceci est représenté par l'exemple de simulation de la figure III.8.
a) Structure
Le bloc diagramme suivant représente le principe du filtre FIR 3éme ordres

X_in(n)[k]
[k]
[2*k]
CLK
a1[k]
Reg_1[2*k]
x-int1[k]
CLK CLK
Reg_2[2*k]
a2[k]
X_int2[k]
Reg_y[2*k+2]
Reg_3[2*k]
a3[k]
DIV
Y_out [k]
Process
Figure III.9 : bloc digramme d'un filtre FIR 3ème ordre
Nous avons utilisé la même procédure pour créer ce filtre que celle exploité dans les deux premiers filtres, nous avons utilisé un autre process pour créer le troisième étage.
b) Simulation et Interprétation :
Dans cette partie nous avons utilisé une autre méthode de test et de simulation, pour ainsi valider notre conception.
Nous avons choisi de réaliser la simulation de ce filtre sur logiciel Modelsim avec une entré de type x(n)= cos (n) ou la résolution sera de 8 bits, nous avons besoin dans ce cas de figure de crée un testbench (banc de test) pour accomplir la simulation.
Par définition, un testbench VHDL est un code VHDL destiné à la vérification, par simulation, du bon fonctionnement d'un système, lui-même décrit en VHDL.
Dans notre testbenchs il faut intégrés un générateur d'horloge pour la synchronisation de ces différents composants avec le filtre qu'on veut tester. Les coefficients du filtre seront fixés dans le code du testbench. L'élément le plus important est le générateur de cosinus, il est basé sur une table de 256 valeurs qui représente un quart de période du cosinus.

Filtre RIF
Générateur d'horloge
(CLK)
Générateur de signal
périodique
Compteur
|
ROM |
ROM |
|
Figure III.10 : Bloc diagramme du testbench avec cosinus d'un filtre RIF
Pour générer le cosinus, il suffit de lire cette table via un générateur d'adresse sous forme d'un compteur cadencé par l'horloge. Pour réaliser une période de cosinus en adresse la table 4 fois avec 4 manières différentes :
|
|
|
|
|
||
|
x_in <= -cosrom(512-cont |
Si |
(cont >= 257) and (cont < 513 |
||||
|
|
|
|
|
||
|
xin <= cosrom(1024-cont) |
Si |
(cont >=769) and (cont<1024) |
||||
Pour régler la fréquence du cosinus il suffit de changer le pas du compteur, la fréquence la plus petite équivaut à un pas de comptage de 1. Pour une fréquence plus grande on peut lire la table de cosinus avec un pas de 50, soit 5 valeurs générées par 1/4 de période.
1ère simulation
Avec les paramètres suivants nous avons les résultats de simulation de la figure III.11 :
· Horloge : 1000ns
· Largeur des données : 8 bits
· Pas de comptage : +10
Soit un cosinus d'une fréquence de 10kHz
Figure III.11 : Résultats de la simulation d'un filtre du 3ème ordre avec f=10khz 2ème simulation
Avec les paramètres suivants nous avons les résultats de simulation de la figure III.11 :
· Horloge : 100ns
· Largeur des données : 8 bits
· Pas de comptage : 60
Soit un cosinus d'une fréquence de 500kHz

Figure III.12 : Résultats de la simulation d'un filtre du 3ème ordre avec f=500khz
Le but de cette méthode est d'avoir une description VHDL générique, qui peut être utilisée
avec n'importe quel système, où il suffit simplement de fixer les paramètres génériques lors de l'instanciation de cette entité.
La figure III.13 donne un aperçu de la manière dont le filtre d'ordre N est décomposé pour permettre sont implantation en VHDL. Une mémoire est déclarée pour sauvegarder les N coefficients que le filtre utilise lors de son exécution. Une pile FIFO est l'élément important de cette réalisation, c'est elle qui permet de faire des calculs en boucle ; de multiplication et
d'addition.
Les coefficients X(n)

Reg
Reg
Reg
Reg
MUX
Coeff(N-1)
Coeff(2)
Coff(1)
Ceff(0)
MUX
ACCU
Y(n)
Figure III.13 : Bloc diagramme d'un filtre N ordre
A cause des exigences du langage VHDL ; plusieurs manipulations sur les signaux internes sont effectuées, de ce fait le signal de sortie doit mis en forme pour le rendre compatible avec le reste du système. Par exemple, il faut éliminer les bits en surplus pour avoir les 8 bits utile du filtre.
Pour tester ce filtre nous aurons plusieurs configurations du filtre lui-même et plusieurs configurations des testbenchs. Nous allons utiliser les méthodes déjà validées au cours de ce travail en les adaptant à ce nouveau filtre.
Au cours de ces simulations nous serrons limité à des bus internes de largeur de 32 bits, ceci est restreint pas le logiciel de simulation ModelSim SE 6.3f
1ère simulation
Avec les paramètres suivants nous avons les résultats de simulation de la figure III.14 :
· Horloge : 50 ns
· Nombre de coefficient : 4
· Largeur des données : 8 bits
· Pas de comptage : 10
Soit un cosinus d'une fréquence de 100 khz
Figure III. 14 : Résultats de simulation d'un filtre d'ordre 4 à 8bits
Pour voir un lissage de signal il faut que les coefficients soient égaux avec un nombre petit
par rapport à la valeur maximum de signal traité.
2ème simulation
Avec les paramètres suivants nous avons les résultats de simulation de la figure III.15 :
· Horloge : 100ns
· Nombre de coefficient : 8
· Largeur des données : 4 bits
Soit un signal triangulaire d'une fréquence de 320 khz
Figure III.15 - Résultats de simulation d'un filtre d'ordre 8 à 4bits
Le but de notre projet étant d'implanter un filtre numérique dans un FPGA, nous allons essayer de faire cette étape du travail dans cette section en implantant de dernier filtre RIF qu'on a développé en VHDL ; nous avons choisit comme support d'élaboration les FPGA de type Xilinx Virtex XCV50. Pour cela, il faut travailler avec le logiciel de développement Xilinx ISE 8.1.
Pour accomplir notre projet sous Xilinx ISE il faut suivre les étapes suivantes :
> Créer le projet : nous avons pris les mêmes fichiers VHDL que celui développé en III.3, et nous l'avons adapté à pour qu'il soit compilable sous Xilinx.
> Compilation (compile) : c'est l'étape de vérification de la syntaxe et structure des codes VHDL.
> Synthèse et optimisation : Il s'agit de réaliser le circuit RTL (Registre-Transfert level) avec des primitives technologiques (CLB, blocs RAM, I/O).
> Placement-routage : Le rôle du placement-routage est double. Cibler les différentes primitives existantes dans le FPGA choisit. Et faire les différentes connexions entre les ces primitives.
Pour effectuer toute ces opérations, il faut en premier valider le FPGA avec le quel nous allons travailler, qui est le Virtex XCV50, Le tableau suivant présente les différentes caractéristiques de cette FPGA.
Le filtre étant générique, il faut lui fixé ses paramètres avec les valeurs suivantes
· Nombre de coefficient = 8
· Largeur du bus de données = 4 bits
Tableau III.2 : Les caractéristiques de circuit programmable FPGA (virtex : xcv50)
|
composant |
portes |
CLB |
Cellules |
E/S |
RAM |
Performance |
|
Xcv50 |
57,906 |
16x24 |
1.728 |
180 |
32.768 |
200 Mhz |
L'étape de la synthèse nous donne le schéma logique du filtre RIF qu'on a développé.

Figure III.16 - Schéma RTL équivalent du FIR à xcv50 sous Xilinx ISE 8.1i L'exécution des différentes étapes de synthèse et placement-routage se résume dans le
tableau suivant :
Tableau III.2 : Les caractéristiques de circuit programmable FPGA (virtex : xcv50) qui est utilisée :
|
Utilisation élément logique |
utilisé |
Existant |
pourcentage |
|
Numbers ne bascules |
24 |
1,536 |
1% |
|
LUTs (table de vérité) |
285 |
1,536 |
18% |
|
Distribution logique |
|||
|
Nombre de CLB utilisé |
185 |
768 |
24% |
|
Nombres total de LUTs à 4 entrées |
318 |
1,536 |
20% |
|
Nombres des entrées sorties |
48 |
94 |
51% |
|
Nombres d'horloges |
1 |
4 |
25% |
Le résultat du placement-routage est donné sur la figure suivante :

Figure III.17 - Implantation de filtre RiF sur un circuit FPGA (xcv50)
Dans ce dernier chapitre, nous avons essayé de réaliser un filtre RIF selon les concepts
qu'on a étudié dans le chapitre deux. Nous avons réussi a développé plusieurs filtres, qui varient selon leur architecture, performance et capacité de traitement.
Enfin nous avons développé une description VHDL qui traduit le fonctionnement du filtre RIF avec un ordre quelconque, et une précision de traitement générique ; que l'utilisateur final du code peut choisir suivant ses besoins. Dans la dernière section, nous avons implémenté se filtre RIF sur un FPGA de la famille Xilinx.
Ce travail a comme objectif principal la conception et la simulation des filtres numériques codés en VHDL, spécialement les filtres non-récursifs RIF, ces filtres otn une large utilisation dans le monde du traitement numérique de signal.
Dans un premier temps, nous avons défini le langage de description matériel ; le VHDL. C'est un moyen indispensable pour la conception des systèmes numériques, subordonné par des outils de développement tel que ModelSim et Xilinx ISE. Ils nous ont permis la synthèse automatique des descriptions VHDL écrites en un schéma logique intégrable dans un les circuits programmable, tel que FPGA.
Une application de traitement numérique du signal à savoir le filtrage numérique est exploré en détail. Ceci nous a aidés dans notre démarche de conception d'un filtre nonrécursif (RIF) sur FPGA.
Evidemment, ce travail n'épuise absolument pas le sujet de la conception des filtres numériques, au contraire, nous espérons avoir contribué à la clarification d'un sujet qui a de plus en plus un rôle important dans les systèmes de traitement numérique de signal

:
.
ÉÔSÐãäÇ
í ÊÌ.ÒÈ~á Ê~~~~áÇ Êí~ØìãáÇ Ë14Ç,ÈáÇ Ë~~~Õ~ í.Ú ÊíãÞÒáÇ ÍÔÒãáÇ Êí4ÓÑÇ,Î Ðí~ìÊ
. äÇ.íãáÇ
ÈiåäÇ
ãÓáÇÇ
~ãÍ~
:
:
ÉÏÇÏ å~
íÞ~ÈáÇ .ÈÚ íÍ4ÇÑ : ÔØ ÄãäÇ
ÕÎå.
ãã.äÇ ÇÒ. åq ÖÔÛäÇ
Ê~-ÔÈåä Êå411äÇ Êò~ØäãäÇ Ë1-ÇìÈäÇ Ë~1ìÕ- Êòã~ ÖÔÚ ì4
Ë ~ ò~ÕÓÇì~ ÒòäÊä
áÅ íÏ Ô í ð~ ìåÚ Ï~ãÊÚáÇ~ ~ ÊòããÔäÇ ËÇÓ1ÔÇáÅÇ Ê~ä1~.
. ÉÏæÐ~~ Ê4.NÊÓÇ ËÇÑ ÊòããÔäÇ ËLNÔÇÔãäÇ ð~
íÏ Ô ì~ ÊÛå~ ~å~ìåÓ
Ét~L~A Ú~ ÞÔØ ÉÐÚ Ø~Ó ìåÚ ËLNÔÇÔãäÇ åÒ. ÈSÔ~ 1ääæ1Í øÊÍæÔØáÇ åÒ. áN~
.
áÅ
áÅ
íÏ Ô í ì~
ÉÏæÐ~~ Ê~~~ÊÓÅ ËÇÑ ÍÔÇÇÔ. ðãã ÔäÇ ÍÔÇÔãäÇ : ÊòÍ~Ë~ Ë~ãåS
. äÇÐòãäÇ ði Ê~ ~ ÔÈåä Êå~~~äÇ Êò:ØäãäÇ
Ë14ÇìÈäÇ Ë ~~ìÕ~
Title : Implantation of algorithm digital filter on FPGA
Name Bendada First Name Mohamed Directed by: Mr Rabhi Abdelbaki Abstract
The aim of this work is to present the interest of FPGA circuits that can have to
support implementation of Digital Signal Processing algorithms in VHDL, such as digital filters specially FIR (Finite impulse response).
We tried in this memory to build FIR filters, basing on several methods of implementation, each description VHDL is checked and tested by behavioral simulation.
Key words : VHDL, Digital Filter, FIR, FPGA
Mémoire : Implantation d'algorithme de Filtrage Numérique sur FPGA Nom : Bendada Prénom : Mohamed Encadreur : Mr Rabhi Abdelbaki Résumé :
l'objectif de ce travail est de présenter l'intér~t des circuits FPGA (réseau de
portes programmables) comme un support pour implanter des algorithmes de traitement du signal numérique en VHDL tel que les filtres numériques de type RIF.
Nous avons essayé dans ce mémoire, de construire des filtres FIR, en nous basant sur plusieurs méthodes d'implantation, chaque description VHDL est vérifiée et testée par des simulations comportementales.
Mots clés : ò VHDL, Filtre Numérique, RIF, FPGA.

