Déterminants des investissements directs étrangers en Afrique subsaharienne

4.2 - Choix du modèle

En s'appuyant sur les résultats issu de l'Analyse Factorielle Discriminante (AFD), nous pouvons postuler la formulation linéaire suivante:

IDE/PIB = f [ IDE/PIB(-1), TIF, T_OUV(-1), T_INVEST(-2), T_DEMO(-2), PETROLE(-2) ]

Les déterminants des investissements directs étrangers en Afrique subsaharienne

Il convient à présent de mettre en oeuvre la procédure décrite dans la méthode d'analyse pour choisir le modèle de panel approprié aux données disponibles. Le test de Fisher effectué a fourni une probabilité de dépassement de la Fisher empirique⁶ de l'ordre de 20%. Ce qui est suffisamment élevé pour que l'on puisse rejeter l'hypothèse nulle. Donc, il n'existe pas d'effets spécifiques entre individus. Le modèle retenu est donc celui à effets communs. Par conséquent, la procédure de choix s'arrête à cette étape. Les résultats des régressions qui ont permis de faire le test sont présentés en annexe (A.5).

Compte tenu de ce résultat, nous pouvons écrire :

IDE/PIBit = â₀ + â₁ IDE/PIBit-1 + ^â2 _TIFit + â₃ T_OUVit-1 + â₄ T_INVESTit-2 + â₅ T_DEMOit-2 + ^â6 _PETROLEit-2 + åit

4.3 - Test de stationnarité des variables

Les données de l'étude ayant une dimension temporelle, Il convent avant toute estimation d'étudier leurs caractéristiques stochastiques afin de savoir si elles sont stationnaires (moyennes et variances constantes dans le temps) ou pas. Les applications de ce procédé ne sont pas rependues sur les données en panel comme sur les données uniquement chronologiques. Im, Pesaran et Shin (1997) ont proposé une démarche largement utilisée permettant d'effectuer le test de racine unitaire sur données de panel (IPS) que nous présentons ci-après.

Encadré 7 : Test de racine unitaire sur données de panel proposé par Im, Pesaran et Shin (1997)¹

Im, Pesaran et Shin (1997) proposent un test de racine unitaire pour données de panel (i = 1, ..., N ; t = 1, ..., T). Le test est basé sur la moyenne t des statistiques t_ñ de Dickey-Fuller Amélioré (ADF) calculés

i

statistique du test ADF sur données individuelles (H0 : ñ_i = 1 ).

Les hypothèses du test de Im, Pesaran et Shin (1997) sont : H0 : ñ_i = 1 pour tout i contre H1 : ñ_i < 1 pour au moins un i.

Pour T ? 8 et N ? 8 et sous l'hypothèse nulle le théorème central limite de Lindeberg-Lévy

assure que la statistique t_IPS de Im, Pesaran et Shin suit une loi normale centrée réduite.

Weiner. Im, Pesaran et Shin (1997) assure que les t_iT sont indépendantes et identiquement distribuées de moyenne et de variance finies.

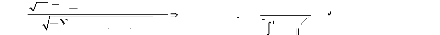
Où 10

t=

W _iz d W i z

0

₂¹2

W

iz

et W ( r )dr est l'intégrale de

iT

V a r

1

N

( t - 1 E t

[ | ñ = 1])

N i = 1 iT i

[ |

t ñ = 1]

iT i

1

N

t IP S = N

N i

=

N ( 0 , 1)

pi

'

y it = E + zitã +åit

j

t = 1 E t

N ñ

i=1

N

sur données individuelles :

i

1

, _ñ est la

t

La mise en oeuvre de ce test à partir des données disponibles montre que (i) le taux d'investissement (IDE/PIB), IDE/PIB(-1) et exportation de pétrole retardée d'ordre 2 sont stationnaires. Le taux d'ouverture retardée d'ordre 1 et les variables retardées d'ordre 2 que sont le taux d'investissement et le taux de croissance démographique sont des marches aléatoires avec dérive. Ce qui signifie qu'elles sont toutes intégrées d'ordre 1. les résultats complets sont présentés dans le tableau 8.

⁶ La statistique du test de Fisher vaut F (22, 569) = 1, 24

VARIABLES	EN NIVEAU				EN DIFFERENCE				CONCLUS ION
	Valeurs du test	Valeurs critiques	Nombre de retards	Avec constante	Valeurs du test	Valeurs critiques	Nombre de retards	Avec constante
		-1,940
IDE/PIB	-2,019	-1,820	2	Oui					I(0)
		-1,750
		-1,940
IDE/PIB(-1)	-2,210	-1,820	2	Oui					I(0)
		-1,750
		-1,940				-1,940
T_OUV(-1)	-1,716	-1,820	2	Oui	-3,145	-1,820	2	Oui	I(1)
		-1,750				-1,750
		-1,940				-1,940
T_INVEST(-2)	-1,818	-1,820	2	Oui	-3,137	-1,820	2	Oui	I(1)
		-1,750				-1,750
		-1,940				-1,940
T_DEMO(-2)	-1,527	-1,820	2	Oui	-2,148	-1,820	2	Oui	I(1)
		-1,750				-1,750
		-1,940
PETROLE(-2)	-2,096	-1,820	2	Oui					I(0)
		-1,750
TIF		-2,652				-2,656
	-0,902	-1,954	1	Non	-4,455	-1,955	1	Non	I(1)
		-1,622				-1,623
NB : Les valeurs critiques	sont rangées par ordre croissant des seuils (1%, 5%, 10%).
I(p) signifie que	la variable est intégrée d'ordre p.
Les valeurs de la variable TIF sont les mêmes pour tous les 23 pays. Donc, nous avons effectué un test Dickey-Fuller Amélioré
(ADF) sur cette variable.
La valeur du test pour IDE/PIB est inférieure aux différentes valeurs critiques (aux différents seuil), donc cette variable est I(0)

Source : Résultats de STATA 7.0

Les résultats (existence de variables intégrées) autorise à postuler le risque de cointégration des variables. Pour se fixer les idées, il convient d'effectuer le test de cointégration sur données de panel proposé par Pedroni P.(1999). Les résultats de ce test seront comparés à ceux du test en deux étapes de Engle et Granger (1987). Pedroni conclut dans son article que les résultats de son test ne sont qu'une extension de la méthode de Engle et Granger aux panels hétérogènes. Ce qui impliquerait que son test suppose l'unicité du vecteur de cointégration. En Toute rigueur, l'on devrait déterminer le nombre de vecteurs de cointégration puisque le nombre de variables non stationnaires est supérieur à 2.

Les résultats du test de Pedroni P. (1999) sont obtenus à partir du logiciel RATS. Les statistiques centrées réduites ont été calculées grâce à la table de moyennes et variances simulées par Pedroni P. (1999) en fonction du nombre de régresseurs. Au seuil de 5%, ces statistiques en valeur absolue sont supérieures à 1,96 sauf le panel t-statistique nonparamétrique (tableau 9). Ce qui nous amène à rejeter l'hypothèse nulle H0 « les variables ne sont pas cointégrées » et donc les variables sont cointégrées. On va de ce fait procéder à l'estimation du modèle à correction d'erreur (MCE).

^à

Ù_i

Encadré 8 : Test de cointégration pour panel hétérogène proposé Pedroni P. (1999)¹

Pedroni P. (1999) propose une série de statistiques basées sur la variance du panel pour tester la

cointégration. Considérons l'équation de long terme

13 +^'zy_it = xitiitã+eit ; ; it est le résidu estimé ete

l'estimateur robuste (comme l'estimateur de Newey-West (1987)) de la matrice de variance-covariance Ù_i de

eit . Soit	à Li la matrice triangulaire inférieure issue de la décomposition de Cholesky de	Ù à i (	L iL i = Ù i ). 2 à à ' à L à i 11 11
- 1 ' E qui est le premier élément de la diagonale s'écrit 2 à 1 - = Ù ? Ù Ù Ù . Soit 2 à 2 2 à à à L i L ó ó ~ = à à 11 11 i 21 22 21 i i i N T , N 11 i i				et et

i=1= 1

ë^à_i = 1 (c'^Ne ) où - _i est la variance empirique et 2

sà_i est la variance empirique corrigée des résidus uà_it de

2

l'autocorrélation eEnfin, la version paramétrique des t-statistiques repose sur les

i , t -1 + t

statistiques de Dickey-Fuller Amélioré (ADF). *

s à_i est la variance corrigée estimée des résidus de ADF et

N

~ =

* 2 ¹ s à * 2

s .Les statistiques de Pedroni P. (1999) sont :

N T

, N i

i1

₌

1

· Panelív --- Statistique :

1_- N NT ^T11 N T2 2 - 2

etet T 2N 31í N , T ,T -- 0 N = (^0,0ö(^'1^'1)y(1)ö(1))).
· Panel ñ - pStatistique :

T NZ

ñ

N

= T N L e

à à

- à ( à

L e Ä -

e à ë à )

, 1

T - 11 , 1

i i t - 11 i i t

, 1

- i t

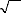
N T

2 3 / 2 2 3 / 2

T N Z í L e

- 2 2

= T N à à

N T

, 11 , 1

i i t ⁱ

= 1

=

t=1
=

-

et T N Z _ñ ZN , T ,- 1--- È ₂ È ₁N N0,ö ( 2 ₍₂₎₍ 2 ) ö( 2 )2)
· Panel t t Statistique (non paramétrique) :

-

N

T -1/ 21N T T

Z t Z2 ² E EN , T,N , T,i , t

1-

EE11 ^-2 i ( ,(Ä eàA_t - ëi)ii = 1 =t=1== 1

=

⁼

t =1

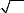
et Z N T ? È ₂ ( È ₁ ®(1 (+ È 3)) ₎1 / 2/N N ( ⁰,0ö(^'(3 3)(3) ö(3 )))

· Panel t t Statistique e aramétrique) :

N

T 1 / 2_N 2_T

Z N , T,s N , T,T E E E11 ² i (ii , i,Ä e^ài ,t,

2

t

i = 1 =t =1 =1 i = 1 ^=t=1=

Cette statistique est de même loi asymptotique que la t t Statistique non paramétrique.e

_- N

T 1 T

· Groupe ñ p Statistique :

TN - 1/ 2 Z2N , T,- 1--1 -- TN -1/ 12 ^2E eà^2i^2. (eà(Ä eàAt - ëi2) t = 1 , t=1=

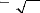
et TN -1 / 2 Z _ñ ZN N T --- È₁ N N( 0,ø₁)_i)

,

· Groupe t t Statistique (non paramétrique) :

1/ ^2/

N - 1/ 2 Z _t ZN , T,= N -1/ 2 12E 2.2eà 2_i 2_.

(eà(Ä eà, _t-_r-- i)t

i= 1 =t = 1 =t=1=

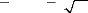
Et N -1 / 2 1Z t N , T,2 N NN ( 0,ø 2)2
· Groupe t t Statistique (paramétrique) :

1/ 2/_N T

N - 1/ 2 Z * _7N -1/ 2 /2E I_si *2 e`à _a*2 *_Ä , t- 1-i = 1 =1 ^It = 1 =t=1= t

Cette statistique est de même loi asymptotique que la -t -- Statistique non paramétrique de groupe

2929

Où ø( _j ), j = 1, 2, 3 est le ^jième élément de la matrice de covariance ø et öj ( ) , j=1, 2, 3 se réfèrent aux

vecteurs

' - 2 ö(1) = -È , ö ' (2) ( 1 - , 2 1 - ) = ? È È È et le 1 2 1

' 1/ 2 1/ 2 1 3/ 2 1/ 2 1 1/ 2

vecteur ö ( - (1 ) - , 3/ 2

= ? È + È ? È È - (1 ) - , 2

+ È ? È È - (1 ) - )

+ È

(3) 1 3 2 2 1 3 2 1 3

Les « groupe statistique » sont calculés à partir du panel formulé en terme de moyenne de groupes (voir Greene W. H. (2003)).

Pedroni P. (1999) a simulé les moments ( È _i et ø_ij i,j = 1, ...,3 ; È_á etø_á á =1,2). Ce qui lui a permis de
tabuler les moyennes et variances de la loi de ses statistiques selon le nombre de régresseurs (variables explicatives non stationnaires) dans la relation de long terme.

Tableau 8 : Résultats du test de Pedroni P. (1999)

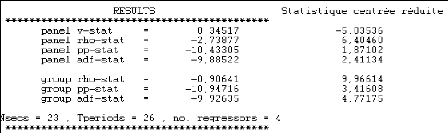
Source : Résultats de RATS 4.30