3.3.3 Other key structural features
CDS tenor choice
Another crucial structural feature of the DPPI is the tenor
investment rule that allows to adapt CDS tenors depending on market spread
levels. Let us call e(S(t), t) the potential tenor of any CDS investment done
on date t, where e is defined below:
e : [0, 1] x [0, T] -? {3, 5, 7, 10} (x,t) 7-? e(x,t)
Removal
of downgraded assets
In order to manage the default risk inherent in owning
leveraged long CDS positions, we shall apply a specific asset-removal rule
based on rating observations: as soon as an obligor's rating has been staying
below a given threshold, say Ba2, for more than 3 straight months, then all CDS
long positions on that obligor must be removed from the portfolio and replaced
by equivalent positions on another obligor whose rating is investment grade,
i.e above or equal to Baa3.
Early cash-in events
The DPPI structure shares with earlier CPPI products an early
cash-in feature that allows the deal to be unwound before the scheduled
maturity date if the deal's NPV is high enough to cover all future liabilities,
i.e future coupons, fees, and principal payments, until the scheduled maturity
date (10 years). However, our DPPI incorporates two extra early cash-in
triggers based on shorter maturity dates, namely 5 years and 7 years. Those
three barrier conditions allow the structure to avoid adverse scenarios where
the NPV would plummet and break the bond floor, hence cash-out, after reaching
its TRV level.
Subordinated note
We add to the DPPI structure an sl := 2% thick subordinated
note, the payoff of which is similar to that of a CSO equity tranche. The
relatively high yield served on that tranche, 250 bps, compensates the
subordinated noteholder for bearing the first loss risk of the structure.
3.4 A study of the DPPI's sensitivities
Given Moody's modelling and calibrating assumptions on risk
factors, we wish to study the DPPI's behaviour as a function of its main
structural features, such as the spread over EURIBOR served to the senior
investor, the CDS tenor investment rule or the parametres of the Target
Notional Exposure function.
Unless otherwise stated, we base our analysis on the portfolio
described in figure (12), on the DPPI optimized parametres listed in figure
(11) on the set of Moody's parametres listed in figures (8), (9) and (10). All
numerical results are based on C++ code developped by both Bear Stearns and
Moody's. As a starting point we plot hereafter the DPPI's simulated discounted
loss and lock-in times distributions based on 30,000 draws..
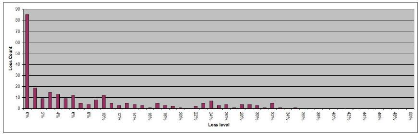
Figure 3.3: DPPI base-case loss distribution conditional on the
structure not cashing in
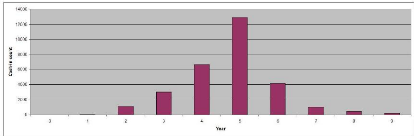
Figure 3.4: Distribution of cash-in times
The Moody's Metric of the base case scenario is 2.697, which is
equivalent to an Aa2 rating.
3.4.1 Tailor-made structural features to achieve target
rating
Senior rated coupon level
The level of the senior rated coupon is obviously a key
parametre in achieving the target rating. The graph below plots the estimated
expected loss and Moodys Metric as a function of S, the senior rated premium
paid above EURIBOR rate and measured in basis points. One shall point out the
jumps in the graph, stemming from the various triggers introduced in the
pay-off loss function L. The rather linear relationship outside jumps is also
fairly straightforward: between two jumps, the subset of cash-out scenarios is
fixed. However, given that the bulk of the loss is explained by scenarios that
cash-out at maturity without paying any single coupon, one would find that the
average loss on those scenarios is proportional to the senior coupon level, as
is the price of a bond paying EURIBOR plus the senior coupon.
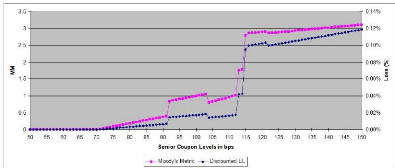
Figure 3.5: Estimated expected loss as a function of S. CDS tenor
choices
Initial and reinvestment CDS tenors have a significant impact
on the shape of the loss distribution and eventually on its expected level. We
now assume that e(.,.) is constant and equal to 0. We then plot the expected
loss level as a function of 0 E {3, 4, .., 10}. The reverse-bell shape of the
diagram accounts for the fact that:
· for short tenors, the lower MtM volatility of the DPPI
does not fully compensate for the loss in contracted CDS spread premia due to
the upward sloping shape of the term structure;
· for long tenors, the gain in contracted CDS spread premia
does not fully offset the impact of a higher MtM volatility.
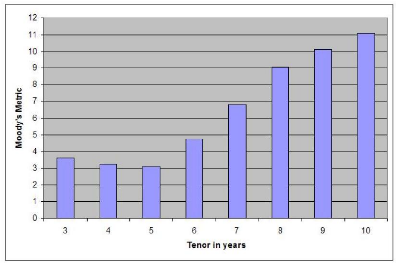
Figure 3.6: Estimated expected loss as a function of è
(2000 simulations per coupon level)
Target Notional Exposure parametrization
In order to get the intuition on how the expected loss behaves
with respect to the
Target Notional Exposure function TNE(.), one shall
slightly simplify the latter and
assume that opportunity leverage and target
multiplier functions, OL(.) and TM(.),
are constant and equal to respectively OL and TM. We then plot
TNE as a function
of both parametres OL and TM. S1 stands for TM = 20 and S9 for
TM = 40 with Si+1 - Si constant.
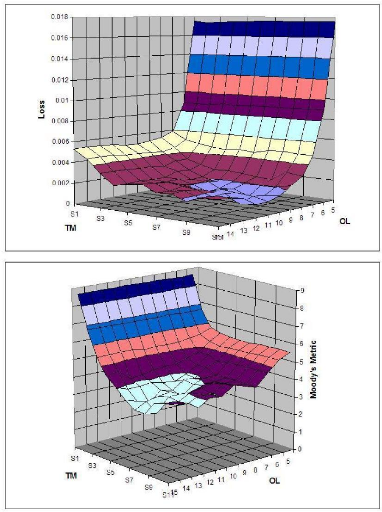
Figure 3.7: Loss and Moody's Metric as a function of OL and TM,
1000 simulations per couple of parametres
One shall point out from the graphs that even with the best
combination of fixed
Opportunity Leverage OL and Target Multiplier TM parametres,
the structure's
Moody's Metric remains significantly higher than 2.697
obtained with dynamic OL
and TM functions. Also, we clearly see that there is a
tradeoff between OL and TM
that allows the structure to improve its rating:
too high values for both parametres
lead to a sub-optimal leverage function,
reflecting the fact the extra MtM volatility
induced by a higher leverage has a negative fat tail effect on
the loss distribution L(M).
| 


