Les principales sources d'inflations en pays sous développés: la cas du Cameroun de 1995 à 2006

CHAPITRE III : MÉTHODOLOGIE DE L'ÉTUDE ET
PRÉSENTATION DES DONNÉES

III.1. Généralités sur le modèle SVAR (p)

Soit X_t un vecteur composé de n variables endogènes, représentant une économie. D'une manière générale, dire que le vecteur X_t suit un processus SVAR(p) (vectoriel autorégressif structurel à n variables et p décalages), signifie que ses observations courantes et passées sont reliées de la façon suivante :

B0Xt = B1X t - ₁+ · · · + _BpXt-p+ å_t (1)

où å_t est tel que E(å_t)= 0 et V(å_t)= Ó_å ?t

Avec Xt

?xt^1 1 ? ? x2 ? ? t = ? ? ? ? . ? ? xt^n

[k1 i ... b1ni Bi = ? ? ? bn1i · · · · · · b:i

B0

?b1^01 ? ? = b20 ? ? ? ?b,^c:r

åt

?å^1 1 t ? ? r å2 åt^n

III.1.1 Estimation des paramètres du modèle

Compte tenu de l'effet feed-back inhérent au système (chaque variable endogène cause contemporainement les autres variables endogènes), les équations du modèle SVAR(p), ne peuvent pas être estimées directement. Pour y parvenir, l'on suit la procédure suivante :

1ère étape : L'on écrit le modèle structurel sous une forme réduite.

Admettons que la matrice B₀ ne soit pas singulière (c'est-à-dire B₀^-1 existe). En prémultipliant l'équation (1) de la forme structurelle par B¹ il vient :

X_t = B₀^-1B₁X+ · · · + _{B0-1BpXt_p+} B₀ ¹å_t

₍₂₎ 12

cette équation est de la forme :

X_t = C1X t - ₁+ · · · + CpX t - p+çt (³)

¹² Cette équation est dite forme réduite du modèle structurel.

-1

[B₀ - B_jr j=E A_jr

j=1j=0

A(L) où les A_j sont des matrices carrées d'ordre n.

avec C_jmB₀^-1B_. j= 1, 2,· · ·,p ; q_t--B₀^-1·å_t et la matrice de variance-covariance des résidus est donnée par :

Ù_ç = V(ç)= V(B₀^-1 · å_t)= B₀^-1 · E(å_tå:)·(B₀¹)' =B₀^-1· Ó_å (B01 y (4)

Les résidus de cette forme réduite, qui sont des combinaisons linéaires des chocs structurels, sont appelés « innovations ».

Ce modèle réduit peut être estimé à l'aide des moindres carrés généralisés (MCG) ou toutes autres techniques d'estimation standard (Estimateur du Maximum de Vraisemblance...)

2^ème étape : Une question importante qui se pose à ce niveau est celle de savoir comment à partir des estimations des paramètres de la forme réduite, l'on pourra estimer ceux de la forme structurelle. Cette interrogation pose le problème d'identification du modèle. Pour l'illustrer, l'on présentera premièrement les liens algébriques qui existent entre les paramètres des formes structurelle et réduite.

L'on a :

[Forme Structurelle] B0Xt =B1Xt-1+ · · · + _BpXt-p+ å_t avec V(å_t)= Ó_å

[Forme Réduite] + · · · + _CpXt-p + avec V(ç_t) = Ù_ç

Ces deux formes peuvent être réécrites à l'aide de l'opérateur retard L qui se définit tel que :

L:R×N?R

(xi) ?»,xt=xt-i

Ainsi, la forme structurelle devient :

B₀ X_t = B _1(L)Xt-1 + å_t

ou encore :

p

(B₀ - B₁(L))· X_t= å_t avec B₁ (L) E B_jL^j

j 1

(⁵)

En considérant que le vecteur X_t soit stationnaire, le polynôme (B₀ - B₁(L)) est inversible, ce qui en vertu du théorème de Wold conduit à :

Ainsi, la forme moyenne mobile vectorielle infinie VMA(8) de X_t est :

8

X? A_jL^jå_t

j 1

qui s'écrit aussi :

8

X? A_j · st-j

j 1

(6)

ou encore de façon plus générale :

Xt = A(L) · å_t

Toujours au moyen du théorème de Wold, la forme réduite peut également se mettre sous la forme moyenne mobile vectorielle infinie. Ce qui donnera les équations algébriques suivantes :

j=1

Xt=[? jX_t +ç_t

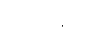
ce qui correspond à :

?p

(7)

I

_

?

j

Xtçt

j=1

Et en inversant le polynôme retard, puis en prémultipliant cette équation par cet inverse, il vient :

· ? D_j · ç_t-j où DM= ?Djr - ? C _jr

88j=1j=1j=1

soit au final :

X_t= D(L) ·ç_t

(8)

La décomposition de Wold étant unique¹³, il vient en rapprochant les deux formes :

?

? ?

X _t=A(L)· å XD(L)·ç_t

Il en résulte que :

¹³ Puisque la représentation moyenne mobile vectorielle est issue de l'inversion d'une forme stationnaire de X_t .

1 · å_t (⁹)

A(L)·å= D(L)·ç_t ? A(L)·å= D(L)· B₀

1

? A(L) = D(L)· B₀

Puisque les paramètres de la forme réduite et ses résidus sont connus (déjà estimés), alors les relations devant nous permettre de trouver les estimations des paramètres de la forme structurelle sont :

çt=B0^1· åt (10) A(L) = D(L)· Bo^1

Ainsi, D(L) étant connu à partir de l'estimation puis l'inversion par le théorème de Wold de la forme réduite, la connaissance de /3₀¹ va nous permettre de déterminer åà_t et A(L). Tout le problème pour y parvenir est de savoir si /3₀¹ est identifiable.

III.1.2 Le problème de l'identification de B₀¹

Ce problème consiste à déterminer si, à partir des paramètres estimés de la forme réduite, nous avons assez d'équations que d'inconnues pour trouver les paramètres de la forme structurelle. Remarquons que : la forme réduite comporte

n² · p +n(n ₂ +1) paramètres¹⁴. En effet, nous avons p matrices carrées d'ordre n de coefficients des endogènes retardés (B_j) soit n²· p paramètres et la matrice de variance-covariance des innovations qui est symétrique soit en plus n(n +1)

2

paramètres.

S'agissant de la forme structurelle, nous avons en plus des paramètres de la forme réduite, ceux de la matrice des variables contemporaines (B₀) soit n²

paramètres supplémentaires. Or tous les éléments de la diagonale de B₀ étant égaux à
l`unité, B₀ n'a en tout que n² - n paramètres inconnus. Comme Ó_å est diagonale, elle

n'a que n paramètres inconnus. En définitive, la forme structurelle a un nombre de paramètres égal à (n² - n)+ n²· p + n .

¹⁴ Il suffit de les compter en utilisant les ordres des différentes matrices.

2

Ainsi, la forme structurelle a n(n -1)

paramètres de plus que la forme réduite ;

l'on dit alors que le système est sous identifié. Pour pouvoir le résoudre, il faudra qu'il

restrictions

soit au moins juste identifié¹⁵, ce qui correspond donc à imposer n(n -1)

2

identifiantes sur les paramètres de la forme structurelle. Dans le cas de la présente

=15 restrictions !!!

étude, puisque n = 6, il faut imposer n(n -1) 6(6 -1)

2 2

=

3ème étape : Démarche pour imposer les restrictions identifiantes.

Les contraintes identifiantes portent presque toujours sur les réponses du

n - 1)

système aux différentes impulsions structurelles : le nombre ⁿ⁽² de contraintes

identifiantes que le modélisateur doit introduire en faisant référence à la théorie économique croit rapidement avec la dimension du système et corrélativement, le degré d'arbitraire inévitablement associé à l'expression des a priori correspondants. En pratique, la théorie économique ne fournit qu'un nombre très réduit de contraintes identifiantes qui ne soient pas sujet à controverse. (Bruneau et De Bandt (1998))

Plusieurs approches ont été proposées dans la littérature pour imposer ces restrictions. Il existe une façon simple, en effet, plus statistique que véritablement économique, d'imposer les contraintes identifiantes supplémentaires. C'est la décomposition de Choleski de la matrice de variance Ù_ç , définie comme l'unique

matrice triangulaire inférieure P telle que

P · P? = Ù .

ç

L'orthogonalisation des impulsions est alors réalisée selon les principes préconisés par Sims (1980), et ne requiert comme a priori que le choix de l'ordre des séries qui doivent être alors rangées de la variable la plus « exogène » à la plus « endogène » : la matrice P correspondant à la décomposition de Choleski est définie de manière unique pour un ordre donné des composantes du modèle.

Quoique l'orthogonalisation obtenue par la méthode de Choleski ait été critiquée à de nombreuses reprises par les partisans de la méthodologie VAR structurel, qui préconisent l'orthogonalisation fondée sur l'imposition de contraintes identifiantes tirées de la théorie économique (voir par exemple Shapiro et Watson

¹⁵ C'est-à-dire que le nombre de paramètres inconnus soit au moins égal au nombre d'équations.

p

D'après la forme réduite estimée, l'on a : Xt = Â0 +?4Xt_j . Les fonctions t

19

LES PRINCIPALES SOURCES D'INFLATION DANS LES PAYS SOUS DÉVELOPPÉS :
Le cas du Cam eroun de 1995 à 2006

(1989) ; Blanchard et Quah (1989), King et al. (1992) etc.), nous utiliserons cette décomposition pour éviter de passer par des algorithmes complexes d'estimation d'équations non linéaires.

III.2. Fonctions Impulsion-réponse

III.2.1. Détermination des fonctions impulsion-réponse

j 1

impulsion-réponse (IRF ou FIR) sont définies par :

?X

t+s = È^(s),s 0,1,2,... (13)

?åà_t

Pour les obtenir, on procède comme suit :

En faisant usage du théorème de Wold, l'on peut écrire un processus vectoriel autorégressif d'ordre p (VAR( p)) en processus moyenne mobile vectorielle infinie (VMA (8) ):

p X Â0+? Â X + 13

j t- j
· t

j 1

c'est-à-dire :

p

X_t Â₀

j 1

(14)

p

Ce qui s'écrit à l'aide de l'opérateur retard L, [1₃ -?ÂjL^j]Xt=Â0 +ii_t et par

j=1

conséquent, en prémultipliant cette équation par l'inverse de ce polynôme retard, il vient :

p p

.

X_t =[I₃ -?Â_jL^jT¹Â₀ +[I₃ -?Â_jv]^-1ii_t

j=1 j=1

(15)

En posant :

[I₃ -L¹ ? È?L^k et [I₃ --EÂ_jLi]^-1Â₀=ê₀

(k)

p 8 p

il vient:

j= 1 k=0 j= 1

8 (k)

X_t =È₀+?È ç_t

k 0

ou alors

8 (k)

X_t=15₀ +?Ô É01êt-k
k 0

(16) à l'instant t + s , l'on a:

8 (k)

à

Xt+s È₀ +?È B01êt+s-k
k 0

(17) Les fonctions impulsion-réponse étant données par :

?Xt+s ê ?åàt

(s)

^16, s=0, 1, 2...

III.2.2. Intervalle de confiance des fonctions impulsion-réponse

Notons que l'analyse économique des fonctions de réponses impulsionnelles n'a de sens que mise en regard du degré de précision de l'estimation.

Il existe des formules analytiques pour mesurer l'intervalle de confiance¹⁷ autour de ces fonctions; mais celles-ci ne s'appliquent généralement pas à des contraintes de long terme¹⁸ ni a fortiori, aux cas où l'identification est réalisée conjointement par des contraintes de court et de long terme. Il est donc commode de procéder par simulation (Monté Carlo ou Bootstrap).

Nous privilégions dans le cas de notre étude la méthode du « Bootstrap » mais on vérifie que les deux méthodes donnent des résultats équivalents dans le cas particulier de cette étude.

III.3. Décomposition de la variance

La décomposition de la variance permet de percevoir dans l'analyse de la variabilité des variables endogènes, les parts de variabilité respectives induites par les différents chocs exogènes. Analytiquement, ces parts se calculent comme suit :

Conformément à l'équation de la forme réduite, nous avons :

¹⁶ Soit au total 36 fonctions impulsion réponse, dans le cas de cette étude !

¹⁷ Voir Lutkepöhl (1990) et Hamilton (1994), cité par Mialou (2002).

¹⁸ Sauf dans Lutkepöhl et Reimers (1992), cité par Mialou (2002).

p

ç_t

X_t +?Aj Xt-j+çt C'est-à-dire, (I -EA_jLi)X_t 4

j

1

en posant A(L)= ? A_jL^j , il vient : (I - A(L))X_t = A0+çt soit :

1

p j

X_t = (I - A(L))^-1 (A₀ +ç_t)

(18)

Sous l'hypothèse que (I - A(L)) soit inversible, ce qui serait le cas d'ailleurs dès lors
que notre VAR( p) est stationnaire, alors en vertu du théorème de Wold, nous

8

avons (I - A(L))^-1 =?C_jL^j où C_j sont des matrices carrées d'ordre 3. Ainsi,

j 0

8

X_t = (?C_jL^j )(A₀ +ç0

j =0

Ce qui est équivalent à :

8 8

X_t = (? Cj _A0+?Cyt-j) ^où 71t-j=B0-1åt-j

j =0 j=0

(19) La matrice de variance-covariance de X_t est définie par :

8 8

XX,0=E(XtXt )= E(?C _jL^j )· E(ç0: )· (? C; L^j) (20)

j=0 j=0

où E(77,77: )=(B₀¹)· E(å_tå_t^')·(e)' = (e)·Ó_å · (e)'

Les å_t étant deux à deux indépendants, il vient :

? ?

0 pour j j

'

= ??C B¹E(e e )(13^-1X avec E(e .e ⁾⁼Ó_å pour j =

0 t-j t-j' 0 t-j'

et donc :

8

=?C_jB7s_å(B7¹)'C;

j 0

(21)

Soit E_å⁽ⁱ⁾ l'élément de rang (i,i) de la matrice Ó_å (matrice diagonale). Nous pouvons alors définir la contribution du i^ème choc structurel à la variance de X_t comme :

8

=?(C_jB₀¹)Ó⁽_å⁰(C_jB₀¹)' (22) - -

j =0

Ainsi le ratio de la variance de X_t expliquée par le i^ème choc est donné par¹⁹ :

, i,k = 1, 2, ...6 (23)

[(0 ] XX ,0	k
[ ] XX,0		i

[(0

]

XX ,0

[ ]

XX,0

De façon plus explicite,

k

i

, i,k =1, 2, ...6

donne les ratios

å _t

ó²(

X_t

=[ r (i) =[:Ê=0(C B₀^-1 )Ó⁽_åⁱ⁾ (CjB0 ¹

XX,0 k jk i,k =1,2,...6 [^rX" Ê(Cj·B0^1)Óå (Cj ?j=0 ? i

(24)

III.4. Les données de l'étude

Du point de vue méthodologique, nous avons choisit comme c'est le cas dans plusieurs travaux sur le sujet, une approche VAR structurelle. Nous ferons donc une modélisation dans laquelle la variable d'intérêt sera l'inflation et les variables explicatives seront celles suggérées par la littérature. A l'instar de Loungani et Swagel (2001, 1996), eu égard au différentes sources présentées ci-dessus, l'on peut retenir les variables suivantes :

· Variables endogènes :

? Indice des prix des produits pétroliers ;

? Indice des prix des produits non pétroliers ;

? Output gap ;

? Le taux de croissance de la masse monétaire ;

? Le taux de change ;

? L'inflation.

· Covariables exogènes :

? Solde budgétaire (mesure de l'influence des dépenses publiques sur le niveau de l'inflation) ;

? Le taux de croissance du PIB dans les pays du G7 (mesure du niveau d'activité dans le monde).

À la suite de la précédente modélisation, nous ferons quelques simulations de chocs aléatoires de façon à déterminer la contribution de la variation d'un point de

¹⁹ Il est important de noter ici que ce n'est pas à proprement parler la part du choc lui-même qui est représentée, mais, la part de ses effets.

pourcentage de chaque variable, à la variation de l'inflation. Nous pourrons ainsi savoir quelles variables contribuent le plus à la détermination de l'inflation.

Pour la mise en oeuvre de notre analyse, nous utiliserons principalement le logiciel statistique Eviews.

Nous utilisons des données trimestrielles couvrant la période 1995-2006.

ü la série du taux d'inflation nous provient de l'Institut National de la Statistique du Cameroun, elle est calculée à partir de la différence du logarithme de l'indice général des prix à la consommation des ménages.²⁰

ü la série du taux de change provient de la BEAC, elle est mesurée par la différence du logarithme du taux de change nominal entre le Cameroun (F.CFA) et les États-unis (dollars $). Le taux de change représente de façon spécifique, le nombre d'unité de monnaie locale par unité de dollar, de telle sorte qu'une augmentation du taux de change corresponde à une dépréciation de la monnaie nationale. Il aurait été souhaitable d'utiliser une mesure du taux de change entre le pays domestique et son principal partenaire commercial (à l'exemple du TCER : taux de change effectif réel). Nous n'utilisons pas ce taux de change réel dans le cadre de cette étude parce que ce dernier comprend déjà l'inflation dans sa détermination or il s'agit de la variable d'intérêt de notre étude.

ü La série du taux de variation de la monnaie nous provient de la BEAC, elle est calculée par la différence du logarithme de la masse monétaire (M2) du Cameroun.

ü La série de l'output gap est obtenue de la base de données de la Banque Mondiale : World Development Indicator et International Financial Statistics. Elle est la différence entre le logarithme du _PIBpotentiel par tête et le logarithme du PIB par tête, de sorte qu'une augmentation de l'output gap représente un ralentissement de l'activité économique effective par rapport à l'activité potentielle. Bien entendu, cela pourrait aussi bien indiquer une augmentation de l'activité potentielle sans que l'activité réelle ne soit influencée. Le _PIBpotentiel est obtenu de la série du PIB par tête au moyen du filtre de Coe et Mc Dermott (1997) qui extrait la composante lourde ou la tendance de fond de la série initiale. Ce filtre est semblable au filtre de Hodrick et Prescott, à la seule différence que les paramètres dans le filtre de Coe et Mc Dermott sont déterminés empiriquement. Il faut noter que les pays en développement sont susceptibles de subir un choc d'offre assez élevé en important les nouvelles

²⁰ Nous ferons empiriquement le choix entre l'inflation et l'inflation en glissement annuel suivant la qualité des résultats.

technologies des pays industrialisés. Cette augmentation du _PIBpotentiel aura tendance à être surestimée par notre choix d'utiliser un filtre pour extraire la composante potentielle. Il est évident qu'une variable du marché du travail, telle que le taux de chômage, serait plus intéressante à la place de l'output gap pour mesurer le niveau d'activité réel dans les pays, malheureusement cette série est indisponible dans notre pays.

ü Les séries de l'indice des prix des produits pétroliers et de l'indice des prix des produits non pétroliers nous proviennent de l'Institut National de la Statistique.

Comme nous l'avons signifié plus haut, nous introduisons dans notre analyse une nouvelle variable pour tenir compte de l'influence des dépenses gouvernementale.

ü la série du solde budgétaire provient de la base de données du Fonds Monétaire International : World Economic Outlook. Elle mesure la différence entre les recettes et les dépenses du gouvernement central, de sorte qu'un signe (-) indique le déficit. Nous utilisons le déficit budgétaire plutôt que le déficit public du fait de l'indisponibilité de toute la série du déficit public.²¹

Nous examinons aussi l'impact sur l'inflation du niveau d'activité économique mondiale, mesurée ici par le taux de croissance du PIB des pays du G7.

ü la série du taux de croissance du PIB des pays du G7 nous provient de la base de l'Organisation pour la Coopération et le Développement Économique.

Dans le cadre de cette étude, nous n'explorons pas l'impact de l'environnement politique ou des caractéristiques institutionnels²² ou encore du climat des affaires au Cameroun, qui pourraient induire des taux d'inflations élevés ou offrir un environnement propice à la stabilité des prix. Nous nous limiterons à l'étude des quatre principales sources susmentionnées.

²¹ Le calcul du coefficient de corrélation entre les deux séries pour la période de disponibilité, dépasse largement la barre des 0,9.

²² Quelques exemples de ces caractéristiques institutionnels seraient selon des étude récentes : l'indépendance de la banque centrale (voir Alesina et Summers (1993)), l'ouverture au commerce extérieur (voir Romer (1993) et la taille du pays et son niveau de développement (voir Campillo et Miron (1996).