|
1
Sommaire
|
RESUME
INTRODUCTION
1. LES TECHNIQUES AU CENTRE DE L'APPRENTISSAGE MATHEMATIQUE
|
|
3
4
5
|
|
1.1 APPROCHE THEORIQUE
|
5
|
|
|
1.2 QUESTION DE RECHERCHE
|
12
|
|
|
1.3 HYPOTHESE DE LA RECHERCHE
|
12
|
|
|
2. METHODOLOGIE
|
|
12
|
|
2.1 CONTEXTE DE LA RECHERCHE
|
12
|
|
|
2.2 RECUEIL DES DONNEES : TRANSCRIPTION ET COPIES
|
13
|
|
|
2.3 LA TRANSCRIPTION : UNE RAISON DES SEANCES FILMEES.
|
13
|
|
|
2.4 L'ENREGISTREMENT DE LA LEÇON
|
14
|
|
|
2.5 LA COPIE DE L'ELEVE : UNE TRACE D'OBSERVATION.
|
14
|
|
|
2.6 ANALYSE A PRIORI
|
15
|
|
|
2.6.1 Présentation et analyse a priori du savoir
|
15
|
|
|
2.6.1.1 présentation
2.6.1.2 analyse a priori du savoir
2.6.1.3 analyse a priori des praxéologies de l'instance
apprenant
2.6.2 Des résurgences des positions diverses des
élèves avec
2.6.3 Marche vers une conjecture
2.6.4 Analyse a priori des problèmes didactiques possibles
|
15
16
16
17
17
18
|
|
|
2.7 SYNOPSIS DE SEANCES
|
19
|
|
|
2.8 LE JEU ET SA DEVOLUTION
|
22
|
|
|
3. ANALYSE DES PRAXEOLOGIES DES ELEVES
|
|
23
|
|
3.1 LA CORRECTION : UN JEU DE VERBALISATION
|
26
|
|
|
3.2 ASCENDANCE ET COMPREHENSION DES PRAXEOLOGIES DES ELEVES.
|
28
|
|
|
3.2.1 Séance 1.b : consolidation ou réajustement ?
|
28
|
|
|
3.2.2 Séance 1.â prolongée :
réaffirmation ou réajustement ?
|
33
|
|
|
3.3 INTRIGUE DE L'INTRUS DANS LA SEANCE 1
|
37
|
|
|
3.4 INTRIGUE ET INTRUS DANS LA SEANCE 2
|
39
|
|
|
3.5 RELANCE DU JEU
|
39
|
|
|
3.6 EXODE DE COMPORTEMENTS
|
40
|
|
|
3.7 PERCEPTION D'OBJETS OSTENSIFS ET NON OSTENSIFS
|
41
|
|
2
3.7.1 Objets ostensifs
|
41
|
|
|
3.7.2 Objets non ostensifs
|
42
|
|
|
3.8 LA MEMOIRE PRATIQUE ET MEMOIRE DU SAVOIR
|
42
|
|
|
3.9 DU POINT DE VUE CHRONOGENETIQUE
|
43
|
|
|
3.10 DU POINT DE VUE TOPOGENETIQUE
|
45
|
|
|
3.11 DU POINT DE VUE MESOGENETIQUE
|
45
|
|
|
4 REPONSE A LA QUESTION DE RECHERCHE
|
46
|
|
|
CONCLUSION
|
|
48
|
|
BIBLIOGRAPHIE
|
|
49
|
3
Résumé
Le spicilège aborde la question d' « en quoi le
milieu de la résolution de problème est un lieu de production de
techniques variées ? ». Le cadre théorique est
principalement articulé autour des travaux d'Y. Chevallard (1998), (M.
Bosch & Y. Chevallard (1999) et Y. et Mathéron & M.-H. Salin
(2002) qui révèlent successivement des éléments
d'analyse comme les façons de faire, les ostensifs et la mémoire.
La méthodologie consiste à utiliser deux caméras (une
centrale et une baladeuse) et les copies sur lesquelles les
élèves déclinent leur pratique. Cette façon de
prélever des données, dans une institution d'apprentissage
(école élémentaire de Marseille en France), nous permet de
les analyser et de lire la présence ou non de ces éléments
dans le milieu de la résolution de résoudre de problème en
mathématique. La conclusion tirée de l'analyse est la
manipulation par les élèves des opérations
mathématiques (addition, soustraction, multiplication et division) aussi
bien que les ostensifs et la mémoire. Cependant l'amélioration ou
l'acquisition des meilleures techniques se fait en fonction des phases de
verbalisation créées par l'enseignant pour laisser entrevoir les
constituants des techniques utilisées par les élèves entre
la tâche déjà effectuée et une nouvelle tâche
à effectuer.
Mots clés : techniques, milieu,
problème, ostensifs, mémoire.
Summary: The scrapbook addresses the question
of «how the world of problem solving is a place of production of various
techniques? «. The theoretical framework is mainly centered around the
work of Y. Chevallard (1998) ( M. Bosch & Y. Chevallard (1999) and
M.-H.Salin & Y.Matheron (2002) successively revévèlent
elements of analysis as ways to the ostensive and memory. methodology is to use
two cameras (one central and wandering ) and copies that students decline their
practice. This way of collecting data in an elementary learning institution
(school of Marseille in France), we can analyze and read the presence or
absence of these elements in the middle of the resolution to solve problems in
mathematics. The conclusion of the analysis is the manipulation by the students
of mathematical operations (addition, subtraction, multiplication and division)
as well as the ostensive and memory. However the improvement or acquisition of
the best techniques is based on the phases of verbalization created by the
teacher, to show the components of the techniques used by students between the
task already performed and a new task. Keywords: technology,
environment, problem, ostensive, memory.
4
Introduction
Les apprentissages réalisés dans toute
institution dont la mission est le partage des valeurs scolaires se
construisent avec une participation des élèves eux-mêmes.
L'intention en général est d'attendre qu'au terme du processus
d'enseignement apprentissage les apprenants fassent montre de
compréhension ; ce qui explique tout l'intérêt de la visite
des travaux de Charlot sur le rapport aux savoirs et ceux de Julio sur la
représentation des problèmes et réussite en
mathématique. Ainsi l'indice qui rassure l'enseignant est la
réponse attendue d'un problème défini.
Dans ce travail nous voulons dépasser le simple regard
orienté sur la réponse ou la technique de l'enseignant. En
admettant que chaque apprenant ait des ressources personnelles dont il s'en
sert devant un problème mathématique que lui présente un
enseignant, l'enseignement pourrait ne plus se focaliser exclusivement vers un
mouvement logique construit pour n'attendre que la réponse de
l'élève. Mais la pensée serait aussi orientée vers
les pratiques des élèves. En conséquence nous pouvons nous
intéresser aux techniques dont met en oeuvre chacun d'eux. D'où
notre question est axée sur « en quoi le milieu de la
résolution des situations problèmes est un lieu de production de
techniques variées ? ».
La première partie de notre mémoire reste
consacrée à la présentation de l'approche théorique
qui permet de comprendre les emplois didactiques des concepts clés (ou
expression) comme « technique », « technologie » et «
type de tâche » définis par Chevallard (1998), ostensifs et
non ostensifs par Bosch et Chevallard (1999) et une articulation sur la forme
compréhensible du savoir qu'abordent certains auteurs comme Brousseau
(1998), Paun (2006) et Mathéron (2011). Cette première partie
dévoile aussi la question de recherche telle qu'exposée un peu
ci-haut. Une seule hypothèse est conduite en raison de sa
complétée.
Dans la deuxième partie, nous définissons une
méthodologie centrée sur l'observation des pratiques des
élèves qui va nous permettre de répondre à la
question posée. Cette observation ne sera possible comme on peut bien
voir à travers nos explications que par un dispositif mis en place
permettant le recueil des données.
Enfin dans la troisième partie, avec l'intention
d'avoir des résultats quelle qu'en soit la nature, nous analysons les
données qui sont essentiellement les productions des
élèves ponctuées par l'étalage des pratiques en
termes de techniques personnelles
5
utilisées pour attaquer une tâche définie
par l'enseignant. Cette analyse porte aussi sur les extraits des
transcriptions, au moyen d'un outil audiovisuel, établies à
partir des phases de verbalisation des élèves qui pourraient
offrir des éléments nécessaires à la confirmation
ou à l'infirmation de l'hypothèse déclinée.
1. Les techniques au centre de l'apprentissage
mathématique
Les pratiques enseignantes montrent
régulièrement un attachement de l'enseignant plus marqué
aux résultats de l'élève qu'à ses techniques. Cet
attachement reste souvent lié aux techniques d'enseignement qu'aux
techniques d'apprentissage. Cette observation nous amène à nous
intéresser aux techniques des élèves. Cet
intérêt justifie alors la diversité de mon cadre qui est
composite : sociologique, psychologique et didactique.
1.1 APPROCHE THEORIQUE
La réussite des élèves dans une
leçon est l'attendu non seulement de l'Enseignant qui donne cours, mais
aussi le leur. Les facteurs pour y parvenir sont multiples : ce qui nous
conduit à nous intéresser aux travaux de Charlot (1999) sur le
rapport au savoir en sociologie et Julio (1995) en psychologie cognitive sur la
représentation des problèmes et réussite en
mathématiques. L'intérêt complémentaire des travaux
de chacun de ces auteurs pour notre recherche se construit simultanément
:
Selon Charlot (1999) la réussite d'un
élève dépend du rapport de soi au savoir. Il situe le
problème au niveau des activités d'apprentissage qui sont sources
de réussite en indiquant que pour qu'il y ait" activité", il faut
que l'élève "se mobilise", pour qu'il se mobilise il faut que la
situation présente pour lui du "sens". Par ailleurs, Il explique que se
mobiliser c'est mettre des ressources en mouvement à travers de bons
mobiles. Pour cela, il faut que le but visé soit mobilisateur d'actions
; car " l'enfant se mobilise dans une activité lorsqu'il s'y investit,
fait usage de soi comme d'une ressource.
Pour Julio (1995) il ne peut y avoir activité de
recherche et de compréhension véritable des mathématiques
que si les élèves parviennent à se représenter les
problèmes qui leur sont proposés. La représentation du
problème est une condition essentielle dans la poursuite du processus de
résolution de problème.
Mais avoir de bons mobiles pour mobiliser les ressources ou
bien se représenter le problème suppose un certain travail de
l'instance enseignante. Ce regard sur l'enseignant nous a conduits à
exploiter les travaux de trois auteurs : E. Paun (2006), G. Brousseau (1998) et
Y. Mathéron (2011).
6
Pour chevallard (1985, 1998) et repris par Paun (2006), la
science constituée ne peut pas être transmise telle quelle aux
élèves. Il conseille le curriculum formel qui est le point final
du processus de transformation externe du savoir. Donc il pose un
problème de la forme du savoir qui va faire l'objet de l'apprentissage
ou qui va susciter un intérêt pour l'apprenant.
Concernant Brousseau(1998) l'agio de ses travaux porte sur le
fait que dans le sens de la modélisation l'apprentissage est
supposé s'accomplir par une adaptation spontanée de l'apprenant
au milieu créé par une situation qu'il y ait ou non intervention
d'un enseignant au cours du processus.
Enfin Mathéron (2011) cherchant à comprendre
pourquoi deux élèves n'abordent pas un problème de la
même façon, examine les raisons pour lesquelles, à travers
un épisode critique pour deux élèves dont les voies
empruntées dans l'attaque d'un problème dévolué
à la classe sont différentes : l'une erronée ne conduit
pas à la solution l'autre permettant de la trouver. La réponse
apportée à cette question est naturellement une difficulté
d'adaptation. Celui comprend le problème et trouve la solution se situe
mieux avec la forme présentée. Celui qui ne trouve pas la bonne
voie pour enfin trouver la réponse n'est pas éclairé par
la forme du savoir.
S'il est vrai que la forme à présenter aux
élèves est une condition déterminante dans
l'apprentissage, elle ne peut à elle seule suffire pour permettre de
réels apprentissages. La théorie des situations didactiques se
propose d'offrir ce que Brousseau (1998) appelle la théorie en acte. Il
indique que c'est dans l'action que la compréhension de la situation
permet d'inférer sur une théorie. Il prend bien l'exemple du jeu
sur « qui dira 20 ? » où le choix des nombres de début
est laissé libre à chaque joueur. Mais un choix qui
nécessite des tactiques personnelles. Nous pouvons construire un lien
entre le jeu et les situations d'apprentissage où « qui dira 20 ?
» serait substitué à une question conduisant à des
choix intelligibles pour trouver la réponse attendue.
Des formes du savoir et l'organisation du jeu se placent donc
au coeur de l'enseignement apprentissage. Ainsi il importe de visiter les
pratiques mathématiques, qui comme dit Chevallard (1991), donnent des
compétences aux individus tels que les enseignants qui les utilisent.
Elles leur offrent la possibilité de créer des formes
particulières du savoir. On peut y voir un lien entre le savoir et
l'individu qu'il convient bien de croire qu'il y a une personnalisation du
savoir. Les formes parfois complexes sont modélisées pour faire
passer le savoir savant au savoir à enseigner ou au savoir
enseigné. Il se construit des efforts de transformation du savoir
à tous les niveaux y compris celui de l'apprenant. On peut donc
s'exulter d'entendre Chevallard (1991) reprendre Michel Verret (1975,
pp146-147) : « une transmission scolaire bureautique
7
suppose quant au savoir en chacune de ces pratiques, la
séparation du savoir et de la personne ;
c'est-à-dire la dépersonnalisation du savoir.
». L'élève peut détacher les liens
qui unissent les mathématiciens au savoir ; car les
mathématiciens ne sont plus les seuls à posséder
le savoir qui a donc fait l'objet d'un apprentissage.
La condition minimale qui permet à l'enseignant
d'être capable d'opérer le renouvellement didactique c'est la
conduite de la lchronogénèse grâce au fait qu'il
sait avant les autres qu'il sait et qu'il sait « plus ».
L'auteur précise que si cette chronogénèse
toujours détruite (par l'apprentissage), toujours reconstruite
(par l'enseignement c'est-à-dire l'introduction
de nouveaux objets transactionnels) se structurerait selon le seul axe temporel
d'un temps progressif cumulatif irréversible il y aurait bien
en décalage chronologique, une identification du temps de
l'enseignement et du temps de l'apprentissage : la fiction d'un temps
didactique unique deviendrait réalité. L'auteur indique par
ailleurs pour donner une place aux élèves dans leur
apprentissage que le pouvoir de l'enseignant dans la classe ça
n'est pas d'interdire (plus précisément :
d'interdire de manière directe) la réponse
6x2 -- 4 = 2(8x2 -- 2),mais bien de produire la
réponse 16x2 -- 4 = (4x + 2)(4x -- 2). Son pouvoir consiste
moins à désigner les « mauvaises » réponses
qu'à susciter la bonne réponse qui
désigne implicitement les autres réponses comme
mauvaises. Cette attitude est une position qui considère celle
de l'élève ; car l'élève a son rôle à
jouer dans ce beau jeu semble dire Chevallard (1985) où
la synchronie du système didactique n'est vraie que lorsque
l'élève est un actant à part entière. L'enseignant
sait en fait jouer sur l'axe topogénique.
Dans cet environnement de pratiques
mathématiques où l'enseignant travaille pour
l'élève un certain nombre de concepts techniques d'usage
est mis en place pour universaliser le discours. Parlant du topos de
l'élève Chevallard (1998) indique que dans le
cadre des systèmes didactiques scolaires S(X ; y ; P), les types de
tâches intégrés dans une praxéologie
mathématique sont, traditionnellement, accomplis par un individu
seul. L'élève x E X doit apprendre à factoriser,
seul, sans l'aide d'autrui certains types d'expressions
algébriques ; à calculer, par ses
propres moyens, la somme des fractions 47 +
2 , etc. En revanche il n'a pas à apprendre
seul : officiellement il reçoit pour cela au moins l'aide du
professeur y.
Chronogénèse Chevallard (1985) :
disposition du savoir sur l'axe du temps. Ensemble des
opérations qui organisent le déroulement chronologique
(le « défilé ») des objets de savoir et du
résultat de ces opérations.
8
Les tâches didactiques, en effet, sont, dans un certain
nombre de contextes, coopératives, en ce sens qu'elles doivent
être accomplies de concert par
plusieurs personnes les acteurs de la tâche. On dira que
chacun des
acteurs doit en ce cas effectuer certains gestes, dont
l'ensemble constitue alors
son rôle dans l'accomplissement de la tâche
coopérative t, ces gestes étant à la fois
différenciés (selon les acteurs) et coordonnés entre eux
par la technique t mise en oeuvre collectivement. Certains de ces gestes seront
regardés comme des tâches à
part entière t' dans l'accomplissement desquelles agira
(momentanément) en
autonomie relative par rapport aux autres acteurs
de la tâche. L'ensemble de ces tâches, sous-ensemble du rôle
de lorsque t est accomplie selon , est nommé alors le topos de dans
t.
Le grec topos (qui correspond au latin locus) signifie «
lieu » : le topos de
c'est le « lieu de », sa « place »
l'endroit où, psychologiquement,
éprouve la sensation de jouer, dans l'accomplissement
de t « un rôle bien à lui ». Dans le cas d'une classe on
parlera ainsi du topos de l'élève et du topos du professeur.
Ainsi, lorsqu'une classe de mathématiques « fait un exercice »
ce qui est une tâche éminemment coopérative, la
sous-tâche consistant à fournir l'énoncé de
l'exercice revient généralement au professeur : elle appartient
à son topos. La tâche consistant à produire - par exemple
par écrit - une solution de l'exercice relève elle du topos de
l'élève tandis que la tâche consistant ensuite, à
fournir un corrigé ressortit, à nouveau, au topos du professeur.
Si, au cours de la résolution de l'exercice un élève pose
une question au professeur, il effectue ainsi ce qui est vu ordinairement comme
un simple geste, appelant un geste homologue de la part du professeur - geste
qui peut consister, quelquefois, à... refuser de répondre
Types de tâches : Il souligne une
solidarité à la racine de la notion praxéologie et des
notions de tâche, t, et de type de tâches, T. Quand une tâche
t relève d'un type de tâches T on écrira parfois : t T.
Dans la plupart des cas, une tâche (et le type de tâches parent)
s'exprime par un verbe : balayer la pièce développer l'expression
littérale donnée, diviser un entier par un autre, saluer un
voisin lire un mode d'emploi monter l'escalier intégrer
la fonction entre
et , etc. Trois points doivent être soulignés
immédiatement.
Techniques : Une manière d'accomplir, de
réaliser les tâches t T : à une telle
manière de faire, , on donne ici le nom de technique
(du grec tekhnê, savoir-faire). Une praxéologie relative au type
de tâches T contient donc, en principe, une technique relative à
T. Elle contient ainsi un « bloc » [T/ ] qu'on appelle bloc
pratico-technique et qu'on identifiera génériquement à ce
qu'on nomme
9
couramment un savoir-faire : un certain type de tâches,
T, et une certaine manière, x, d'accomplir les tâches de
ce type.
Technologies. - On entend par technologie, et
on note généralement 6, un discours rationnel (logos)
sur la technique - la tekhnê - x, discours ayant pour objet
premier de justifier « rationnellement » la technique x, en
nous assurant qu'elle permet bien d'accomplir les tâches du type T
c'est-à-dire de réaliser ce qui est prétendu.
Les pratiques mathématiques semblent exigeantes sur les
concepts et les objets d'emploi : ce qui occasionne un intérêt aux
travaux de Bosch & Chevallard (1999). Dans leur double questionnement ils
explicitent le problème de la « nature » des objets
mathématiques et celui de leur « fonction » dans
l'activité mathématique. C'est ce qui les a conduit à
établir une dichotomie fondamentale en distinguant deux types
2d'objets : les objets ostensifs d'une part et les objets non
ostensifs d'autre part, ils précisent que le terme ostensif vient du
latin ostendere , « montrer, présenter avec insistance
» qui renvoie à une référence à tout objet
ayant une nature sensible, une certaine matérialité, et qui, de
ce fait, acquiert pour le sujet humain une réalité
perceptible.
A côté des travaux de Marianna Bosch & Y
Chevallard (1999), nous avons estimé que la mémoire est
sollicitée activement par le savoir en construction ; ce qui semble
important pour notre outil d'analyse. Aussi nous avons été
amenés à visiter les travaux Yves3 Matheron &
Marie-Hélène Salin (2002) ensuite ceux de Bertrand & P.-H.
Garnier (2005, p.121),
Pour ce qui est de Mathéron & Salin (2002), ils
impriment dans la conscience éducative qu'une pratique suppose un
dispositif constitué de moyens matériels (feuille, stylo,
règle, énoncé, écrit, compas, etc.) et de
techniques (essentiellement les savoir-faire mathématiques,
institutionnellement mis à la disposition, et attendus pour la
réalisation de la tâche). Ce dispositif doit être
outillé par des gestes appropriés, afin que la pratique puisse se
déployer ; son activation
2 Les objets ostensifs sont constitués
essentiellement des mots, des phrases, des graphismes, des écritures,
des gestes ou tout un long discours pour exprimer les objets non ostensifs
comme une « fonction » ou « la primitive d'une fonction.
»
Les objets non ostensifs sont formés essentiellement
des idées, des intuitions ou des concepts qui existent dans une
institution au sens où on leur attribue une existence sans pourtant
être vus, dits, entendus, perçus ou montrés par
eux-mêmes. Ils ne peuvent qu'être évoqués ou
invoqués par la manipulation adéquate de certains objets
ostensifs associés comme le mot ou le geste.
10
nécessite la mobilisation de moyens personnels. Ils
indiquent assez bien que pour produire un geste, il faut en posséder une
mémoire : celle-ci permet de reproduire la pratique
antérieurement apprise : ce qu'ils nomment « mémoire
pratique de la personne » qui résulte de l'incorporation de
chaînes opératoires (Leroi-Gourhan, 1964) portées par
« une communauté mathématique ». L'étude du
travail des élèves permet l'accès à certaines
couches de leur mémoire pratique ; ce que Mercier(1995) nomme «
l'accès à des fragments de leur biographie didactique ».
Cette assertion est illustrée par deux réponses en classe de
2nde à la question « démontez que ABCD est un
rectangle après leur avoir demandé de placer
quatre points A(4 ;1),B( ;4),C( ;1) et
D(-2 ;-2) ». Un premier élève répond
laconiquement : ABCD est parallélogramme AB//CD. AC coupe BD en leur
milieu s'appuyant de ses acquis de la classe de 5ème.Alors
4que le deuxième élève active la mémoire
de pratiques spécifiques de la
classe de 2nde en employant les ostensifs
langagiers
(« colinéaires », « déterminants
») ou scripturaux (||) gestes pour l'accomplissement des calculs comme
chercher à savoir si les vecteurs CD et AB sont colinéaires.

Illustration 1 : calcul du déterminant
Concernant A. Bertrand & P.-H. Garnier (2005), ils
indiquent que la mémoire implicite correspond en fait au rappel
accidentel d'expériences passées.
Comme dans toutes les oeuvres d'enseignement ou
d'apprentissage on ne peut se démarquer du système didactique,
nous nous sommes intéressés aux 5travaux de Assude
& Mercier (2007) qui présentent qu'on ne peut vraiment rendre
intelligible l'action du professeur sans prendre en compte dans le même
temps l'action des élèves et qu'il leur parait tout aussi vrai
que l'action de ces derniers dépend
11
fondamentalement de l'action du professeur. Toute
activité d'une instance(le professeur ou les élèves) ne
trouve l'intégralité de son sens qu'à travers l'autre
instance l'une et l'autre rendues solidaires par le savoir en travail.
Il revient pour ce travail de savoir comme les auteurs du
présent ouvrage l'indiquent dans l'hypothèse selon laquelle
l'action didactique est une action conjointe qui puise sa forme dans les
savoirs et qui s'est faite non pas seulement par les méthodes classiques
de l'observation ethnographique ou clinique jugées insuffisantes, mais
par des formes de réduction appropriée de ces données
particulières que sont les films des séances de classe ou les
transcriptions des dialogues produits dans ces séances ; et imaginer des
formes de description de l'action qui puissent rendre justice à sa
complexité, et surtout, des manières nouvelles de mettre en
regard la pluralité des descriptions obtenues : vue synoptique dont
l'élaboration à la fois conceptuelle et technique paraissant
constituer l'un des enjeux majeurs de la recherche pour les années
à venir.
Ils avancent que les « manières de faire » en
tant que techniques peuvent être ramenées dans le vocabulaire de
la recherche à des tâches. Ils énoncent par ailleurs que la
notion de « type de tâches » ne peut permettre à elle
seule la description correcte de l'action mais qu'il faut y ajouter les
situations et les milieux qui donnent leur forme à ces tâches.
Puis ils affirment qu'il faut considérer les techniques non pas comme
des manières d'accomplir une tâche mais comme des manières
d'accomplir tel type de tâches dans un milieu (dans une situation
particulière). Ils Caractérisent les techniques et indiquent que
: « avec la technique invisible, l'élève
produit une réponse. avec la technique faible,
l'élève produit la réponse et met en place un
discours associé à la technique et avec la technique forte :
l'élève produit la réponse explicite un discours
associé à la technique et le valide comme technologie.
Nous nous sommes intéressés aux travaux de G.
Sensevy (2011) parce qu'il oriente dans le sens du savoir ;
éléments pour une théorie de l'action conjointe en
didactique pourquoi décrire les évènements : « Cela
suppose tout d'abord dans un premier temps, une suspension des
conceptualisations théoriques. On a affaire à une certaine
pratique et on cherche à décrire aussi précisément
qu'il est possible sans faire usage de termes théoriquement
chargés. On tente, autant que faire se peut, de saisir la logique
première des événements sans introduire d'autres concepts
que finalement comme si l'analyse épuisait le point de vue des agents
dans un effort de compréhension de ce qu'ils font. Ils doivent pouvoir
s'y retrouver. Ils devraient pouvoir dire quelque chose comme oui c'est bien
cela qui se passe de mon point de vue .
ieux ils devraient pouvoir préciser oui c'est bien cela
qui est essentiel dans ce qui se passe de mon point de vue . »
12
1.2 QUESTION DE RECHERCHE
La résolution de problèmes occupe une place
considérable dans les pratiques didactiques des mathématiques
à l'école élémentaire en France et bien dans
d'autres pays. C'est un moyen qui permet à l'apprenant la
dévolution aux problèmes, la manifestation des connaissances dans
ses interactions avec le milieu (Brousseau, 1998) et occupe un espace non moins
important dans les programmes (MEN, 2008) et le socle commun des connaissances
et des compétences (décret, 2006) en France. Cette
dévolution n'est possible qu'à travers des phases bien
déterminées indique
athéron (2011). Les travaux de l'Institut national de
recherche pédagogique, équipe de recherche en didactique des
mathématiques, menés dans le sens de susciter des apprentissages
par la résolution de problèmes, définissent à
travers le manuel « apprentissages numériques et résolution
de problèmes » les objectifs de chaque contenu et les phases de
résolution de problèmes subdivisée en étapes
successives.
Dans notre recherche, tout en nous inscrivant dans un champ
comparatiste existant de l'agir ensemble (Assude T. & Mercier,A. 2007),
nous voulons comprendre en quoi le milieu de résolution de
problème est un lieu de production de techniques variées ?
1.3 HYPOTHESE DE LA RECHERCHE
Notre cadre théorique suffisamment édifiant sur
les techniques qu'utilise l'homo-sapiens quelle que soit la tâche
à laquelle il se confronte, nous amène à penser que les
élèves vont utiliser dans la conduite de leur topos des
manières de faire en s'appuyant sur les ostensifs , les non ostensifs et
la mémoire pour expliquer les opérations.
2. Méthodologie
2.1 CONTEXTE DE LA RECHERCHE
Ce travail de recherche est certes produit aux fins
d'obtention d'un master 2 de recherche mais il s'inscrit
précisément dans un champ d'actions dont l'articulation se fait
autour du savoir-faire de l'apprenant lors d'une rencontre avec le savoir que
lui propose l'enseignant. Un intérêt qui pourrait nous conduire
à étendre notre observation au plus grand nombre. Nous avons
plutôt choisi de travailler dans une classe d'une école primaire
d'AIX-Marseille composée de CM1 et CM2 où les
élèves sont supposés avoir accumulés des
réflexes de raison. Cette classe, dont les effectifs de CM1 et CM2
étaient de 10 et 13, est un milieu de résolution de situation
problème en mathématique et surtout qu'elle a l'habitude de la
présence de la caméra et/ou des personnes
étrangères.
13
2.2 RECUEIL DES DONNEES : TRANSCRIPTION ET
COPIES
Deux séances composées de quatre tâches du
même type peuvent suffire pour offrir au chercheur la possibilité
de collecter des données nécessaires à l'analyse. La
première tâche que nous pouvons qualifier de moyen de
révélation des techniques empruntes d'originalité ; parce
que produite sans référence à une technique d'emploi dans
la classe. A partir de la deuxième tâche, il peut avoir des
influences langagières qui modifient de façon significative les
pratiques des élèves, donc il y a la possibilité de voir
un élève utiliser une technique déjà
utilisée par un autre élève de la classe. Pour ce faire
nous transcrirons l'oral de la leçon afin d'avoir la matière de
structuration du synopsis, mais plus le champ de la recherche pratique
présentant divers aspects des discours possibles. Nous exploiterons
également à côté des transcriptions, les copies des
élèves. Nous utilisons la méthode quantitative en raison
de son principe qui veut que les hypothèses soient testées lors
du travail de collecte de données à travers l'emploi
d'instruments ou de documents qui permettent une vérification
quantifiable.
2.3 LA TRANSCRIPTION : UNE RAISON DES SEANCES
FILMEES.
Les séances filmées ont la tendance de
présenter une diversité de phénomènes non
perceptible à une simple observation faite en une fois. Le film a un
attribut avéré de reprise du défilé d'actions
produites par les acteurs de la scène. Le film nous permet de structurer
le synopsis (le déroulement des opérations de l'enseignant et
celles des élèves le dosage à travers les phases ou
tâches du même type) grâce à un moment fastidieux mais
riche de transcription et donc de voir les interventions des
élèves dans l'action conjointe du professeur et des
élèves afin d'établir une analyse possible. Il peut donc
permettre de voir certains écrits des élèves d'enregistrer
les justifications orales (logos) de ce que les élèves utilisent
comme moyen (technique) pour arriver à la réponse attendue.
14
2.4 L'ENREGISTREMENT DE LA LEÇON
Tableau
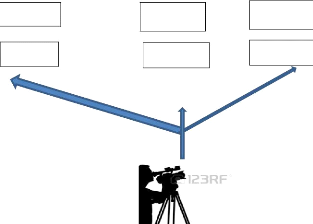
Table 1
Table 4
Table 2
Table 5
Table 3
Table 6
Illustration 2 : Plan du dispositif d'enregistrement
vidéofilmé des données
Nous avons utilisé deux caméras en affectant
à chacune d'elles une mission bien précise :
Une caméra comme présentée dans le
schéma ci-avant qui est une caméra posée sur l'axe
centrale de la classe. Elle nous permet d'enregistrer toutes les actions
produites ensemble dans les communications du groupe classe. Elle nous montre
particulièrement comment l'enseignant définit les tâches de
travail les dévolue les régule ou les institutionnalise. Elle
permet certes de voir les justifications des élèves mais aussi de
voir les interactions entre le professeur- élèves et entre les
élèves.
Une autre caméra portable gardée dans la main du
chercheur permet de filmer toutes actions individuelles de l'apprenant. Il
s'agira à ce niveau de prendre ce qu'écrit chaque
élève,
2.5 LA COPIE DE L'ELEVE : UNE TRACE
D'OBSERVATION.
Pour observer comment les élèves de ces deux
niveaux, mis ensemble, réagissent pour fournir l'attendu de l'enseignant
qui les dévolue à quelques tâches définies dans le
manuel scolaire « Apprentissages numériques et résolution de
problèmes. » dont chacune intègre la question ci pertinente
de la recherche de trois nombres qui se suivent dont la somme d'avance
fixée. Les copies des élèves sont
toutes aussi importantes que le film, car elles offrent au
chercheur le déroulement des opérations qui devra se montrer
comme un mouvement continu d'étapes intelligibles ou plutôt comme
un mouvement entrecoupé de marques de reprise susceptibles d'amener
à la réponse.
2.6 ANALYSE A PRIORI
Avant de regarder au détail, les productions des
élèves à partir d'un problème il nous semble
important d'établir une certaine compréhension autour :
? du savoir choisi contenu dans une ressource d' Hatier ER EL C
1
? des praxéologies possibles de l'instance apprenant
? des problèmes didactiques que peut rencontrer
l'enseignant dans le cadre du déroulement de ce savoir.
2.6.1 Présentation et analyse a priori du
savoir 2.6.1.1 Présentation
Ce savoir mathématique a été
modélisé par l'Equipe de recherche en didactique des
mathématiques à l'Institut national de recherche
pédagogique et prescrit dans la collection d' Hatier 6ERMEL
dont le titre est « apprentissage numériques et résolution
de problèmes CM1 cycle 3. » (2005, p.62-66).Dans ce manuel
l'articulation de l'apprentissage se fait en trois phases
découpées en deux étapes chacune.
Le type de tâche est défini tel que le
maître doit prendre un exemple au début pour expliquer en quoi
consiste le problème. « Les nombres 5,6 et 7 sont trois nombres qui
se suivent et leur somme est 18. Je vais vous donner un nombre qui va
être la somme de trois nombres qui se suivent et vous, vous allez
chercher ces trois nombres. » :
Première phase : appropriation du problème et
premières recherches
1ère étape : recherche pour s=96. Consigne :
« vous allez chercher trois nombres qui se suivent dont la somme est 96.
Ecrivez tous les calculs que vous faites, il faudra ensuite expliquer comment
vous avez trouvé. ».
2ème étape : On fait avec un nombre plus grand ;
s=354
15
6 ERMEL : Equipe de Recherche sur les athématiques dans
l'Enseignement Elémentaire.
16
Deuxième phase : expliciter les propriétés
qui permettent de prouver
1ère étape : recherche individuelle avec s=25 et
s=45.l'objectif est de faire découvrir qu'il n'est pas toujours possible
de trouver trois nombres qui se suivent correspondant à une somme
donnée.
2ème étape : attendre des élèves
une formulation des propositions apportant la preuve que c'est impossible avec
s=25
2.6.1.2 Analyse a priori du savoir
Il s'agissait d'un cas de problème pouvant être
assimilé aux équations du premier degré à une
inconnue de la forme de : trouver x s'il existe tel que ( x -- 1) + x + (x
+ 1) = n (avec n E N) ou x + (x + 1) + (x + 2) = n (avec n E N) ;
car si l'on considère x + (x + 1) + (x + 2) = n, on a : n =
3x + 3 = 3(x + 1) . Dans cette forme,
on sait que n est multiple de 3. Donc après la
division de a , (x + 1) est
considéré
comme deuxième terme successif. Le premier
naturellement étant x si on introduit -1 à (x + 1)
et le troisième en ajoutant + 1 sur (x + 1). L'idée
de trois nombres qui se suivent est bien du domaine d'une suite de raison r = 1
; ce qui peut bien sûr faire l'objet d'un apprentissage ou qui apporte le
problème aux apprenants des niveaux de CM1 et CM2. La raison r est la
condition de résolution à un degré superieur que demander
simplement de trouver trois nombres identiques dont la somme se trouve
être n multiple de 3 ou n= 3. x . Il y a un
réel besoin de communication qui peut se produire entre
l'arithmétique et l'algèbre. Chacun prenant appui sur l'autre
pour expliquer le schéma de la résolution.
2.6.1.3 Analyse a priori des praxéologies de
l'instance apprenant
Nous savons que les tâches ou les types de tâches
provoquent généralement chez l'homo-sapiens, des manières
de faire qui sont parfois les mêmes. Le début du jeu est un moment
nous semble-t-il tout indiqué pour voir à quoi
l'élève va-t-il s'en tenir. Ainsi nous imaginons des techniques
possibles(T) que pourraient dérouler les élèves
de la classe choisie devant le problème présenté sous la
façon suivante : trouvez trois nombres qui se suivent dont la somme
(n) est donnée.
1 : multiplication d'un nombre x E N (pris au hasard)
par 3 et voir si le produit donne . Puis considérer qu'ils sont trois
nombres identiques et faire -- 1 pour le plus petit et x + 1 pour le
plus grand.
T2 : décomposition du chiffre des dizaines et
celui des unités pour trouver les trois nombres dont le nombre somme est
96. On a : 9 = 3+3+3 et 6= 3+2+1 pour le résultat suivant 31-32-33 ou
décomposition des dizaines et essai d'unités. On a 96= 90+6 et
on
17
écrit 90 = 30+30+30 ensuite à chaque 30, on y
met un chiffre à la place de 0 et on voit si les trois chiffres
constituent la suite dont le total est 6.
T3 : division du nombre somme ( n) par 3
pour trouver le deuxième nombre dans cette suite. Et successivement, on
retranche 1sur le deuxième pour trouver le premier et on ajouter 1 au
deuxième pour obtenir le troisième.
T4 : Technique intuitive. Elle relève des
opérations mentales ne donnant pas l'occasion à l'enseignant de
voir quelle est la procédure de résolution utilisée. Sur
la feuille, on voit juste les trois nombres qui se suivent dont la somme est
effectivement celle que l'enseignant a donnée. Cette technique peut
être rangée parmi les techniques invisibles si
l'élève ne l'explicite pas pour qu'une trace écrite nous
situe.
T5 : tirage d'une suite quelconque au sein des
entiers naturels et vérification de la proximité de leur somme
à la somme donnée : il s'agit d'opérer dans un intervalle
possible. 96 est la somme de trois nombres qui se suivent de deux chiffres et
non un ou trois chiffres.
T6 : retrait du surplus des deux plus grands nombres
du nombre somme, ensuite division par 3 pour obtenir le plus petit et ajouter
successivement + 1 et +2 au plus petit. On a 96-3=93, puis 93/3=31
et 31+1=32 ; 31+2=33.
2.6.2 Des résurgences des positions diverses des
élèves avec
Certains élèves qui pensent que ça marche
avec tous les nombres, vont prendre du recul en se posant la question s»il
n'y a pas des cas pour lesquels ça marche bien et d'autres pour lesquels
ça ne marche pas.
Des élèves qui pensent que ça marche
toujours pour vue qu'on accepte les nombres décimaux
Des élèves qui trouvent des nombres très
proches dont la somme n ne vérifie pas le nombre donné.
Exemple 25, ils peuvent trouver 7-8-9 avec n= 24 et 8-9-10 avec
n= 27. Mais pour n =25, la solution n'existe pas !
2.6.3 Marche vers une conjecture
La condition d'existence indiquée ci-haut de x
qui existe tel que (x -- 1) + x + (x + 1) = n (avec n E N) est
« n doit être multiple de 3 ». C'est pourquoi, il
importe d'introduire deux cas de figure pour provoquer des interrogations
à vocation ascendante dans leurs manières de faire :
18
n multiple de 3 ; c'est-à-dire n = 3(x + 1) et savoir
s'il existe une solution car x existe. Exemple n =12 ; on sait que 12=3x4 ou
12= 3x (3+1). On peut utiliser les tables de multiplication ou la calculatrice
pour vérifier 3x4 = ?
n non multiple de 3 ; c'est-à-dire n # 3(x + 1) et
savoir s'il y a une solution car x n'existe pas. Exemple n =13 ; on sait que
13? 3 x un nombre entier. On peut utiliser les tables de multiplication et/ou
la calculatrice pour vérifier qu'il n'existe aucun entier naturel qui
soit multiplié par 3 pour obtenir 13.
2.6.4 Analyse a priori des problèmes didactiques
possibles
Organiser le jeu pour mettre en action l'élève
est ce qui explique la présence du professeur à l'école.
Nous savons que les deux acteurs ont une histoire construite en classe autour
des premiers savoirs donnés qui servent de point d'appui à la
construction d'une nouvelle histoire. La modélisation
réalisée sur le problème par l'équipe de recherche
en mathématique a certes donné une forme accessible au savoir
mais il reste à l'enseignant le pouvoir de réalisation. Dans le
contrat didactique le professeur attend une réponse produite par l'usage
d'une technique qui produit un intérêt à notre recherche.
Si l'enseignant parvient à établir la compréhension
suffisante du problème de recherche aux élèves nous
pouvons penser qu'il s'appuiera sur les prés requis ou les acquis des
élèves qui sont divers ; par exemple sur la maîtrise de la
division euclidienne la multiplication les caractères de
divisibilité d'un nombre par 3 ou les caractères de nombre
multiple de 3.
Bien que l'enseignant sache compter sur les
élèves mais il ignore les représentations réelles
de ces derniers vis-à-vis du problème présenté.
C'est pourquoi il peut s'agir de voir l'enseignant définir
réguler et dévoluer la première tâche : ce que lui
impose l'action didactique conjointe du professeur-élève.
19
2.7 SYNOPSIS DE SEANCES
|
Séance
|
Temps en
minutes
|
Nombre de
tours de parole
|
Organisation : Faire jouer le jeu
|
Jeu : étapes de
l'activité
|
Observations
|
|
1. (á)
|
0mn
6mn
|
Professeur : 11 Elèves : 9
|
? L'Enseignant définit et dévolue le type de
tâche et la tâche1 aux élèves.
? L'écoute
individuelle des élèves
|
Type de tâche (T) :
trouver trois
nombres qui se
suivent dont la
somme est donnée !
Exemple : somme
= 18 ; les trois
nombres sont 5 ; 6 et 7.
t1 : trouver trois
nombres qui se
suivent dont le total est 96
|
Réactions de
compréhension
|
|
0mn
27,5mn
|
Professeur : 24 Elèves : 23
|
Travail individuel
|
Résolution du
problème :
Les élèves résolvent le problème
chacun avec une technique. correction
|
|
20
1.(â )
|
28mn53s
|
professeu r :
élèves :
|
· Rappel des techniques utilisées à la
séance 1.a distribution feuilles vierges.
|
t 2 :
· trouver trois nombres qui se suivent dont la somme
connue est un grand nombre ; 354
|
|
|
|
|
Résolution du
problème : les élèves résolvent le
problème chacun en maintenant sa technique ou en utilisant une technique
présentée par un autre élève lors des
justifications à la séance 1.a
|
Production de la réponse au moyen des techniques
invisibles et faibles
|
|
|
complément ou approfondis sement
|
1.â
· 00mn
5mn
|
Professeur : 63
|
Rappel du jeu sur les trois nombres qui se suivent et des
techniques.
|
t 3
trouver trois nombres qui se
suivent pour sept sommes
connues (324 ; 645 ; 915 ; 144 ; 273
; 489 et 552)
· un nouveau nombre
724 pour les élèves
qui ont fini.
|
|
|
|
|
· Résolution du problème : les
élèves résolvent le problème chacun en
|
|
|
21
10mn
22mn02s
|
Elèves : 34
|
avec tableau à 4
entrées et lignes
pour explications.
· Travail individuel
des élèves.
|
maintenant sa technique ou en utilisant une technique
présentée par un autre élèves
· Les élèves qui travaillent sur 724
indiquent un reste de 1 ou le nombre moyen est décimal
|
|
|
|
|
|
|
· Travail individuel et
|
|
|
|
32mn12
|
|
Ramassage des feuilles ; pas de correction au tableau
|
|
|
|
00mn
|
|
· Rappel du
caractère de
|
t4 :
|
Réactions positives
|
|
|
|
nombre divisible
|
· trouver trois nombres
|
:
|
Séance 2
|
4mn11 s
|
|
par 3 et des
techniques utilisées
|
qui se suivent pour sept
sommes connues (141 ;
|
impossib ilité ;
|
|
|
|
lors de la séance 1.a
|
309 ; 251 ; 624 ; 563 ;
|
reste 1 et
|
|
|
|
prolongée en 1.b et
|
701 et 414)
|
ne sont
|
|
|
17mn12s
|
Prof : 101
|
approfondissement
|
· Deux nouvelles sommes pour les élèves qui
ont fini
|
pas
divisible
|
|
|
|
Distribution de
|
(525 et 421)
|
|
|
19mn05s
|
Elèves : 73
|
feuilles récupérées
à la fin
· Régulation
|
· Extension avec cinq
nombres dont la somme est 525,
quatre nombres dont la somme est
|
s par 3
|
|
|
|
|
324 et sept nombres dont la somme est
|
|
|
|
|
|
1267
|
|
|
33mn45s- 51mn30
|
|
· Travail individuel des élèves.
|
Résolution de problèmes et discussion pour 324
|
|
|
|
récréation
|
|
|
|
Correction.
|
|
|
|
|
0mn-4mn45
|
|
|
|
|
22
2.8 LE JEU ET SA DEVOLUTION
Le recueil de données qui s'est fait en dates du 28mars
et du 02 avril 2013 et qui portait sur le travail des élèves
à travers les tâches (t1- t2- t 3- t4) susmentionnées dans
le tableau synoptique ci-dessus, présente quelques aspects y
résumés. Au début de la tâche (t1) l'enseignant dans
l'esprit de la présentation du savoir tel qu'indiqué dans la
ressource exploitée, définit le type de tâche (T) en
prenant un exemple avec le petit nombre somme 18. Le professeur (y) effectue la
somme de 5 ; 6 et 7 pour montrer deux choses :
- Que la somme est 18
- Que les trois nombres se suivent.
Cet exemple choisi est un moyen de dévolution des
élèves au problème et d'adaptation que le professeur (y)
met en action dans son topos pour faire comprendre la règle du jeu qui
est de trouver trois nombres qui se suivent dont la somme (multiple ou non
multiple de 3) est donnée. Des comportements de recherche de
compréhension se manifestent par des questions pertinentes des
élèves. L'enseignant qui compte sur les ressources individuelles
des élèves leur donne l'occasion de travailler seul. Cette
façon permet à chaque apprenant de générer des
éléments de technique personnelle. C'est un travail qui se fait
entre d'importants moments des séances. Pour la tâche (t1) on
observe 27mn 30s d'activité accordées aux élèves
dont l'attendu de l'enseignant est la réponse au problème
posé. Pour la tâche (t2), on a 6mn45s ; la tâche (t3),
12mn02s et la tâche (t4) ,17mn45s. On voit bien que les
élèves ont pris assez de temps lors de leur premier contact avec
le savoir.
S'il est vrai que le travail individuel pour le chercheur
permet de voir ce qu'utilise chaque acteur ( i) comme technique dans ce jeu, il
est aussi vrai que la mise au net ou correction lui permet de voir les causes
des changements des techniques par certains élèves ( 1 ... 23)
lors d'une autre tâche.
23
3. Analyse des praxéologies des
élèves
Séance1(á) : naissance d'embryons de techniques
|
Tendance de Techniques r
utilisées
|
1
|
2
|
3
|
4
|
5
|
6
|
|
Effectif d'élèves du C 1
|
1
|
1
|
0
|
2
|
4
|
0
|
|
Effectif d'élèves du C 2
|
3
|
2
|
1
|
2
|
4
|
0
|
|
Effectif total par technique
|
4
|
3
|
1
|
4
|
8
|
0
|
|
Effectif de la classe
|
20
|
Tableau 1:effectifs des élèves ayant
utilisés une technique
Le jeu, défini comme indiqué dans le synopsis
à la séance 1 et à la partie ( a), amène chaque
élève à une rencontre de soi et du savoir. Cette rencontre
est interactive entre le savoir et l'apprenant. Autrement dit elle provoque
dans tous les cas un regard personnel, une compréhension plus
approfondie de la de la question de recherche. La compréhension pour ce
problème impose à chaque élève de consulter dans
son répertoire cognitif, des problèmes déjà
rencontrés pour induire des représentations favorables à
la résolution du nouveau problème.
Au cours de cette partie, 4 élèves
(Andréa, Alexandre, Lucie et Illian) sur 20, ont utilisé la
technique x1 prenant appui sur la multiplication. Parmi eux, trois
élèves ont fait simplement 30x3 =90 et ensuite ils ont
associé à chaque 30 ; les chiffres 3-2-1 pour avoir 96. Sauf
Lucie qui s'est servie de la multiplication pour vérifier qu'elle est
proche de la somme. Elle fait 3 fois 30 ça donne 90 ; après elle
écrit 30+31+32 = 93 pas assez ; 32+33+34=99 trop et écrit
31+32+33 = 96 bonne réponse.
3 élèves (Pacôme, Erwan et Valéria)
sur 20, ont utilisé la technique x2 dite de décomposition. Deux
d'entre eux en exploitent la même stratégie : dans 96, on a : 9
c'est 3+3+3 et 6 c'est 3+2+1 et donc un chiffre de dizaine associé
à un chiffre des unités, on obtient 33-32-31. Le troisième
exploite la multiplication comme stratégie. Dans 96, Valeria voit 9
dizaines qui peuvent être réparties pour les trois nombres
recherchés et associer 1 ; 2 et 3 qui composent 6 pour obtenir
effectivement les trois nombres qui se suivent.
Production d'Yves
24
Yves, le seul élève sur 20, a utilisé la
technique 3 sans faire de division. Mais 32 est un nombre moyen que
l'on obtient bien par un calcul de division euclidienne.

4 élèves (Léon, Garance, Rayan et Mayeul)
sur 20, ont utilisé la technique 4 dite magique lors de la
verbalisation en fonction de ses opérations uniquement mentales et non
transcrites sur la feuille de recherche. L'un d'entre eux, pour cette
technique, utilise certainement une bonne logique qui peut conduire à un
résultat satisfaisant, mais il n'explicite pas à l'écrit
ces opérations mentales. Il déclare : « j'ai cherché
le nombre rond ; puis combien plus combien faisait 90 ; puis je me suis
rapproché du nombre et j'ai trouvé le résultat. »
8 élèves sur 20, à travers les feuilles
employées pour la recherche de la solution du problème, ont
utilisé la technique 5 dont le sens est établi
à l'analyse à priori des techniques aux précédentes
lignes du présent mémoire. Si le fait d'utiliser le principe est
le même c'est-à-dire poser une addition des nombres qui se suivent
et changer les nombres en raison de la proximité de leur total à
la somme indiquée, il demeure cependant des justificatifs au choix de
ces nombres qui singularisent les pratiques de ces élèves.
Sara présente trois opérations barrées de
trois nombres qui se suivent, 24+25+26 =75 ; 30+31+32 = 93
et 33+34+35= 102 et une opération jugée bonne 31+32+33
=96. Elle écrit à la suite de ces opérations : « J'ai
calculé dans les vingt et ça m'a fait un nombre trop petit et
après j'ai calculé dans les trente et ça a marché.
La réponse pour un total de 96 est 31-32-33. ».
Production de Zoé
25
Zoé du CM2 écrit : « 96/3 =32 » et
pose quatre opérations de trois nombres qui se suivent en
intégrant 32 d'abord au début à la fin ensuite au milieu
pour trois opérations et une opération qui ne contient pas 32 ;
c'est 34+35+36. Puis elle mentionne pour le nombre 96, les trois nombres sont :
31 ; 32 ; 33.
Lefèvre, élève de CM1, prend dans les
vingt mais évolue progressivement en changeant différents nombres
pour atteindre 96 comme somme.
Romain, Telma et Steeve savent que les trois nombres
commencent par 3 et changent de nombre en fonction de la somme obtenue qui est
soit grande, soit petite. Chacun fait des choix personnels en fonction de ses
estimations d'atteinte de la somme 96. Ils ont écrit
simultanément :
- Romain : « pour un total de 96, les trois nombres sont
31 ; 32 ; 33. J'ai additionné 31+32+33 et j'ai trouvé 96. J'ai
essayé ces nombres car ils commencent tous par trois. ».
- Steeve : « j'ai fait 30-31-32 ça faisait 93 et
j'ai essayé 31-32-33 et j'ai trouvé 96 ».
- Telma : « 34 35 36 =105 ; 33 34 37=102 ;
35 36 37 ; 30-31-32= 93 ; 29-3031=90 ; 31-32-33=96 »
26
Sheryne n'a pas fait long. Elle dit : « on fait 31+32+33
; ça fait 96 et au début, j'ai fait 30+31+32 donc j'ai fait
après comme c'était proche ».
Inès applique l'essai erreur avec les nombre
commençant par 3. Elle pose successivement des suites qu'elle supprime
après parce que n'aboutissant pas à la réponse. 30 31
32 ; 34 35 36 ; 32 33 34 et 31-32-33 =96
3.1 LA CORRECTION : UN JEU DE VERBALISATION
Un moment important dans la séance 1.a est
réservé aux explications des élèves de leur
procédure de résolution du problème rencontré. Il
faut pour cela accepter que certains élèves n'aient pas vraiment
expliqué réellement ce qu'ils ont fait parce que l'enseignant
prenait un ou deux par groupe d'élèves mis ensemble en raison de
l'approche utilisée ou simplement de l'hésitation dont ont fait
montre certains d'entre eux .
En leur donnant l'occasion d'expliciter les procédures
utilisées on voit plus clairement le non-dit sur les feuilles de
recherche.
Par exemple Sara du CM1 qui a écrit : « j'ai
calculé dans les vingt et ça m'a fait un nombre trop petit et
après j'ai calculé dans les trente et ça a marché !
»,déclare : « j'ai d'abord pris dans les vingt 24+25+26=75 ;
après j'ai pris dans les trente c'est trop petit après j'ai fait
30+31+32 = 93 ensuite j'ai fait 33+34+35 =102 ; j'ai vu que c'était trop
alors j'ai pris 31+32+33 =96 j'ai vu que c'était la bonne
réponse. ».Le discours nous présente un détail bien
qu'il soit le même car ici en plus de l'idée de faire les calculs
progressifs d'addition on voit la raison de suppression de deux
opérations exprimées en « trop petit ». Elle fait bien
allusion au total trouvé qui est inférieur à la somme
donné. Mais on ne voit pas celle qui permet de supprimer 33+34+35 =102.
C'est dans le discours de l'élève que l'expression « trop
»nous édifie.
L'élève du CM2, Zoé, qui place 32 au
début (32 ; 33 ; 34), à la fin (30 ; 31 ; 32) et au milieu (31 ;
32 ; 33), indique : « j'ai divisé 96 par 3 pour voir de quel nombre
ça allait se rapprocher j'ai essayé 30 ; 31 ; 32 et ça
faisait 93 ce n'était pas assez après j'ai essayé 31 ; 32
; 33 et ça faisait 96 ». Son écrit n'explique pas pourquoi
elle abandonne la division qu'elle a effectuée. ais nous comprenons
qu'elle s'en sert juste pour être proche des nombres
recherchés.
Après lecture par le professeur de l'écrit de
Valéria « les nombres qui se suivent et qui donnent un
résultat de 96 sont 31 ; 32 ; 33. J'ai pensé que 3 fois 3 c'est
9. J'ai tout de suite pensé à 1 ; 2 ; 3 et puis j'ai
trouvé le résultat en les additionnant ».
27
L'élève du CM2, Léon, qui a écrit
: « j'ai trouvé car j'ai réfléchi. Les trois nombres
qui se suivent sont 31 ; 32 ; 33 » explique : « je disais dans les
unités ça doit faire 6 ; donc 1 ; 2 ; 3 et ça fait 6 et
dans les dizaines ça doit faire 9 j'ai pensé à 3 ; 3 ; 3
ça fait 9. Donc total 96. On voit ici clairement que cet
élève change complètement le discours ; il passe d'un
état très mentaliste à un état opératoire.
alheureusement, Garance du C 2 qui écrit « quand on m'a dit le
résultat les nombres sont venus tout seul. » ne prend pas un tour
de parole. Cette phase de verbalisation nous montre qu'elle est un moment
d'interaction et d'appropriation du savoir à travers l'écoute de
l'autre (professeur ou condisciple).
L'unique élève (CM2), Yves, qui a écrit :
« j'ai fait 32+32+32 =96 ; on compense le 32+1=33 pour compenser le 1
», explique : « en fait j'ai décomposé j'ai presque
décomposé j'ai cherché combien trois nombres pour faire 96
32+32+32 ; j'ai trouvé 3 fois 32 ; je me suis dit comme ça fait 3
fois de suite, il faut faire quelque chose, après j'ai compensé
j'ai... » et à la demande du professeur, il développe que
compenser : « c'est par exemple un jour on avait hein ... comme si on
avait une méthode où on prend 1 chiffre et on donne à
côté, on ne met pas en dessus , alors que nous on prend en dessous
et on n'est pas obligé de donner au-dessus bon là c'est 32 on
enlève le 1 du premier 32 et on le donne au dernier 32, et ça
fait 31 ;32 ;33. ». La copie sur laquelle il a produit son
résultat, ne permet pas de saisir explicitement sa pratique ! Mais
prendre 1 chiffre et donner à côté ou enlever le 1 du
premier 32 et donner au dernier c'est bien l'idée ingénieuse de
(x - 1) et (x + 1) que l'on saisit grâce à la
verbalisation.
Romain qui a écrit : « J'ai additionné
31-32 et 33 j'ai trouvé 96 ; j'ai essayé ces trois nombres car
ils commencent tous par trois ».déclare : « en fait j'ai
essayé d'additionner entre 31 ; j'ai pris 6 d'abord donc ça
faisait 1+2+3 =6 et j'ai pris 9 ça faisait 3+3+3 = 9 et j'ai vu que 3 et
1 ça faisait 31 ; 3et 2 ça fait 32 puis 3 et 3 ça fait
33.
Andréa du CM1 qui a écrit : « j'ai
trouvé en multipliant 3x30 = 90 ; puis j'ai additionné trois
nombres qui se suivent et qui font 6 ; 3+2+1, déclare après le
professeur qui voulait savoir pourquoi il s'est arrêté ?
«Parce qu'au début j'ai trouvé trois nombres, mais
égaux ! » . Cette verbalisation offre dans tous les cas un
éventail des manières de faire. Ceux qui ne terminent pas ou qui
se bloquent dans leur procédure se retrouvent dans une situation de
compréhension des techniques utilisées par les uns et les
autres.
Alexandre, élève du CM2 et qui écrit :
« j'ai fait 30 x 3 ça fait 90 donc j'ai pris 90 et 6 ça me
fait 96 » en déclarant : « j'ai fait pareil que Romain, mais
ma feuille est ici ! » ne fait pas exception à la règle.
Dans cette réaction du rangement de la copie mise
28
ailleurs qu'à côté de celle de Romain nous
y voyons une identification à une technique bien que faible ; mais une
manière de faire établie pour résoudre le
problème.
3.2 ASCENDANCE ET COMPREHENSION DES PRAXEOLOGIES DES
ELEVES.
Il nous vient que critiquer ou analyser un
phénomène passe avant tout par la connaissance de celui-ci ;
c'est pourquoi nous présentons les productions des élèves
sous leur forme originale afin de mieux comprendre leurs pratiques. Les
élèves qui ont commencé avec une quelconque peuvent
changer en fonction de la pertinence d'efficacité d'une autre . Il peut
aussi s'agir du maintien d'une technique qui a permis d'obtenir les
résultats ; ou simplement de poursuivre avec la même technique
étant donné qu'une explication peut apporter à un
élève, un détail nécessaire pour la suite.
3.2.1 Séance 1.b : consolidation ou
réajustement ?
|
Tendance de Techniques utilisées
|
1
|
2
|
3
|
4
|
5
|
6
|
|
Effectif d'élèves du C 1
|
0
|
1
|
1
|
0
|
6
|
0
|
|
Effectif d'élèves du C 2
|
0
|
1
|
2
|
0
|
9
|
0
|
|
Effectif total par technique
|
0
|
2
|
3
|
0
|
15
|
0
|
|
Effectif de la classe
|
20
|
Tableau 2: praxéologies des élèves.
Le jeu redéfini à la partie 1.b donne une
occasion aux élèves de se réaffirmer ou d'utiliser des
ressources capitalisées à la partie dite 1.a ; car on sait que
l'esprit humain infère ou induit du sens à partir de
différents éléments du contexte et de la culture. Nous
pensons qu'à cette première partie de la séance 1, s'il
n'y a pas eu fixation sur une façon de faire, cependant des idées
peuvent se restructurer pour réaliser cette nouvelle tâche qui
exige une utilisation efficace d'une technique.
Andréa du CM1 devant la nouvelle tâche avec 354
établit que 100+100+100 = 300. Il essaie la division 54/3 = 1 et
l'abandonne après avoir posé pour le reste de la division (54 -
24= ? ) ; il essaie cette fois par multiplication 15x 3= 45 ; 17 x3 =511 ; 19
x3 =57 et 18 x 3 = 54 ; puis il pose 18-18-18. Il retire 1 du premier 18 ; il
reste 17 et le donne au dernier 18 pour obtenir 19, alors il forme 117 +118+119
=354. Il écrit
29
ensuite : « j'ai fait la méthode de compensation.
Pour un total étant de 354, les trois nombres sont 117 ; 118 ; 119
». Le professeur, qui a regroupé les productions des
élèves en fonction des approches utilisées explique
qu'Andréa s'est servi de toutes les techniques : la division pour
chercher à trouver le nombre moyen, mais il abandonne en raison de la
non maîtrise de la technique opératoire. Il utilise la technique
essai-erreur ( ) mais avec la multiplication jusqu'à ce qu'il trouve la
bonne réponse 18 x3 = 54, il utilise la compensation à partir de
18 (17-18-19). Il a au départ appliqué la décomposition
100+100+100 = 300. Finalement par addition, il obtient 100+17 = 117 ; 100+18
=118 et 100+19 =119. Rappelons qu'à la partie 1.a de cette séance
Andréa avait multiplié 3x30 = 90 ; puis additionné trois
nombres qui se suivent dont le total est 6 ; 3+2+1 pour avoir les
différents nombres par addition 30+3 ; 30+2 ; 30+ 1. On comprend que la
correction de la tache donnée à 1.a : plus
précisément les justificatifs des collèges ont
impacté sur la manière de faire d'Andréa à cette
partie 1.b de la séance 1. Car la division qu'elle a tentée
d'effectuer le montre très clairement. Il est resté aussi
lui-même par endroit avec l'utilisation de la multiplication pour obtenir
54.
Zoé du CM2, qui à la partie 1.a après la
division, sachant que le nombre moyen faisait partie des nombres qu'elle
trouvait par essai-erreur (tirage d'une suite contenant le nombre moyen),
obtient directement les trois nombres après la division. Cette fois elle
trouve directement le premier nombre plus petit que le nombre moyen obtenu de
la division ; et par ricochet le plus grand. Il apparait un réel
exercice de mémoire implicite du fait du rappel accidentel
d'expériences passées qui se construit dans l'agir de cette
élève ; car elle sait désormais la place attendue du
nombre moyen. On peut aussi constater qu'elle a choisi une technique qui
permettra désormais d'attaquer ce type de tâche. Cette
manière de faire ne s'éloigne pas totalement de ce qu'Yves a fait
en parlant de compensation. Car trouver le petit nombre pour Zoé
c'est
reculer d'un à partir du nombre moyen ( ) ou encore moins
trouver le grand
nombre c'est avancer d'un à partir du même nombre
moyen ( ).
Yves utilise, à cette partie 1.b, des emprunts pour
obtenir de façon technique le nombre moyen contrairement à ce
qu'il a fait à la partie 1.a de la présente séance. Il
fait une décomposition multiplicative de 354 c'est 3 x 100 et 3 x18 mais
il vérifie par division si 3x18 donnent 54. Puis il trouve le nombre
moyen en additionnant simplement 100 +18 = 118. On observe qu'Yves se sert bien
de la multiplication comme Alexandre et Andréa qui ont
présenté comment ils ont procédé à la
correction de la partie 1.a de la présente séance ; car pour
trouver 96, ils ont fait 3 x30 ou 30 x3 pour avoir 90 et additionner à
chaque 30 , 1 ;2 et 3. Bien sûr que ce qui différencie ces deux
élèves à Yves c'est le fait que dans cette nouvelle
démarche d'Yves il s'agit
plutôt de trouver 2 comme nombre moyen d'unités
à partir de la division 6/3 = 2 ; donc on prendrait 32 comme nombre
moyen. Nous voyons très bien qu'Yves a été impacté
par la verbalisation du milieu ; puisque autant cet élève agit
sur le milieu que ce même milieu agit sur lui.
Inès utilise la décomposition additive et
multiplicative. 354 c'est 300+50+4 et 3x100 ; 5x10 et 4x1. ais 100+10+1 = 111
qui malheureusement n'est pas un nombre exploitable ! Cette
décomposition qu'elle utilise pour attaquer le même type de
tâche semble encore lui échapper. On voit qu'elle veut
procéder comme Yves qui s'est servi de la technique adoptée par
Alexandre et Andréa. La verbalisation, une fois de plus, semble faire
avancer les schèmes pour donner du sens à ce qu'elle fait.
L'essai-erreur qui demande plus de temps et qu'elle continue d'utiliser par
défaut de bonne exploitation de la technique, ne lui a pas permis de
trouver la bonne réponse !
Erwan s'emploie lui à utiliser la technique de
décomposition à en juger par sa première ligne où
il écrit 300-50-4. ais il considère qu'avec 300 le nombre moyen
est 100 et on peut avoir comme grand nombre 101 et 99 comme petit nombre.
Malheureusement il n'exploite pas 50 et 4. Il pose la combinaison 118-117119
alors qu'il n'a que 99-100-101. Bien que des difficultés subsistent
encore, cette nouvelle manière de faire est emprunte d'influence
extérieure ; car il est passé d'une décomposition du
chiffre des dizaines puis à celui des unités (dans 96 9 c'est
3+3+3 et 6 c'est 3+2+1) pour obtenir la combinaison correcte à un autre
type de décomposition (96 c'est 90+6) qui permet d'avoir des nombres
proches.
Dans cette même partie 1.b de la séance 1, il y a
un conglomérat de 15 élèves sur 20 qui se rechignent
à utiliser la technique de l'essai-erreur( 5). On est donc passé
de 8 à 15 ; ce qui est un exode important et qui nous montre que ces
élèves ont été influencés par la phase de
correction qui est un moment réel de verbalisation explicative des
élèves et de validation des procédures comme l'enseignant
le conseille ci bien aux élèves qui éprouvent des
difficultés à utiliser une technique :
Professeur (16mn47s) : oui on a déjà fait sur
des opérations méthode essai avec un s et erreur avec un s
(essais-erreurs) mais j'aimerais qu'il y en a le moins possible ; merci. Quand
on est bloqué par contre hein, tu ne sais pas ; méthode
essai-erreur ; tu essaies quelque chose, tu regardes si ça va ! , si
c'est plus petit ou plus grand tu essaies si ça te convient très
bien ! Si ça ne te convient pas tu réajustes : ça c'est
une méthode quelques soient les situations les jeux etc... on peut
utiliser cette méthode d'essai-erreur, il ne faut pas hésiter
!
31
Pacôme, qui avait commencé avec un peu de
décomposition, semble avoir été
entrainé par la technique d'essai-erreur('r5)
très en usage par un groupe important de la classe
(8élèves), essaie directement avec une combinaison de trois
nombres dont la somme est plus élevée 151+152+1523 =456. Il
diminue les nombres et obtient la bonne réponse. Lui qui avait
utilisé un discours de justification pour 96, quand il posait 6 ; c'est
1+2+3 et 9 ; c'est 3+3+3 tente trouver un nouveau discours ; mais il n'explique
que la technique opératoire : « on sait que 7+8+9 ça fait 24
et que 1+1+1 plus 2 de retenue ça fait 5 et que 1+1+1 ça fait 3.
Donc le résultat est 354.
Telma, dans cette démarche conseillée aux
élèves qui éprouvent des difficultés à
utiliser une autre technique, reste rattachée à ses
représentations de départ. Elle utilise une succession
d'additions pour avancer vers la bonne réponse qu'une division
contraignante. Les additions choisies sont aussi loin de lui offrir des
tendresses car par endroits on voit des erreurs liées au rangement des
nombres composés de deux chiffres et ceux composés de trois
chiffres dans une addition. Elle s'en sort mieux quand les nombres ont le
même nombre de chiffres.
Sheryne pratique, dans l'ensemble des taches données
par le professeur, l'essai-erreur ('r 5). Elle n'a donc pas tenu compte de ce
qu'elle a vu lors de la correction.
Sur la copie de Léon, à cette même partie
1.b de la séance 1, il cherche par essai-erreur la bonne combinaison,
déroule 15 opérations additives et ne trouve la bonne
réponse qu'à la seizième opération. Ce qui est
contraire à ce qu'il avait fait lors de la partie 1.a. Cette variation
de pratiques à son niveau prouve qu'il a été
influencé par les interventions des autres élèves et par
la validation de cette pratique par le professeur.
Valeria utilise l'essai-erreur('r5) à 1.b alors qu'elle
avait utilisé la décomposition ('r2). Elle commence très
rapidement avec les nombres proches dont la somme est inférieure
à 354 ; notamment avec 114+ 115+ 116.
ayeuil s'inscrit lui aussi dans la même pratique en
commençant directement par 116 + 117 + 118 = 351 et augmente chaque
nombre de 1 et obtient 117 +118 + 119 =354. On observe bien qu'il y a
également une variation de pratiques à son niveau. Dans ces
explications on y perçoit clairement l'emploi de la technique
essai-erreur ('r5), mais pas le choix des nombres proches de ceux qui sont
attendus.
Lucie utilise la multiplication comme à 1.a pour se
rapprocher de la somme et se situer par rapport au choix des nombres à
prendre. Elle pose 100 x3 =300 et prend les
32
nombres qui composent cette première addition 130 + 131
+132 = 393 ; puis elle se retrouve avec un intervalle de nombres à
essayer après avoir conclu « trop » pour 120 +121 + 122 = 363
et « pas assez » pour 115 +116+ 117 = 348.
Sara, quant à elle, a repris simplement ce qu'elle a
fait à la partie 1.a en choisissant les nombres dont le premier chiffre
des centaines est 1 les essayer jusqu'à ce qu'elle trouve 117 ; 118 et
119 qui vérifient la somme de 354.
Steven qui voulait utiliser la division, revient comme
à 1.a à l'essai-erreur avec plusieurs additions commençant
par 120 +121+ 122 =363.
Rayan lui aussi se déploie à utilise
l'essai-erreur alors qu'il avait utilisé le parachutage de la
réponse. Il passe ainsi de la technique dite magique dont les
opérations sont effectuées dans le mental de
l'élève. Il pose 114 +115+ 116 = 345 ; puis augmente
jusqu'à obtention du résultat.
Ilian lui commence avec 111 +112+ 113 = 336 et écrit
c'est trop petit. Il pose ensuite 120 +121 +122 =363 et constate que c'est
« trop grand » ; il finit par régler son intervalle de choix.
Il y a pour lui une variation de pratiques à cette partie 1.b de la
séance1, car il avait fait 30 x3 90 et 3 +2 +1 = 6 pour construire les
nombres 31 ; 32 ; et 33. Cette variation intervient après la correction
de 1.a.
Alexandre qui faisait partie des quatre élèves
qui avaient utilisé la décomposition de 96 en 30 x3 = 90 et 6 en
1 + 2 + 3, trouve nécessaire de pratiquer La technique ('r5). Ce
changement serait lié aux éléments intervenus lors de la
correction.
Romain qui avait essayé trois nombres qui se suivent
était convaincu qu'ils commençaient tous par 3. Ici, il fait la
même chose ; il commence avec 127 parce qu'il sait que 1 est le premier
chiffre en vérifiant par multiplication la proximité du produit
à la somme 354. Ainsi 127 x3 = 381 ; il varie pour diminuer avec 125 x3
= 375 jusqu'à obtention de 118 x3 = 354 et il pose 117 +118+119 =
354.
Lefèvre poursuit dans le même sens qu'à la
première tâche définie pour commencer le jeu didactique. Il
fait un sursaut sur les nombres de trois chiffres commençant par 1 avec
125 +126 127 et obtient 388 et il les diminue de 10 ; de 4 ; de 7 ; puis de 8
et obtient 117 +118 119 = 354. Il s'agit donc d'une diminution dans la pratique
de l'essai-erreur ('r5). Ce qui montre que cet élève n'a pas
connu l'influence d'éléments développés lors de la
verbalisation.
Garance qui a voulu utiliser la multiplication en posant 30
x10 = 300 s'est rapidement orientée vers une technique plus accessible
pour le plus grand groupe ; car elle ne peut utiliser sa technique avec des
nombres davantage plus grands qu'avec 96 où elle exprimait la
spontanéité de la réponse. Elle pose 111 + 111 + 111 = 333
; puis
33
elle augmente à 120 +121 +122 = 363 ; opération
qui l'amène à faire une régression nécessaire.
3.2.2 Séance 1jâ prolongée :
réaffirmation ou réajustement ?
Il est de tradition que si une personne attaque un type de
tâche avec beaucoup d'aisance elle laisse penser qu'elle a
développé une forte compétence pour réaliser ce
type de tâche. Le professeur veut marquer cette fin de séance 1
par deux lots de sept sommes chacun (grands et petits nombres) comme clairement
indiquées sur les feuilles de résultat des élèves.
Il s'agit toujours de trouver trois nombres qui se suivent dont la somme est
connue.
Romain qui a presque tout trouvé, n'explique pas
malheureusement comment il a fait pour trouver toutes les réponses
correctes. On observe cependant sur sa feuille de recherche qu'il pratique
parfois la division-compensation ('r3) le cas de 552 et 489, parfois la
multiplication ('r1) le cas de 144-273-915-645 et aussi l'addition ('r5)
à pieds joints c'est le cas 324. Il montre par sa pratique plurielle
pour lui qui au départ n'avait pas utilisé de division, que les
multiples communications intérieures à la séance 1,
modifient ses schèmes de façon significative.
Andréa fait preuve de mutation intérieure, car
il avait au départ utilisé la multiplication pour vérifier
54 = (18 x3) dans 354 . Puis additionner après la compensation du nombre
18 chacun des nombres 17-18-19 à chaque 100 obtenu par
décomposition. Ici, il utilise la division sur sa feuille de recherche.
Mais il inscrit aussi par endroit la décomposition car avec 915, en plus
de la division de 15/3, il pose 300 +300 +300 = 900, puis il additionne 300 +5
= 305 qui est le nombre moyen et il vérifie 304 + 305 + 306 = 915.
Mayeul change de pratiques, car à la partie
précédente de la séance 1, il avait plutôt
préféré l'essai-erreur en plaçant 1 comme
étant le premier chiffre qui commence ces nombres pour la somme de 354.
Ce changement se caractérise sur le fait de voir apparaitre sur sa
feuille de recherche des divisions pour les sommes 552 ; 489 ; 273 ; et 144. On
note en outre l'emploi du parachutage du nombre moyen pour 645 ; 324 et 915. On
peut s'imaginer à l'évidence qu'il s'agirait toujours de la
division qui semble être le moyen rapide.
Bien que steven n'explique pas comment il a fait pour trouver
toutes ses réponses correctes, il déroule sur la feuille de
recherche un ensemble d'additions successives qui caractérisent l'emploi
de la technique dite essai-erreur ('r5) comme il l'avait utilisée
34
à la partie précédente de la
séance1. Cependant on observe la présence de trois divisions qui
donnent lieu à une simple approximation au nombre moyen pour 489 ; 645
et 552. Ensuite il y a un retour à l'emploi de l'essai-erreur.
Rayan est un élève du CM1 qui a totalement
changé sa pratique. Il avait commencé par le parachutage des
réponses. Puis il avait avancé en exploitant l'essai-erreur ; et
là il pratique la division pour trouver chaque suite.
Sheryne, élève du CM2, chemine dans la pratique
absolue de l'essai-erreur à travers l'ensemble de toutes les parties de
la séance 1 quelle que soit la tâche définie pour ce type
de tâche. Elle a tenté d'effectuer la division 915 par 3. Pour
elle, le début de la réponse était 9 ; malheureusement
elle manque d'assurance et de confiance en soi : ce qui la ramène
à un repli de technique.
Lucie qui à la tâche précédente
s'était servie de la multiplication pour se rapprocher des nombres
à prendre comme réponse a trouvé la
nécessité de s'aider de la division pour chaque somme. Elle
utilise la multiplication à cette tâche juste pour vérifier
si le nombre moyen trouvé est le bon.
Ilian n'utilise que des divisions pour trouver le nombre moyen
quelle que soit la somme. L'addition ( ex :107+108+109 = 324 ?) lui sert
à compenser et à vérifier si la somme est obtenue à
travers les nombres qu'il opérationnalise. Précisions qu'il se
servait de l'essai-erreur ; ensuite de la multiplication pour trouver le nombre
moyen. Cette nouvelle pratique qu'il met en place, vient après le jeu de
la correction de la tâche précédente. D'où nous
comprenons qu'il y a eu des facteurs importants de la correction l'entrainant
ainsi à changer de façon de faire.

Erwan
35
Erwan qui a choisi de travailler avec le lot de petits nombres
semble désormais inspiré par la compensation qu'il
représente assez bien par une flèche. On voit comment il trouve
le nombre moyen par la division et la flèche qui reste le signe de sa
compréhension de la compensation pour 45 et 15. On observe une
flexibilité à changer de façon de faire pour terminer plus
rapidement et plus facilement les tâches définies par le
professeur.
Yanis bien qu'absente aux deux premières parties de la
séance1, en bénéficiant de l'assistance de l'enseignant ,
s'incline vers l'essai-erreur alors qu'elle avait commencé par poser une
division pour attaquer l'avant dernière somme de la liste. On comprend
qu'elle n'a pas encore intégré une ressource suffisante
(compensation) pour agir lorsqu'elle se retrouve devant un cas comme 33 + 33 +
33 = 99. Ici on voit qu'elle a abandonné la suite et le tableau reste
vide.
Yves qui sait utiliser la compensation dès le premier
jeu didactique défini, se rapproche entre ('r2) et ( 'r3). Il
décompose par exemple 645 en 600 et 45. Il pose 600 = 3x200 ; il divise
45/3=15. Et il regroupe 200+15 = 215 qu'il considère comme nombre moyen.
Puis il pratique simplement la compensation. Cette technique malheureusement ne
fonctionne qu'avec les nombres dont le chiffre de centaine est un multiple de 3
et les deux derniers chiffres constituent un nombre multiple aussi de 3. Ce qui
n'est pas le cas pour 144 et 489. Il aborde la division pour 144 ; 273 ; 489 et
552. On peut comprendre qu'il s'oriente vers la pleine division par
nécessité d'affronter cette catégorie de nombres dont le
chiffre de centaine n'est pas un multiple de 3 encore moins les deux derniers
chiffres ne forment pas un multiple de 3. Bien qu'étant mal à
l'aise avec ces nombres, il a cependant utilisé 'r3 .
Garance
36
Garance fait montre de flexibilité par le fait qu'elle
utilisait comme techniques la multiplication et l'essai-erreur ; maintenant
elle utilise la division pour loger le nombre du centre pour remplir facilement
le tableau à quatre entrées comme cela apparait bien dans les cas
présentés ci-dessus. Et elle fixe les autres nombres selon que
les vides sont exigeant des critères clairement précisés
(nombre précédent et nombre suivant). Cette étape de
l'écriture du nombre précédent et/ou du nombre suivant
n'est pas présentée sur la feuille de recherche ; sinon
directement sur la feuille des résultats.
Inès adopte la division comme opération pour
trouver les trois nombres qui se suivent. Elle vérifie la
fiabilité des résultats par addition après une
compensation faite mentalement. Son passage de la décomposition qu'elle
se servait aux tâches précédentes à la division pour
finir avec la compensation, est la preuve du changement de technique d'attaque
pour ce type de tâche. Cette nouvelle approche lui a permis de terminer
avec le lot de petits nombres et de commencer le lot des grands nombres dans la
limite du temps de travail donné pour la production des
résultats.
Pacôme qui utilise l'essai-erreur à la
troisième tâche après utilisation de la
décomposition à la première tâche a finalement
recourt à la division bien que l'essai-erreur est intervenu pour la
première somme qui semble facile (107 +108+109 = 324). Toutes les autres
sommes (645 ; 915 ; 144 ; 273 ; 489 et 552), ont un traitement établi du
point de vue de la division euclidienne. On voit une nouvelle adoption de
technique
37
après l'intervention du professeur qui définit
la troisième tâche en reprenant l'exemple de 96 comme somme vue
à la première tâche.
Telma fidèle à l'essai-erreur, ne termine
malheureusement pas la tâche. Elle traite cinq sommes sur sept. On voit
sur sa feuille de recherche une tentative de résolution par division
mais qu'elle barre rapidement parce qu'elle est convaincue des erreurs
possibles y contenues ; car elle trouve 144/3 = 40 et 489/3 =38. Cependant, on
peut comprendre par cet essai que l'intervention de l'enseignant a un impact
sur sa manière de faire.
Sara utilise comme aux tâches précédentes
l'essai-erreur avec moins d'essais pour chaque somme. Dans cette pratique
malheureusement, elle ne termine pas la tâche. Mais ce regard qui
amène rapidement à une combinaison qui serait la réponse
attendue tend vers une division. On voit qu'elle situe les nombres dans un
intervalle d'espoir ; car pour 144 par exemple elle prend 50 +51 + 52 = 153 et
descend jusqu'à obtenir la réponse ; ou pour 915, elle pose 306
+307 +308 = 924 et elle diminue un peu jusqu'à obtention de la
réponse souhaitée.
Léon recherche les réponses autant qu'à
la partie précédente par l'essai-erreur et la maîtrise de
l'addition semble pour lui une forte compétence qui lui permet de
trouver toutes les réponses dans la limite du temps de travail
accordé à l'ensemble des élèves. Cette confiance de
soi à travers la maîtrise de l'addition ne fait entrevoir en aucun
endroit le besoin de recourir à la division.
Paul Alexandre et Valeria choisissent chacun pour ce qui le
concerne l'essai-erreur comme technique d'attaque de cette troisième
tâche. Seul Alexandre termine la tâche donnée alors que les
deux autres n'obtiennent pas le temps nécessaire pour traiter le dernier
cas centré sur le nombre 552.
3.3 INTRIGUE DE L'INTRUS DANS LA SEANCE 1
La recherche des nombres qui se suivent dont la somme est
d'avance fixée est un jeu qui semble désormais entrainer tous les
élèves de la classe quelle que soit la manière dont ils
s'y accrochent. ais l'imprévisible condition qui s'impose au nombre
somme est la source du rébus. Pour être donc un bon joueur, il
faut connaître la caractéristique centrale du nombre somme.
Le professeur vers la fin de la séance 1
s'intéresse aux élèves qui ont terminé la
tâche composée des nombres contenus dans le tableau rempli par
chaque élève. Il
38
leur demande de travailler avec le nombre 724 en
précisant : « ça ; c'est pour ceux qui ont fini ! »
Des difficultés commencent alors à se pointer
avec ce nombre comme le montre une partie de la transcription de la fin de la
première séance.
Professeur (19mn29s) : 1 ; 2 ; 3 ; ceux qui
n'ont pas fini vous essayez d'expliciter la méthode ! Pour ceux qui ont
fini vous explicitez aussi la méthode, sinon vous faites ça
regardez ! Il écrit la somme vaut 724. Ça c'est pour ceux qui ont
terminé !
Professeur (20mn19) : régule, il
revient chez Paul qui ne décolle toujours pas ! Il essaie de l'amener
à la division !
Professeur (21mn54) régule : il
s'arrête chez un élève qui était absent à la
première séance, il dit en 24 il y a combien de fois 3, il y a 8
fois.
Un élève (27mn58s) : est-ce qu'
on peut trouver des décimaux ?
Professeur (28mn00s) : non, on cherche des
entiers hein ! Qui sont ceux qui font avec 724 ? Vous n'arrivez pas ?
Les élèves concernés (28mn)
: non, on n'arrive pas !
Professeur (28mn42s) : pourquoi vous
n'arrivez pas ? Zoé, Garance ? Léon ? Pourquoi vous n'arrivez pas
?
Zoé (28mn52s) : il reste 1
Garance (28mn59) : il reste 1
Léon (29mn07s) : la réponse se
serait un nombre à virgule
Professeur (29mn12s) : toi aussi tu vas
essayer ?
Un élève (30mn02) : moi, j'ai
trouvé un entier ... mais j'ai divisé par 4 ce n'était pas
par 3
Professeur (31mn05s) : pourquoi on divise par
3
Iliane (31mn10s) : parce que c'est trois
nombres qui se suivent
Une élève (31mn33s) :
lève le doigt, on garde la partie entière et on enlève les
nombres après la virgule ;
Professeur (32mn) : bon, vous allez me
vérifier vos deux noms, ça va être deux feuilles, votre nom
et votre prénom, sur les feuilles que vous avez fait et vous allez me
poser ça ici ! La feuille de recherche aussi
lèves Pour les (32mn12s)
: élèves oui dont la pratique à la fin de la
séance 1 est focalisée sur la division et la compensation qui est
la technique qui permet d'aller vite il y a un ressenti de
difficultés présentées par le nombre
choisi sur le fait du reste et d'autres sur le fait d'avoir un nombre
décimal. On voit d'ailleurs un élève qui change de
diviseur pour tenter de rendre son opération possible.
39
3.4 INTRIGUE ET INTRUS DANS LA SEANCE 2
|
Tendance de Techniques utilisées
|
1
|
2
|
3
|
4
|
5
|
6
|
|
Effectif d'élèves du C 1
|
0
|
0
|
6
|
0
|
3
|
0
|
|
Effectif d'élèves du C 2
|
0
|
0
|
10
|
0
|
1
|
0
|
|
Effectif total par technique
|
0
|
0
|
16
|
0
|
4
|
0
|
|
Effectif de la classe
|
20
|
Tableau 2: praxéologies des élèves à
la séance 2
Comme dans tous les jeux l'excellente connaissance des
règles comme ressources qui organisent un jeu permet au joueur de se
servir régulièrement de celles-ci afin d'échapper aux
multiples occasions de rebut dont l'ultime dessein est l'apprentissage. Celui
qui consiste à trouver trois nombres dont la somme est connue ne peut
donc déroger à ce principe. L'enseignant introduit dans une liste
des nombres déstabilisants 141 ;309 ;251 ;624 ;563 ;701 et 414 pour
amener les élèves à découvrir qu'il n'est toujours
pas possible de trouver trois nombres qui se suivent dont un nombre
(somme ) est d'avance donné : que le jeu marche avec
certains nombres.
3.5 RELANCE DU JEU
Le professeur récapitule les approches techniques et
redéfinit le type de tâche pour attendre des réactions sur
la base desquelles la conjecture pourrait se structurer autour des nombres qui
se suivent connaissant le nombre identifié comme somme de ces trois.
Voici comment le professeur conduit l'interaction pour obtenir
l'implication des élèves dans cette tâche :
Professeur (3mn25s) : alors pour
résumer, on avait effectivement cherché trois nombres qui se
suivent et avait dit qu'il y avait plusieurs façons d'y parvenir donc
plusieurs méthodes : certains avaient fait des additions pour trouver un
total, on faisait des essais et on recommence etc. ou multiplication par 3,
là aussi on faisait des essai-erreurs, puis il y avait la méthode
divisive qui permet de trouver quoi ? Inès ?
Inès (4mn11s) : le nombre du milieu, mais
après il faut compenser.
Professeur (4mn23s) : oui après il
faut compenser. C'est bon pour tout le monde ? On essaye ? Vous pensez à
un détail ? Bon vous faites sur ces feuilles ! (et il distribue les
feuilles) mettez vos noms sur les deux feuilles s'il vous plait ! Vous mettez
les nombres que je donne ici et vous faites votre recherche, puis vous mettez
vos résultats ! Je vous donne juste la liste des sommes dont les nombres
se suivent : 141 ; 309 ; 251 ; 624 ; 563 ; 701 ; 414 (et il intègre les
différents nombres dans un tableau à quatre entrées dont
la première porte les différents nombres sommes.)
40
3.6 EXODE DE COMPORTEMENTS
|
classement
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CM1
|
|
|
|
|
|
|
|
|
|
|
CM1
|
|
|
|
|
|
|
|
|
|
|
CM1
|
Andréa
|
|
|
|
|
|
|
|
|
|
CM1
|
|
|
|
|
|
|
|
|
|
|
CM1
|
Inès
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CM1
|
|
|
|
|
|
|
|
|
|
|
CM1
|
|
|
|
|
|
|
|
|
|
|
CM1
|
|
|
|
|
|
|
|
|
|
|
CM1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
âge
|
niveau
CM2
|
élève
|
|
S1.á
|
S1.â
|
S1.â.p
|
S.2
|
|
|
|
1
|
sexe
F
|
10
|
CM2
|
Sara
|
|
5
|
5
|
5
|
5
|
|
|
2
|
G
|
10
|
CM2
|
Romain
|
|
5
|
5
|
3
|
3
|
|
|
3
|
G
|
10
|
CM2
|
|
|
1
|
3
|
1
|
3
|
|
|
4
|
G
|
11
|
CM2
|
Mayeul
|
|
4
|
5
|
1
|
3
|
|
|
5
|
F
|
10
|
CM2
|
|
|
5
|
2
|
3
|
3
|
|
|
6
|
G
|
10
|
CM1
CM2
|
Lefev
|
|
5
|
5
|
5
|
5
|
|
|
7
|
F
|
11
|
CM2
|
Valéria
|
|
2
|
5
|
5
|
3
|
|
|
8
|
F
|
10
|
CM2
|
Rayan
|
|
4
|
5
|
3
|
3
|
|
|
9
|
F
|
10
|
CM2
|
Yanis
|
abs
|
|
abs
|
5
|
5
|
|
|
10
|
F
|
11
|
CM2
|
Océane
|
abs
|
|
abs
|
abs
|
abs
|
|
|
|
|
CM2
|
|
|
|
|
|
|
|
|
1
|
G
|
11
|
CM2
|
Ugo
|
abs
|
|
abs
|
abs
|
abs
|
|
|
G
11
F
11
F
11
G
10
F
11
Techniques utilisées
|
Alexandre
1
5
Sheryne
5
5
Séance 1
|
5
3
5
3
Séance 2
|
total
|
|
Steven Yves Telma 1 . a
|
1. f.?
|
5
5
3
3
5
5
1. f.? prolongée
|
5
3
3
3
5
3
|
|
F
11
G
11
T 1
|
Lucie
Erwan
4
|
0
|
1
5
2
2
7
|
1
3
3
3
0
|
11
|
|
G
10
G
11
T 2
|
Ilian
Léon
3
|
2
|
1
5
4
5
0
|
1
3
5
5
0
|
5
|
|
F
11
F
11
T 3
|
Zoé
Garance
1
|
3
|
5
3
4
5
5
|
1
3
1
3
16
|
25
|
|
T 4
|
4
|
0
|
0
|
0
|
4
|
|
T 5
|
8
|
15
|
9
|
4
|
36
|
|
T 6
|
0
|
0
|
0
|
0
|
0
|
observations même technique tendance
au chang tendance au chang tendance au chang tendance au chang même
technique tendance au chang tendance au chang même technique
rien
rien
tendance au chang tendance au chang tendance au chang
tendance au chang même technique tendance au chang tendance au chang
tendance au chang tendance au chang même technique tendance au chang
tendance au chang
Tableau 4: relâchement des techniques faibles et
adhésion à T3
41
Les tableaux ci-dessus laissent entrevoir que la
majorité d'élèves avaient recours à la technique
essai-erreur ( 'r5) 36 fois contre 25fois pour la technique ('r3) durant les
deux séances qui ont constitué l'essentiel de notre milieu
d'étude en tâches de même type. Cependant, il y a des
élèves flexibles qui abandonnent leurs techniques ( 'r2 et 4) se
montrant surement difficiles d'emploi et intègrent d'autres pratiques
mises en évidence à travers les moments comme nous l'avions
déjà dit de verbalisation des élèves et de
validation du professeur.
Mais il est aussi visible que la séance 2 offre aux
élèves (16/20) une possibilité de réemploi de ce
qui semble efficace comme technique appropriée pour résoudre les
problèmes de la même famille ou les tâches du même
type en parlant bien sûr de la compensation qui suit automatiquement la
division. On voit bien qu'il y a eu plus de sollicitation de 'r5 que de 'r3 ;
car à la seule tâche de la séance 2, pour 20
élèves, 16 ont utilisé 'r3 pour résoudre le
problème devant 4 élèves qui ont plutôt
réussi avec 'r5.
3.7 PERCEPTION D'OBJETS OSTENSIFS ET NON
OSTENSIFS
3.7.1 Objets ostensifs
Nous identifions des embryons de techniques utilisées
par les élèves à travers les tâches de la
première séance certes, mais nous pouvons aussi y percevoir ou
voir une création par les élèves d'objets auxiliaires
à l'apprentissage : des mots, des phrases, des idéogrammes ou
écrits pour mieux étayer la technique choisie.
Yves, qui produit le mot « compenser » après
avoir trouvé trois fois 32 alors qu'il ne s'agit pas d'avoir trois fois
un nombre (32+32+32 = 96), pour atteindre la réponse attendue, se
déploie à faire émerger quelque chose de personnel comme
le montre bien l'extrait de texte suivant :
|
Yves (21mn30s) : en fait, j'ai
décomposé, j'ai presque décomposé, j'ai
cherché combien trois nombres pour faire 96 ,32+32+32, j'ai
trouvé 3 fois 32 ; je me suis dit comme ça fait 3 fois de suite,
il faut faire quelque chose, après j'ai compensé, j'ai ...
Professeur (22mn) : tu peux expliquer ce que
tu veux dire par compenser, c'est quoi compenser ?
Yves (22mn04s) : compenser c'est par exemple
un jour on avait hein... comme si on avait une méthode où on
prend 1 chiffre et on donne à côté, on ne met pas en
dessous, alors que nous on prend en dessous, et on n'est pas obligé de
donner au-dessus bon là c'est 32, on enlève le 1 du premier 32 et
on le donne au dernier 32, et ça fait 31, 32 ,33
|
42
Erwan, qui a désormais bien dévisagé les
pratiques de ses condisciples qui se reposent essentiellement en manipulant -1
et +1 sur le nombre moyen pour obtenir la combinaison recherchée, fait
rentrer lui par contre les flèches comme matériel
contrôlable ou matériel d'opérationnalisation des nombres
pour parvenir à la réponse. C'est semble-t-il un moyen qui va lui
permettre de construire sa mémoire à traiter ce type de
tâche.

Tableau 5: une pratique d'ostensifs
3.7.2 Objets non ostensifs
Comme une maxime dirait « la faim justifie les moyens
» : il est évident qu'un chercheur ou un enseignant manque
suffisamment d'outils pour bien cerner au cours d'une séance de
mathématique tout ce sur quoi peut s'appuyer un élève pour
résoudre un problème. Cependant nous pouvons observer à
travers les productions des élèves présentées
ci-haut que certains n'ont de problème qu'à avoir le nombre
moyen. ais dès qu'ils se sont rassurés que le nombre moyen
trouvé est le bon intuitivement ou instinctivement, ils produisent les
deux autres (celui qui vient avant et celui qui vient après).
3.8 La mémoire pratique et mémoire du
savoir
Toujours en passant notre observation sur les
praxéologies des élèves au rythme des tâches
données par le professeur, il se montre que certains
élèves reprennent les techniques qui les ont conduits à la
bonne réponse. De même les
43
élèves qui ont participé à
l'activité de mathématique s'approprient les techniques qui ont
amené leurs collègues à la résolution des
problèmes de la même famille. Nous pouvons retenir quelques
exemples comme pour les élèves qui commencent par la division,
ils savent que pour attaquer ce type de tache, il faut effectuer la division
par 3 pour avoir le nombre moyen.
Cet effort d'appel à la mémoire pratique
s'appuie aussi sur les pratiques antérieures personnelles ou collectives
pour construire des nouvelles pratiques ; car on voit bien que les chemins
choisis tiennent compte des ressources dont dispose chaque
élève.
3.9 Du point de vue
chronogénétique
Plusieurs opérations professionnelles sont
déroules de façon successive pour faire avancer l'apprentissage
par l'enseignant dans le temps certes mais leur activation intervient à
des moments bien précis. Il faut naturellement une action, en
perspective d'un résultat bien établie de l'élève
pour que l'enseignant change d'opération. On dira simplement que la
réaction de l'élève conditionne l'avancée
temporelle des opérations de l'enseignant.
Exemple 1
A la définition du type de tâche
(séance1.a) l'enseignant déclare aux élèves
à 2mn36s : « Eh alors il s'agit d'un petit d'une petite situation
problème d'un petit problème que vous allez devoir vous allez
d'abord chercher j'espère que vous allez trouver c'est entre la
situation problème voir même un petit jeu , hein un petit jeu
mathématique , on va travailler donc en mathématique sur des
nombres en numération ; pas d'opérations pas d'additions pas de
soustractions de multiplications comme on vient de faire sur les
décimaux en fin d'année. Ici on vous demande de ... allez je vous
le dis en une phrase ; de trouver trois nombres qui se suivent, trois nombres
qui se suivent, et dont je vous donne le total ; exemple, petit exemple : le
total doit être égal à 12, vous devez trouver les trois
nombres qui permettent de faire un total de 12. 5 6 et 7 ; car 5+6=11 et 11+7
=18. Oh pourquoi je vous dis 12 ? C'est 18 excusez-moi ! 5+6=11 et 11+7=18.
Vous avez compris le système ? ». Mais la réaction des
élèves lui rassure de leur compréhension de ce qu'il
attend d'eux. Comme Illian qui dit à 5mn17s: « ils peuvent se
suivre à l'envers ? » ; « par exemple 9-87 ? » ; à
5mn48s « hein ! Ils peuvent être pareils ? Hé non c'est
bon... ». Alors on voit l'enseignant après ce moment donner la
première tâche à 6mn07s : «alors il faut trois nombres
qui se suivent pour un total de 96. Allez c'est parti vous pouvez chercher vous
notez sur la feuille ! Tout ce que vous pensez vous essayez de me
l'écrire c'est parti ! ».
44
Exemple 2
Après 15mn de travail l'enseignant décide de
faire verbaliser les élèves pour découvrir la technologie
avancée par les élèves. On voit bien que le travail ou la
production raisonnée des élèves conditionne la
compréhension par l'enseignant des techniques utilisées par ces
derniers. Il désigne ainsi Sara qui doit dire comment elle a fait pour
avoir la réponse et Sara répond à 16mn09s: « j'ai
d'abord pris dans les vingt 24+25+26 = 75 ; après j'ai pris dans les
trente c'était trop petit après j'ai fait 30+31+32 = 93 ensuite
j'ai fait 33+34+35 =102 ; j'ai vu que c'était trop alors j'ai pris
31+32+33 = 96, j'ai vu que c'était la bonne réponse. ».
Exemple3
L'enseignant va du petit nombre au plus grand nombre lorsqu'il
constate que les élèves s'en sortent aisément ! il donne
354(1.b) après 96(1.a), ensuite une liste de nombres
(324-645-915-144-273-489-552)(1.b prolongée). Il introduit
également à 4mn23s de la séance 2 des nombres qui sont des
cas d'impossibilité (141 ; 251 ; 563 ; 414) dans une liste
hétérogène après les sommes possibles pour ensuite
y faire déduire par les élèves une règle des
nombres susceptibles d'être les sommes de trois nombres successifs. Cette
tâche, on voit bien, est placée à la suite de la liste
homogène des nombres sommes. La raison pratique d'impossibilité
ou de possibilité est développée dans la séance 2
à travers la manipulation des nombres donnés.
|
Professeur (35mn08s) : après 309 ?
Telma
Telma (35mn37s) : sans parler, elle écrit
102 ; 103 ; 104
Professeur (35mn49s) : tout le monde a
trouvé celui-là ? Ou vous n'avez pas trouvé !
Elèves (35mn52s) : oui
Professeur (35mn59s) : le le le le suivant ?
251 ? Lucie. Léandre aussi combien tu as trouvé à la
division ?
Léandre (36mn04) : j'ai trouvé 3
6
Professeur (36mn10s) : on a dit qu'on
s'arrêtait aux entiers. Donc 83 avec un reste de 2 ; donc impossible !
Pourquoi ce n'est pas possible ? Lucie
Lucie (36mn28s) : parce que on rajoute des
chiffres.
|
45
3.10 Du point de vue
topogénétique
Nous pouvons rappeler que dans les divers niveaux de
co-détermination didactique, il y a ceux qui sont constitués
essentiellement des opérations qui organisent les différents
« lieux » qu'occupent les acteurs de la relation didactique et le
résultat inhérent à ces opérations dont l'ensemble
est appelé topogénèse. Dans ce jeu tout indiqué
nous voyons comment l'enseignant manipule son lieu en changeant les
tâches : de la plus simple aux tâches plus complexes (grands
nombres et nombres impossibles), en régulant quand cela est
nécessaire, faire une mise au net (instituer) avec les
élèves en introduisant des éléments qui font
exception à la règle pour apporter les cas
d'impossibilité. ais nous voyons par ailleurs les élèves
et ce qui nous intéresse le plus, manipuler également leur lieu ;
ils suivent l'enseignant qui définit la tâche à effectuer,
ils posent des questions de compréhension pour bien être dans le
jeu comme Alexandre qui demande : « on peut les additionner ? » qui
est une question dont l'allure d'action est la vérification de
l'exactitude des nombres trouvés par une certaine pratique. Ce qui se
montre comme un refus du hors sujet, ils utilisent leur savoir-faire devant les
tâches que leur donne l'enseignant ils font appel à leur
connaissances d'appui pour attaquer le type de tâche proposée. Ils
s'engagent réellement dans le jeu au moyen de leurs pratiques pour y
découvrir le résultat attendu. Exemple à 1.b, un
élève chuchote pour trouver la suite qui donne 54 après
avoir posé 100+100+100 =300 « non c'est trop il faut diminuer un
peu !». Cette communication avec soi où l'élève met
son potentiel culturel ou ses ressources intérieures en mouvement
relève d'une pratique ou technique en construction. C'est
également un lieu d'utilisation des concepts nouveaux «
compensation », « nombre du milieu ou moyen », « avant
» ou « après ».
Rappelons que la compensation s'emploie lorsqu'on obtient
trois fois le nombre du milieu ou moyen par l'usage de la division. Appliquer
-1 sur l'un des trois nombres permet d'avoir le nombre avant et +1 sur l'un des
autres permet de trouver le nombre après. C'est également le lieu
de la comparaison libre et individuelle des techniques utilisées.
Exemple d'Illian : « j'ai fait essai-erreur ; j'ai fait comme Sara mais
j'ai fait 30 x3 = 90 ; 3+2+1 ça fait 6 et j'ai fait 3+30 =33 ; 2+30 =32
; 30+1 =31 ».
3.11 Du point de vue
mésogénétique
Dans ce jeu de recherche des nombres qui se suivent connaissant
une somme multiple ou non de 3, les clés (techniques) utilisées
par le professeur semblent ne plus être la seule propriété
de celui qui sait avant les élèves, mais une
propriété désormais
46
bien partagée ; telle est le principe de la
mésogénèse. Ainsi au niveau des mots actions du discours
l'enseignant s'en sert pour les besoins de communication.
A l'entendement de la classe trois moments fixent la technique
3 vers laquelle l'enseignant et la majorité des
élèves y vont :
ssi
est admis comme nombre de milieu
Compenser signifie et dès que est trouvé.
4 REPONSE A LA QUESTION DE RECHERCHE
Notre prospection aux voisinages des praxeologies des
élèves est une action qui impose un esprit assez souvent
méticuleux pour regarder au détail les éléments
constitutifs de chaque pratique. Nous estimons l'avoir eu tout au long de
celle-ci. L'analyse établie à la séance 1 sur le travail
individuel à travers la feuille de recherche et les moments de mise au
net sinon lors de la verbalisation, laisse entrevoir toujours une
manière de faire soutenue par une technologie émergente comme l'a
indiqué Y. Chevallard (1998). La mise au net a souvent été
un moment au cours duquel les éléments constitutifs d'une
technologie en construction permettaient aux autres élèves soit
de changer complètement leur pratique soit d'offrir un
élément suffisant pour parachever une pratique dont les
élans étaient bien amorces, ou simplement de confirmer la voie
choisie. Une pratique qui consiste à trouver un nombre moyen et
réaliser une compensation de -1 pris sur l'un des trois nombres
identique et ajouter +1 sur l'autre la technique qui se rapproche le plus de
3 définie a priori : « division du nombre somme ( ) par
3 pour trouver le deuxieme nombre dans cette suite. Et successivement, on
retranche 1sur le deuxième pour trouver le premier et on ajouter 1 au
deuxième pour obtenir le troisième ».
ais dans ces différentes manières de faire
l'appui a été la mémoire ; car certains
élèves et nous l'avons déjà dit soit changent de
façon de faire parce qu'une phase de mise au net leur a permis de
retenir comment faire ou de maintenir la pratique qui a justifié la voie
de la réponse ce que mettent en évidence Mathéron &
Salin (2002). L'appui c'est également l'usage des ostensifs comme
l'emploi des flèches pour expliquer la transaction de la compensation
que certains élèves utilisent soit à l'écrit soit
mentalement pour les deux autres nombres à partir du nombre moyen
trouvé par division comme l'indiquent Bosch et Chevallard (1999). Si
l'ostensif ?
47
flèche » est bien ce qui donne du sens à
une action mais l'idée de compenser est une opération qui trouve
une place importante dans le siège mental et qui justifie des
réponses données après la division.
A partir de ces trois phénomènes (façon
de faire, ostensifs et mémoire), nous affirmons que l'hypothèse
est confirmée. Cependant nous indiquons qu'il est possible que des
évènements nous aient échappés en raison de notre
dispositif qui ne pouvait permettre au même temps T d'enregistrer les
pratiques de tous les élèves ! Nous imaginons qu'après
notre passage avec la camera baladée il se construisait d'importants
éléments que nous aurions pu examiner également !
48
Conclusion
Nous avons vu que les pratiques mathématiques exigent
une utilisation des techniques de résolution de problèmes
mathématiques pour agir sur les tâches de même type comme
pour le problème qui a bien porté sur la recherche de trois
nombres dont la somme est donnée au départ. Nous avons fait une
analyse a priori pour voir les emplois possibles.
Savoir « en quoi le milieu de résolution de
problème en mathématique est un lieu de production de techniques
variées ? » est plus que le souci de voir dans les pratiques des
élèves les éléments qui leur permettent de mettre
en place une façon de faire avec des ostensifs personnels aidant
à résoudre la situation problème présentée
par l'Enseignant et la mémoire.
Nous avons défini une méthodologie
centrée sur l'observation de la leçon au moyen des transcriptions
(vidéo) de l'interaction dans l'action conjointe du professeur et des
élèves et des copies des élèves.
Cette observation nous a présenté les
éléments constitutifs des techniques utilisées dans ce
milieu de résolution de problème pour le savoir
mathématique choisi. Ils oscillent non seulement autour des
opérations traditionnelles (division, multiplication, addition et
soustraction) mais aussi autour des ostensifs et de la mémoire pour
attaquer les tâches de même type. Bien que les manières de
faire étaient différentes au début de la première
séance, mais les mouvements de communication ou de validation
créés par l'enseignant ont offert des occasions de regroupement
des élèves autour des mêmes pratiques :
de la classe attaquent la deuxième séance avec la
technique 3 (16élèves) de la classe utilise lui, la
technique 5.
Nous pouvons à travers ces différentes raisons
affirmer la confirmation de notre hypothèse.
Des lectures exploratoires nous ont fourni d'importants
éléments pour construire le cadre théorique qui nous a
permis certes d'y retirer la substance nécessaire à l'analyse des
données, mais peut-on penser que la caractérisation des
techniques des élèves dans un processus de résolution de
situation problème ne se limite qu'à ces aspects visibles ?
49
Bibliographie
Assude T. & ercier A. (2007). L'action conjointe
professeur-élèves dans un système didactique
orienté vers les mathématiques. Agir ensemble. L'action
didactique conjointe du professeur et des élèves,
153-185.
Bertrand, A., & Garnier, P.-H. (2005). Psychologie cognitive
(Vol. 611). Studyrama. Consulté à l'adresse
http://books.google.fr/books?hl=fr&lr=&id=1xjpJSZ_0FoC&oi=fnd&pg=PA9&dq=psycho
logie+cognitive&ots=ix_NhBlccK&sig=HzHDlgiEaJU4XImzqcmx6T9Kd3Q
Bosch . & Chevallard Y. (1999). La sensibilité de
l'activité mathématique aux
ostensifs: Objet d'étude et problématique.
Recherches en didactique des mathématiques, 19(1), 77 123..
Brousseau, G. (2011). La théorie des situations
didactiques en mathématiques. Education & didactique, vol.
5(1), 101-104.
Charlot B. (2006). La question du rapport au savoir: convergences
et différences entre deux approches. Savoirs, n° 10(1),
37?43. doi:10.3917/savo.010.0037
Chevallard, Y. (1991). La transposition didactique - Du
savoir savant au savoir enseigné. Grenoble: La Pensée
sauvage (1985).
Chevallard, Y. (1998). Analyse des pratiques enseignantes et
didactique des mathématiques: l'approche anthropologique. Actes de
l'École d'été de la Rochelle 91- 118.
Julo, J. (1995). Représentation des problèmes et
réussite en mathématiques: un apport de la psychologie cognitive
à l'enseignement. Presses universitaires de Rennes.
Lebeaume, J. (2008). REUTER Yves (éd.)(2007). Dictionnaire
des concepts fondamentaux des didactiques. Bruxelles: De Boeck, 272 p.
Recherche et formation, (57), 159-161.
Matheron, Y. (2011). Le travail du professeur de
mathématiques relatif à la conception et la réalisation
des phases de dévolution. Education & didactique, vol. 5(3),
81-100.
Mettoudi, C., Tempez, B., Yaïche, A., & Chérel,
I. (2010). Mettre en oeuvre les programmes de mathématiques - Du CP au
CM2. Hachette Éducation Technique.
Paun, E. (2006). Transposition didactique: un processus de
construction du savoir scolaire. Carrefours de l'éducation, n°
22(2), 3-13. doi:10.3917/cdle.022.0003
50
Salin, M.-H., & Matheron, Y. (2002). Les pratiques
ostensives comme travail de construction d'une mémoire officielle de la
classe dans l'action enseignante. Revue française de pédagogie,
141(1), 57 66.
| 


