Les déterminants de l'offre de monnaie dans l'économie congolaise de 1980 à 2013.

Section 3. L'analyse économétrique de données

3.1. L'estimation

? Les variables utilisées

Dans le cadre de ce travail, les variables qui font l'objet de l'analyse économétrique sont : le taux directeur; le taux d'inflation et le taux de croissance économique ; sont toutes, des données ou des séries annuelles.

? Les sources des données

Les principales sources des données que nous avons consultées sont les rapports annuels et les condensées d'informations statistiques de la Banque Centrale du Congo.

? La spécification du modèle théorique ? La règle de Taylor

Il ne suffit pas d'évaluer la politique monétaire de la Banque Centrale sur base des éléments de sa stratégie, tout particulièrement en fonction de l'objectif de la stabilité monétaire qui lui a été assigné. Il faut prendre un point de vue plus extérieur pour que cette évaluation soit complète. La stabilité monétaire n'est pas le seul critère pour se prononcer sur l'action de la Banque Centrale. On ne peut pas ignorer les évolutions des grandeurs réelles, performantes en matière de croissance et d'emploi et des variables financières, stabilité des taux d'intérêt, des marchés financiers, des taux de change, etc.

Le recours à la règle de Taylor permet de prendre en compte les premières, mais il faut aller plus loin si l'on veut aussi intégrer les seconds. Le recours à la règle proposée par John Taylor, permet une évaluation de la politique monétaire prenant en compte à la fois les performances réalisées dans le domaine de

Serge KASEREKA KANYAMA Page 103

« Les Déterminants de l'Offre de Monnaie dans l'Economie Congolaise de 1980 à 2013»

l'inflation et les résultats en matière de croissance économique. Elle fournit une valeur de référence pour les taux d'intérêt de telle sorte qu'il soit égal à sa valeur d'équilibre, le taux d'intérêt réel correspondant à la réalisation du plein emploi dans le long terme, corrigée en fonction de l'écart de production et de l'écart d'inflation⁵⁰.

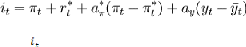
En effet, La règle de Taylor est un dispositif d'encadrement rigoureux des politiques monétaires présenté en 1993 par J.B. Taylor dans « Discrétion Versus Policy Rules in Practice », puis popularisé en 1996 par une étude de Goldman Sachs « The International Economic Analyst ». Elle définit une trajectoire de variation optimale du taux d'intérêt de court terme au cours du cycle économique, en fonction de l'objectif d'inflation de la Banque Centrale et de l'évolution de l'output gap. Ainsi, en comparant le taux de Taylor avec le taux d'intérêt à court terme mis en oeuvre par les autorités monétaires, il est possible de juger de l'adéquation de la politique monétaire avec les données économiques fondamentales⁵¹. Taylor présente cette règle comme suit :

Avec le taux directeur fixé par la Banque Centrale à l'instant t, le

taux d'inflation, la cible d'inflation de la Banque Centrale, le taux d'intérêt réel à

l'instant t, et les niveaux respectifs du PIB et du PIB potentiel, et des
coefficients.

Dans ce modèle, les coefficients et sont déterminés
économétriquement par les économistes des Banques Centrales, pour la zone monétaire concernée ; l'équation de Taylor (ou bien une de ses variantes) permet alors de calculer la valeur optimale à fixer pour le principal taux directeur de la Banque Centrale, ce dernier ayant une grande influence sur les taux d'intérêt de la zone économique.

Selon cette règle et doivent être positifs (Taylor proposait dans

son article de 1993 ). Cette règle suggère un taux d'intérêt relativement
haut quand l'inflation dépasse sa cible ou quand l'économie semble être « en surchauffe » et un taux d'intérêt relativement bas (une politique monétaire accommodante) dans les situations opposées.

Parfois, les objectifs des politiques économiques peuvent être contradictoires, par exemple lorsqu'il y a stagflation, l'inflation dépassant sa cible alors que l'économie est en situation de sous-emploi. Dans ce cas, la règle de Taylor aide à mettre en balance ces différentes considérations pour fixer le taux d'intérêt.

Plus précisément, en spécifiant , Taylor suggère que les Banques Centrales
doivent augmenter le taux d'intérêt nominal de plus d'un point pour chaque augmentation d'un point de l'inflation.

En d'autres termes, en considérant que le taux d'intérêt réel est approximativement le taux d'intérêt nominal moins l'inflation, poser que

⁵⁰MISHKIN F., Monnaie, banque et marchés financiers, 9èmeéd. Pearson(nouveau horizon), Paris, 2010, p.233.

51 Décrite dans l'article de référence de 1993: «Discretion versus Policy Rules in Practice», Carnergie-Rochester conference, n^°39

Serge KASEREKA KANYAMA Page 104

« Les Déterminants de l'Offre de Monnaie dans l'Economie Congolaise de 1980 à 2013»

revient à dire que lorsque l'inflation augmente, le taux d'intérêt réel doit également augmenter.

Présentée comme ci-haut, la règle de Taylor est théorique, appropriée peut être à l'économie américaine de 1993, et ne peut être d'application dans toutes les économies du monde. Simplement parce que le poids accordé aux objectifs assignés à la Banque Centrale (stabilité des prix, stabilité de l'activité économique) que capte les coefficients n'est pas le même d'une économie à une autre, au sein d'une même économie, d'une période à une autre.

D'où certains économistes suggèrent que les coefficients doivent être estimés pour chaque pays, étant donné la différence dans les objectifs. Ainsi, de cette manière, on a l'information sur le poids qu'une économie accorde à ces objectifs.

Il convient de signaler à ce niveau que la règle de Taylor n'a pas été élaborée pour des fins économétriques, sa vocation initiale était plus descriptive que normative. Et à ce propos, la critique de Mc Callum qui note que la formulation de Taylor n'est pas opérationnelle étant donné qu'elle a besoin des informations dont les décideurs politiques ne disposent pas.

En effet, l'estimation de règle de Taylor pose certains problèmes liés à la

détermination de certaines variables. La production potentielle est une variable
inobservable, et pour un pays qui vient d'adopter la stratégie du ciblage de l'inflation, on n'aura pas non plus le nombre d'observations nécessaire pour la cible , du coup elle aussi devient une information manquante ; à moins que l'on se propose d'estimer en prenant une valeur fixe, année après année, de la cible (15 par exemple).

Ces faiblesses ont déclenché l'émergence des modèles du type de Taylor que l'on rencontre çà et là. Mais nous proposons ici, un modèle émanant de la règle de Taylor, que certains auteurs se proposent d'estimer, appelé parfois la « fonction de réaction de la Banque Centrale » :

Où :

: masse monétaire ;

: solde de finance publique ;

: output gap (ou gap de la production Y)

Avec c est écarte parce que nous n'en avons pas toutes les
observations.

Les conclusions de Taylor restent valables, nous tentons seulement de proposer un modèle plus manipulable et susceptible d'usage économétrique.

Nous avons déjà noté plus haut que la Banque Centrale resserre d'autant plus la politique monétaire que l'inflation observée dépasse son objectif (sa

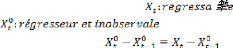
Serge KASEREKA KANYAMA Page 105

« Les Déterminants de l'Offre de Monnaie dans l'Economie Congolaise de 1980 à 2013»

cible). Donc et varient dans le même sens, c'est-à-dire que si augmente, on

augmente également pour diminuer la volatilité de l'inflation⁵².

Donc le paramètre associé à doit être positif, s'il est supérieur à 1, on dit

qu'il a un effet stabilisateur. Et si , on en conclut que l'attention des autorités
politiques est plus accordée à la stabilité du niveau des prix qu'à la stabilité de l'activité économique.

Ainsi, le paragraphe qui suit est consacré à l'estimation de notre modèle, mais qui n'interviendra que tard après quelques transformations dont l'importance est démontrée plus loin.

? L'estimation de la règle : Application de l'approche de Cagan

La présentation de l'approche de Cagan, nous permet de spécifier le modèle économétrique que nous allons estimer. L'utilisation de cette approche est justifiée par le fait que, dans la fonction de réaction de la Banque Centrale, y* est non

observable, et par conséquent devient aussi inobservable. Il se pose donc un
problème, ce modèle non plus ne peut être estimé. Nous recourons, pour contourner cette difficulté, à l'approche proposée par Cagan, en vue de transformer notre modèle et ainsi de le rendre estimable.

Revenons à nos modèles spécifiés ci-haut:

Dans notre modèle à estimer de l'équation (a), on se rend compte, du fait que soit non observable, que le gap de la production devient aussi inobservable. Il se pose donc un problème, ce modèle non plus ne peut être estimé.

Nous recourons, pour contourner cette difficulté à l'approche proposée par Cagan, en vue de transformer notre modèle et ainsi de le rendre estimable.

Soit le modèle de régression simple ci-après :

Où :

Cagan établit que :

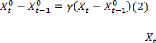
Puisqu'il n'y a aucune raison qui pousse à établir cette égalité, on introduit un coefficient d'ajustement (gamma) pour assurer l'égalité :

De l'équation (2), en tirant, il vient que :

⁵²Volatilité de l'inflation: taux de croissance du taux d'inflation

« Les Déterminants de l'Offre de Monnaie dans l'Economie Congolaise de 1980 à 2013»

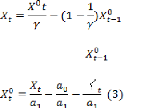
Et de (1), tirons, on a :

Serge KASEREKA KANYAMA Page 106

Ainsi, à partir de (3), on peut écrire :

(3) et (4) dans (2a), après réaménagement, on trouve :

L'équation (5) peut s'écrire :

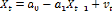
En appliquant cette approche de Cagan à notre modèle ; on peut établir

que :

Si on tire de (1), on trouve :

(2)

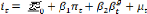
Et de notre modèle , on tire , puis on

a : (3)

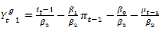
Ainsi, de (3) on peut écrire : (4)

? (3) et (4) dans (2), on a :

En tirant , on trouve :

(5)

En simplifiant, on a la fonction de réaction de la banque centrale (note modèle de l'équation (a) transformé) ci-après :

Où :

« Les Déterminants de l'Offre de Monnaie dans l'Economie Congolaise de 1980 à 2013»

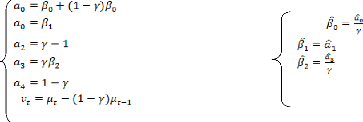
Donc notre modèle de l'équation (a) (fonction de réaction de la Banque Centrale) estimé sera :

? La spécification du modèle économétrique

Notre modèle transformé devant être estime se présente comme suit :

Avec :

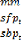
: Masse monétaire

: La série des soldes de finance publique de 1980 à 2013 ; : La série des balances de paiement de 1980 à 2013 ;

, et : des paramètres inconnus (à estimer) ;

: Le terme d'erreur.

Et notre modèle du départ :

Où : est le gap des solde de balance de paiement.

? L'analyse exploratoire des données

Les différents tests statistiques sont importants dans un travail économétrique car ils permettent de confirmer ou d'infirmer la validité du modèle, et de voir le pouvoir explicatif de chaque variable exogène. Ainsi, dans le cadre de ce travail nous avons effectué un ensemble de tests⁵³.

Serge KASEREKA KANYAMA Page 107

53 Ces différents tests auront comme source les résultats générés par E-views.

Serge KASEREKA KANYAMA Page 108

« Les Déterminants de l'Offre de Monnaie dans l'Economie Congolaise de 1980 à 2013»

Tableau n°19. Les données de l'estimation

Année	Masse Monétaire	Besoin de financement	Solde de la balance de paiement
1980	1 237,73	-237,454	55.629
1981	1 060,48	-291,829	-162.20
1982	1 401,29	-710,096	73.511
1983	1 085,42	-151,68	21.235
1984	520,11	-113,527	-197.31
1985	479,74	-210,539	332.3
1986	636,33	39276,84	144.0
1987	664,96	-32855,6	-578.0
1988	908,05	-624,21	435.4
1989	700,64	158925,7	-298,49
1990	1 092,60	-721,614	-232,085
1991	1 172,91	-1440,84	-167,77
1992	1 579,44	-0,00118	-409,26
1993	9 809,52	-0,00038	-257,45
1994	2,566875	-0,47344	-600,59
1995	226,56	3527,333	-866,4
1996	203,540566	-33438,7	-1138,1
1997	250,20	-203888	71,535
1998	524,8714286	-155109	571,14
1999	973,95	-655453	63,27
2000	471,16128	-210803	-560,7
2001	245,99	3958,409	-287,9
2002	258,63	59,6354844	-32,2
2003	349,2932	-23,6888087	-314,2
2004	500,4088	47,5142426	-244,30
2005	642,5326	-99,4699499	-176,6
2006	882,2512	-50,2622013	-430,8
2007	1309,007	-43,3402255	-271
2008	1628,882	-55,1046424	-632,2
2009	1709,986	48,9251767	-912
2010	2,214553473	161,684785	-1 198,00
2011	2,661873638	-249,145969	75,3
2012	3,21421574	469,825841	601,2
2013	3,799238717	-114,028276	66,6

Source : rapports BCC de 1980 à 2013

Serge KASEREKA KANYAMA Page 109

« Les Déterminants de l'Offre de Monnaie dans l'Economie Congolaise de 1980 à 2013»

1. Estimation du modèle d'analyse (en appliquant la méthode de moindre carre ordinaire)

? Première estimation du modèle

Dependent Variable: MM Method: Least Squares

Date: 08/29/15 Time: 02:50 Sample: 1980 2013 Included observations: 34
Variable	Coefficient	Std. Error t-Statistic	Prob.
C	4.87E+08	2.13E+08 2.288933	0.0291
SFP	-0.016488	0.077899 -0.211659	0.8338
SBP	6609.224	4648.150 1.421904	0.1650
R-squared	0.063113	Mean dependent var	4.27E+08
Adjusted R-squared	0.002669	S.D. dependent var	1.20E+09
S.E. of regression	1.20E+09	Akaike info criterion	44.73870
Sum squared resid	4.49E+19	Schwarz criterion	44.87338
Log likelihood	-757.5579	F-statistic	1.044150
Durbin-Watson stat	1.769790	Prob(F-statistic)	0.364043

Estimation Command:

=====================

LS MM C SFP SBP

Estimation Equation:

=====================

MM = C(1) + C(2)*SFP + C(3)*SBP

Substituted Coefficients:

MM = 487052021.6 - 0.0164881522*SFP + 6609.224055*SBP

Correlogram of residuals

Date: 08/29/15 Time: 03:08 Sample: 1980 2013 Included observations: 34
Autocorrelation		Partial Correlation			AC	PAC	Q-Stat	Prob
. | .	|	. | .	|	1	-0.008	-0.008	0.0024	0.961
. |* .	|	. |* .	|	2	0.146	0.146	0.8230	0.663
. |* .	|	. |* .	|	3	0.070	0.074	1.0171	0.797
. | .	|	. | .	|	4	-0.036	-0.057	1.0700	0.899
. *| .	|	. *| .	|	5	-0.102	-0.128	1.5096	0.912
. | .	|	. | .	|	6	-0.050	-0.048	1.6204	0.951
. *| .	|	. *| .	|	7	-0.127	-0.090	2.3495	0.938
. | .	|	. |* .	|	8	0.040	0.070	2.4259	0.965
. *| .	|	. *| .	|	9	-0.093	-0.061	2.8459	0.970
. *| .	|	. *| .	|	10	-0.127	-0.155	3.6722	0.961
. *| .	|	. *| .	|	11	-0.107	-0.132	4.2822	0.961
. |* .	|	. |* .	|	12	0.120	0.160	5.0825	0.955
. |* .	|	. |**.	|	13	0.140	0.233	6.2169	0.938
. *| .	|	. *| .	|	14	-0.100	-0.170	6.8285	0.941
. |**.	|	. |* .	|	15	0.290	0.180	12.251	0.660
. *| .	|	. *| .	|	16	-0.097	-0.154	12.892	0.681

Serge KASEREKA KANYAMA Page 110

« Les Déterminants de l'Offre de Monnaie dans l'Economie Congolaise de 1980 à 2013»

? Test auto corrélation

Une des hypothèses de moindre carré veut que les erreurs de la période précédente n'aient aucune relation avec celles de périodes à venir.

Rejeter H1 : Si Probability > 0.05 Rejeter H0 : Si Probability = 0.05

Test d'autocorrelation des erreurs de breusch godfrey

Breusch-Godfrey Serial Correlation LM Test:

F-statistic 0.435833 Probability 0.650892

Obs*R-squared 0.992132 Probability 0.608921

Test Equation:

Dependent Variable: RESID Method: Least Squares

Date: 08/29/15 Time: 03:30

Variable Coefficient Std. Error t-Statistic Prob.

C 13362411 2.18E+08 0.061329 0.9515

SFP -0.010525 0.080541 -0.130679 0.8969

SBP -136.8890 4744.458 -0.028852 0.9772

RESID(-1) -0.006432 0.212194 -0.030314 0.9760

RESID(-2) 0.198867 0.213322 0.932242 0.3589

R-squared 0.029180 Mean dependent var -7.01E-08

Adjusted R-squared -0.104726 S.D. dependent var 1.17E+09

S.E. of regression 1.23E+09 Akaike info criterion 44.82673

Sum squared resid 4.36E+19 Schwarz criterion 45.05120

Log likelihood -757.0545 F-statistic 0.217917

Durbin-Watson stat 1.826659 Prob(F-statistic) 0.926294

Ainsi, nous constatons qu'il y a autocorrélation car la probabilité est > à o.o5.

? Test d'hétéroscédacticité

Ce test est utilisé, pour vérifier si les variances des erreurs ne sont plus sur la première diagonale, donc la variance de l'erreur est alors liée aux valeurs de la variable explicative. Utilisons le test de White afin de détecter tout risque d'Hétéroscédasticité.

« Les Déterminants de l'Offre de Monnaie dans l'Economie Congolaise de 1980 à 2013»

Test d'hétéroscédasticité conditionnelle autorégressive : Test ARCH ARCH Test:

F-statistic 0.009728 Probability 0.922065

Obs*R-squared 0.010353 Probability 0.918956

Test Equation:

Dependent Variable: RESID^2

Method: Least Squares

Date: 08/29/15 Time: 03:32

Sample(adjusted): 1981 2013

Included observations: 33 after adjusting endpoints

Variable Coefficient Std. Error t-Statistic Prob.

C 1.37E+18 7.01E+17 1.959544 0.0591

RESID^2(-1) -0.019802 0.200763 -0.098633 0.9221

R-squared 0.000314 Mean dependent var 1.35E+18

Adjusted R-squared -0.031934 S.D. dependent var 3.79E+18

S.E. of regression 3.85E+18 Akaike info criterion 88.48393

Sum squared resid 4.59E+38 Schwarz criterion 88.57463

Log likelihood -1457.985 F-statistic 0.009728

Durbin-Watson stat 1.807429 Prob(F-statistic) 0.922065

Test d'hétéroscédasticité de white pour les variables croisées et non croisées

White Heteroskedasticity Test:

F-statistic 2.595930 Probability 0.057016

Obs*R-squared 8.964275 Probability 0.061999

Test Equation:

Dependent Variable: RESID^2 Method: Least Squares

Date: 08/29/15 Time: 03:36 Sample: 1980 2013

Included observations: 34

Variable Coefficient Std. Error t-Statistic Prob.

C 1.53E+18 6.48E+17 2.355073 0.0255

SFP -1.34E+08 2.49E+08 -0.538027 0.5947

SFP^2 -0.023850 0.035755 -0.667036 0.5100

SBP 7.67E+13 2.47E+13 3.101668 0.0043

SBP^2 3.26E+08 1.21E+08 2.692332 0.0117

R-squared 0.263655 Mean dependent var 1.32E+18

Adjusted R-squared 0.162090 S.D. dependent var 3.73E+18

S.E. of regression 3.42E+18 Akaike info criterion 88.32387

Sum squared resid 3.39E+38 Schwarz criterion 88.54834

Log likelihood -1496.506 F-statistic 2.595930

Durbin-Watson stat 2.356582 Prob(F-statistic) 0.057016

Comme la probabilité est superieure à 5%, on conclut qu'il n y a pas hétéroscédasticité.

Serge KASEREKA KANYAMA Page 111

Serge KASEREKA KANYAMA Page 112

« Les Déterminants de l'Offre de Monnaie dans l'Economie Congolaise de 1980 à 2013»

? Test de normalité de résidus

^6.E+09 4.E+09 2.E+09 0.E+00 -2.E+09

^{80 85 90 95 00 05}

2. Test de stationnarité

Ce test permet de voir si la série est stationnaire en comparant la valeur de la statistique d'ADF aux valeurs de McKinnon⁵⁴. S'il s'avérait qu'une série n'est pas stationnaire, il y a nécessité de la stationnariser, avant de faire les estimations.

Ce test permet de voir si la série est stationnaire en comparant la valeur de la statistique d'ADF aux valeurs de McKinnon⁵⁵. S'il s'avérait qu'une série n'est pas stationnaire, il y a nécessité de la stationnariser, avant de faire les estimations.

La masse monétaire

Date: 08/29/15 Time: 03:15 Sample(adjusted): 1982 2013 Included observations: 32 after

adjusting endpoints

Standard errors & t-statistics in parentheses

MM

MM(-1) 0.068042

(0.21013)

(0.32380)

MM(-2) 0.198966

(0.20982)

(0.94828)

C 3.66E+08

(2.4E+08)

(1.51984)

R-squared 0.035529

Adj. R-squared -0.030986

Sum sq. resids 4.58E+19

S.E. equation 1.26E+09

F-statistic 0.534146

54 Pour tous nos tests, nous considérons le seuil de 5 (généralement utilisé en économie). Si |Stat - ADF| > | p - values|, conclut par la stationnarité de la série. Au cas contraire, la série n'est pas stationnaire.

55 Pour tous nos tests, nous considérons le seuil de 5% (généralement utilisé en économie). Si |Stat - ADF| > |p - values|, conclut par la stationnarité de la série. Au cas contraire, la série n'est pas stationnaire.

Serge KASEREKA KANYAMA Page 113

« Les Déterminants de l'Offre de Monnaie dans l'Economie Congolaise de 1980 à 2013»

Log likelihood -714.2999

Akaike AIC 44.83124

Schwarz SC 44.96865

Mean dependent 4.54E+08

S.D. dependent 1.24E+09

Le solde des finances publiques

Date: 08/29/15 Time: 03:18 Sample(adjusted): 1982 2013 Included observations: 32 after

adjusting endpoints

Standard errors & t-statistics in parentheses

SFP

SFP(-1) -0.176301

(0.17371)

(-1.01490)

SFP(-2) 0.374990

(0.18381)

(2.04013)

C -2.08E+08

(4.7E+08)

(-0.44420)

R-squared 0.189624

Adj. R-squared 0.133736

Sum sq. resids 1.93E+20

S.E. equation 2.58E+09

F-statistic 3.392929

Log likelihood -737.3365

Akaike AIC 46.27103

Schwarz SC 46.40844

Mean dependent -3.19E+08

S.D. dependent 2.77E+09

Le solde des balance de paiements

Date: 08/29/15 Time: 03:19 Sample(adjusted): 1982 2013 Included observations: 32 after adjusting endpoints

Standard errors & t-statistics in parentheses

SBP

SBP(-1) 0.203818

(0.18490)

(1.10232)

SBP(-2) 0.092019

(0.18512)

(0.49707)

C -7298.693

(8588.20)

(-0.84985)

R-squared 0.058347

Adj. R-squared -0.006595

Serge KASEREKA KANYAMA Page 114

« Les Déterminants de l'Offre de Monnaie dans l'Economie Congolaise de 1980 à 2013»

Sum sq. resids	6.30E+10
S.E. equation	46604.50
F-statistic	0.898453
Log likelihood	-387.8135
Akaike AIC	24.42584
Schwarz SC	24.56325
Mean dependent	-10400.25
S.D. dependent	46451.58

Nous trouvons que finances publiques est toujours négatif de 1980 à 2013 qui est respectivement de -237,454 à -114,028276 en millions USD et les soldes de balance des paiements pendant notre période a été de 55.629 et 66,6 en millions de USD.

Par rapport aux estimations faites de notre modèle : MM = 487052021.6 - 0.0164881522*SFP + 6609.224055*SBP dans le cadre de cette étude, il se dégage que le poids accordé par la Banque Centrale congolaise à l'objectif de stabilité des prix et celui de stabilité de l'activité économique sont respectivement (en prenant trois

chiffres après la virgule) de 0,8338 et 0,1650. Et comme > , on en conclut que l'attention des autorités monétaire congolaises est plus accordée à la stabilité du

niveau des prix qu'à la stabilité de l'activité économique. Et puisque <1, il n'y a pas d'effet stabilisateur sur notre modèle.

Il résulte également de nos estimations que le solde de finance publique ou encore solde budgétaire et le solde de la balance de paiement évoluent en sens inverse, ce qui montre à suffisance que pour la période considérée, la politique monétaire a été inefficace et la politique budgétaire a été sous mis à une rigueur par les institutions de Brettons Wood. Les échecs répétés de la situation de la monnaie et du crédit au niveau des opérations de la politique monétaire durant la période considérée sont dus au fait qu'avant 2002, la Banque Centrale utilisait exclusivement une politique monétaire discrétionnaire d'une part et d'autre part, la Banque Centrale ne bénéficiait pas d'indépendance.

En effet, toutes ses actions s'inscrivant dans le cadre de la politique du gouvernement. Ainsi, pour les années avant 2001, l'inflation a été nourrie par le Crédit à l'Etat qui augmentait de façon considérable le niveau de la masse monétaire.

La lecture de ces résultats nous renseigne qu'au seuil de 5 %, toutes les séries sont stationnaires. Etant rassuré de la stationnarité de toutes les séries, nous pouvons d'ores et déjà présenter les différentes estimations et les différents tests jugés nécessaires.

Serge KASEREKA KANYAMA Page 115

« Les Déterminants de l'Offre de Monnaie dans l'Economie Congolaise de 1980 à 2013»