Modélisation et implémentation d'un système d'information pour la gestion des abonnés en eau potable.

II.4.4 Construction du graphe Pert

Le PERT (Program of Evaluation and Review Technique) est une méthode consistant à mettre en ordre sous forme de réseau plusieurs tâches qui, grâce à leur dépendance et à leur chronologie, concourent toutes à l'obtention d'un produit fini. La méthode PERT est la plus souvent synonyme de gestion de projets important à long terme. C'est pourquoi, plusieurs actions sont nécessaires pour réussir sa mise en oeuvre¹⁶. Il est une méthode anglo-saxonne, A on A, c'est-à-dire Activité sur l'Arc¹⁷.

II.4.4.6.1. Graphe PERT non ordonné

5

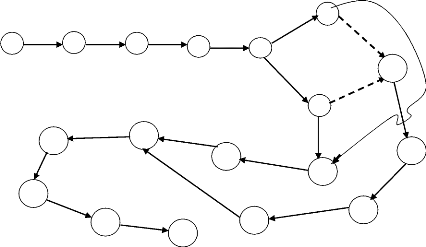
C'est en fonction des contraintes explicitées au point II.4. Que nous construisons le graphe PERT ci-dessous :

e

j

10

f

g

6

n 13

14

m

k

12

l

7

p

11

q r

16 17

18

o

9

h

8

i

Figure n°01 : Graphe PERT non ordonné

5

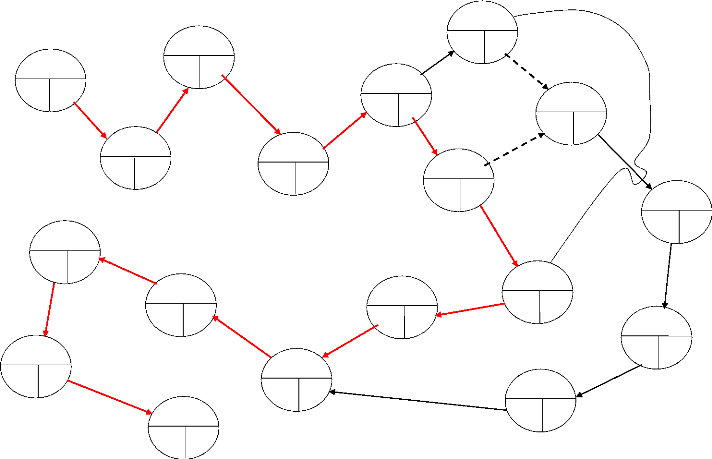
Ce graphe ne répond pas aux exigences d'un réseau d'où il faut le ramener à la structure d'un réseau avec une origine et une et une seule extrémité, qui nous amène à l'arrangement à savoir :

e

6 jours

1 jour

j

a b c d

0 1

5 jours 3 jours 2 jours 6 jours

2 3 4

10

f

10 jours

6

2 jours

g

7 jours

p

13

14 2 jours

n

3 jours

m

12

2 jours

l

22 jours

11

k

2 jours

7

o h 4 jours

16

6 jours

8

17

r

9

18

q

i

5 jours

1 jour

Figure n°02 : Graphe PERT ordonné

¹⁶ Guide méthodologie du travail en commun, Planifiet - Organiser le Projet, IAAT 2005.

¹⁷ SULA, opcit.

a b c

0 1 2d

3 4

NZINGA ANTOINE Dickembers

Modélisation et l'implémentation d'un système informatique pour la gestion des bonnes

24

II.4.5. Matrice Booléenne

Cette matrice nous permettra, par les différents rangs à obtenir, de pouvoir ordonner facilement le graphe PERT se rapportant à notre étude.

P(x) S(x)	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R
A	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
B	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
C	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0 0 0	0 0 0
D	0	0	0	0	1	1	0	0	0	0	0	0	0	0	0	0
E	0	0	0	0	0	0	1	0	0	1	0	0	0	0	0	0
F	0	0	0	0	0	0	1	0	0	0	1	0	0	0	0	0	0	0
G	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0
H	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0
I	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0
J	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0
K	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0 0 0
L	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0
M	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0
N	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0
O	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0
P	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0
Q	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1
R	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

NZINGA ANTOINE Dickembers

Tableau n°05 : Matrice Booléenne

NZINGA ANTOINE Dickembers

Modélisation et l'implémentation d'un système informatique pour la gestion des bonnes 25

H(2)

P(7)

Figure n°03 Réseau pert

68 68

62 62

J(1)

22 39

E(6)

8 8

0 0

A(5)

B(3)

C(2)

D(6)

16 16

F(10)

26 39

G(2)

5 5

10 10

26 26

K(22)

28 41

Q(5)

55 55

50 50

L(2)

48 48

N(2)

M(3)

30 43

67

67

R(1)

53 53

O(4)

I(6)

f

36 49