4.2. Importance des courbes caractéristiques du
sol
Si la conductivité hydraulique K est connue, les flux
hydriques tels que les remontées capillaires et le drainage peuvent
être déduits en mesurant les paramètres de
l'équation de Darcy à l'aide de tensiomètres et
d'humidimètres (Musy et Soutter, 1991). La teneur en eau (6) et la
conductivité hydraulique (K) sont liés par les relations
caractéristiques du milieu :
? La courbe de rétention h(6) lie la teneur en eau
volumique à la tension hydrique et exprime la capacité du sol
à retenir l'eau en fonction de la succion exercée. Grâce
à elle, il est possible de connaître les humidités
volumiques correspondant aux données tensiométriques (et
vice-versa). C'est une grandeur macroscopique fondamentale en physique du sol
car elle exprime l'influence de la structure, de la porosité et de
l'adsorption sur l'état de l'eau du sol.
Etat de l'art-Chapitre 4. Caractérisation hydrodynamique
des sols
? La courbe de conductivité hydraulique K(è) ou
K(h) caractérise la capacité du milieu à transmettre l'eau
en fonction de son état énergétique ou de son état
de saturation.
L'importance que revêt la conductivité
hydraulique pour la description de la dynamique de la phase liquide fait de sa
détermination un aspect essentiel de l'évaluation des processus
de transfert. La détermination de la phase liquide en laboratoire
s'effectue à l'aide d'échantillons non remaniés et aussi
représentatifs que possible de l'ensemble du terrain dont ils sont
issus. Ces deux conditions sont en général très difficiles
à respecter (ce qui induit souvent de grosses erreurs), par contre les
techniques de mise en place au laboratoire sont plus simples et fournissent des
mesures relativement précises.
4.3. Direction d'écoulement de l'eau dans le
sol
Les mouvements d'eau dans le sol, leur direction et leur
importance sont naturellement fonction des différences d'énergie
dans le sol. La détermination de la direction des écoulements
repose sur l'étude de la forme de la pente des profils de charge totale,
déduits des profils tensiométriques (Musy et Soutter, 1991). En
effet, la loi de Darcy dans le cas d'un écoulement vertical
s'écrit :
q=-K(è) ?H (4-5)
?z
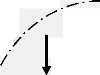
Ainsi, un gradient de charge négatif indique un
drainage des eaux (Figure 3); un gradient de charge positif
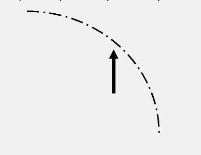
stipule un mouvement ascendant de l'eau (Figure 4) et un
gradient de charge nul traduit un flux nul (redistribution et
évaporation) comme le montre la Figure 5.
Z[m]
-4,0 -3,0 -2,0 -1,0
H[m]
Zone plus humide
Direction de l'écoulement
- 0,1
- 0,2
- 0,4
- 0,6
Zone plus sèche
20
Figure 3: Profil de charge totale -
écoulement descendant
Etat de l'art-Chapitre 4. Caractérisation hydrodynamique
des sols
Z[m]
H[m]
- 0,1
- 0,2
- 0,4
- 0,6
-4,0 -3,0 -2,0 -1,0
Zone plus sèche
Direction de l'écoulement
Zone plus humide
Figure 4: Profil de charge totale -
écoulement ascendant
Z[m]
|
-4,0 -3,0
|
-2,0
|
-1,0
|
|
- 0,1
- 0,2 Zo
- 0,4
- 0,6
|
H[m]
|
21
Figure 5: Profil de charge totale -
redistribution Source: Musy et Soutter (1991)
| 


