Entwicklung einer steuerung mit grafische oberfläche auf einem mini-computer zur durchführung von fahrzyklen an einem motorprüfstand.

5.2.1.2 Button

Ein Button ist eine Tkinter-Klasse, die eine interaktive Kommunikation mit dem Nutzer vereinfacht. Jeder Button führt zu einer bestimmten Aktion. Für die Realisation der GUI werden verschiedene Buttons erzeugt.So wird z.B. ein Button benötigt, um sich anzumelden bzw. damit der Nutzer die Möglichkeit hat, das Programm zu beenden. Ferner ist ein Button für den Sprung zur nächsten Seiteerforderlich und ein weiterer, um den Prüfstand ein- bzw. auszuschalten. Der Folgende Code zeigt, wie der Button<anmelden> mit dem Tkinter-Modul erzeugt wird:

Import tkinter as tk

root = tk.Tk()

Login_Button = tk.Button(root, text="anmelden",

font=("Helvetica",12,"bold"), width=46,

fg="#000000",bg="white")

Login_Button.pack()

root.mainloop()

Abbildung 19: Programmausschnitt für das Erzeugen des "Anmelden" Buttons

5.2.1.3 Canvas

Canvas dient dazu, grafische Elemente zu erzeugen. Somit wird in diesem Bereich das Zeigerinstrumentfür die Drehzahlanzeige realisiert. Das Canvas enthält unter Tkinter unterschiedliche Artengrafischer Elemente,wie z.B. Linie, Rechteckt, Kreis. Das Canvas-Element wird im Tkinter wie folgt erstellt:

Import tkinter as tk

root = tk.Tk() #erzeugt das Tkinter Fenster

Canvas_breite = 350 #die Breite der Canvas-Element wird gesetzt

Canvas_Höhe= 250 #die Höhe der Canvas-Element wird gesetzt

Canvas = tk.Canvas(root, width= Canvas_breite ,height=Canvas_Höhe,

background="#41B77f",highlightthickness=0)

Canvas.grid()

root.mainloop()

Abbildung 20: Programmausschnitt für das Erzeugen eines Canvas in einem Tkinter-Fenster.

· Der Zeigerinstrument

Canvas Breite

5

6

4

7

3

È₅=È₁*5

8

sin(è₅)

2

Canvas Höhe

È₁

9

1

sin(è₁)

0

10

Max. Teilstrich

cos(è₅) =0

Min. Teilstrich

Cos(è₁)

Canvas Fenster

Abbildung 21: Vorgehensweise für Das Zeichnen der Teilstriche der Zeigerinstrument

Die Skalenlinien des Zeigerinstruments werden durch das Erstellen von Linien mit unterschiedlichen Koordinaten erzeugt, die einen Kreisbogen bilden.Die Methode Create_linie der Klasse Canvas nimmt als Argument 4 Parameter. Das bedeutet, dass die Linien jeweils vom Punkt Innenradius für Teilstriche(siehe Abb.22) mit Koordinaten (X_i,Y_i) zum PunktAußenradius für Teilstrichemit Koordinaten (Xj,Y_j) verlaufen wird.i und j gehören zum Intervall [0, 10] mit 0 der minimalen Anzahl von Teilstrichen und 10 der maximalen Anzahl von Teilstrichen.

Ändert sich der Winkel Theta, dann ändert sich auch sein Cosinus und Sinus.

Für eine maximale Anzahl von Teilstrichen (N=10) wird der maximale Winkel auf 180⁰, für eine minimale Anzahl von Teilstrichen(N=0) wirdes auf 0⁰gesetzt.

Anz. Von Teilstriche	Nmin=0	1	2	3	4	5	6	7	8	9	Nmax=10
Winkel in Grad ^0	0	18	36	54	72	90	108	126	144	162	180

Tabelle 4: Berechnung der Teilstriche Winkel der Zeigerinstrument

Der Winkel allerTeilstriche wirdanhand der Dreisatz-Regel berechnet.

Also: N_max - N_min è_max- è_min

N=1 è₁

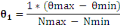
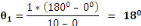
Innenradius für Teilstriche

Außenradius für Teilstriche

Canvas_breite / 2

X

175

40

175

80

175 Pixel

250 Pixel

(0,0)

Y

350 Pixel

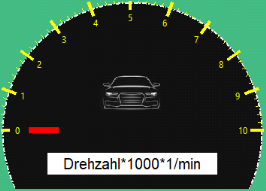
Abbildung 22: Zeigerinstrument für die Drehzahlanzeige in Canvas

Der folgende Python-code erläutert, wie die obenstehende Abbildung mit dem Modul Tkinterrealisiert wird.

Import math

From math import pi

Import tkinter as tk

Width=350 #Breite der Canvas-Fenster

Height=250 #Tiefe der Canvas-Fenster

Theta_min=0 # minimal winkel

Theta_max=180 # maximale winkel

Teilstrisch_min=0 # minimale Anzahl von Teilstrische

Teilstrisch_max=10 # maximale Anzahl von Teilstrische

Delta_Theta= Theta_max - Theta_min

Delta_N = Teilstrisch_max - Teilstrisch_min

root = tk.Tk()

canvas= tk.Canvas(root, width=width,height=height, bg="#41B77f",

bd=3, highlightthickness=0)

canvas.grid()

Gauge=canvas.create_oval(5 , 5, width, 350, fill="#111111", width=2,

outline="#EEEEEE", activedash=7,

dash=(12,1,1,1) )

red_line=canvas.create_Line(80,175,40,175,fill="red",width=8)

for i in range(11):

Teilschritte=canvas.create_line((width/2)-160*math.cos(((delta_Theta / Delta_N)*i)*pi/180),

(width/2)-160*math.sin(((delta_Theta / Delta_N)*i)*pi/180),

(width/2)-180*math.cos(((delta_Theta / Delta_N)*i)*pi/180),

(width/2)-180*math.sin(((delta_Theta / Delta_N)*i)*pi/180),

fill="yellow",width=4)

text=self.canvas.create_text(((width/2)-150*math.cos(((delta_Theta / Delta_N)*i)*pi/180),

(width/2)-150*math.sin(((delta_Theta /Delta_N)*i)*pi/180),

text=i,fill="yellow")

root.mainloop()

Abbildung 23: Programmausschnitt für die Realisierung der Gauge-meter