II.4.1.1. La population de l'étude
La population de notre étude est constituée de
l'ensemble des consommateurs de la bière des différents sexes,
âgés de 18 ans et plus ayant déjà consommé ce
produit (bière) et résidant dans la ville de Bukavu
précisément dans la commune de Kadutu.
2.4.1.2. La taille de l'échantillon
La population cible de notre étude est constitué
de la population de la commune de Kadutu chiffré à 2867
consommateurs de la bière. La taille de notre échantillon est
trouvée par la formule suivante :
Avec n : la taille de l'échantillon
Zá2 : le coefficient de fiabilité
pris à 1,96 pour un intervalle de confiance de 95%
ä : l'écart - type de
l'échantillon
E : la marge d'erreur
A partir de cette formule, nous remarquons que la taille
cherchée est fonction de la l'écart - type de la population
qui ne pas connue. Comme la taille est une fonction d'une autre inconnue qui
est l'écart - type, la théorie propose trois solutions pour
résoudre le problème
ANDERSON, D. et al. (2001) préconisent trois solutions
suivantes :
- Possibilité d'organiser un pré test ou une
étude pilote sur une trentaine d'individus de la population cible et
estimer l'écart-type sur cette base ;
- Si les valeurs extrêmes de la variable
étudiée (maximum et minimum) sont connues dans la population et
si la règle de l'approximation normale est acceptable, l'écart
type peut être estimé à partir de la différence
entre les deux valeurs extrêmes divisée par quatre.
- Si on dispose les résultats d'une étude
similaire effectuée dans le passé récent, on utilise
l'écart type observé à cette époque.
Dans le cadre de notre travail nous optons sur pour la
troisième solution. Une étude portant sur le déterminant
de la consommation des bières étrangères au Sud - Kivu
mené par MAROTI Bahati Elizabeth (2009) a donné un écart -
type de 10,203. A partir de la formule et les valeurs des paramètres
nous avons trouvé la taille de l'échantillon.
  = 82,59 = 83 consommateurs
Après avoir passé aux près enquête
nous avons remarqué que certaines consommateurs ont changés leur
comportement de consommations et d'autre ont dût rester fidèle
à l'ancienne marque. Les raisons qui ont poussées les uns
à changer et les autres à rester fidèle sont multiples.
Pour les uns les raisons de changement sont les suivantes : la
disponibilité sur le marché, le prix, les anciens produits
présentent la fatigue le lendemain une fois consommé une grande
quantité « effet murumbé ». Pour ceux qui
sont resté fidèle à la marque les raison de cette
fidélité sont les suivantes : certains sont des agents de la
maison productrice (Bralima), l'habitude, goût des anciens produits
(Primus, Mützig, Turbo king) est meilleur par rapport au goût des
nouveaux produits (Skol, Simba, Dopel), la capacité en alcool aussi fait
à ce que certains restent fidèle à l'ancien marque.
II.5. Quelques statistiques descriptives
.LaMoyenne arithmétique :
c'est la somme des termes divisés par leurs nombre. Elle est
calculée à l'aide de la formule suivante :
  =  Avec N : nombre des vendeurs suivant notre échantillon
.La variance : c'est la somme
arithmétique des carres des écarts des valeurs par rapport a la
moyenne appliquée a un échantillon de taille n. Elle est obtenue
à l'aide de la formule suivante :
V= 
.L'écart type : on la
symbolise par .Plus est faible, plus il y a une concentration des valeurs
autour de la moyenne ; plus il est élevé, plus les
données sont dispersées autour de la moyenne. C'est la racine
carrée de la variance
= 
.Coefficient de variation(CV) :
c'est une mesure de l'homogénéité d'une série qui
exprime l'écart-type en pourcentage de la moyenne. Il est mesuré
par :
CV= 
II.6. Statistique inférentielle
TEST DE KHI-CARRE (Laurence L. Lapin, 1987) :
a)Définition
La distribution de Khi-carré est semblable à la
distribution de Student parce qu'elle a une distribution distincte pour chaque
nombre de degré de liberté. Plusieurs applications statistiques
font appel à la distribution du Khi-carré. Tout comme la
distribution de Student, il n'y a pas une distribution différente pour
chaque valeur du  , selon le nombre de degré de liberté qui s'applique
à un test particulier.
Pour effectuer ce test, on dispose en premier lieu des
données observées rangée dans un tableau de contingence
comprenant une rangée ipour chaque
caractéristique de la 1ere variable et colonne
j pour chaque caractéristique de la seconde
variable. Les cases de ce tableau,   correspondent aux fréquences théoriques observées
pour chaque couple caractéristique. On calcule ensuite les
fréquences théoriques espérées, 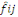  au moyen de l'équation suivante :
Ou n
correspond à la taille de l'échantillon.
Une fois toutes les valeurs   obtenues, on peut les disposer dans un deuxième tableau.
Pour comparer les fréquences observées et les
fréquences théoriques espérées, on se sert de
l'équation suivante pour calculer la valeur de la statistique de Khi
carré :
Il s'agit toujours des tests unilatéraux à
droite et pour un seuil de signification donnée de á, il y a une
valeur critique correspondante   á qu'on retrouve en consultant le tableau C).On
calcule ensuite le nombre de degré de liberté :
  Ou s : nombre des colonnes
r : nombre des rangées
Si la valeur du   qu'on obtient est superieur a la valeur du  calculé, on rejette l'hypothèse nulle de
l'indépendance ; dans le cas contraire, on l'accepte.
| 
