L'impact des événements politiques, économiques, sociaux et du terrorisme sur la volatilité boursière: cas du marché financier tunisien

Section 2 : Validation empirique

Dans cette deuxième section, tout d'abord on va présenter et analyser les statistiques descriptives des trois indices boursiers. Ensuite, nous allons étudier la normalité et l' hétéroscédasticité. Enfin, nous allons présenter le modèle à estimer.

2.1) Analyse statistique descriptive des variables endogènes Tableau 4: Statistiques descriptives des variables financières

	R_TUNINDEX	EURO_TND	LN_INDSF
Mean	6.39E-05	0.000106	8.071671
Median	0.000111	0.000139	8.054980
Maximum	0.041086	0.011654	8.256192
Minimum	-0.041439	-0.012561	7.968015
Std. Dev.	0.005876	0.002527	0.064316
Skewness	-0.718972	-0.115847	0.827714
Kurtosis	15.60355	5.401614	3.102524
Jarque-Bera	7415.597	272.3945	126.8878
Probability	0.000000	0.000000	0.000000
Sum	0.070684	0.119070	8935.340
Sum Sq. Dev.	0.038159	0.007165	4.575041
Observations	1106	1123	1107

63

D'après le tableau (4), nous allons analyser les propriétés statistiques de trois variables ainsi que le critère de la normalité, en effet, nous calculons le coefficient d'asymétrie (skwenes) et l'aplatissement (kurtosis) et la statistique de jarque-bera (JB).

Pour le rendement de l'indice Tunindex, on remarque que la moyenne est de 6.39E-05 avec un minimum de -0.041439 et un maximum de 0.041086 au cours de la période étudiée. Son écart type est égal à 0.005876. Concernant le test de l'hypothèse de normalité du r_Tunindex, son kurtosis est largement supérieur à 3 soit (15.60355 >3), ce qui engendre des distributions leptokurtiques. En effet, ce rendement présente une valeur du skewnes égale à -0.718972 <0 et par conséquent, une asymétrie négative (asymétrie à gauche).

Concernant l'Indsf, on constate qu'il présente une moyenne de 8.071671 avec un minimum 7.968015 et un maximum de 8.26192. Son écart type est égal à 0.064316. Son kurtosis est supérieur à 3 soit (3.102524), ce qui ramène à des observations leptokurtiques (absence d'aplatissement). En effet, il admet des valeurs de skewnes positives (0.82771) supérieur à zéro et par la suite, une asymétrie vers la droite.

La variable Eur/ Tnd possède une moyenne de 0.000106 avec un minimum de -0.012561 et un maximum de 0.011654. Son écart type est de valeur 0.002527. Passant au test de l'hypothèse de normalité de cette variable, son kurtosis est égale à 5. 401614.Il est supérieur à 3 ce qui entraine des observations leptorkurtiques. La valeur du skewnes est négative, c'est-à-dire, inferieur à zéro (-0.115847) et par conséquent, il y a une asymétrie vers la gauche.

2-2) Etude de la normalité

Les valeurs de skewnes, kurtosis et la P_value de la statistique de JarqueBera montrent certaines asymétries dans les variables étudiées (P_value pour les trois indices est inférieure à 0.05). Donc, la distribution est non normale. Ainsi, la mesure de la variance conditionnelle est la plus adéquate pour mesurer la sensibilité de nos trois variables en faveur des effets des diverses nouvelles. En effet, la probabilité de Jarque-Bera est inférieur à 0.05 pour r_tunindex et r_eur/tnd et ln Indsf, d'où le rejet de l'hypothèse nulle et l'acceptation de l'hypothèse alternative d'hétéroscedasticité qui suppose l'existence d'un effet ARCH/GARCH .

64

2.3) Test de Fisher : Test d'hétéroscédasticité

On va utiliser le Test de Fisher afin de renforcer notre hypothèse testée sur le Tunindex, le taux de change EUR/TND et l'indice INDSF qui suivent un processus autorégressif d'ordre (P) :

Xt = 0 + + åt (1)

Ht = á0 + (2)

: Variable endogène

: Variance conditionnelle

: Terme d'erreur idN (0.h²t)

Le test se présente de la sorte :

Ho : Absence d'effet ARCH

H 1 : Présence d'effet ARCH

Tableau 5:Test d'effet ARCH au Tunindex

Heteroskedasticity Test: ARCH

F-statistic 71654.76 Prob. F(1,1104) 0.0000

Obs*R-squared 1089.218 Prob. Chi-Square(1) 0.0000

Tableau 6: Test d'effet ARCH à l'Indsf

Heteroskedasticity Test: ARCH

F-statistic 59581.72 Prob. F(1,1104) 0.0000

Obs*R-squared 1085.880 Prob. Chi-Square(1) 0.0000

Tableau 7: Test d'effet ARCH au taux Eur/Tnd

Heteroskedasticity Test: ARCH

F-statistic 178168.2 Prob. F(1,1121) 0.0000

Obs*R-squared 1115.978 Prob. Chi-Square(1) 0.0000

65

D'après ces trois tableaux, on remarque que la probabilité associée à la statistique du test de Fisher est en dessous du seuil de risque. (Prob<0.05), ce qui entraine le rejet de l'hypothèse nulle et par conséquent, l'acceptation de l'existence de l'effet ARCH.

2.4) Présentation du modèle et des variables à tester

Nous présentons successivement le modèle ainsi que les variables à tester. Pour bien comprendre l'effet des mauvaises nouvelles et conformément au modèle EGARCH proposé par Gewek (1986) et Pantula (1986) qui ont utilisé le modèle ARCH spécifique non paramétrique. Le modèle se compose de deux équations :

? Equation du rendement

rx1,t = 0 + 1rx1, t-1 + ₂ Dummy + åx1,t

? Equation de la volatilité

log(h² x1,t) = æ + á1?x1,t (Zx1,t-1) + â log(h² _x1,t) + á2Dummy

Où,

?x1,t (Zx1,t-1) = (|Zx1,t-1| - E | Zx1,t-1|) + ä Zx1,t-1 ^and Zx1,t-1 = åx1,t-1 | hx1,t-1|.

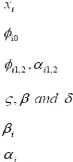
: Différentiel de ln Tunindex, Différentiel du ln Eur/Tnd , ln indsf

: Constante

: Coefficients

: Paramètres de la variance conditionnelle

: Effet de la dernière période sur la variance conditionnelle.

: Contribution de la période précédente dans l'explication de l'information liée aux résidus, affectant la volatilité de la période.

: Effet qui distingue entre les mauvaises et les bonnes nouvelles. Un coefficient négatif t signifie que les mauvaises nouvelles ont un effet plus important sur la volatilité.

Les variables « événements » sont construites comme suit :

66

ev_glob : représente le total des événements, on attribue 1 suite à la présence d'événement, 0 sinon

ev_soc : représente les événements sociaux, on attribue 1 à la présence d'événement, 0 sinon

ev_eco : représente les événements économiques, on attribue 1 à la présence d'événement, 0 sinon

ev_pol : représente les événements politiques, on attribue 1 à la présence d'événements, 0 sinon

ev_terro : représente les événements du terrorisme, on attribue 1 à la présence d'événements, 0 sinon