Modélisation en risques de crédit : dérivés de crédit et calibration de modèles structurels

N° d'ordre :

REPUBLIQUE TUNISIENNE

****

MINISTERE DE L'ENSEIGNEMENT SUPERIEUR ET DE LA RECHERCHE SCIENTIFIQUE

****

UNIVERSITE DE SFAX

FACULTE DES SCIENCES DE SFAX(FSS) ANNÉE UNIV 2010/2011

FACULTE DES SCIENCES DE SFAX Ecole Doctorale sciences fondamentales

Ecole Doctorale : SCIENCES FONDAMENTALES (Mathématiques)

MÉMOIRE

Présenté pour l'obtention du diplôme de :

MASTÈRE

Spécialité :

ASSURANCE ET MATHÉMATIQUES POUR LA FINANCE

Par :

Mr. JELLALI Mohamed Néji

Sujet :

Modélisation en Risques de Crédit :

Dérivés de crédit et Calibration de modèles structurels

Encadré par :

Mr.Yacin JERBI, Encadreur académique, enseignant

chercheur en Mathématiques & Finance Quantitative,FSEGS.

Mr.Mohamed Raouf JEMAA, Directeur octroi des crédits

au PME : pôle Risque, Direction Centrale Analyse Risques.

L'Union Internationale de Banques(UIB) Tunis, groupe SOCIETE GENERALE

Soutenu le 01 Juin 2011, devant le jury composé :

Noms et prénoms Fonctions / Entreprise

Pr. Mr JERIBI Aref Président Enseignant-chercheur/FSS

Pr. Mr. MASMOUDI Afif Examinateur Enseignant-chercheur/FSS

Pr. Mr. DABBECH Mohamed Membre Chef d'agence/Axis Bourse

Pr. Mr. JERBI Yacin Encadreur Enseignant-chercheur/FSEGS

Laboratoire : Probabilités et statistiques (Code ED : ED08FSSf01/ LR : 00/UR/15-02) Département : Mathématiques

Remerciements

Ce rapport est préparé après un stage de fin d'études au sein de L'Union Internationale de Banques(UIB), groupe SOCIETE GENERALE de Tunis et plus précisément au Pôle Risques : Direction Centrale Analyse Risques ; Direction Analyse et Octroi des Crédits aux Particuliers, Professionnels, TPE et Associations (au Berge du lac-Tunis) et aussi au sein du Pôle Commercial : l'agence MISR (à la Fayette).

Je tiens à remercier mon maitre de stage Mr. Raouf JEMAA(Directeur octroi des crédits au PME) , Mr .Hichem RBAI (Directeur du pole Risque) et Madame Raoudha ESSID (Directeur département des crédits) pour ses aides et ses conseils.

Je remercie aussi Madame Houda ELGHRIBI, chef de l'agence MISR, pour l'intérêt qu'elle a montré à l'égard de mon travail.

Je remercie également mon encadreur académique Mr .Yacin JERBI qui m'a guidé et répondu à l'ensemble de mes questions. J'ai particulièrement apprécié sa rigueur en matière de rédaction et la qualité de ses relectures.

Ensuite, je remercie également Mr Aref JERIBI le président du jury de ce mémoire.

J'adresse également mes remerciements à Mr Afif MASMOUDI le coordinateur du Mastère `Assurance et Mathématiques pour la finance ', pour sa grande disponibilité et ses précieux conseils et je suis très honoré qu'il soit examinateur sur mon mémoire.

Je suis également très heureux que Mr Mohamed DABBECH, chef d'agence /Axis Bourse, aient bien voulu être membre du jury.

Je tiens également ici à exprimer ma gratitude envers Mr le professeur Abdelhamid HASSAIRI, responsable du Laboratoire de Recherche `Probabilités et Statistique' (et à travers lui plusieurs de mes professeurs de mathématiques) qui à un moment charnière a, par son enseignement, développé et renforcé mon attrait pour les mathématiques.

Je souhaite enfin remercier mon entourage, qui de près ou de loin, a su m'apporter sa confiance et son soutien.

JELLALI Mohamed Neji

SOMMAIRE

Remerciement

INTRODUCTION 5

Chapitre 1 Présentation des produits dérivés 10

1.1Introduction aux marchés financiers 10

1.2 Titres de base et produits dérivés 10

1.2.1Titres de base 10

1.2.2 Les contrats à terme 11

1.3 Caractéristiques financières des contrats d'options 12

1.3.1 Les options négociables 12

1.3.2 Les options de gré à gré 15

1.3.3 Utilité des produits dérivés 15

Chapitre2 Outils et concepts de base pour modéliser le risque de

crédit 16

2.1 Zoologie des risques 16

2.2 Enjeux 17

2.3 Modèles du risque de crédit 18

Chapitre 3 Produits dérivés de crédit 20

3.1 Le marché des produits dérivés de crédit 20

3.2 Les obligations risquées 23

3.3 Credit default swap (CDS) 23

3.3 .1 Description du produit 23

3.3 .2 Evaluation de la marge d'un CDS 24

3.3 .2 .1 Exemple. (Pricing d'un CDS) 25

3.4 Collateralized Debt Obligations 27

3.4 .1 Titrisation 27

Chapitre 4 Les modèles structurels 29

4.1.2 Les obligations risquées 30

4.1.3 La modélisation du défaut d'une entreprise 34

4.1.4 La Différence entre actions et obligations 35

4.2 Modèle de Merton : présentation du modèle de base 35

4.2.1 Produits dérivés sur la valeur des actifs de la firme 36

4.2.2 Probabilités de défaut et Loss Given Default 37

4.2.3 Distance-to-default 38

4.2.4 Levier d'endettement 39

4.2.5 Spread implicite 39

4.2.6 Une première implémentation du modèle de Merton 40

4.2.7 Spread implicite et smile de volatilité 41

4.2.8Limites du modèle et extensions 44

4.3 Modèles de premier instant de passage 44

4.3.1 Préliminaires mathématiques 45

4.3.2 Lemme 45

4.3.3 Proposition 45

4.4 Modèle Credit Grade 46

4.4.1 Description du modèle 46

4.4.2 Probabilité de défaut et spread de crédit 47

4.4.3 Calibration du modèle sur les données de marche 48

Chapitre 5 Les modèles structurels en pratique (Exemples de modèles) 50

5.1 Exemples de modèles 50

5.1 .1 Modèles KMV (Kealhofer, McQuown et Vasicek) de Moody's 50

5.1 .2 Forces et Faiblesses 52

5.1 .2 CreditMetrics de JPMorgan 53

5.1 .2.1 Principe du modèle : portefeuille à une

obligation 53

5.1 .2.2 Principe du modèle : portefeuille à deux obligations 59

5.1 .2.2 .1Exemple de Portefeuille de 2 titres BBB et A 63

5.1 .2.3 Principe du modèle : portefeuille à plusieurs

obligations 64

5.1 .2.3.1 Forces et Faiblesses 66

Chapitre 6 CONCLUSION : 67

6.1 L'amélioration théorique de ces modèles 68

6.2 Etude empirique 69

6.3 RESULTATS ATTENDUS 70

ANNEXE 1 Lemme d'Itô 71

ANNEXE 2 Equation de Black & Scholes (modèle standard) 73

ANNEXE 3 Démonstration du Lemme 4.3.2 76

Bibliographie 79

INTRODUCTION

Introduction

Le mémoire que je présente se décompose en trois parties assez distinctes, mais qui ont tout attrait à la modélisation stochastique du risque de crédit en finance.

Objectif

· Découvrir les grands domaines de la modélisation du risque de crédit.
·Présenter les principaux dérivés de crédit (CDS et CDO). Nous y décrivons leurs payoffs et donnons quelques indications sur leur intérêt financier.

· Comprendre l'approche structurelle en pratique pour modéliser le risque de crédit.

· Savoir utiliser et calibrer les modèles de risque de crédit sur des portefeuilles de créances.

Partie 1

Le premier volet de ce présent travail est un chapitre introductif aux produits dérivés en finance, nous faisons une introduction aux marchés financiers, les titres de base des produits dérivés, ainsi que les caractéristiques financières et les stratégies des contrats d'options .

Dans cette première partie de ce mémoire et dans le chapitre 2 nous passons à présenter quelques outils et concepts qui peuvent servir de base à la modélisation du risque de crédit ; ils sont plus spécifiquement orientés vers la valorisation des produits dont la valeur dépend du risque de crédit auquel il est exposé. Dans ce chapitre et après avoir rappelé quels sont les principaux risques auxquels sont confrontées les institutions financières, nous expliquons quels sont les enjeux de la modélisation du risque de crédit.

Le marché du risque de crédit est depuis une dizaine année en pleine expansion. Ce marché a pour objet d'échanger des produits financiers qui sont essentiellement des protections contre le risque de défaut d'une ou de plusieurs entreprises. On attribue souvent le développement récent de ce marché à la prise de conscience qu'a constitué la crise asiatique à la fin des années 1990, puis aux faillites retentissantes de la société ENRON ou de l'Etat d'Argentine en 2001. En Europe, la faillite en décembre 2003 de Parmalat a également fait couler beaucoup d'encre. Cela étant, si l'apparition de produits liquides traitant du risque de faillite est récente, les faillites et le problème de recouvrement de la dette existent eux depuis bien longtemps. On peut donc légitimement se

demander pourquoi ce type de marché traitant du risque de défaut n'est pas apparu plus tôt. Nous ne nous étendrons bien évidemment pas sur cette question

Introduction

qui sort du cadre d'une thèse de mathématiques financières. Cependant, il est certain que les idées de Black, Merton et Scholes (1973) qui ont permis de voir un marche financier comme une source d'information et un moyen de se couvrir du risque sous-jacent au marche ne sont pas étrangères à l'émergence de nouveaux marches, et pas seulement celui du risque de crédit. Le temps qui s'est

écoulé entre ces travaux et l'émergence des dérivés de crédit peut s'expliquer au moins par deux raisons. D'une part il a fallu le temps nécessaire à la diffusion et l'acceptation de ces idées au sein des acteurs du marché. D'autre part, la spécificité des produits dérivés de crédit, avec notamment leur profil de paiement " tout ou rien", a certainement retardé leur développement.

Ainsi, nous commencerons par présenter dans le chapitre 3 de manière précise ce marche du risque de crédit en donnant la définition des principaux produits qui sont traités aujourd'hui.

On en distingue deux grandes classes. Tout d'abord, les produits traitant du défaut d'une seule entité (single-name). Le plus répandu est le Crédit Default Swap qui est une protection contre le défaut d'une entité. Dans ce chapitre nous citons un exemple de fonctionnement d'un CDS qui constitue le produit à la vanille de ce marché et nous décrivons les caractéristiques du Crédit Default Swap (CDS).

Ensuite on passe à présenter les principaux dérivés de crédit. Nous y décrivons leurs payoffs et donnons quelques indications sur leur intérêt financier.

En revanche, ces produits ne permettent pas de se couvrir contre le risque de plusieurs faillites en cascades. Pourtant, il est fréquent que la faillite d'une grande entreprise entraine la faillite d'autres entreprises.

Pour citer un exemple, ENRON a entrainé dans sa chute le cabinet d'audit Arthur Andersen. Ce phénomène d'entrainement a certainement atteint son paroxysme durant la crise de 1929. Ce type de risque, appelé risque de contagion est en un certain sens plus dangereux car il a un impact financier plus grand pour les banques, mais également un impact économique et social pour les états. C'est afin de limiter ce risque que des règles plus contraignantes sur la gestion du risque de crédit ont été fixées lors des accords de Bâle I et II. Pour traiter ce risque de dépendance entre les différents défauts, plusieurs

Introduction

types de produits sont apparus, mais les plus répandus aujourd'hui sont certainement les tranches de CDO (Collateralized Debt Obligation) appelés aussi simplement CDO et dans ce chapitre nous expliquons le fonctionnement de ces tranches.

Il est donc crucial de remarquer comment les CDS sont donc à la base de produits exotiques plus complexes, et sont utilisés à la fois en tant que produits de couverture (diversification du risque, couverture d'un risque en préservant la relation commerciale, réduction du risque de concentration, transfert du

risque de crédit (balance sheet CDO),...), et d'investissement (long d'un risque de crédit à l'aide d'un instrument hors-bilan, effets de levier, création de position de crédit synthétique (CDO synthétiques),...).

Partie 2

Dans cette deuxième partie on s'intéresse aux modèles structurels qui sont les plus utilisés par les praticiens du marché.

Nous regardons quelques modèles structurels dont le principe est d'expliquer le défaut d'une entreprise à partir d'autres variables économiques.

Par exemple, Merton lie le défaut d'une entreprise à sa capacité à rembourser sa dette, et le modèle de Black et Cox explique le temps de défaut d'une entreprise comme le premier temps de passage en dessous d'un certain seuil de la valeur de cette entreprise. Les modèles structurels sont aussi le point de vue utilisé par les agences de rating. Les principales agences sont Standard&Poor's, Moody's et Fitch. Elles fournissent régulièrement des notes sur la qualité de crédit de differentes entreprises ou collectivités publiques. La note d'une entité est établie en fonction de nombreux critères (son bilan, ses projets en cours,...). Elle est ainsi construite à partir d'autres variables et est en ce sens structurel.

Le chapitre 4 est consacré aux modèles structurels dont leur principe est d'expliquer le défaut d'une entreprise à partir d'autres variables économiques ,on commence par définir et présenter ce type de modèle et après avoir présenter le modèle de base(Le modèle de Merton ou le modèle de la firme (1974)) tel que l'introduit Merton dans son article fondateur , nous expliquons

comment le modèle de Merton est une adaptation au risque de crédit de modèle de Black-Scholes-Merton sur les produits dérivés, et le pricing d'un call.

Introduction

Ensuite nous décrivons une méthode d'implémentation présentée par Hull, Nelken et White (Hull (J. C.), Nelken (I.), White (A.). Merton's Model, Credit Risk, and Volatility Skews. Working Paper. University of Toronto (2003).)

Dans le chapitre 5 on s'intéresse à la coté pratique de l'approche de Merton, vue que dans la pratique, les outils de gestion du risque de crédit reposant sur cette approche sont le modèle KMV de Moody's et la méthode Credit Metric de JPMorgan entre autres, on va présenter et décrire ces deux modèles en mettant en vigueur les avantages et les limites de chaque modèle.

L'une des limites du modèle de Merton réside dans le fait que le défaut de l'émetteur ne peut intervenir qu'à la maturité de la dette, pour combler cette lacune on s'installa dans des modèles appelés modèles de premier instant de passage dans les quels l'instant de défaut est (un temps d'arrêt) de la forme

ô = inf{t > 0 ; At < Bar(t)}, où Bar est une barrière qui peut être aléatoire et A est une variable de type «valeur de la firme». Après quelques préliminaires mathématiques, nous présenterons un exemple de modèle de premier instant de passage : le modèle Credit Grade développé par JP Morgan.

Il est très important de noter que toute une autre famille de modèles appelés modèles à intensité de défaut ou encore modèles à forme réduite cherchent à expliquer le défaut à partir d'un processus exogène appelé intensité de défaut. Ce processus décrit la probabilité instantanée qu'une entreprise donnée a de faire faillite. L'objet est alors d'extraire à partir des prix observés sur le marché du risque de crédit cette probabilité telle qu'elle est perçue par le marché.

Bien évidemment, cette probabilité est influencée par les analyses structurelles puisque notamment les acteurs du marché tiennent compte des notations des agences de rating. Cependant, il peut y avoir quelques écarts entre la vision du marché et celle des analyses financières. Un exemple récent et très net de ce type d'écart a eu lieu sur le marché action lors de " la bulle internet" où le marché a anticipé des scénarios trop optimistes. En ce sens, on peut dire que les modèles à intensité sont par nature plus proches de l'opinion du marché tandis que les modèles structurels cherchent à donner une explication économique du défaut (endettement excessif, mauvais choix stratégiques...).

Partie 3

Enfin, la troisième partie est une conclusion qui mette en exergue les points forts ainsi que les faiblesses des deux approches structurelle et à formes réduite.

Les modèles structurels de la dette risquée actuels ne parviennent pas à rendre compte convenablement de la structure des spreads observés et de leur sensibilité à certaines variables.

Pour discuter ce problématique et proposer quelques raisonnement qui peuvent être utile pour combler ces faiblesse, on s'intéresse dans cette conclusion d'une part à un approfondissement théorique dans l'approche structurelle pour modéliser le risque de crédit et d'autre part, à une étude empirique visant à induire (à partir du modèle élaboré) une estimation des primes de risque sur action à partir des spreads de crédit observés.

Nous nous intéressons, dans cette conclusion, plus à l'approche structurelle que celle à forme réduite, vue qu'il est le plus utilisée en pratique sur le marché.

Chapitre 1

Présentation des produits

dérivés

1.1Introduction aux marchés financiers

Une révolution de grande ampleur a eu lieu depuis une trentaine d'années sur les marchés financiers, suite a une politique affirmée de dérégulation. Ce nouveau paysage financier est né notamment des déséquilibres et des incertitudes qui pèsent sur les relations économiques internationales depuis le début des années 1970 (endettement des pays en voie de développement, instabilité des taux de change). Le développement de l'inflation et la grande volatilité des taux d'intérêt ont perturbe les anticipations des investisseurs. D'autre part, l'internationalisation des capitaux, les progrès technologiques en informatique et communication ont modifié les relations entre les différentes places financières : New-York, Londres, Tokyo, etc. . . : il est maintenant possible à tout instant d'intervenir sur tous les marchés.

En France, les réformes ont commencé à la mi-1984 avec comme objectifs, le décloisonnement des marchés et la création d'un unique marché des capitaux, la modernisation des réseaux financiers. Un élément majeur de cette politique a été la création de deux marchés financiers très actifs, et avec de grandes liquidités, sur lesquels vont être négociés de nouveaux instruments financiers :

- le MATIF ou Marché à Terme International de France (1985) (d'abord nommé Marché à Terme des Instruments Financiers) et actuellement membre d'Euronext.

- le MONEP ou Marché des Options Négociables de Paris (1987).

1.2 Titres de base et produits dérivés

1.2.1Titres de base

L'activité financière se développe travers un certain nombre d'instruments tels que la circulation de monnaie exprimee dans differentes devises, les operations de prêts et d'emprunts qui sont assorties de paiements d'intérêts dépendant de la maturité des operations, et bien sur des actions émises par les entreprises qui refletent leur capitalisation. Des indices ont été créés (SP500, CAC 40..) afin de permettre aux investisseurs étrangers d'avoir une information rapide sur le niveau économique et le comportement des actions d'un pays.

La très grande variabilité de ces paramètres ou de ces titres a conduit naturellement à une demande de transfert des risques de la part d'un certain nombre d'intervenants, comme les entreprises industrielles,

les compagnies d'assurance Les banques jouent évidemment

Chapitre 1 Présentation des produits dérivés

un rôle fondamental dans cette transformation, notamment en proposant un certain nombre de produits financiers, qui seront appelés produits dérivés. Elles peuvent d'ailleurs utiliser elles-mêmes ces produits dans leur gestion pour compte propre.

Ces produits "d'assurance" existent de fait depuis fort longtemps, puisqu'on a trouvé la description de contrats a terme sur le blé dans des textes de l'Antiquité. Il y avait aussi un marché de contrats à terme sur les métaux très actif à Amsterdam au 18 éme siècle. Mais l'existence de marchés organisés (le premier est créé a Chicago en 1973) organises pour diminuer le risque de contrepartie sur des opérations dénouées dans le futur, contribue à faciliter l'accès par un grand nombre d'intervenants à ce genre de produits. En France, le MATIF et le MONEP ouvrent entre les années 1985-1987.

Nous distinguerons les contrats à terme et les produits optionnels, que nous retrouverons en

fonction de la nature du sous-jacent sur lequel ils sont écrits dans différents marchés :

- Le marché des changes : achat/vente de devises

- le marché des matières premières : métaux, pétrole, denrées agro-alimentaires...

- le marché des actions et des indices boursiers

- le marché des taux d'intérêt

1.2.2 Les contrats à terme

Une opération à terme est une opération au comptant différée dans le temps : l'acheteur et le vendeur se mettent d'accord sur les conditions d'un échange, qui s'effectuera à une date future précisée par le contrat, dite la maturité.

1. Les conditions de l''echange sont définitivement fixées à la date où le contrat est noué, mais l'échange d'argent n'a lieu qu' à maturité. Ces contrats peuvent porter aussi bien sur des tonnes de pétrole, des instruments financiers, ou tout autre bien dont la qualité ou la quantité sont clairement spécifiées.

2. A la date d'échéance, il peut y avoir livraison physique du sous-jacent, contre le paiement de la totalité de la somme prévue dans le contrat. On parle de "physical settlement". Il est aussi possible que les contreparties n'échangent que la différence entre la valeur de marché du titre à l'échéance et le cours garanti. On parle de "cash settlement".

3. Il y a un risque de voir la contrepartie avec laquelle on a noué le contrat ne pas satisfaire à ses obligations. C'est le risque de non-exécution ou de contre-partie. Son élimination a

conduit les marchés financiers à adopter des règles de fonctionnement concernant ces contrats légèrement différentes. On parle alors de contrat futures.

4. Les contrats à terme sont symétriques, c'est à dire qu'à priori chaque contrepartie a autant de chances que l'autre de gagner ou de perdre de l'argent dans le futur.

5. Pour les intervenants, l'intérêt des contrats à terme est de connaitre le cours d'une opération dans le futur. Il s'agit dans ce cas d'une opération de couverture :

6. Toute opération dans le futur peut être mise en place à des fins de spéculation. Un operateur qui anticipe (contre le marché) un certain type de mouvement peut acheter un contrat en espérant réaliser un gain.

7. Comme le souligne Aftalion et Poncet, ces marchés jouent aussi un rôle important en terme de diffusion de l'information. Les prix à terme reflètent en un certain sens

Chapitre 1 Présentation des produits dérivés

les prévisions des participants du marché, même si nous verrons que des arguments d'arbitrage les contraignent de manière importante.

8. Un autre risque est présent en permanence sur les marchés à terme : c'est le risque de liquidité. Un intervenant qui voudrait échanger son contrat à une date antérieure à l'échéance peut ne pas trouver rapidement de contrepartie. Les marchés organisés ont essayé de mettre en place des règles de fonctionnement qui limitent à la fois le risque de contrepartie et de liquidité. Ces risques restent importants dans les marchés de gré à gré.

9. Les produits dérivés permettent aussi de faire le lien entre différents marchés, (taux, change, actions) de telle sorte que l'ensemble des prix disponibles forment un tout cohérent. En effet, des combinaisons de plusieurs opérations sur différents marchés peuvent permettre de gagner de l'argent à coup sûr sans prendre aucun risque : On réalise ce qu'on appelle un arbitrage.La présence de nombreux professionnels très compétents dans les salles de marché aboutit par la loi de l'offre et de la demande à des ajustements de prix qui réduisent ces possibilités d'arbitrage. Nous verrons que cette "loi" des marchés liquides est à la base de la modélisation mathématique que nous présenterons dans les chapitres suivants.

1.3 Caractéristiques financières des contrats d'options

1.3.1 Les options négociables

Une option est un contrat qui permet à son détenteur d'acheter ou de vendre une certaine quantité d'un bien ou un actif à un cours convenu à l'avance, appelé prix d'exercice (Strike), à (ou jusqu' à) une date fixée, dite échéance de l'option.En contrepartie, l'acheteur verse immédiatement au vendeur de l'option une prime qui est le prix de l'option. Les options européennes sont les options exercées seulement le jour de l'échéance, et les options américaines celles qui peuvent être exercées à tout moment avant leur échéance. Les options cotées sur le marché à Paris sont américaines, mais les options de gré à gré sont souvent européennes.

Chaque contrat porte sur un nombre fixé d'actifs supports : 100 dans le cas des actions. Dans le cas du MONEP, il s'agit essentiellement d'options sur actions, ou éventuellement sur le CAC 40, qui est un indice reflétant le marché des actions en France. Dans le cas du MATIF, les options portent sur les contrats à terme sur taux PIBOR, ou sur le Notionnel, qui est un titre fictif de maturité dix ans, versant des coupons de 10%.

Les options d'achat et de vente Les options traitées sont essentiellement des options d'achat (call) ou de vente (put). Chaque contrat porte sur un nombre fixé d'actifs supports (100 dans le cas des actions). Le prix fixé dans le contrat auquel l'opération peut se faire s'appelle le prix d'exercice, ou strike.

Les opérations sur les options

Achat d'une option d'achat :

L'acheteur paye au vendeur une prime qui lui donne le droit d'acheter à la date d'échéance de l'option, 100 actions à un prix d'exercice convenu à l'avance. C'est le principe d'une " promesse de vente". Ce droit n'est "exercé" que si les cours ont monté et dépassé le prix d'exercice. Les risques sont limités à la prime payée, et les gains dépendent de l'écart entre le prix d'exercice et le cours à l'échéance.

Chapitre 1 Présentation des produits dérivés

Vente d'une option d'achat :

Le vendeur a l'obligation de livrer à l'échéance 100 actions au prix convenu, si l'acheteur le demande, c'est à dire exerce son droit. Son gain est constitué de la prime. Il espère que les cours vont baisser pour ne pas avoir à livrer. Les pertes peuvent être grandes en cas de hausse. Le vendeur est en général un investisseur professionnel.

Achat d'une option de vente :

L'acheteur a le droit de vendre 100 actions à un prix convenu. Les gains sont importants si les cours baissent ; la perte maximale est égale à la prime.

Vente d'une option de vente :

Le vendeur à l'obligation d'acheter au détenteur de l'option 100 actions au prix convenu si l'option est exercée. Il espère que les cours vont monter pour ne pas avoir à les acheter.

Straddel : Un straddel est une combinaison de deux options d'achat et de vente.

Les paramètres des options

· La durée d'exercice

Dans les marchés organisés, trois échéances sont cotées simultanément : 3, 6 et 9 mois sur les mois suivants : mars, juin, septembre, décembre. La cotation cesse la veille de l'échéance, ce qui signifie que les options sont négociables jusqu' à l'avant-dernier jour du mois d'échéance.

Toutefois, sur le CAC 40 l'échéance des options est mensuelle. Les pages financières des quotidiens donnent simultanément en plus des cours, le nombre de contrats traités. Les échéances les plus liquides sont traditionnellement les plus proches.

· Le prix d'exercice

C'est le cours auquel l'option peut être exercée. Trois prix d'exercice au minimum sont cotés sur chaque action, et chacune des trois échéances. Ils respectent entre eux des écarts standards. Les trois prix d'exercice sont fixés à des cours proches de celui de l'action. Les options les plus liquides sont les options à la monnaie, pour lesquelles le prix d'exercice est

proche de la valeur du cours. Les options dans la monnaie sont des options pour lesquelles la valeur intrinsèque n'est pas nulle. Les autres sont dites en dehors de la monnaie.

· Le prix d'exercice

C'est le cours auquel l'option peut être exercée. Trois prix d'exercice au minimum sont cotés sur chaque action, et chacune des trois échéances. Ils respectent entre eux des écarts standards. Les trois prix d'exercice sont fixés à des cours proches de celui de l'action. Les options les plus liquides sont les options à la monnaie, pour lesquelles le prix d'exercice est

proche de la valeur du cours. Les options dans la monnaie sont des options pour lesquelles la valeur intrinsèque n'est pas nulle. Les autres sont dites en dehors de la monnaie.

· La prime

La prime est le prix du contrat payé par l'acheteur au vendeur de l'option. Comme un contrat porte sur 100 actions support, l'acheteur doit payer 100fois la prime. Elle fait l'objet de cotations et peut être négociée : on peut acheter une option pour essayer de la

revendre plus chère, ou l'inverse. Le prix de l'option évolue tout au long de sa durée de vie. Le prix de l'option est décomposé en valeur intrinsèque et valeur temps.

· La valeur intrinsèque

C'est la différence positive ou nulle entre le cours coté du titre support et le prix d'exercice.

Call Valeur intrinsèque= sup (Cours de l'action- Prix d'exercice, 0) Put Valeur intrinsèque = sup (Prix d'exercice Cours de l'action, 0)

· La valeur temps C'est la différence entre le cours de l'option et sa valeur intrinsèque. Elle est nulle à l'échéance pour une option européenne.

Chapitre 1 Présentation des produits dérivés

Les straddles :Un straddle est un dérivé constitué d'un call et d'un put de même paramètres. La figure 1.2 représente le payoff vis à vis du vendeur. L'intérêt de traiter un straddle à la monnaie plutôt qu'une option réside dans le fait que sa sensibilité par rapport à une variation du sous-jacent est très faible à la date de négociation du contrat. C'est un pur produit de volatilité tant que le spot ne dérive pas. Si le spot S(t) dérive trop loin de K, l'une des deux jambe du straddle fait encourir des risques inutiles au vendeur pour un prix dérisoire. Il a donc intérêt à la racheter. Le rôle des marchés organisés d'options

Les marchés organisés contribuent par la grande lisibilité des prix affichés, la garantie qu'ils offrent aux intervenants en se substituant en cas de défaut de l'une des contreparties, àmaintenir une grande liquidité sur les titres négociés ou du moins sur certains d'entre eux les plus traités. La contrepartie est une certaine rigidité dans les produits fournis, qui sont de type standard. Ils sont le lieu privilégié vers lequel se tournent les traders qui cherchent à

couvrir des produits complexes à l'aide d'options standards. Ils peuvent être perçus comme les supermarchés de la finance.

Fig. 1.1: Profil de prix et valeur intrinsèque.

Fig. 1.2: Payof d'un straddle vis a vis du vendeur

Chapitre 1 Présentation des produits dérivés

1.3.2 Les options de gré à gré

En dehors des marchés organisés, il existe un grand nombre d'options négociées de gré à gré, c'est à dire directement entre l'acheteur et le vendeur, sans la garantie d'un marché, notamment sur les taux de change qui sont les supports d'un très grand nombre d'options de tout prix d'exercice et de toutes maturités. Les prix de telles options ne sont pas affichés sur les écrans Reuter, et peuvent varier d'une banque à l'autre. Toutefois, la grande liquidité de ces options et la présence sur les marchés d'arbitrageurs qui essayent de tirer profit de disparités sur les prix contribuent à rendre ces différents prix convergents.

1.3.3 Utilité des produits dérivés

Comme nous l'avons vu, la principale utilité des produits dérivés est de permettre de transférer les risques financiers entre les différents agents économiques rapidement. En particulier, certains agents, les banques notamment, sont disposés à prendre des risques supplémentaires moyennant un rendement accru de leurs opérations. Nous retrouverons tout au long de ce mémoire cette idée que rendement et risque sont fortement corrélés.

D'autre part, en transférant sur les banques les risques financiers associés à leur activité industrielle, les grandes entreprises n'ont plus qu' à gérer les risques d'exploitation, qui sont leurs risque spécifiques. En particulier, elles ont besoin d'immobiliser des réserves moins importantes de fonds propres, dont la rentabilité devient ainsi plus importante.

Les produits dérivés ont conduit à une plus grande spécialisation des investisseurs, qui peuvent se concentrer sur des portions de marché qu'ils connaissent bien, par exemple dans le secteur action. Par l'intermédiaire des produits dérivés, il peut diversifier son risque en échangeant la performance du CAC contre d'autres références en vigueur. Les produits dérivés offrent un fort effet de levier, dans la mesure où l'acheteur d'un dérivé ne risque de perdre au maximum que la prime, c'est à dire le prix qu'il a payé.

Chapitre2

Outils et concepts de base pour

modéliser le risque de crédit

Lobjectif de ce chapitre est de présenter quelques outils et concepts qui peuvent servir de base à la modélisation du risque de crédit ; il est plus spécifiquement orienté vers la valorisation des produits dont la valeur dépend du risque de crédit auquel il est exposé. Les modèles et techniques présentes peuvent néanmoins être utilises aussi bien pour la mesure que

pour l'évaluation du risque de crédit ( autrement dit, ces techniques servent aussi bien sous la probabilité historique que sous une probabilité risque-neutre).

Les avancées théoriques autour de la modélisation du risque de crédit est l'un des facteurs qui ont rendu possible l'essor d'un marché des produits dérivés de crédit.

Le développement du marché des produits dérivés de crédit, qui a atteint cette année un encours total d'environ 2300 milliards de dollars, a révolutionné en retour la gestion du risque de crédit ainsi que l'ingénierie financière qui lui est liée. Les gestionnaires de portefeuille et les investisseurs disposent désormais d'instruments financiers permettant le transfert efficace du risque de crédit.

D'après Alan Greenspan, la diffusion (et donc la mutualisation) des risques que génère ce marché des produits dérivés de crédit augmenterait la résistance de l'économie mondiale aux chocs systémiques comme l'aurait prouvé son bon comportement face aux récentes faillites d'Enron et de WorldCom.

Dans ce chapitre introductif et après avoir rappeler quels sont les principaux risques auxquels sont confrontés les institutions financières, nous expliquons quels sont les enjeux de la modélisation du risque de crédit. Nous présentons alors, brièvement, les deux grandes classes de modèles du risque de crédit : les modèles structurels et les modèles à forme réduite.

2.1 Zoologie des risques

On distingue traditionnellement quatre grands types de risques financiers [1] :

1. Le risque de marché

Le risque de marché peut se définir comme le risque de perte lié aux variations des conditions de marché (prix, taux, taux de change, volatilités, etc...)

2. Le risque de crédit

Le risque de crédit est définir comme le risque de perte lié à l'évolution de la qualité de la signature d'un émetteur. On peut distinguer deux types de risque de crédit: le risque de contrepartie et le risque de référence. Pour un émetteur donné, ce risque peut se matérialiser sous la forme :

-- du changement de sa note (upgrade ou downgrade) telle celle émise par les grandes agences de

notations Moody's et Standard & Poor's,

-- d'une variation de son spread de crédit,

-- d'un événement de crédit (credit event) tel le défaut de paiement ou la restructuration

de sa dette.

Ces trois risques sont, bien évidemment, corrélés. Une augmentation brutale du niveau du spread émetteur augmente la probabilité d'un événement de crédit. De la même manière, un changement de notation influe fortement sur la probabilité du défaut d'un émetteur. Lorsque A entre en relation avec une contrepartie B via un instrument financier, il peut être soumis au risque que B soit dans l'impossibilité d'honorer ses engagements.

Par exemple, si A est en possession d'une obligation émise par B, il court le risque qu'à maturité B ne puisse lui rembourser le capital investi. On parle dans ce cas de risque de contrepartie unilatéral puisque B n'est pas soumis au risque de crédit de A.

Si A et B sont les deux contreparties d'un swap, ils sont tout deux soumis au risque de contrepartie : on parle alors de risque de contrepartie bilatéral.

Supposons maintenant que la qualité de la signature des contreparties A et B soit de qualité infinie (de sorte que le risque de contrepartie bilatéral soit nul). Les parties A et B peuvent entrer dans un contrat qui fait intervenir le risque de crédit d'une troisième contrepartie C( un credit swap dont le payoff dépend de l'occurrence d'un événement de crédit est un exemple de tel contrat).

Le risque de crédit associé à C est appelé risque de référence. Nous verrons que le but des produits dérivés de crédit est le transfert de ce risque de référence.

La distinction entre ces risques n'est pas toujours aisée : le risque de crédit lié à la variation des spread de crédit default swap peut être considéré comme un risque de marché. Les portefeuilles de produits dérivés OTC sont, bien évidemment, soumis aux risques de marché mais ils sont aussi exposés au risque de contrepartie.

3. Le risque de liquidité.

Il s'agit, pour une entreprise, du risque de ne pas pouvoir mobiliser à un instant donné assez de liquidités pour pouvoir faire face à ses engagements.

4. Le risque opérationnel.

Dans cette catégorie sont regroupés, par exemple, les risques de fraude, d'erreurs des opérateurs, de pannes des systèmes, etc...

2.2 Enjeux

Le risque de crédit peut être défini, en première approximation, comme le risque de perte lié au changement de la qualité de la signature d'une contrepartie. Toutes les institutions

Chapitre 2 Outils et concepts de base pour modéliser le risque de crédit

financières (ainsi que tout les acteurs du marché) accumulent une grande quantité de risque de crédit: soit directement par l'intermédiaire de leurs portefeuilles de créances, soit indirectement sous la forme de risques de contrepartie dans leurs portefeuilles d'actifs et de produits dérivés OTC. L'enjeu que représente la modélisation de ce risque est donc très important : il s'agit de pouvoir : -- mesurer le risque de crédit contenu dans les portefeuilles,

-- évaluer les instruments financiers sensibles au risque de crédit et, plus généralement, tout instrument exposé à ce risque (risque de contrepartie), et ce à un niveau agrégé. Il est, en effet, important de pouvoir contrôler l'exposition au risque de crédit contrepartie par contrepartie ainsi que l''evolution de cette exposition par secteurs géographiques et industriels. De telles pratiques permettent, par exemple, de réduire le risque de concentration.

La production de résultats quantitatifs robustes permet alors à l'institution concernée

-- d'allouer à chaque centre de profit un capital économique adéquat,

-- d''evaluer la performance des centres de profit au regard des risques pris,

-- de fournir des informations fiables sur son intégrité financière aux régulateurs, aux investisseurs et aux agences de notation,

-- de diversifier et réduire le risque en imposant, par exemple, des limites à l'exposition au risque de crédit par contrepartie.

La mise en place de tels processus de gestion du risque correspond à l'évolution de la réglementation prudentielle et aux trois piliers du nouvel accord de Bale .

2.3 Modèles du risque de crédit

Dans cette section, nous exposons les approches classiques de la modélisation du risque de défaut à partir de l'étude du concept central d'obligation zéro-coupon risquée (C'est-à-dire soumise au risque de défaut). Il existe deux grandes familles de modèles d'évaluation de la dette risquée : -- les modèles structurels,

-- les modèles à forme réduite.

Nous mentionnons aussi les modèles de corrélation d'instants de défaut qui sont nécessaires à l''evaluation des produits dérivés exotiques de crédit ainsi que les modèles dit hybrides dont le but est de permettre l''evaluation précise du risque de contrepartie des portefeuilles de produits dérivés OTC.

Dans la suite, nous nous plaçons dans le cadre de l''evaluation risque-neutre des actifs financiers :

nous supposons donnés un espace probabilisé filtré sur lequel est défini le

processus des taux d'intérêt instantanés (rt)t=0 et une probabilité risque-neutre P*.

Rappelons qu'alors la valeur des actifs contingent (c'est-à-dire dont la valeur est contingente à l'évolution des conditions de marché) est calculée comme l'espérance sous cette probabilité de ses flux futurs actualisés au taux sans risque. Une obligation zéro coupon (sans risque) est un actif qui paye 1 à sa maturité T.

La valeur B(t; T) de cet actif est :

Chapitre 2 Outils et concepts de base pour modéliser le risque de crédit

Si le risque de contrepartie de l'émetteur du zéro-coupon n'est pas nul, l'évaluation du zéro-coupon doit tenir compte de la possibilité du défaut de celui-ci : deux nouveaux risques entrent en jeu -- l'instant du défaut,

-- la perte en cas de défaut (Loss Given Default).

La perte en cas de défaut s'exprime en termes d'un taux de recouvrement #177; éventuellement

aléatoire et d'une hypothèse de recouvrement. Noter que ces hypothèses de recouvrement, que nous présentons maintenant, s'étendent immédiatement à d'autres actifs que les zéro -coupons risqués. Nous notons D(t; T) la valeur en t du zéro -coupon risqué de maturité T et ô l'instant du défaut de l'émetteur de ce titre.

L'hypothèse de recouvrement la plus courante s'appelle fractional recovery of par value et consiste en le recouvrement à l'instant du défaut d'une fraction #177; du nominal du titre. Dans ce cas, on a

Si, en cas de défaut, la fraction recouvrée l'est à maturité, on parle de fractional recovery of Treasury value. Dans ce cas, on a

Une autre hypothèse classique dite fractional recovery of market value suppose qu'à l'instant de défaut le propriétaire du titre perçoit une portion #177; de la valeur précédant immédiatement le défaut. Dans ce cas

où D(ô-,T) (Si f est une fonction à valeurs réelles, nous notons f (t-) la limite lims?t;s<t f(s).) est la valeur avant défaut de l'instrument considéré.

Chapitre 3

Produits dérivés de crédit

Dans ce chapitre, nous présentons les principaux dérivés de crédit. Nous y décrivons leurs payoffs et donnons quelques indications sur leur intérêt financier. Après un rapide état des lieux du marché des dérivés de crédit, nous décrivons les caractéristiques du Credit Default Swap (CDS), qui constitue le produit à la vanille de ce marché.

Les CDS sont à la base de produits exotiques plus complexes, et sont utilisés à la fois en tant que produits de couverture (diversification du risque, couverture d'un risque en préservant la relation commerciale, réduction du risque de concentration, transfert du risque de crédit (balance sheet CDO),...), et d'investissement (long d'un risque de crédit à l'aide d'un instrument hors-bilan, effets de levier, création de position de crédit synthétique (CDO synthétiques),...).

Enfin, nous présentons les produits de corrélation les plus courants : les nth-to default, et les Collateralized Debt Obligations(CDO).

Dans la suite, r désigne le taux sans risque, B le processus :

Et ô l'instant de défaut d'une entreprise.

3.1 Le marché des produits dérivés de crédit

Le marché des produits dérivés connait une croissance exponentielle depuis le début des années 1990. Pour fixer les idées, précisons tout de suite que le nominal total des encours sur produits dérivés de crédit est de 2306 milliards de dollars (Risk Magazine 2003) en augmentation de plus de 50% par rapport à l'année dernière. La standardisation des CDS est devenue une réalité grâce aux nouvelles normes et définitions mises en place par l'ISDA(International Swap & Derivatives Association.).

Evolution du volume des dérivés de crédit échangés dans le monde depuis 1997 (La Tribune 13/10/03).

L'année 2003 a été marquée par les faits suivants :

Généralisation de l'utilisation des produits synthétiques, accroissement de la liquidité sur les produits de corrélation (cotation bid-ask de tranches synthétiques), croissance du marché des credit default swaptions (credit option). Ils restent, cependant, de nombreux problèmes à résoudre. Citons, par exemple, le besoin de liquidité sur le court et le long terme de la courbe de crédit qui se fait parfois sentir et les méthodologies de calibration de taux de recouvrement qui demandent à être améliorées. L'essentiel de l'encours se répartit sur : les credit default swaps (73%) et les produits sur paniers de crédit (22%), en particulier, les nth-to-default swap à hauteur de 0.3% et toutes les transactions synthétiques tels les CDO (Collateralized Debt Obligations) et les TDP (Tranche Default Product). Le reste de l'encours est constitué de Credit Linked Notes, de Total Rate of Return et de Spread Option.

	Fig
3.1-Répartition des encours sur produits dérivés de crédit.

Le marché vanilla (celui des credit default swaps) est essentiellement concentré sur l'Amérique du nord et l'Europe. Le point de plus grande liquidité est celui des CDS de maturité comprise entre 4 et 6 ans sur des signatures investment grade.

Chapitre 3 Produits dérivés de crédit

Cette répartition géographique est intéressante compte tenu du fait qu'elle ne correspond pas à celle des obligations (la proportion d'obligations européennes est significativement plus faible).

La croissance de ce marché est en partie due à la demande toujours plus forte de produits permettant de couvrir les positions synthétiques (CDO).Les banques sont les principales utilisatrices de produits dérivés de crédit. Ceci est dû à leur utilisation massive des CDS pour couvrir leurs portefeuilles de créances et leurs positions synthétique (Une position synthétique est une position de crédit courte ou longue (c'est-à-dire acheteuse ou vendeuse de protection) obtenue à partir d'un portefeuille de CDS donc sans prêt effectif de capital).

L'activité de couverture engendrée par l'émission de CDO synthétiques a, pour la première fois, permis de satisfaire à la demande d'achat de protection provenant des gestionnaires de portefeuille de créances.

Les principaux investisseurs dans les positions synthétiques restent les compagnies d'assurance : elles détiennent 65% des TDP et 81% des CDO de bilan (Ces produits sont émis par les banques qui veulent couvrir le risque de crédit de leur portefeuille de créances en vue de réduire leur charge en capital économique.). Les hedge funds participent désormais activement à ce marché : ils sont, par exemple, régulièrement acheteurs de CDS pour leur activité d'arbitrage d'obligations convertibles.

Fig 3.2-Répartition des utilisateurs de produits dérivés de crédit.

Chapitre 3 Produits dérivés de crédit

3.2 Les obligations risquées

Outre les prêts traditionnellement accordés aux entreprises, une part importante du marché de la dette risquée consiste en obligations émises par les entreprises et certains états. Contrairement aux prêts, les obligations s'échangent sur les marchés organisés et sont ainsi soumis au risque de marché (risque de taux), au risque de crédit (risque de contrepartie) et, dans une certaine mesure, au risque de liquidité. Le rendement de ces obligations est, en général, supérieur au rendement d'obligations identiques dont le risque de contrepartie est considéré comme nul (par exemple, les obligations du Trésor pour les pays de l'OCDE). La différence de rendement ou spread est une prime demandée par le marché pour prendre en charge les risques de contrepartie et de liquidité (En pratique, il est difficile de modéliser le risque de liquidité. On considère souvent, en première approximation, qu'il est pris en compte dans le spread de crédit.)

inhérents à l'instrument. On distingue, pour un émetteur donné, le spread calculé à partir d'obligations à taux fixe de celui coté dans les obligations à taux variables.

Noter que les obligations peuvent présenter des caractéristiques particulières : elles peuvent être rappelées par l'émetteur avant maturité (callable bond), être convertible en actions (convertible bond).

3.3 Credit default swap (CDS) 3.3 .1 Description du produit

Le crédit default swap (CDS) est le plus simple des produits dérivés de crédit et doit être considéré comme la brique de base (ou le sous-jacent) des produits dérivés plus exotiques.

Le CDS permet le transfert de risque de crédit de référence d'une entreprise C (entité de référence) entre deux contrepartie A et B. Dans le contrat standard, l'une des parties en question, disons A, achète une protection contre le risque de perte en cas de défaut de l'entité de référence C. Ce défaut est déclenché par un événement de crédit formel spécifié dans le contrat. Cet événement peut être la faillite de l'entreprise, un défaut de paiement ou la restructuration de sa dette.

La protection est valable jusqu'à la maturité du swap. En échange de cette protection, l'acheteur A verse périodiquement (en général, tous les 3 mois) au vendeur B une prime et ce jusqu'au défaut de C ou jusqu'à maturité du swap. La jambe du swap correspondante est appelé premium leg.

Si le défaut intervient avant la maturité du swap, le vendeur de protection effectue un paiement à l'acheteur de protection. Ce paiement équivaut à la différence entre le nominal de la dette couverte par le swap et le taux de recouvrement observé à l'instant du défaut.

Ce paiement peut être effectué selon deux modalités : physical settlement ou cash settlement.

Dans le premier cas, l'acheteur de protection A livre au vendeur de protection B un nombre d'obligations émises par C correspondant au nominal du swap et reçoit en retour le nominal du swap payé en cash.

Chapitre 3 Produits dérivés de crédit

Dans le deuxième cas, un paiement en cash qui correspond au pair moins le taux de recouvrement est effectué par le vendeur de protection B vers l'acheteur de protection A. Ce taux de recouvrement est calculé à partir de cotations obtenues quelques temps après que le défaut se soit produit.

La prime (aussi appelé spread ou marge) qui annule la valeur du CDS est dite à la monnaie (fair margin ou fair spread ou simplement spread).

Fig. 3.3 - Un credit default swap : CDS

Soient T0 la date d'entrée dans le swap, T sa maturité, T0 < T1 < ... < TN = T, les dates de paiements, ä le taux de recouvrement en cas de défaut et s la valeur de la marge. Le payoff (payé en T) correspondant à la jambe fixe s'écrit

.

Tandis que le payoff associé à la jambe variable s'écrit

.

3.3 .2 Evaluation de la marge d'un CDS

Un raisonnement simple d'absence d'opportunité d'arbitrage permet d'obtenir une première approximation du spread (fair margin) d'un credit default swap. Nous notons C l'entité de référence. Considérons les deux portefeuilles suivants :

P1 {long d'une obligation à taux variable émise par C de spread U court d'une obligation à taux variable sans risque}

P2 {court d'un crédit default swap sur C de spread S}

Chapitre 3 Produits dérivés de crédit

Nous supposons que toutes les obligations et le CDS considérés ont même maturité, même dates de tombée de coupon et même nominal. Nous supposons aussi que le défaut ne peut intervenir qu'immédiatement après une tombée de coupon.

Les cash-flows générés par le portefeuille P1 sont décrits dans la figure 3.4.

Ils Correspondent à une position acheteuse de protection sur un CDS de spread U. Les deux portefeuilles P1 et P2 étant à coût d'entrée nul, on a nécessairement par absence d'opportunité d'arbitrage U = S.

Ainsi, en première approximation, la fair margin d'un CDS est égale au spread d'une obligation à taux variable (FRN = floating rate note) de même maturité et ayant les mêmes dates de tombée de coupons.

Remarque : L'égalité précédente n'est pas toujours observée dans la pratique. Ceci est du au fait que les hypothèses implicites à notre raisonnement (telle l'absence de coût de transaction (spread bid-ask) sur le marché du cash et des obligations à taux fixes) ne sont pas toujours vérifiées.

Remarque. Ce genre de raisonnement n'est valide que pour déterminer la marge à la monnaie d'un CDS. Pour déterminer sa valeur en cours de vie (NPV = net present value) qui n'est plus nécessairement égale à 0, il faut avoir recours à un modèle.

3.3 .2 .1 Exemple. (Pricing d'un CDS.)

Nous considérons un CDS de maturité T. Nous supposons que le taux de recouvrement en cas de défaut ä, le taux d'intérêt sans risque r et le taux de défaut A. > 0 sont constants. L'instant de défaut

ô suit une loi exponentielle de paramètre A. :

Chapitre 3 Produits dérivés de crédit

Fig 3.4-Synthèse d'un CDS.

On cherche à calculer la marge s* qui annule la valeur du CDS à l'origine. En considérant que la prime est payée jusqu'au défaut, et sans tenir compte du coupon couru, la valeur de la jambe fixe s'écrit :

En supposant que le flux variable est payé à l'instant d'occurrence du défaut, la valeur de la jambe variable est :

Le fair spread s* est tel que JF(s*) = JV soit S* = (1-ô) ë, Cette égalité est connue sous le nom d'égalité du triangle

Chapitre 3 Produits dérivés de crédit

3.4 Collateralized Debt Obligations

Les Collateralized Debt Obligations ou CDO sont des produits obligataires adossés à des dettes, résultant d'un mécanisme relativement complexe d'ingénierie financière appelé titrisation (securitization).

A partir d'un panier de titres de dette (de 50 à 10000 créances), l'émetteur synthétise des actifs obligataires. Les CDO se distinguent selon la nature de la dette sous-jacente : s'il s'agit de produits obligataires, on parle de «Collateralized Bond Obligations» ou CBO. Dans le cas ou le panier est constitué uniquement de titres de prêts, on parle de «Collateralized Loan Obligations» ou CLO.

Bien entendu, dans le cas général, le panier est mixte. Depuis sa création dans le milieu des années 1990, le marché des CDO n'a cessé de se développer.

En 2000, il dépassait les 100 Milliards de dollars d'émission. Nous présentons les enjeux du processus de titrisation ainsi que ses mécanismes, puis les techniques récentes liées à la génération synthétique de tranches utilisées en trading de corrélation.

3.4 .1 Titrisation

La titrisation est une technique de gestion de bilan consistant à créer des produits obligataires à partir d'un ensemble de créances par le truchement d'une entité juridique particulière appelée Special Purpose Vehicle (SPV). Un établissement financier possédant un ensemble de créances ou de crédits auprès d'emprunteurs individuels ou institutionnels peut ainsi choisir de les titriser. Pour ce faire, il crée un SPV juridiquement indépendant, à qui il vend ses créances. Cette étape est fondamentale, car elle lui permet, d'une part, de transférer le risque de crédit au SPV, et d'autre part de retirer les créances titrisées de son bilan. Enfin, le SPV émet les CDO (voir figure 3. 5).

Les CDO émis comportent différentes tranches d'investissement, chacune d'elle possédant une qualité de crédite, et donc une notation différente :

- la tranche junior ou equity supporte les premières pertes sur l'ensemble de créances. Il s'agit donc d'un produit très risqué, payant un spread très élevé à l'investisseur. Il s'agit d'un produit purement spéculatif ;

- la tranche intermédiaire, dite mezzanine supporte les pertes au delà de la tranche equity, c'est un produit moyennement risqué, offrant un spread intéressant ;

- la tranche senior supporte les pertes restantes, si elles ont lieu. Elle est la moins soumise au risque de crédit, et offre donc un coupon faible.

Fig 3.5-Le mécanisme de Titrisation

Comme chacune de ces tranches porte sur un ensemble de crédit, leur valorisation fait intervenir la corrélation entre les défauts du panier. Il est à noter que l'établissement financier peut parfois conserver une partie du risque de crédit, ce qui améliore la notation des tranches. Alternativement, il peut aussi faire appel à une compagnie d'assurance externe pour augmenter la qualité du crédit. On parle alors de credit enhancement.

L'intérêt de la titrisation est double : tout d'abord, elle permet d''economiser des fonds propres et ainsi d'améliorer leur rentabilité. En effet, étant donné que les créances titrisées peuvent être sorties du bilan, l'exigence de fonds propres sera moindre. De plus, la titrisation offre un accès simple et économique au marché financier à des entreprises de faible notation, qui devraient autrement se refinancer `a des coûts prohibitifs. Elle permet l'assainissement de leur structure de capital.

Chapitre 4

Les modèles structurels

Les modèles structurels sont des modèles du risque de crédit où une entreprise donnée est considérée en cessation de paiement lorsque la valeur de ses actifs ne suffit plus à faire face à sa dette. Dans cette approche initiée par Merton (1974) ;la valeur de la dette est évaluée à l'aide de la théorie des options : l'action de l'entreprise et sa dette y apparaissent comme des produits dérivés sur la valeur totale de ses actifs.

La popularité de ce modèle a permis la diffusion des idées de Merton et a transformé en quelques décennies la vision du risque de crédit. Le modèle développé par Moody's KMV pour estimer les probabilités de défaut ou le modèle Credit Grade de JP Morgan sont de parfaites illustrations de cette tendance. Les modèles à la Merton» sont toujours largement utilisés pour valoriser la dette risquée, modéliser le spread de crédit, évaluer la qualité d'une signature, établir des liens entre le risque equity et le risque de crédit, etc.

Après avoir présenté le modèle de base tel que l'introduit Merton dans son article fondateur, nous décrivons, suivant Hull, Nelken et White, comment il peut être implémenté. Nous étendons ensuite le modèle de Merton dans la direction des modèles dits «de premier instant de passage» et traitons l'exemple du modele Credit Grade de JP Morgan. Les exemples retenus mettent en évidence le lien entre risque de crédit et risque equity.

4.1 Modélisation du défaut d'une entreprise :

4.1.1 Préteurs, emprunteurs, produits

Les marchés de la dette regroupent plusieurs types d'intervenants :

. Les emprunteurs

. Les préteurs (investisseurs privés ou institutionnels)

. Les agences de notation qui sont des organismes indépendants dont le métier est d'attribuer une note représentative du risque de crédit associé ua n'importe quel type d'émission obligataire.

Les produits traités sur les marchés financiers sont divers. Les plus simples et les plus anciens sont les obligations, qui sont émises par des Etats (en France Obligation au Trésor (OAT), emprunts russes, Government Bonds americains, etc...), des administrations (Unedic en France qui a lancé en 2006 une opération de titrisation de ses créances pour un montant de 1.5 Mds ), des villes (Municipality bonds aux Etats-Unis), des grandes entreprises (France Telecom, EDF, Sodexho) dont des banques (BNPP, Société Générale, Crédit Agricole, etc ). Des produits dérivés sont ensuite apparus : les CDS (Crédit Default Swap) ou plus généralement les dérivés de crédit classiques et enfin encore plus récemment des produits plus complexes tels que les CDO (Collateralized Debt Obligations) ou First-to-Default

Chapitre 4 Les modèles structurels

Notons enfin l'existence de produits dits hybrides tels que les obligations convertibles qui permettent d'échanger de la dette contre des actions.

Le marché de la dette représente un volume important des échanges. Au premier trimestre 2005, 360 milliards d'Euros d'obligations avaient été émis (en Europe) pour un total de 805 milliards de dollars au niveau mondial. Par ailleurs, le montant de produits structurés s'élevait à 67 milliards d'euros et l'ensemble des prêts syndiqués ua 250 milliards de dollars. Enfin, notons que le marché de la dette est en croissance soutenue depuis plusieurs années, et notamment la standardisation des produits structurés.

Figure 4.1.1: Croissance du marché de la dette (source :J.P.Morgan) 4.1.2 Les obligations risquées

Reprenons notre exemple France Telecom. Aujourd'hui, en 2006, France Telecom souhaite lever des fonds pour financer une acquisition importante ou une avancée technologique. En raison de contraintes fiscales, d'un cours boursier défavorable, France Telecom souhaite

Chapitre 4 Les modèles structurels

financer son opération via l'émission d'un emprunt sur les marchés financiers sous la forme de bons aux porteurs. L'intérêt proposé est de 6% et la maturité de l'opération 4 ans.

France Telecom va se tourner vers une banque qui s'engage à placer sur les marchés financiers les titres émis, au prix de 100. Afin de parvenir à ce chiffre, la banque "testera" les marchés et demandera-en conséquence à France Telecom d'ajuster à la hausse ou à la baisse le taux d'intérêt proposé (le coupon).

La banque garantira ensuite à France Telecom la vente de tous les titres, s'engageant ainsi à prendre ceux qu'elle n'aura pas placés. On dira alors que la banque est collée (risque de colle) aux titres France Telecom.

Les titres sont émis au 1er septembre 2006. Un échéancier est mis en place suivant lequel :

l Au 01.09.2006, FT perçoit 100

l aux 01.09.2007, ..., 01.09.2009, France Telecom verse le coupon de 6 au porteur

l le 01.09.2010, France Telecom verse au porteur le dernier coupon de 6 et rembourse le principal de 100.

Figure 4.1.2:Echéancier des paiements pendant la durée de vie de l'obligation.

Chapitre 4 Les modèles structurels

Un porteur qui a acheté l'obligation France Telecom au 01.09.2006 peut la revendre sur le marché obligataire. Le prix d'échange est fixé par le marché et on assiste à une cotation de

l'obligation France Telecom aux cotés d'autres obligations. Un exemple de cotation est le suivant :

Plusieurs informations sont rassemblées autour de la cotation :

l nom de l'émetteur

l qualité de crédit de l'émetteur (rating attribué par une agence de notation)

l maturité de l'obligation

l coupon

La cotation est un prix (en l'occurrence 111.93) auquel on associe un taux, le taux actuariel. Le taux actuariel est le taux qui égalise prix d'achat (la jambe fixe) et flux à venir (la jambe variable).Il reflète la rémunération exigée pour le risque pris (risque de taux et risque de non-remboursement), qui dépend donc de la qualité de crédit de l'emprunteur (l'émetteur), du coupon et de la maturité de l'obligation. Le taux de rendement actuariel ñ est donc solution de l'équation :

.

Figure 4.1.4:Comparaison des taux actuariels entre une obligation sans risque (emprunt d'état (OAT)) et une obligation risquée(Société Générale)

Chapitre 4 Les modèles structurels

Figure 4.1.3: Le prix de l'obligation - et le taux de rendement actuariel dépendent de la qualité de l'emprunteur. Comparaison de taux de rendement actuariels pour des maturités similaires.

La différence entre le taux de rendement actuariel et le taux sans risque mesure le risque de crédit sous-jacent à l'émetteur et supporté par le préteur.

Chapitre 4 Les modèles structurels

Un investisseur qui porte l'obligation quelques mois entre deux versements de coupons doit être rémunéré pour le risque porté bien qu'il ne puisse, en théorie, avoir droit à aucun versement de coupon puisqu'il ne possède pas l'obligation lors des versements de coupon. Aussi, le prix d'une obligation est-il corrigé du coupon couru qui est simplement l'intérêt linéaire (au taux du coupon) sur la période entre le dernier versement coupon et aujourd'hui.

Le coupon couru est donc Coupon (Aujourd'hui-Dernière date de paiement du coupon). Le prix coté de l'obligation est généralement le prix pied de coupon (Clean Price), c'est à dire le prix réel de l'obligation auquel on retranche le coupon couru. En conséquence, le prix de l'obligation dans le temps ne subit pas de sauts dus aux versements de coupons.

Certaines obligations vont être cotées différemment. Il s'agit des obligations convertibles. Les obligations convertibles sont des obligations normales auxquelles est ajoutée une option de conversion en actions. Le nombre d'actions en lesquelles l'obligation peut être convertie est spécifié à l'avance, ainsi que les dates d'exercice de l'option. Cette option permet pour l'émetteur de réduire le coût de la dette ainsi que les cash-flows à verser. Ce type de produit est attractif lorsque les marches actions sont très volatiles. Il justifie enfin l'intérêt de modèles structurels permettant de décrire dans une même dynamique actions et obligations.

4.1.3 La modélisation du défaut d'une entreprise

Pour un investisseur dans la dette de l'entreprise, le défaut est en général un événement soudain. Il intervient lorsque l'entreprise ne peut plus faire face à ses engagements, ce qui a inspiré l'approche structurelle dans la modélisation du défaut d'une entreprise. L'approche structurelle est une modélisation de l'actif et du passif de l'entreprise. Le défaut est un événement qui survient lorsque la structure du bilan ne permet plus à l'entreprise de tenir ses engagements.

Regardons le bilan d'une entreprise :

Chapitre 4 Les modèles structurels

L'entreprise, ou la firme, possède des actifs : ce sont des machines, des locaux, ou, dans le cas d'une banque, des prêts accordés. Ces actifs sont financés par les actionnaires et des créanciers qui ont acheté les actions et les obligations émises par l'entreprise.

4.1.4 La Différence entre actions et obligations:

l flux de paiement : pour les obligations, les paiements sont fixés contractuellement, et pour les actions il n'y a pas de paiements fixes. Les actionnaires reçoivent le solde des avoirs, après paiements de créanciers. C'est cela la définition de l'action.

l Séniorité : à liquidation de l'entreprise, on rembourse prioritairement les créanciers, on rembourse les actionnaires en denier.

A la date t = 0, une entreprise est en besoin de financements pour lancer son activité. Prenons quelques chiffres. Les besoins en capitaux sont évalués ua 100 000 EUR, qui vont être financés par des actionnaires et des créanciers. Imaginons que les entrepreneurs apportent 200 000 EUR, il reste 800 000 EUR à financer sous forme de créance. Les entrepreneurs pensent que leur entreprise produira ses premiers résultats dans un an.

Ils empruntent donc aujourd'hui une somme S0 et devront rembourser une somme ST à la date T = 1 an. Dans un an, les actifs de l'entreprise auront évolué (achat de brevets, vente de produits, acquisition et amortissement de machines, etc.).

Soit l'entreprise peut rembourser, auquel cas elle verse ST aux créanciers (éventuellement après avoir vendu certaines activités, cf Vivendi Universal), et on retranche ST de la valeur des actifs, les actionnaires (soit les entrepreneurs) pouvant vendre le reste de l'entreprise pour un montant d'actifs égal a AT - ST , soit l'entreprise ne peut rembourser la somme ST ua ses créanciers, les actifs sont vendus, et le produit de la vente est versé aux créanciers a concurrence de ST .

On peut donc résumer les flux financiers a la date T dans le tableau suivant :

4.2 Modèle de Merton : présentation du modèle de base

Dans le modèle de Merton, l'action et la dette d'une entreprise sont considérées comme des produits dérivés sur sa valeur de marché peuvent donc être évaluées dans le cadre de la théorie des options. Pour pouvoir appliquer cette théorie, il nous faut faire l'hypothèse de complétude suivante : il existe une classe d'actifs (comprenant le cash) permettant de répliquer les futurs cash-flows de l'entreprise. Cette hypothèse nous permet de justifier la valorisation des actifs de l'entreprise par absence d'opportunité d'arbitrage.

Chapitre 4 Les modèles structurels

Soit par A la valeur totale des actifs de l'entreprise (A est la valeur de marché de l'ensemble des futurs cash-flows générés par l'activité de l'entreprise) et nous supposons que ce processus satisfait à l'équation différentielle stochastique suivante (mouvement brownien géométrique) : dAt /At = p dt + o- dBt ; (p, o- > 0) où B est un mouvement brownien unidimensionnel. Nous supposons aussi que les propriétaires de cette entreprise ont choisi de structurer son capital sous la forme d'actions (pure equity) et d'un unique zéro-coupon de maturité T et de nominal L (debt) (Cette hypothèse simplificatrice n'est que tr`es rarement vérifiée. En pratique, la structure de capital d'une firme est infiniment plus complexe et peut comprendre, par exemple, des portions de

dette convertible en action).

Le bilan d'une telle entreprise est résumé dans le tableau suivant :

Actif	Passif
Actifs At = Et + Dt	Equity Et Debt Dt

4.2.1 Produits dérivés sur la valeur des actifs de la firme :

A maturite, si la valeur de l'entreprise est inferieure à la somme L due aux detenteurs d'obligations (zero-coupon), nous considerons que la firme fait defaut. Dans ce cas, elle passe aux mains des détenteurs de sa dette qui ne recuperent qu'une portion AT/L de leur capital initial. Ainsi, les detenteurs d'obligations reçoivent min(AT ;L) à maturit'e tandis que les actionnaires percoivent le reliquat (AT - L) +.

Fig. 4.2 - Valeurs liquidatives pour une entreprise de dette 100.

Chapitre 4 Les modèles structurels

Notons Et et Dt les valeurs respectives en t des actions et de la dette et B(t; T) la valeur en t d'un zéro-coupon sans risque de maturité T. D'après la théorie des options et en vertu de l'hypothèse de complétude, les processus E et D peuvent s'écrire sous la forme de l'espérance, sous la probabilité risque neutre, de leur valeur finale actualisée.

Autrement dit, si nous avons

.

Posons Lt = B(t; T) L. Appliquer la formule de Black & Scholes permet alors d'obtenir la formule de Merton pour la valeur de la dette risquée :

(4.1) Dt = AtN(-d1) + LtN(d2)

Ou

Et

La valeur de la dette apparait comme celle d'un zéro-coupon au taux sans risque de nominal L auquel on retranche un put (appelé put-to-default) sur la valeur de la firme de strike L et de maturité T. La valeur de actions apparait, quant a elle, comme celle d'un call sur la valeur de la firme de strike L et de maturité T.

4.2.2 Probabilités de défaut et Loss Given Default

La formule (4.1) peut se réécrire

Où P* est la mesure martingale équivalente pour le numéraire A, c'est-à-dire la probabilité définie par

Chapitre 4 Les modèles structurels

Les probabilités de défaut conditionnelles

Sont données par les formules

, En utilisant ces notations, la formule de Merton

suivantes

devient

Où ät est le taux de recouvrement (Recovery Rate) en cas de défaut défini par

Et ou

4.2.3 Distance-to-default

La probabilité de défaut s'interprète naturellement comme une fonction de la distance-au-défaut (distance-to-default) définie par

Xt = (lnAt -ln L)/ó=1/ó ln(At / L).

Plus précisément, si m* = (r -o²/2) / o, on peut écrire que

Où

La distance au défaut est la distance entre la valeur des actifs de la firme et le niveau L de la dette mesuré en nombre d''ecarts-type. Il est facile de vérifier que X est un mouvement brownien avec dérivé de drift m*.

Chapitre 4 Les modèles structurels

4.2.4 Levier d'endettement

Introduisons la variable lt =Lt /At appelée levier d'endettement (leverage ratio) de l'entreprise. Ce ratio mesure le taux d'endettement de la firme. Il permet de réinterpréter les formules de Merton. Les formules de Merton peuvent ainsi s'exprimer sous la forme

ET .

Où
	ET

Les trois paramètres At, lt et ó sont des paramètres-clefs de l'analyse du risque de crédit d'une entreprise.

4.2.5 Spread implicite

Le spread de crédit S(t, T) peut se définir comme la différence de rendement (yield) entre une dette sans risque (par exemple une obligation du Trésor) et la dette émise par une entreprise (corporate bond). Ainsi, si D(t, T) désigne la valeur d'un zéro-coupon risqué, on a

Où

Etant donné un modèle, nous appellerons spread implicite, le spread induit par ce modèle. Remarquons que dans le cas du modèle de Merton.

Chapitre 4 Les modèles structurels

Le spread de crédit ne dépend ainsi que de la variabilité (volatilité) des actifs de la firme, du levier d'endettement et de la distance à la maturité. Lorsquet_? ?T,on observe le comportement suivant :

4.2.6 Une première implémentation du modèle de Merton

La difficulté majeure de toute implémentation d'un modèle financier est sa calibration: comment peut-on estimer de manière fiable les paramètres apparaissant dans les formules précédentes? En pratique, l'on peut estimer le paramètre L en évaluant la dette de l'entreprise. Les paramètres At et ó n'étant pas directement observables; néanmoins, ils peuvent être estimés implicitement à partir des

données de la volatilité (historique) óE de l'action et de sa valeur spot Et. Rappelons que la valeur de l'action est donnée par la formule

(4.2)

La formule d'Itô montre alors que Et est un processus de volatilité

(4.3)

Chapitre 4 Les modèles structurels

Par suite, si l'on connait ót et Et, on connaît, en principe, la valeur des variables At et óA. Il suffit pour cela de résoudre en At et ó le système suivant :

Et = AtN(d1) LtN(d2) óE(t) =(At / Et )* N(d1)ó

La relation (4.3) n'ayant lieu qu'instantanément les résultats obtenus par cette méthode risque d'être instables .

4.2.7 Spread implicite et smile de volatilité

Nous preesentons maintenant une nouvelle meethode pour implémenter le modele de Merton, d'apres Hull, Nelken et White .Il s'agit d'utiliser l'information contenue dans le smile de volatilité implicite pour calibrer le modèle de Merton et en particulier estimer le spread implicite.

Cette implémentation permet de classer les emetteurs de dette risquete selon la qualité de leur signature. L'intérêt d'un tel classement est important : d'une part, il permet de comparer le risque de crédit entre plusieurs firmes et d'autre part, il peut servir de base à une estimation des probabilités de defaut à horizon donné. Enfin, ce modèle permet de relier risque equity et risque de crédit.

Dans le modèle de Merton, un put de maturité ô < T et de strike K apparaît comme une option composee sur la valeur de l'entreprise. Ainsi, la valeur du put sur l'action est donnée par la formule suivante :

Avec :	,

Où M désigne la fonction de répartition d'une gaussienne bivariée :

et A*ô représente la valeur de la firme telle qu' à l'instant ô, l'on ait

Chapitre 4 Les modèles structurels

Autrement dit, A*ô est la valeur en dessous de laquelle le put sur l'action sera exercé. Notons í la volatilité implicite du put et posons

Le paramètre ? est souvent appelé moneyness de l'option (lorsque ? = 1, l'option est à la monnaie du forward). Le paramètre á est la moneyness du point de vue de la valeur de la firme. Par définition, la volatilité implicite y du put est solution de l'équation

Où

En utilisant alors l'équation

(4.4)

il vient

(5.5)

	En
utilisant une nouvelle fois l'équation (4.4), nous pouvons aussi écrire que

Chapitre 4 Les modèles structurels

Où

de sorte que (4.6)

Pour un jeu de paramètres (l0; ó; T) du modèle de Merton et une maturité d'option ô (< T), les équations (4.5) et (4.6) définissent une relation implicite de la forme y = Fonction(?);qui conduit à un smile de volatilité. Les propriétés de cette relation peuvent se résumer en quelques faits stylisés :

(1) le spread de crédit est une fonction croissante de la volatilité implicite ;

(2) la relation entre la pente (skew) du smile de volatilité et le spread de crédit est plus complexe : pour des spreads faibles, la pente est une fonction croissante du spread ; pour des niveaux de spread plus élevés, la variation de la pente devient négligeable ;

(3) enfin, la pente est une fonction croissante de la volatilité implicite à la monnaie.

Ces résultats suggèrent une nouvelle méthode pour implémenter le modèle de Merton : étant données deux volatilités implicites et une valeur pour T, on peut résoudre les équations (4.5) et (4.6) pour obtenir l0 et ó. Cette implémentation permet donc d'estimer directement le spread de crédit et la probabilité risque-neutre de défaut à partir du smile de volatilité tout en évitant le recours à la relation instantanée (4.3).

Ces résultats peuvent ensuite être utilisés comme un indicateur du risque de crédit. Les auteurs ont testé cette approche en comparant le classement des spreads obtenus par cette méthode avec les spreads du marche des CDS et ont montré que ces classements sont proches. Cette méthode permet donc, par exemple, d'étudier la qualité de la signature d'entreprises dont le marché de CDS n'existe pas ou n'est pas très liquide.

Chapitre 4 Les modèles structurels

4.2.8Limites du modèle et extensions

La principale limitation du modèle de Merton est que les spreads implicites court terme sont nécessairement proches de zéro contrairement aux spreads réellement observés sur les marchés de capitaux. Cette propriété du modèle est liée à la continuité de la filtration brownienne (ou, de manière équivalente, à la prévisibilité de l'instant de défaut). Duffie et Lando expliquent cette apparente contradiction par le fait que l'asymétrie d'information qui existe entre les actionnaires et les détenteurs de la dette n'est pas prise en compte par ce modèle. Ils ont montré [10] que si ces derniers ne disposent que d'une information comptable partielle (ou «bruitée») l'instant de défaut leur apparait comme totalement inaccessible. Ces résultats permettent de justifier l'utilisation des modèles à forme réduite dont nous aborderons l'étude dans le prochain chapitre.

Le modèle de Merton peut être étendu dans différentes directions : Nous verrons dans la section 4.3 consacrée aux modèles de premier instant de passage comment l'on peut incorporer des défauts se produisant à un instant quelconque de l'intervalle [0; T] ; Vasicek [11] propose un modèle de Merton prenant en compte l''echelonnement de la dette ; Longstaff & Schwartz [12] introduisent un modèle de Merton intégrant des taux stochastiques.

Notons enfin que si l'on souhaite tenir compte des imperfections de marché (telle l'incomplétude ou le contrôle que peuvent exercer actionnaires et détenteurs de la dette sur la conduite de l'entreprise), la théorie s'éloigne sensiblement de la théorie des options. Sur ce sujet, l'on pourra se référer à Leland [13].

4.3 Modèles de premier instant de passage

L'une des limites du modèle de Merton réside dans le fait que le défaut de l'émetteur ne peut intervenir qu' à la maturité de la dette. Dans les modèles de premier instant de passage, au contraire, l'instant de défaut est (un temps d'arrêt) de la forme ô = inf{t > 0 ; At < Bar(t)} où Bar est une barrière qui peut être aléatoire et A est une variable de type «valeur de la firme». Dans les modèles de ce type, il est possible de spécifier une grande variété d'hypothèses de recouvrement en cas de défaut .

Apres quelques préliminaires mathématiques, nous présenterons un exemple de modèle de premier instant de passage : le modèle Credit Grade développé par JP Morgan.

Chapitre 4 Les modèles structurels

4.3.1 Préliminaires mathématiques

Nous commençons ce paragraphe par un lemme bien connu de la théorie des diffusions Dans la suite, Y désigne un mouvement brownien avec dérive de sorte que

Yt = y0 + pt + óBt ; (y0 > 0; p ? IR; ó > 0) où B est un mouvement brownien unidimensionnel.

4.3.2 Lemme

Une preuve de ce lemme est donnée en Annexe

Considérons le temps d'arrêt v = inf{t > 0 ; Yt < 0 }.Appliquer le lemme précédent à Yy0 suffit à prouver :

4.3.3 Proposition La variable aléatoire ô est distribué selon la loi gaussienne inverse. Plus précisément,

où

Exemple. Nous considérons une entreprise dont la valeur A est décrite comme dans le modèle de Merton et nous supposons que l'instant de défaut de la firme se présente sous la forme v = inf{t > 0 ; At < v } où v est un réel inferieur `a A.

Dans ce cas, nous avons :

Ou

Chapitre 4 Les modèles structurels

4.4 Modèle Credit Grade

Dans ce paragraphe, nous présentons un modèle de premier instant de passage développé par JP Morgan (Credit Grade, voir [14]).

Nous avons choisi de présenter ce modèle car il nous semble qu'il contient des intuitions puissantes sur ce que sont les déterminants du risque de défaut et les liens qui existent entre le risque de crédit et le risque equity.

4.4.1 Description du modèle

Nous supposons que la «valeur» V d'une entreprise est décrite par un processus satisfaisant à l'EDS dVt / Vt = ó dWt ; (ó > 0);où W est un mouvement brownien unidimensionnel et ó > 0 est la

volatilité de V.

Ici, V n'est pas réellement la valeur de la firme mais plutôt un indice mesurant l'évolution temporelle de la qualité du crédit de l'entreprise. Dans ce modèle, le défaut est défini comme le premier instant ou V atteint une barrière LD où

(1) D est le ratio debt-per-share,

(2) L est une grandeur aléatoire représentant le taux de recouvrement moyen global en cas de défaut.

La variable L est supposée log normale de moyenne L et d'écart-type de sorte que LD = LDexp (AZA ²/2 ) où Z suit une loi normale centrée réduite.

La moyenne L et l'écart-type ë sont estimés historiquement en utilisant des données de taux de recouvrement telles celles fournies par Standard & Poor's. Dans [14], les auteurs mentionnent les valeurs L = 0,5 et ë = 0,3 obtenues à partir des données de défaut de 300 entreprises américaines (hors institutions financières) entre 1987 et 1997.

Le ratio debt-per-share D est obtenu en divisant le nominal de la dette globale par le nombre d'actions émises par l'entreprise. Pour une valeur V0 donnée, l'instant ô de défaut est donc

r = inf{t > 0 ; Vt < LD}

et si l'on pose Xt = óWt -ëZ- 1/2ó ² t-1/2ë²

Xt ~ N(-Y2 At ², At ),o`u At ²= ó ² t + ë², cette formule peut se réécrire r = inf{t > 0 ; Xt < ln (LD/V0) - ë²}

Pour appliquer les formules présentées dans le paragraphe précédent (afin d'obtenir une formule fermée pour la structure par terme de probabilité de défaut), les auteurs proposent de remplacer Xt avec un mouvement brownien Yt de loi N(ìt; è²t), où è²t = At² = ó ²t + ë² et

ìt =-Y2 At ², D'après le lemme 4.3.2, l'on a

Chapitre 4 Les modèles structurels

et en posant y = ln(LD/V0)- ë², l'on obtient la formule :

Où

Remarque. L'introduction dans un modèle structurel d'une barrière aléatoire implique que la probabilité de défaut instantanée n'est plus nulle. Ceci conduit à un spread court-terme non nul et permet de résoudre l'un des problèmes inhérents aux modèles à la Merton.

4.4.2 Probabilité de défaut et spread de crédit

Dans ce paragraphe, nous désignons par spread de crédit la valeur de la marge d'un Credit Default Swap qui annule sa valeur au moment de l'entrée dans le swap. Autrement dit, le spread est donné par la formule

Il faut bien prendre garde au fait que R est le taux de recouvrement spécifique au titre couvert par le CDS et n'est donc pas nécessairement égal à L qui est un taux de recouvrement moyen global. Typiquement, le taux de recouvrement pour une dette unsecured sera plus faible que L, alors que celui lié à une dette secured sera plus grand que L.

Remarque.

Si l'on note

p(t) = -1/t . ln P(t);

le taux de défaut moyen et si l'on suppose que

(1) p(t) p constant,

(2) P(0) 1,

alors l'approximation suivante est justifiée s(t) (1-R)p.

Chapitre 4 Les modèles structurels

4.4.3 Calibration du modèle sur les données de marche

Nous cherchons maintenant à calibrer ce modèle sur des données de marché observables(données equity). Soient S et óS respectivement la valeur de l'action et la volatilité de l'action de l'entreprise considérée. La méthode proposée par JP Morgan consiste à examiner les conditions aux bords à long terme sur une expression de type distance-au-défaut pour les deux régimes extrêmes

§ prés du défaut c'est- à-dire S--0,

§ loin de la barrière c'est-à-dire S LD.

Soit donc ç la distance-au-défaut mesuré en écart-type de V et définie par

Reprendre le raisonnement qui nous a conduit à la formule 4.3 permet d'exprimer la distance-au-défaut sous la forme :

(4.7)

Nous allons établir les conditions aux bords pour. Prés du défaut (S--0), nous

Avons

En utilisant l''equation précédente et (4.7), on montre que lorsque S--0

Lorsque S »LD, on suppose que S/V--1 (ce qui est cohérent avec le comportement d'un modèle de Merton standard). Par suite,

L'expression la plus simple pour qui satisfasse simultanément à ces deux conditions aux bords est

En comparant l'équation précédente avec (4.7) nous sommes conduits à

Chapitre 4 Les modèles structurels

V = S + LD ; et donc V0 = S0 + LD:

Finalement, l'on obtient

ó= ó*S . {S*/(S* + LD)}

pour une valeur de l'action égale à S et sa volatilité (historique ou implicite) correspondante.

La formule suivante pour la probabilité (risque neutre) de défaut ne fait plus intervenir que des variables observables

Où

Chapitre 5

Les modèles structurels en

pratique (Exemples de modèles):

5.1 Exemples de modèles :

Dans la pratique, les outils de gestion du risque de crédit reposant sur cette approche sont le modèle KMV de Moody's et la méthode CreditMetrics de JPMorgan entre autres.

5.1 .1 Modèles KMV (Kealhofer, McQuown et Vasicek) de Moody's

KMV ont développé plusieurs modèles de quantification du risque de crédit : Credit Monitor, Credit Edge et Private Firm Model pour le risque de crédit individuel et Portfolio Manager pour le risque de crédit des portefeuilles. Les produits CreditMark pour le calcul de la valeur marked-to-market des instruments peu liquides et CDO Analyser pour l'analyse des risques des Collateralised Debt Obligations ont été développés par M-KMV suite à l'acquisition de KMV Corporation par Moody's.

Les modèles KMV reposent sur la notion de "distance au défaut" ("distance to default") qui est calculée en regard de la barrière qui enclenche le défaut. Une fois la distance au défaut calculée, elle est convertie en probabilité de défaillance (appelée aussi "fréquence de défaut espérée" ou "Expected Default Frequency" ou EDF).

La distance au défaut est définie de la façon suivante :

oÙ VA correspond à la valeur de marché des actifs de l'entreprise, óA la volatilité des actifs et X est le point de défaut qui correspond à la somme de la dette à long terme et de la moitié de la dette à court terme.

Plus la DD est grande, moins il y a de chance que l'entreprise soit en défaut.

On suppose dans le modèle de Merton que l'entreprise a émis des actions et des obligations en t = 0. A la date de maturité T, les actionnaires reçoivent (VA - X) lorsque VA > X et 0 lorsque VA ? X. En résumé, ils reçoivent max(VA - X, 0) en T. Cette situation s'apparente à

l'achat pour les actionnaires d'une option d'achat (ou call) sur la valeur de marché des actifs de l'entreprise et dont le strike X correspond à la valeur comptable de la dette. En supposant,

Chapitre 5 Les modèles structurels en pratique

comme le fait Merton, que VA évolue suivant un processus de diffusion géométrique de la forme salivate :

dVA / VA = u dt + aA dWt , où Wt est le processus de Wiener standard, la valeur boursière de l'entreprise est donnée par (il s'agit du prix d'une option d'achat européenne fourni par Black et Scholes (1973)) :

VE = VAN(d1) - exp(-rT )X N(d2), où N(.) désigne la fonction de répartition de la loi normale avec :

KMV fait l'hypothèse d'une structure de capital uniquement composée d'actions, de dettes à

court terme, de dettes à long terme de maturité infinie (perpétuité)etdetitres convertibles.Dans la réalité, la valeur de marché VA et la volatilité des actifs aA ne sont pas observables.Elles seront déduites à partir des valeurs des options VE. En supposant que VE = f(VA, aA, X,c, r) et aE = g(VA, aA, X, c, r) où c désigne le coupon payé sur la dette long terme et r le taux d'intérêt sans risque et en appliquant le lemme d'Itô à ces 2 fonctions et en arrangeant les termes, on obtient :

Or

,

puisque la valeur VE est définie par VE = VA N(d1) - e-rT X N(d2).

D'où :

Nous obtenons alors un système de 2 équations à 2 inconnues VA et aA :

Chapitre 5 Les modèles structurels en pratique

Une fois les expressions de VA et óA déterminées, nous pouvons en déduire la formulation suivante de la distance au défaut :

A partir de la distance au défaut, on peut inférer la probabilité de défaut de la façon suivante :

Dans la réalité, la probabilité de défaut ne correspond pas à une loi normale. C'est pourquoi KMV ont défini des tables basées sur des données historiques qui associent aux différentes valeurs possibles de DD sur un horizon donné une probabilité de défaut constatée empiriquement (elles montrent combien de sociétés faisant état d'un DD similaire ont effectivement fait défaut sur l'horizon temporel considéré).

Pour le calcul du Credit Value-at-Risk ou CreditVaR destinée à la constitution d'une réserve de capital pour faire face aux pertes potentielles liées aux variations du portefeuille, KMV se

basent sur la détermination de la grandeur aléatoire L des pertes du portefeuille définie de la manière suivante sur un horizon H :

L = VH/ND - VH, où VH/ND est la valeur du portefeuille en H en l'absence de pertes et VH est la valeur de marché du portefeuille en H. KMV montrent que la distribution de L peut être approchée par une distribution normale inverse. La CreditVaR est alors calculée à partir des quantiles de la distribution de L.

5.1 .2 Forces et Faiblesses

Forces :

? Le modèle relie les probabilités de défaut aux informations du marché.

? Les débiteurs sont spécifiques. On peut les distinguer par leur propre probabilité de défaut,

leur propre structure de capital et leurs propres actifs (contrairement aux modèles de CreditMetrics

et de CreditRisk+).

? Contrairement à l'approche de Merton, le seuil de défaut est défini de manière empirique

comme la somme de la dette financière à long terme de la firme et de la moitié de sa dette

à court terme.

Faiblesses :

? L'hypothèse que la dette de la firme est constituée d'obligations zéro-coupon et d'actions

n'est pas réaliste.

? Le prix des actifs est supposé suivre un mouvement brownien géométrique.

Chapitre 5 Les modèles structurels en pratique

Cette modélisation par un processus continu exclut donc tout défaut non anticipé.

· Taux d'intérêt supposés constants (hypothèse trop simpliste).

· La méthode est difficile à mettre en place car elle nécessite de nombreux données en entrées qui sont pour la plupart soit inobservables soit difficilement accessibles.

5.1 .2 CreditMetrics de JPMorgan

CreditMetrics, lancé en 1997 par la banque JPMorgan, est un outil destiné à évaluer, pour un

portefeuille, ses variations de valeur provoquées, d'une part, par les changements de la qualité de crédit de l'émetteur des obligations (migration du crédit) et d'autre part, par le défaut de la contrepartie. A la différence de l'approche KMV, les probabilités de défauts sont données ici par les agences de rating (notation externe) concernant les entreprises importantes et par les méthodes de scoring et de mapping (notation interne) pour les petites et moyennes entreprises.

CreditMetrics permet de calculer la CreditVaR. Il fait partie des modèles structurels car, à l'instar du modèle KMV, il repose sur le modèle de Merton (1974) pour définir les seuils de migration du crédit.

Pour calculer la CreditVaR, la méthode repose sur les 4 étapes suivantes :

· Détermination du risque isolé de chaque actif du portefeuille (prise en compte d'un système de notation).

· Construction de la matrice des probabilités de transition d'une notation à une autre (CreditMetrics utilise les matrices fournies par les agences de rating : Standard & Poor's ou Moody's).

· Valorisation des actifs du portefeuille selon les scénarios de transition d'une notation à une autre.

· Calcul de la CreditVaR.

5.1 .2.1 Principe du modèle : portefeuille à une obligation

Le système de notation pris en compte par CreditMetrics est celui des agences de rating telles que Moody's ou Standard & Poor's. Les émetteurs de titres (de créance) sont notés à partird'une échelle allant de AAA à CCC (échelle de Standard and Poor's) en fonction de leur solidité financière. Les entreprises saines financièrement sont notées AAA tandis que les plus mauvaises sont notées CCC.

Les agences de notation publient régulièrement des informations relatives à l'évolution de lanotation des émetteurs dans le temps. Ces informations sont regroupées dans des tableaux qui indiquent, soit directement le taux de défaut historique des émetteurs selon leur notation et sur un horizon donné, soit les changements de notation au cours du temps. Les tableaux décrivant l'évolution dans le temps de la notation d'un ensemble d'émetteurs sont appelés "matrices de transition(1)". La matrice annuelle de transition décrit le changement de notation, sur un horizon d'un an, d'un ensemble d'émetteurs

Chapitre 5 Les modèles structurels en pratique

(1) La matrice de transition est à interpréter avec soin car les probabilités de migration ont été déterminées en regroupant plusieurs entreprises entre elles et en mêlant plusieurs phases économiques entre elles (par exemple pour la notation BBB, plusieurs types d'industrie au cours des phases de récession et d'expansion de l'économie sont pris en compte alors que l'on sait que la probabilité de défaut est beaucoup plus élevée durant une phase de récession qu'au cours d'une période de croissance et elle est aussi beaucoup plus forte pour une PME que pour une grande entreprise).

Cette table s'analyse comme suit, en lisant par exemple la ligne BBB du tableau ci-dessus :

La probabilité pour notre actif de notation initiale BBB de rester BBB après une période d'un an est de 86,93 %, celle de devenir B est de 1,17%, celle de faire défaut est de 0,18%.

on refait le même calcul avec les autres catégories de rating et on utilisant le tableau précédent on obtient sur Excel les résultats suivants:

Chapitre 5 Les modèles structurels en pratique

Les hypothèses du modèle sont :

? Absence de transition multiple:

Le nombre de transitions pour un horizon temporel donné est au maximum de 1 transition.

? Stabilité de la matrice de transition au cours du temps:

Au sein d'une classe de notation, deux entreprises dans des secteurs différents ou dans des pays différents ont la même probabilité de migrer d'une notation à une autre. Des travaux ont montré que cette hypothèse n'était pas souvent vraie. Il a été constaté une volatilité plus forte des transitions de rating pour les banques que pour l'industrie.

? Matrice de transition de type Markov:

La probabilité de migrer d'une classe à une autre au cours d'une période est indépendante de ce qui s'est passé au cours des périodes passées (hypothèse émise pour simplifier les calculs de la matrice de transition pour les périodes postérieures : en effet, la matrice de transition à 3 ans est obtenue en calculant A1 x A1 x A1 où A1 est la matrice de transition à 1 an). Des études ont montré que l'erreur d'approximation commise en procédant à des produits matriciels successifs augmentait au cours du temps.

Pour le calcul de la CreditVaR, CreditMetrics détermine la valeur actuelle de l'obligation en utilisant la courbe des taux zéro coupon (lorsqu'il n'y a pas eu faillite de l'émetteur). Exemple : Calcul de la valeur d'une obligation notée BBB

Tableau des taux forward(taux sans risque+prime de risque)

On considère un émetteur noté BBB qui émet une obligation de 100 euros sur 4 ans avec un taux annuel de 6%. Dans ce cas la valeur actuelle de l'obligation est donnée par l'équation suivante :

Chapitre 5 Les modèles structurels en pratique

		^5,22322	^86,81
		^5,21574	^86,64
		^5,19341	^86,15
		^5,14618	^85,14
		^4,92812	^80,06
		^4,75903	^76,43
		^4,04663	^63,83
^5,791506	^5,529246
^5,788712 ^5,784805	^5,523942 ^5,513357
^5,763689	^5,476547
^5,68451	^5,337964
^5,657709	^5,238674
^5,194805	^4,535284
^Notation		^Proba
^AAA		^0.02

^{Valeur act 108,64 107,53 102,01 98,09 83,61 Valeur}

^109,35

^AA

^0.33

^109,1724

^A

^5.95

^108,643

^BBB

^86.93

^107,5309

^BB

^5.3

^102,0064

^B

^1.17

^98,08591

^CCC

^0.12

^83,60547

^D

^0.18

^51,13

Remarque :

109,35 = ? 5,79150579 5,529246123 5,223215445 86,80894

On détermine ainsi, toute les valeurs possibles du titre BBB en fonction des ses migrations possibles vers d'autres notations l'année suivante.

Lorsqu'il y a eu faillite de l'entreprise, la valeur du titre est déterminée en utilisant le taux de récupération moyens calculés par CreditMetrics sur des données historiques (moyenne sur ce que récupèrent les créanciers lorsqu'une entreprise tombe en faillite).

Les différentes valeurs du titre BBB en fonction des migrations possibles sont données dans le tableau suivant :

Chapitre 5 Les modèles structurels en pratique

Valeur d'un titre BBB

Ces résultats sont traités sur une feuille Excel comme suivant :

^categorie

^AAA

^AA

^A

^BBB

^BB

^B

^CCC

^AAA

^90,81%

^8,33%

^0,68%

^0,06%

^0,12%

^0,00%

^0,00%

^0,00%

??

^AA

^0,70%

^90,65%

^7,79%

^0,64%

^0,06%

^0,14%

^0,02%

^0,00%

^A ^BBB

^0,09% ^2,27% ^0,02% ^0,33%

^91,05% ^5,95%

^5,52% ^0,74% ^86,93% ^5,30%

^0,26% ^1,17%

^0,01% ^0,06% ^0,12% ^0,18%

^BB

^0,02% ^0,14%

^0,67%

^7,73% ^80,53%

^8,84%

^1,00% ^1,06%

^B

^0,00% ^0,11%

^0,24%

^0,43% ^6,48%

^83,46%

^4,08% ^5,20%

^CCC

^0,22% ^0,00%

^0,22%

^1,30% ^2,38%

^11,24%

^64,85% ^19,79%

^DEFAULT categorie

^0,00% ^0,00% ^Année 1

^0,00%Année 2

^0,00% ^0,00% Année 3 ^5,25

^0,00% Année 4 ^5,63

^0,00% ^100,00%

^AAA

^3,6

^4,17

^4,73

^5,12

^AA

^3,65

^4,22

^4,78

^A

^3,72

^4,32

^4,93

^BBB

^4,1

^4,67

^BB

^5,55

^6,02 ^6,78

^DEFAULT

^5,17

^5,32

^7,27

^B

^6,05

^7,02

^8,03

^8,52

^CCC

^15,5

^15,02

^14,03

^13,52

^{Tableau des taux forward (taux sans risque} + ^{prime de risque)}

A partir du tableau des différentes valeurs de BBB selon sa migration, on peut déduire la distribution des variations de prix de l'obligation, comme le montre l'exemple suivant :

En s'aidant d'une feuille Excel, on obtient les résultats suivants ;

Chapitre 5 Les modèles structurels en pratique

^SOURCE :

^{DISTRIBUTION OF THE BOND VALUES AND CHANGES IN VALUE OF BBB BOND,IN 1 YEAR}

^{year-end rating}

^{pobability of state:p%}

^{forward price:V($)}

^AAA

^0.02

^AA

^0.33

^A

^5.95

^BBB

^86.93

^BB

^5.3

^B

^1.17

^CCC

^0.12

^D

^0.18

^{CreditMetrics de JPMorgan}

Year-endthe end of a financial year or calendar year

^{change in value:Äv($)}

^1,8190561

^1,641426998

^1,112048194

⁰

^-5,524558376

^-9,445030719

^-23,92547137

^-56,4009439

On voit que la distribution n'est pas normale car non symétrique. La distribution ci-dessus est

Chapitre 5 Les modèles structurels en pratique

obtenue en mettant en abscisse les différentes valeurs de variation du prix du titre (seul titre présent dans le portefeuille) et en ordonnée, les probabilités de migration.

La CreditVaR à 1% (c'est-à-dire perte maximale attendue pour une probabilité de 1%) ou en d'autres termes pour un niveau de confiance de 99% est obtenue en prenant le premier percentile de la distribution des variations de prix de l'obligation, soit CreditVaR = -23,91.

On prend 1% de l'aire de la distribution ci-dessus en partant de la gauche car les valeurs de variation du prix du titre sont rangées dans un ordre ascendant (des nombres négatifs = pertes vers les nombres positifs = gains).

5.1 .2.2 Principe du modèle : portefeuille à deux obligations

Dans le cas de plusieurs actifs dans le portefeuille, la migration des différents crédits est corrélée (les valeurs des titres d'un même secteur d'activité ou d'une même région géographique sont en principe fortement corrélées). Il est alors nécessaire d'estimer ces corrélations. Le problème est qu'il n'y a pas de bonnes données observables. Par conséquent,

pour le calcul des corrélations entre migrations des crédits, CreditMetrics utilise les corrélations entre les valeurs des actifs des émetteurs des crédits qui sont approchées par les

corrélations entre les prix des actions de ces émetteurs (il est possible d'utiliser aussi les

obligations mais leur historique est moins important que celui des actions).

Cependant, pour pouvoir dériver les corrélations des migrations des crédits des corrélations des valeurs des actifs, il faut disposer d'un modèle liant la qualité d'un crédit à la valeur des actifs. Le modèle utilisé est une extension du modèle de Merton (1974) qui incorpore les migrations des crédits.

Dans le cadre de ce modèle, en considérant les probabilités de migration d'une entité initialement notée BB qui sont données par le tableau de Standard & Poor's suivant :

On suppose que le comportement du rendement d'un titre est modélisé par : r = u+o€où €~>N(0,1). La probabilité de défaut d'un émetteur du titre est donnée par : Pr{défaut} = Pr{ r < ZDef } = Pr{ u+o€< ZDef } = Pr{ o€< ZDef } si on suppose u= 0. D'où Pr{défaut} = Pr{ € < ZDef /o} = cJ(ZDef /o) où cJ est la fonction cumulative de la loi normale.

où 1-4(ZAA/o) désigne la probabilité pour l'entité BB de passer à la notation AAA, ZAA représentant le seuil à partir duquel l'entité BB passe à AAA.

Chapitre 5 Les modèles structurels en pratique

Graphiquement, les données du tableau apparaissent de la façon suivante (si on suppose que les rendements des actifs de l'entité BB suivent une loi normale)

Sachant que Zdef = cb-1(1.06%).a = -2.30 a, nous obtenons la valeur de chacun des seuils ZAAA, ZAA, ZA, ... en fonction de a qui correspond à l'écart-type de la distribution normale des rendements des actifs de l'entité BB :

Z BBB ZAA

On a P(Z B B G r = Z BBB, ZAA = r' = ZAAA) = f f f(r,r',a,a') drdr'

Z B B ZA

Comme on a cb(Zdef /a)=1.06% alors on a Zdef /a = cb-1(1.06%)4 Zdef = a cb-1(1.06%)

On utilisant la fonction NORMSINV function (normal standard inverse) d'un tableau Excell,on obtient Zdef = a cb-1(1.06%)=-2,3044 a ; avec cb-1 : NORMSINV

De même, et toujours d'après le tableau précédent on a aussi:

cb(ZCCC /a)- cb(Zdef /a)= 1% 4 cb(ZCCC /a)= cb(Zdef /a)+ 1%

4 ZCCC /a = cb-1 (cb(Zdef /a)+ 1%)

4 ZCCC = a cb-1 (cb(Zdef /a)+ 1%)

=a cb-1 (1.06% + 1%)

= a cb-1 (2.06%)

= -2,0415 a

On refait le même raisonnement de calcul pour déterminer les autres seuils ZB, ZBB, ZBBB, ZA, ZAA et

on obtient le tableau suivant :

Chapitre 5 Les modèles structurels en pratique

^ZAA
^SEUIL
^ZA
^ZBBB

^ZCCC	^2,04a
^Zdef
	^VOCAB
^EN		^FR
^thresholds		^seuil
^value
^asset
^according to
^over
^remains

Chapitre 5 Les modèles structurels en pratique

Supposons que nous ayons un second émetteur noté A et dont les rendements des actifs

suivent une loi normale avec un paramètre a', nous obtenons alors le tableau suivant (construit de la même façon que pour BB) :

Disposant de ces deux tableaux d'informations pour les 2 entités notées BB et A, nous pouvons calculer les probabilités de migration jointes de la façon suivante :

où r et r' représentent respectivement les rendements des actifs de BB et de A et f(r,r',a,a') désigne la fonction de densité jointe de la loi gaussienne qui dépend du coefficient de corrélation p. La fonction de densité jointe de la loi gaussienne des variables X et Y se

présente comme suit (la moyenne de X et Y est supposée nulle) :

Chapitre 5 Les modèles structurels en pratique

Pour ñ = 20%, on obtient la matrice de transition jointe suivante qui tient compte de la corrélation des deux entités BB et A :

Les colonnes "Total" représentent les probabilités marginales pour les titres BB et A (somme des probabilités jointes de la ligne ou de la colonne). Ces probabilités marginales correspondent aux probabilités de migration de BB et de A prises individuellement.

Pour chacune des probabilités jointes, on calcule la variation du portefeuille des 2 titres. Par exemple, pour la probabilité jointe de 7.10% (BB passe à BBB et A reste A). La valeur du portefeuille après migration est de VBBB + VA. La variation de la valeur du portefeuille sera alors de : (VBBB + VA) - (VBB + VA).

5.1 .2.2 .1Exemple de Portefeuille de 2 titres BBB et A :

1. Régression des rendements rt des titres sur les indices sectoriels. Dans le cas de 3 titres et de 2 indices sectoriels, on a :

Chapitre 5 Les modèles structurels en pratique

A partir du tableau des probabilités jointes de migration et du tableau des valeurs possibles du portefeuille, on peut déduire la distribution des valeurs du portefeuille comme suit :

5.1 .2.3 Principe du modèle : portefeuille à plusieurs obligations

Pour plus de 2 titres, il est plus compliqué de calculer la probabilité jointe entre tous les titres

du portefeuille.CreditMetrics utilise alors les simulations de Monte-Carlo et la décomposition de Cholesky pour générer les trajectoires corrélées des titres et construire la distribution des valeurs du portefeuille à un certain horizon.Pour générer les trajectoires corrélées des variables suivant la distribution normale N(ì,?) où ? représente la matrice des variances-covariances, les étapes sont les suivantes :

Chapitre 5 Les modèles structurels en pratique

On obtient les valeurs estimées :

2. Calcul des variances et covariances entre 2 titres i et j :

et

On obtient alors la matrice des variances-covariances Ó. Les étapes 1 et 2 permettent de réduire les temps de calcul pour obtenir la matrice Ó lorsque le nombre de titres est très important.

3. Décomposition de Cholesky de la matrice des variances-covariances Ó de la façon suivante :

Ó = A

où A désigne la matrice triangulaire inférieure et la transposé de la matrice A.

4. Simulation des variables Zi,t ~>N(0,1). Il y a autant de Zi,t qu'il y a de titres i à simuler.

5. Simulation des valeurs des variables corrélées V ~>N(/1,Ó) à l'aide de

dV/ V = /1dt + A Z (processus de diffusion géométrique) où

,dt=Ä

Chapitre 5 Les modèles structurels en pratique

5.1.2.3.1 Forces et Faiblesses : Force :

· Les deux aspects du risque de crédit (risque de défaut et risque de dégradation de la qualité du crédit) sont pris en compte.

Faiblesses :

· Les entreprises doivent être correctement notées (sinon les matrices de transition ne valent rien). Les agences de rating appliquent des cotes de crédit identiques à travers les différentes industries ou pays.

· Les émetteurs ayant la même notation ont des probabilités de défaut et des probabilités de migration identiques. Une entreprise importante notée BB a par conséquent les mêmes probabilités de défaut et de migration qu'une société notée BB.

· Il y a une relation entre la conjoncture économique et la probabilité de défaut. Il faudrait avoir des matrices de transition associées à chaque cycle économique.

· Les taux d'intérêts sont supposés constants.

· La variabilité du prix des actifs d'une entreprise est approchée par la variabilité des actions de l'entreprise. Or il n'a pas été prouvé que les variations des actions soient un bon proxy pour les variations des actifs de la firme. Le modèle peut manquer de précision.

Chapitre 6

CONCLUSION

Les modèles structurels de la dette risquée actuels ne parviennent pas à rendre compte convenablement de la structure des spreads observés et de leur sensibilité à certaines variables.

Pour discuter ce problématique et proposer quelques raisonnement qui peuvent être utile pour combler ces faiblesse, on s'intéresse dans cette conclusion d'une part a unapprofondissement théorique dans l'approche structurelle pour modéliser le risque de crédit et d'autre part, a une étude empirique visant à induire (à partir du modèle élaboré) une estimation des primes de risque sur action à partir des spreads de crédit observés.

Les modèles d'évaluation de la dette risquée, qui sont en même temps des modèles explicatifs du niveau et de la structure des «spreads de crédit", et servent de base à l'évaluation des produits dérivés de crédit, ont fait l'objet d'une abondante littérature depuis le début des années 70. A la suite de Duffie-Singleton (98), ces modèles sont généralement rangés en deux catégories :les

«modèles structurels» et les «modèles sous forme réduite".

Dans les «modèles sous forme réduite", le temps du défaut est défini de manière exogène

(cf. Jarrow Turnbull (95), Jarrow Lando Turnbull (97) et Duffie Singleton (98)). Le principal

avantage de ces modèles est leur souplesse. Leurs paramètres peuvent aisément être estimés à partir de l'observation de la structure des spreads de crédit. Ces modèles permettent aussi un pricing (évaluation du prix) des titres dérivés de crédit compatible avec les prix observés de la dette risquée. Cependant, ils sont très pauvres sur le plan théorique et rompent le lien théorique entre les variables économiques de base (valeur de l'entreprise, taux du marché) et l'événement «défaut». En effet, le prix de la dette risquée apparait exposé à deux sortes de facteurs de risque :

1. le risque de défaut associé au risque de marché, ou risque d'exploitation affectant la valeur de l'entreprise : dans un modèle où le risque d'exploitation qui affecte la valeur de l'entreprise est le seul facteur de risque, le risque de défaut n'est qu'un sous produit de ce risque d'exploitation sous jacent.

2. le risque lié à l'évolution du taux de marché.

Même dans les modèles, comme celui deMerton (1974), où ce taux d'intérêt est supposé constant, le prix de la dette risquée apparaît comme une fonction de ce taux d'intérêt. Dans un modèleà deux

facteurs où le taux d'intérêt est stochastique, la probabilité de défaut, sauf à supposer
l'indépendance des deux facteurs de risque, dépend en principe du niveau du taux d'intérêt. En statique comparative il devient possible de comparer la sensibilité au taux d'intérêt du marché de la dette risquée à celle d'une dette non risquée ayant la même chronique de coupons nominaux.

CONCLUSION

En conclusion, les modèles sous forme réduite ne fournissent aucune formule «a priori" du risque de taux de la dette risquée contrairement aux modèles structurels. Les «modèles structurels" ont pour variable d'état le plus souvent la valeur de l'entreprise (ou son cash flow

d'exploitation), variable observable ou non selon les cas. Elle est modélisée par un certain processus de diffusion. Le «défaut» y est un évènement endogène qui survient lorsque la valeur heurte une barrière absorbante elle même exogène ou un seuil résultant d'un calcul d'optimisation de l'actionnaire. L'avantage essentiel des modèles structurels est en outre de permettre une évaluation intégrée et cohérente des divers titres émis par l'entreprise (exposés à des degrés divers aux deux catégories de risque définies ci-dessus) qu'il s'agisse des actions pour aller à la dette fortement sécurisée au moyen de collatéraux (hypothèques ou garantie d'un tiers) ou d'obligations convertibles ou encore de dettes risquées de premier ou de deuxième rang.

Toutefois les modèles structurels ont généralement du mal à rendre compte d'une manière convenable de la structure des spreads de crédit observée et de leur sensibilité à certaines variables(comme le taux d'intérêt). Par exemple, ils ne rendent pas compte de la non convergence vers 0 des spreads de crédit sur échéance courte, même pour des entreprises peu endettées (La convergence du spread vers zéro dans les modèles structurels tient à la prédictibilité du défaut dans le cadre des hypothèses standards voir Gieseke 2003).

6.1 L'amélioration théorique de ces modèles

La prise en compte de la dynamique de la dette : un titre de dette particulier émis par une entreprise ne peut être valorisé indépendamment des autres titres d'emprunt émis par la firme. C'est la totalité de la dette de l'entreprise qui détermine son risque de défaut et qui influence donc la valorisation de chaque titre de dette particulier quel que soit son rang de priorité ou les garanties dont il est assorti. Le défaut est un évènement qui affecte l'ensemble des dettes émises. Sa survenance est déterminée par la totalité des engagements contractés par la firme. Bien plus la valeur d'une dette d'échéance T dépend en t < T non seulement des emprunts déjà au bilan en t mais de tous les nouveaux emprunts qui pourront être émis entre t et T et dont l'importance contribuera à déterminer la probabilité de défaut de l'entreprise durant l'intervalle.

Autrement dit, une dette risquée ne peut être évaluée comme si elle était seule au bilan. Elle ne peut l'être que dans le cadre d'une dynamique présumée de l'endettement global de la firme. Retenir un niveau de dette constant quel que soit t, revient à supposer que le taux d'endettement anticipé décroît et conduit à réduire les spreads de crédit à long terme relativement aux spreads de court terme. P. Colin-Dufresne et R. S. Goldstein (2001), pour pallier cette difficulté, supposent un ratio d'endettement maintenu stationnaire à long terme, par un processus de retour à la moyenne (cf. processus de Ornstein-Uhlenbeck). On obtient donc une forme plus satisfaisante de la courbe par terme des spreads de crédit.

Nous nous proposons d'étudier l'influence de l'introduction de nouveaux modèles stochastiques sur la dynamique de l'endettement. En particulier, la prise en compte des emprunts éventuellement émis entre t et T donne lieu à des problèmes de calcul stochastique anticipatif ou de grossissement de filtration.

CONCLUSION

L'endogénéisation du seuil de défaut : le défaut de l'entreprise suppose réunies deux conditions. D'une part la firme n'est pas en mesure de faire face à ses échéances courantes et d'autre part ses actionnaires ne sont pas disposés à lui fournir les fonds dont elle aurait besoin

pour survivre. Il y a donc toujours une décision des actionnaires. Il convient ainsi, afin d'apprécier le risque de défaut de la firme, de spécifier et de modéliser quel peut être le comportement de ces derniers dans ce domaine.

La prise en compte d'asymétries d'informations sur le seuil de défaut ou la valeur de l'entreprise (cf. Duffie et Lando (2001)) parait en mesure de produire un spread qui ne tend pas vers zéro lorsque la maturité devient très faible( l'asymétrie d'information est un moyen de remettre en cause la prédictibilité du défaut par les acteurs du marché). On s'attachera aussi à modéliser les asymétries d'information des investisseurs sur le seuil de défaillance. En effet, les écarts de signaux détenus par les agents modifient leur niveau d'investissement et ont ainsi une incidence sur la prime de risque et le spread de crédit.

La modélisation du processus de la valeur de l'entreprise avec des sauts ou des mouvements browniens fractionnaires : le projet est d'examiner si de tels modèles ne sont pas eux aussi propres à rendre compte de la non convergence vers zéro des spreads de crédits sur échéances

courtes, même pour des entreprises de très bon rating (faible endettement). En effet, la«prévisibilité» d'un brownien standard rend le non défaut presque sûr pour des échéances très rapprochées lorsque la firme (aux yeux de tous) est éloignée du seuil de défaut.

6.2 Etude empirique

La modélisation structurelle établit un lien entre le prix des actions et le prix de la dette risquée. Elle doit permettre d'approcher de manière novatrice le problème de l'évaluation de la prime de risque des actions (ou de la «prime de risque du marché»). On peut identifier deux méthodes standards d'estimation de cette prime de risque :

- les méthodes statistiques estimant la prime de risque, avec des techniques plus ou moins sophistiquées, à partir des excédents de rentabilité passées en posant des hypothèses de stationnarité nécessaires ;

- les méthodes des analystes financiers (comme «associés en finance» en France et divers établissements financiers). Elles utilisent des prévisions de dividendes et en induisent le taux de rendement interne de la chronique des flux espérés diminuée du prix de l'action.

Ces approches sont peu satisfaisantes et donnent de médiocres résultats de sorte que le niveau lui-même et les fluctuations de la prime de risque sont, en fait, fort mal connus. Par ailleurs, dans l'estimation d'un modèle structurel, certains paramètres (le taux d'intérêt, la valeur de l'entreprise, le taux d'endettement...) ne posent guère de problème d'estimation.

En revanche d'autres paramètres ne sont pas directement observables, tels la volatilité de la valeur de l'entreprise ó et la prime de risque X associée à l'aléa affectant cette valeur.

CONCLUSION

6.3 RESULTATS ATTENDUS

En conclusion, le développement de modèles structurels d'évaluation de la dette risquée est un enjeu essentiel pour les établissements financiers à la fois :

- dans leur gestion des risques de portefeuilles formés de titres différents émis par une même entreprise,

- dans leurs stratégies d'arbitrage (au sens non technique) entre les différents titres de l'entreprise, ce qui suppose une bonne maîtrise des risques pris et une bonne compréhension des corrélations entre les fluctuations de prix,

- dans le contrôle de leurs engagements vis-à-vis d'une contrepartie.

ANNEXE 1

Lemme d'Itô

Le lemme d'Itô, ou encore formule d'Itô est l'un des principaux résultats de la théorie du calcul stochastique. Ce lemme offre un moyen de manipuler le mouvement brownien ou les solutions d'équations différentielles stochastiques (EDS).

Énoncé

Soit un processus d'Itô processus stochastique de la forme

Autrement formulé, on a

avec et deux fonctions aléatoires satisfaisant quelques hypothèses techniques d'adaptation au

processus (mouvement brownien).

Si est une fonction de classe alors la formule d'Itô s'écrit

Un exemple : le modèle Black-Scholes

Le mouvement brownien géométrique est souvent utilisé en finance comme le plus simple modèle d'évolution de cours de bourse. Il s'agit de la solution de l'équation différentielle stochastique :

où

? est le prix de l'action sous-jacente,

? (constant) est le taux de dérive jen) du prix de l'action,

ANNEXE 1

? (constante) est la volatilité du prix de l'action,

? est un mouvement brownien.

Si alors nous sommes face à une équation différentielle ordinaire dont la solution est

En posant on obtient grâce à la formule d'Itô :

On peut alors intégrer et il en découle que :

Applications

? La formule d'Itô est l'une des pierres angulaires du calcul stochastique, et est utilisée dans de

très nombreux domaines: mathématiques appliquées, physique, finance, biologie, Mécanique quantique, traitement du signal, etc..

En calcul stochastique,

? Elle permet de faire le lien entre les solutions d'EDS et des opérateurs différentiels du

second ordre, et donc entre la théorie des probabilités et celle des équations aux dérivées partielles.

? Elle permet d'affirmer l'existence de solutions d'EDS sous des conditions (très) faibles de

régularité sur les coefficients.

ANNEXE 2

Equation de Black & Scholes (modèle standard)

Nous allons étudier ici le modèle BS dans sa forme simple avant l'apport de Robert Merton sur la volatilité déterministe et les taux aléatoires.

Considérons un marché sans coût de transaction où sont échangés 2 types d'actifs avec absence de possibilité d'arbitrage: risqué et non risqué. La cotation est réalisée en continue à un taux constant r. Le spot du sous-jacent à l'émission est noté S0 et son évolution est déterminée par un mouvement brownien. On notera p la tendance ou dérive (i.e. l'espérance de rentabilité du support sur son historique de cours), ó la volatilité du sous-jacent (le paramètre de diffusion) et Wt un mouvement brownien.

Cette équation est donc une équation différentielle stochastique (EDS) qui régit un mouvement brownien géométrique (MBG) St avec p et ó connues et constants. On peut déduire la dérive du mouvement :

Car d'après le lemme d'Itô on obtient pour ln(St) :

Ce qui nous permet d'écrire :

On retrouve donc bien le terme de dérive du mouvement. On peut également montrer que ce MBG est log-normalement distribué en rappelant que S0 ne peut être négatif car le cours d'une action n'est jamais négatif en vertu de la responsabilité limité de l'actionnaire:

St est donc log-normal et la solution de St s'écrit :

ANNEXE2

Définissons à présent la valeur ât de l'actif sans risque en t.	On peut définir le rendement de l'actif

sans risque au taux constant r comme la différentielle de ât : La solution de cette

équation est :

Introduisons à présent une option européenne avec pour sous-jacent St. Notons qu'aucun dividende n'est versé.

L'intuition de F. Black et M. Scholes s'exprime par la recherche dans les stratégies autofinançantes de celle(s) qui duplique(nt) le call et dont la ou les valeur(s) s'exprime(nt) comme une fonction déterministe de St et de t que l'on notera it(t, St). L'idée est donc qu'il existe un portefeuille autofinancé composé du sous-jacent et de l'actif sans risque dont la valeur en T est égale au payoff ØT de l'option. On tente donc de trouver le processus itt qui représente la valeur d'un portefeuille autofinançant et dont la valeur en T est celle du payoff à dupliquer. L'expression it doit donc être suffisamment régulière au sens d'Itô ; i.e. la fonction it doit être 1 fois continûment différentiable sur t et 2 fois continûment différentiable sur St. Sous ces conditions, nous pouvons appliquer la formule d'Itô :

De notre 1^ère équation

on déduit et on remplace :

On cherche à présent à respecter

l'égalité suivante ()

Afin que it(t, St) représente à tout instant t la valeur d'un tel portefeuille. Remanions cette égalité :

ANNEXE2

On a ainsi obtenu l'équation aux

dérivées partielles de Black & Scholes (EDP d'évaluation). A ce stade il reste à vérifier que le portefeuille autofinançant synthétise l'option :

Rappelons que nous sommes en absence de possibilité d'arbitrage, ce qui implique que la valeur du portefeuille dupliquant est, à chaque instant, égale à celle du titre dupliqué :

Dans le cas où le payoff est égal à celui

- d'un call ( )

- ou d'un put ( ) ,la solution est donnée par la formule de Black & Scholes :
,

Notons que N(u) fait référence à la fonction de répartition de la loi normale centrée réduite :

ANNEXE 3

Démonstration du Lemme 4.3.2

Dans cette partie, nous allons démontrer le résultat suivant :

Posons

La démonstration revient à prouver le lemme suivant : Lemme E.1

En

effet :

et donc

ANNEXE3

L'extension au cas général est alors immédiate en écrivant :

La démonstration du lemme 4.3.2 repose sur le Principe de réflexion dont nous rappelons l'énoncée :

Proposition E.2 (principe de réflexion) Parmi les trajectoires browniennes qui atteignent le niveau y avant l'instant t, il y en a autant en dessous de x qu'au dessus de 2y-x en t. Autrement dit :

ce qui se réécrit de la façon suivante :

Nous allons à présent prouver le lemme. D'âpres le théorème de Girsanov il existe une probabilité'e P 'équivalente à P définie par sa densité de Radon-Nikodym

Telle que

Soit un -mouvement brownien, et une probabilité équivalente à

définie par la densité

	Telle que Wt = Xt + ìt soit un e -mouvement brownien.
Soit x=y, on a

ANNEXE3

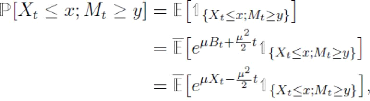
et d'âpres le principe de réflexion :

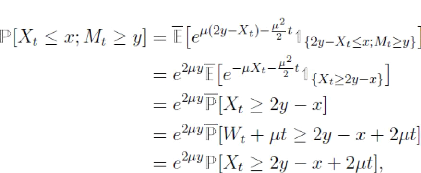
car W est un e -mouvement brownien. Ceci achève la démonstration

Bibliographie

Vivien BRUNEL- Benoît ROGERT-version: September 23, 2009

Risque de crédit-Ecole Nationale des Ponts et Chausses

Couverture des risques dans les marchés financiers

Nicole El Karoui Ecole Polytechnique, CMAP, 91128 Palaiseau Cedex

Aurelien ALFONSI, Thèse de doctorat ,L'ECOLE NATIONALE DES PONTS ET CHAUSSÉES,

David KURTZ & Thomas B. PIGNARD,Modélisation du risque de crédit, DEA de Statistique et Modèles

aléatoires en économie et finance Université Paris 7 -- Université Paris 1

[1] Aven (T.). A theorem for determining the compensator of a counting process. Scandinavian Journal of Statistics, 12(1), pp. 69-72 (1985).

[2] Bielecki (T. R.), Rutkowski (M.). Credit Risk : Modeling, Valuation and Hedging. Springer (2002).

[3] Bomfim (A. N.). Credit Derivatives and Their Potential to Synthesize Riskless Assets. The Journal of Fixed Income December 2002, Vol. 12, No. 3, pp. 6-16 (2002).

[4] Crosbie (P. J.). Modeling Default Risk. KMV Corporation, San Francisco, www.kmv.com (1997).

[5] Dellacherie (C.) Meyer (P.A.). Probabilités et potentiels, chapitres I `a IV, Hermann, Paris (1975).

[6] Duffie (D.), Filipovi_c (D.) & Schachermayer (W.). Affine Processes and Applications in Finance. Annals of Applied Probability, Vol.13, No 3, August 2003 (2003).

[7] Duffie (D.). A Short Course on Credit Risk Modeling with Affine Processes. Working Paper. Stanford University and Scuola Normale Superior (2002). Disponible sur http ://fibonacci.dm.unipi.it/ finance/duffie notes.pdf.

[8] Duffie (D.), Lando (D.). The Term Structure of Credit Spreads with Incomplete Accounting Information. Econometrica 69, pp. 633-664 (2001).

[9] Duffie (D.), Pan (J.), Singleton (K.). Transform Analysis and Asset Pricing for Affine Jump Diffusions. Econometrica, Vol. 68, pp. 1343-1376 (2000).

[10] Duffie (D.), Singleton (K. J.). Modeling Term Structure of Defaultable Bonds. The Review of Financial Studies Special 1999 Vol. 12, No. 4, pp. 687-720 (1999).

[11] Duffie (D.), Singleton (K. J.). Credit Risk . Princeton University Press (2003).

[12] _Emery (M.). Classical Probability Theory : An Outline of Stochastic Integrals and Diffusions. Quantum Probability Communications, QP-PQ, Vol. XI,World Scientific (1999). Disponible sur http :// www-irma.u-strasbg.fr

[13] El Karoui (N.) & Mazliak (L.). Backward Stochastic Differential Equations. Pitman Research Notes in Mathematic Series (1997).

[14] Geske (R.). The valuation of compound options. J. Finan. Econom. 7, pp. 63-81 (1979).

[15] Hull (J. C.), Nelken (I.), White (A.). Merton's Model, Credit Risk, and Volatility Skews. Working Paper. University of Toronto (2003).

[16] ISDA 2003 Credit Derivatives Definitions. www.isda.org.

[17] Krylov (N. V.). Introduction to the theory of diffusion processes. American Mathematical Society, Providence.

[18] Laurent (J.-P.). I will survive. Risk, June 2003. www.risk.net (2003).

[19] Leland (H. E.). Corporate debt value, bond covenants, and optimal capitalstructure. J.Finance 49, pp. 1213-1252.

[20] Longstaff (F. A.), Schwartz (E. S.). A simple approach to valuing risky fixed and floating rate debt. J. Finance 50, pp. 789-819 (1995).

[21] Merton (R. C.). On the pricing of corporate debt :The risk structure of interest rates. J.Finance 29, pp. 449-470 (1974).

[22] Pan (G.). Equity to credit pricing. Risk, November 2001. www.risk.net (2001).

[23] Protter (P.). Stochastic Integration and Differentiel Equations. Springer (1990).

[24] Pye (G.). Gauging the Default Premium. Financial Analyst's Journal, January-February, pp.49-50 (1974).

[25] Credit Derivatives Survey. Risk, February 2003. www.risk.net (2003).

[26] Roncalli (T.). La gestion des risques financiers. Cours du DESS de Gestion des risques et des actifs de l'universit'e d' Evry. gro.creditlyonnais.fr.

[27] Rudin (W.). Real and Complex Analysis. McGraw-Hill, New York, third edition(1987).

[28] Schonb
·ucher (P.), Rogge (E.). Modeling Dynamic Portfolio Credit Risk.Working Paper. ETH Z·urich (2002). Disponible sur www.schonbucher.de.

[29] Schonb
·ucher (P.), Schubert (D.). Copula-Dependent Default Risk in Intensity Models. Working Paper. University of Bonn (2000). Disponible sur www.schonbucher.de.

[30] Vasicek (O.). Credit Valuation. Working Paper. KMV Corporation. www.kmv.com (1984). Merton R. (1974). On the pricing of corporate debt : The risk structure of interest

rates, Journal of Finance, Vol. 29, pp. 449-470.

Black F., Cox J. C. (1976), Valuing corporate securities : Some e_ects of bond indenture provisions, Journal

of Finance, Vol. 31, pp. 351-367..

Laure Coutin, Laboratoire de Probabilités-Statistiques, Université Paul Sabatier Toulouse,

Jean-Claude Gabillon, Groupe de Finance, ESC Toulouse,

Laurent Germain, Groupe de Finance, ESC Toulouse,

Monique Pontier, Laboratoire de Probabilités-Statistiques, Université Paul Sabatier Toulouse,

Clémentine Prieur, Laboratoire de Probabilités-Statistiques, Université Paul Sabatier Toulouse,

Anne Vanhems, Groupe de Finance, ESC Toulouse

Correspondant du projet: Laurent Germain, ESC Toulouse.