III.4. Liaison entre IPC et
recettes fiscales
Pour appréhender l'impact de l'inflation sur les
recettes fiscales, nous avons construit un modèle, dont REC
représente les recettes fiscales et IPC l'indice des prix à la
consommation.
Comme signifié plus haut, nous avons utilisé le
logiciel Eviews 3.1 pour estimer le modèle et réaliser les
différents tests dont les résultats sont présentés
dans les lignes suivantes.
Après traitement de données avec le logiciel
Eviews 3.1, nous avons trouvé que REC = 1,020IPC - 15915 ; cette
équation signifie que lorsque l'IPC augmente d'une unité, les
recettes fiscales augmentent de 1,020 millions de CDF.
La figure n°4 ci-dessous retrace l'impact des IPC sur les
recettes fiscales durant la période de notre investigation.
Fig. n° 4 : Évolution des recettes fiscales
en fonction des indices des prix à la consommation
La figure ci-haut nous montre que les recettes fiscales sont
corrélées positivement avec les indices des prix à la
consommation. L'augmentation d'une unité des indices prix à la
consommation entraine une augmentation de 1,020 millions de CDF des recettes
fiscales.
III.4.2. Différents
tests du modèle
A. Tests individuels
Ce test permet d'étudier la signification des
paramètres. Il pose les hypothèses suivantes :
H0 : ai = 0, la variable exogène
n'influence pas la variable endogène c'est-à-dire le
paramètre n'est pas significatif.
H1 : ai ? 0, la variable exogène
influence la variable endogène c'est-à-dire le paramètre
est significatif.
Règle de décision : si la
probabilité associée à ce test est inférieure
à 5%, on rejette l'hypothèse nulle.
Le test T de Student du coefficient de la variable IPC est de
9.107659 (tableau n°3 en annexe), sa probabilité est de 0,00%
inférieure à 5% ; ce qui signifie que la variable IPC est
significative, c'est-à-dire une variation de l'IPC occasionne
également une variation des recettes fiscales.
B. Test global
Pour mesurer le degré d'explication du modèle,
nous faisons recours au coefficient de détermination
donné par l'équation ci-après :
 avec
0 R2 1
Parfois, R2 a tendance à croître avec
le nombre de variables explicatives du modèle, même si ces
variables n'ont rien à avoir avec le phénomène
étudié. Pour pallier à cet inconvénient, certains
chercheurs ont proposé d'introduire un R2 corrigé,
noté par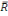 
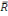 2 qui est défini par :
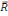
 2 R2 si 
 2  
R2. Il n'est utilisable que dans le modèle avec le terme
constant.
Selon le résultat du tableau n°3 en annexe, le
coefficient de détermination R2=0.907899,
soit 90,79%. Il est ajusté à 0.901759, soit 90,18% exprimé
par son R2 ajusté. Cela signifie que 90,07%
des recettes fiscales sont expliquées par l'augmentation des indices
prix à la consommation.
Pour déterminer si le modèle est globalement
significatif, nous émettons les hypothèses suivantes :
H0 : R² = 0, le modèle n'est
pas significatif.
H1 : R2 ? 0, il y a
présomption que le modèle est significatif. Le modèle est
globalement significatif.
Règle de décision : Il faut que Fcal soit
supérieur à F th pour que le modèle soit
significatif ; ou bien si la probabilité associée à
ce test est inférieure à 5%, on rejette l'hypothèse
nulle.
Le test F de Fischer donne 147.8642 (tableau n°3 en
annexe) ; et la probabilité associée à ce test est de
0,0%, inférieure à 5% ; cela veut dire que le modèle
est globalement significatif donc on rejette H0.
| 
