3.2.5.2. La dimension
fractale
La dimension fractale est une mesure de la façon dont
la fractale occupe l'espace la dimension fractale des frontières de ces
agrégats peut être calculée à partir des estimations
de périmètre et d'aire, en partant de la relation suivante :
 (14) (14)
où K est une constante appelé facteur de
graduation reliant aij à pij et Df j est la dimension fractale de la
classe j. Ce qui donne alors
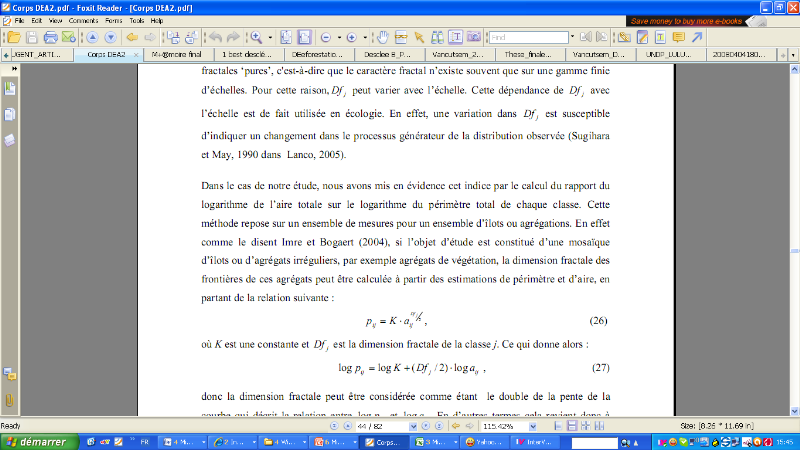
(Y = A+ B X) (15)
Donc la dimension fractale peut être
considérée comme étant le double de la pente de la courbe
qui décrit la relation entre log pij et log aij. En d'autres termes
cela revient donc à estimer périmètre et aire de chaque
tache de la classe à une échelle donnée et à
représenter ces valeurs en coordonnées logarithmiques. La pente
de la régression entre aires et périmètres correspondants
est une estimation de la moitié de Dfj. La régression devra
être significative.
La dimension fractale (notée D) est
considérée comme une mesure de complexité du paysage
(Kenkel, 1996). Cette valeur varie entre (Df1) les paysages fortement
anthropisés (D1) et les paysages tout à fait naturels,
sans impact humains notables (D2)
Df =2B Avec Df la dimension fractale, B la pente de la droite
, K le facteur de graduation k reliant A à P
3.2.5.3. Identification
des processus de transformation spatiale
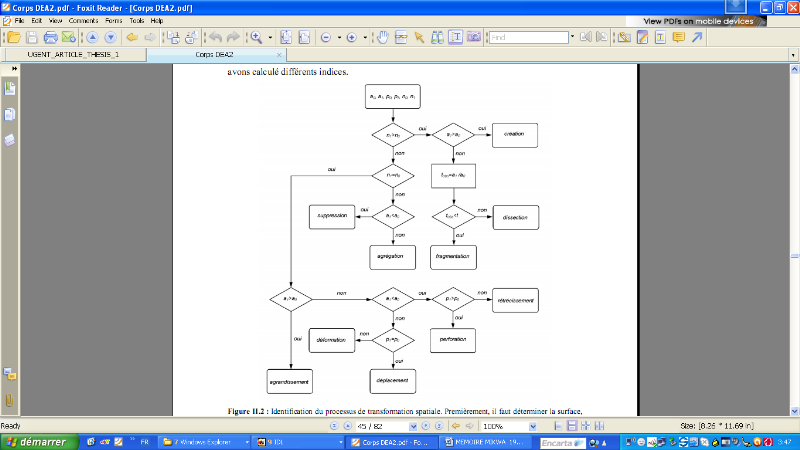
Afin d'identifier les types de changements
opérés dans chacune des classes d'occupation du sol, nous avons
utilisé l'arbre de décision présenté par (Bogaert
et al., 2002). Cet arbre permet de cerner le processus dominant de la
transformation du paysage. Les données d'entrées à
introduire dans l'arbre de décision sont les données d'aire, de
périmètre et celles qui concernent le nombre de taches
observées appartenant à la classe mise à l'étude.
Elles seront calculées avant (notées comme a0, p0 et n0 et
à l'issue (notées comme a1, p1 et n1 de la transformation.
Figure 5.1.: Identification du processus de
transformation spatiale. Premièrement, il faut déterminer la
surface, le périmètre et le nombre de taches du type
considéré avant (a0, p0 et n0) et après (a1, p1 et n1) la
transformation. Deuxièmement, le changement de chacune des trois
caractéristiques est utilisé pour aboutir à un processus
représentatif de la dynamique observée. Selon le modèle,
il faut d'abord analyser l'évolution du nombre de taches (comparaison de
n0 avec n1). Par suite, le changement de la surface (comparaison de a0 avec a1)
du type considéré mènera directement vers un des
processus, ou indirectement via l'évolution du périmètre
(comparaison de p0 avec p1). Afin de faire une distinction entre
fragmentation et dissection, une valeur prédéfinie de diminution
d'aire (t) est utilisée (Bogaert et al., 2008)
| 


