Approximation et simulation des signaux sur Matlab

TP2: Analyse des systèmes linéaires au spectre des fréquences
(représentation de BODE et de nYQYUIST d'une fonction de
transfert)

Soit la fonction de transfert suivante: H(s) = z(s) / n(s) = (s²-2s+3) / (s³+3s²+1) En langage MATLAB son écriture sera : H(s) = z(s) / n(S) = (s. A2-2^*s+3)/ (s. A3+3^*s. A2+1)

2.1 Code du vecteur z sous forme z = Ia3 a2 a1 a0] et également celui de n

z= 10	1	-2	3];
n= 11	3	0	1];

2.2 Verifier que le code : Printsys (z, n) affiche la fonction de transfert H sur l'ecran

Code :

z= [0	1	12	3];
n= [1	3	0	1];

printsys (z, n)

Le resultat est le suivant:

num/den = (SA2 - 2 s + 3)/(SA3 + 3 sA2 + 1)

2.3 Calcul du gain statique H (0)

Code :

z=[0	1	12	3];
n=[1	3	0	1];

dcgain (z, n) solution:

ans =

3

2.4 Représentation graphique des pôles et des zéros de H :

Code :

z= 10	1	-2	3];
n= (1	3	0	1];

pzmap (z, n)

Graphe :

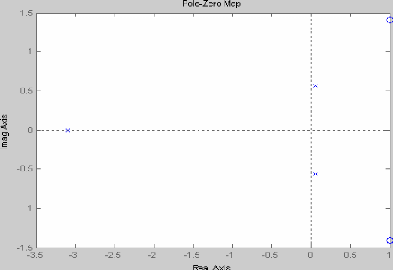
2.5 Representation graphic:ue de la reponse impulsionnelle

Code :

z=10	1	-2	3];
n=11	3	0	1];

Impulse(z,n)

Graphe :

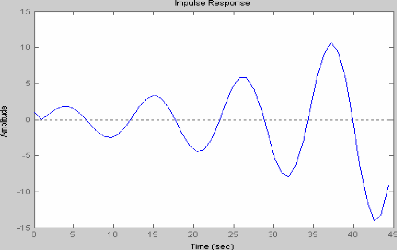
Representation graphic:ue de la reponse a la fonction de
Heaviside du systeme

code :

z= [0	1	-2	3];
n= [1	3	0	1];

Step (z. n)

Graphe :

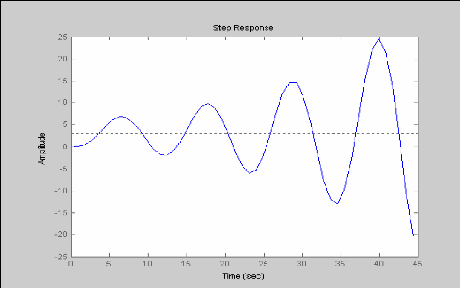
2.7 Representation graphic:ue du diagramme de Bode code:

z= [0	1	-2	3];
n= [1	3	0	1];

bode (z, n)

graphe:

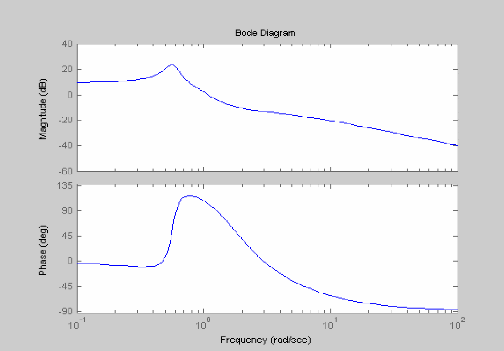
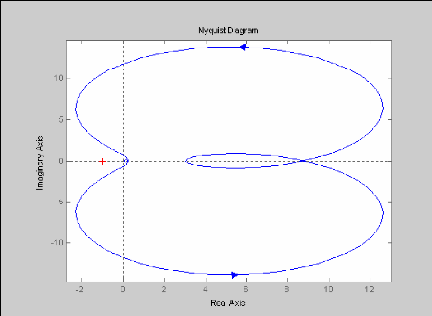
eoresentation qraohique de la courbe d'espace de nyquist

code:

z= [0	1	-2	3];
n= [1	3	0	1];

nyquist (z, n) graphe: