Effets des dispositifs d'amortissement sur les déplacements, vitesses et accélérations des structures

Chapitre III : Formulation du problème

d'amortissement et méthode de

dimensionnement des amortisseurs

Formulation du problème d'amortissement et méthode de
dimensionnement des amortisseurs

III. 1. Introduction

L'équation du mouvement dynamique est fondée sur trois composantes principales qui caractérisent une construction et sa structure : la masse mise en mouvement, la rigidité des éléments structuraux et les différents systèmes d'amortissement.

Ces composantes sont reliées respectivement aux grandeurs du mouvement : le déplacement, la vitesse et l'accélération.

Notre travail porte sur l'impact de l'addition de nouvel appareil d'amortissement sur le mouvement.

Nous allons ainsi procéder dans ce chapitre à la formulation de l'équation de mouvement avec intégration des amortisseurs, ensuite au dimensionnement des amortisseurs ;

III.2. Caractéristiques des amortisseurs visqueux

Ces dispositifs sont assimilables à un vérin hydraulique à doubles effets et à forte capacité de dissipation d'énergie. Ils comportent couramment deux chambres remplies d'un fluide (huile hydraulique ou pâte silicone). Celles-ci sont reliées l'une à l'autre par des soupapes calibrées de façon à permettre des déplacements lents et une dissipation d'énergie générée par frottement visqueux du fluide sous l'effet du mouvement sismique (rapide).

La relation entre la force d'amortissement et la vitesse relative V peut s'écrire comme suit [6]:

F = C V^á (III-3)

V : la vitesse du piston (soupape),

C et á : sont des paramètres qui dépendent de la loi de comportement du fluide.

Tableau III.1 : différents types d'amortisseurs selon les différentes valeurs de l'exposant á [6].

Type d'amortisseur	Valeur de á	Force d'amortissement	Remarques
Amortisseur linéaire	á =1	F = C V	Amortisseur hydraulique classique
Amortisseur non linéaire	á =0	F = C	Amortisseur idéal à frottement sec
Amortisseur non linéaire	á ? 0, 1	F = C V^á	Amortisseur visqueux intermédiaire

En général la valeur de l'exposant á varie entre 0.1 et 1.8 [6].

Les figures suivantes, montrent la loi de comportement des différents types d'amortisseurs soumis à une excitation sinusoïdale.

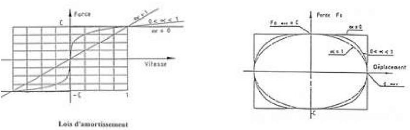
Figure III.1 : lois de comportements de différents types d'amortisseurs

Remarque

L'amortisseur liquide assure seulement l'amortissement dans sa direction axiale.

III.3. Formulation de l'équation du mouvement avec des amortisseurs

Le problème posé par les déplacements excessifs peut être résolu par l'augmentation de l'amortissement

En général l'équation d'équilibre dynamique de n'importe quel modèle est sous la forme suivante:

F_m + F_c + Fk= P(t) (III-1)

F_m : Force d'inertie.

F_c : Force d'amortissement due à la structure.

F_m : Force de rigidité.

P(t) : Charge dynamique (variable en fonction du temps).

On peut donc écrire l'équation comme suit :

& & &

M U + CU + KU = P( t ) (III-2)

M : matrice de la masse de la structure,

C : matrice d'amortissement,

K : matrice de rigidité,

U&& ,U^& etU sont respectivement l'accélération, la vitesse et les déplacements du système.

La force d'amortissement due à un amortisseur est donnée par l'expression suivante [11] :

F = C Vá

Pour un système où l'on utilise des amortisseurs l'équation de mouvement devient :

F_m + F_c +F_c' +Fk= P(t) (III-4)
F'c : force d'amortissement due à l'amortisseur ajouté au système, d'où l'équation de mouvement devient [11] :

.. .

M U + C_s U+C_aV^á + K U = P t (III-5)

( )

Lors de mouvement de système, la vitesse du piston V est égale à la vitesse de mouvement du

.

système, donc U = V

D'où l'équation devient [11] :

M U & & + C _s U & + CaU & á + KU = P(t) (III-6)

Et pour une excitation sismique l'équation s'écrit [11]:

& & &

M U s U C _a U

+ C + ^á + K = -

U MU_g (III-7)

& & &

U& & g : Accélération sismique du sol

On remarque bien que si á est égal à l'unité l'équation devient linéaire comme suit [11]:

& & & & &

M U + ( C _s +C_a)U +KU=MU_g (III-8)

La résolution de cette équation devient classique comme elle a été introduite dans le chapitre IV par la méthode de Newmark ou par d'autres méthodes [11].

Si a ? 1 l'équation du mouvement précédente reste non linéaire et parmi les nombreuses méthodes d'intégration directe pour résoudre cette équation, la méthode d'intégration de Newmark semble être la plus efficace avec de très petites erreurs numériques. Dans la méthode de Newmark, on supose que l'accélération est linéaire pendant le temps à t + Ä t . Pour l'intervalle de temps Ät, les relations sont [11]:

. . .. ..

Ut +Ä t = Ut + - â + â +Ä Ä [(1 ) U t U t t t ]

(III-9)

. .. ..

U t +Ä t = U_t +U_t Ät + [( ₂ -á )U t+áUt+Ät]Ät

2 (III-10)

á et â sont les paramètres employés pour obtenir l'exactitude et la stabilité d'intégration. Dans le cas oil 4

á = et 2

¹ â = , la méthode d'accélération moyenne constante rapportera la

1

stabilité sans conditions dans le procédé d'itération.

. ..

Les équations précédentes, Ut _+Ät et Ut _+Ät peuvent être résolues en termes de Ut + Ä t comme

suit [11]: .

. ..

..

U t + Ä t t + Ä t (1 - â )U t+âÄtUt +Ät

&&

( U t+Ä t - U_t -U_t- - 1U t

1 1

1

&&

áÄ

t áÄt

₂

á

(III-11)

(III-12)

Pour obtenir le déplacement, la vitesse et l'accélération au temps t + Ä t , l'équation d'équilibre est écrite comme [11]:

M U & & C s U & C K ( g ) t t t t t t a t t U + & á + + U = - M & U & + Ä + Ä + Ä t t + Ä +Ä

.

(III-13)

C & : Terme de la non linéairité.

á

aUt +Ä t

Pour éviter d'employer la technique d'itération pour détérminer le vecteur de déplacement à

á

chaque étape, le terme non linéaire Ut +Ä t est développé par une série de Taylor comme montré dans l'équation suivante: [11]

& á t +Ä t = U _t^á+r · diag

( ¹ )(

á

U & - U & - U & )

t t t

+ Ä t

U

(III-14)

On suppose que les limites d'ordre supérieur peuvent être négligées sans perte d'exactitude

diag : Opérateur de diagonalisation d'un vecteur à une matrice. Les étapes de résolution sont comme suit [11] :

~ ~

~	..
P M U g t t Ma M C s a C C a C + + t t + Ä = - ( ) + Ä + a a s		(III-17)

K Ut +Ä t = Pt+Ät

.

~ 1 â r â

K K

= + + + C _a diag U t á

M C m (

t 2

á Ä á Ä t á Ä t

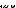
(III-15)
(III-16)

)

-1

1 t 2 U t +áÄt Ut+( _2á 1) U_t

1 . 1

â

U_t + ( á 2á-1)U _t + Ä t( -1) U_t

& .. .

..

â U

t - U t á + râ diag( Ut ^á- )W_t + â Ä t( 1 - 1) U t - rÄ t(1 - â ) diag( Uá t )U t

2á

·
·

a Cd

á Ä

â â

..

áÄt

. .

áÄ t

·

=

a_M

=

aC_s

(III-18)

(III-19)
(III-20)

La vitesse U

t+ Ät et l'accélération U t+ Ät peuvent être obtenues à partir des équations III-11 et

4-12 [11].

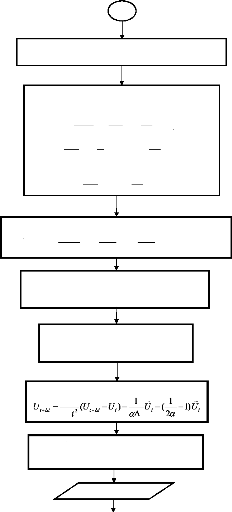
Nous présentons sous forme d'organigramme le cheminement des étapes de déterminations des grandeurs déplacements, vitesses et accélérations.

1

n

ö

ö j n

ö n n

Détermination de la matrice modale Ö

1 j n

ö ö ö

1 1 1

? ? ? ? ? ? ? ??

j n

ö ö

j j

Ö

1

ö

j

Détermination de la matrice d'amortissement diagonale

C m

=

ci

c j

? ? ? ? ? ? cn ?

1

ORGANEGRAMME DE DETERMINATION DES DEPLACEMENTS,
VITESSES ET ACCELERATIONS

Début

Lecture des données

Matrices de masse et de rigidité

Détermination des pulsations propre du système
det(K-ù²M)=0

Détermination des modes propres du système (K- ù j²M)Ö^j=0

Chapitre III Formulation du problème d'amortissement et méthode de dimensionnement des amortisseurs

	FIN

Détermination de la matrice d'amortissement modale
C_s=(MÖ[Ö^TMÖ]^-1)Cm ([Ö^TMÖ]^-1 Ö^TM)

Calcul de la rigidité effective Keff

1 â r â .

Keff = K+ ( )

r -

+ 1

M C + C _d diag U

P t + Ä t = - M(Ug) t +Ä t Ma_M + C sa _C +C aa C

s

&& 1

1_- t + Ä t = ₂ ( U t+Ä t U _t) - 1 U t 2á 1) U t

~

Détermination du déplacement Ut+Ät

acs=

U t + Ä t = U _t +Ä t (1 -â )U _t +âÄ tUt+Ät

Calcul de la charge effective Peff

aM=

Détermination de l'accélération

áÄ

. .

â

U_t + ( -1) U_t + Ä t( -1) U t

áÄ t á 2á

Détermination des coefficients

. t 2 m

á Ä á . Ä t á . Ä t t

Détermination de la vitesse

acd=

â â

áÄ t

1

áÄ

..

r

^âu_t - u t+

.

1 1

U _t + U _t + ( - 1)

2 áÄt 2á

K Ut + Ät = Pt+Ät

~ ~

t

Résultats

1

.

râ

..

..

á

táÄ_t&

diag(u

.

U_t

..

..

a