b) Test de Duckey et Fuller Augmenté
Dans le modèle de Duckey-Fuller simple, le processus
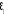 est par hypothèse bruit blanc c'est-à-dire un processus
de moyenne nulle et de variance constante non auto-corrélé. Or,
il n'ya aucune raison pour que, à priori, l'erreur soit non
corrélée. est par hypothèse bruit blanc c'est-à-dire un processus
de moyenne nulle et de variance constante non auto-corrélé. Or,
il n'ya aucune raison pour que, à priori, l'erreur soit non
corrélée.
Ce test est appelé ADF (1981) et va prendre en compte
cette hypothèse alternative | è |=1. Les tests sont fondés
sur l'estimation par les moindres carrées ordinaires des trois
modèles qui suivent :
o quatrième modèle : 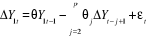
o cinquième modèle : 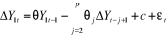
o sixième modèle : 
Avec 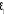 ?iid (indépendant et identiquement distribué) ?iid (indépendant et identiquement distribué)
Ce test se déroule de manière similaire aux
tests de Dickey-Fuller simple, seules les statistiques sont différentes.
La valeur de è peut être déterminée selon les
critères d'Akaike et de Schwartz ou encore en partant d'une valeur
suffisamment importante de p ; on estime un modèle à p-1
retards jusqu'à ce que le coefficient de pième retards
soit significatif.
c) Le test de Philips et Perron (1988)
Le test de Philips et Perron est un prolongement des tests de
Dickey- Fuller. Ce test est construit sur une correction non
paramétrique de statistique de Dickey- Fuller pour prendre en compte des
erreurs hétéroscédastiques. Il s'agit d'un prolongement
des tests de Dickey et Fuller.
D'une façon simple ce test est plus souvent
préconisé pour résoudre les problèmes liés
à un non respect des hypothèses habituelles faites sur les
perturbations (absence d'auto corrélation, etc.). Philips et Perron
proposent une correction non paramétrique de deux statistiques de
Dickey-Fuller.
Il se déroule de la manière suivante en deux
étapes :
1) estimations par les moindres carrés ordinaires de
trois modèles de Dickey et Fuller et calculs des statistiques
associées ;
2) estimation d'un facteur correctif établi à
partir de la structure «j» covariance des erreurs des modèles
précédemment estimés de telle sorte que les
transformations réalisées conduisent à des distributions
identiques à celles de Dickey et Fuller standard. Cela nous conduit
à celles de Dickey-Fuller.
De ce fait, la formulation des hypothèses en ce qui
concerne la stationnarité et la fixation des critères de rejet
est effectuée de la même façon que pour le test de Dickey
et Fuller et conduit sur un modèle avec constance et trend. Tous ces
tests permettent de vérifier la stationnarité des séries.
D'où, la règle de décision est la
suivante :
o si la valeur calculée d'ADF test ou de PP test est
inférieure à la valeur critique (vc), la série sous
étude est dite stationnaire en niveau et est notée I(0).
o si par contre la valeur calculée d'ADF test ou de PP
test est supérieure à la valeur critique (vc), la série
étudiée est non stationnaire ou encore elle est
intégrée d'un ordre supérieur ou égal à
un.
De façon formalisée, la régression
à estimer est la suivante :
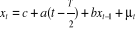 Avec T : nombre d'observations Avec T : nombre d'observations
Z est la statistique de PHILIPS et PERRON et se
calcule de la façon suivante :
Z = t (s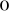 /s /s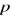 )-(s )-(s -s -s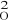 ) T ) T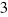 /4s /4s (3Dx)1/2 (3Dx)1/2
Avec T = valeur de la statistique de Student pour
b=1
s = racine résiduelle de la régression = racine résiduelle de la régression
Dx = déterminant de la matrice
 où où 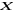 est la matrice des variables est la matrice des variables
explicatives du modèle
s = ( = (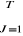 û û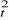 +2 +2 w w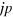  û û û û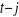 ) / T ) / T
w = (1-j) / (p+1) et û sont les résidus estimés de
la régression. = (1-j) / (p+1) et û sont les résidus estimés de
la régression.
Ce test se ramène donc au test de Dickey- Fuller simple
dans le cas où les erreurs seraient homoscédastiques. Sa mise en
oeuvre est identique à celle du test de Dickey-Fuller du fait qu'il suit
la même procédure séquentielle descendante. Il est, en
définitive, à une autocorrélation et à une
hétéroscédasticité de forme inconnue qui est aussi
une recommandation pour vérifier s'il y a une relation entre les
variables dans le long terme (ces variables sont non stationnaires en niveau et
intégrées d'ordre un).
| 


