III.3.
Définition et propriétés de la stationnarité ou
test de racine unitaire
Plusieurs étapes préliminaires sont
nécessaires et sont disponibles à un théoricien pour
mieux réaliser et effectuer tout test spécifique sur une
série chronologique ou temporelle et pour enfin chercher à la
modéliser. Il est opportun d'analyser la stationnarité ou la
présence de la racine unitaire dans cette série.
III.3.1. Définition
Selon R. BOURBONNAIS (2000) : «Avant tout traitement
d'une série chronologique, il convient de s'assurer de la
stationnarité des variables étudiées autrement dit,
étudier les caractéristiques stochastiques. Si ces
caractéristiques c'est-à-dire son espérance et sa
variance se trouvent modifiées dans le temps, la série
chronologique est considérée comme non stationnaire ; dans
le cas contraire d'un processus stochastique invariant, la série
chronologique (temporelle) est alors stationnaire.»
Il existe deux types de processus non stationnaires : les
processus TS (Trend Stationary Processes) qui présentent une
non-stationnarité de type déterministe et les processus DS
(Difference Stationary Processes) pour lesquels la stationnarité est de
type aléatoire.
III.3.2.Test de présence de
racine unitaire
Ces tests de racine unitaire ont comme finalité
préliminaire de vérifier la stationnarité des
séries. Une série chronologique est stationnaire lorsque ses
caractéristiques, c'est-à-dire son espérance
mathématique (ou sa moyenne) et sa variance sont invariables dans le
temps. Dans le cas d'un processus stochastique invariant, la série
temporelle est alors stationnaire. (Bourbonnais R. ; 1998)
Pour approfondir le cadre théorique des tests de racine
unitaire, faisons un bref aperçu sur le test de Duckey et Fuller, Duckey
et Fuller Augmenté ainsi que le test de Phillips et Perron.
a) Test de Duckey et Fuller simple
Initialement, Duckey et Fuller (1979) considèrent trois
modèles de base pour une série Y1t, avec t=1,.....,
T ; ces trois spécifications des modèles de base se
présentent de la manière suivante :
· Premier modèle : modèle
autorégressif avec constance ou modèle avec constance sans
tendance déterministe. (1-èL)(Y1t -ì)
= 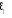 . .
· deuxième modèle : modèle
autorégressif avec tendance c'est-à-dire modèle avec
constance et tendance déterministe. (1-èL)(Y1t
-á- ât) = 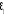 . .
· troisième modèle : modèle
autorégressif d'ordre un, autrement dit modèle sans constance ni
tendance. (1-èL)Y1t = 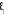 . .
Dans chacune des trois modèles, on suppose que 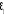 ?iid (c'est-à-dire, un processus de moyenne nulle, de
variance constante et non autocorrélé), en d'autres termes le
Bruit Blanc. ?iid (c'est-à-dire, un processus de moyenne nulle, de
variance constante et non autocorrélé), en d'autres termes le
Bruit Blanc.
Le principe des tests est le suivant : si dans l'une des
trois modèles è=1, cela signifie qu'une des racines du
polynôme opérateur est égal à un.
En d'autres termes, Y1t est un processus non
stationnaire et la non stationnarité est de la nature stochastique. Le
choix de la spécification dépend des données
traitées.
Pour tester l'hypothèse nulle (H0) de la
racine unitaire (Y1t est intégré d'ordre un,
c'est-à-dire non stationnaire) contre l'hypothèse alternative
(HA) d'absence de racine unitaire (Y1t est
intégré d'ordre zéro : I(0) c'est-à-dire
stationnaire).
D'une manière plus concrète et plus
précise, les hypothèses nulles et alternatives des trois
modèles spécifiques considérés s'écrivent
comme suit :
· premier modèle : H0 :
è=1? Y1t = Y1t-1 + 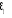
HA : | è |<1 ?
Y1t = èY1t-1 + 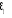
· deuxième modèle :
H0 : è=1? Y1t = Y1t-1 +
 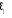
HA : | è |<1 ?
Y1t = èY1t-1 + 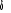 + +  avec avec 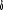 = ì (1- è) = ì (1- è)
· troisième modèle :
H0 : è=1? Y1t = Y1t-1 +
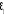
HA : | è |<1 ?
Y1t = èY1t-1 +ë +  + + 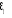 avec ë= á (1- è) +áâ et avec ë= á (1- è) +áâ et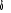 = â (1- è) = â (1- è)
Alors, on en déduit ce qui suit:
· si | è |<1, la série Y1t
est stationnaire ; les observations présentes ont un poids plus
important que les observations passées ;
· si | è |=1, la série Y1t n'est
pas stationnaire, sa variance augmente de façon exponentielle avec t, on
parle de processus explosif. Les observations passées ont une
considération plus élevée que les observations
présentes ;
· si | è |>1, Y1t n'est pas
stationnaire, sa variance augmente de façon exponentielle avec le temps.
On parle également de processus explosif ; les observations
passées ont une pondération considérable et plus
élevée que les observations présentes.
| 


