Simulation de modèles de diffusion appliqués aux taux d'intérêts

Simulation de Modèles de Diffusion

Appliqués aux Taux d'Intérêts

BOUATTA Mohamed Adel

Département de Probabilités & Statistiques
Faculté de Mathématiques,
Université des Sciences et de la Technologie Houari Boumediene,
U. S. T. H. B.
Mémoire présenté dans le cadre de l'obtention du diplôme de
MASTER en MATHEMATIQUES FINANCIERES.

Promotion: 2011/2012

Table des matières

Introduction générale 1 Introduction					1 1
	1.1		Problématique		1
	1.2		Les marchés financiers		1
	1.3		Le marché obligataire		2
	1.4		Définition d'un bon du trésor		3
2	Rappels de probabilité				4
	2.1		a--Algèbre		4
	2.2		Espérance conditionnelle par rapport a une a--algèbre		5
	2.3		Théorème central limite		5
	2.4		Filtration		6
	2.5		Processus stochastique		6
	2.6		Martingale		8
	2.7		Temps d'arrêt		9
3	Les processus de diffusion				10
	3.1		Le mouvement brownien		10
			3.1.1 Définition du mouvement brownien		11
			3.1.2 Propriétés du mouvement brownien		12
TABLE DES MATIERES 3.1.3 Simulation du mouvement brownien 3.2 Mouvement brownien multidimensionnel 3.3 Mouvement brownien avec dérive 3.4 Mouvement brownien géométrique 3.5 Calcul stochastique						ii 13 14 15 16 17
				3.5.1 Intégrale stochastique d'Itô		17
				3.5.2 Processus d'Itô		19
				3.5.3 Lemme d'Itô		20
				3.5.4 Equations différentielles stochastiques		20
		3.6		Les processus de diffusion		22
				3.6.1 Méthodes de simulation des processus de diffusion		24
4		Simulation des processus de diffusion				26
		4.1		Présentation des données		26
		4.2		Modèle de Vasicek (processus d'Ornstein-Uhlenbeck)		26
				4.2.1 Mesure objective (Monde réel)		27
				4.2.2 Estimation des paramètres du modèle de Vasicek		27
				4.2.3 Simulation du modèle de Vasicek		28
				4.2.4 Simulation de la solution exacte du modèle de Vasicek		29
				4.2.5 Calcul du prix du bon dans le modèle de Vasicek		29
		4.3		Modèle de Cox, Ingersoll & Ross (CIR)		30
				4.3.1 Estimation des paramètres du modèle de Cox, Ingersoll & Ross . . .		30
				4.3.2 Simulation du modèle de Cox, Ingersoll et Ross		31
				4.3.3 Simulation de la solution exacte du modèle CIR		32
				4.3.4 calcul du prix du bon dans le modèle CIR		33
		4.4		Modèle de Vasicek a 2 facteurs		33

4.4.1 Estimation des paramètres du modèle de Vasicek a 2 facteurs 34

4.4.2 Simulation du modèle de Vasicek a deux facteurs 35

4.4.3 Simulation de la solution exacte du modèle de Vasicek a 2 facteurs . 36

4.4.4 calcul du prix du bon pour le modèle de Vasicek 2f 36

4.5 Simulation du processus d'Ornstein-Uhlenbeck exponentiel 37

4.6 Simulation du modèle d'Eraker de volatilité stochastique 38

4.7 Simulation du modèle de Heston de volatilité stochastique 40

5 Conclusion générale 43

6 Annexes 44

6.1 Annexe I : Programmes en R 44

6.1.1 Code R pour simulation d'un mouvement brownien standard 44

6.1.2 Code R pour simulation de 30 trajectoires d'un mouvement brownien 44

6.1.3 Code R pour covariance empirique du mouvement brownien 45

6.1.4 Code R pour simulation d'une marche aléatoire 45

6.1.5 Code R pour simulation d'un mouvement brownien de dimension 2 45

6.1.6 Code R pour simulation d'un mouvement brownien de dimension 3 46

6.1.7 Code R pour simulation d'un mouvement brownien avec dérive. . . 47

6.1.8 Code R pour simulation de 30 trajectoires d'un brownien avec dérive 47
6.1.9 Code R pour simulation d'un mouvement brownien géométrique . . . 48

6.1.10 Code R pour estimation des paramètres du modèle Vasicek 49

6.1.11 Code R pour simulation du modèle de Vasicek 49

6.1.12 Code R pour simulation de la solution du modèle de Vasicek 50

6.1.13 Code R pour le calcul du prix du bon dans le modèle de Vasicek . . 51

6.1.14 Code R pour estimation des paramètres du modèle CIR 51

6.1.15 Code R pour simulation du modèle de Cox, Ingersoll & Ross 52

6.1.16 Code R pour simulation de la solution exacte du modèle CIR 53

6.1.17 Code R pour le calcul du prix du bon dans le modèle CIR 53

6.1.18 Code R pour estimation des paramètres du modèle de Vasicek 2f . . 54

6.1.19 Code R pour simulation du modèle de Vasicek a 2 facteurs 55

6.1.20 Code R pour simulation de la solution exacte du Vasicek 2f 56

6.1.21 Code R pour le calcul du prix du bon dans Vasicek 2f 58

6.1.22 Code R pour simulation d'un processus d'O-U exponentiel 59

6.1.23 Code R pour simulation du modèle d'Eraker de volatilité stochastique 59
6.1.24 Code R pour simulation du modèle de Heston de volatilité stochastique 60

6.2 Annexe II : Les données 62

6.2.1 Daily Treasury Bill Rates Data 62

Chapitre 1

Introduction

1.1 Problématique

Nous allons, tout au long de ce mémoire, proposer des algorithmes de simulation de modèles de diffusion appliqués aux taux d'intérêts et proposer leurs codes de simulation en logiciel R. Certains produits financiers sont liés aux taux d'intérêts tels que le prix d'une obligation ou celui d'un bon du trésor.

Les modèles que nous allons présenter dans ce mémoire sont le modèle de Vasicek, le modèle de Cox, Ingersoll & Ross ainsi que le modèle de Vasicek a 2 facteurs, ces modèles sont caractérisés par un effet de retour vers la moyenne comme les taux d'intérêts observés sur les marchés financiers.

Une applications sur les bons du trésor des Etats-Unis d'Amérique avec estimation des paramètres de ces modèles sera faite en utilisant des données historiques, ces données sont journalières et s'étalent sur la période allant du 03/01/2012 au 02/10/2012. Nous proposerons au lecteur des formules pour le calcul du prix des bons du trésor.

1.2 Les marchés financiers

Les marchés financiers sont un lieu géograhique ou virtuel on différnets types d'acteurs s'échangent des capitaux au comptant ou a terme.

Ce sont également les marchés on sont effectuées les transactions sur des actifs financiers et, de plus en plus, leurs produits dérivés.

Il s'agit, par ordre de volumes négociés décroissants :

- du marché des taux d'intérêt, c'est-à-dire du marché de la dette, qu'il est d'usage de séparer en :

1. marché monétaire pour les dettes à court terme (moins d'un, deux ou même parfois trois ans à son émission);

2. marché obligataire pour les dettes originellement à moyen ou long terme;

- marché des changes, ou FOREX, on l'on échange des devises les unes contre les autres; - marché des actions, c'est-à-dire des titres de propriété des entreprises;

- marché des métaux précieux (or et argent).

1.3 Le marché obligataire

Le marché obligataire est le marché sur lequel les entreprises ainsi que les états se financent, les produits traités sont les obligations, lorsqu'un état ou entreprise souhaite s'endetter, elle émet une obligation. Dés lors, un créancier prêtera la liquidité nécessaire à l'agent économique contre un taux d'intérêt. Ce taux d'intérêt sera le reflet du risque. Plus le risque est élevé, plus le taux d'intérêt le sera.

Une obligation zéro-coupon est une obligation qui ne donne pas droit à détachement de coupon, d'oñ le terme. L'acquéreur souscrit l'obligation à un prix inférieur à sa valeur faciale, laquelle est payée à l'échéance du contrat. Le zéro-coupon est généralement indexé

sur l'inflation. C'est une forme très utilisée par les emprunts d'Etat notamment ceux des Etats-Unis, les T-bills.

Parmi les obligations, seules les zéro-coupon permettent d'éliminer réellement tout risque de taux entre deux dates. Une obligation à taux fixe classique génère en fait autant de risques de taux supplémentaires qu'elle est dotée de flux financiers intermédiaires, le taux de réinvestissement de chacun des coupons entre sa date de paiement et la date de remboursement final est, en fait, inconnu, même s'il est implicite dans le prix de l'obligation.

- l'expression marché primaire designe les émissions de nouvelles obligations, dont le placement auprès des investisseurs institutionnels, et éventuellement particuliers, est assuré, généralement en prise ferme par un groupe de banques d'investissement choisies par l'emetteur.

- l'expression marché secondaire designe les transactions sur les obligations déjà émises.

1.4 Définition d'un bon du trésor

Un bon du Trésor est un titre de créance représentatif d'un emprunt dont l'émetteur est un Etat, comme les obligations, elles représentent un titre de créance détenue par le prêteur sur l'emprunteur, plusieurs sortes de bons du Trésor coexistent, ils procurent une rémunération à leur détenteur suivant certaines caractéristiques.

Le fait de détenir un bon du Trésor rend alors son propriétaire (investisseur-épargnant) créancier de l'Etat, de son côté, l'Etat s'engage à le rembourser à une échéance déterminée et à verser un intérêt à son porteur.

En Bourse, les bons du Trésor sont négociables sur le marché monétaire. Ils font partie de la catégorie des Titres de créances négociables (TCN).

Les obligations émisent par l'état, que l'on appelle aussi OAT ou obligation assimilable au trésor, sont le support de l'endettement à long terme de l'état. La maturité de ces titres est comprise entre sept et cinquante ans.

Chapitre 2

Rappels de probabilité

2.1 cr--Algêbre

Une tribu ou o--algebre sur un ensemble , est un ensemble non vide de partie de ~, stable par passage au complémentaire et par union dénombrable (donc aussi par intersection dénombrable).

Définition 1 a--algêbre ou tribu

Soit un ensemble non vide. une collection A de sous ensemble de est appelé a--algébre si elle satisfait les propriétés suivantes :

i1)A =6 ø
i2)ø 2 A

i3)VA 2 A = A 2 A

i4)siVm 2 N, A C A alors U A C A

La o---algebre engendrée par les ouverts de , notée BR, est appelée tribu des boréliens de R.

Définition 2 Mesurabilité par rapport a une a--algêbre

Soit X une variable aléatoire de et A une a--algêbre d'événements de 1. Alors X est

A--mesurable si

{X 2 B} 2 A,VB 2 BR

2.2 Espérance conditionnelle par rapport a une cr--algèbre

Théorème 3 Théorême de Radon-Nikodym

Soit (~, A) un espace mesurable, une mesure a--finie et u une mesure tq u << (u

dominée par ) i.e : si A 2 A (A) = 0 = u(A) = 0

Alors il existe f une fonction mesurable essentiellement unique tq

_J

u(A) = fd

A

On note f = d

d

essentiellement unique veut dire si il existe h mesurable telle qu'elle vérifie aussi le théorême alors

{w,h(w) =6 f(w)} = 0

Théorème 4 Soit (~, A, IP) un espace probabilisé et X une variable aléatoire sur (~, A, IP). Si E(X) existe et C A une sous a--algébre. Alors il existe une variable aléatoire essentiellement unique qu'on note E(X/ ) définie sur (~, ) telle que VA 2

_{J J}

XdIP = E(X/ )dTP

A A

Remarque 5 E(X/ ) est --mesurable.

2.3 Théorème central limite

Théorème 6 Théorême central limite

Soit S = X1 + X2 + ... + X la somme de ii variables aléatoires indépendantes ayant la même densité d'espérance et de variance a2

Soit S , = Sn~Pm

pn~ : alors, pour tout a < b :

uim

fl-400

J b

1 _e--x²

TP(a < S n < b) = ,,2 2 dx

a

En d'autres termes, on a

uim

fl-400

Fs _n(t) = 0,1(t)

(on parle alors de "convergence en loi")

Ce théorème indique que si S est la somme de ii variables aléatoires mutuellements indépendantes et identiquement distribuées, alors la distribution de S peut être correctement approximée par la densité normale (et ce quelque soit la distribution initiale!), l'approximation est d'autant plus précise que ii est grand.

Ce théorème et ses généralisations offrent une explication a l'omniprésence de la loi normale dans la nature, de nombreux phénomènes sont dus a l'addition d'un grand nombre de petites pérturbations aléatoires.

(voir [3])

2.4 Filtration

Definition 7 Le concept de filtration

Une filtration d'un ensemble c est une suite {Fn}n>0 de a--algêbre de plus en plus fine F0 c F1 c ... c F_n...

avec F0 = {ø, c}

La filtration F_n représente l'information accumulée jusqu'au temps ii

(voir [3])

2.5 Processus stochastique

Definition 8 Processus Stochastique

Un processus stochastique (ou processus aléatoire) represente une évolution, généralement dans le temps, d'une variable aléatoire.

Soit (c, A, P) un espace de probabilité et (A, £) un espace mesurable. On appelle processus
aléatoire a valeur dans (A, £), une famille de variables aléatoires {Xt, t ~ 0}, Xtest a valeur

dans (A, £). Pour w 2 Q fixé, la fonction de R+ dans A qui a t associe Xt (w) est appelée la trajectoire associée a la réalisation de w.

Le théorême de kolmogorov assure la continuité des processus stochastiques. Xt est un processus centré si son espérance est nulle E(Xt) = 0 et si Xt est dans L² (E1Xt1² < oo)

on définit :

La moyenne du processus

E(Xt) = I Xt(w)dP(w)

La variance

V ar(Xt) =E[IXt -- E(Xt)1²]

La fonction de covariance

F(s, t) = E(X, --E(X₈))(Xt -- E(Xt))

= E(X,Xt) -- E(X₈)E(Xt)

La continuité des trajectoires est déterminé par le théorême de Kolmogorov

(voir [18])

Theoreme 9 Théorême de Komogorov

Soit (Xi) un processus stochastique tel que pour tout t, t+h dans [a, b], il existe des constantes p > 0, c > 0, r > 0 vérifiant

E[1Xt+h -- XtI^P] < c 1h1^1+r

alors presque toutes les trajectoires sont continues

(voir [13])

Definition 10 Processus stochastique adapté

Un processus stochastique X = (X_n)_n>0 est adapté a la filtration (T_n)_n>0 si X_n est .F_n--mesurable

Vn 2 N

Un processus adapte signifie qu'une interpretation probabiliste de ce processus est realisable.

Definition 11 Processus stochastique prévisible

On dit qu'un processus stochastique X = (Xn)n>0 est prévisible conditionnellement a la fil-

tration _(Fn)n>0 si X est F_n_i--mesurable Vm 2 N

(voir [13])

2.6 Martingale

Une martingale est une stratégie de jeu, basée sur des calculs de probabilité, qui cherche a optimiser les chances de gain.On les appelle aussi "montantes", il en existe différentes formes mais leur principe est commun. il consiste a rattraper des pertes antérieures en augmentant la mise, voir ensuite a degager des bénéfices.

Le théorie des martingales a eu de grandes répercussion dans de nombreux champs d'application, en probabilité, mais aussi pour la résolution numérique des équations aux dérivées partielles (EDP), en assurance (théorie de la ruine) et en finance.

Definition 12 Martingale

Un processus stochastique X = (Xn)n>0 est une martingale par rapport a une filtration

(FTh)fl~O (on dit aussi F--martingale) si X est adapté a F et

E(Xk+1=Fk) = Xk

Ainsi, a F donnée, la valeur espérée de _Xk+1 est simplement Xk, une martingale modélise donc des "jeux justes".

Definition 13 Sous-martingale

Une suite de variables aléatoires X1, X2, ..., X_n est dite sous martingale (respectivement surmartingale) par rapport a une filtration _(Fn)n>0 si

i1)X est intégrable Vm 2 N

i2)X adapté a F

i3)E(Xn+1/Fn) ~ X, p.s Vm 2 N (respectivement _E(Xn+1/Fn) Xn)

(voir [17],[2])

2.7 Temps d'arrêt

Dans un jeu de hasard (la roulette par exemple), un temps d'arrêt est un temps lors duquel un joueur décide d'arrêter de jouer, selon un critère ne dépendant que du passé et du présent. Les temps d'arrêts ont donc deux propriétés importants : ils sont aléatoires, puisqu'ils dépendent du déroulement antérieur du jeu, et il ne peuvent pas dépendre du futur, puisque le joueur doit a tout moment pouvoir décider s'il arrête ou non (par exemple quitter la bourse aprés une chute des cours).

On note le temps d'arrêt par T (ou r ), T peut être fixé en avance si on décide d'arrêter aprés un nombre m de parties, mais en général T dépend du déroulement passé

Definition 14 temps d'arrêt

Une variable aléatoire T a valeur dans N U {oc} est dite temps d'arrêt par rapport a la filtration _(Fm)m~0 si Vm 2 N

{T = m} 2 F_m

ou bien, de maniêre équivalente si

{T < m} 2 F_m

La définition d'un temps d'arrêt traduit le choix de l'instant aléatoire T(w) et dépend seulement du passé (au sens large incluant le present)

Chapitre 3

Les processus de diffusion

3.1 Le mouvement brownien

Le botaniste Robert Brown a observé en 1828 le mouvement irregulier de particules de pollen en suspension dans l'eau. En 1877 Delsaux a expliqué les changements incessant de direction de trajectiore par les chocs entre les particules de pollens et les molecules d'eau. Un mouvement de ce type est qualiflé de mouvement au hasard.

En 1900, Louis Bachelier, en vue d'étudier les cours de la bourse, a mis en évidence le caractère markovien du mouvement brownien : la position d'une particule a l'instant t + s dépend de sa position en t et ne dépend pas de sa position avant t .il convient d'insister sur le caractère précurseur de Bachelier et le fait que la théorie du mouvement brownien a été développée pour la bourse, avant de l'étre pour la physique.

En 1905, Albert Einstein a déterminé la densité de transition du mouvement brownien par l'intermédiaire de l'équation de la chaleur et relie ainsi le mouvement brownien aux équations aux dérivées partielles de types parabolique, il montra également que ce mouvement (maintenant appelé mouvement brownien) pouvait être éxpliqué par le "bombardement continuel de particule éxercé par les molécules du liquide". La même année, Smoluchowski a décrit le mouvement brownien comme une limite de promenades aléatoires.

La première étude mathématique rigoureuse de ce processus est faite par Norbert Wiener (1923) qui a exhibé également une démonstration de l'existence du brownien, ce mouvement sera donc parfois appelé processus de Wiener. Paul Levy (1948) s'est interessé aux proprietés

fines des trajectoires du brownien. Depuis, le mouvement brownien continue de passionner les probabilistes, aussi bien pour l'étude de ses trajectoires que pour la théorie de l'integration stochastique (Wiener, Ito, Watanabe, Meyer, Yor, Le Gall, Salminen, Durrett, Chung, Williams, Knignt, Pitman,...)

On utilise le mouvement brownien pour modéliser les phénomènes aux mouvements trés erratiques en physique, en economie, en finance et en biologie.

3.1.1 Définition du mouvement brownien

Le mouvement brownien est un processus stochastique a incréments stationnaires, indépendants et distribués selon une loi normale. Les trajectoires de ce processus sont continues. exemples :

- trajectoire du pollen dans l'eau

- trajectoire de la pollution dans une rivière;

- prix des actifs dans un marché financier

On le note de la façon suivante :

{Wt, t ~ 0} avec W : (t, w) E T x -p W(t, w) (3.1)

(voir [14])

De la marche aléatoire au mouvement brownien

Une autre manière d'expliquer et de définir le mouvement brownien est la suivante : supposons une marche aléatoire symétrique telle que :

11 avec la probabilité 2 1

xi ⁼--1 avec la probabilité 1 2

Ensuite, accélérons ce processus en prenant des pas de plus en plus petits (i.eLx -p 0) et en prenant des intervalles de temps de plus en plus petits (i.eLt -p 0). En passant a la limite, on obtient le mouvement brownien.

3.1.2 Proprietes du mouvement brownien

Soit (Wt)t>0 un mouvement brownien, alors pour tout t, T > 0, (Wt+_T -- Wt) est indépendant de W_u, 0 < u < t et est distribué selon une loi normale centrée de variance T

Ses principales propriétés sont d'être :

fini : l'échelonnage de la variance du mouvement brownien en fonction du temps garantit que le mouvement brownien reste fini ;

continu : les trajectoires du mouvement brownien sont continues ;

markovien : la distribution conditionnelle de Wt sachant toute l'information jusqu'à T < t dépend uniquement de W_T;

une martingale : l'espérance conditionnelle de Wt sachant toute l'information jusqu'à T < t est W_T (E[Wt/F_~] = WT);

E[W_t²/F₈] >W_s², s < t et {W_t² -- t, t > 0} est une martingale.

de variation quadratique fini : si on divise [0, T] en rt-F1 points ti = ⁱ_n^t alors Eni_1(Wti --

Wti_1)^2

! n-->o

T

L'accroissement suit une loi normale : (Wti -- Wti_1) " N(0, ti -- ti_1)

Fonction de covariance Cov(Wt, W₅) = E(WtW₈) = t A s = min{t, s}

Symetrie : --W est un mouvement brownien ;

Propriété d'échelle (scaling : pour tout c > 0 : {Wt = 1 Wot, t > 0} est un mouvement brownien ;

Retournement du temps : pour tout t > 0 ; { cWtT = WT -- Wt, t E [0, T]} est un

mouvement brownien ; Inversion du temps : {
	Wt = tW1 t	, t > 0, rs^, Wo = 0} est un mouvement brownien

(continuité en zéro) (voir [15])

Figure 1.1 : Le mouvement

brownien Figure 1.2 : Flux de trajectoires

3.1.3 Simulation du mouvement brownien

Il ne nous est pas possible de simuler le mouvement brownien en temps continu, nous le simulons en temps discret, aux instants 0 = t0 < t1 < ... < t_a, et en se basant sur la relation:

Wti = Wti_1 + Wti - Wti_1 (3.2)

Wt% - Wti_1 '-" .,A/(0, t, - ti 1) (3.3)

Ainsi, Wt% = Wti_1 + Jt - ti 1Z avec {Zi, i 2 N} est formée de variables aléatoires indépendantes de loi .Af(0, 1)

(voir [11])

Algorithme 16 mouvement brownien

1.Simuler n réalisations (yi...y_Th) de la variable aléatoire y '-" .Af(0, 1) 2.Initialiser w0

3.Pour j = 1...m, calculer :

/ wj = wj 1 + A tyj

(3.4)

3.2 Mouvement brownien multidimensionnel

Le mouvement brownien multidimensionnel est utilisé dans les modéles de marché en temps continu. Par exempe lors de la modélisation simultanée des prix de plusieurs actifs risqués. Cependant, les chocs que subissent ces actifs risqués ne devraient pas 'tre indépendants. C'est pourquoi il y a lieu de construire un mouvement brownien multidimensionnel dont les composantes sont corrélées.

Definition 17 Mouvement brownien multidimensionnel

Soit Wt = (W (1)

t ; W ⁽²⁾

t ; :::; W ⁽ⁿ⁾

t )T un processus n-dimensionnel. On dit que Wt est un mouvement brownien multidimensionnel si les processus(W ⁽ⁱ⁾

t ; i < n) sont des mouvements brow-

niens independants.

A partir d'un mouvement brownien standard W de dimension n, il est possible de creer un mouvement brownien de dimension n, dont les composantes sont correles.

Le processus n-dimensionnel W est un mouvement brownien si et seulement si les processus WO et W⁽ⁱ⁾W⁽i⁾ -- sont des martingales (avec = 0 pour i _L j et 8i,i = 1).

On dira que les mouvements browniens a valeurs reelles B1 et B2 sont correles de coefficient de correlation p si B1(t)B2(t) -- pt est une martingale.

On "decorrele" les mouvements browniens en introduisant le processus B3 defini par B3(t) = 1 (B2(t) -- pBi(t)). Ce processus est un mouvement brownien independant de B1

v 1-p2

(voir [11])

Figure 3.1 : Mouvement brownien
de dimension 2

Figure 3.2 : Mouvement brownien
de dimendion 3

3.3 Mouvement brownien avec derive

Le mouvement brownien avec dérive, que l'on appelle aussi mouvement brownien arithmétique, est connu en finance sous le nom de modèle de Merton (1973).

Le mouvement brownien standard comporte certaines lacunes, comme le fait que la dérive est nulle or plusieurs processus stochastiques comportent une tendance prenons comme exemple les indices boursiers qui font preuve d'une tendance a la hausse sur le long terme.

Le mouvement brownien avec dérive corrige cette lacune du processus de Wiener.

Definition 18 Mouvement brownien avec dérive Il s'agit d'un processus stochastique de la forme

{1ut + Zt,t ~ O} (3.5)

oh est une constante et (Zt) un mouvement brownien

Propriétés :

ii)Wo = 0;

i2)(Wt)t>o suit une loi normale de moyenne 1ut et de variance cr²t;

i3)(Wt)t>o est un processus a acroissement stationnaire. Ainsi Wt - W₈ suit une loi normale de moyenne (t - s) et de variance cr²(t - s);

i4)(Wt)t>0 est un processus a acroissement indépendants.

N'importe quel mouvement brownien {Wt, t ~ 0} de dérive et de variance cr² peut alors s'écrire Wt = 1ut + aZt oh {Zt, t ~ 0} est un mouvement brownien standard.

(voir [3])

Remarque 19 Si = 0, nous retrouvons le mouvement brownien standard.

Remarque 20 A court terme, c'est la partie stochastique du processus qui domine, sur le long terme, c'est la tendance.

FIGURE 4.1 : Brownien avec dérive FIGURE 4.2 : Flux de trajectoires

3.4 Mouvement brownien géométrique

Un mouvement brownien géométrique est un processus stochastique continu dont le logarithme suit un mouvement brownien. Il est appliqué dans la modélisation mathématique de certains cours dans les marchés financiers

Le mouvement brownien géométrique représente une approximation raisonnable de l'évolution des cours en bourse parce qu'une quantité qui suit un mouvement brownien géométrique prend toute valeur strictement positive et seuls les changements élémentaires de la variable aléatoire sont significatifs.

Définition 21 Mouvement brownien géométrique

Un processus stochastique de la forme {e^Wt, t ~ 0} oh {Wt, t ~ 0} est un mouvement brownien, est appelé mouvement brownien géométrique.

(voir [11])

FIGURE 5 : Mouvement brownien géométrique.

3.5 Calcul stochastique

3.5.1 Intégrale stochastique d'Itô

L'intégrale stochastique est appelée aussi intégrale d'Itô en l'honneur du mathématicien japonais kiyoshi Itô (1915-2008). L'intégrale stochastique se construit de façon semblable a l'intégrale classique de Riemann. L'intégrale est d'abord définie sur une classe de processus constants par morceaux et ensuite est étendue a une classe plus large par approximation. Il y a cependant deux grandes différences entre l'intégrale de Riemann et l'intégrale d'Itô.

La première est le type de convergence, les approximations de l'intégrale de Riemann converge dans tandit que l'intégrale d'Itô est approchée par des sequences de variables aléatoire qui converge dans L²'l'espace des variables aléatoires de carrés intégrables (variance finie).

La deuxième différence est la suivante, les sommes de Riemann approchant l'intégrale d'une fonction f : [0, T] -p sont de la forme:

_Xn~ 1 f(si)(ti+i - tj) (3.6)

j=0

avec 0 = t0 < t1 < ... < t = T et s3 un point arbitraire dans [ti, t3+i] pour tout j

La valeur de l'intégrale de Riemann ne dépend pas du choix des points s3 2 [ti, t3+i]. Dans le cas stochastique, les sommes approximantes prennent la forme:

I(f_n) = _Xn~ 1 f(sj)(Wtj+1 - Wtj) (3.7)

j=0

La limite de telles approximations dépend du choix des points intermédiaires s3 2 [ti, t3+1]. De façon a lever l'ambiguité on prend s3 = t3 pour tout j.Comme on prend la borne inférieure de l'intervalle, les approximations a une certaine date ne dépend que de l'information connue a cette date et pas des événements futurs.

L'intégrale d'Itô se note

Z0 1 f(s)dW₅ (3.8)

et est définie de telle façon que

fl-400

uim E f(s)dW₅ - I(f_n) = 0 (3.9)

"~~~~ Z 1 ~ ~~ 2#

0

L'intégrale stochastique bénéficie des propriétés suivantes ii)linéarité :

Z0 t (af(u) + /3g(u))dW_u = a f(u)dW_u + /3 g(u)dW_u (3.10)

Z t Z t

0 0

i2)isométrie :

E[

_~Z

~~~

0

~

t 2 Z t

~

f(u)dWu ~] = E[ jf(u)j² du] (3.11)

~

0

i3)propriétés de martingale, pour s < t :

Z t Z 8

E[ f(u)dW_u=F₈] = f(u)dW_u (3.12)

0 0

L'intégrale stochastique est un des outils fondamentaux du calcul stochastique et sert de base a la définition des processus de diffusion.

(voir [5])

3.5.2 Processus d'Itô

Si W suit un processus de Wiener (mouvement brownien) standard alors la variation 8Wdurant un court intervalle 8t s'écrit :

_J

8W = € 8t, on € ~ N (0_; 1)

tout processus de Wiener général X (avec tendance) peut s'écrire :

dX = bdt + adW (3.13)

ainsi, dans un intervalle de temps 8t, la variation 8W de W s'écrit

../

8X = b8t + a€ 8t, on € .,A/(O, 1) (3.14)

/

Les paramètres b et a d'un processus de Wiener (8X = b8t + a" 8t) sont constants.

Definition 22 Un processus stochastique encore plus général, appelé processus d'Ito, auto-rise les paramétres b et a a être des fonctions de la variable X et du temps t :

dX = b(X, t)dt + a(X, t)€dW (3.15)

_s/

ou : 8X = b(X, t)8t + a(X, t)" 8t (3.16)

(en supposant que la tendance et la variance restent constants entre t et t + 8t)

Une analyse des actifs dérivés nécessite donc une bonne compréhension du comportement des fonctions de variables aléatoires.

Un résutat important dans ce domaine a été établi par le mathématicien Kiyosi Itô en 1951. Ce résultat est connu sous le nom de "lemme d'Itô".

3.5.3 Lemme d'Itô

Lemme 23 Lemme d'Itô

Soit (Xi) un processus stochastique de dimension1.

Z t Z t

X = x + b(s, X₅)ds + a(s, X₅)dW₅

0 0

oIl _(Wt)t~0 est un mouvement brownien standart de dimension 1.

Soit f(t, x) une fonction de classe C¹par rapport a t et C² par rapport a x alors f vérifie :

Z t Z t Z t

@f @f

f(t, Xt) = f(0, x)+ @t (s_; Xs)ds+ _@x(s; Xs)dXs+ ¹ a²(s_; X_s)^@2f

@x2 (s_; X_s)ds (3.17)

2

0 0 0

Le lemme d'Itô est aux variables stochastiques ce que les series de Taylor sont au cas déterministe, ce lemme offre un moyen de manipuler le mouvement brownien ou les solutions d'équations différentielles stochastiques.

3.5.4 Equations différentielles stochastiques

Les équations différentielles stochastiques sont des équations différentielles qui contiennent un ou plusieurs termes qui est un processus stochastique. La solution de ces équations est un processus stochastique aussi. Normalement les EDS (ou équations différentielles stochastiques) incorporent du bruit blanc qui ici peut être vue comme la dérivée d'un mouvement brownien. Les EDS permettent de modéliser des trajéctoires aléatoires, tels des cours de bourse ou les mouvements de particules soumises a des phénomènes de diffusion.

tique réelle est une équation de la forme :

Z t Z t

X = x + b(s, X₅)ds + a(s, X₅)dW₅ (3.18)

0 0

Ou sous une forme différentielle :

dX = b(t,Xt)dt + a(t,Xt)dWt (3.19)

X0 = x

Soit b et a deux fonctions de R+ x Rⁿ a valeurs réelles, données :

i1) b(t, Xt) est appelé coefficient de transport ou de dérive (ou drift);

i2) a(t, Xt) est appelé coefficient de diffusion ou volatilité.

On se donne également un .7--mouvement brownien _(Wt)t>o sur cet espace. Une solution de

l'EDSprécédente est unprocessus _(Xt)t>o continu,.F--adapté tel que les intégrales f 0 t b(s, X₅)ds et f 0 a(s, X₅)dW₅ aient un sens et l'égalité

Z t Z t

X = x + b(s, X₅)ds + a(s, X₅)dW₅ (3.20)

0 0

soit satisfaite pout tout t. IP presque slirement. (voir [1],[10])

Théorème 25 (Théorême d'existence)

Sous les hypotheses suivantes :

(a) il existe K tel que pour tout t 2 [0,T],x 2 R,y 2 R. :

(i) b(t, x) - b(t, y) + a(t, x) - a(t, y)j ~ K x - yj :

(ii) b(t, x)j² + a(t, x)j² (1 + xj²).

(b) la condition initiale X0 est indépendante de _(Wt)t>o et est de carré intégrable,

il existe une unique solution de l'EDS a trajectoires continues pour t 2 T. De plus cette solution vérifie

Théorème 26 Théoréme de Girsanov

Dans la théorie des probabilités, le théoréme de Girsanov indique comment un processus

stochastique change si l'on change de mesure. Ce théoréme est particuliérement important en mathématiques financiéres dans le sens oh il donne la maniére de passer de la probabilité historique qui décrit la probabilité qu'un actif sous-jacent (comme le prix d'une action ou un taux d'intérêt) prenne dans le futur une valeur donnée a la probabilité risque neutre qui est un outil trés utile pour évaluer la valeur d'un dérivé du sous-jacent.

Soit _(Ot)t>oun processus aléatoire .F--adapté tel que :

Z T

E[exp(¹ kO₅M² ds)] < +00 (3.22)

2 0

Le processus W^° défini par:

Z t

W t ° = Wt - O_sds (3.23)

0

est un mouvement brownien sous la probabilité 1P0 de densité (par rapport a IP) :

dP~

dIP

Z T Z T

O5dW5 - 1

= exp( k~_sk² dt) (3.24)

2

0 0

3.6 Les processus de diffusion

Définition 27 Processus de diffusion

Un processus de diffusion est un processus de markov a trajectoires continues vérifiant le lemme d'Itô.

Soit _(Xt)t>oun processus stochastique défini sur l'espace probabilisé (~, A, IP)a valeurs reéls muni d'une filtation .F. On dit que _(Xt)t>0 est un processus de diffusion caractérisé par: i1) la limite donnant la dérive :

uim h!0		E(Xt+h - Xt/Xt = x)	= b(x, t) (3.25)
		h
uim h!0	E([Xt+h - Xt]^2/X = x)			= a^2(x,t) (3.26)
	h

i2) la limite donnant la diffusion:

i3) la condition de Dynkin

lim h-)	11^1(1Xt#177;h -- Xt1 > E/Xt = x)	= 0, 8 > 0 (3.27)
	h

Une diffusion obéit a une equation differentielle stochastique de la forme

dXt = b(X(t), t)dt + a(X(t), t)dW (t) (3.28)

Sous forme integrale, le systeme peut s'ecrire sous les formes.

X(t) = X(0) + I b(X(u), u)du + I a(X(u), u)c/W(u) (3.29)

k t

Xi (t) = X f

(0) + I bt(X(u), u)du + ^E atj(X(u), u)dWi(u) (3.30)

j=i

Les processus de diffusion sont construits a partir du mouvement brownien. Le terme b(x) peut s'interpreter comme la force deterministe agissant sur une particule dans un fluide au point x, et s'appelle donc le coefficient de derive. le terme a(x) mesure l'effet de l'agitation thermique des molecules du fluide en x, et s'appelle le coefficient de diffusion. Il y a des conditions de regularitees sur les fonctions b et a pour que le systeme d'equations differentielles stochastiques admette une solution

i1) Les fonctions a et b sont des fonctions mesurables qui veri...ent la condition de Lipschitz, soit V(xi, 0), (x2, 0) E R^d * :

11a(xi : 0) -- a(x2 : 0)11 < C 11x1 -- x211 11b(x1 : 0) -- b(x2 : 0)11 < C 11x1 -- x211

avec C une constante positive quelconque.

i2) Les fonctions a et b sont bornees lineairement telles que :

11a(xi : 0)11² +11b(xi : 0)11² < C²(1 + 11411²)

avec C une constante positive quelconque et 11.11 symbolise la norme euclidienne.

i3) La valeur initiale Y0 appartient a L²(Q, s, P) et est indépendante de la a--algebre a(Wt, t 2 [0, T]), alors il existe une solution pour tout t 2 [0, T] appartenant a L²(Q, =, continu et unique sur l'intervalle.

(voir [5],[13])

3.6.1 Méthodes de simulation des processus de diffusion

Lorsqu'il s'agit de simuler des processus de diffusion, il y a les méthodes exactes et celle qui sont basées sur la discrétisation du temps.

Les méthodes exactes sont employées lorsque l'on connait la distribution de X(t + u) conditionnellement a la valeur de X(t)

Les méthodes basées sur la discrétisation du temps simulent une approximation du processus original. pour cette raison, la méthode exacte est généralement préférable aux méthodes de discrétisation du temps.

Schéma d'Euler

une façon trés intuitive de simuler un processus de diffusion est a l'aide de l'approximation d'Euler.

Soit l'équation différentielle stochastique originale

k

dX,(t) = b_z(X(t),t)dt + J=1 aid(X(t), t)dWi(t) (3.31)

Soit l'approximation d'Euler sur une courte période de temps de longueur h

k

^bX,(t + h) -- ^bX,(t) = b,( ^bX(t),t)h + J=1 aij( ^bX(t),t)(Wi(t + h) -- W;(t))

k

= ^1°ibi( ^bX(t),t)h + J=1 aij( (t), OhZi on Z1, ..., Zk sont iidAr (0,1)

Sous sa forme intégrale, l'EDS originale est, pour t, h > 0 :

Z t+h k p t+h

Xi(t + h) = Xi(t) + bi(X(u), u)du + ai3(X(u), u)dW3(u)

t t

j=1

Z t+h _Xk Z t+h

' Xz(t) + bi(X(t), t)du + ai3(X(t), t)dW3(u)

t t

j=1

si h est suffi sament petit

Z t+h > k Z t+h

= Xi(t) + bi(X(u), u) du + ai3(X(t), t) dW3(u) (3.32)

t t

j=1

=l° Xi(t) + bi(X(u), u)h +

Xk j=1

V' ai3(X(t), t) hZ3 on Zi, ..., Zk sont i i dLA/(0, 1) (3.33)

Afin de bien marquer le fait que l'approximation d'Euler est un processus différent de la solution du systéme d'EDS original, nous la notons différemment :

^bXi(t + h) = ^bXi(t) + bi( ^bX(t), t)h +

Xk j=1

V' aij( ^bX(t), t) hZ3, i = 1, ...d (3.34)

(voir [11])

Chapitre 4

Simulation des processus de diffusion

4.1 Présentation des données

Afin d'estimer les paramètres des modèles de diffusion nous utiliserons l'historique des taux d'intérêts des bons du trésor Américain téléchargé sur le site suivant :

http :// www.treasury.gov/resource-center/data-chart-center/interest-rates/Pages/default.aspx.

Nous disposons de données concérnant le taux d'intérêt court (short rate) ainsi que le taux d'intérêt a long terme (long term interest rate)

(voir annexe II : Daily Treasury Bill Rates Data)

4.2 Modêle de Vasicek (processus d'Ornstein-Uhlenbeck)

Définition 28 Processus Ornstein-Uhlenbeck

Dans le modéle de Vasicek, le taux sans risque est modêlisé par un processus d'Ornstein-

Uhlenbeck, sous la probabilité neutre au risque Q

dr = k(0 - rt)dt + adW'² (4.1)

t

oh k, 0 et a sont des constantes positives avec 0 la moyenne a long terme du procesus, k le taux de retour a la moyenne, a est le coéfficient de diffusion de la volatilité et r est le taux d'intérêt sans risque. Ce modêle autorise des taux d'intérêts négatifs avec probabilité positive (mais petite) !(voir [7],[4])

4.2.1 Mesure objective (Monde reel)

Le modele de Vasicek est modélisé en monde neutre au risque (ou mesure martingale qui désigne l'absence d'opportunité d'arbitrage), quoique la distribution dans le management du risque est la mesure objective (monde réel), nous passons de la mesure martingale a la mesure objective de la façon suivante :

dW_t^c? = dWt + Artdt (4.2)

d'ori : drt = (k0 -- (k + Acr)rt)dt + dW_t^c? (4.3)

avec Ats'écrit sous la forme :

At = Art (4.4)

(Voir [6])

4.2.2 Estimation des paramètres du modèle de Vasicek

Afin d'estimer les parametres du modele de Vasicek, nous utiliserons l'historique des taux d'intérets des bons du trésor Américain, ces données sont journalieres et s'étalent sur la période allant du 03/01/2012 au 02/10/2012.

L'estimation se fera en utilisant le maximum de vraissemblance (EMV)

= E(rt -- art-1)

avec

n(1 -- a)

(4.5)

72 En i=1 r2 i~1 ~ (Pn i=1 ri~1)²

^b =

n E_i riri_i -- E_i ri E_i ri_i

bk =	-- log(a) (4.6) dt

2k ₁₇' 2

(1 -- e-2idt)

avec 9^.2 = ¹ V(ri -- arj_i -- E(1 -- a))² (4.7)

n

0" =

(voir [19],[6])

bO	=	0.06494378
bk	=	2.88582778
^b	=	0.05732961

4.2.3 Simulation du modèle de Vasicek

Discrétisation du modèle de Vasicek, le processus d'Ornstein-Uhlenbeck d'écrit :

_s/

^drt+h = ^brt + k(O - ^brt)h + a hZ avec Z '-" .A/(0, 1) (4.8)

Algorithme 29 modêle de Vasicek

1.Simuler m réalisatioms (z1...z_n) de la variable aléatoire z '-" .Af(0, 1) 2.Imitialiser r0

3.Pour j = 1...m, calculer :

_V

r3 = r3_1 + k(O - ri_1) A t + cr A tz3 (4.9)

FIGURE 7.1 : Simulation du modèle FIGURE 7.2 : Un echantillon de 30

de Vasicek. trajectoires.

4.2.4 Simulation de la solution exacte du modèle de Vasicek

Aprés application du Lemme d'Itô, la solution du modèle de Vasicek est :

_r

1

rti+1 = e_k(ti+1_ti)rtj + 0(1 - e_k(ti+1_ti)) + ~ _2k(1 - e_^2k(^ti+^1_ti))Zj+i (4.10)

(voir [4])

Nous simulerons le processus aux instants 0 = to < ti < ::: < t_n

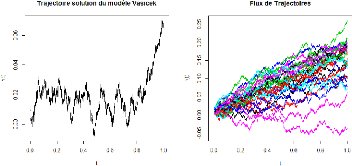
FIGURE 8.1 : Simulation de la solution FIGURE 8.2 : Un echantillon de

exacte du modèle de Vasicek. 30 trajectoires.

4.2.5 Calcul du prix du bon dans le modèle de Vasicek

Soit P(t, T) le prix d'une obligation zéro-coupon a l'instant t dont l'échéance est a T

Le prix du bon est donné par:
P(t, T)	=
avec A(t, T )	=
et B(t,T)	=

R T

P (t, T ) = Et(e t --rudu) (4.11)

A(t, T)e_B(t;T)rt (4.12)

{ }

(0 - 2

2k2 )[B(t, T ) -- T + t] - 2

exp _4kB(t, T )² (4.13)

_k(1 - e_k(t_T))

1 (4.14)

(voir [6])

4.3 Modèle de Cox, Ingersoll & Ross (CIR)

Définition 30 Processus racine-carrée

Cox, Ingersoll et Ross utilisent le rocessus racine carrée étudié par Feller comme modêle de taux

drt = k(0 - rt)dt + aJrtdW Q (4.15)

t

oh k, 0 et a sont des constantes positives avec 0 la moyenne a long terme du procesus, k le taux de retour a la moyenne, a est le coéfficient de diffusion de la volatilité et r est le taux d'intérêt sans risque.Ce modêle garantit la positivité du taux court, la solution de cette EDS reste strictement positive sous la condition 2k0 > a².

(voir [1])

4.3.1 Estimation des paramètres du modèle de Cox, Ingersoll & Ross

Contrairement au modèle de Vasicek, il n'est pas possible d'utiliser le maximum de vraissemblance pour estimer les paramètres du modèle CIR, cela est dii au fait que le taux d'intérêt rt ne suit plus la loi normale mais un khi-deux décenté.

Nous utiliserons l'optimisation numérique pour obtenir les paramètres du modèle CIR La fonction de répartition de rt est :

P(r(t) y/r(u)) = FX2 (d,A)( 4ky

a²(1 - ek(tu))) (4.16)

La fonction desité de probabilité est la suivante :

on _p(d,A)(cy) est la densité de probabilité du Khi-deux non central et

c =

4k
cr²(1 - e_k(t_u))

Nous pouvons définir la vraissemblance et la log-vraissemblance de la facon suivante :

L(k,O,a;y) =	Yn z=2	cp(4.18) X2 (d,A)(cyi/yi_1) avec y = r1, r2, ..., r
l(k,O,a;y) =	Xn z=2		log(c) +	Xn z=2	log(p(4.19) X2 (d,A)(cyi/yi_1))

(voir [6],[12])

Le code en R pour calcul de la fonction log-vraissemblance ainsi que pour l'optimisation numérique est présenté en annexe.

Nous utilisons l'historique des taux d'intérêts des bons du trésor Américain pour obtenir les paramètres du modèle de Cox, Ingersoll & Ross (du 03/01/2012 au 02/10/2012)

bO	=	0.05494378
bk	=	2.26582778
^b	=	0.05132961

\/ /

^brt + k(O - ^brt)h + a ^brt hZ (4.20)

4.3.2 Simulation du modèle de Cox, Ingersoll et Ross

Aprés discrétisation du temps :

^drt+h =

Algorithme 31 modêle de Cox, Ingersoll et Ross

1.Simuler n réalisations (z1...z_n) de la variable aléatoire z '-" .Af(0, 1) 2.Initialiser r0

3.Pour j = 1...m, calculer :

r = rj_1 + k(O - ri_1) A t + a/rj_1 A tzj

FIGURE 10.1 : Simulation du modèle CIR FIGURE 10.2 : Flux de trajectoires

4.3.3 Simulation de la solution exacte du modèle CIR

Pas de solution explicite pour rt en fonction de r0 et W, mais nous savons que la distribution est un x² decentré.

La densité de transition de r(t) s'écrit :

cr²(1 - e_k(t_u)) d ( 4ke_k(t_u)

r(t) = X 2 ²(1 - e_1c(t_u))r(u)), t > u (4.21)

4k

2

4_ke_k(t_u)

~ =

40k

d =

cr²(1 - e_1(t_u))r(u)

(voir [4])

Nous simulons aux instants 0 = t0 < t1 < ::: < t_n

FIGURE 11 : Simulation de la solution du modèle CIR.

4.3.4 calcul du prix du bon dans le modèle CIR

Le prix du bon dans le modèle P(t, T) = avec A(t; T ) = et B(t, T ) =	de Cox, Ingersoll et Ross est donnée par A(t, T)e_B(t;T)rt 2he[(k+h)(T _t)1I2 2 (	(4.22) (4.23) (4.24)
	2h + (k + h)e(T _t)h_1 )2k~=~2e(T_t)h_1
	h V" k^2 2o-^2
	2h + (k + h)e(T _t)h_1 avec = +

(voir [6])

4.4 Modèle de Vasicek a 2 facteurs

Definition 32 Modéle de Vasicek a deux facteurs

Le modéle de Vasicek a deux facteurs se présente comme la somme d'un premier facteur, xt_;representant le taux d'intérêt court instantané (short rate) et d'un autre facteur, yt,representant le taux d'intérêt a long terme (long term interest rate).

Dams le ynodéle de Vasicek a deux facteurs, le taux court imstamtamé sous la probabilité meutre au risque Q, est dommé par

Tt = Xt + yt (4.25)

dx = kx(Ox - xt)dt + a_xdW¹ (4.26)

t

dyt = ky(Oy - yt)dt + aydW t 2 avec d (W1, w²) = pdt (4.27)

(voir [8])

4.4.1 Estimation des paramètres du modèle de Vasicek a 2 facteurs

L'estimation des paramètres du modéle de Vasicek a deux facteurs se fait de la même façon que pour le modeèle de Vasicek a un facteur, nous estimerons les paramètres des processus Xt et yt par EIVV.

Nous utilisons l'historique des taux d'intérêts a court terme des bons du trésor Américain dont l'échéance est a 4 semaines pour estimer les paramètres du processus Xt.

Les resultats obtenus pour Xt sont les suivants :

^b~_x = 0:05747338 bk = 2:90211453 ^b~_x = 0:05136251

Nous utilisons l'historique des taux d'intérêts a long terme des bons du trésor Américain dont l'échéance est a 52 semaines pour estimer les paramètres du processus Yt
·

Les resultats obtenus pour Yt sont les suivants :

^b~_y = 0:18038052 ^b1c_y = 0:42094486 ^b~_y = 0:02654436

4.4.2 Simulation du modèle de Vasicek a deux facteurs

Afin de simuler, nous discrétisons le modèle et obtenons ce qui suit :

^brt = ^bxt + ^byt (4.28)

/

^dxt+h = ^bxt + k_x(O - ^bxt)h + a_x hZ (4.29)

t

yt+h =

/ ^byt + ky(Oy -- ^byt)h + ay hZ (4.30) t

Algorithme 33 modêle de Vasicek a deux facteurs

1.Simuler m réalisatioms (zi...z_n) de la variable aléatoire z '-" .N(O, 1) 2.Simuler m réalisatioms (z^' ₁...z^' _n) de la variable aléatoire z^' '-" .,A/(O, 1) 3.Imitialiser x0

4.imitialiser yo

5.Pour j = 1...m, calculer :

_{s/ p}

xj = xj-i + k(O - xj-i) A t + a A t(p * zj + 1 - p²*z^' _j) (4.31)

6.Pour j = 1...m, calculer :

_-s/
yi = yj-1 + k(O - yj-i) A t + cr A tz3 (4.32)

7.faire

rj = x3 + y3 (4.33)

FIGURE 12.1 : Simuation du modèle FIGURE 12.2 : Flux de trajectoires

4.4.3 Simulation de la solution exacte du modèle de Vasicek a 2 facteurs

Par application du lemme d'Itô xt et yt, on trouve :

xti+1 = e

r 1 _kx(ti+1_ti)xti + Ox(1 - e_kx(ti+1_ti)) + x (1 - e_2k(ti+1_ti))Zl ti+1 (4.34) 2kx

_s

1

yti+1 = e_ky(t%+1~t%)yt. + O_y(1 - e_ky(ti+1_ti)) + _y (1 - e_2k(ti+1_ti))Z2 ti+1 (4.35)

2k_y

Tt. = xti + yti (4.36)

Il suffit de simuler la solution exacte de chacun des deux processus de taux et ensuite de prendre la somme.

(voir [6])

FIGURE 13.1 : Simulation de la solution FIGURE 13.2 : Flux de trajectoires

4.4.4 calcul du prix du bon pour le modèle de Vasicek 2f

Le prix d'un bon du trésor dans un modèle de Vasicek a deux facteurs est donné par

P(t, T) = _e_R(t,T )rt (4.37)

avec R(t, T) est la rentabilites au temps t d'un bon du tresor de maturite T.

1 -- e^-kx(T-t) 1 -- e-ky(T-t)

R(t, T) =

O_X + kx(T-t) (Xt ~O) + By #177; ky(T-t) (yt -- By)

CT2 1 -- e-2kx(T-t) 1 -- _ekx(T-t) \ 0-2 (1 1 -- e-2ky(T-t)

(1 + 0

2 1 -- eky(T-t) \

21q 2k_x(T -- t) kx(T-t) i 21:^k' #177; 2k_y(T -- t) ' ky(T-t) ) y

1 -- e^-kx(T-t)

Pa ^{xa Y} (1 + 1 -- e_kyv_t) 1 -- e_kyv_0(kx+ky)(T-t)

k_x + ky kx(T-t) ky(T-t) (kx+ky)(T-t) ) (4.38)

(voir [6])

4.5 Simulation du processus d'Ornstein-Uhlenbeck exponentiel

Ce processus fut etudie par Jean-Francois Begin dans son article paru en 2010 : "Analyse MCMC de certains modeles de diffusion avec application au marche europeen du carbone".

Ce modele ressemble au processus d'Ornstein-Uhlenbeck toutefois il est exponentiel. Il se presente sous la forme suivante :

d(log r) = k(19 -- (log rt))dt + o^-dWt (4.39)

La difference par rapport aux autres modeles est qu'ici on considere le logarithme du prix et non le prix en temps que tel, ce modele permet le retour a la moyenne.(voir [1])

Apres discretisation du temps :

log(rt+h) = log(P_t) + k(19 -- log(P_t))h + as/hZ (4.40)

Afin de simuler le processus, nous utiliserons les parametres obtenus par Begin en utilisons la methode MCMC (Markov chain monte carlo)

E = 0.0632

bk = --0.0240 a = 0.0573

Algorithme 34 Processus d'Ornstein-Uhlenbeck

1.Simuler n réalisations (zi...z_n) de la variable aléatoire z '-" N(0, 1) 2.Initialiser r0

3.Pour j = 1...m, calculer :

_V"

log(r3) = log(r3_i) + k(O - log(r3_i)) A t + cr A tz3 (4.41)

FIGURE 15.1 : Simulation d'un FIGURE 15.2 : Flux de 30 trajectoires

processus d'O-U exponentiel. du processus d'O-U exponentiel.

4.6 Simulation du modêle d'Eraker de volatilité stochastique

Le processus suivant a été proposé par Eraker dans son article paru en 2001 : "MCMC analysis of diffusion models with application to finance".

dr = (O_r + k_rrt)dt + _r exp(¹ ₂Vt)dW¹ (4.42)

t

dVt = k_vVtdt + avdW t 2 avec d(W1, W²) = pdt (4.43)

Aprés discrétisation du temps :

rt+h = Vt+h =

p ^brt + (Or + kr^brt)h + ar exp(^1 2Vt) hZ^1 / ^bVt + kv( ^bit)h + av hZ^2, avec Z^1'^2 JV(0, 1)

Afin de simuler le processus, nous utiliserons les paramètres obtenus par Eraker en utilisons la méthode MCMC.

^bO_r = 0.00127

^bk_r = 0.01271, k = 0.03873

^b;. = 0.24297, ^b = --0.38174

Algorithme 35 Modéle d'Eraker

1.Simuler m réalisatioms (zi...z_n) de la variable aléatoire z '-" .Af(0, 1)

2.Simuler m réalisatioms (z^' ₁...z^' _n) de la variable aléatoire z^' '-" .,A/(0, 1)

3.Imitialiser v0 4.imitialiser r0 5.Pour j = 1...m, calculer :

_s/ \/

vj = vj_i + kv(vj_1) A t + a A t(p * zj + 1 - p²*z^' _j) (4.44)

6.Pour j = 1...m, calculer :

_p

rj = rj_1 + (O_r + krrj_i) A t + _r exp(¹ _{2Vj_i)} A tzj (4.45)

(voir [9])

FIGURE 18.1 : Simulation de la volatilité FIGURE 18.2 : Flux de 30 trajectoires.

FIGURE 19.3 : Simulation du modèle FIGURE 19.4 : Flux de 30 trajectoires

4.7 Simulation du modêle de Heston de volatilité stochastique

Définition 36 Modéle de Heston de volatilité stochastique (SV)

Le modéle de Heston de volatilité stochastique est trés utilisé pour le pricing de produits dérivés

/

dS = rStdt + VtStdW ¹ (4.46)

t

/ t avec d (W 1, W ²⁾

dVt = k(O - Vt)dt + a VtdW ² = pdt (4.47)

Ici S représente l'actif sous-jacent de l'option (taux d'intérêt, taux de change, actions,...) et (St)t>o est le processus de son cours a la date t, (V)

t,t>o est le processus de sa volatilité. _{(Wt1)t>o,(Wt2)t>0} sont deux mouvements browniens standard corrélés, de paramétre de corrélation p.

W t 1 = 1 t

_p

W t 2 = 1 _t + 1 -- p²4q avec 01,4q v.a.i.i.d de loi .A1(0,1)

Le processus (Vt)t>0 est un processus du type CIR (Cox-Ingersoll-Ross).

(voir [14],[16])

Aprés discrétisation du temps :

St#177;h = St + (r St)h + St VVo/hz¹

+ k(19 --17t)h + av VVZ² avec Z¹'² Ji(0, 1)

Vt#177;h =

Afin de simuler le modele de Heston, nous utiliserons les parametres obtenus par Najed Ksouri dans le rapport technique qu'il publia en Mai 2007 intitulé "Méthodes d'approximation numérique pour le pricing des options vanilles et asiatiques dans le modele de Heston de volatilité stochastique".

	b = 0:04
	bk = 0:3
	^b = 0:15

Algorithme 37 Modele de Heston de volatilité stochastique 1.Simuler n réalisations (zi...z_n) de la variable aléatoire z J1(0,1)

2.Simuler n réalisations (z⁰₁:::z⁰ ) de la variable aléatoire J1(0,1)

3.Initialiser vo 4.initialiser so 5.Pour j =1...n, calculer :

6.Pour j = 1...m, calculer :

s3 = sj_1 + _{(rsi_1)} A t + sj_1\/vj_1\/A tz3 (4.49)

FIGURE 16.1 : Simulation volatilité FIGURE 16.2 : Flux de 30 trajectoires

FIGURE 17.1 : Simuation du modèle FIGURE 17.2 : Flux de 30 trajectoires

Chapitre 5

Conclusion générale

Nous avons tout au long de ce mémoire intitulé "Simulation de modèles de diffusion appliqués aux taux d'intérêts" proposé des algorithmes de simulation de processus de diffusion appliquées aux taux d'intérêts ainsi que leurs programmes de simulation sous le logiciel R.

R est un langage de programmation et un environnement mathématique utilisé pour le traitement de données et l'analyse statistique. C'est un projet GNU fondé sur le langage S et sur l'environnement développé dans les laboratoires Bell par John Chambers et ses collègues.

R est considéré par ses créateurs comme étant une exécution de S, avec la sémantique dérivée du langage Scheme. R est un logiciel libre distribué selon les termes de la licence GNU GPL et est disponible sous GNU/Linux, FreeBSD, NetBSD, OpenBSD, Mac OS X et Windows. R représente aujourd'hui l'un des objectifs techniques majeurs de la communauté hacker GNU1.

Les processus stochastiques de taux que nous avons étudié sont le modèle de Vasicek, le modéle de Cox, Ingersoll & Ross ainsi que le modèle de Vasicek a 2 facteurs, qui sont les modèles les plus utilisés pour la dynamique des taux d'intérêts.

Des programmes en R pour la simulation du processus d'Orstein-Uhlenbeck exponentiel ainsi que les modèles de Heston et d'Eraker ont été ajoutés et proposés au lecteur.

Nous espérons avoir atteint l'objectif fixé, a savoir initier le lecteur a la simulation des processus de diffusion appliqués aux taux d'intérêts par l'utilisation de l'outil informatique.

Chapitre 6

Annexes

6.1 Annexe I : Programmes en R

6.1.1 Code R pour simulation d'un mouvement brownien standard

SimulationBrownien<-function(n){

# n ... nombre de simulations

temps = seq(0,1,length=n+1) ## discretisation du temps

pas.temps = 1/n

B.acc = rnorm(n,sd=sqrt(pas.temps)) ## Simulation des accroissements B.sim = c(0,cumsum(B.acc))} ## Simulation d'une trajectoire

6.1.2 Code R pour simulation de 30 trajectoires d'un mouvement brownien

SimulTrajectoires<-function(n.sim,n.point){ # n.sim ... nombre de simulation

# n.point ... points de discrétisation

temps = seq(0,1,length=n.point)

pas.temps = 1/(n.point-1)

B.acc = matrix(rnorm((n.point-1)*n.sim,sd=sqrt(pas.temps)),nrow=n.sim) B.sim = matrix(NA,ncol=n.point,nrow=n.sim)

for (i in 1 :n.sim)

{B.sim[i,] = c(0,cumsum(B.acc[i,]))}

B.mean = apply(B.sim,2,mean)} ## apply calcule la moyenne pour chaque colonne

6.1.3 Code R pour covariance empirique du mouvement brownien

B.cov.emp = cov(B.sim) ## estimation de la matrice de variance-covariance image(temps, temps, B.cov.emp,col=terrain.colors(20),xlab="temps",ylab="temps", main="Covariance empirique du mouvement Brownien")

contour(temps, temps,B.cov.emp, add=TRUE)

6.1.4 Code R pour simulation d'une marche aléatoire

SimulationRandomWalk<-function(n){

# n ... nombre de simulations

temps = seq(0,1,length=n-l-1) ## discretisation du temps

pas.temps = 1/n

M.tr = runif(30,-1,1)

M.sim = c(0,cumsum(M.tr))}

6.1.5 Code R pour simulation d'un mouvement brownien de dimension 2

SimulBrowDim2<-function(n,rho){

# n ... nombre de simulations

# rho ... coéffi cientde corrélation

R<-matrix(c(1 ,rho,rho,1),nrow=2) ## Matrice des Corrélation

L<- t(chol(R)) ## decomposition de Cholesky

Z<- matrix(rnorm(n*2),nrow=2)

Z<- L%*%Z ## variables aléatoires corrélées

Z2=t(Z) ## transposé de la matrice Z pas.temps = 1/n

B.acc1 = sqrt(pas.temps)*Z2[,1] B.sim1 = c(0,cumsum(B.acc1)) B.acc2 =sqrt(pas.temps)*Z2[,2] B.sim2 = c(0,cumsum(B.acc2))}

6.1.6 Code R pour simulation d'un mouvement brownien de dimension 3

SimulBrowDim3<-function(n,rho){

# n ... nombre de simulations

# rho ... coéffi cientde corrélation

R<-matrix(c(1 ,rho,rho,rho,1,rho,rho,rho,1),nrow=3)

L<- t(chol(R))

Z<- matrix(rnorm(n*3),nrow=3)

Z<- L%*%Z Z3=t(Z)

pas.temps = 1/n

B.acc1 = sqrt(pas.temps)*Z3[,1] B.sim1 = c(0,cumsum(B.acc1)) B.acc2 = sqrt(pas.temps)*Z3[,2] B.sim2 = c(0,cumsum(B.acc2)) B.acc3 = sqrt(pas.temps)*Z3[,3] B.sim3 = c(0,cumsum(B.acc3))}

6.1.7 Code R pour simulation d'un mouvement brownien avec derive

SimulationBrownienDrifté<-function(n,u){

# n ... nombre de simulations

# u ... Coéfficient de dérive

temps = seq(0,1,length=n+1) ## discretisation du temps

pas.temps = 1/n

B.acc =rnorm(n,sd=sqrt(pas.temps)) ## simulation des accroissements y=u*pas.temps+(B.acc)

B.sim = c(0,cumsum(y))} ## simulation d'une trajectoire

6.1.8 Code R pour simulation de 30 trajectoires d'un brownien avec derive

SimulTrajectoires<-function(n.sim,n.point,u){ # n.sim ... nombre de simulation

# n.point ... points de discrétisation

# u ... Coéfficient de dérive

temps = seq(0,1,length=n.point)

pas.temps = 1/(n.point-1)

B.acc = matrix(rnorm((n.point-1)*n.sim,sd=sqrt(pas.temps)),nrow=n.sim) B.sim = matrix(NA,ncol=n.point,nrow=n.sim)

for (i in 1 :n.sim)

{B.sim[i,] = c(0,cumsum(u*pas.temps+(B.acc[i,])))}

B.mean = apply(B.sim,2,mean)} ## apply calcule la moyenne pour chaque colonne

6.1.9 Code R pour simulation d'un mouvement brownien géométrique

SimulBroGéo<-function(para,x0,dt,n){ # x0 ... valeur intiale du processus

# n ... nombre de simulations

# u ... coéfficient de dérive

# sigma ... volatilité

u=para[1]

sigma=para[2] dt=1/n

x=c(0,n)

tvector=dt*0 :n dW=sqrt(dt)*rnorm(n)

x[1]=x0

for(i in 1 :n) {x[i+1]=x[i]+mu*x[i]*dt+sigma*x[i]*dW[i]}}

6.1.10 Code R pour estimation des paramètres du modèle Vasicek

EstimationVasicek<-function(data,dt){

#data ... vecteur contenant les données des taux #dt ... intervalle de temps entre les données

N=length(data)

rate=data[2 :N]

lagrate=data[1 :(N-1)]

alpha=(N*sum(rate*lagrate) - sum(rate)*sum(lagrate))/ (N*sum(lagrate^2)- (sum(lagrate)) 2)

k_hat = -log(alpha)/dt

theta_hat = sum(rate-alpha*lagrate ) / (N*(1-alpha)) v2hat<-sum((rate-lagrate*alpha-theta_hat*(1-alpha)) 2)/N sigma_hat<-sqrt(2*k_hat*v2hat/(1-exp(-2*k_hat*dt))) c(theta_hat,k_hat,sigma_hat)}

6.1.11 Code R pour simulation du modèle de Vasicek

VasicekSimulation<-function(para,r0,dt,n,m){ # r0 ... valeur intiale du processus de taux

# n ... nombre de simulations

# dt ... pas du temps

# m ... nombre de trajectoires simulées k=para[1]

theta=para[2]

sigma=para[3]

r=matrix(0,m+1,n)

r[1,]=r0

for(j in 1 :n){

for(i in 2 :(m+1)){

dr=k*(theta-r[i-1,j])*dt + sigma*sqrt(dt)*rnorm(1,0,1) r[i,j]=r[i-1,j] + dr }}}

6.1.12 Code R pour simulation de la solution du modèle de Vasicek

VasicekSimulSolution<-function(para,r0,dt,n,m){

# r0 ... valeur intiale du processus de taux

# n ... nombre de simulations

# dt ... pas du temps

# m ... nombre de trajectoires simulées

k=para[1]

theta=para[2] sigma=para[3] r=matrix(0,m+1,n)

r[1,]=r0

for(j in 1 :n){

for(i in 2 :(m+1)){ dr=k*(1-exp(-sigma*dt))+(theta*sqrt((1-exp(-2*sigma*dt))/(2*sigma))*rnorm(1,0,1)) r[i,j]=r[i-1,j]*exp(-sigma*dt)+dr }}}

6.1.13 Code R pour le calcul du prix du bon dans le modèle de Vasicek

VasicekPrix<-function(r,tau,para){

# r ... valeur actuelle du taux d'intérêt

# Para ... vecteur des paramètres du modèle de Vasicek

# tau ... maturité

theta=Para[1]

k=Para[2]

sigma=Para[3]

B=(1-exp(-k*tau))/k

A=exp((B-tau)*(k 2*theta-0.5*sigma 2)/k 2 - sigma 2*B 2/(4*k)) P=A*(exp(-B*r))} # P : prix du bon du trésor

6.1.14 Code R pour estimation des paramètres du modèle CIR

CIRloglike<-function(para,data){

#Calcul de la fonction log-vraissemblance du modèle CIR theta=para[1]

k=para[2]

sigma= para[3]

N=length(data)

rate=data[1 :(N-1)]

lagrate=data[2 :N]

ncp= rate*((4*k*exp(-k*dt))/(sigma 2*(1-exp(-k*dt)))) d= 4*theta*k/sigma 2 #degr" de liberté

c= 4*k/(sigma 2*(1-exp(-k*dt))) R=sum(dchisq(c*lagrate,df=d,ncp=ncp,log=TRUE)+log(c))}

#Code R pour l'optimisation Numérique OptimCIR<-optim(par=c(0.1,0.1,0.1),fn=CIRloglike,method="L-BFGS-B", lower=c(0.05,0.05,0.05),upper=c(0.7,0.7,0.7),data=read.table("dataUS.dat"))$par

6.1.15 Code R pour simulation du modèle de Cox, Ingersoll & Ross

CIRsimulation<-function(para,r0,n,dt,m){

# r0 ... valeur intiale du processus de taux

# n ... nombre de simulations

# dt ... pas du temps

# m ... nombre de trajectoires simulées

k=para[1]

theta=para[2] sigma=para[3] r=matrix(0,m+1,n)

r[1,]=r0

for(j in 1 :n){

for(i in 2 :(m+1)){

dr=k*(theta-r[i-1,j])*dt +sigma*sqrt( r[i-1,j]*dt)*rnorm(1,0,1)

r[i,j]=r[i-1,j] + dr }}}

6.1.16 Code R pour simulation de la solution exacte du modèle CIR

CIRsimulSolution<-function(para,n,dt,m){ # r0 ... valeur intiale du processus de taux # n ... nombre de simulations

# dt ... pas du temps

# m ... nombre de trajectoires simulées

# c... terme multiplicatif distribution khi-2 # df... degré de liberté

# ncp... parametre de non centralité k=para[1]

theta=para[2]

sigma=para[3]

c= sigma 2*(1-exp(-k*dt))/(4*k)

df= 4*theta*k/sigma 2

r=c(0,m)

r[1]=r0

for(i in 1 :(m)){

ncp= r[i]*exp(-k*dt)/c

r[i+1]=c*rchisq(m,df=df,ncp=ncp)}}

6.1.17 Code R pour le calcul du prix du bon dans le modèle CIR

CIRprix<-function(r,tau,para){

# r ... valeur actuelle du taux d'intérêt

# Para ... vecteur des paramètres du modèle CIR

# tau ... maturité

theta=Para[1]

k=Para[2]

sigma=Para[3]

h=sqrt(k 2+2*sigma 2)

B= 2*(exp(h*tau)-1) / (2*h+(k+h)*(exp(tau*h)-1))

A= ((2*h*exp((k+h)*(tau)/2)) / (2*h+(k+h)*(exp(tau*h)-1))) (2*k*theta/sigma 2) P=A*(exp(-B*r))} # P : prix du bon du trésor

6.1.18 Code R pour estimation des paramètres du modèle de Vasicek 2f

EstimationVasicek2f<-function(data,data2,dt){ #data ... vecteur des données du taux court

#data2 ... vecteur des données du taux a long terme #dt ... intervalle de temps entre les données N=length(data)

rate=data[2 :N]

lagrate=data[1 :(N-1)]

alpha=(N*sum(rate*lagrate) - sum(rate)*sum(lagrate))/

(N*sum(lagrate 2)- (sum(lagrate)) 2) k_hat = -log(alpha)/dt

theta_hat = sum(rate-alpha*lagrate ) / (N*(1-alpha)) v2hat<-sum((rate-lagrate*alpha-theta_hat*(1-alpha)) 2)/N

sigma_hat<-sqrt(2*k_hat*v2hat/(1-exp(-2*k_hat*dt))) c(theta_hat,k_hat,sigma_hat)

N=length(data2)

rate=data2[2 :N]

lagrate=data2[1 :(N-1)]

alpha2=(N*sum(rate*lagrate) - sum(rate)*sum(lagrate))/ (N*sum(lagrate^2)- (sum(lagrate)) 2)

k_hat2 = -log(alpha2)/dt

theta_hat2 = sum(rate-alpha2*lagrate ) / (N*(1-alpha2)) v2hat2<-sum((rate-lagrate*alpha2-theta_hat2*(1-alpha2)) 2)/N sigma_hat2<-sqrt(2*k_hat2*v2hat2/(1-exp(-2*k_hat2*dt))) c(theta_hat2,k_hat2,sigma_hat2)

corr=cor(T,T2)} #coéffi cient de corrélation

6.1.19 Code R pour simulation du modèle de Vasicek a 2 facteurs

Vasicek2fSimulation<-function(param,x0,y0,dt,n,d){ # x0 ... valeur intiale du processus de taux x

# y0 ... valeur intiale du processus de taux y # n ... nombre de simulations

# dt ... pas du temps

# m ... nombre de trajectoires simulées k_x =param[1]

theta_x =param[2]

sigma_x=param[3]

k_y =param[4]

theta_y =param[5] sigma_y=param[6] rho =param[7]

x=matrix(0,m+1,n) y=matrix(0,m+1,n) r=matrix(0,m+1,n) x[1,]=x0

y[1,]=y0

r[1,]=x[1]+y[1]

for (j in 1 :(n)){

for(i in 2 :(m+1)){ norm1=rnorm(1,0,1) norm2=rnorm(1,0,1)

norm3=(rho*norm1)+(sqrt(1-rho 2)*norm2) dx=k_x*(theta_x-x[i-1,j])*dt+sigma*sqrt(dt)*norm3

x[i,j]=x[i-1,j] + dx

dy=k_y*(theta_y-y[i-1,j])*dt + sigma_y*sqrt(dt)*norm1

y[i,j]=y[i-1,j] + dy r[i,j]=x[i,j]+y[i,j] }}}

6.1.20 Code R pour simulation de la solution exacte du Vasicek 2f

Vasicek2fSimulSolution<-function(param,x0,y0,dt,n,d){

# x0 ... valeur intiale du processus de taux x

# y0 ... valeur intiale du processus de taux y

# n ... nombre de simulations

# dt ... pas du temps

# m ... nombre de trajectoires simulées

k_x =param[1]

theta_x =param[2] sigma_x=param[3] k_y =param[4]

theta_y =param[5] sigma_y=param[6] rho =param[7]

x=matrix(0,m+1,n) y=matrix(0,m+1,n) r=matrix(0,m+1,n) x[1,]=x0

y[1,]=y0

r[1,]=x[1,]+y[1,]

for (j in 1 :(n)){ for(i in 2 :(m+1)){ norm1=rnorm(1,0,1) norm2=rnorm(1,0,1)

norm3=(rho*norm1)+(sqrt(1-rho 2)*norm2) dx=k_x*(1-exp(-sigma_x*dt))+(theta_x*sqrt((1-exp(-2*sigma_x*dt))/(2*sigma_x))*norm3)

x[i,j]=x[i-1,j]*exp(-sigma_x*dt)+dx dy=k*(1-exp(-sigma_y*dt))+(theta_y*sqrt((1-exp(-2*sigma_y*dt))/(2*sigma_y))*norm1) y[i,j]=y[i-1,j]*exp(-sigma_y*dt)+dy

r[i,j]=x[i,j]+y[i,j] III

6.1.21 Code R pour le calcul du prix du bon dans Vasicek 2f

PrixVasicek2F<-function(t,para,x,y,tau){

# t ... valeur du taux d'intérêt (modele vasicek2f)

# x ... valeur du processus y(t)

# y ... valeur du processus x(t)

# Para ... vecteur des parametres du modele Vasicek2f)

# tau ... maturité

k_x =para[1]

theta_x =para[2]

sigma_x=parm[3]

k_y =parm[4]

theta_y =para[5]

sigma_y=para[6]

rho =para[7] R=theta_x+(1-exp(-k_x*tau))/(k_x*tau)*(x-theta_x)+theta_y+(1-exp(-k_y*tau))/ (k_y*tau)*(y-theta_y)-sigma_x^-2/(2*k_x^-2)*(1+(1-exp(-2*k_x*tau))/ (2*k_x*tau)-2*(1-exp(-k_x*tau))/(k_x*tau))-sigma_y^-2/(2*k_y^-2)*(1+(1-exp(-2*k_y*tau))/ (2*k_y*tau)-2*(1-exp(-k_y*tau))/(k_y*tau))-(rho*sigma_x*sigma_y)/(k_x*k_y)*(1-

(1-exp(-k_x*tau))/

(k_x*tau)-(1-exp(-k_y*tau))/(k_y*tau)+(1-exp(-(k_x+k_y)*tau))/((k_x+k_y)*tau)) P=exp(-R*t)} #P : prix du bon du trésor

6.1.22 Code R pour simulation d'un processus d'O-U exponentiel

SimulationOUexponentiel<-function(para,rO,dt,n,m){

# rO ... valeur intiale du processus OUexpo

# n ... nombre de simulations

# dt ... pas du temps

# m ... nombre de trajectoires simulées

k=para[1]

theta=para[2] sigma=para[3] r=matrix(O,m+1,n)

r[1,]=log(rO) for(j in 1 :n){

for(i in 2 :(m+1)){

dr=k*(theta-log(r))*dt + beta*sqrt(dt)*rnorm(1,O,1)

r[i,j]=r[i-1,j] + dr }}}

6.1.23 Code R pour simulation du modèle d'Eraker de volatilité stochastique

SimulationEraker<-function(para,rO,vO,m,dt,n){ # vO ... valeur intiale du processus de volatilité # rO ... valeur intiale du modèle proposé par Eraker

# m ... nombre de simulations

# dt ... pas du temps

# n ... nombre de trajectoires simulées

k=para[1]

theta=para[2]

sigma=para[3]

rho=para[4]

v=matrix(0,m+1,n) r=matrix(0,m+1,n) v[1,]=v0

r[1,]=r0

for(j in 1 :n){ for(i in 2 :(m+1)){

norm1=rnorm(1,0,1) norm2=rnorm(1,0,1) norm3=(rho*norm1)+(sqrt(1-rho 2)*norm2)

dv=k*v[i-1,j]*dt +sigma*sqrt(dt)*norm3

v[i,j]=v[i-1,j] + dv

dr=(theta+k*r[i-1,j])*dt +sigma*exp(0.5*v[i-1,j])*norm1

r[i,j]=r[i-1,j] + dr }}}

6.1.24 Code R pour simulation du modèle de Heston de volatilité stochastique

Simulationlleston<-function(para,s0,v0,r,m,dt,n){ # v0 ... valeur intiale du processus de volatilité

# s0 ... valeur intiale du modèle de Heston

# r ... taux d'intérêt sans risque

# m ... nombre de simulations

# dt ... pas du temps

# n ... nombre de trajectoires simulées

k=para[1]

theta=para[2]

sigma=para[3] #volatilité de la volatilité

rho=para[4]

v=matrix(0,m+1,n) s=matrix(0,m+1,n) v[1,]=v0

s[1,]=s0

for(j in 1 :n){

for(i in 2 :(m+1)){ norm1=rnorm(1,0,1) norm2=rnorm(1,0,1)

norm3=(rho*norm1)+(sqrt(1-rho 2)*norm2)

dv=k*(theta-v[i-1,j])*dt +sigma*sqrt(v[i-1,j]*dt)*norm3

v[i,j]=v[i-1,j] + dv

ds=r*s[i-1,j]*dt +s[i-1,j]*sqrt(v[i-1,j]*dt)*norm1

s[i,j]=s[i-1,j] + ds }}}

6.2 Annexe II : Les données

6.2.1 Daily Treasury Bill Rates Data

Nous présentons ici les données s'étallant sur la période allant du 05/01/2012 au 21/05/2012.

Bibliographie

[1] Bégin Jean-Francois, (Aoüt 2010), "Analyse MCMC de certains modèles de diffusion avec application au marché européen du carbone", Département de Mathématiques et statistiques, Université de Montréal, Montréal, Canada.

[2] Berglund Nils, (Janvier 2012), "Martingales et calcul stochastique", Université d'Orléans.

[3] Bourlès, R, "Mathématiques pour la finance", Ecole Centrale Marseille.

[4] Bruno Bouchard, (2010), "Introduction a l'évaluation d'actifs financiers par absence d'opportunité d'arbitrage", Université Paris-Dauphine, Ceremade, et Ensae, Crest.

[5] Christophe Chorro, (Septembre 2006), "Cours de calcul stochastique", Master M2 IRFA.

[6] Dagistan Cagatay, (2010), "Quantifiying the Interest Rate Risk of Bond by Simulation", B.S, Industrial Engineering, Istanbul Technical University, Submitted to the Institut for Graduate Studies in Science and Enginnering in partial fulfillement of the requirements for the degree of Master Of Science, Graduate Program in Indusrial Engineering, Bogazici University.

[7] Eraker Bjørn, (2010), "The Vasicek Model", Wisconsin School of business.

[8] Eraker Bjørn, (2008), "Two Factor Models", Wisconsin School of business.

[9] Eraker Bjørn, (2001),"MCMC Analysis Of Diffusion Models With Application To finance",American Statistical Association, Journal of Business & Economic Statistics April 2001, Vol. 19, No. 2.

[10] Fima, C Klebaner, (2005), "Introduction to stochastic calculus with applications", Second Edition, Imperial College Press.

[11] Geneviève Gauthier, "Simulation des processus de diffusion 6-601-09 Simulation Monte Carlo", HEC Montréal.

[12] Gourieroux, C, Monfort, A., (Fevrier 2007), "Estimation Of The Historical Mean-Reverting Parameter In The CIR Model", CREST, CEPREMAP & University of Toronto., CNAM & CREST.

[13] Guidoum Arsalane Chouaib, (2012), "Concetion d'un Pro Logiciel Interactif Sous R Pour La Simulation de Processus de Diffusion", Mémoire présenté pour l'obtention du diplôme de Magister en Mathématiques spécialité : Probabilité & Statistique, USTHB, Université des Sciences et de la Technologie Houari Boumedienne.

[14] Ksouri Najed, (Mai 2007), "Méthodes d'approximation numérique pour le pricing des options vanilles et asiatiques dans le modèle de Heston de volatilité stochastique", INRIA, Institut National De Recherche En Informatique et En Automatique.

[15] Nizar, T, (2007), "Calcul Stochastique et Finance", IMFSE, Département de Mathématiques appliquées.

[16] Nimalin Moodley, (2005), "The Heston Model : A Pratical Approach With Matlab Code", An Honours Project submitted to the Faculty Of Science, University of the Witwatersrand, Johannesbourg, South Africa, In partial fulfillement of the requirements of the Bachelor Of Science Honours, Programme in Advanced Mathematics of Finance.

[17] Roustant Olivier, (Janvier 2009), "Matingales Support de Cours", Ecole des Mines de Saint-Etienne.

[18] Roustant, O, (Janvier 2008), "Processus Aléatoires : Généralités et exemples", Ecole Nationale Supérieure des Mines, Saint-Etienne.

[19] Sorensen, H, (Septembre 2002), "Parametric inference for diffusion processes observed at discrete points in time, a survey",Centre Ror Analytical Finance, University Of Aahrus, Aahrus School Of Business, ISSN 1398-6163.

[20] Xie Dejun, (2008), "Parametric Estimation for Treasury Bills", Department of mathematics, university of delaware, Newark, DE 19711, USA, International Research Journal Of Finance And Economics, ISSN 1450-2887 issue 17 (2008).