Annexes
Annexe A
Notions fondamentales d'élasticité
Une déformation produite en un point d'un milieu
élastique se transmet de proche en proche dans ce milieu et ce
phénomène de propagation met en jeu les propriétés
élastiques du milieu, propriétés que nous allons
maintenant rappeler.
A.1 Contraintes
Une contrainte est une force par unité de surface qui
agit sur un élément de volume élémentaire, sa
notion permet de décrire la répartition des forces à
l'intérieur d'un solide soumis à une charge [107].
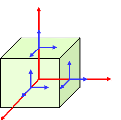
Considérons un parallélépipède
élémentaire. Sur chacune de ces faces s'exerce une contrainte qui
peut se décomposer en trois composantes selon les axes du trièdre
(????1??2??3) (cf. figure A). Ces composantes, notées ?????? ; ??, ?? =
1 a 3), sont les sont les éléments du tenseur des
contraintes« ?? a , l'indice «??» repérant la
direction dans laquelle s'exerce la contrainte et l'indice « ??
a~ se référant à la face sur laquelle elle s'exerce.
Les éléments ?????? sont dites contraintes normales, car elles
agissent perpendiculairement à la face. Les éléments
?????? = ?????? ; ?? ? ??~ sont dites contraintes tangentielles (ou de
cisaillement) puisqu'elles agissent dans le plan de la surface. Le
tenseurI des contraintes est donc symétrique et
s'écrit [108]:
|
|
??11
|
??12
|
??13
|
|
|
??????
|
=
|
??21
|
??22
|
??23
|
(??. 1)
|
|
|
??31
|
??32
|
??33
|
|
??12
??11
??21
??
??31
??22
??32
??13
??23
??33
??3
??2
??1
Fig. A - Notation des contraintes sur un volume
élémentaire
I Le concept du tenseur à été introduit,
à la fin du dix-neuvième siècle, par le physicien W.Voigt
pour définir l'état de tension
mécanique d'un solide (le mot tenseur vient
de tension), sa notation apparaît dis qu'on cherche à
établir des relations linéaires entre effets et causes dans les
milieux anisotropes. Dans un cristal, une cause appliquée suivant une
direction donne en générale naissance à un effet
orienté suivant une autre direction. Le rang d'un tenseur correspond au
nombre d'indices nécessaires pour définir un de ses
éléments : un tenseur de rang « r » est un ensemble de
3r éléments repérées par « r » indices
[51].
A.2 Déformations
Lorsque des forces extérieures sont appliquées
à un solide, celui-ci se déplace et se déforme. Cette
déformation est décrite au moyen du tenseur des
déformations « S » qui lui aussi est symétrique. Les
éléments de ce tenseur peuvent s'écrire [109]:
1 +??????
?????? = 2 ?????? (??. 2) ?????? ??????
Ou (???? ??
?????? ???? ???? ??
??????) sont les gradients des déplacements.
Les éléments Sii représentent l'allongement
dans chacune des directions des axes principaux et les éléments
Sij ; i ? j~ représentent les déformations de cisaillement.
| 


