Chapitre 4
Tâche incarnee : la tâche de
survie minimale
A` l'instar du chapitre pr'ec'edent, nous allons dans ce
chapitre tout d'abord pr'esenter
l'exp'erience dans un premier temps, et
dans un second nous analyserons les r'esultats.
4.1 Experience
La tàache de survie minimale que nous utiliserons ici
est fortement inspirée de [Girard et al., 2003]. Il s'agit pour un robot
de sélectionner efficacement ses comportements afin d'assurer sa survie,
en maintenant ses variables d'état interne dans des intervalles
tolérables, sa zone de viabilité[Ashby, 1952]. Cette survie
dépend directement de la capacitédu robot a` se ravitailler
auprès de deux types de ressources différents, en un temps
limitépar son niveau de recharge. L'utilisation de deux ressources
différentes force le robot a` se déplacer dans l'environnement
pour accéder a` l'une puis a` l'autre et le met en situation de conflit
pour déterminer quelle ressource est prioritaire a` un instant
donné, susceptible de générer des oscillations
comportementales. Cette tàache sera simulée sur ordinateur.
Le robot sera placédans un environnement o`u il pourra
trouver deux types de ressources : des zones d'ingestion qui lui permettront de
faire des réserves et des zones de digestion o`u il pourra assimiler ses
réserves et les transformer en énergie utilisable. Sachant que
tous les comportements du robot consomment de l'énergie, il va donc
devoir alterner phases d'ingestion et de digestion pour survivre.
L'environnement expérimental est une surface plane de
400x400 unités entourée de
murs. Elle est recouverte de 25
carreaux de 80x80 unités, de trois types différents : 21
carreaux gris (zones neutres), 2 carreaux noirs (zones
d'ingestion), dont les ressources sont inépuisables, et 2 carreaux
blancs (zones de digestion). La figure 4.1 montre l'environnement.

FIGURE 4.1: Environnement de la tâche de survie
minimale. Nous y voyons 21 carreaux gris, 2 carreaux noirs et 2 carreaux
blancs, tous les carreaux étant de la même taille. Le cercle jaune
représente le robot.
Le robot est un disque de rayon 20 unités et
possède 2 variables internes :
- l'Energie Potentielle (EP) correspond aux
réserves puisées sur les zones d'ingestion, entre 0 et 1;
- l'Energie (E) est l'énergie
réellement utilisable pour survivre dans l'environnement, elle est
obtenue par digestion de l'EP sur les zones claires. Pour survivre, le robot
doit maintenir E au dessus de 0 et le maximum de E est 1.
Le robot a accès a` 4 capteurs externes :
- un pare-choc gauche (BL pour left bumper),
valeur binaire, a` 1 si contacts avec le mur, a` 0 sinon;
- un pare-choc droit (BR pour left bumper),
valeur binaire, a` 1 si contacts avec le mur, a` 0 sinon;
- un capteur de carreau noir (LD pour light
darkness), valeur binaire, a` 1 si sur un carreau noir, a` 0 sinon;
- un capteur de carreau blanc (LB pour light
brightness), valeur binaire, a` 1 si sur un carreau blanc, a` 0 sinon.
Le robot a 5 actions a` sa disposition :
- Explorer aléatoirement (wander) : le
robot se déplace aléatoirement (rotation aléatoire entre 0
et 9° suivie d'un déplacement vers l'avant de 5
unités). A` noter qu'en l'absence de capacités de navigation et
de mémoire sur l'environnement, seul ce comportement permet de trouver
des zones de recharges (carreaux blancs ou noirs). Cette action dure 2
unités de temps.
- 'Eviter un obstacle (avoid) : le robot
effectue une marche arrière de 60 unités suivie d'une rotation de
180°. Cette action dure 2 unités de temps.
- Recharger sur zone noire (reload on dark) :
le robot s'arrête et recharge son EP : äEP = 0.027 × LD. Nous
remarquons que le robot ne recharge réellement son EP que s'il se trouve
sur une zone noire. Cette action dure 1 unitéde temps.
- Recharger sur zone blanche (reload on
light) : le robot s'arrête et recharge son E : äE = 0.027 × LB
et äEP = -0.027 × LB. Nous remarquons que le robot ne recharge
réellement son E que s'il se trouve sur une zone blanche. Cette action
dure 1 unitéde temps.
- Se reposer (rest) : le robot ne fait rien.
Cette action dure 1 unitéde temps.
A` chaque unitéde temps, le robot consomme 0.002 de son
énergie, même lorsqu'il choisit de se reposer. Si l'énergie
devient négative ou nulle, alors le robot meurt.
Afin de choisir une action, la mRF reçoit en
entrée la salience de chacune des
actions
calculée a` partir des variables internes et externes. La
salience correspond au degréd'urgence ou de motivation a`
effectuer une action. Les formules utilisées ici pour le
calcul des saliences sont les mêmes que dans
l'évaluation du modèle de la mRF par [Humphries et al., 2005]
ainsi que dans l'évaluation d'un modèle des ganglions de la base
par [Girard et al., 2003].
- Swander = -BL - BR + 0.8(1 - PE) + 0.9(1 - E)
- Savoid = 3BL + 3BR
- Sreload on dark = -2LB - BL - BR + 3LD(1 - PE)/
- Sreload on light = -2LD - BL - BR + 3LB(1 - E) 1 - (1 -
PE)2
Si la mRF ne réussit pas a` converger avec les
saliences données en entrée, alors l'action de repos est
sélectionnée. Dans notre expérience, un nouveau vecteur de
salience est propagépendant 100 itérations (1 itération
durant 1ms) dans la mRF et nous considérons qu'il y a convergence
dès lors que sur les 50 dernières itérations la variation
de chacune des valeurs du vecteur de sortie de la mRF est inférieure a`
0.001. Lorsque la mRF converge, alors nous considérons que l'action
sélectionnée correspond a` la sortie la plus élevée
de la mRF. Nous testerons également une variante o`u l'action
sélectionnée est modulée en fonction du contraste du
vecteur de sortie de la mRF.
4.2 Résultats
Pour 'evaluer chaque contrôleur du robot, nous avons
simul'e 5 tàaches de survie mini-male dans la fonction fitness, en
plaçant a` chaque fois le robot a` un endroit al'eatoire sur la carte et
initialis'e avec comme valeurs 0.5 en 'energie et 1 en 'energie potentielle.
Comme a` chaque unit'e de temps le robot consomme 0.002 de son 'energie, sa
dur'ee de vie minimale est de 500 unit'es de temps. Afin que l''evaluation
prenne un temps raisonnable de calcul, nous avons limit'e les simulations a`
3000 unit'es de temps chacune.
Tout d'abord, afin de v'erifier une suffisante complexit'e de
la tàache, nous avons 'evalu'e un contrôleur al'eatoire, qui
d'ecidait au hasard une action parmi les cinq possibles. Les r'esultats de ce
contrôleur montre une survie moyenne entre 500 et 600 unit'es de temps,
ce qui confirme que la tàache ne peut être r'esolue par un
contrôleur al'eatoire et fournit une base de comparaison.
Une seconde v'erification pr'ealable que nous avons effectu'ee
fut de tester un contrôleur de type Winner-Takes-All (WTA), ce dernier
choisissant l'action en se basant sur la plus forte salience. Nos premiers
r'esultats ont montr'e que ces contrôleurs avaient une dur'ee de vie
approchant souvent les 3000 unit'es de temps, ce qui signifiait que la
tàache 'etait trop simple pour 'evaluer notre modèle de la mRF
correctement. Nous avons subs'equemment essay'e de trouver un facteur
complexifiant la tàache et nous avons trouv'e que la vitesse de
d'eplacement du robot, non sp'ecifi'ee dans [Humphries et al., 2005], influe
grandement sur les r'esultats. Initialement, dans notre exp'erience, lorsque le
contrôleur du robot choisit l'action a` explorer al'eatoirement, il se
d'eplace en avant de 10 unit'es après avoir effectu'e une rotation
al'eatoire. Lorsque nous diminuons la vitessse d'eplacement a` 5 unit'es, la
tàache devient plus difficile et un contrôleur WTA n'a plus qu'une
dur'ee de vie moyenne d'environ 1250 unit'es de temps, ce qui est loin de la
dur'ee de vie maximum (3000 unit'es de temps). Par cons'equent, la
tàache semble non triviale a` r'ealiser. La figure 4.2 compare les temps
de survie des contrôleurs al'eatoire et WTA sur 1000 tàaches de
survie.
Les r'esultats du contrôleur mRF montrent qu'en quelques
g'en'erations seulement le robot r'eussit a` vivre plus de 2500 unit'es de
temps, voire le maximum 3000. N'eanmoins, il faut plusieurs centaines de
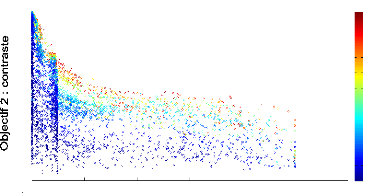
g'en'erations pour que le contraste devienne important. La figure 4.3 pr'esente
l''evolution du front de Pareto 2D d'un contrôleur mRF au bout de 500
g'en'erations : le temps de survie est proche ou 'egal a` la valeur maximum, le
contraste est d'environ la moiti'e du maximum th'eorique pour les meilleurs
individus. Les scores de l'objectif de plausibilit'e anatomique montrent que la
mRF respecte presque exactement les donn'ees connues sur la mRF. Concernant le
temps pass'e sur chacune des actions en moyenne pendant une tàache de
survie, la figure 4.5 montre qu'il n'y a pas de diff'erence notable entre les
diff'erents contrôleurs, a` l'exception
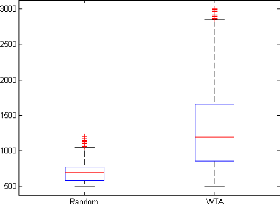
FIGURE 4.2: Comparaison des temps de survie des contrôleurs
aléatoire et WTA sur 1000 tâches de survie.
triviale du contrôleur aléatoire.
Nous avons essayéde forcer la mRF a` avoir un contraste
élevéen modulant les actions en fonction du contraste. A` cet
effet, nous avons redéfini chacune des 5 actions en incluant la valeur
du contraste, f étant la fonction de modulation du contraste :
- Explorer aléatoirement (wander) : le
robot se déplace aléatoirement (rotation
aléatoire entre 0 et f(contrast)x9° d'un
déplacement vers l'avant de f(contrast)x
5 unités).
- 'Eviter un obstacle (avoid) : le robot
effectue une marche arrière de f(contrast)x 60 unités suivie
d'une rotation de f(contrast) x 180°. Cette action dure 2
unités de temps.
- Recharger sur zone noire (reload on dark) :
äEP = f(contrast) x 0.027 x LD. - Recharger sur zone blanche
(reload on light) : äE = f(contrast) x 0.027 x LB et äEP =
-f(contrast) x 0.027 x LB.
- Se reposer (rest) : le robot ne fait rien.
En prenant comme fonction de modulation f(x) = /x et en
évaluant toujours chaque réseau sur 5 tàaches de survie,
les réseaux mRF obtenus présentent des durées de survie
similaires voire un peu inférieure aux contrôleurs WTA. Cependant,
le contraste est un peu meilleur que lorsque nous introduisons une fonction de
modulation, comme le
0.2
0
Numéro de génération
1
500
0.8
400
0.6
300
0.4
500 1000 1500 2000 2500 3000 3500
200
100
0
Objectif 1 : durée de survie
FIGURE 4.3: Front de Pareto 2D de l''evolution d'un
contrôleur mRF repr'esentant les scores des objectifs de dur'ee de survie
(abscisse) et de contaste (ordonn'ee) obtenus par chaque individu de chaque
g'en'eration au cours de l''evolution. Le contrôleur mRF a 'et'e 'evalu'e
sur 5 tâches de survie.
montre la figure 4.6. Par conséquent, la fonction de
modulation introduit une pression de sélection favorisant le contraste
aux dépens de la durée de survie. L'objectif de
plausibilitéanatomique a toujours un score entre -1 et 0, ce qui
signifie que les réseaux ont bien une structure de type mRF.
Autre variante de l'expérience initiale, nous avons
essayéde rendre la tàache plus
réaliste en supprimant
le calcul des saliences et donnant directement en entrée
des
réseaux les 4 variables externes (BL, BR, LD et LB) ainsi que les
2 variables internes
(E et EP), ce qui a pour effet de complexifier la
tàache. Nous avons également donnéen entrée 1-- E
et 1-- EP afin d'éviter que la tàache soit trop complexe, en
reprenant
ainsi la configuration de l'expérience de [Humphries and
Prescott, 2006]. Les réseaux ont donc dans cette variante 8
entrées et 4 sorties.
Le graphique 4.7 montre les fronts de Pareto obtenus au bout
de 1000 générations : nous voyons que certains réseaux ont
une durée de vie dépassant 2000 unités de temps,
néanmoins le contraste est très faible (inférieur a` 0.1).
Par comparaison avec les résultats obtenus avec le modèle de
Humphries [Humphries and Prescott, 2006], ce dernier indique que la plupart des
réseaux obtenus par évolution réussissent a` faire a`
peine mieux qu'un contrôleur aléatoire, mais les actions sont
modulées en fonction du contraste a` l'instar de ce que nous avons fait
dans l'expérience précédente. Ici,
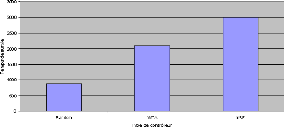
FIGURE 4.4: Comparaison des meilleures moyennes de temps de
survie sur 5 tâches obtenues par des contrôleurs aléatoire,
WTA et mRF. Pour chaque type de contrôleur, nous avons effectué20
000 évaluations, chacune d'entre elles consistant a` faire 5
tâches de survie et calculer la moyenne de la durée de survie.
Nous n'avons gardéici que la meilleure moyenne trouvée pour
chaque type de contrôleur.
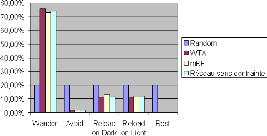
FIGURE 4.5: Comparaison du temps passésur chacune des
actions par les contrôleurs aléatoire, WTA et mRF. Ces
statistiques agrègent les données 500 tâches de survie pour
chacun des contrôleurs ayant les durées de survie les plus
élevées parmis 50 000 tâches de survie simulées.
nos réseaux réussissent clairement mieux qu'un
contrôleur aléatoire, cependant les actions ne sont pas
modulées.
Ces résultat montrent que la mRF est globalement plus
efficace qu'un simple réseau WTA et encore plus qu'un contrôleur
aléatoire, comme le résume la figure 4.4, contrairement aux
expériences de [Humphries et al., 2005] qui n'avaient pas réussi
a` évoluer la mRF de façon suffisamment optimale pour
dépasser le WTA. Cela signifie que la mRF est non seulement apte a`
faire de la sélection de l'action, mais que celleci peut faire face a`
des situations complexes o`u un réseau WTA ne suffirait pas.
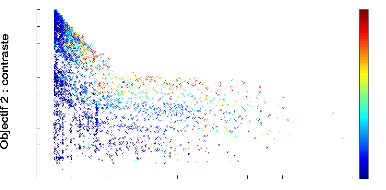
Numéro de génération
500
400
300
200
100
0
400 600 800 1000 1200 1400 1600 1800 2000 2200
1
0.8
0.6
0.4
0.2
0
Objectif 1 : durée de survie
FIGURE 4.6: Front de Pareto 2D de l''evolution d'un
contrôleur mRF repr'esentant les scores des objectifs de dur'ee de survie
(abscisse) et de contaste (ordonn'ee) obtenus par chaque individu de chaque
g'en'eration au cours de l''evolution, avec modulation des actions en fonction
du contraste. La fonction de modulation est f(x) = /x et le contrôleur
mRF a 'et'e 'evalu'e sur 5 tâches de survie.
Néanmoins, dans les variantes o`u nous essayons de
rendre la tàache de survie plus réaliste, en modulant les actions
en fonction du contraste des vecteurs de sortie de la mRF ou en donnant a`
cette dernière directement les variables internes et externes sans
calcul préalable de saliences, les résultats que nous avons
obtenus sont moins probants : il faudrait approfondir davantage ces variantes.
Autre point a` creuser, il serait intéressant de quantifier la
propension de nos réseaux mRF a` généraliser leurs
performances en les évaluant sur un nombre plus important de
tàaches de survie.
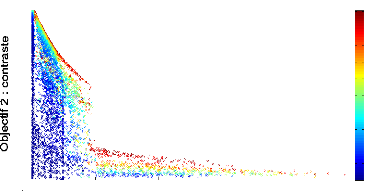
Numéro de génération
1000
1
0.8
0.6
0.4
0.2
0
800
600
400
200
0
500 1000 1500 2000 2500 3000
Objectif 1 : durée de survie
FIGURE 4.7: Front de Pareto 2D de l''evolution d'un
contrôleur mRF repr'esentant les scores des objectifs de dur'ee de survie
(abscisse) et de contaste (ordonn'ee) obtenus par chaque individu de chaque
g'en'eration au cours de l''evolution. Le r'eseau recoit directement
en entr'ee toutes les variables externes et internes, et le contrôleur
mRF a 'et'e 'evalu'e sur 5 tâches de survie.
| 


