Modélisation et simulation d'un robot mobile sur roues avec le logiciel Matlab/Simulink

EPIGRAPHE

1. « On parle parfois du rôle du hasard dans la découverte scientifique, mais le mérite du savant servit par l'imprévu, c'est d'avoir ^étésavant, d'avoir eu l'esprit tendu vers la solution du problème. » J. LALOUP

2. « Le hasard ne favorise que les esprits qui y ont ^étépréparés. »

Albert EINSTEIN

3. « Le hasard, c'est le chemin que DIEU emprunte lorsqu'IL veut rester anonyme. »

Albert EINSTEIN

IN MEMORIUM

A vous, papa Jean TENFUMA LULENGA, papa Boniface et papa William MULENGA NGOMBE, vous que la mort a arrachés de la portée de nos yeux, mais pas de nos coeurs. Que le fruit de cette oeuvre, que vous aviez vue commencer et que vous aviez désiré voir s'achever, soit une gerbe de fleurs sur vos tombes. Aujourd'hui, pendant qu'elle s'achève, vous êtes incapables de nouer un pagne aux hanches pour danser la victoire qui visite votre camp. Nous manquerons d'ouïr vos ovations et cris de joie.

DEDICACE

A notre Seul Sauveur et Seigneur ;

A nos aimables et dynamiques parents ;

A notre précieuse et compatissante épouse ; A nos rejetons ;

A nos oncles et tantes ;

A nos biens aimés frères et soeurs ;

A nos cousins et cousines ;

A nos neveux et nièces ;

A nos amis et connaissances ;

Au monde scientifique ;

A tous les humains ;

Nous dédions ce travail, couronne de sacrifices indescriptibles.

MATANDA KINAMA Tristan

AVANT PROPOS

Il est une exigence académique que tout étudiant présente et défende un mémoire devant sanctionner la fin de ses études universitaires. Nous n'avons pas été exempté de cette condition et c'est la raison d'être de ce mémoire. Sa rédaction n'a pas été l'oeuvre de notre mais seule, mais bien une sommation de plusieurs forces partielles, tant positives que négatives, que nous tenons de remercier.

Avant toutes choses, qu'il nous soit permis de remercier notre Seul Seigneur et Sauveur, le CHRIST JESUS, en qui DIEU nous a élu avant qu'aucune poussière de la terre ne soit créée à être Ses enfants d'adoption, selon le bon plaisir de Sa volonté.

Nos sentiments de gratitude vont à l'endroit du Professeur docteur ingénieur Alain DELCHAMBRE pour avoir proposé le sujet de ce travail et avoir accepter d'en assurer la direction en dépit de la distance et de ses multiples engagements à l'ULB (Université Libre de Bruxelles) et dans plusieurs universités du monde.

Nous ne saurons combien remercier l'ingénieur Vincent VANDAELE, chercheur au service de mécanique analytique de la faculté polytechnique de l'ULB, pour nous avoir fait bénéficiaire, de sa part, d'un encadrement rigoureux et scientifique à la hauteur de nos aspirations.

Nous nous faisons, à travers ce travail, le noble devoir de remercier tous les professeurs, chefs des travaux, assistants et techniciens de la faculté polytechnique de l'université de Lubumbashi (UNILU), de l'université de Kinshasa (UNIKIN), de l'université libre de Bruxelles (ULB), de l'université catholique de Louvain (UCL), de l'université de Mons qui se sont disposés pour nous engendrer « ingénieur ». De manière particulière, nous pensons aux professeurs : MULAPI WA LUMENGE, SUMUNA TEMO, KALENGA NGOIE,

KAMABU TSONGO, LIASSA NKOY, MUTONDO Ruffin, FRANCOIS NTAMBWE, LIVIU MASALAR, Augustin MPANDA pour leur sacrifice en notre faveur.

Nous remercions de tout coeur notre cher papa Félix Emmanuel KAZEMBE MATANDA KINAMA pour avoir beaucoup investi dans notre vie en général et nos études en particulier, et notre chère mère Philomène Wernemine Marie-Emman KASONGA MESOLENGA MASHAMO pour ses grands sacrifices visant à faire de nous des vases utiles.

Il serait impardonnable si nous manquons de remercier notre précieuse épouse, Jackie Suzanne Nadine KAMIN NAWEJ NAMBUND pour son affection et sa présence remarquable dans notre vie.

Ne pas honorer l'apport de nos frères et soeurs, oncles et tantes, cousins et cousines, beaux-frères et belles-soeurs, amis et connaissances serait un péché. Nous pensons à : Oncle Chadrac KAZEMBE et tantine BANZA, papa Benoît MATANDA, maman Guislaine MUJINGA et maman Agnès LUMBWE, papa Norbert MAMBWE et maman Charlotte MWISHIBWE, papa Honoré NGOIE et maman Phalonne NGOIE, vieux Placide KINKUKU et da Mamie, tonton Louis MASENGO et tantine Constance ILUNGA, tonton Dieudonné KABOBA et tantine Rose NGONGA, vieux Johny KAPEND et da Espérance MUJINGA, vieux Hubert KAUMBA et da Pélagie, vieux Pierre NGOIE et da Euphrasie,vieux Gerard KILOLO, Maurice KASONDE, Olivier MUSONA, Clément MWEPU, Micky MUKINGA, Auguy KAZEMBE, David KAZEMBE, Daniel KAZEMBE, Esther KASONGO, Seraya KAZEMBE, Mishael WAMALELE, Abigaïl KIPETE, Rabbim MWAPE, Thethe MILAMBO, Ignace LUKUNSHA, Priscille, da Marie, vieux Jean, Tshetshe NAWEJ , da Kannie, Aimé, Gabby et Francine, Yannick MBUMB et Jolie, Clémence URUNG, Julie MWAD, MUMBA, Florence MUJINGA, Prince MWAZAZ .

Nous remercions également nos beaux-parents, papa NAWEJ WANKAMB et maman Benedicte MUJINGA CHANDA, qui, dans notre vie, ont surgie au temps décisif pour donner leur part.

Que notre grand ami et frère dans le Seigneur, Donat KITAMBILE, trouve ici l'expression de notre profonde gratitude.

Nous ne saurons combien remercier les contributions de notre bien aimé frère dans le Seigneur, ingénieur Bertin POLOMBWE et son épouse Chouchou NYUNDU.

Enfin, nous remercions nos amis de lutte et nos frères en CHRIST, les un pour leur sympathie et les autres pour leur soutien et leurs prières. Particulièrement, nous pensons à : Erick SHIMBI, Mao NGOIE MWEPU, Jonathan MUMBA, Victor MUGANZA, Jean MBAZ...

Que tous celui qui lira ces phrases se voie honoré !

Pour cela et pour plus encore, nous disons à chacun grand merci.

INTRODUCTION

1. Problématique

Depuis la genèse, l'homme a toujours été condamné à suer, c'est - à - dire travailler durement, pour avoir son pain quotidien. Conscient de sa condition, il s'est décidé de se faire aider dans son labeur tout en gardant une position centrale de toute activité. Ce souci a vite engendré trois autres qui sont :

· La croissance de la productivité ;

· L'optimisation des procédés de fabrication ; et

· L'amélioration de la qualité des produits finis.

Il a donc inventé des machines, appelées robots, qu'il peut néanmoins contrôler et commander. Les robots sont maintenant présents presque partout dans les usines ainsi que dans notre vie de tous les jours et ils sont indiscutablement les nouveaux partenaires de l'homme.

Le contrôle et la commande nécessitent une bonne connaissance du système qui, d'ailleurs, n'est toujours pas très évidente. Une tâche importante de l'ingénieur est donc la réalisation d'un modèle censé réunir, dans un environnement choisi, un certain nombre de données représentatives de la réaliser, afin de résumer, sous forme condensée aisément manipulable, les aspects essentiels du système étudié. C'est la modélisation. Deux raisons importantes, qu'il convient de relever, motivent celle-ci:

· Prédire le comportement du système pour différentes conditions de fonctionnement : analyse de son comportement devant des actions possibles ou non et en tirer des informations significatives utiles tant au chercheur pour la conception et l'amélioration du système, qu'à l'exploitant pour la bonne conduite du système ;

· Elaborer une loi de commande à appliquer au processus pour qu'il réalise « au mieux » l'objectif assigné.

En ingénierie, la simulation est un moyen efficace et économique couramment utilisé pour faire des études préliminaires et / ou comparatives, tant au stade du développement (conception) qu'au cours du fonctionnement normal du système. Elle consiste à déduire le comportement d'un système sur base d'un modèle mathématique correspondant et remplit toutes les fonctions d'un laboratoire didactique virtuel. L'outil se prêtant le mieux est l'ordinateur. La simulation sur ordinateur exigera donc des logiciels. Parmi ceux qui existent, MATLAB/SIMULINK fait déjà parler de lui.

De ce fait, le présent travail consistera à modéliser la cinématique et la dynamique et élaborer un programme de simulation d'un robot mobile sur roues avec le logiciel MATLAB/SIMULINK en utilisant divers degrés de complexité.

2. Subdivision du travail

Pour bien répondre à ses objectifs, notre travail aura cinq chapitres, hormis l'introduction et la conclusion :

· Dans le premier, nous établirons le modèle cinématique du robot dans sa plus simple expression ;

· Dans le second, nous établirons son modèle dynamique dans sa forme la plus simple ;

· Ensuite les diverses améliorations (voir plus loin) seront introduites ;

· Dans le quatrième chapitre, nous décrirons l'architecture du programme de simulation ;

· Finalement, il s'agira de valider le code et interpréter les résultats.

PRESENTATION DU PROBLEME

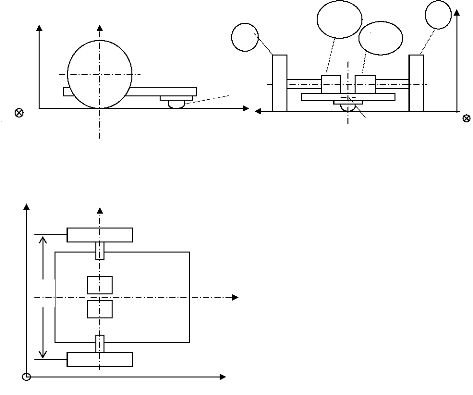
Le robot est constitué de deux roues motrices (1 et 3) actionnées indépendamment par deux moteurs à courant continu (M1 et M3) solidaires au châssis (2) du robot. Le troisième point d'appui est constitué d'une bille libre (B) qui n'est pas motorisée (Figure 1). Le robot se déplace sur un plan incliné d'un angle â par rapport à l'horizontale.

y1

y

O

z1

G1

x

M3

M1

G

G1

1

z

G3

B

3

z

y

O

y

l13

x1

x

Figure 1 : Projections orthogonales du robot

Par ce projet, on devra arriver à prédire la position, la vitesse et l'accélération du centre de masse du robot (sorties) à partir des valeurs de couples fournis par les moteurs ou à partir des courants appliqués à ceux-ci (entrées).

Nous partirons d'un modèle simple sans frottement, roulant sans glisser sur un sol plat. Ensuite, différentes améliorations seront prises en compte. C'est notamment ;

· La prise en compte de l'inclinaison â ;

· La prise en compte du frottement dans les différentes liaisons du robot (roues - châssis, roues-sol) ;

· La prise en compte de la dynamique des moteurs à courant continu ;

· La prise en compte de la limite d'adhérence des roues (roulement avec glissement sur le sol).

Nous considérerons que le robot est parfaitement symétrique (les axes des roues coïncident aussi parfaitement) et que les roues sont infiniment fines (existence d'un seul point de contact avec le sol).

Pour établir les équations de mouvement, deux méthodes équivalentes seront utilisées pour être comparées. Il s'agit de la méthode analytique ou méthode de LAGRANGE et celle des théorèmes généraux ou méthode synthétique. Une d'elle sera implémentée dans MATLAB pour la résolution et il faudra choisir l'outil de résolution numérique entre SIMULINK et les solveurs ODE (Ordinary Differential Equation).

Les chiffres entre crochets renvoient à la bibliographie.

Chapitre 1 : MODELE CINEMATIQUE

Ce modèle aura pour entrées, les angles de rotation theta1 et theta3 ( è₁ et è₃ ) des roues, et

? ? ?

pour sorties, la position rG , la vitesse vG , l'accélération aG et l'orientation alpha du robot.

1. Terminologie

Symboles		Désignation
		l13
distance entre roues		R
rayon des roues		G1
centre de roue 1		G2
centre de masse du châssis		G3
centre de roue 3		A
point médian entre roues, appartenant au châssis		G
centre de masse du robot		I1
point de contact de la roue1 avec le sol		I3
point de contact de la roue3 avec le sol		? ? ? ? = 1 . 1 + 1 . 1 + 1 . 1 rG rG x x rG y y rG z z 1
Vecteur position de la roue 1		? ? ? ? rG rG x x rG y y rG z z 2 = 2 . 1 + 2 . 1 + 2 . 1
Vecteur position du châssis		? ? ? ? rG rG x x rG y y rG z z 3 = 3 . 1 + 3 . 1 + 3 . 1
Vecteur position de la roue 3		? ? ? ? = 1 . 1 + 1 . 1 + 1 . 1 vG vG x x vG y y vG z z 1
Vecteur vitesse de G1		? ? ? ? = 2 . 1 + 2 . 1 + 2 . 1 vG vG x x vG y y vG z z 2
Vecteur vitesse de G2		? ? ? ? = 3 . 1 + 3 . 1 + 3 . 1 vG vG x x vG y y vG z z 3
Vecteur vitesse de G3		? ? ? ù1 , ù2 et ù3
Vitesses angulaires respectivement de la roue 1, du châssis et de la roue 3 dans la base d'étude.		? ? ? ? = 1 . 1 + 1 . 1 + 1 . 1 aG a G x x aG y y aG z z 1
Vecteur accélération de G1

? ? ? ? = 2 . 1 + 2 . 1 + 2 . 1 aG aG x x aG y y aG z z 2		Vecteur accélération de G2	? ? ? ? = 3 . 1 + 3 . 1 + 3 . 1 aG aG x x aG y y aG z z 3
Vecteur accélération de G3

Tableau 1 : Terminologie du modèle cinématique

2. Description des différents mouvements

? ? ?

La base d'étude est la base (x, y, z) ayant 1x , 1y et 1z comme vecteurs de

base. Cette base est liée au sol. Nous la considérerons donc comme galiléen à condition de
substituer à la force de gravitation la notion de poids et d'exclure les mouvements très précis (la

? ?

déviation vers l'est) ou très rapides. [2.4]. Au robot est lié la base (x1, y1 et z1) ayant 1x1 , 1y1 et

?

1 z1 comme vecteurs de base. La relation entre les deux bases est définie par les expressions :

? ? ?

1 x 1 = cosá .1 x+siná.1 y (1)

? ? ?

1 y 1 = - siná .1 x+cosá.1 y (2)

? ?

1 z 1 = 1z (3)

Les différents mouvements sont :

· Roue 1 par rapport au châssis : rotation d'angle theta1 autour de l'axe y1 (figure 1).

· Roue 3 par rapport au châssis : rotation d'angle theta3 autour de l'axe y1.

· Châssis par rapport au référentiel d'étude : mouvement quelconque dans le plan xoy c.à.d. rotation d'angle alpha autour de l'axe z et translation suivant les axes x et y.

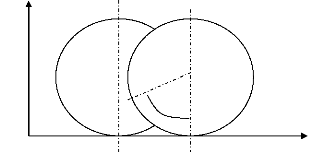
3. Etablissement du modèle cinématique Pour un roulement sans glissement, on a : (figure 2)

? ?

vG 1 = R.è& ₁ . 1 x ₁ (4)

x

z

G1

è

dè

G1'

Figure 2 : Déplacement infinitésimal d'une roue

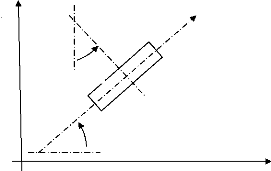
Dans la base fixe, la vitesse de G1 sera donnée par : (figure 3)

? ? ?

vG = R è&

1 . ₁ .(cos . 1 sin . 1 )

á x + á y (5)

De même, pour la roue 3 :

? ? ?

vG = R è&

3 . ₃ .(cos . 1 sin . 1 )

y

á

G1

á

x

?

vG₁

á x + á y (6)

	tan	á	=
					Et :

Figure 3 : Roue1 suivant une orientation á

?

Vu la non-linéarité du problème (á est variable avec le temps), la position rG du robot sera trouvée par intégration numérique.

? ?

rG ? vG dt

1 = 1 (7)

Et :

? ?

rG ? vG dt

3 = 3 (8)

Pour un solide indéformable, la connaissance du mouvement d'un point quelconque suffit pour décrire complètement le comportement cinématique de tout le solide. [2.3]. Donc le mouvement du point médian A est identique à celui du centre de masse G2 du châssis et à celui du centre de masse G de tout le robot.

De (7) et (8), on a :

? ?

? rG rG

1 + 3

rG = (9)

2

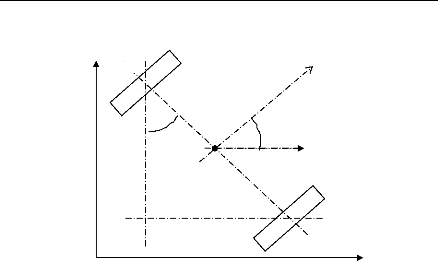
L'orientation du robot sera donnée par : (figure 4)

(10)

rG x

¹

- rG x

3

y

rG y rG

-

3 1

DG₁

=

DG₃

? rG x rG x

- ?

1 3

á arctan

= ? ? (11)

? rG y rG y

-

3 1 ?

Modélisation et simulation d'un robot mobile sur roues avec le logiciel - 9 -

MATLAB/SIMULINK

G3

x1

y

á

á

A

G1

D

x

Figure 4 : Robot suivant une orientation á

La vitesse et l'accélération du robot seront :

? R ? ?

vG = ( è & è &

+ ).(cos . 1 sin . 1 )

á x + á y (12)

2 1 3

?

dvG

dt

(13)

?

aG

Chapitre 2 : MODELE DYNAMIQUE

Ce modèle aura pour entrées, les couples C1et C3 appliqués aux roues, et pour sorties les angles de rotation è₁ et è₃ des roues.

1.Terminologie

Symboles		Désignation
		Ec1, Ec2 et Ec3
Respectivement énergie cinétique de la roue 1, du châssis avec ses sous-ensembles (moteurs et bille) et de la roue 3		EcR=Ec1+Ec2+Ec3
Energie cinétique totale du robot		I1 , I2 et I3
Respectivement tenseur central d'inertie de la roue 1, du châssis et de la roue 3		Ep1, Ep2 et Ep3
Respectivement énergie potentielle de la roue 1, du châssis et de la roue 3		EpR=Ep1+Ep2+Ep3
Energie potentielle totale du robot		Q1 et Q3
Respectivement force généralisée appliquée à la roue 1 et à la roue 3		? MC
Moment cinétique		? Mext
Moment des forces extérieures		g=9,81
Accélération de la pesanteur

Tableau 2 : Terminologie du modèle dynamique

2 .Méthode de LAGRANGE

2.1. Expression de l'énergie cinétique

Par le théorème de KOENIG relatif à l'énergie cinétique, on a :

Ec1 = Energie cinétique de la roue dans son référentiel barycentrique

+

Energie cinétique de son centre de masse dans le référentiel lié au sol

Ceci conduit alors à l'expression :

2

1 ? 1? ?

Ec = m vG + 1 1 1

ù I ù

. . (14)

1 1 1

2 2

Avec :

? & ? ?

ù 1 = è ₁ . 1 y ₁ + á & . 1 z 1 (15)

0 0 2 m 1 R	? ? ? ? ? ? ?? ?		(16)	4

?

?

I= 1 ? ?

??

?

0 0

Et

2

R

0

m 1

4

2

m R

1

0

2

dans les axes principaux d'inertie de la roue 1.

2

1

1 = m R è & + á &

. 2 2

Ec (6 ) (17)

1

8

De même :

2

3

3 = m R è & + á &

. 2 2

Ec (6 ) (18)

3

8

Le robot étant considéré parfaite ment symétrique :

m1=m3=m (19)

et posons :

m2=M (20).

(17) et (18) deviennent :

2
Ec 1 = m R è & + á &

. 2 2

(6 ) (21)

1

8

2
Ec 3 = m R è & + á &

. 2 2

(6 ) (22)

3

8

Pour le châssis, le théorème de KOENIG donne :

2

? ? ?

1 M vG 1

Ec = + 2 2 2

ù ' ù

. . (23)

2 2

2 2

Avec :

? ?

ù 2 = á & . 1 z 1 (24)

?

' = ?

² 12 ?

?

0 0

b

² + c ²

M ?

d b

2 2

0 + 0 ? (25)

c d

2 2

+

0 0

Et

dans les axes principaux d'inertie du châssis. (Figure 6)

MR ² M

2 2 2 2

Ec = è & è &

( + ( ). (26)

2 1 3 ) + c d á &

+

8 24

Et finalement, on a :

2 2 2 2

) MR ²

(27)

(6 m M R

+ mR M c d

? ( + ) ?

2 2 2

= ( è è

& &

Ec_R + ) è è

& &

+

1 3 1 3

. + + á &

8 4 ?? 4 24 ??

2.2. Expression de l'énergie potentielle

Comme le robot se déplace sur un sol plat, son énergie potentielle sera nulle :

EpR=0

2.3. Expression du lagrangien Le lagrangien L aura pour expression :

2 2 2 2 + ) MR ^2 (6 m M R ? mR M c d ( + ) ? 2 2 2 L = EcR = ( è è & + & ) + è è & & 1 3 1 3 . + + á & 8 4 ?? 4 24 ??

(28)

2.4. Expression des forces généralisées

Q1=C1 (29) et _Q3=C3 (30)

2.5. Expression des équations de LAGRANGE

d

2.5.1. Equation relative à è1

? L ? L

( ) - = Q (31)

1

dt

? è^& ? è

1 1

2.5.2. Equation relative à è₃

d ? L ? L

( ) - = Q

dt ? è^& ? è

(32)

3

3 3

Il nous sera difficile de développer analytiquement les équations (31) et (32) à cause de leur non-linéarité.

3. Méthode des théorèmes généraux

Il est intéressant d'appliquer ces théorèmes à la fois dans le référentiel fixe (absolu) et dans le référentiel mobile lié au châssis pour comparer les résultats. Mais, par soucis de simplification, nous ne travaillerons que dans le référentiel mobile. Les résultats du référentiel fixe seront repris dans les annexes (Annexes 2).

R15

z1

y1

x1

R6

è2

R16

R11

R8

R13

R9

è1

R4

R10

R7

R5

R7

R12

R12

R3

R4

R10

R13

R8

R9

R1

R11

R14

R6

R5

R2

3.1. Diagrammes des corps rendus libres

Roue 1

z1

x1

R4

y1

y1

R2

r

R6

R8

R5

R3

z1

R6

x1

R4

R3

R1

R1

R2

R7

R5

Figure 6 : Projections orthogonales de la roue 1 rendue libre

R14

R11

R5

R10

R8

R6

R13

R14

R11

R9

b

R4

R6

f

R9

R12

R5

R7

e

R10

R4

O2

d

l

c

Châssis

R12

R10

R9

X3

R15

Roue 3

z3

y3

Z3

R11

X3

R16

R15

R11

R13

R10

R9

R15

Y3

MR

& & & &

(39)

2

(è ₁ +è₃) =

R R

-

4 9

3.2. Théorème de la résultante cinétique

3.2.1 Roue 1

Ce théorème, appliqué à la roue 1, donne :

? ? ? ?

d?

m . vG mg z R R x R R y R R z

= - . 1 (

- + - + + +

1 1 1 4 ) . 1 (

1 2 5 ) . 1 (

1 3 6 ) . 1 (33)

1

dt

De l'expression (4):

d ? ? d ? ? ?

è & & + . . 1

è & x R x R

dt

è & & + . . . 1

& & y (34)

è á

vG R x R

= . . 1

= . . 1

1 1 1 1 1 1 1 1 1

dt

Comme nous dérivons dans un référentiel mobile, nous pouvons aussi faire usage du vecteur de DARBOUX pour arriver au même résultat (Voir plus loin).

Soit, en le projetant sur différents axes:

mR è& & 1 = - ( R₁+R₄) (35)

mR .è & 1 .á & = - (R₂ +R₅) (36)

R ₃ + R₆ = m.g (37)

3.2.2 Châssis

Appliqué au châssis, il donne :

? ? ? ? ?

d

m . vG Mg z R R x R R y R R R z

= - . 1 (

+ - + - + + -

2 1 4 9 ) . 1 (

1 5 10 ) . 1 (

1 11 14 6 ) . 1 (38)

1

dt

Soit, en le projetant sur les axes :

MR
2

.

d dt

? MCG

1

=

d dt

? MCG1 rel

? ? + ù 1 ? MC Darb 1 (48) G

(è^&₁ + è & á & = - (40)

3 ). R R

5 10

R ₁₄ + R 11 - R 6 = M . g (41)

3.2.3 Roue 3

Appliqué à la roue 3, il donne :

? ? ? ?

d?

m . vG mg z R R x R y R R z

= - . 1 (

+ - + + -

3 1 9 15 ) . 1 1 10 . 1 (

1 16 11 ) . 1 (42)

1

dt

Soit, en le projetant sur différents axes:

mR è& & 3 = R 9 - R 15 (43)

mR . è & 3. & á= R 10 (44)

R 16 - R 11 = m . g (45)

3.3 Théorème du moment cinétique

3.3.1 Roue 1

Le moment cinétique de la roue 1 en son centre de masse est donné par :

? ?

MCG 1 = I₁ .ù 1 (46)

Soit :

? mR

2

? ?

MC_G = (2 . 1

è & y + z

á & . 1 ) (47)

1 1 1 1

4

La dérivée, dans la base mobile, de l'expression (47) sera :

?

ùDarb 1 est le vecteur de Darboux et vaut :

? ?

ù Darb 1 = á & . 1 z 1 (49)

d

? mR

2

? ? ?

. MC = ( 2 . . 1 2 . 1

- & áè & x á & & . 1 ) (50)

1 1 1 + y

è & & 1 1 + z

dt

G 1

4

Le moment des forces extérieures dans la base (x1, y1, z1) est :

? ? ? ? ? ? ? ? ? ? ? ?

Mext R z R x R y R z r y R x R y R z R x C y R z

= - 1 ( 1 - 1 1 ) 1 ( 1 1 1 ) 1 1 1 )

1 1 × - 1 1 2 ₁ + +

3 1 1 × - 4 1 - 5 ₁ + -

6 1 7 1 + (51)

1 ₁ + 8 1

Soit :

? ? ? ?

Mext R r R R R x R R C y R r R z

= ( . - - + + + + (52)

1 6 2 . ) . 1 ( . ) . 1 ( . ) . 1

7 1 1 1 1 4 8 1

Partant des expressions (50) et (52), le théorème du moment cinétique, projeté sur différents axes, s'écrit :

mR 2

2

è & á & =

1 . R r R R R

- (53)

6 . - 2 . 7

mR 2

2

mR 2

è& & = R R C

+ (54)

1 1 . 1

á& & = +

R R r

. (55)

8 4

4

3.3.2. Chassis

Le moment cinétique du châssis en son centre de masse est donné par :

? ?

MCG 2 = I₂ .ù₂ (56)

Avec :

? ?

ù 2 = á&. 1 z 1 (57)

Soit :

2 2

? M c d

( + ) ?

MC_G = á& (58)

. 1 z

2 1

12

La dérivée, dans la base mobile, de l'expression (58) sera :

.

d dt

? MC G

2

=

d dt

? MCG2 rel

? ? + ù 2 ? MC Darb 2 (59) G

?

ùDarb 2 est le vecteur de Darboux relatif au châssis et vaut :

? ?

2 2

d ? +

M c d

( ) ?

ùDarb 2 = á&. 1 z₁ (60)

. MC

= á&& (61)

. 1 z

dt

G 2 1

12

Le moment des forces extérieures dans la base (X1, y1, z1) est :

? Mext

? ? ? - e ? ? ? f = ? - ? 2 ? 2 ? ? ? b ? ? ? 2 ?

(

x1 , y 1 , z1 )

(

?

?

?

? [ ?

R₄ l 0

? R₅ + 0 A 0 + A - RH

R6

^? ?( x1 , y 1 , z 1 )-b R 14
?(x1 , y 1 , z 1 )f2b e

(

2

?

x1 , y 1 , z1 )

R 11

R₉

? ?

? R R

-

7 12 ?

(62)

+ 0

? ?

? ? R R

- ?

1 , y1 , z1 )

x y z

1 , 1 , 1 ) 13 8 (

? x

Ou bien :

(

2

?

x1 , y 1 , z1 )

( +R₁₁).

₆

b

(R 10 - R5). 2 + R₇ -

f₊ 2

R12 ?

R

2 = I (R 4 - R₉ ).

b +(R 11 , R₆ ).

e-R14

²

.l (63)

Mext

( )e + (R ₄ +R9).

R 13 - R₈

x1 , y 1 , z1 )

f₊ 2

(

R ₁₀ R5

Partant des expressions (61) et (63), le théorème du moment cinétique, projeté sur différents axes, s'écrit :

(R ₆ + R₁₁ )+b (_R10 - R ₅ ) + R 7 - R₁₂ = 0 (64)

2 2

b (R₄ - R₉ ) + e.( R 11 - R₆ )- l. R 14 = 0 (65)

²

(66)

2 _d2 \

M ( c + ⁾á&& = 2

f

12 (R ₄ + R ₉) + e. (R 10 - R ₅) + R 13 - R₈

3.3.3. Roue 3

Comme pour la roue 1, on aura :

? ?

MCG 3 = I ₃ .ù 3 (67)

Soit :

? mR

2

? ?

MC_G = (2 . 1

è & y + z

á & . 1 ) (68)

3 3 1 1

4

La dérivée, dans la base mobile, de l'expression (68) sera :

a

? mR

2

?

? ?

. MC = ( 2 . . 1 2 . 1

- á & è & x á & & . 1 ) (69)

3 3 1 + y

è & & 3 1 + z

at

G 1

4

Le moment des forces extérieures dans la base (x1, y1, z1) est :

? ? ? ? ? ? ? ? ? ? ?

1 ( 1

1 ) 1 ( 1

1 ) 1 1

Mext = - R z R x R z r y R x R y R z R x C y R z

1 11 1

1

× - + - × + - - + -

3 1 15 1 16 1

1 9 1 10 1

12 1 3 1 13 1

(70)

Soit :

? ? ? ?

Mext R r R x R R C y R r R z

= ( . ) . 1 ( . ) . 1 ( . ) . 1

+ + + + - (71)

3 11 12 1 15 3 1 9 13 1

Partant des expressions (69) et (71), le théorème du moment cinétique, projeté sur différents axes, s'écrit :

2

mR

2

2

mR

2

2

mR

è & á & = R r R

+ (72)

3 . 11 . 12

è& & = R R C

+ (73)

3 15 . 3

á& & = R r R

4

- (74)

9 . 13

3.4. Système d'équations à résoudre

Les équations (35), (36), (37), (39), (40), (41), (43), (44), (45), (53), (54), (55), (64), (65), (66), (72), (73) et (74) constituent le système de 18 équations différentielles à 18 inconnues à résoudre avec MATLAB.

Les simplifications et substitutions conduisent au système suivant : De l'équation (54), on trouve :

2 . 2

R R + C

1 1

è& & = 1 (75)

.

m R ²

De (73), on a :

.

i₌2 /65 +2C3 (76) m R 2

(76) dans (35), on tire :

R1 = R4. R +2 C1 (77)

3R

De (36), on tire :

R2 = 2m+M (-R10 -m.R . di. et) (78)

M

De (37), on a :

R ₃ = m. g - R₆ (79)

De (65), on tire :

R =

4 [ ( 6

2 e R R l R R

- +

11 ) . 14 ] 9

+ (80)

b

(44) et (36) dans (40), avec (78), on a :

M

R 5 = R10-

2 m+MR2 (81)

(75), (76) et (80) dans (39) donne :

R6= b .m (R1 +R15) - l R14-R11 (82)

e

(2 m+M).e

(53), avec (36), donne :

R 7 = r . R₆ + mR2 _uA1 xi R. R₂ = 2r.R ₆ 3R.R₂ R.R5 (83)

2 2

2

mR

R = á&& - (84)

r R
.

8 4

4

De (66), on a:

M c d

2 2

2 (

? + ) ?

R = á&& + e R R R R

.( - + -

9 5 10 ) R (85)

8 13 4

?? -

f ?? 12

De (64), on a :

2 ? -

b ?

R = ( 5

R R R R R

10 ) 12

+ - - (86)

11 7 6

f ?? 2 ??

De (72), avec (44), on tire :

(87)

mR ² R R

. + 2 .

r R

10 11

R = - è & á & -

. r R

. = -

12 3 11

2 2

(74) devient :

2

mR

R = r R -

. á&& (88)

13 ⁹ 4

(65) devient :

R14 = R6-R11+Mg (89)

(76) dans (73), on tire :

R R C

. ₉ 2 3

-

3

(90)

R15

R

(45) devient :

R16 = m. g +R₁₁ (91)

4. Comparaison entre les deux méthodes

Il est vrai que le formalisme de lagrangien est intéressant pour les systèmes à plusieurs poins libres ou liés [1.3], car par la méthode des théorèmes généraux il faut écrire n équations à n inconnues (18 pour notre cas). Mais ici, la puissance du formalisme est réduite sensiblement car la résolution de l'équation fournie demande d'abord l'évaluation du lagrangien

donné par l'expression (28) et ensuite le calcul de ses variations par rapport à è₁ , è^&₁ , è₃ et è^&₃ .

Encore, le formalisme est inutilisable en présence des frottements. Ceci dit, dans la suite du projet, nous ne travaillerons plus qu'avec la méthode des théorèmes généraux.

Chapitre 3 : AMELIORATIONS

1. Prise en compte de la dynamique des moteurs

Les moteurs à courant continu sont caractérisés par leur type d'excitation. Dans les variateurs de vitesse, on trouve essentiellement ceux à excitation indépendante ou série. [1.8]

Le bilan des puissances montre que :

Cem = Cu + Cpertes (92)

Or Cpertes est faible et comme le rendement a une expression complexe, il est plus commode de raisonner sur le couple électromagnétique et c'est ce que l'on fait toujours. [2.2]

Il y'a deux manières d'exprimer la dynamique des moteurs à courant continu, selon qu'on a pour paramètres de couple :

-la tension appliquée u, le courant d'induit ia et la résistance d'induit ra :

C ( - . ) .

u ra ia ia

= (93)

è&

-le courant d'induit et le flux par pôleö :

C=K. ia.ö (94)

K est une constante du moteur, qui dépend du nombre de paires de pôles p, du nombre de brins actifs n et du nombre de paires de voies d'enroulements a, et vaut :

p n

.

K 2 . .

ð a

= (95)

Des modèles (93) et (94), nous retiendrons le dernier parce qu'il ne fait pas intervenirè^& , qui est une sortie du modèle dynamique.

Dans l'expression (94), on voit qu'il y'a deux moyen de faire varier le couple :

· Par variation du flux ö , donc du courant d'excitation ;

· Par modification du courant d'armatureia .

Ici, nous ne considérerons que la variation par modification de ia à cause des inconvénients suivants de la variation de flux : [1.8]

· Saturation du fer ne permettant pas d'atteindre des valeurs de flux ^aussiélevées que l'on désire (réglage de vitesse dans des rapports 1 à 4

seulement alors que par modification de ia on a des gammes de vitesses allant jusqu'à des rapports de 1 à 200, et ce, dans des laps de temps très courts) ;

· Importance de l'inductance du circuit d'excitation conduisant à une constante de temps relativement grande et empêchant des variations rapides du courant d'excitation ;

· ie p ia et peut, de fois, conduire au désamorçage des thyristors du variateur de vitesse (ie plus petit que le courant de maintient).

2. Prise en compte du frottement dans les liaisons du robot

Le couple de frottement est donné par la relation :

Cf = N. re . fa (96) [1.7]

Où re est le diamètre des essieux et fa, le coefficient de frottement entre les essieux et les moteurs (Ce frottement sera considéré sec) et N la réaction normale de la liaison châssis - roue (résultante de R6 et R4, et celle de _R11 et R9).

Pour ce projet, nous prendrons fa compris entre 0.05 et 0.1. [1.7]

La présence du frottement dans les liaisons du robot se manifestera par une réduction du couple moteur. Comme le frottement dans les articulations du robot n'a pour effet que de réduire le couple moteur appliqué à la roue, la seule modification à faire sera donc la considération d'un couple réduit Cred tel que :

Cred 1 = C₁ - Cf

Quatre expressions seulement vont changer, toutes les autres seront maintenues.

R R + C - re fa R + R

2 . 2 . ( . . )

1 1 6 4

2 2

è& & = (97)

¹ m R ²

.

2

2 R + C - re fa R + R

2

2 . ( . .

15 3 11 9

)

è& & = (98)

³ m R ²

	+	R ^2 4		)	(99)

.

R R

. 2 . (

+ C re fa

- . .

4 1

R 1 3 R

						) (100)	R 15
R R . 9	- 2. ( C re fa - . . 3
	3 R

3. Prise en compte de l'inclinaison â du plan d'appui du robot par rapport au sol (horizontal)

Si le plan d'appui est incliné d'un angle â par rapport à l'horizontal, le robot ne sera pas toujours sur la plus grande pente (pente apparente), mais plutôt sur une pente ? (pente réelle) telle que représentée sur la figure 8 et donnée par :

y2=y

x1

z2

x

á

?

â

^â

x2

Figure 9 : Différents axes relatifs au plan incliné

L'amélioration ici sera le fait que le poids de chaque corps ne sera plus suivant l'axe des z, mais plutôt suivant l'axe z2 de la base (x2 ,y2, z2) telle que :

? ? ? ? ? ?

1 x = cos . 1 sin . 1 cos . cos . 1 cos . sin . 1 sin . 1

â x - â z = â á x - â á y - â z (101)

2 1 1 1

? ? ? ?

1 1 2 sin . 1 ₁ cos . 1 1

y y

= = á x + á y (102)

? ? ? ? ? ?

1 z = sin . 1 cos . 1 sin . cos . 1 sin . sin . 1 cos . 1

â x + â z = â á x - â á y + â z (103)

2 1 1 1

3.1. Théorème de la résultante cinétique

3.1.1. Roue 1

Ce théorème, appliqué à la roue 1, donne :

? ? ? ?

d?

m . vG mg z R R x R R y R R z

= - . 1 (

- + - + + +

1 2 1 4 ) . 1 (

1 2 5 ) . 1 (

1 3 6 ) . 1 (104)

1

dt

Soit :

d

? ? ? ? ? ? ?

(105)

m . vG mg

= - .(sin . cos . 1 sin . sin . 1 cos . 1 ) (

â á x - â á y + â z - +

R R x R R y R R z

- + + +

1 1 1 1 1 4 ) . 1 (

1 2 5 ) . 1 (

1 3 6 ) . 1 1

dt

Ou bien :

mR è^&& = - ( . . sin . cos

m g â á + +

R R ) (106)

1 1 4

mR . .

è & á & = m g

. . sin . sin (

â á - R R

+ ) (107)

1 2 5

R ₃ + R₆ =m.g . cos â (108)

3.1.2. Chassis 2

Appliqué au châssis, il donne :

? ? ? ?

d?

m . vG Mg z R R x R R y R R R z

= - . 1 (

+ - + - + + -

2 2 4 9 ) . 1 (

1 5 10 ) . 1 (

1 11 14 6 ) . 1 (109)

1

dt

Ou bien :

? ? ? ? ? ?

d ?

1 (110)

m . vG Mg

= - .(sin . cos . 1 sin . sin . 1 cos . 1 ) (

â á x - â á y + â z + R R x R R y R R R z

- + + + + -

2 1 1 1 4 9 ) . 1 (

1 5 10 ) . 1 (

1 11 14 6 ) . 1

dt

MR

Soit, en le projetant sur les axes :

& & & &

2 1

MR

2

( è è

+ 3 R ₄ R ₉ M g

) = - - . . sin . cos

â á (111)

(è & 1 + è & á & =

3 ). M g

. . sin . sin

â á + -

R R (112)

5 10

R ₁₄ + R₁₁ - R₆ =M.g . cos â (113)

3.1.3. Roue 3

Appliqué à la roue 3, il donne :

d

? ? ? ? ? ? ?

(114)

m . vG mg

= - .(sin . cos . 1 sin . sin . 1 cos . 1 ) (

â á x - â á y + â z + R R x R y R R z

- + + -

3 1 1 1 9 15 ) . 1 1 10 . 1 (

1 16 11 ) . 1 1

dt

Et sur les différents axes, on a :

mR & & 3 = R 9 - R 15 - m . g . sin . cos

è â á (115)

mR è & á & = m g â á + R (116)

. ₃ . . . sin . sin 10

R 16 - R₁₁ =m.g . cos â (117)

3.3. Théorème du moment cinétique

Aucune modification n'est à faire ici car le bras de levier du poids est nul.

m g .

. . sin . co s R â á + R R . 2. ( + C re fa - . . 4 1

R R 2 2 + 6 4

)

R R m g . - . 9

. . sin . cos 2 . ( R â á - C re fa - . . 3

R R 2 2 + 11 9

)

3 R

3 R

R 1 =

R 15

(124)

(125)

Après simplifications et substitutions, les expressions modifiées seront:

2 m M

+

R m g

= . . sin . cos

â á - -

R m R

. . .

è á

& & = ( . . sin . cos

m g â á - m R

. . .

è á

& & - R ) (118)

2 5 1 1 10

M

R 3 = m. g . cos â -R₆ (119)

mR .è & 3 .á& - m.g . sin â.sin á = R₁₀ (120)

R 14 = R6 -R₁₁ +M.g . cos â (121) - . . . sin . cos 2

R 15 =

â á - C

. R m g R

3R

R 9 ³ (122)

R 16 = m. g . cos â +R₁₁ (123)

4. Modèle complet

Le modèle complet est celui reprenant toutes les améliorations. L'utilisateur n'aura donc plus qu'à considérer les valeurs adéquates de chaque paramètre pour son cas d'étude. Il est constitué des expressions (80), (81), (82), (83), (84), (85), (86), (87), (88), (97), (98), (118), (119), (120), (121), (123), (124) et (125), auxquelles il faut ajouter :

Chapitre 4 : DESCRIPTION DE L'ARCHITECTURE DU
PROGRAMME

Intervalle d'intégration

Equation différentielle d'ordre n

Changement des variables

Système d'équations
différentielles d'ordre 1
[Y']=f ([Y])

Intégration du système

Vecteur [Y]

Conditions initiales

1. Généralités

1.1 But du chapitre

Ce chapitre a pour but de décrire et représenter l'enchaînement des opérations à

effectuer par ordre chronologique dans l'exécution du programme.

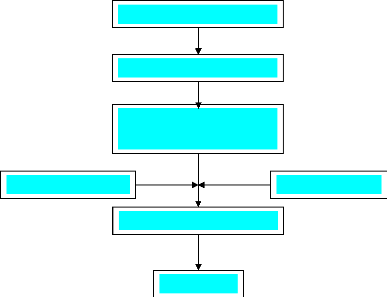
1.2 Résolution numérique d'une équation différentielle ordinaire d'ordre n Pour résoudre numériquement une équation différentielle ordinaire, on suit les

étapes suivantes :

· Changement de variables ;

· Transformation de l'équation en un système d'équations différentielles d'ordre un ;

· Intégration du système avec un solveur ode.

En résumé, on a :

1.3. Développement des intégrateurs numériques utilisés par le logiciel MATLAB

1. Forme canonique d'une EDO (équation différentielle ordinaire).

Equation : f ( y , t ) dy = dt

(126)

Condition initiale : y ( t _o ) = yo

Solution exacte : y = F (t)

Ou bien = + ?

t

f (y , t )dt

(127)

0

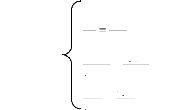
2. Transformation vers une forme canonique

d z

2

n - 1

dz d z

ⁿ d z

Soit l'équation : = G z

( , , ,..., ₁ , )

t

ⁿ dt ²

dt dt dt n -

y 2

1 =

dt

dt

n

n

d

dy

z

=

dt

n

dt

z y

= 1

dz

dy

On posera :

n

-

dy

dt

1 =

y n

1

-

n

d

z

=

1

-

n

dt

(128)

f

( t , y)

Si :

dy

=

dt

y t _o= y_o

t

(129)

alors, la solution exacte sera : = + ?

y t y o f t y dt

( ) ( , )

0

Pour une solution numérique y_j , l'erreur commise sera : e j = y_j-y( t _j) (130)

3. Méthodes à pas constant

1) Méthode d'EULER ou de la tangente Soit à résoudre l'équation différentielle :

dy = dt

f ( y , t )

Considérons le développement de TAYLOR de y(t) autour de t_o, qui s'écrit :

) (131)

n

y t

' ' ( ) y t

( ) ( )

o n o

y t y t

( ) ( ) ( ) . ' ( ) ( ) .

2

= + -

t t y t + -

t t + + -

( ) .

t t + R t

n (

o o o o o

n

²! !

En se limitant à l'ordre 1 dans ce développement, on a :

y ( t ) = y(t _o ) + ( t - t _o ) .y ' ( t _o) (132)

Ou bien :

y n + = y _n + h f t _n y n (133)

. ( , )

1

Avec :

h = t n +1 -t n (134)

Les expressions (133) et (134) définissent la méthode d'EULER. Elle revient à estimer la solution au voisinage de t_n sur la tangente à la fonction f (t, y). Elle est assez précise pour des pas petits.

2) Méthode de HEUN

C'est une méthode en 4 étapes qui sont :

· Calcul de la fonction f en tj-1 :

k₁ = f( t j -1, y j -1) (135)

· Calcul de yj^* par la méthode de EULER explicite :
y j * = y j - + h.k (136)

1 1

· Calcul de la pente en (tj , yj *) :
k₂ = f(t _j , y _j ) (137)

· Calcul final de la solution finale entre k1 et k2 :

y j y j = - 1

k k + 1 2 + h . (138) 2

3) Méthodes de RUNGE-KUTTA (RK)-ODE 23 et ODE 45

Elles sont une amélioration de la méthode de HEUN et elles font la moyenne entre m

pentes.

Formule générique :

y j = y+ w₁. k ₁ + w₂ .k ₂ + + wm.k m (139)

Avec :

k1 = f ( t j -1, y j-1)

k 2 = f ( t + c2.h , y + a21.k1

)

)

k = f t j - + c h y j - + a k + a k

( . , . .

3 1 3 1 31 1 32 2

k f t

= ( + c h y

. , + a k a k

. + . ....

+ + a . )

k (140)

m j - 1 m j - 1 m 1 1 m 2 2 m m

( 1 )

- m - ¹

L'ordre m de la méthode dépend de l'ordre du développement de la série de TAYLOR correspondante.

Les termes wi, ci et ai sont choisi par identification avec les termes du développement de TAYLOR à l'ordre m. Pour faire cette identification, on arrive toujours à un système de n équations à n+1 inconnues. On doit alors fixer un paramètre au choix, lequel choix étant fait de manière à minimiser l'erreur d'intégration.

On voit bien que la méthode de HEUN est une méthode de RK d'ordre 2 avec c2=a21=1, w1= w2=1/2.

La méthode de RK d'ordre 4(RK4), s'écrit :

1 1 1 1

y j y j h k k k k

= - +

1 .( 1 + + + ) (141)

2 3 4

6 3 3 6

Avec :

k1 = f ( t j -1 , y j-1)

)
)

k 2 = f( t +^h ,y + h .

2 j2

k 3 = f( t +h 2 j2

, y + h k2

k_m = f( t j - ₁+ h,y j - ₁+ h.k₃ ) (142)

La précision de la méthode dépend de l'ordre, cependant l'utilisation d'ordres supérieurs n'est pas très intéressante. Cette précision augmente lorsque le pas h diminue. [3.3]

4. Méthode à pas variable

C'est une méthode numérique qui ajuste le pas d'intégration au cours de la résolution. Pour cela, il faut estimer l'erreur commise à chaque pas d'intégration. Si l'erreur d'intégration est trop grande, par rapport à un critère fixé, alors on réduit le pas h. Si l'erreur est petite, par rapport au même critère, on peut alors se permettre d'augmenter le pas pour aller plus vite. Deux solutions sont en vue :

· Solution 1 : Calculer une solution à un point donné avec deux valeurs de h différentes :

o Si le résultat est le même, alors on conserve la valeur grande de h pour le pas suivant ;

o Si le résultat est différent, on suppose que le meilleur résultat est obtenu avec la petite valeur de h qu'on conserve pour le pas suivant.

· Solution 2 : Utiliser deux méthodes en parallèle avec le même pas h mais avec des ordres différents.

Cette solution nous conduit aux solveurs ODE 45 et ODE 23 implantés dans MATLAB :

o ODE 23 : C'est la méthode de RK-FEHLBERG 23 qui utilise les méthodes de RK d'ordres 2 et 3 :

On calcule successivement yjavec RK2, yj^* avec RK3 et ?j = yj - yj^* (avec un même pas h) :

Si la valeur de ?j est inférieure à la tolérance fixée, alors on accepte yj tout en maintenant h ;

Si la valeur ?j est très petite que la tolérance fixée, alors on accepte yj et on augmente h ;

Si la valeur de ?j est supérieure à la tolérance fixée, alors on recommence avec h plus petit.

Comme c'est la méthode numérique qui choisit le pas, on n'a pas la
solution aux temps désirés. Il est alors nécessaire d'interpoler les résultats.

Cet intégrateur a un bas niveau d'exactitude et est utilisé pour des problèmes non raides avec tolérances brutes ou pour résoudre des problèmes modérément raides.[]

o ODE 45 : Ici les ordres sont 4 et 5. Cet intégrateur est employé la majeur partie du temps et il est le premier en vue pour tout problème. Il a un niveau moyen d'exactitude. [3.3], []

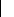
Pour ces deux méthodes, le pas d'intégration est fixé de manière à avoir :

ô -< max(Re lTol * y_j ,AbsTol) (143)

ti étant une estimation de l'erreur locale produite par la méthode numérique .

La tolérance relative (RelTol) et la tolérance absolue (AbsTol) sont respectivement 1^e-3 et 1e-6 par défaut.

5. Méthodes à pas liés

Elles consistent à évaluer yj à partir de plusieures valeurs yj-1, yj-2,....yj-k :

t_j

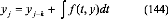
k

-

tj

Avec ces méthodes, f(t,y) sera évalué avec un polynôme d'interpolation. 1) Méthode ouverte

On utilise les k+1 dernières valeurs de f pour construire un polynôme de degrés k(f_n, fn- 1, fn-2,..., fn-k+1), lequel sera utilisé pour déduire la valeur de la fonction f en n+1 (une extrapolation). C'est la méthode d'ADAMS - BASHFORH (à pas fixe).

Pour k=1 :

y n + 1 = yn + h.f ( y n) (145)

Pour k=2 :

y j = yj-k + ? f( t , y ) dt (144)

3 1

2

y n + 1 = y _n h . ₂ .f( y _n ) - .f( yn-01_] (146)

Pour k=3 :

= + ? 23 16 5 ?

y y h f y

. . ( ) - . ( )

f y + . ( )

f y (147)

n + 1 n n n - 1 n - 2

?? 12 12 12 ??

Pour k=4 :

? 55 59 37 9 ?

y = +

y h f y

. . ( ) - . ( )

f y + . ( )

f y - . ( )

f y (148)

n + 1 n n n - 1 n - 2 n - 3

?? 24 24 24 24 ??

2) Méthode fermée

Contrairement à la méthode ouverte, on utilise cette fois le point qu'on cherche dans la détermination du polynôme d'interpolation de degré _k+1(fn+1, ^fn, fn-1, fn-2,..., fn-k+1). La méthode étant implicite, la résolution est donc lourde. C'est la méthode d'ADAMS - MOULTON (à pas fixe).

Pour k=0 :

y n + 1 = y_n + h. f ( y n +1) (149)

Pour k=1 :

1 1 ?

y y h f y

+ = + ? + +

. . ( ) . ( )

f y (150)

n 1 n n 1 n

?? 2 2 ??

Pour k=2 :

= + ? 5 8 1 ?

y y h f y

. . ( ) + . ( )

f y - . ( )

f y (151)

n + 1 n n + 1 n n - 1

?? 12 12 12 ??

Pour k=3 :

? 9 19 5 1 ?

y = +

y h f y

. . ( ) + . ( )

f y - . ( )

f y + . ( )

f y (152)

n + 1 n n + 1 n n - 1 n - 2

?? 24 24 24 24 ??

3) Méthode prédicteur - correcteur-ODE 113

Dans cette méthode, on utilise les avantages des méthodes ouvertes et fermées. Elle s'effectue en trois étapes :

· Etape 1 : Phase de prédiction :

^

On prédit une valeur 1

y n + de par la méthode ouverte ;

· Etape 2 : Phase d'évaluation :

^ ^

)

f n + = f t n + y n +

( , 1

1 1

· Etape 3 : Phase de correction :

^

On corrige la valeur de 1

y n +

^

.

en utilisant 1

f n +

Amélioration :

par une méthode fermée pour trouver yn+1

o La phase de correction peut être répétée plusieurs fois ;

o Usage d'une méthode à pas variable ;

o Usage d'une méthode à ordre du polynôme d'interpolation variable. Cette méthode a pour inconvénient majeur quelle n'est pas auto démarrante.

Si l'ordre est 1, la méthode est dite de EULER modifiée.

y n + prédit = y _n + h f t _n y n

1 , . ( , ) (153)

y corrigé y h f t y prédit

, = + . ( , , ) (154)

n + 1 n n + 1 n + 1

Le solveur ODE 113 de MATLAB utilise la méthode prédicteur - correcteur (méthode d'ADAMS - BASHFORTH - MOULTON à pas variable et ordre de polynôme variable entre 1 et 13). Il est utilisé pour des problèmes non raides avec des tolérances rigoureuses ou pour résoudre des problèmes intensifs avec une exactitude allant du niveau bas au haut niveau

A forte précision demandée, le solveur ODE 113 est plus rapide, tandis qu'à faible précision, les solveurs ODE 23 et 45 sont plus rapides.

6. Méthodes « stiff »

1) Equation différentielle « stiff »

Un système d'équations différentielles est « stiff » ou raide quand les dynamiques qu'il représente sont à la fois très lentes et très rapides.

¹ f y y y t

= 1 ( ₁ , ₂ ,..., , )

n

dt

dy

² f y y y t

= 2 ( ₁ , ₂ ,..., , )

n

f ( y ₁ , y ₂ ,..., y , t )

n n

(155)

dy n

dt

dy

dt

La matrice jacobienne de ce système s'écrira :

. ?

dy n ?

.... ?

?

df n

. ?

dy ? ?

n

df ?

1

(156)

df₁

1

dy

df n

1

dy

Pour laquelle on calculera les valeurs propres. Pour cette méthode, il faut intégrer sur une longueur importante à cause des dynamiques lentes, avec de petits pas en raison des dynamiques rapides. C'est une méthode inefficace et de fois infiniment longue.

2) Méthode de GEAR (ou BDF : backward differentiation formulas)

Par cette méthode, on cherche à interpoler la fonction y(t) grâce aux valeurs précédentes ( _yn+1, y_n, yn-1, yn-2, ,yn-k+1) avec un polynôme d'interpolation noté q(t). Il y' a donc une contrainte supplémentaire :

q'(tn+1)=f(tn+1)

c'est une méthode à pas d'intégration et ordre variables.

Pour k=1 :

y n+ 1 = y_n + h. f ( y n +1) (157)

Pour k=2 :

3 1

h

f y n + = y n + - y _n + y n - . ( ) 2 (158)
1 1
2 2 1
Pour k=3 :

11 3 1

h f y

. ( ) = y - +

3 y y - y (159)

n + 1 n + 1 n n - 1 n - 2

6 2 3

Pour k=4 :

25 4 1

h f y

. ( ) = y - 4 3

y y

+ - y + y (160)

n + 1 n + 1 n n - 1 n - 2 n - 3

12 3 4

Pour k=5 :

137 10 5 1

h f y

. ( ) = y - +

5 5

y y - y + y - y (161)

n + 1 n + 1 n n - 1 n - 2 n - 3 n - 4

60 3 4 5

Pour k=6 :

147 15 20 15 6 1

h f y

. ( ) = y - 6 y + y - y + y - y + y (162)

n + 1 n + 1 n n - 1 n - 2 n - 3 n - 4 n - 5

60 2 3 4 5 6

3) ODE 15s

Ce solveur est une amélioration de la méthode de GEAR. C'est une méthode à pas variable et ordre variable entre 1 et 6, avec une exactitude allant du bas niveau à un niveau moyen. On l'emploi généralement lorsque l'ODE45 est lent.

4) ODE 23s

Il permet la résolution des problèmes raides, avec un bas niveau d'exactitude. 4) ODE 23t

Il permet la résolution des problèmes modérément raides, avec un bas niveau d'exactitude.

5) ODE 23tb

Il permet la résolution des problèmes raides, avec un bas niveau d'exactitude.

2. Fichier parametresrobot.m

C'est un script dans lequel on affecte des valeurs aux différents paramètres du robot et aux entrées de la fonction dynamique_moteurCC. Comme ces entrées doivent varier dans le temps, la contrainte est qu'il faut qu'elles aient ( + 1 )

tfin valeurs, avec tfin qui est le temps d'intégration et

h

h le pas d'intégration. Pour saisir facilement ces entrées, nous allons générer 4 tranches de di ou di1 valeurs chacune, et ce, partant de leurs bornes et ensuite faire la concaténation de liste. Ce fichier est repris en annexe 3.

di = entier le plus proche de )

( h

tfin (163)

4 .

tfin

di 1 = -3* di+1 (164)

h

3. Fichier dynamiquemoteurCC.m

Les entrées sont les courants et les sorties, les couples moteurs. Après la déclaration des variables et différents paramètres du robot, la fonction parametres_robot est appelée et les couples sont calculés par la relation (94) et (95), pour finir par la visualisation de ces couples en fonction du temps.

Début

Déclaration des variables globales

Calcul de K, C1 et C3

Affichage des résultats

Fin

4 Fichier bouclerobot.m

Dans ce script, nous faisons le traitement dynamique et cinématique du robot. Il s'agit ici de trouver les angles de rotation de rotation des roues et les différentes réactions connaissant les couples appliqués aux moteurs, sortis de dynamique_moteurCC (traitement dynamique) et, des angles de rotation des roues, trouver les positions, les vitesses, les accélérations et l'orientation du robot. Nous avons été contraint de faire les deux traitements dans une même boucle par la non linéarité des équations (alpha dépend des ces angles). Ses temps forts sont :

· Déclaration des différents paramètres globaux ;

· Initialisation de la variable t, faisant office du temps dans les différents calculs, du compteur i et des conditions initiales ;

· Création des matrices de dimensions adéquates pour le stockage des différentes sorties ;

· Tant que t=120 secondes, les opérations suivantes seront exécutées :

o i=i+1 : actualisation du compteur ;

o Affectation de la valeur de C1(i) et C3 (i) aux couple de calcul C1c, C3c , valeurs à considérer dans les calculs au temps t ;

o Calcul des valeurs des réactions au temps t par les relations (80), (81), (82), (83), (84), (85), (86), (87), (88), (118), (119), (120), (121), (123), (124) et (125);

o Lancement de l'intégration de la dynamique avec le solveur ODE45 ; o Mémorisation de la valeur actuelle de yd dans la matrice sorties_d ;

o Mémorisation des valeurs des réactions dans des matrices respectives ; o Lancement de l'intégration de la cinématique avec le solveur ODE45 ; o Mémorisation de la valeur actuelle de yc dans la matrice sorties_c ;

o Calcul de alpha au temps t (alp) et de ses deux dérivées (dalp et ddalp) ;

o Mémorisation de la valeur actuelle de alp et dalp dans leurs matrices

respectives ;

o Mémorisation de la valeur actuelle de t dans la liste temps ;

o fin de la boucle

· Calcul des positions, vitesses et accélérations du robot ;

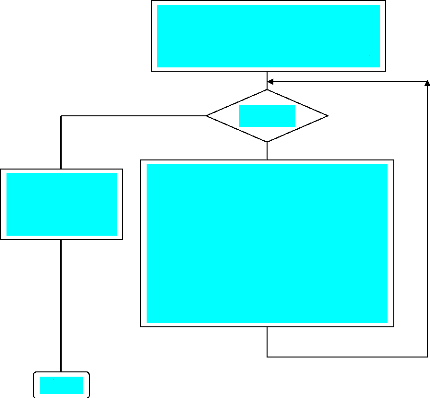
Calcul des positions, vitesses et

accélérations du robot.

Fin

i=i+1 ;

affectation des couples de calcul ;

calcul des réactions ;

lancement de l'intégration dynamique ; Mémorisation de la valeur actuelle de yd dans la matrice sorties_d ;

Lancement de l'intégration cinématique ; Mémorisation de la valeur actuelle de yc dans la matrice sorties_c ;

Calcul de alp, dalp et ddalp ;

t=t+h

mémorisation du temps ;

t=0 ;
i=0 ;
conditions initiales ;
création des matrices sorties_d et sorties_c ;

t=tfin-h

Le script possède 2 fonctions internes dans lesquelles les équations à intégrer{(5) et (6) pour la cinématique, (97) et (98) pour la dynamique} ont été définies. Son ordinogramme est le suivant :

Début

Déclaration des
paramètres du modèle

Appel des paramètres du robot et des entrées
du modèle

A l'instant initial, toutes les réactions sont nulles sauf R3, R6, R7, R11, R12, R14 et R16.Leurs valeurs sont obtenues en traduisant l'équilibre statique du robot (figures 5, 6, 7 et 8).

Mg l

.

R R mg

3 = = +

16 (165)

2 . ( )

l e

+

Mg l

.

R R

6 = =

¹¹ l e (166)

2 . ( )

+

Mg l r

. .

R R

= = (167)

7 ¹² 2 . ( )

l e

+

Mg e

.

R 14 l

e

= (168)

( )

+

5. Fichier robotmobile.m

Ce modèle a pour entrées les courants ia1 et ia3 et pour sorties les accélérations, les vitesses et les positions du robot (aG, vG et rG). Il a la structure suivante :

ia1 ia3

Dynamique moteur
CC

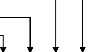
C1

C3

Dérivation

Dynamique robot

° è1

° è3

Cinématique robot

?

aG

á

?

rG

?

vG

L'ordinogramme du modèle est le suivant :

Chapitre 5 : VALIDATION DU CODE ET RESULTATS

1. Choix de la méthode de validation

Pour valider le code, trois moyens sont possibles :

· 1^er moyen : Comparaison entre les résultats obtenus par le code et ceux des expériences au laboratoire sur modèle physique réel ;

· 2^ème moyen : Comparaison entre les résultats obtenus par le code et ceux d'un soft
approprié (sorte de laboratoire virtuel, le VISUAL NASTRAN par exemple) ;

· 3^eme moyen : Par analyse du comportement du robot devant certaines actions préméditées.

Le troisième moyen sera retenu pour ce projet pour les raisons suivantes qui disqualifient les deux autres :

> Absence d'un laboratoire de mécanique analytique à Lubumbashi ; > Méthodes coûteuses (les deux premières).

Nous partirons donc de quelques actions pour lesquelles on peut imaginer le comportement du robot. Les actions choisies sont :

> C 1 = C3 = 0 : Le robot reste stationnaire si â = 0 et se meut inconditionnellement

vers le bas en ligne droite avec une certaine accélération en l'absence du frottement ou à condition que le frottement soit vaincu pour â ? 0 ;

> C 1 = C3 ? 0 : Il se meut en ligne droite quelque soitâ ;

> C 1 = 0 et C3 ? 0 : Il décrit un cercle de rayon l13 si â = 0 et de rayon plus grand que l13 si â ? 0 , dans le sens horlogique ;

> C 1 ? 0 et C3 = 0 : Il décrit un cercle de rayon l13 si â = 0 et de rayon plus grand que l13 si â ? 0 , dans le sens trigonométrique ;

> C1 supérieur à C3 : Il prend un virage vers la droite ; > C3 supérieur à C1 : Il prend un virage vers la gauche.

2.Comportement du robot

2.1. C 1 = C3=0 ; 2.2. C 1 = C3?0 ;

2.3. C 1 = 0 et C3?0 ; 2.4. C 1 ? 0 et C3=0;

2.5. C1 supérieur a C3 ; 2.6. C3 supérieur a C1.

3.Conclusions

CONCLUSIONS GENERALES

1. Objectifs accomplis

Dans le présent travail, nous avons modélisé et simulé la cinématique et la dynamique d'un robot mobile sur roues se mouvant sur un plan incliné. Par superposition des lois élémentaire relatives aux mouvements simples, nous sommes arrivé à un modèle mathématique dépendant des différents paramètres du robot (rayon des roues, masse des roues et du châssis, pente du plan incliné).

Nous sommes parti d'un modèle simple sans frottements et sur sol horizontal, que nous avons ensuite amélioré jusqu'à avoir un modèle assez complexe représentant globalement le robot :

· nous avons introduit la dynamique des moteurs à courant continu. Il s'agissait d'établir la relation liant les couples aux signaux électriques ;

· nous avons tenu compte de l'adhérence des roues en utilisant la loi approximative de COULOMB ;

· nous avons considéré le frottement dans les liaisons paliers - essieux des roues.

Pour arriver aux équations de mouvement, nous avons utilisé deux méthodes équivalentes afin de les comparer :

· la méthode des théorèmes généraux ; et

· le formalisme lagrangien.

La méthode synthétique ou méthode des théorèmes généraux a été retenue parce qu'elle nous a fournit des équations faciles à intégrer.

Le logiciel MATLAB nous a permis de résoudre les équations obtenues et de les

simuler.

2. Méthodes de résolution

2.1. Performances

2.2. Limitations

3. Intérêt du projet

Ce projet constitue une fiche technique du robot étudié. Il servira donc de guide dans son analyse, sa synthèse et sa conduite. Il est ensuite un exemple de résolution d'un problème concret de mécanique analytique avec MATLAB/SIMULINK et il contribuera à accroître le volume documentaire en mécanique analytique.

4. Validité des résultats

5. Problèmes en suspens

Pour ne pas compliquer le modèle, plusieurs paramètres ont été mis à l'écart. C'est

notamment :

· Le frottement dans la liaison bille - châssis ;

· Le rendement de la transmission moteur - roue.

Ils peuvent cependant être pris en compte pour réalise un modèle assez complet. On pourra aussi envisager d'autres lois de frottement plus complexes (BOWDEN - TABOR, par exemple) mais plus exactes que celle de COULOMB.

Une comparaison quantitative entre les deux méthodes d'étude peut être faite. Il faut, pour cela, faire un programme de résolution des équations obtenues avec la méthode de LAGRANGE et comparer les résultats obtenus avec ceux relatifs aux théorèmes généraux.

6. Perspectives

A l'avenir, il faudra aussi penser à résoudre le problème avec l'interface SIMULINK pour conclure sur l degré d'exactitude des programmes établis. On pourra aussi changer d'intégrateur (ODE 15s ou ODE 113) pour s'assurer ou non de l'amélioration du temps de résolution et de la précision des calculs.

ANNEXES

Annexes1 : Les différents scripts

Annexes 2 : Théorèmes généraux appliqués au robot dans la base fixe

1. Théorème de la résultante cinétique

Roue 1

Ce théorème, appliqué à la roue 1, avec l'expression (5), donne :

d ? ?

? [ ] ? [ ] ?

m . . (cos . 1 sin . 1 ) (

R è^& á x + á y R R

= + ) sin (

á - + ) cos . 1 (

R R á x R R

- + ) sin (

á + R R

+ ) cos . 1 (

á y R R m g z

+ + - . ) . 1 (169)

1 2 5 1 4 1 4 2 5 3 6

dt

Soit, en le projetant sur différents axes:

m R

. . ( 1 . cos

è & & á è & á & á

- 1 . . sin ) sin ( 2 5) cos ( 1 4)

= á R R

+ - á R R

+ (170)

m R

. . ( 1 . sin

è & & á è & á & á

+ 1 . . cos ) sin ( 1 4) cos ( 2 5)

= - á R R

+ - á R R

+ (171)

R 3 + R6=m.g (172)

Châssis

Appliqué au châssis, il donne :

M R

.

2
M R

.

2

. ( . cos

[ è á è á á è á è á á

& & - & &

. . sin ) ( . cos

+ & & - & &

. . sin ) ] cos (

= á R R

- ) sin (

+ á R R

- ) (173)

1 1 3 3 4 9 10 5

. ( . sin

[ è á è á á è á è á á

& & + & &

. . cos ) ( . sin

+ & & + & &

. . cos ) ] sin (

= á R R

- ) cos (

+ á R R

- ) (174)

1 1 3 3 4 9 5 10

R ₁₁ + R₁₄ -R₆ =M.g (175)

Roue 3

d

Appliqué à la roue 3, il donne :

? ?

? [ ] ? [

. . (cos . 1 sin . 1 ) ] ?

m è&

R á x + á y = - R sin (

á + R R ) cos . 1 (

- á x R R

+ - ) sin á + R cos . 1 (

á y R R m g z

+ - - . ) . 1 (176)

3 1 1 10 9 15 9 15 10 16 11

dt

Et sur les différents axes, on a :

(177)

m R

. . ( . cos

è & & á è & á & á

- . . sin ) = - R . sin cos (

á + á R R

- )

3 3 10 9 15

m R

. . ( . sin

è á è á á

& & + & &

. . cos ) sin (

= á R R

- ) . cos

+ R

3 3 9 15 10

á (178)

R 16 - R₁₁ =m.g (179)

1. Théorème du moment cinétique

Roue 1

? ? mR

2

? ?

Et :

d

.

dt

MC G 1 = 4 (-2 è ₁ sin á . 1 x+ 2è ₁ cos á .1y+ (1.1 z ) (180)

MC O 1 = - mR ² [

2( 01 sin á + 01 .ci . cos á) .1 x+ 2( è ₁ cos á - è1.a. sin á) .1 y+ 4.1 91 (181)

4

Le moment des forces extérieures, dans la base fixe (x, y, z), est :

?

?

?

??

(182)

? 0 ? ? R á R á ? - R -

2 . sin - ?- ? . sin ? . cos á

1 . cos á ? r R

. sin ? á - R . cos á C . sin á

5 4 7 1

? ? ? ? ? ? ? ? ? ?

Mext = 0 ? - R . sin á - R . cos á + r . cos á ? - R á - R á + C á - á

1 ? ? ? 1 2 ? ? ? ? 5 . cos 4 . sin ? ? 1 . cos R ₇ . sin

? ? ? ? ? ? ? ? ? ?

? - R ? ? R 3 ? ? 0 ? ? R 6 ? R8

Soit :

?

? ? ? ??

Mext

1

=

)

? ? ? ? ?

(x, y ,

z

)

(183)

-

sin

á(R1 .R + C1) + cos á(R6

. r - R2. R - R7

sin

)

á( .

R r R R R

- - á

6 2 . 7 ) cos ( .

+ +

R R C

1 1

R₄ .r + R₈

Partant des expressions (87) et (89), le théorème du moment cinétique, projeté sur différents axes, s'écrit :

mR 2

(ei sin a +O1 ti cosa)= sin a(R R+C)+ cosá(R ₇ + R₂ .R - R₆ .r) (184)

1 - - 1^- 1

2

mR

(o1 . cosá - d1. ci. sin á)= sin á(R₆ .r - R₂ .R - R₇ ) + cos á(R₁ .R + C₁) (185)

2

2

mR

4 ift = R ₈ + R₄.r (186)

2

Chassis

Pour le châssis :

d ? M(c ^2 + d2) ? ei.1 . dt MCG 2 = 12

z (187)

Le moment des forces extérieures appliquées au châssis dans la base fixe (x, y, z), sera :

? ? ?

? ?

? ^fsin á

2 e. cos á r

COSa R₅

. sinal / 0 1

. - f sin á

2 e .cosá^?

R 4

á - R₁₂ ) . cos á

Mext 2 r [R14 b?R 11 R10 .sin

₂ = - COS a - e.sin a A [R₄ . sin a + R₅.cosa+ 0 ? 0 + cos á - e .sin á ? [ - R 10

2

- R 6 - b

2?

₁₀.cos á - R 9

.sin á + (R R - R₈

- R₁₂ ) . sin á

b

?? f R9 . COS a 1 (R_1:

i ? ?2 ??

Ou bien :

sin á.

?
??

á.

+

?
??

+ cos

l. R14

( R₆

? ? ? ? ? ? ? ? ?

?
??

?
??

(189)

2

b +(R 11 - R₆ ). e-R14

b

(R 10 - R5). 2 + R₇ -

.l

( R 4 - R₉ ).

R12

^f+

2

).

R11

? b

- + .( - ) +

6 11 9 4

?? e R R

. ( ) R R

2

.

?
??

? ?? f b ?

Mext = ? sin . (

á + + ( - ). + - + á

2 cos

6 11 10 5 7 12

?? R R R R

). R R

2 2 ??

?

( ). e + (R ₉ + R₄).

R 13 - R₈

^f+

2

R 10 - R ₅

Partant des expressions (187) et (189), le théorème du moment cinétique fournit les équations suivantes, après projection sur différents axes :

sin á .P. (R 6 - R₁₁ ) + b 2 .(R 9 - R ₄ ) + LR14 ^-1¹, + cosá .[(R ₆ + R ₁₁ ).^f + (R 10 - R₅ ).^b + R 7 - R 12^-1¹.= 0 (190)

J 2 2

cos á .Le . (R 11 - R₆ ) + b 2 .(R 4 - R ₉ ) - l.R14 1+ sin á . (R ₆ + R ₁₁ ).^f + (R 10 - R₅ ).^b + R 7 - R 12^-1¹,= 0 (191)

2 2 J

M ( c ^2 + d2) á&& = 2 f 12 (R 4 + R 9) + e.(R 10 - R 5) + R 13 -R

8 (192)

Roue 3

Comme pour la roue 1, on aura :

? 0 ? ? - R . cos á ? ? r . sin á ? ? - R á R á ? ? - 10 . sin + á C á 15 12 . cos 3 . sin 9 . cos R ? ? ? ? ? ? ? ? ? ? Mext 3 = 0 ? - R . sin á + - r . cos á ? R á + R á + C á + R ? ? ? 15 ? ? ? ? 10 . cos 9 . sin ? ? 3 . cos 12 . sin á ? ? ? ? ? ? ? ? ? ? ? R - ? ? R ? ? 0 ? ? - R ? - R 16 11 13				? ? ? ??
Et :	mR	2

(193)

(è

. sin á + è^&

h. cos á) = - sin á ( R

₃

₃

₁₅

₃

12

2

.R + C

) + cos á(R + R₁₁ .r) (194)

mR

03 . cos á - è^&₁ .(i . sin á) = sin _á(R11 .r + R₁₂ ) + cos á( R₁₅ .R + C₃) (195)

2

2

mR 2

4

á&& = R₉. r - R₁₃ (196)

Et le système S2 obtenu dans la base fixe, d'équations :

m . R. ( è1 . cosá - è^&1 . ci. sin á)= sin á(R 2 + R5) - cosá(R 1 + R4) (197)

m . R. ( è^&&1 . sin á + è^&1 . et . cos á) = - sin á (R 1 + R4) - cos á(R 2 + R5) (198)

R 3 + R6 = m.g (199)

M .R
2

M .R
2

.[ ( è ₁ . cosá - d₁ rit. sin á )+( è ₃ . cosá -d₃ .6t. sin á)] = cosá(R 4 - R₉ ) + sin á(R 10 - R₅)

(200)

IA . sin á + d₁ rit. cos á )+ ( è ₃ . sin á +d₃ .6t. cos á)] = sin á(R 4 - R₉ ) + cos á(R 5 - R10)

(201) R ₁₁ + R₁₄ - R₆ = M.g (202)

m . R. ( è₃ . cosá - è^&₃ h. sin á)=- R₁₀ . sin á + cosá(R 9 - R₁₅) (203)

m . R. ( ij ₃ . sin á + d3 .d. cos á)= sin á(R 9 - R₁₅ ) + R ₁₀ . cos á (204)

R 16 - R₁₁ = m.g (205)

mR 2

è^&&

in á

è^&

.ci. cos á)= sin á (

+

)+ cosá (

2

₍

₁ . s

+

₁

R₁

.

R

C ₁

R ₇

R₂ .

R

R₆

+

-

.r) (206)

mR

è^&&1 . cos á - th. ci. sin á)= sin á(R₆ .r - R₂ .R - R₇ ) + cos á(R₁ .R +C)₁ (207)

2

2

(

mR

ii = R ₈ + R ₄.r (208)

4

2

sin á.Le . (R 6 - R₁₁ )+^b .(R 9 - R ₄ ) + l.R14 ?,+ cosá .[(R ₆ + R ₁₁ ). 2 f + (R 10 - R₅ ). b 2 + R 7 - R 12 ? L_I= 0 2 J

(209)

? ?

cos á.p. (R 11 - R₆ ) + b .(R 4 - R ₉ ) - l.R14 l_i+ sin á .[(R ₆ + R ₁₁ ). 2 f + (R 10 - R₅ ). 2 b + R 7 - R _12??= 0

2 J

(210)

M ( c ^2 + d2) && = 2 f 12 á - (4 + R 9) + e.(R 10 - R 5) + R 13 -R

8 (211)

mR 2

(è^&&

. sin á + è

.á&. cos á) =- sin á( R

. R+ C

)+ cosá(R

₃

₃

₁₅

₃

₁₂

₁₁

2

+ R

.r) (212)

mR 2

(

è

cos á - è^&

h. sin á)= sin _á(R

₃

₁

₁₁

12 15

2

.r + R ) + cos á( R. R+ C₃ ) (213)

mR 2

4

á& & = R r R

- (214)

9 . 13

On peut constater que les deux systèmes, projetés sur les axes fixes sont équivalents, mais celui exprimé dans les axes mobiles est plus simple.

BIBLIOGRAPHIE

1. Cours

CASADEVALL : Introduction à MATLAB

Université de PARIS - DAUPHINE. Deug science mention Mass. 2ème année 2004

DELCHAMBRE A. : Mécanique rationnelle 1

P.U.B. Librairie cours - 42 avenue Paul Héger - 1000 Bruxelles

DELCHAMBRE A. : Mécanique rationnelle 2

P.U.B. Librairie cours - 42 avenue Paul Héger - 1000 Bruxelles

HOANG L.H. : Introduction à MATLAB et SIMULINK.

Département de génie électrique et de génie informatique. Université

de LAVAL. QUEBEC, CANADA 1998

KAMABU Ts. : Machines électriques

2ème graduat électromécanique. UNILU. 2000-2001

KAMABU Ts. : Complément machines électriques

2ème grade électromécanique. UNILU. 2003-2004

LEDUC B. : Cinématique et dynamique des machines

LIASA NK. : Electronique de puissance

2ème grade électromécanique. UNILU. 2003-2004

MPANDA M. : Complément d'électrotechnique

2ème grade électromécanique. UNILU. 2003-2004

2. Ouvrages

ANNEQUIN ET BOUTIGNY : Cours de physique : Mécanique 2

2ème édition. Librairie VUIBERT. 1974. 269 pages

FOUILLE A. : Electrotechnique à l'usage des ingénieurs. Tome 3 : Machines continues - électronique de puissance

10^ème édition. DUNOD. 264 pages

GRECIAS P. et MIGEON J.P. : Physique 2

Techniques de documentation LAVOISIER. 1988. 536 pages

PEREZ J.P. : Mécanique : Fondements et applications

6ème édition. DUNOD 2001. 748 pages

2.5 PROVOST P. et JOYAL M. : Mécanique

Masson et Cie. 1972. Paris.

3. Sites Web

WWW. enstimac.fr/~louisnar/matlab/polymatlab.pdf

WWW.devinci.fr/cs/manifestations/matlab 2002/09 Plain.pdf WWW. itp.nat.uni-magdeburg.de/matlab/techdoc/ref/ode45.html WWW.sciences.univ-nantes.fr/physique/perso

INDEX

A.

F. Flux

Acceleration ADAMS-BASHFOR-MOULTON Adhérence

Force Frottement

G. Glissement

H. HEUN

I.

Inclinaison Inconnue

Intégration

L.

LAGRANGE Lagrangien

Liaisons

Linéarité

Améliorations

Angle de rotation

B.

Barycentre Bille

C.

Centre

Châssis

Cinématique Cinétique

Code

Coefficient Complexité Couple

Courant

D.

DARBOUX Dynamique E.	Masse MATLAB Modèle Moment Mouvement N.
Energie Entrée Equation Erreur Essieux EULER Evaluation
	Numérique

M.

O. V.

Variable Vecteur Vitesse

Orientation

P.

Paliers Paramètre

Pente Poids Position

Potentiel Précision

R.

Rayon Référentiel Résistance Résultats

Robot Rotation

Roues RUNGE-KUTTA

S.

Simulation SIMULINK Sol

Solution

Sortie

Symétrique

T.

Tangente TAYLOR Temps

Tension Théorème Tolérance Transformation Translation

TABLE DES FIGURES ET TABLEAUX

Figure 1 : Projections orthogonales du robot

Figure 2 : Déplacement infinitésimale d'une roue ; Figure 3 : Roue 1 suivant une orientation á

Figure 4 : Robot suivant une orientation á

Figure 5 : Vue éclatée du robot avec ses corps rendus libres Figure 6 : Projections orthogonales de la roue 1 rendue libre Figure 7 : Projections orthogonales du châssis rendu libre Figure 8 : Projections orthogonales de la roue 3 rendue libre Figure 9 : Différents axes relatifs au plan incliné

Figure 10 : Schémas de résolution numérique d'une équation différentielle Figure 11 : Ordinogramme relatif au script dynamique_moteurCC

Figure 12 : Ordinogramme relatif au script boucle_robot Figure 13 : Vue d'ensemble des différents traitements Tableau 1 : Terminologie du modèle cinématique

Tableau 2 : Terminologie du modèle dynamique

TABLE DE MATIERE

EPIGRAPHE I

IN MEMORIUM II

DEDICACE III

AVANT PROPOS IV

INTRODUCTION - 1 -

1. PROBLEMATIQUE - 1 -

2. SUBDIVISION DU TRAVAIL - 2 -

PRESENTATION DU PROBLEME - 3 -

Chapitre 1 : MODELE CINEMATIQUE 1. TERMINOLOGIE 2. DESCRIPTION DES DIFFERENTS MOUVEMENTS 3. ETABLISSEMENT DU MODELE CINEMATIQUE	- 5 - - 5 - - 6 - - 7 -
Chapitre 2 : MODELE DYNAMIQUE	- 10 -
1. TERMINOLOGIE	- 10 -
2. METHODE DE LAGRANGE	- 10 -
2.1. Expression de l'énergie cinétique	- 10 -
2.2. Expression de l'énergie potentielle	- 12 -
2.3. Expression du lagrangien	- 12 -
2.4. Expression des forces généralisées	- 13 -
2.5. Expression des équations de LAGRANGE	- 13 -
3. METHODE DES THEOREMES GENERAUX	- 13 -
3.1. Diagrammes des corps rendus libres	- 14 -
3.2. Théorème de la résultante cinétique	- 18 -
3.3 Théorème du moment cinétique	- 19 -
3.4. Système d'équations à résoudre	- 24 -
4. COMPARAISON ENTRE LES DEUX METHODES	- 26 -

Chapitre 3 : AMELIORATIONS - 27 -

1. PRISE EN COMPTE DE LA DYNAMIQUE DES MOTEURS - 27 -

2. PRISE EN COMPTE DU FROTTEMENT DANS LES LIAISONS DU ROBOT - 28 -

3. PRISE EN COMPTE DE L'INCLINAISON â DU PLAN D'APPUI DU ROBOT PAR RAPPORT AU SOL (HORIZONTAL) ... -

29 -

3.1. Théorème de la résultante cinétique 3.3. Théorème du moment cinétique 4. MODELE COMPLET		- 30 - - 32 - - 33 -
Chapitre 4 : DESCRIPTION DE L'ARCHITECTURE DU PROGRAMME		- 34 -
1. GENERALITES		- 34 -
1.1 But du chapitre		- 34 -
1.2 Résolution numérique d'une équation différentielle ordinaire d'ordre n		- 34 -
1.3. Développement des intégrateurs numériques utilisés par le logiciel MATLAB		- 35 -
2. FICHIER PARAMETRES_ROBOT.M		- 44 -		3. FICHIER DYNAMIQUE_MOTEURCC.M
- 44 -
4 FICHIER BOUCLE_ROBOT.M		- 45 -
5. FICHIER ROBOT_MOBILE.M		- 47 -
Chapitre 5 : VALIDATION DU CODE ET RESULTATS	- 49 -
1. CHOIX DE LA METHODE DE VALIDATION	- 49 -
2. COMPORTEMENT DU ROBOT	- 50 -
3. CONCLUSIONS	- 50 -

CONCLUSIONS GENERALES - 51 -

-

- - - - - - - -

Modélisation et simulation d'un robot mobile sur roues avec le logiciel
MATLAB/SIMULINK

		- 68
1. OBJECTIFS ACCOMPLIS		- 51
2. METHODES DE RESOLUTION		- 51
2.1. Performances		- 52
2.2. Limitations		- 52
3. INTERET DU PROJET		- 52
4. VALIDITE DES RESULTATS		- 52
5. PROBLEMES EN SUSPENS		- 52
6. PERSPECTIVES		- 52
ANNEXES ANNEXES1 : LES DIFFERENTS SCRIPTS ANNEXES 2 : THEOREMES GENERAUX APPLIQUES AU ROBOT DANS LA BASE FIXE BIBLIOGRAPHIE INDEX	- 53 - - 53 - - 54 - - 62 - - 64 -
A.	- 64 -
B.	- 64 -
C.	- 64 -
D.	- 64 -
E.	- 64 -
F.	- 64 -
G.	- 64 -
H.	- 64 -
I.	- 64 -
L.	- 64 -
M.	- 64 -
N.	- 64 -
O.	- 65 -
P.	- 65 -
R.	- 65 -
S.	- 65 -
T.	- 65 -
V.	- 65 -

TABLE DES FIGURES ET TABLEAUX - 66 -

TABLE DE MATIERE - 67 -