|
RÉPUBLIQUE ALGÉRIENNE DÉMOCRATIQUE
ET POPULAIRE
MINISTÈRE DE L'ENSEIGNEMENT SUPÉRIEUR ET
DE LA RECHERCHE SCIENTIFIQUE
UNIVERSITÉ L'ARBI BEN M'HIDI D'OUM EL
BOUAGHI
INSTITUT DES SCIENCES TECHNOLOGIQUES DE AIN
BEIDA
DEPARTEMENT DE GENIE MÉCANIQUE
MÉMOIRE
Présenté en vue d'obtenir le diplôme de
Magister en Génie Mécanique
Option
Robotique et systèmes intelligents
Par
CHEMAMI SABAH
Ingénieur d'état en électronique
ETUDE DES DIFFÉRENTES LOIS DE COMMANDE POUR UN
ROBOT MANIPULATEUR À 6DDL COMPORTANT UNE LIAISON PRISMATIQUE
Soutenue le 13/05/2009
Devant le jury constitué de :
|
-Président :
|
Mr Golea Noureddine
|
Prof
|
Université d'Oum El Bouaghi
|
|
-Rapporteur :
|
Mr Mahfoudi Chawki
|
M.C
|
Université d'Oum El Bouaghi
|
|
-Examinateurs:
|
Mr Zaatri Abdelouahab
|
Prof
|
Université de Constantine
|
|
Mr Nini Brahim
|
M.C
|
Université d'Oum El Bouaghi
|
|
-invité
|
Mr Chibani Abdelhakim
|
M.A.A
|
Université d'Oum El Bouaghi
|
Remerciements
Je tiens à remercier tout d'abord DIEU le tout
puissant qui m'a donné, durant toutes ces années, la
santé, le courage et la foi pour arriver à ce jour.
Je ne peux, réellement, trouver les expressions
éloquentes que mérite Mr. Mahfoudi Chawki, Maître de
conférence à l'université d'Oum El Bouaghi, afin de le
remercier pour ses encouragements, son aide, son dévouement pour le
travail et sa présence totale, au cours de cette étude.
Je remercie le professeur Golea Nouredinne de m'avoir fait
l'honneur d'accepter d'être le président de jury.
J'adresse mes remerciements aux messieurs: Zaatri
Abdelouahab, professeur à l'université de Constantine, Nini
Brahim, Maître de conférence à l'université d'Oum El
Bouaghi, d'avoir bien voulu accepter d'examiner et d'enrichir mon modeste
travail.
Je remercie également Monsieur Chibani Abdelhakim,
Maître de conférence à l'université d'Oum El Bouaghi
de nous avoir fait l'honneur de faire partie du jury comme invité.
Mes remerciements vont également à tous les
enseignants qui ont contribués à notre formation et les
responsables de notre Institut.
Enfin, j'exprime mes remerciements à tous ceux qui ont
contribué de prés ou de loin à l'élaboration de ce
travail surtout Mme S. Zaamta.
Dédicaces
Aux êtres qui me sont les plus chers « MES
PARENTS» Pour leur AMOUR, leur EDUCATION et leurs SACRIFICES.
A mes frères
A mes Soeurs
A ma grand-mère
A toute ma petite et ma grande famille
A toutes mes amies et mes collègues
A tous ceux qui m'ont aidé de faire ce travail
Je dédie ce modeste travail
Sommaire
Introduction Générale
1
Chapitre I: Le Modèle
géométrique direct du robot (MGD)
5
I.1. Introduction
5
I.2. description de la géométrie des robots
à structure ouverte simple
5
I.2.1. Paramétrage de Denavit Hartenberg
6
I.3. Le MGD d'un robot manipulateur
8
I.4. Représentation des coordonnées
opérationnelles
9
I.4.1. Les angles de Cardans (Roulis - Tangage - Lacet
« RTL »)
9
I.5. Le MGD du robot
10
I.5.1 La chaîne cinématique du robot
10
I.5.2. Application
13
I.6. Espace de travail
15
I.6.1. Définition
15
I.6.2. Application numérique
16
I.7. Conclusion
18
Chapitre II: Le Modèle
géométrique inverse du robot (MGI)
19
II.1. Introduction
19
II.2. Position du problème
19
II.3. Calcul du MGI par la méthode de Paul
21
II.3.1. Principe
21
II.3. 2. Le découplage cinématique
23
II.4. le MGI du robot choisi
24
II.5. Application
27
II.5. Conclusion
29
Chapitre III:Etude cinématique du robot
30
III.1. Introduction
30
III.2. Le modèle cinématique direct (MCD)
30
III.2.1 Calcul Indirect de la matrice Jacobienne
31
III.2.2. Calcul direct de la matrice Jacobienne
31
III.2.3. le calcul du MCD par les équations de
récurrence
33
III.2.4. la jacobienne analytique
33
III.2.5. Utilisation de la matrice jacobienne
35
III.2.5. 1. Calcul des efforts statiques
35
III.2.5.2. Les positions de singularité
35
III.3. Vitesse et accélération inverses
36
III.4. Application sur le robot choisi
37
III.4.1. calcul de la jacobienne géométrique
37
III.4.2. calcul de la jacobienne analytique
40
III.4.3. Les positions de singularité
41
III.5. Conclusion
43
Chapitre IV: L'étude dynamique du robot
44
IV.1. Introduction
44
IV.2. Notation
44
IV.3. Le modèle dynamique inverse (MDI)
45
IV.3.1. Formalisme de Newton Euler
46
IV.3.2. Formalisme de Lagrange
49
IV.4. Application sur le robot choisi
52
IV.4.1. Résultats obtenus par le formalisme de Newton
Euler
52
IV.4.2. Résultats obtenus par le formalisme de Lagrange
59
IV.5. Le modèle dynamique direct (MDD)
61
IV.6. Application numérique
62
IV.7. Conclusion
64
Chapitre V:Commande de mouvement
65
V.1. Introduction
65
V.2. Commande PID
65
V.3. Commande par découplage non linéaire
67
V.3.1. Commande dans l'espace articulaire
67
V.3.2.Commande dans l'espace opérationnel
74
V.3.2.1. Commande dans l'espace
opérationnel avec correction dans l'espace articulaire
74
V.3.2.2. Commande dans l'espace
opérationnel avec correction dans l'espace opérationnel
78
V.3.3. Commande au voisinage des positions
singulières
81
V.4. Conclusion
85
Conclusion générale
86
Références bibliographiques
89
Liste des figures
Figure 1. Schéma hiérarchique de
la commande. 2
Figure I.1. La chaîne cinématique
d'un robot série 6
Figure I.2. Paramètres de Denavit et
Hartenberg 7
Figure I.4. Le robot à l'état de
repos où d1=3, y1=2, 0=pi/3 13
Figure I.5. La position du robot lorsque :
d1=1, y1=2, 0=pi/6, 6=0.6*t, t=0:5 13
Figure I.6. La position du robot lorsque : d1=
-3, y1=2, 0=pi/6, 2=0.3*t, t=0:5 14
Figure I.7. La position du robot lorsque :
d1=3, y1=2, 0= -pi/3, 1=0.5*t, t=0:5 14
Figure I.8. L'espace de travail du robot
lorsque : 0<i<2ð, 0<r3<0.5 17
Figure I.9. L'espace de travail du robot
lorsque : 0<1,2<ð, 0<4,5 <2ð,
0<r3<0.5 17
Figure II.1. Transformation entre organe
terminal et repère atelier. 21
Figure II.2. Suivi de la trajectoire
donnée 28
Figure II.3. Suivi de la trajectoire
donnée (vue de dessus) 29
Figure III.1. Influence du type de
l'articulation sur le repère terminal 31
Figure III.2. Les coordonnées
articulaires et les coordonnées opérationnelles correspondantes
39
Figure III.3. Les vitesses calculées par
les deux méthodes ; équations de récurrence, et la
jacobienne 39
Figure III.4. Description du programme
utilisé pour la validation de la jacobienne analytique 40
Figure III.5. Les vitesses
opérationnelles par l'utilisation de la jacobienne analytique 41
Figure III.6. Quelques positions
singulières du robot 42
Figure IV.1. Bilan des efforts au centre de
gravité 47
Figure IV.2. Les couples calculés, par
les deux formalismes 63
Figure IV.3. La force F3, par les deux
formalismes 63
Figure V.1. Schéma classique
d'une commande PID
66
Figure V.2. Commande dynamique pour
un mouvement complètement spécifié.
69
Figure V.3. (a) positions
articulaires (b) vitesses articulaires
71
(c) la commande PID
71
(d) la commande dynamique
71
Figure V.4. L'erreur de
position et de vitesse
72
(a)et (b) la commande PID
72
(c) et (d) la commande dynamique .
72
Figure V.5. (a) positions
articulaires (b) vitesses articulaires
73
(c) la commande PID
73
(d) la commande dynamique
73
Figure V.6. L'erreur de
position et de vitesse
74
(a)et (b) la commande PID
74
(c) et (d) la commande dynamique .
74
Figure V.7. Commande dans l'espace
opérationnel avec correction dans l'espace articulaire
75
Figure V.8. Les
coordonnées de la trajectoire désirée dans l'espace
opérationnel (a, b) et dans l'espace articulaire(c, d).
76
Figure V.9. L'erreur de
position et l'erreur de vitesse dans l'espace articulaire
76
Figure V.10. L'erreur due au
problème de la non unicité du MGI.
77
Figure V.11. La commande dans
l'espace opérationnel avec correction dans l'espace opérationnel
79
Figure V.12. L'erreur
d'orientation et de translation dans l'espace opérationnel..
80
Figure V.13. L'erreur de
vitesse dans l'espace opérationnel
81
Figure V.14. La trajectoire
désirée.
82
Figure V.15. La position de
l'effecteur et les erreurs de position dans l'espace
opérationnelle.
83
Figure V.16.
« à gauche » l'erreur de vitesse
opérationnelle
83
« à droite »les positions
et les vitesses articulaires calculées.
83
Figure V.17. Le cas
d'utilisation de l'inverse généralisée.
84
La position de l'effecteur et les erreurs de
position dans l'espace opérationnelle
84
Figure V.18. Le cas
d'utilisation de l'inverse généralisée.
85
« à gauche » l'erreur de
vitesse opérationnelle
85
« à droite »les positions
et les vitesses articulaires calculées.
85
Liste des tableaux
Tableau I.1. Paramètres
géométriques relatifs au mécanisme
....................................11
Tableau II.1. Types d'équations
(Méthode de Paul) ................................................23
Tableau IV.1. Paramètres entrant dans le
calcul du modèle dynamique ......................... 62
Introduction Générale
Le problème de la commande d'un robot manipulateur peut
être formulé comme la détermination de l'évolution
des forces généralisées (forces ou couples) que les
actionneurs doivent exercer pour garantir l'exécution de la tâche
tout en satisfaisant certains critères de performance.
Différentes techniques sont utilisées pour la
commande des bras manipulateurs. La conception mécanique du bras
manipulateur a une influence sur le choix de schéma de commande. Un
robot manipulateur est une structure mécanique complexe dont les
inerties par rapport aux axes des articulations varient non seulement en
fonction de la charge mais aussi en fonction de la configuration, des vitesses
et des accélérations.
La plupart des robots utilisent des servomoteurs
électriques comme actionneurs. Les caractéristiques des
servomoteurs ont un rôle important pour la sélection du
système de commande.
Dans le cas où, les articulations sont
actionnées par l'intermédiaire de réducteurs à
forts rapports de réduction, l'inertie vue par les moteurs varie peu.
Dans ce cas, les asservissements peuvent être assurés axe par axe
par des boucles de commande classiques PID [TEC 07]. Ses avantages sont la
facilité d'implantation et le faible coût de calcul. En
contrepartie, la réponse temporelle du robot varie selon sa
configuration, on constate des dépassements de consigne et une
mauvaise précision de suivi dans les mouvements rapides [KHA 99].
En opposition, quand le robot utilise des servomoteurs avec de
faibles rapports de réduction, les boucles de commande doivent compenser
les effets des variations des forces d'inertie et de gravité fonctions
de la configuration. Les lois de commande basées sur les modèles
dynamiques des robots (appelée commande dynamique) donnent de
très bons résultats dans ce cas. Ils permettent de maintenir la
réponse dynamique du système dans certains critères de
performance. En utilisant ce type de techniques les robots peuvent
évoluer à grandes vitesses [AGU 07].
En effet la majorité des tâches confiées
aux robots sont délicates et exigent une très grande
précision sous des trajectoires rapides. Dans ce cas le type de commande
nécessaire est la commande par découplage non linéaire,
méthode qui est considérée comme la solution
théorique idéale pour la commande de ce type de robot [KHA 78],
[BEJ 85], [LUH 80],....
Notre travail porte sur la commande d'un bras manipulateur en
supposant que son application exige des évolutions rapides et une grande
précision et nous n'abordons pas sa construction.
Le schéma de commande que nous proposons n'utilise que
des capteurs proprioceptifs et reste ouvert pour l'inclusion de capteurs
extéroceptifs (systèmes de vision, capteurs d'effort, capteurs
tactiles,...) pour les boucles de commande de plus haut niveau. Le
schéma de la figure 1 présente cette idée de façon
simplifiée [SPO 04].
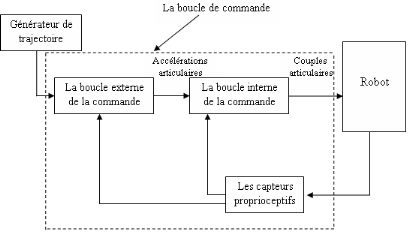
Figure 1.
Schéma hiérarchique de la commande.
La commande se fait soit dans l'espace opérationnel,
soit dans l'espace articulaire, le coût de calcul de la commande dans ce
dernier cas est quasiment égal au nombre d'opérations
nécessaires pour établir le modèle dynamique [KHA 99].
Ainsi, pour réaliser cette commande, on doit essentiellement disposer
d'un algorithme de calcul du modèle dynamique performant, deux
méthodes sont utilisées dans le cadre de ce travail.
Dans le cas où les modèles du robot sont
parfaitement connus, cette méthode de commande présente des
performances très satisfaisantes. Cependant, en pratique, cette
condition n'est pas simple pour un robot à plus de trois ddl, on doit
disposer d'un langage évolué, qui nous permet d'extraire les
expressions de tous les modèles nécessaires, sous forme
symbolique. Le logiciel Maple répond à ce critère.
Problématique :
L'objectif de ce travail est :
Ø l'élaboration de tous les modèles du
robot nécessaire à la commande : les modèles
géométrique, cinématique, et dynamique : directs et
inverses.
Ø trouver une loi complète de commande,
permettant de contrôler le mouvement du bras manipulateur, en tenant
compte de tous les problèmes qui surviennent lors du mouvement.
Durant notre travail on prend en considération les
suppositions suivantes :
Supposition 1
Le robot manipulateur utilisé est de type série
à 6 ddl de structure (RRPRRR), il est composé de corps
rigides.
Supposition 2
Tous les paramètres inertiels sont connus, on ne
s'intéresse pas à l'étape de l'identification de ces
paramètres.
Supposition 3
Les déformations non linéaires tels que les
frottements et les perturbations internes sont négligeables.
Supposition 4
Toutes les positions et les vitesses articulaires sont
mesurables.
Supposition 5
Nous avons supposé que le système et sa commande
sont continus. Dans la pratique, la commande étant
réalisée par calculateur (systèmes discrets).
Supposition 6
Les efforts extérieurs de l'organe terminal sur
l'environnement sont supposés statiques (donnés
aléatoirement), on ne tient pas en compte comment les
calculés.
Organisation du mémoire :
Ce mémoire est scindé en cinq chapitres et une
conclusion :
Dans le premier chapitre on présente la méthode
du calcul du modèle géométrique direct des bras
manipulateurs à structure ouverte simple. On applique la méthode
de Denavit Hartenberg pour représenter les transformations entre
repères, et les angles de Roulis Tangage Lacet pour la
représentation de l'orientation de l'effecteur dans l'espace
opérationnel.
Dans le deuxième on résout le modèle
géométrique inverse du robot, la solution retenue nous servira
à transformer la trajectoire opérationnelle suivie par le robot
en trajectoire articulaire correspondante.
Le troisième chapitre traite l'étude
cinématique du robot pour pouvoir calculer ses vitesses
opérationnelles à partir des vitesses articulaires et vice
versa. Dans ce chapitre, on voit aussi l'intérêt de la matrice
jacobienne et comment déterminer les positions singulières.
Le quatrième chapitre est dédié
à l'étude dynamique du robot permettant de calculer les couples
qui doivent être fournis par les actionneurs. Nous présentons deux
formalismes du calcul dynamique des bras manipulateurs puis on les applique au
robot pour déterminer ces couples.
Enfin, le dernier chapitre est consacré à la
commande du robot. Dans une première phase nous faisons un bref rappel
sur la commande classique PID, ensuit nous appliquons la loi de commande
dynamique dans l'espace articulaire, puis dans l'espace opérationnel.
Nous proposons des améliorations permettant de traverser les
configurations singulières sans divergences des résultats.
Dans la conclusion générale nous portons
un regard critique sur ce travail et nous finissons cet exposé par
quelques propositions.
Chapitre I
Le Modèle
géométrique direct du robot (MGD)
I.1. Introduction
Un robot manipulateur se compose d'un ensemble de corps
reliés par des articulations, ces derniers peuvent être simples
« 1ddl » rotoïde ou prismatique, ou bien complexes,
« 2 ou 3ddl »une rotule ou un cardan. On suppose que toutes
les articulations ont seulement 1ddl, puisque une articulation complexe peut
être considéré comme une succession des articulations
simples avec des liaisons de longueur zéro, avec cette supposition,
l'action de chaque articulation peut être décrit par un nombre
réel simple : l'angle de rotation dans le cas d'une articulation
rotoïde ou le déplacement dans le cas d'une articulation
prismatique.
L'objectif du modèle géométrique direct
(MGD) est de déterminer l'effet cumulatif des variables articulaires,
dans ce chapitre nous développerons un ensemble de conventions qui
fournissent une procédure systématique pour calculer ce
modèle. Il est, naturellement, possible d'effectuer le MGD même
sans respecter ces conventions, mais pour un manipulateur de n
liaisons le MGD peut être extrêmement complexe et les conventions
présentées ci-dessous simplifient largement la
modélisation et donnent une langue universelle avec laquelle les
ingénieurs de la robotique peuvent communiquer [SPO 04].
I.2. Description de la
géométrie des robots à structure ouverte simple
Un robot manipulateur à structure ouverte simple avec
n articulations est composé de n+1 corps notés
 , puisque chaque articulation relie deux corps, nous numérotons
les articulations de 1 à n, et nous
numérotons les corps de 0 à n,
à partir de la base. On associe à chaque corps i du
mécanisme un repère orthonormé direct , puisque chaque articulation relie deux corps, nous numérotons
les articulations de 1 à n, et nous
numérotons les corps de 0 à n,
à partir de la base. On associe à chaque corps i du
mécanisme un repère orthonormé direct  noté noté . Les repères particuliers sont d'une part celui de la base . Les repères particuliers sont d'une part celui de la base  noté noté  et d'autre part et d'autre part  celui de l'organe terminal. Le repère de la base occupe une
position et une orientation connues par rapport à un repère fixe
noté Ratelier, si le robot est à un
poste fixe dans un atelier. celui de l'organe terminal. Le repère de la base occupe une
position et une orientation connues par rapport à un repère fixe
noté Ratelier, si le robot est à un
poste fixe dans un atelier.
Le robot manipulateur pourrait lui-même être
mobile (par exemple, il pourrait être monté sur une plateforme
mobile ou sur un véhicule autonome), et il peut être
manipulé facilement en prolongeant légèrement les
techniques présentées ici [SPO 04].
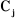
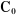
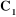
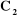
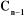
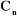
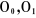
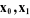
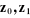
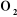
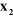
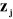
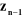
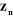
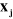
Figure I.1. La
chaîne cinématique d'un robot série
Dans la littérature il existe plusieurs méthodes
et notations pour la description de la morphologie des robots, les plus
répondues sont : [BEN 06]
· La méthode de Denavit-Hartenberg qui est
très bien adaptée pour les mécanismes à structures
de chaînes simples où toutes les liaisons sont
élémentaires, mais, elle présente des difficultés
lorsqu'il s'agit de mécanismes à structures de chaînes
complexes.
· La méthode de Khalil-Kleinfinger vient palier
les inconvénients cités précédemment, mais elle
présente des redondances pour les mécanismes à structures
de chaînes simples [FLÜ 98].
On ne s'intéresse ici qu'à la première
méthode puisque nous travaillons sur un robot à chaîne
ouverte simple.
I.2.1. Paramétrage de
Denavit Hartenberg
Les paramètres de Denavit et Hartenberg sont quasi
universellement adoptés par les roboticiens pour définir, avec un
nombre minimum de paramètres, les matrices de transformations
homogènes élémentaires qui permettent de passer du
repère associé à un corps du robot au corps qui le suit
dans la chaîne cinématique, les corps sont supposés
parfaitement rigides et les articulations sont considérées comme
idéales.
Un repère de référence  est assigné pour chaque corps est assigné pour chaque corps  du robot à l'articulation i où elle
rencontre le corps précédent du robot à l'articulation i où elle
rencontre le corps précédent , ce repère est défini comme suit : , ce repère est défini comme suit :
-- L'axe  se dirige le long de l'axe de l'articulation i. se dirige le long de l'axe de l'articulation i.
-- l'axe  est aligné suivant la direction de la perpendiculaire
commune aux axes est aligné suivant la direction de la perpendiculaire
commune aux axes  et et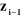
-- l'axe , non représenté sur la figure, est choisi de
manière à former un trièdre orthonormé direct
avec , non représenté sur la figure, est choisi de
manière à former un trièdre orthonormé direct
avec et et  . .
Les transformations élémentaires qui
permettent d'exprimer le passage du repère  au repère au repère  (Figure I.2) sont : (Figure I.2) sont :
· une translation di suivant
 égale à la longueur de la perpendiculaire commune. égale à la longueur de la perpendiculaire commune.
· une rotation d'angle  autour de l'axe autour de l'axe . . est l'angle entre est l'angle entre  et et . .
· une rotation d'angle  autour de l'axe autour de l'axe . . est l'angle entre l'axe xi-1 et l'axe est l'angle entre l'axe xi-1 et l'axe . .
· xj
zi-1
i
i
di
Oj
xi-1
zi
rj
Oi-1
une translation suivant l'axe . L'amplitude de cette translation, notée . L'amplitude de cette translation, notée , est donnée par la distance (signée) entre l'axe , est donnée par la distance (signée) entre l'axe  avec l'axe avec l'axe [GRE 05]. [GRE 05].
Figure I.2.
Paramètres de Denavit et Hartenberg
Il est à noter que les angles sont positifs quand la
rotation est dans le sens inverse des aiguilles d'une montre.
Les paramètres  sont les paramètres de Denavit et Hartenberg. On remarque que
seul quatre paramètres sont nécessaires pour passer d'un
repère sont les paramètres de Denavit et Hartenberg. On remarque que
seul quatre paramètres sont nécessaires pour passer d'un
repère  au repère au repère , grâce notamment au choix de l'emplacement de ces derniers. , grâce notamment au choix de l'emplacement de ces derniers.
La variable articulaire  associée à la iième
articulation se traduit par la relation : associée à la iième
articulation se traduit par la relation :
 (I-1)
(I-1)
|
tel que :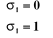
|
si l'articulation i est rotoïde
|
et 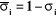
|
(I-2)
|
|
si l'articulation i est prismatique
|
En terme de matrice de transformation homogène, les
quatre transformations élémentaires donnent la matrice
suivante :
 (I-3) (I-3)
après son développement, on obtient :
(I-4) 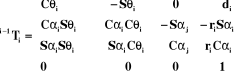
avec : 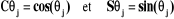
la matrice de transformation homogène est souvent notée sous la forme : est souvent notée sous la forme :
 (I-5) (I-5)
tel que :
 :est la matrice de rotation (3x3), appelé aussi matrice
d'orientation ou matrice des cosinus directeurs, elle représente la
rotation entre les deux repères :est la matrice de rotation (3x3), appelé aussi matrice
d'orientation ou matrice des cosinus directeurs, elle représente la
rotation entre les deux repères  et et , Les colonnes de la matrice , Les colonnes de la matrice  représentent les composantes des vecteurs unitaires du
repère représentent les composantes des vecteurs unitaires du
repère  dans le repère dans le repère  . .
 est la matrice de position (3×1) qui définit l'origine du
repère est la matrice de position (3×1) qui définit l'origine du
repère  dans le repère dans le repère  . .
I.3. Le
MGD d'un robot manipulateur
Il exprime la position et l'orientation du repère de
référence  lié à l'outil, relativement à un repère
fixe lié à l'outil, relativement à un repère
fixe  , celui de l'atelier par exemple, en fonction des variables
articulaires motorisées (et asservies électroniquement)
q1, q2 ... qn du
mécanisme. , celui de l'atelier par exemple, en fonction des variables
articulaires motorisées (et asservies électroniquement)
q1, q2 ... qn du
mécanisme.
Après avoir donner les quatre paramètres  de tous les repères du robot, ainsi que la façon dont sa
base est située dans l'espace, on peut complètement indiquer la
géométrie du bras à n'importe quelle moment. de tous les repères du robot, ainsi que la façon dont sa
base est située dans l'espace, on peut complètement indiquer la
géométrie du bras à n'importe quelle moment.
Le MGD est obtenu par la multiplication successive des
matrices de passage entre repères, il est exprimé donc sous forme
d'une matrice définit comme suit :
 (I-6)
(I-6)
Il peut aussi être représenté par la
relation :  (I-7) (I-7)
où :
X : est le vecteur des
coordonnées opérationnelles, il peut être défini
avec les éléments de la matrice tel que : tel que :
 (I-8) (I-8)
q : est le vecteur des variables
articulaires, noté :
 (I-9)
(I-9)
I.4.
Représentation des coordonnées opérationnelles
Pour définir la situation de l'organe terminal du robot
dans l'espace, il faut préciser sa position et son orientation.
Soit  (I-10)
(I-10)
où  représente les trois coordonnées opérationnelles
de position et représente les trois coordonnées opérationnelles
de position et  représente les coordonnées opérationnelles
d'orientation. représente les coordonnées opérationnelles
d'orientation.
Pour les coordonnées  tout le monde s'accorde pour choisir les composantes
cartésiennes, mais pour spécifier une rotation, la matrice tout le monde s'accorde pour choisir les composantes
cartésiennes, mais pour spécifier une rotation, la matrice  présente un nombre surabondant de paramètres (neuf),
tandis que, seul trois paramètres indépendants sont suffisants
pour une telle représentation. présente un nombre surabondant de paramètres (neuf),
tandis que, seul trois paramètres indépendants sont suffisants
pour une telle représentation.
Plusieurs choix sont possibles et adoptés en pratique
pour les coordonnées  : :
-- angles d'Euler
quaternions d'Euler
angles de Cardans (Roulis - Tangage - Lacet) : c'est la
méthode qu'on a choisi pour notre travail.
I.4.1. Les angles de Cardans
(Roulis - Tangage - Lacet « RTL »)
Par analogie avec la terminologie des pilotes de
véhicules, des avions notamment, dont la direction du mouvement est
supposée dans le sens de l'axe z, les angles de roulis
( ), tangage ( ), tangage ( ) et lacet ( ) et lacet ( )?, présentent trois rotations successives défini comme
suit [KHA 99] : )?, présentent trois rotations successives défini comme
suit [KHA 99] :
 (I-11)
(I-11)
ce qui donne la
matrice de rotation suivant:
 (I-12) (I-12)
L'expression de ces angles en fonction des cosinus directeurs
est comme suit :
 (I-13)
(I-13)
Les coordonnées opérationnelles sont donc
données par le vecteur:  (I-14)
(I-14)
I.5.
Le MGD du robot
I.5.1 La chaîne
cinématique du robot
Le robot manipulateur utilisé dans ce travail est de
type série à 6 degrés de liberté, constitué
par 6 corps mobiles supposés parfaitement rigides .le porteur est de
type RRP et le poignet comporte trois rotations d'axes concourants, ce robot a
une position connue par rapport à un repère atelier et le dernier
repère choisi pour le calcul du MGD est celui de l'outil .voir
figure (I.3)
Figure I.3. La chaîne
cinématique du robot
RRPRRR
r1
L6
Z2
X4 X5
X6
Z1 X2
X3
X1
Z5
Z4 Z6
1
2
4
5
6
r3
Z3
RL4
ZE
XE
il
Z0
X0
6TE
0T6
ZF
XF
YF
F T0
L2
Ce robot est caractérisé par les
paramètres suivants :
|
j
|
|
|
d
|
|
r
|
|
1
|
0
|
0
|
d1
|
1
|
r1
|
|
2
|
0
|
/2
|
0
|
2+ /2
|
0
|
|
3
|
1
|
/2
|
0
|
0
|
L2+r3
|
|
4
|
0
|
0
|
0
|
4
|
RL4
|
|
5
|
0
|
-/2
|
0
|
5
|
0
|
|
6
|
0
|
/2
|
0
|
6
|
0
|
Tableau I.1 Paramètres
géométriques relatifs au mécanisme
Le long du projet, on a attribué aux
différentes longueurs du mécanisme, les mêmes valeurs qui
sont :
r1 =1.5 m
L2 = 0.75 m
RL4 = 0.75 m
L6 = 0.20 m
La transformation du repère  au repère au repère  et celle du repère et celle du repère  au repère au repère  sont représentées par les translations et les rotations
suivantes : sont représentées par les translations et les rotations
suivantes :
 (I-15) (I-15)
 (I-16)
(I-16)
Le vecteur des variables articulaires comporte cinq angles
(rad) et une translation (m), il est exprimé comme suit: (I-17) (I-17)
Le calcul des matrices de transformation homogène sous
Maple nous a donné :
 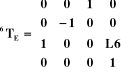
     
avec :  (I-18)
(I-18)
Le modèle géométrique direct est
donné selon la relation :
 (I-19)
(I-19)
Puisque on a choisi de représenter les rotations par
les angles de RTL, Le vecteur des coordonnées
opérationnelles X simplifié (en fonction de
q), extrait de l'expression de la matrice , est comme suit: , est comme suit:
 (I-20-a)
(I-20-a)
 (I-20-b)
(I-20-b)
avec :
 (I-21) (I-21)
I.5.2. Application
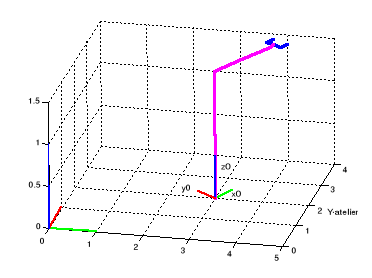
Puisque X est en fonction de
q et des paramètres de , on a joué sur les valeurs de ces variables pour obtenir
différentes configurations de l'effecteur. Les figures (I.4),
(I.5), (I.6) et (I.7) montrent les résultats
et les coordonnées opérationnelles obtenues pour plusieurs
positions et mouvements simples. , on a joué sur les valeurs de ces variables pour obtenir
différentes configurations de l'effecteur. Les figures (I.4),
(I.5), (I.6) et (I.7) montrent les résultats
et les coordonnées opérationnelles obtenues pour plusieurs
positions et mouvements simples.
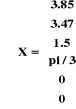
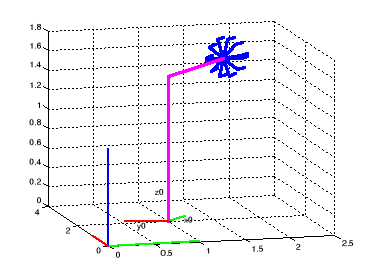
Figure I.4. Le robot à
l'état de repos où d1=3, y1=2, 0=pi/3
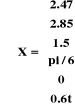
Figure I.5. La position du robot
lorsque : d1=1, y1=2, 0=pi/6, 6=0.6*t, t=0:5
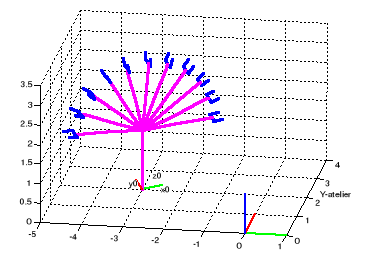
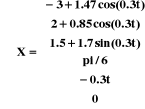
Figure I.6.la
position du robot lorsque : d1= -3, y1=2, 0=pi/6, 2=0.3*t, t=0:5
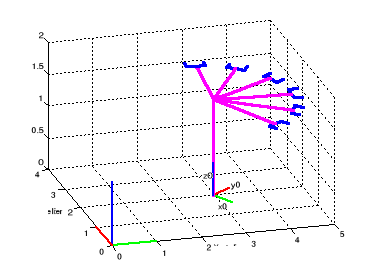
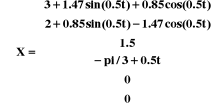
Figure I.7.
La position du robot lorsque : d1=3, y1=2, 0= -pi/3,
1=0.5*t, t=0:5
I.6.
Espace de travail
I.6.1. Définition
L'espace de travail est l'ensemble des positions et /ou
orientations accessible par l'organe terminal du robot.
Le volume ou l'espace de travail d'un robot dépend
généralement de trois facteurs :
- De la géométrie du robot,
- De la longueur des segments,
- Du débattement des articulations (limité par
des butées)
Soit  une configuration articulaire donnée et soit X
l'élément de l'espace opérationnel correspondant, tel que
: une configuration articulaire donnée et soit X
l'élément de l'espace opérationnel correspondant, tel que
: 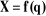
On note Q l'ensemble des configurations
accessibles compte tenu des butées articulaires, Par conséquent,
Q sera appelé domaine articulaire.
L'image de Q par le modèle géométrique
direct f définit l'espace de travail W du robot:
 (I-21)
(I-21)
Dans le cas général, Les orientations de
l'organe terminal n'apparaissent pas dans la définition de ce volume de
travail car ce n'est pas facile de les représentées.
W est donc la projection dans l'espace des positions [FIS
04].
Comme on l'a définie précédemment, la
position de l'organe terminal dans le repère atelier est donnée
par le vecteur position P dans la matrice de transformation
FTE.
On a développé un programme qui a comme
paramètres d'entrée les limites articulaires de chaque
articulation et comme sortie toutes les configurations possibles (les
positions) de l'organe terminal, l'algorithme associé à ce
programme est : [BEN 06]
Début
Entrer (qmin et qmax)
pour chaque articulation ;
i =1
Pour q1 allant de qmin à
qmax faire
Pour q2 allant de qmin à
qmax faire
......
.......
Pour qn allant de qmin à
qmax faire
px(i)=f(q)
py(i)=f(q)
pz(i)=f(q)
i=i+1
fin pour
......
fin pour
fin pour
Sortie (Px,Py,Pz)
fin du programme
I.6.2. Application
numérique
Si on admet que chaque liaison rotoïde permet une
rotation d'un tour complet (2) et que l'origine
OE du repère outil est le point de
référence, dans l'absence des butées articulaires et sans
tenir compte les positions singulières, l'espace de travail dans ce cas
est une sphère creuse du centre O2 l'origine
du repère R2 et de rayons intérieur
et extérieur L-L6 et L+r3 (où
L=RL4+L2), Figure (I.8).
La figure (I.9), montre la
représentation de cette espace dans le cas où :
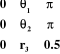
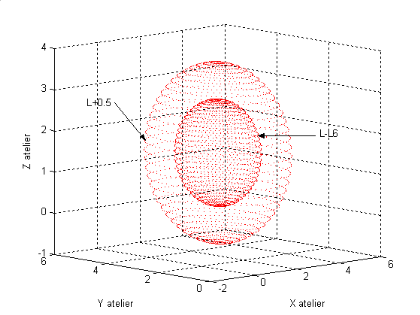
Figure I.8.
L'espace de travail du robot lorsque : 0<i<2ð,
0<r3<0.5
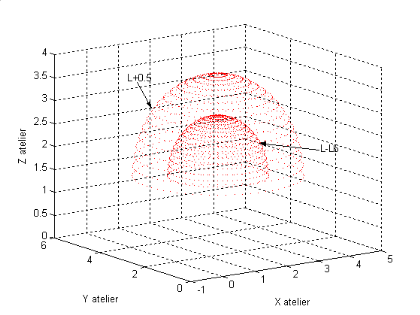
Figure I.9.
L'espace de travail du robot lorsque : 0<1,2<ð,
0<4,5 <2ð, 0<r3<0.5
I.7.
Conclusion
On a exposé dans ce chapitre une méthode de
calcul du modèle géométrique direct des robots à
structure ouverte simple, qui est fondée sur l'utilisation du
paramétrage de Denavit Hartenberg et nécessite le bon choix des
repères.
On a vu que la représentation des coordonnées
opérationnelles de rotation est faite par les cosinus directeurs puis
par les angles de Cardans.
On a terminé le chapitre par le calcul de l'espace de
travail du robot en dehors de ses positions singulières.
Comme on a présenté dans ce chapitre, le MGD
d'un manipulateur est de déterminer la configuration (position et
orientation) de son effecteur terminal en fonction de ses variables
articulaires, le problème inverse de celui ci, c.-à-d.,
déterminer les variables articulaires en donnant une configuration
désirée de l'effecteur terminal, est appelé le
modèle géométrique inverse et c'est le sujet du chapitre
suivant.
Chapitre II
Le Modèle
géométrique inverse du robot (MGI)
II.1. Introduction
L'organe terminal d'un robot manipulateur doit effectuer des
mouvements et/ou exercer des efforts dans un repère qui est lié
à l'espace opérationnel (l'atelier). L'opérateur qui
programme un robot par des moyens évolués lui fournit des
instructions définies dans cet espace. Par contre, même s'il est
doté de capteurs extérieurs (de position, de force) permettant de
l'asservir localement à la tâche, le robot a ses asservissements
élémentaires bouclés sur les informations issues de ses
capteurs internes (articulaires) et mesurant plus ou moins directement les
qi et/ou les forces fi
. L'armoire de commande du robot doit donc contenir un module (un programme
implanté sur calculateur numérique) qui calcule les consignes
à envoyer aux asservissements « articulaires » en
fonction des valeurs des variables de position, d'orientation et/ou d'efforts
désirées dans l'espace opérationnel. Ces calculs font
appel aux modèles théoriques des transformations de
coordonnées inverses. Une condition nécessaire d'existence de ces
modèles (nombre fini de solutions) est que le robot ne soit pas
redondant vis-à-vis de la tâche : le nombre de variables
opérationnelles spécifiées est égal à
n, nombre de degrés de liberté du
mécanisme. [TEC 07]
II.2.
Position du problème
Le problème général de la
géométrique inverse peut être énoncé comme
suit. Donner une transformation homogène (4×4) , trouver (un ou tous) les solutions de l'équation : , trouver (un ou tous) les solutions de l'équation :  (II.1)
(II.1)
où
Ø H représente la position et
l'orientation désirées de l'outil.
 Ø
(II.2) Ø
(II.2)
 Ø est la matrice de transformation homogène
définissant la situation du repère de base Ø est la matrice de transformation homogène
définissant la situation du repère de base  du robot dans le repère atelier du robot dans le repère atelier ; ;
 Ø est la matrice de transformation homogène du
repère terminal Ø est la matrice de transformation homogène du
repère terminal  dans le repère dans le repère  (calculée par MGD) ; (calculée par MGD) ;
 Ø est la matrice de transformation homogène
définissant le repère outil Ø est la matrice de transformation homogène
définissant le repère outil  dans le repère terminal dans le repère terminal . .
En remplaçant la relation (II.2) dans
l'équation
(II.1) et en regroupant dans le coté droite
tous les termes connus, on peut écrire :
 (II-3)
(II-3)
Notre tâche est de trouver les valeurs des variables
articulaires  de sorte que de sorte que . .
Il est, trop difficile de résoudre directement ces
équations, par conséquent, nous devons développer des
techniques efficaces et systématiques qui exploitent la structure
cinématique particulière du manipulateur.
Considérant que le MGD a toujours une solution
unique, le MGI peut n'avoir pas une solution et même si elle existe,
elle peut être pas unique.
À résoudre le MGI on s'intéresse
à trouver une solution de forme analytique plutôt qu'une solution
numérique. Chercher une solution analytique signifie de trouver un
rapport explicite :  (II-4)
(II-4)
Les solutions analytiques sont préférables pour
deux raisons. D'abord, les équations géométriques inverses
doivent être résolues à une vitesse rapide, disent toutes
les 20 millisecondes, et avoir des expressions plutôt qu'une recherche
itérative est une nécessité pratique. En second lieu, le
MGI en général a des solutions multiples, les solutions de forme
analytique permettent de développer des règles pour choisir une
solution particulière parmi plusieurs [BIL 05].
Une fois une solution aux équations
mathématiques est identifiée, il doit encore vérifier pour
voir si elle satisfait toutes les contraintes sur la gamme de mouvement commun
possible.
Outil
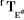
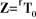
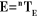
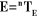
Bras manipulateur
Figure II.1.
Transformation entre organe terminal et repère atelier.
Le nombre de solutions dépend de l'architecture du
robot, il est égal au produit de solutions possibles pour chaque axe
[AIS 06].
Plusieurs méthodes, analytiques et numériques,
sont proposées pour trouver le MGI d'un robot, parmi eux on
s'intéresse à la méthode de Paul ; une méthode
analytique qui traite séparément chaque cas particulier et
convient pour la plupart des robots industriels.
II.3.
Calcul du MGI par la méthode de Paul
II.3.1. Principe
La situation de l'organe terminal d'un robot manipulateur
à  degrés de liberté est décrite par le modèle
géométrique direct qui a pour expression : degrés de liberté est décrite par le modèle
géométrique direct qui a pour expression :
 (II-5)
(II-5)
Cette même situation désirée
sera notée par la matrice de transformation homogène  telle que : telle que :
 (II-6)
(II-6)
On cherche à résoudre le système
d'équations suivant :
 (II-7)
(II-7)
Pour trouver les solutions du système
(II-3), Paul [KHA 99] a
proposé une méthode qui consiste à pré multiplier
successivement les deux membres de l'équation (II-7) par les
matrices  pour pour variant de variant de à à , opérations qui permettent d'isoler et d'identifier l'une
après l'autre les variables articulaires que l'on cherche. , opérations qui permettent d'isoler et d'identifier l'une
après l'autre les variables articulaires que l'on cherche.
Pour un robot à 6 ddl à titre d'exemple, on
procède comme suit :
- on multiplie à gauche l'expression (II-7) par  : :
 (II-8)
(II-8)
- par identification terme à terme des deux membres de
l'équation (II-8), On se ramène à un système
d'équations, fonction de  uniquement, qu'on résout selon le uniquement, qu'on résout selon le
Tableau II-1.
- ensuite on multiplie à gauche l'expression (II-8) par
 et on calcule et on calcule , ,
La succession des équations permettant le calcul de
tous les  est la suivante: est la suivante:
 (II-9) (II-9)
avec : 
Ces équations peuvent avoir des solutions
évidentes, ou se ramènent aux principaux types rencontrés
en robotique, mentionnés dans le tableau (II.1)
ci-dessous [KHA 99]:
|
Types
|
Système
|
|
Type1
|
|
|
Type2
|
|
|
Type3
|
|
|
Type4
|
|
|
Type5
|
|
|
Type6
|
|
|
Type7
|
|
|
Type8
|
|
|
avec :  variable de l'articulation prismatique variable de l'articulation prismatique 
 sinus et cosinus de la variable sinus et cosinus de la variable  de l'articulation rotoïde de l'articulation rotoïde 
|
Tableau II.1. Types d'équations
(Méthode de Paul)
II.3. 2. Le découplage
cinématique
Pour un manipulateur 6ddl avec un poignet rotule, le MGI peut
être découplé en deux problèmes plus simples,
à savoir d'abord trouvant la position de point d'intersection des axes
du poignet, ce dernier appelée le centre de poignet, et puis à
conclure l'orientation du poignet.
Puisque le mouvement autour des axes du poignet, ne change
pas la position de son centre, la position du poignet est en fonction des
trois premières variables seulement . Afin d'avoir l'organe terminal du robot au point donné par les
coordonnées P et une orientation donnée par
A, il est suffisant que le centre du poignet
(Oc) a des coordonnées données
par : . Afin d'avoir l'organe terminal du robot au point donné par les
coordonnées P et une orientation donnée par
A, il est suffisant que le centre du poignet
(Oc) a des coordonnées données
par :
 (II-10)
(II-10)
En utilisant l'équation (II-10) nous pouvons trouver
les valeurs des trois premières variables articulaires. Ceci
détermine la transformation d'orientation  qui dépend seulement de ces variables. Nous pouvons maintenant
déterminer l'orientation de l'organe terminal relativement au
repère R 3 de l'expression : qui dépend seulement de ces variables. Nous pouvons maintenant
déterminer l'orientation de l'organe terminal relativement au
repère R 3 de l'expression :
 (II-11)
(II-11)
Noter que le côté droite de (II-11) est
complètement connu puisque ;  est indiqué (l'orientation désirée) et est indiqué (l'orientation désirée) et  peut être calculée, une fois les trois premières
variables articulaires sont connues[FIS 04], [SPO 04]. peut être calculée, une fois les trois premières
variables articulaires sont connues[FIS 04], [SPO 04].
II.4.
le MGI du robot choisi
Le MGD du robot a été déjà
établi au chapitre I, Les paramètres
géométriques sont donnés dans Tableau
I.1. .Puisque le robot a un poignet rotule (de centre
O4)on a utilisé la méthode de Paul
avec découplage cinématique.
La position désirée de l'outil par rapport au
repère atelier est donnée par la matrice  : :

On a calculé la matrice de transformation qui exprime le repère qui exprime le repère dans le repère dans le repère  suivant la relation: suivant la relation:
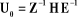
Le système d'équations qu'on doit
résoudre est:

· Calcul de  : :
Puisque , on peut écrire que la quatrième colonne de , on peut écrire que la quatrième colonne de est égale à la quatrième colonne du produit des
transformations est égale à la quatrième colonne du produit des
transformations  : :
 (II-12) (II-12)
En prémultipliant l'équation
précédente par , on obtient : pour les éléments de droite (la
quatrième colonne de , on obtient : pour les éléments de droite (la
quatrième colonne de ): ):
 (II-13)
(II-13)
En identifiant les éléments de l'équation
en remarquant que :
 (II-14) (II-14)
Cette équation est de type 2, elle admit les deux
solutions suivantes pour : :
 (II-15) (II-15)
En prémultipliant encore par , on obtient : , on obtient :

Par identification terme à terme de ce système
d'équations on peut trouver  et et  ; la résolution de la première équation
(équation de type 2) et après simplification, nous donne pour ; la résolution de la première équation
(équation de type 2) et après simplification, nous donne pour les solutions suivantes : les solutions suivantes :
 (II-16) (II-16)
Connaissant , on peut calculer , on peut calculer  à partir de la deuxième équation (équation
de type 1), la solution obtenu est : à partir de la deuxième équation (équation
de type 1), la solution obtenu est :  (II-17) (II-17)
· Calcul de  : :
Les variables  étant connues, on s'intéresse maintenant aux
équations d'orientation (II-11). étant connues, on s'intéresse maintenant aux
équations d'orientation (II-11).
On note :  (II-18)
(II-18)
où :  est la matrice d'orientation de la matrice est la matrice d'orientation de la matrice 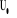
Les expressions de F, G et H
s'écrivent :
 (II-19-a)
(II-19-a)
 (II-19-b)
(II-19-b)
 (II-19-c)
(II-19-c)
A partir de l'équation (II-18) on a :
 (II-20)
(II-20)
Les éléments de  représentent les termes d'orientations de représentent les termes d'orientations de  déjà calculés pour le MGD : déjà calculés pour le MGD :
 (II-21) (II-21)
En prémultipliant cette équation par , on obtient : , on obtient :
 (II-22)
(II-22)
 (II-23) (II-23)
A partir des éléments de (2,3) on obtient une
équation de type 2 en , qui donne les deux solutions : , qui donne les deux solutions :
 (II-24)
(II-24)
A partir des éléments de (1,3) et (2,3) on
obtient un système d'équations de type 3 en , qui a pour solution : , qui a pour solution :
 (II-25)
(II-25)
Enfin, en considérant les éléments (2,1)
et (2,2) on obtient un système d'équations de type 3 en , qui a comme solution : , qui a comme solution :
 (II-26)
(II-26)
Le nombre total de solutions pour le modèle
géométrique inverse est égal à huit ( ) : c'est à dire que l'outil de robot peut atteindre un
point désiré de son espace opérationnel atteignable par
huit configurations possibles. ) : c'est à dire que l'outil de robot peut atteindre un
point désiré de son espace opérationnel atteignable par
huit configurations possibles.
Si on veut donner la position désirée en
utilisant les angles de RTL, dans ce cas le MGI se fait en calculant d'abord
les cosinus directeurs en fonction de ces angles , puis remplacer les valeurs
trouvées dans les solutions calculées, sachant que :
 (II-27) (II-27)
II.5.
Application
On a prend comme exemple de trajectoire, la poursuite d'une
tache de soudure d'un objet de forme cylindrique associé à un
repère Robj, ce dernier est
relié au repère atelier par la matrice : :
 (II-28)
(II-28)
La description du trajet de l'outil par rapport à
Robj est donnée par la transformation
homogène : :
 (II-29) (II-29)
la position désirée de l'outil par rapport au
repère atelier est donc :

 (II-30) (II-30)
avec :
pas signifié le pas du temps
choisi : 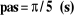
Les résultats de cette simulation sont montrés
par les figures (II.2 et II.3),
ils ont validé le MGI calculé.
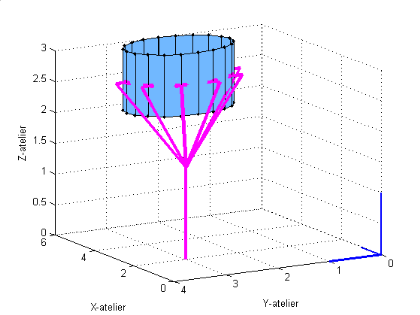
Figure
II.2. Suivi de la trajectoire donnée
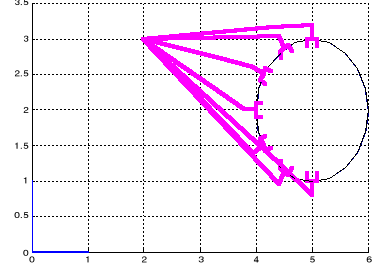
Figure II.3.
Suivi de la trajectoire donnée (vue de dessus)
II.5.
Conclusion
On a exposé dans ce chapitre
la méthode de Paul pour le calcul du MGI, cette méthode
intuitive en ce sens qu'elle laisse à l'utilisateur le choix des
équations à résoudre, elle est applicable à un
grand nombre de chaînes cinématiques possédant surtout des
paramètres géométriques particuliers : distance
nulles ou angles dont les sinus et cosinus sont égaux à 0, 1, -1,
en plus, cette méthode analytique donne toutes les solutions possibles
du modèle géométrique inverse.
Nous avons également résolu le
modèle géométrique inverse du robot proposé
grâce à cette méthode.
Après cette modélisation
géométrique inverse du robot, on va aborder dans le chapitre qui
suit l'étude cinématique qui va nous permettre de calculer ses
vitesses cartésiennes et articulaires.
Chapitre III
Etude cinématique du robot
III.1. Introduction
Le modèle cinématique est,
littéralement, un modèle des vitesses. Il exprime les relations
entre les vitesses articulaires de chaque joint et les vitesses
cartésiennes d'un point de la chaîne cinématique,
généralement l'organe terminal. Ce modèle est donc un
modèle par accroissements infinitésimaux: chaque variation
élémentaire de la valeur d'une articulation implique une
variation de position de l'organe terminal, et inversement. Lorsque ces
variations infinitésimales sont exprimées par rapport au temps,
on peut les considérer comme des vitesses.
Le modèle cinématique permet donc non seulement
de compléter éventuellement le modèle
géométrique en tenant compte des vitesses, mais aussi de
remplacer le modèle géométrique: en agissant par
accroissements successifs, on peut se déplacer d'un point donné
à un autre. [FLÜ98].
III.2.
Le modèle cinématique direct (MCD)
L'outil principalement utilisé pour traiter le
problème de la cinématique des robots est la matrice jacobienne.
Elle représente un opérateur permettant de lier les vitesses des
corps d'un robot exprimées dans différents espaces vectoriels
[FLÜ98].
Le Modèle Cinématique Direct (MCD) permet de
calculer les composantes du torseur cinématique  à partir des vitesses articulaires dites
généralisées à partir des vitesses articulaires dites
généralisées , dérivées par rapport au temps des coordonnées
généralisées , dérivées par rapport au temps des coordonnées
généralisées . Le torseur cinématique est défini par : . Le torseur cinématique est défini par :
 (III-1)
(III-1)
Le MCD fait intervenir la matrice jacobienne, fonction de la
configuration du robot manipulateur, tel que :
 (III-2)
(III-2)
III.2.1 Calcul Indirect de la
matrice Jacobienne
Le calcul indirect de la matrice jacobienne consiste à
utiliser le modèle géométrique du robot manipulateur.
 (III-3)
(III-3)
Et par définition, la matrice jacobienne est la
matrice des dérivées partielles de la fonction f
par rapport aux coordonnées généralisées,
ainsi :
 (III-4)
(III-4)
Cette méthode de dérivation est
facile à mettre en oeuvre pour des robots à deux ou trois
degrés de liberté dans le plan, mais pour des robots ayant plus
de trois degrés de liberté la dérivation manuelle devient
presque impossible.
III.2.2. Calcul direct de la
matrice Jacobienne
On peut utiliser une méthode très
répandue pour le calcul cinématique, qui permet d'obtenir la
matrice jacobienne par un calcul direct fondé sur l'influence que
produit chaque articulation d'ordre  de la chaîne sur le repère terminal de la chaîne sur le repère terminal . .
a) articulation prismatique
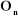
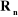
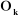
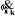
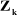
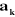
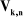
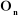
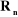
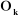
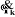
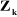
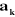
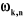
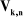
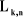
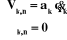
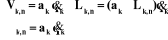
z j
On peut calculer  en considérant séparément les cas d'une
articulation prismatique et d'une articulation rotoïde: en considérant séparément les cas d'une
articulation prismatique et d'une articulation rotoïde:
Figure
III.1. Influence du type de l'articulation sur le repère
terminal
où :
 : désigne le vecteur d'origine et d'extrémité : désigne le vecteur d'origine et d'extrémité
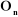
 : est le vecteur unitaire porté par l'axe : est le vecteur unitaire porté par l'axe  de l'articulation de l'articulation  . .
En introduisant le coefficient binaire , les vecteurs , les vecteurs  s'écrivent : s'écrivent :
 (III-5)
(III-5)
Grâce au théorème de la composition des
vitesses, on peut sommer toutes les contributions élémentaires de
chaque articulation afin d'obtenir les vecteurs finaux des vitesses de
translation et de rotation  du repère terminal par l'expression : du repère terminal par l'expression :
 (III-6)
(III-6)
Par identification avec la relation (III-2), la matrice
Jacobienne exprimée dans le repère , notée , notée , s'écrit : , s'écrit :
 (III-7) (III-7)
D'une façon générale,
projetée dans le repère , la matrice jacobienne notée , la matrice jacobienne notée s'écrit : s'écrit :
 (III-8) (III-8)
En remarquant que :
 (III-9)
(III-9)
avec :
 · : matrice d'orientation de dimension · : matrice d'orientation de dimension  du repère du repère  dans le repère dans le repère , ,
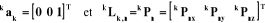
· On calcule alors la  colonne de la matrice Jacobienne, notée colonne de la matrice Jacobienne, notée , projetée dans le repère , projetée dans le repère  par la formule : par la formule :
 (III-10) (III-10)
où :
·
isk,
ink et
iak : sont
respectivement le  vecteurs de la matrice
iAk. vecteurs de la matrice
iAk.
·
kPnx et
kPny : sont
respectivement la  composantes du vecteur composantes du vecteur qui est la quatrième colonne de qui est la quatrième colonne de  calculée précédemment par le modèle
géométrique direct. calculée précédemment par le modèle
géométrique direct.
III.2.3. le calcul du MCD par les équations de
récurrence
Connaissant Jn
les vitesses de translation et de rotation du repère
Rn peuvent être obtenus à partir de la
relation (III-2). De point de vue nombre d'opérations, il est cependant
plus judicieux d'utiliser les équations de récurrence
suivantes :
 (III-11)
(III-11)
On initialise la récurrence avec les vitesses
opérationnelles  et et  de la base du robot. de la base du robot.
La vitesse obtenue dans ce cas est  , pour trouver , pour trouver  on fait la projection de ce vecteur dans le repère
R0 : on fait la projection de ce vecteur dans le repère
R0 :
 (III-12)
(III-12)
Le calcul du MCD, par la matrice jacobienne ou bien par les
équations de récurrence, donne le vecteur  où où  est la dérivée par rapport au temps du vecteur de
position est la dérivée par rapport au temps du vecteur de
position , mais le , mais le  ne représente pas la dérivée de l'orientation, il
faut trouver donc une relation entre les coordonnées
opérationnelles X et le modèle
cinématique. ne représente pas la dérivée de l'orientation, il
faut trouver donc une relation entre les coordonnées
opérationnelles X et le modèle
cinématique.
III.2.4. la jacobienne analytique
La matrice jacobienne développée ci-dessus
s'appelle parfois la jacobienne géométrique pour la distinguer de
la jacobienne analytique, dénoté
Ja(q), qui est basée sur une
représentation minimale pour l'orientation du repère de
l'effecteur .
Soit  une représentation de la situation du repère
Rn dans R0, où
xp représente les trois coordonnées
opérationnelles de position et xr
représente les coordonnées opérationnelles d'orientation,
les vitesses opérationnelles sont donc une représentation de la situation du repère
Rn dans R0, où
xp représente les trois coordonnées
opérationnelles de position et xr
représente les coordonnées opérationnelles d'orientation,
les vitesses opérationnelles sont donc  , on doit trouver la relation entre ces vitesses et les vecteurs
vitesses , on doit trouver la relation entre ces vitesses et les vecteurs
vitesses  telle que : telle que :
 (III-13)
(III-13)
Ou sous forme matricielle :
 (III-14)
(III-14)
Partant de la relation (III-13), on peut déduire
que :
 (III-15)
(III-15)
avec : 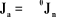
En général, la sous matrice  est égale à la matrice unité
I3 car les coordonnées
opérationnelles de position sont simplement les coordonnées
cartésiennes de la position de l'outil. Par contre, la matrice est égale à la matrice unité
I3 car les coordonnées
opérationnelles de position sont simplement les coordonnées
cartésiennes de la position de l'outil. Par contre, la matrice  dépend du choix effectué pour les coordonnées
opérationnelles de rotation. Cette matrice est parfois singulière
; par exemple dans le cas des quaternions d'Euler, elle est tout simplement non
carrée c.-à-d. non inversible. Les cas pour lesquels la matrice dépend du choix effectué pour les coordonnées
opérationnelles de rotation. Cette matrice est parfois singulière
; par exemple dans le cas des quaternions d'Euler, elle est tout simplement non
carrée c.-à-d. non inversible. Les cas pour lesquels la matrice
 complète n'est pas inversible constituent des
singularités mathématiques : ces
singularités sont uniquement dues au choix des coordonnées
opérationnelles, elles n'ont rien à voir avec le manipulateur lui
même. [SPO 04] complète n'est pas inversible constituent des
singularités mathématiques : ces
singularités sont uniquement dues au choix des coordonnées
opérationnelles, elles n'ont rien à voir avec le manipulateur lui
même. [SPO 04]
Comme il est défini dans le premier chapitre le vecteur
d'orientation qu'on a choisi est : 
dans ce cas [KHA 99]:
 (III-16)
(III-16)
et  (III-17)
(III-17)
Singularité lorsque . .
III.2.5. Utilisation de la matrice jacobienne
La matrice jacobienne  est l'une des quantités les plus importantes dans l'analyse et
la commande du mouvement de robot. Elle survient pratiquement dans chaque
aspect de manipulation robotique : dans la planification, dans la
détermination des configurations singulières, dans la
dérivation des équations dynamiques du mouvement, et dans la
transformation des forces et les couples du terminal aux joints de manipulateur
[SPO 04] est l'une des quantités les plus importantes dans l'analyse et
la commande du mouvement de robot. Elle survient pratiquement dans chaque
aspect de manipulation robotique : dans la planification, dans la
détermination des configurations singulières, dans la
dérivation des équations dynamiques du mouvement, et dans la
transformation des forces et les couples du terminal aux joints de manipulateur
[SPO 04]
III.2.5. 1. Calcul des
efforts statiques
À partir du modèle cinématique, on peut
écrire le modèle différentiel :
 (III-18)
(III-18)
Supposons que les variables
qi soient directement les variables
associées aux déplacements relatifs des moteurs rotatifs ou
linéaires. Chacun de ces derniers exerce une force ou un couple
noté , d'où pour l'ensemble des degrés de liberté un
vecteur des efforts , d'où pour l'ensemble des degrés de liberté un
vecteur des efforts  .
(III-19) .
(III-19)
Si l'on note F le vecteur à six
composantes de la force et du moment exercés par l'organe terminal sur
l'environnement, le principe des travaux virtuels permet
d'écrire :
 (III-20)
(III-20)
d'où :  (III-21)
(III-21)
qui donne la répercussion des efforts moteurs sur
l'environnement, en dehors des singularités.
On utilise la matrice jacobienne  ou ou  selon que l'effort F est défini dans le
repère Rn ou dans
R0 respectivement. [TEC 07] selon que l'effort F est défini dans le
repère Rn ou dans
R0 respectivement. [TEC 07]
Dans le cas inverse, où on veut calculer le  que doivent fournir les actionneurs pour que l'organe terminal puisse
exercer un effort F, on peut déduire à partir de
la relation (III-21) que : que doivent fournir les actionneurs pour que l'organe terminal puisse
exercer un effort F, on peut déduire à partir de
la relation (III-21) que :
 (III-22)
(III-22)
III.2.5.2. Les positions de singularité
Le nombre de degrés de liberté ddl
disponible à l'outil est égal à la dimension de
l'espace engendré par le vecteurs  et et  . Par exemple, cet espace est de dimension six si la structure (et la
configuration instantanée) du manipulateur permet tous les mouvements de
translation et de rotation imaginables pour l'outil. Considérant la
relation (III-2), on constate que l'espace en question est
généré par une combinaison linéaire des colonnes de
la matrice . Par exemple, cet espace est de dimension six si la structure (et la
configuration instantanée) du manipulateur permet tous les mouvements de
translation et de rotation imaginables pour l'outil. Considérant la
relation (III-2), on constate que l'espace en question est
généré par une combinaison linéaire des colonnes de
la matrice , ces colonnes sont en nombre égal au nombre d'articulations, on
a donc normalement : ddl=n, sauf si la matrice jacobienne est
de rang moindre que n, les configurations (c.-à-d. les
valeurs de q) pour lesquelles il y a perte de rang de cette
matrice sont les configurations singulières du manipulateur. Il s'agit
cette fois de singularités qui n'ont rien de mathématique ;
elles résultent du manipulateur lui-même et de la configuration
dans lequel il se trouve. , ces colonnes sont en nombre égal au nombre d'articulations, on
a donc normalement : ddl=n, sauf si la matrice jacobienne est
de rang moindre que n, les configurations (c.-à-d. les
valeurs de q) pour lesquelles il y a perte de rang de cette
matrice sont les configurations singulières du manipulateur. Il s'agit
cette fois de singularités qui n'ont rien de mathématique ;
elles résultent du manipulateur lui-même et de la configuration
dans lequel il se trouve.
En conclusion, l'examen du rang de la jacobienne nous donne un
moyen de déterminer quelles seront les éventuelles configurations
singulières, lorsque la jacobienne est carrée, les
singularités sont solution de où où  désigne le déterminant de la jacobienne. désigne le déterminant de la jacobienne.
III.3.
Vitesse et accélération inverses
C'est peut-être un peu
étonnant que les rapports inverses de vitesse et
d'accélération sont conceptuellement plus simples que la position
inverse. Rappel de
(III-2) que les vitesses articulaires et les
vitesses de terminal sont relié par la jacobienne en tant que 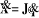
Ainsi le problème inverse de vitesse devient :
 (III-23)
(III-23)
qui est conceptuellement simple dans le cas régulier
où la matrice jacobienne est carrée d'ordre  et son déterminant est non nul. et son déterminant est non nul.
Différencier (III-2) donne les équations
d'accélération :
 (III-24)
(III-24)
Ainsi, donné le vecteur des
accélérations de terminal , le vecteur d'accélération articulaire , le vecteur d'accélération articulaire  est donné comme solution de : est donné comme solution de :
 où : où :  (III-25)
(III-25)
Pour les manipulateurs 6ddl les équations de vitesses
et d'accélérations articulaires peuvent être donc
écrit comme suit :
 (III-26)
(III-26)
La matrice  doit être remplacée par la jacobienne analytique doit être remplacée par la jacobienne analytique , dans le cas où on n'a pas présenté la rotation
par les cosinus directeurs. Dans ce cas on a : , dans le cas où on n'a pas présenté la rotation
par les cosinus directeurs. Dans ce cas on a :
 (III-27)
(III-27)
III.4.
Application sur le robot choisi
III.4.1. calcul de la jacobienne
géométrique
A partir de la relation (III-10) et des résultats
obtenus par le MGD on a calculé la jacobienne dans des différents
repères :  en utilisant le logiciel Maple. en utilisant le logiciel Maple.

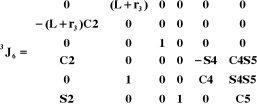
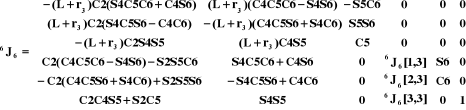
Avec :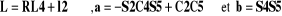
Puisque les cordonnées opérationnelles sont les
cordonnées de la position de l'outil dans le repère R
F , les vitesses qu'on doit calculer sont  et et  . .
En appliquant la relation (III-2), on trouve que :
 (III-28)
(III-28)
avec :
 (III-29)
(III-29)
où :
 (III-30)
(III-30)
et
 (III-31)
(III-31)
 (III-32)
(III-32)
on peut conclure donc que :
 (III-33)
(III-33)
A partir de (III-11) on a pu calculé les vitesses  et et  , ensuite on les a remplacées dans l'équation (III-32)
pour trouver les vitesses cherchées. , ensuite on les a remplacées dans l'équation (III-32)
pour trouver les vitesses cherchées.
Afin de vérifier les résultats trouvés
ainsi que la jocobienne, on a fait une comparaison entre les vitesses
calculées par la relation
(III-28) et celles calculées par la
méthode de récurrence. le programme est réalisé
sous Matlab et l'application sous Simulink
Les coordonnées articulaires utilisées dans ce
programme ainsi que les coordonnées opérationnelles
correspondantes sont celles de la figure (III.2).
La figure (III.3) montre bien que les
mêmes valeurs sont obtenues par les deux méthodes, ainsi on a pu
valider la jacobienne calculée.
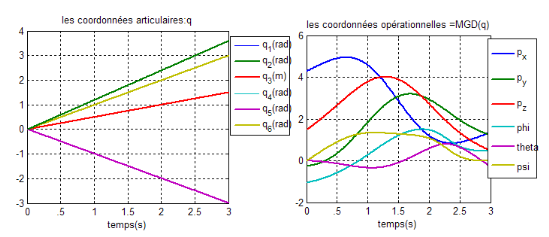
Figure III.2. Les
coordonnées articulaires et les coordonnées
opérationnelles correspondantes
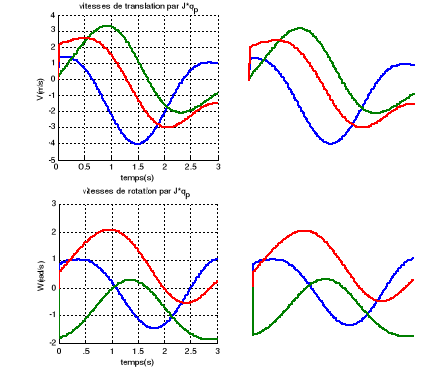
Figure III.3. Les
vitesses calculées par les deux méthodes ; équations
de récurrence, et la jacobienne
III.4.2. calcul de la jacobienne
analytique
Puisque la rotation est
spécifiée par les angles de RTL, les vitesses sont
calculées par la relation . Un programme de vérification a été fait, toujours
afin de valider les résultats, il est indiqué par le
schéma présenté ci dessous : . Un programme de vérification a été fait, toujours
afin de valider les résultats, il est indiqué par le
schéma présenté ci dessous :
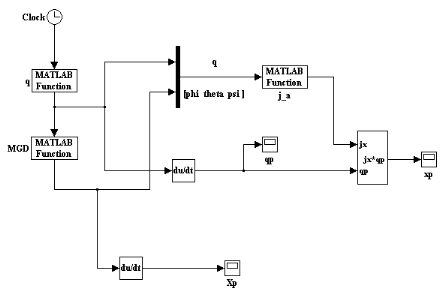
Figure III.4.
Description du programme utilisé pour la validation de la
jacobienne analytique
Les valeurs de q et X sont
les mêmes que ceux de la section précédente.
Les résultats de la simulation du programme
(Figure III-5), interprètent la validité de la
jacobienne analytique utilisée et donc le modèle
cinématique calculé.
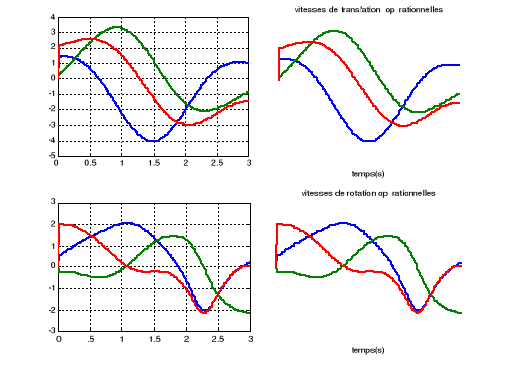
Figure III.5. Les
vitesses opérationnelles par l'utilisation de la jacobienne
analytique
III.4.3. Les positions de singularité
Les positions singulières (Figures III-6.a, b
et c ) sont les solutions de l'équation
:
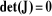
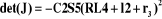
La résolution de cette équation donne les
positions singulières suivantes :
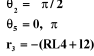
La singularité  (figure III-6.a), correspond à une
configuration dans laquelle le centre du poignet est confondu avec l'axe
z0 et le robot est en extension maximale (singularité
d'épaule). (figure III-6.a), correspond à une
configuration dans laquelle le centre du poignet est confondu avec l'axe
z0 et le robot est en extension maximale (singularité
d'épaule).
Pour  , les deux articulations commandant , les deux articulations commandant  et et ont leurs axes confondus et le poignet se plis sur lui-même
lorsque ont leurs axes confondus et le poignet se plis sur lui-même
lorsque  (figure III-6.b) , ce qui fait perdre un
degré de liberté au robot . Dans cette configuration le
modèle cinématique ne permet pas de commander une rotation
autour de la normale au plan contenant les axes 4,5 et 6 (singularité du
poignet). (figure III-6.b) , ce qui fait perdre un
degré de liberté au robot . Dans cette configuration le
modèle cinématique ne permet pas de commander une rotation
autour de la normale au plan contenant les axes 4,5 et 6 (singularité du
poignet).
Lorsque , le centre du poignet est confondu avec le point
O2 (figure III-6.c), mais c'est
impossible de tomber dans ce cas puisque , le centre du poignet est confondu avec le point
O2 (figure III-6.c), mais c'est
impossible de tomber dans ce cas puisque  est toujours positive (articulation prismatique). est toujours positive (articulation prismatique).
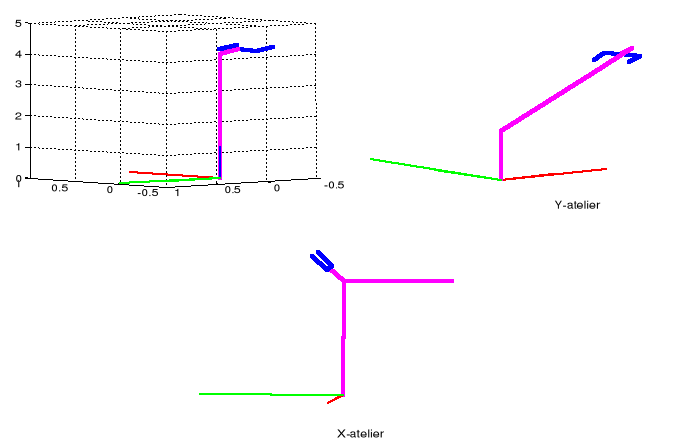
Figure III.6.
Quelques positions singulières du robot
III.5.
Conclusion
On a vu dans ce chapitre comment obtenir le
modèle cinématique direct d'un robot en calculant ses matrices
jacobienne, géométrique et analytique, ainsi que la
détermination de son modèle cinématique inverse du premier
et du deuxième ordre, ensuite on a appliqué ces principes sur le
robot choisi.
On a vu aussi l'intérêt de la matrice
jacobienne dans la dynamique, la cinématique et dans la
détermination des positions singulières.
On a remarqué que pour des vitesses faibles, quelques
rad/s en rotation et quelques dizaines de cm/s en translation, les vitesses de
l'organe terminal avoisinent quelques m/s.
Il faut noter que pour les robots manipulateurs, les
vitesses de rotations articulaires maximales sont de 1 rad/s à 1 tour/s,
et de l'ordre de 1 à 3 m/sec en translation, compte tenu des vitesses de
rotation des moteurs (1000 à 3000 tr/min), cela implique des rapports de
réduction assez élevés [FIS 04].
Chapitre IV
L'étude dynamique du robot
IV.1.
Introduction
Tandis que les équations cinématiques
décrire le mouvement du robot sans considération des forces et
des moments produisant le mouvement, les équations dynamiques
décrivent explicitement le rapport entre les couples (et/ou forces)
appliqués aux actionneurs et le mouvement (positions, vitesses et
accélérations articulaires).
Les principaux problèmes dans la dynamique du robot
sont [FEA 07] :
· La dynamique directe : (donner les
forces et établir les accélérations), elle est
employée principalement pour la simulation.
· La dynamique inverse : (donner les
accélérations, établir les forces), elle a des diverses
utilisations, incluant : commande en ligne des mouvements et des forces de
robot, conception de trajectoire et optimisation, conception du
mécanisme du robot et le calcul des coefficients de l'équation
du mouvement.
· L'identification des paramètres inertiels.
IV.2. Notation
Les principales notations utilisées sont les
suivantes :
 : la masse du corps Ci : la masse du corps Ci
 : accélération de la pesanteur. : accélération de la pesanteur.
 : vecteur d'origine : vecteur d'origine  et d'extrémité et d'extrémité égal à égal à  . .
 : vecteur d'origine : vecteur d'origine  et d'extrémité et d'extrémité égal à égal à  . .
 et et  : vitesse et accélération de rotation du corps
Ci. : vitesse et accélération de rotation du corps
Ci.
 et et  : vitesse et accélération du point : vitesse et accélération du point 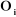
 et et  : vitesse et accélération du centre de
gravité (Gi) du corps
Ci : vitesse et accélération du centre de
gravité (Gi) du corps
Ci
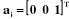
 résultante des forces extérieures sur le corps
Ci. résultante des forces extérieures sur le corps
Ci.
 moment des effort extérieurs exercés sur le corps
Ci autour de
Oi. moment des effort extérieurs exercés sur le corps
Ci autour de
Oi.
 vecteur d'origine Oi et
d'extrémité Gi. vecteur d'origine Oi et
d'extrémité Gi.
 le tenseur du vecteur le tenseur du vecteur  tel que : tel que :
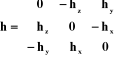
 :désigne le produit vectoriel. :désigne le produit vectoriel.
 tenseur d'inertie du corps Ci par rapport
au repère Ri qui s'exprime
par : tenseur d'inertie du corps Ci par rapport
au repère Ri qui s'exprime
par :
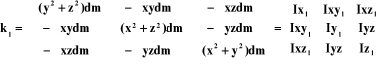
 tenseur d'inertie du corps Ci par rapport
à un repère parallèle à
Ri et d'origine
Gi. tenseur d'inertie du corps Ci par rapport
à un repère parallèle à
Ri et d'origine
Gi.
 et et  résultante et moment du torseur dynamique exercé sur le
corps Ci par son
antécédent et par l'actionneur i. résultante et moment du torseur dynamique exercé sur le
corps Ci par son
antécédent et par l'actionneur i.
 et et  résultante et moment du torseur dynamique exercé par le
corps Ci sur l'environnement. résultante et moment du torseur dynamique exercé par le
corps Ci sur l'environnement.
 , avec , avec  le paramètre de frottement sec de l'articulation
i. le paramètre de frottement sec de l'articulation
i.
 , avec , avec  le paramètre de frottement visqueux de l'articulation
i le paramètre de frottement visqueux de l'articulation
i
IV.3. Le modèle dynamique
inverse (MDI)
Le modèle dynamique inverse (ou le modèle
dynamique tout court) d'un robot permet de déterminer les
équations du mouvement, c'est-à-dire : la relation entre les
couples appliqués aux actionneurs et les positions, vitesses et
accélérations articulaires [FEA 07].
Il est exprimé sous la forme :
 (IV-1)
(IV-1)
Dans cette équation  sont, respectivement, les vecteurs de position, vitesse,
accélération et force, dans l'espace articulaire. Chacun est
un vecteur de dimension n. Les variables de force sont
définies tels que sont, respectivement, les vecteurs de position, vitesse,
accélération et force, dans l'espace articulaire. Chacun est
un vecteur de dimension n. Les variables de force sont
définies tels que  est la puissance fournie par est la puissance fournie par  au système. Ainsi, au système. Ainsi,  et et  qualifiés comme ensemble de variables
généralisées de vitesse et de force pour le
système. qualifiés comme ensemble de variables
généralisées de vitesse et de force pour le
système.
 est un vecteur (6) ; dénote la force externe agissant sur le
robot, dû au contact avec l'environnement ,ainsi le robot exerce une
force de est un vecteur (6) ; dénote la force externe agissant sur le
robot, dû au contact avec l'environnement ,ainsi le robot exerce une
force de  sur l'environnement. sur l'environnement.
Les deux principaux formalismes utilisés pour obtenir
les équations différentielles qui décrivent le
comportement d'un mécanisme à plusieurs corps articulés
sont le formalisme de Newton (théorèmes généraux de
la mécanique classique) et celui de Lagrange. [AIS 06]
IV.3.1.
Formalisme de Newton Euler
Cette méthode est fondée sur une double
récurrence ; la récurrence avant de la base du robot vers
l'effecteur, calcule successivement les vitesses et accélérations
des corps, puis leur torseur dynamique, une récurrence arrière
de l'effecteur vers la base, permet le calcul des couples des actionneurs en
exprimant pour chaque corps le bilan des efforts. [KHA 99]
Les équations de Newton Euler expriment le torseur
dynamique en  des efforts extérieurs sur un corps i par les
équations : [CRA 89] des efforts extérieurs sur un corps i par les
équations : [CRA 89]
 (IV-2)
(IV-2)
Cette méthode permet d'obtenir un MDI non
linéaire par rapport aux paramètres inertiels, pour qu'il soit
linéaire, le MDI doit être calculé en exprimant le torseur
dynamique des efforts extérieurs en plutôt que plutôt que . .
Les équations de Newton Euler ainsi modifiées
s'écrivent :
 (IV-3)
(IV-3)
· Récurrence avant : elle
permet de calculer  et et  à partir de la relation (IV-3). Pour ce faire, il faut
calculer à partir de la relation (IV-3). Pour ce faire, il faut
calculer . .
Les formules de composition des vitesses donnent :
 (IV-4)
(IV-4)
La dérivée de l'équation (IV-4) par
rapport au temps s'écrit :
 (IV-5) (IV-5)
Ce qui donne :
 (IV-6) (IV-6)
On peut finalement calculer et et , on initialise cette récurrence par , on initialise cette récurrence par et et . .
· Récurrence arrière :
Les équations composant la récurrence arrière
sont obtenues à partir du bilant des efforts sur chaque corps,
écrit à l'origine , on obtient (FigureIV.1) , on obtient (FigureIV.1)
i-1
i+1
Oi+1
Oi
Gi
Li+1
Si
i
-fi+1
fi - fei
 (IV-7)
(IV-7)
Figure IV.1.
Bilan des efforts au centre de gravité
On peut faire intervenir l'effet de la gravité
sans avoir à la prendre en compte dans le bilan des efforts, pour
cela on prend:
 (IV-8)
(IV-8)
D'où l'on tire les équations suivantes :
 (IV-9)
(IV-9)
On obtient alors les couples aux actionneurs  en projetant, suivant la nature de l'articulation i,
les vecteurs en projetant, suivant la nature de l'articulation i,
les vecteurs ou ou sur l'axe du mouvement : sur l'axe du mouvement :
 (IV-10)
(IV-10)
Les frottements doivent être pris en compte dans
l'équation dynamique. Le modèle du type frottement sec (ou de
Coulomb) fait l'hypothèse d'un couple constant de frottement en
opposition au mouvement. Au début du mouvement (vitesse nulle), un
couple supérieur au couple de frottement sec doit être
développé pour amorcer le mouvement. De nombreuses études
ont été réalisées afin de mieux analyser les
frottements, menant à l'approximation suivante [VIV 04] :
 (IV-11) (IV-11)
On ajoute à 'équation (IV-10) les termes
correctifs représentant l'effet des frottements et des inerties des
actionneurs, , ce qui nous donne la relation suivante : , ce qui nous donne la relation suivante :
 (IV-12)
(IV-12)
Les inerties des actionneurs sont calculées comme
suit :
 (IV-13)
(IV-13)
 est le moment d'inertie du rotor de l'actionneur i, est le moment d'inertie du rotor de l'actionneur i,
 est le rapport de réduction de l'axe i
égal à est le rapport de réduction de l'axe i
égal à  et et  désigne la vitesse du rotor de l'actionneur i. désigne la vitesse du rotor de l'actionneur i.
On déduit directement de l'équation (IV-9)
que les termes  et et ne dépendent que des paramètres inertiels du corps
i et de ceux des corps situées en aval qui sont
introduit par les termes ne dépendent que des paramètres inertiels du corps
i et de ceux des corps situées en aval qui sont
introduit par les termes  et et  de la récurrence. de la récurrence.
Pour utiliser pratiquement l'algorithme de Newton Euler
exposé ci-dessus, il faut projeter dans un même repère les
vecteurs et tenseurs qui apparaissent dans une même équation. [BOI
88]
Les équations de la récurrence avant peuvent
être présentées par l'algorithme suivant:
· Récurrence avant :
Conditions initiales :
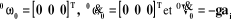
 (IV-14) (IV-14)
 (IV-15)
(IV-15)
Les équations de la récurrence arrière
peuvent être présentées par l'algorithme suivant:
· Récurrence
arrière :
Conditions initiales:
  (IV-16) (IV-16)
Dans cette formulation (Newton Euler), l'effet de la pesanteur
est introduit par une accélération verticale de la base du robot.
Si le robot manipulateur est situé sur un véhicule dont le
mouvement est connu, on peut donc également introduire les fonctions du
temps correspondantes (vitesses et accélérations) dans les
premières récurrences directes qui partent de la base [TEC
07].
IV.3.2.
Formalisme de Lagrange
Les équations de Lagrange permettent d'obtenir
directement les relations entre les efforts moteurs aux articulations et les
mouvements. Par rapport aux équations de Newton, on perd au passage les
informations sur les efforts de réaction aux articulations qui sont
utiles au dimensionnement des parties mécaniques, mais n'interviennent
pas dans un modèle utile à la commande automatique puisque les
corps sont supposés indéformables [CHE 03].
Il s'agit de n équations
différentielles non linéaires du second ordre obtenues à
partir de :
 (IV-17)
(IV-17)
avec :
L est le Lagrangien du système, c'est
la différence entre  l'énergie cinétique du système, et l'énergie cinétique du système, et  l'énergie potentielle du système. l'énergie potentielle du système.
 (IV-18)
(IV-18)
Pour tous les systèmes mécaniques,
l'énergie cinétique est une forme quadratique des
vitesses :
 (IV-19) (IV-19)
où  est une matrice est une matrice symétrique définie positive dépendant des masses
et des inerties de chaque corps du mécanisme, et de la configuration
q . En effet : symétrique définie positive dépendant des masses
et des inerties de chaque corps du mécanisme, et de la configuration
q . En effet :
 (IV-20)
(IV-20)
et on a vu que les vitesses de translation et de rotation de
chaque corps sont des fonctions linéaires des vitesses articulaires.
D'autre part, l'énergie potentielle est fonction de la
configuration du mécanisme:
Il en résulte que les équations de Lagrange
peuvent s'écrire :
 (IV-21)
(IV-21)
où le premier vecteur représente les forces ou
couples d'inertie sur les articulations motorisées, le deuxième
(du second degré par rapport aux vitesses) correspond aux effets
centrifuges et de Coriolis, le troisième traduit les efforts dus
à la pesanteur et aux ressorts. [éEF 05]
Le modèle dynamique lorsqu'on applique la force  peut s'écrit sous la forme : peut s'écrit sous la forme :
 (IV-22) (IV-22)
où :

La matrice d'inertie est obtenue directement à partir
de l'expression de l'énergie cinétique  ; L'élément ; L'élément  est égal au coefficient de est égal au coefficient de  dans l'expression de l'énergie cinétique, tandis que
l'élément dans l'expression de l'énergie cinétique, tandis que
l'élément  est égal au coefficient de est égal au coefficient de . .
Le calcul des éléments de C se
fait à partir du symbole de Christophell  selon la relation : selon la relation :
 (IV-23) (IV-23)
Le calcul de Q se fait à partir de
l'énergie potentielle :
 (IV-24)
(IV-24)
Si on prend en compte l'effet du frottement dans les liaisons
sur le mouvement, on doit ajouter au deuxième membre de l'expression
(IV-24) le vecteur . .
L'équation dynamique devient :
 (IV-25) (IV-25)
Si on tient compte des inerties des actionneurs , l'élément , l'élément  de la matrice d'inertie doit être augmenté de de la matrice d'inertie doit être augmenté de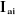
Il est évident que pour trouver les
éléments de M, C et
Q, il faut tout d'abord calculer les énergies
cinétique et potentielle de tous les corps du
robot.
Calcul de l'énergie
cinétique :
L'expression de l'énergie cinétique total d'un
système composé de n corps rigides
est :
 (IV-26)
(IV-26)
Où  désigne l'énergie cinétique du corps désigne l'énergie cinétique du corps , qui s'exprime par : , qui s'exprime par :
 (IV-27) Etant donné que :
(IV-27) Etant donné que :
 (IV-28) Et sachant que :
(IV-28) Et sachant que :
 (IV-29) La relation (IV-28)
devient :
(IV-29) La relation (IV-28)
devient :
 (IV-30) Dans
l'équation (IV-32), tous les éléments doivent être
exprimés dans le même repère. La façon la plus
simple est de les exprimer dans le repère
Ri, l'équation devient donc : (IV-30) Dans
l'équation (IV-32), tous les éléments doivent être
exprimés dans le même repère. La façon la plus
simple est de les exprimer dans le repère
Ri, l'équation devient donc :
 (IV-31) (IV-31)
Le calcul de  et de et de  se fait par la relation (III-11). se fait par la relation (III-11).
Calcul de l'énergie
potentielle :
L'énergie potentielle s'écrit :
 (IV-32) En projetant
les vecteurs de cette relation dans (IV-32) En projetant
les vecteurs de cette relation dans , on obtient : , on obtient :
 (IV-33) (IV-33)
Les énergies cinétiques et potentielles
étant linéaires par rapport aux paramètres inertiels, le
modèle dynamique l'est également.
IV.4.
Application sur le robot choisi
Nous avons supposé que, en raison de symétrie,
les centres de masse , , , , , , et et  sont respectivement situés sur les supports de
Z1, Y2, Z3, Z4,
Y5 et Z6 et que les matrices sont respectivement situés sur les supports de
Z1, Y2, Z3, Z4,
Y5 et Z6 et que les matrices
 de chaque corps, sont diagonales, donc : de chaque corps, sont diagonales, donc :
 
L'effet extérieur sur l'organe terminal est : 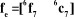
Les efforts extérieurs sur les autres corps du robot
sont supposés nuls.
Le logiciel Maple a été utilisé pour
développer les expressions des différents termes du modèle
dynamique par les deux méthodes.
Les résultats ainsi obtenus sont les suivants :
IV.4.1. Résultats obtenus par le formalisme de Newton
Euler
L'étape 1 : les vitesses
angulaires
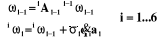
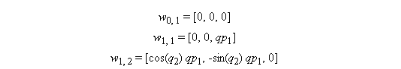
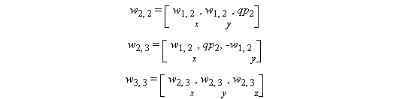
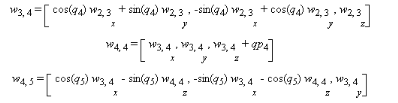
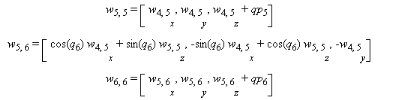
L'étape 2 : les
accélérations angulaires
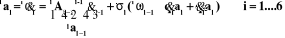
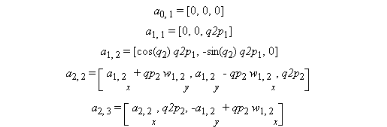
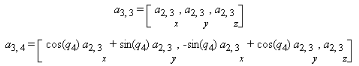
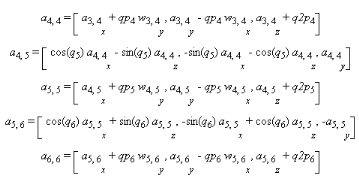
L'étape 3 : opérateurs
tensoriels

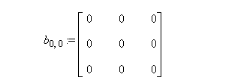
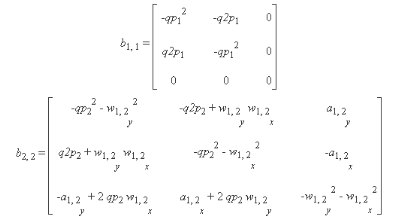
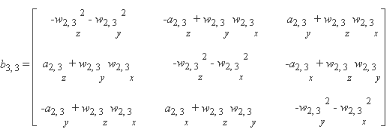
Par la même méthode, on calcule les autres 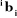
L'étape 4 : Les
accélérations linéaires :
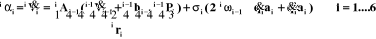
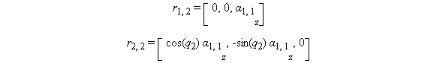
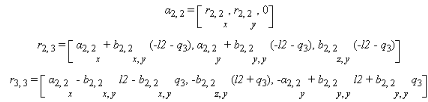
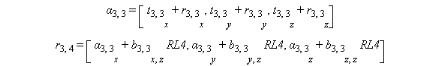
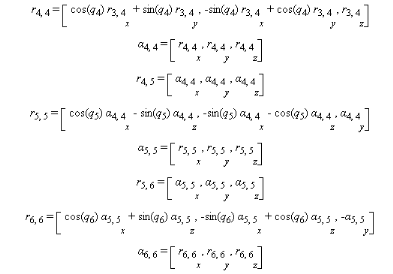
L'étape 5 : Les efforts sur les
articulations :
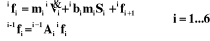
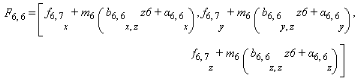
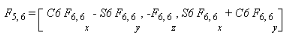
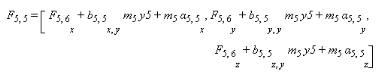
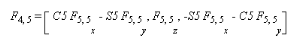
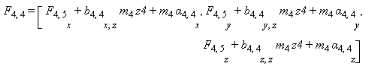
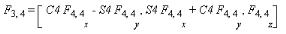
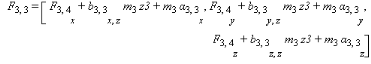
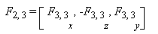
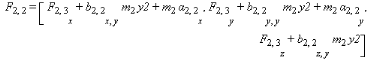
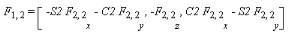
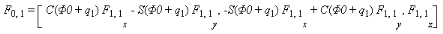
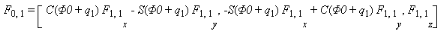
L'étape 6 : Les moments aux
niveaux des articulations :
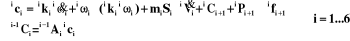
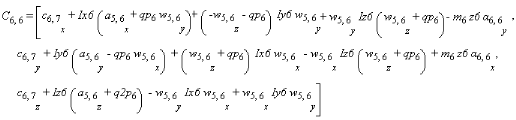
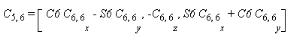
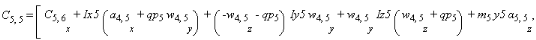
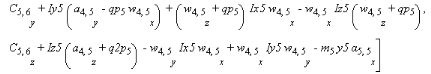
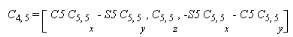
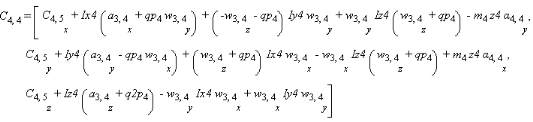
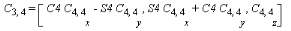
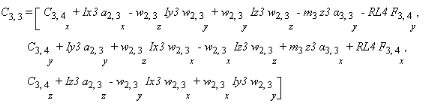
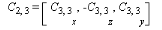
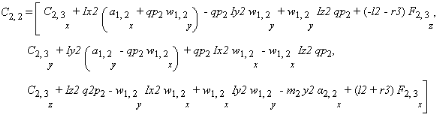
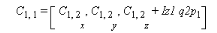
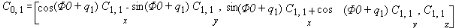
L'étape 7 : Calcul des couples
résultants pour chaque articulation
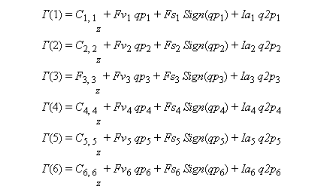
IV.4.2. Résultats obtenus
par le formalisme de Lagrange
· Matrice d'inertie M:
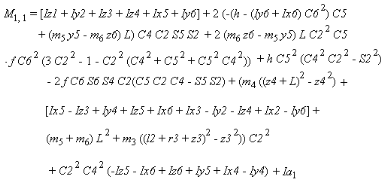
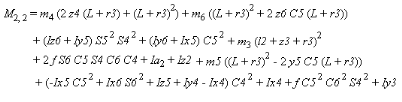
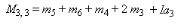
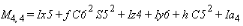
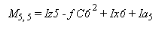
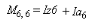
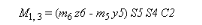
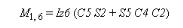
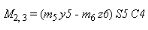

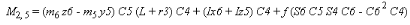
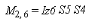
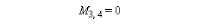
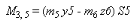
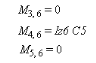
· Les éléments de la matrice
C se déduisent des expressions de la matrice
M grâce à la relation (IV-21).
· Le vecteur Q :
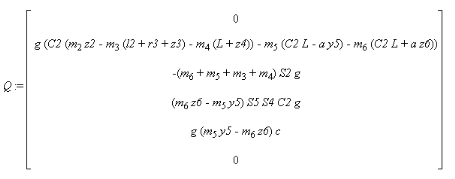
avec :
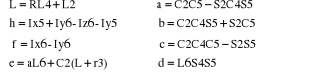

IV.5. Le modèle dynamique
direct (MDD)
On peut simplifier l'écriture du modèle
dynamique inverse comme par la relation :
 (IV-34) (IV-34)
avec :
 (IV-35)
(IV-35)
On utilise le modèle dynamique direct pour simuler le
comportement du robot dans la boucle de commande, il est donné
par :
 (IV-36) (IV-36)
 : L'inverse de la matrice
d'inertie. : L'inverse de la matrice
d'inertie.
Le calcul de la matrice M et le vecteur
H par la méthode de Lagrange se fait explicitement
(§ IV.3.2), et on peut aussi les tirer à partir du formalisme de
Newton Euler comme suit :
H est obtenu en considérant les
accélérations nulles dans l'équation (IV-34).
( si si ).
(IV-37) ).
(IV-37)
La matrice M est obtenue en remarquant
que sa iéme colonne est égal
à  si: si:  (IV-38)
(IV-38)
 étant le vecteur (nx1) dont tous les
éléments sont nuls sauf la
iéme composante qui égale
à 1. étant le vecteur (nx1) dont tous les
éléments sont nuls sauf la
iéme composante qui égale
à 1.
IV.6.
Application numérique
On a supposé que l'effort extérieur , est exprimé dans le repère
R6, pour cela le couple , est exprimé dans le repère
R6, pour cela le couple est égal à : est égal à :
 (IV-39)
(IV-39)
Les frottements sont négligeables sur toutes les
articulations.
En plus des paramètres géométriques du
Tableau (I.1), les paramètres entrant dans le calcul du
modèle dynamique sont donnés par le tableau suivant :
|
i
|
li
(m)
|
mi
(kg)
|
Gi
|
Ixi
Kg.m2
|
Iyi
Kg.m2
|
Izi
Kg.m2
|
|
1
|
1.00
|
25
|
[0,0,- l1/2]
|
0.01
|
0.05
|
0.06
|
|
2
|
0.75
|
30
|
[0,- l2/2,0]
|
0.10
|
0.20
|
0.30
|
|
3
|
0.50
|
15
|
[0, 0, l3/2]
|
0.40
|
0.40
|
0.20
|
|
4
|
0.25
|
4
|
[0, 0,- l4/2]
|
0.30
|
0.50
|
0.01
|
|
5
|
0.10
|
4
|
[0,- l5/2,0]
|
0.01
|
0.60
|
0.03
|
|
6
|
0.10
|
2
|
[0,0, l5+l6/2]
|
0.20
|
0.20
|
0.60
|
Tableau IV.1. Paramètres entrant dans
le calcul du modèle dynamique
avec :
li est la longueur du corps
Ci le long des axes Z1,Y2,Z3,Z4,Y5,Z6
respectivement.
g =9.81 m/s2
fe =[20,20,20,12,30,25]t
Nous avons considéré une trajectoire de
référence complètement spécifiée assurant
une continuité en position, vitesse et accélération,
figure (III.2)
Nous avons fait un test de comparaison entre les couples
calculés par les deux formalismes pour la trajectoire
désirée.
Les figures (IV.2), (IV.3)
montrent clairement que les résultats obtenus, par l'application des
deux formalismes, sont égaux avec une erreur de l'ordre de10-14
N.m pour les couples, et de 10-13 N pour la force
f3
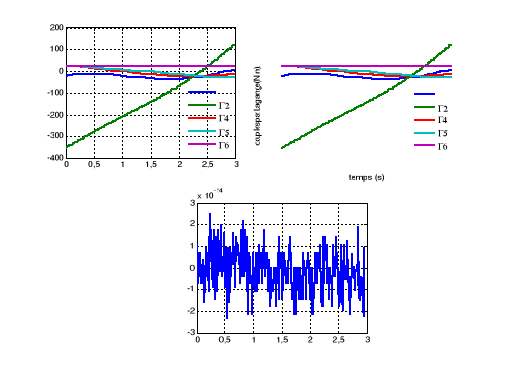
Figure IV.2. Les couples calculés, par
les deux formalismes
 Figure IV.3. La force F3, par les deux
méthodes Figure IV.3. La force F3, par les deux
méthodes
Lors de la simulation, on a
utilisé différentes trajectoires, et on a trouvés toujours
les mêmes résultats, ce qui nous a conduit à valider le
modèle dynamique obtenu par l'utilisation des deux formalismes.
IV.7.
Conclusion
On a présenté dans ce chapitre les deux
formalismes les plus utilisés pour le calcul du modèle dynamique
direct et inverse des robots.
L'extraction des différents éléments
constituants le modèle dynamique par le formalisme de Lagrange est faite
hors ligne, tandis que par celui de Newton Euler tous les calculs sont faits en
ligne, ça nous a permit de jouer sur les paramètres
géométriques et dynamiques du robot sans faire des changements
sur le programme réalisé.
Historiquement, les deux formulations ont été
évoluées en parallèle, et chacune a été
perçu en tant qu'ayant certains avantages. Par exemple, la formulation
de Newton Euler est mieux convenue au calcul récursif que la formulation
lagrangienne. Cependant, la situation actuelle est que toutes les deux
formulations sont équivalentes à presque tous les égards.
Il doit peut-être loyalement dire que dans l'ancien type
d'analyse, la formulation lagrangienne est supérieure tandis que dans le
dernier cas la formulation de Newton Euler est supérieure. Pensant
à l'avenir, si on souhaite étudier des phénomènes
mécaniques plus avancés tels que les déformations
élastiques des corps (c.-à-d., si on n'assume plus la
rigidité des corps), alors la formulation lagrangienne est nettement
supérieure [SPO 04].
Chapitre V
Commande de mouvement
V.1. Introduction
La commande par découplage non linéaire
« commande dynamique » est un asservissement non
linéaire dont les paramètres utilisent un modèle de la
dynamique du robot, la mise en oeuvre de cette méthode exige le calcul
en ligne du modèle dynamique et la connaissance des valeurs
numériques des paramètres inertiels et de frottements ce qui ne
constitue plus maintenant une limite rédhibitoire grâce aux
évolutions technologiques en micro-informatique et le
développement de techniques d'identification. [KHA 99]
La commande dynamique n'est pas dans tous les cas le type de
commande nécessaire pour obtenir une bonne précision et une bonne
stabilité. En effet une commande classique suffit lorsque le robot
manipulateur évolue sans contraintes de performance, de rapidité
et de précision car dans ce cas, les inerties ont une influence moins
importante [AGU 07], Pour évaluer ces performances, nous comparons cette
stratégie (commande dynamique) à la commande classique de type
PID. Ainsi, nous rappelons dans un premier temps très brièvement
le schéma ainsi que la méthode de réglage de la loi PID.
Ensuite, nous présentons la démarche adoptée pour
synthétiser la stratégie dynamique dans le contexte de la
commande de robots
V.2. Commande PID
Les commandes de type PID sont implantées dans tous les
contrôleurs de robots industriels actuels. Le système est
considéré comme un système linéaire et chacune de
ses articulations est asservie par une commande décentralisée de
type PID à gains constants. Dans la pratique, une telle commande est
implémentée selon le schéma de la figure
(V.1)
+
+
+
-
+
-
Robot
Kp
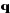
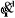
+
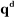
Kvp

Figure V.1.
Schéma classique d'une commande PID
La loi de commande s'exprime par :
 (V-1) (V-1)
où  et et  représentent les positions et vitesses courantes dans l'espace
articulaire, représentent les positions et vitesses courantes dans l'espace
articulaire,  et et  les positions et vitesses désirées et les positions et vitesses désirées et  , ,  et et  sont des matrices diagonales définies positives, de
dimension (n x n), représentant les gains proportionnels sont des matrices diagonales définies positives, de
dimension (n x n), représentant les gains proportionnels  , dérivés , dérivés  et intégraux et intégraux  de chaque articulation i. de chaque articulation i.
La solution la plus courante en robotique consiste à
choisir les gains de façon à obtenir un pôle triple
réel négatif, ce qui donne une réponse la plus rapide
possible sans oscillations. On en déduit alors les valeurs de gains de
l'articulation i [KHA 99] :
 (V-2)
(V-2)
où :
 désigne la valeur maximale de l'élément désigne la valeur maximale de l'élément
 de la matrice d'inertie du robot, de la matrice d'inertie du robot,  est une pulsation choisie la plus grande possible sans
dépasser la pulsation de résonance est une pulsation choisie la plus grande possible sans
dépasser la pulsation de résonance  , et , et  est la valeur du frottement visqueux pour chaque articulation. est la valeur du frottement visqueux pour chaque articulation.
Les avantages de la commande PID sont la facilité de
mise en oeuvre, le faible coût en temps de calcul et elle n'exige pas la
connaissance du modèle dynamique du système commandé [XIE
03]. Néanmoins, la réponse temporelle du robot peut varier en
fonction de sa configuration, en entraînant des dépassements de
consigne et un écart de poursuite important dans les mouvements rapides.
Pour le cas de robots avec une dynamique très importante, ce type de
commande peut s'avérer non efficace.
V.3. Commande par découplage non
linéaire
La commande par découplage non linéaire
consiste à transformer par retour d'état un problème de
commande d'un système non linéaire en un problème de
commande d'un système linéaire. [KHA 99] L'élaboration
d'une loi de commande qui linéarise et découple les
équations est simplifiée par le fait que le nombre d'actionneurs
est égal au nombre de variables articulaires et que le modèle
dont on dispose est un modèle inverse qui exprime l'entrée du
système en fonction du vecteur d'état  et de et de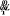  . [MAH 06]. . [MAH 06].
Ce type de technique permet la commande dans l'espace des
articulations ou dans l'espace cartésien, avec l'avantage que les
articulations sont découplées et peuvent évoluer à
grandes vitesses avec de fortes inerties.
V.3.1. Commande dans l'espace articulaire
On suppose que les positions et vitesses articulaires
sont mesurables et que les mesures ne sont pas bruitées,
l'équation dynamique du robot peut s'exprimer sous forme
compacte :
 (V-3)
(V-3)
où  et et  les estimations respectives de M et
H. les estimations respectives de M et
H.
alors, dans le cas idéal où le modèle
est supposé parfait, le système est régi par
l'équation :
 (V-4) (V-4)
 peut être considéré comme un nouveau vecteur de
commande. On se ramène donc à un problème de commande de
n systèmes linéaires, invariants,
découplés et du second ordre (doubles intégrateurs). peut être considéré comme un nouveau vecteur de
commande. On se ramène donc à un problème de commande de
n systèmes linéaires, invariants,
découplés et du second ordre (doubles intégrateurs).
On désigne respectivement par  l'accélération, la vitesse et la position
désirées dans l'espace articulaire, si le mouvement est
complètement spécifié, alors w(t) est
donné par la relation : l'accélération, la vitesse et la position
désirées dans l'espace articulaire, si le mouvement est
complètement spécifié, alors w(t) est
donné par la relation :
 (V-5) (V-5)
où  et et  sont des matrices constantes, diagonales et positives de dimension (n x
n). sont des matrices constantes, diagonales et positives de dimension (n x
n).
 (V-6)
(V-6)
avec :
 facteur d'amortissement facteur d'amortissement
 : Pulsation propre : Pulsation propre
Pour un modèle parfait, l'évolution du vecteur
des erreurs articulaires
 (V-7)
(V-7)
est régie par
l'équation :
 (V-8)
(V-8)
Les erreurs articulaires sont découplées et
chacune se comporte comme un système du second ordre dont on peut fixer
la rapidité de réponse (choix de ) et l'amortissement (choix de ) et l'amortissement (choix de , étant donné , étant donné ), En général, on choisit un amortissement égal
à 1 pour avoir une réponse sans
dépassement [CRE 97] ), En général, on choisit un amortissement égal
à 1 pour avoir une réponse sans
dépassement [CRE 97]
Cette dernière équation a pour solution un
signal e (t) qui tend exponentiellement vers zéro. Le
système en boucle fermée, avec cette loi de commande, dans le cas
où le modèle du robot est connu avec exactitude, est
asymptotiquement stable. Le schéma bloc de cette loi de commande est
représenté sur la figure (V.2).
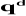
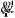
+
+
+
+
+
-
+
-
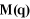
Robot
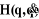
Kp
Kv
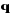
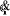
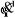
+
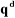
Figure V.2.
Commande dynamique pour un mouvement complètement
spécifié
Le signal de commande aux actionneurs comporte trois
parties :
· la première compense les couples et forces de
Coriolis, centrifuges, de gravité et de frottements (H)
· la deuxième est une correction de position et de
vitesse à gains variables représentée respectivement
par . .
· La troisième constitue une anticipation des
forces d'accélération désirées 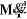
Le modèle dynamique est calculé soit par le
formalisme de Lagrange soit par le formalisme de Newton Euler, dans ce dernier
cas le  est calculé explicitement, on n'a pas besoin de calculer
séparément le M et le H, sauf
lors de la simulation du comportement du robot (le calcul du MDD). est calculé explicitement, on n'a pas besoin de calculer
séparément le M et le H, sauf
lors de la simulation du comportement du robot (le calcul du MDD).
· Application sur le
robot choisi
Afin de montrer l'apport de cette technique de commande, une
simulation numérique a été effectuée sur le robot
choisi. On a considéré une trajectoire de référence
complètement spécifiée assurant une continuité en
position, vitesse et accélération.
L'effet extérieur sur l'organe terminal est tenu en
compte fe, les efforts extérieurs sur les
autres corps du robot sont supposés nuls, les frottements sont
négligeables sur toutes les articulations.
fe =[20,20,20,12,30,25]T
Le modèle dynamique du robot est calculé par
l'un des deux formalismes décrits précédemment.
Pour la simulation du robot on a utilisé le
modèle dynamique direct, (IV-36) en suite on a
intégré; le  pour trouver pour trouver  et cette dernière pour trouver et cette dernière pour trouver . .
Les valeurs des paramètres des contrôleurs ont
été réglées selon les formulations
présentées précédemment. Les lois de commande ont
été testées en simulation dans l'environnement
Matlab/Simulink®.
· Réglage du PID
D'après les équations vues dans le paragraphe
V.2, les paramètres nécessaires pour
régler la commande PID d'une articulation, sont la fréquence  et la valeur de et la valeur de . .
Après le calcul nécessaire, les valeurs de  trouvées sont données par : trouvées sont données par :
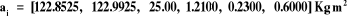
Les valeurs calculées et ajustées des gains, lors
de la simulation, sont :
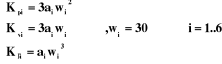
· Réglage de la commande
dynamique
De la même façon, les valeurs à choisir pour
régler la commande dynamique sont la pulsation  et le facteur d'amortissement et le facteur d'amortissement , selon l'équation (V.6) et après
ajustement en simulation, les valeurs de gains sont fixées à: , selon l'équation (V.6) et après
ajustement en simulation, les valeurs de gains sont fixées à:
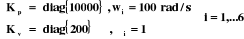
Nous avons utilisé deux tests séparés,
l'un utilise la commande PID et l'autre utilise la commande dynamique.
La figure (V.4) montre le comportement
du robot, pour les deux tests, en poursuite de la trajectoire
présentée par la figure (V.3.a).
Les résultats de simulation montrent un meilleur
comportement de la commande dynamique par rapport à la commande PID,
L'erreur de position est de l'ordre de 10-5(rad) pour la commande
dynamique, et elle est de l'ordre de 10-3(rad) pour la commande PID.
De même, l'erreur de vitesse est voisine de
10-5(rad/s) pour la commande dynamique, et elle est de l'ordre de
10-3(rad) pour la commande PID.
On voit bien, « figure (V.3.c,
d) », que les couples / force donnés par
l'application des deux lois de commande, sont les mêmes,
ce qui nous amène à dire que pour les deux cas de
commande le système converge, mais avec une grande précision pour
la commande dynamique par rapport à la commande PID.
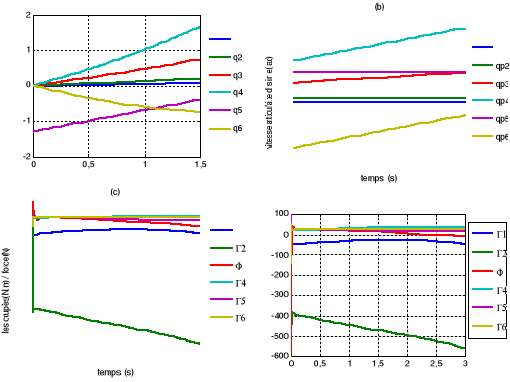
Figure
V.3. (a) positions articulaires (b) vitesses articulaires
(c) la commande PID
(d) la commande dynamique
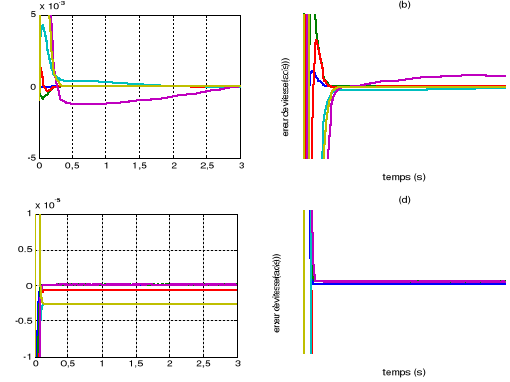
Figure V.4.
L'erreur de position et de vitesse
(a)et (b) la commande PID
(c) et (d) la commande
dynamique.
En suite on a répété le même travail,
pour une trajectoire caractérisée par des grandes vitesses
articulaires figure (V.5)
On voit bien que le système lorsqu'il
est contrôlé par la commande dynamique reste toujours stable,
contrairement au cas de la commande PID, qui est malgré qu'au
début du mouvement (t=[0, 2.5s]) le système est un peut stable
(figure (V.6.a, b)), mais il a divergé
complètement à l'extérieur de cet intervalle.
La divergence du système dans ce dernier cas, est
justifié, par le fait que la matrice d'inertie M(q)
n'est pas diagonale et dépend fortement de la configuration
q. De plus, aux grandes vitesses, les forces centrifuges et de
Coriolis « vecteur C(q) » peuvent
être importantes.
Pour ces raisons, l'utilisation d'asservissements
linéaires classiques conduit à des performances de
rapidité et de précision inconstantes et difficiles à
estimer étant donné le caractère fortement non
linéaire du processus commandé. Cet inconvénient est
notablement réduit par le schéma de la commande dynamique du
mécanisme (figure (V.6.c,d)).
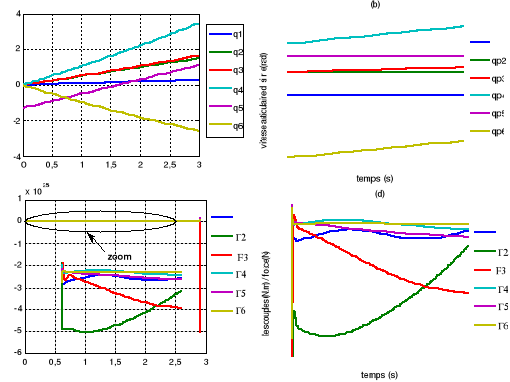
Figure
V.5. (a) positions articulaires (b) vitesses articulaires
(c) la commande PID
(d) la commande dynamique
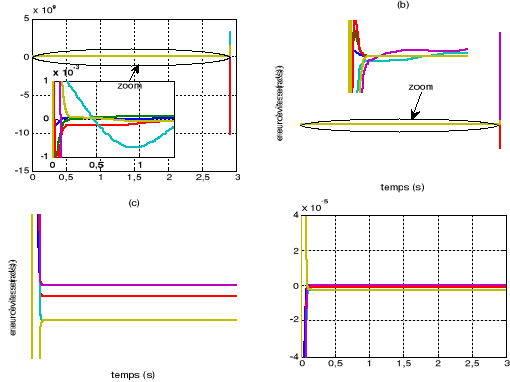
Figure V.6.
L'erreur de position et de vitesse
(a)et (b) la commande PID
(c) et (d) la commande
dynamique.
V.3.2.Commande dans l'espace opérationnel
Le problème de l'asservissement dans l'espace
cartésien pour un bras manipulateur, consiste à produire des
consignes capables de réaliser le mouvement opérationnel [AGU
07], une des deux solutions suivantes peut être choisie pour
réaliser la commande par découplage non linéaire :
V.3.2.1. Commande dans l'espace
opérationnel avec correction dans l'espace articulaire
Dans ce cas, on transforme le mouvement défini dans
l'espace opérationnel en un mouvement dans l'espace articulaire, puis on
met en oeuvre la commande dans l'espace articulaire du
§V.3.1. Le signal d'erreur est exprimé alors dans
l'espace articulaire [VIV 04].
On utilise le MGI pour trouver les variables articulaires
désirées, puis avec une procédure numérique on
dérive ces dernières pour obtenir la vitesse et
l'accélération (Figure V.7).
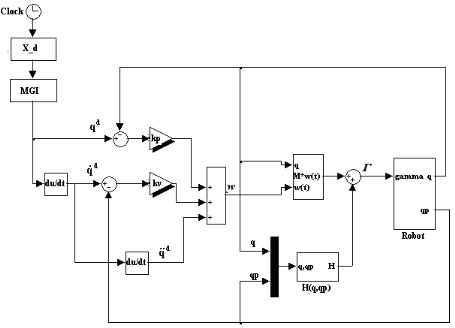
Figure V.7.
Commande dans l'espace opérationnel avec correction dans l'espace
articulaire
· Application sur le robot choisi
Les valeurs de  sont les mêmes de la section précédente. sont les mêmes de la section précédente.
On considère que le robot se déplace selon la
trajectoire donnée dans le chapitre III (la poursuite
d'une tache de soudure). Cette trajectoire est caractérisée par
les coordonnées opérationnelles de translation et de rotation
présentées par les figures (V.8.(a, b))
respectivement.
La figure (V.8.c, d) montre les
coordonnées (positions et vitesses) articulaires correspondantes
à la trajectoire désirée.
La figure (V.9.a, b) représente
l'évolution des erreurs au niveau des coordonnées articulaires
lors du suivi de la trajectoire désirée. On remarque la bonne
convergence de la loi de commande établie. Cette erreur est très
faible, elle est de l'ordre de 10-4rad pour
l'erreur de position et de 10-2 rad/s pour
l'erreur de vitesse.
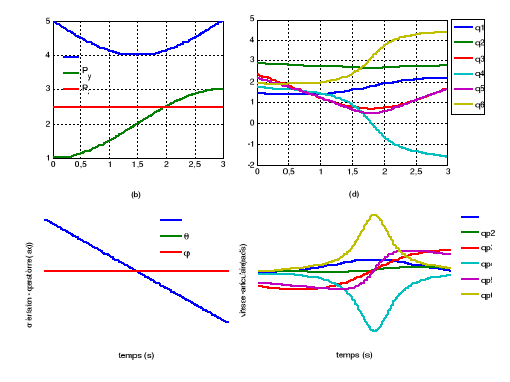
Figure V.8.
Les coordonnées de la trajectoire désirée dans l'espace
opérationnel (a, b) et dans l'espace articulaire(c, d)
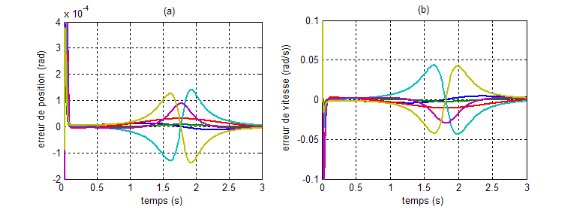
Figure V.9. L'erreur de position et
l'erreur de vitesse dans l'espace articulaire
Lors de la simulation, on a utilisé différentes
trajectoires, et on a trouvé qu'il a des cas où le système
diverge et l'erreur pour quelques articulations devient très grande.
Cette divergence est due par le fait que le MGI a plusieurs solutions (8
solutions dans notre cas).
On prend, comme exemple, la trajectoire donnée par la
figure (V.10.a).
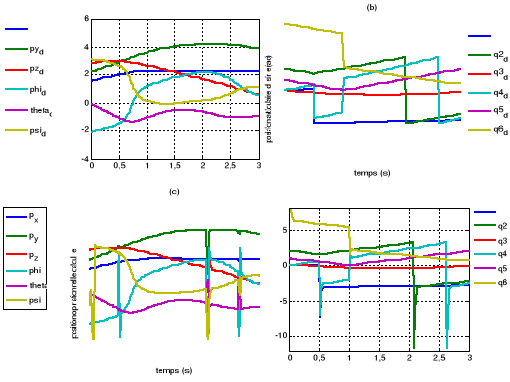
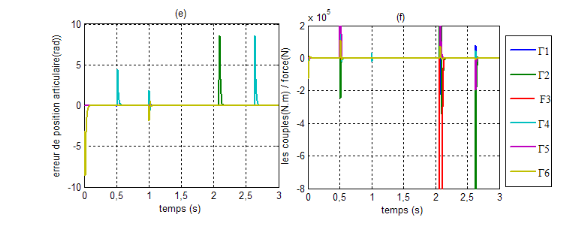
Figure
V.10. L'erreur due au problème de la non unicité
du MGI
Les résultats de simulation sont montrés dans la
figure (V.10). On voit, bien que, les couples atteint des
valeurs très grandes quand les positions articulaires changent
d'aspect.
Pour remédier à ce problème on doit poser
des contraintes ayant une relation avec la géométrie du robot,
afin de minimiser le nombre de solutions. Ces contraintes diffèrent d'un
robot à l'autre.
La deuxième solution est de penser à une loi de
commande qui ne passe pas par le MGI.
V.3.2.2. Commande dans l'espace
opérationnel avec correction dans l'espace opérationnel
Le mouvement dans l'espace de tâche peut être
réalisé en modifiant notre choix de la commande de la boucle
externe  dans l'équation (V-4), tout en laissant la commande de la
boucle intérieure inchangée (le calcul de dans l'équation (V-4), tout en laissant la commande de la
boucle intérieure inchangée (le calcul de  ). ).
Soit  la position du terminal en utilisant n'importe quelle
représentation minimale. Puisque X est une fonction
des variables communes nous avons : la position du terminal en utilisant n'importe quelle
représentation minimale. Puisque X est une fonction
des variables communes nous avons :
 (V-9)
(V-9)
où  est la jacobienne analytique. est la jacobienne analytique.
Etant donné l'équation du double
intégrateur (V-4) dans l'espace articulaire, si  est choisi comme: est choisi comme:
 (V-10)
(V-10)
le résultat est une équation du double
intégrateur dans l'espace opérationnel :
 (V-11) (V-11)
Comme pour la commande dans l'espace articulaire, on peut
proposer plusieurs schémas. On détaille ici le cas d'une
correction PD lorsque le mouvement est complètement
spécifié. On pose alors :
 (V-12) (V-12)
Avec cette loi, dans l'hypothèse d'une
modélisation parfaite et d'erreurs initiales nulles, le comportement du
robot est décrit par l'équation:
 (V-13) avec :
(V-13) avec :  (V-14) Le schéma bloc correspondant
est représenté par la figure (V.8), la valeur de
(V-14) Le schéma bloc correspondant
est représenté par la figure (V.8), la valeur de
 est calculée par la relation : est calculée par la relation :
 (V-15)
(V-15)
w(t)=
-
+
+
+
+
+
+
-
+
-
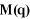
Robot
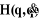
MGD
Kp
Kv
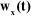
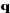
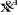
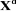
 MCD MCD
+
Figure
V.11. La commande dans l'espace opérationnel avec
correction dans l'espace opérationnel.
· Application sur le robot choisi
La représentation de l'orientation de l'effecteur est
faite toujours (durant notre travail) par les angles de RTL, pour cela on peut
décomposer le vecteur d'erreur en deux sous vecteurs ;  définit les écarts en position, et définit les écarts en position, et  pour indiquer les écarts en orientation, de tel sorte
que : pour indiquer les écarts en orientation, de tel sorte
que :
 (V-16)
(V-16)
On considère que le robot se déplace selon la
trajectoire donnée dans le chapitre II (la poursuite d'une tache de
soudure).
Les valeurs du  sont : sont :
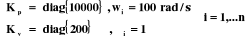
Les coordonnées opérationnelles
calculées et les erreurs de position  et et , sont représentés dans la figure
(V.12). , sont représentés dans la figure
(V.12).
On remarque la bonne convergence de la loi de commande
établie ; la valeur de l'erreur est très faible, elle est de
l'ordre de 10-4m pour l'erreur de translation , et de l'ordre de 10-3 rad pour l'erreur
d'orientation. , et de l'ordre de 10-3 rad pour l'erreur
d'orientation.
De même, la figure (V.13)
représentent les vitesses opérationnelles et les erreurs
correspondantes, ces dernières sont très faibles, elles sont de
l'ordre de 10-5 m/s pour les vitesses de
translation et de l'ordre de 10-5 (rad/s) pour les
vitesses de rotation.
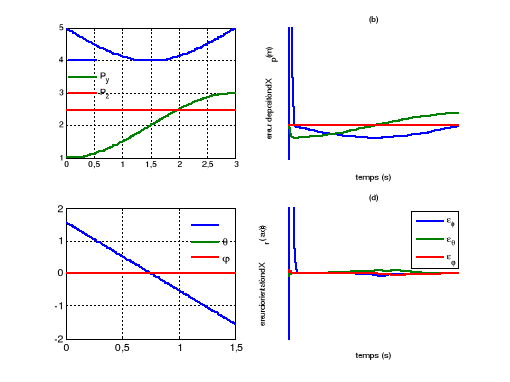
Figure
V.12. L'erreur d'orientation et de translation dans l'espace
opérationnel.
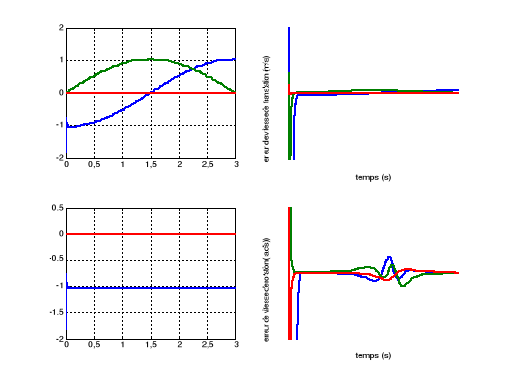
Figure
V.13. L'erreur de vitesse dans l'espace
opérationnel.
V.3.3.
Commande au voisinage des positions singulières
Pour cette loi de commande, nous utilisons l'inverse de la
matrice jacobienne. Le plus grave inconvénient de ce type de commande
est dû au fait que cette matrice peut devenir singulière.
Au niveau d'une configuration singulière, l'inverse
de la matrice jacobienne n'existe plus. Ce qui produit des vitesses
articulaires infinies. L'utilisation de l'inverse
généralisée résout ce problème.
Pour le calcul de la matrice inverse
généralisée au voisinage des singularités, Nakamura
propose une méthode robuste [NAK 91]. Cette matrice est définie
par :
 (V-17)
(V-17)
où  est utilisé comme paramètre d'amortissement de l'inverse
de la matrice jacobienne. En choisissant est utilisé comme paramètre d'amortissement de l'inverse
de la matrice jacobienne. En choisissant , nous assurons l'existence de l'inverse de la matrice jacobienne. Ceci
permet de traverser les positions singulières. Une valeur de , nous assurons l'existence de l'inverse de la matrice jacobienne. Ceci
permet de traverser les positions singulières. Une valeur de  donne des résultats satisfaisants [AGU 07]. donne des résultats satisfaisants [AGU 07].
· Application sur
le robot choisi
Pour valider la solution de Nakamura, sur notre travail, on a
donné une trajectoire qui passe par des positions singulières du
robot (Figure V.14)
 et et 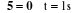
Figure
V.14. La trajectoire désirée
La figure (V.15) montre la position de
l'effecteur et les erreurs qui la correspondante, lors du passage par les
positions singulières choisis sans tenir en compte l'inverse
généralisée de la matrice jacobienne.
Au niveau de position opérationnelle; la valeur
maximale de l'erreur de translation est 6*10-3(m), et l'erreur de
rotation est de l'ordre de 10-2 (rad). Ces erreurs sont multiples
de 100 à 1000 fois des erreurs trouvées dans le cas d'une
trajectoire ne contient pas des positions singulières. Mais on peut dire
que le système converge.
Tandis qu'au niveau des coordonnées articulaires
mesurées, les valeurs des vitesses sont très grandes, de l'ordre
de 5000 rad/s. De même les positions articulaires dépassent ses
limites naturelles (2*pi rad), figure (V.16).
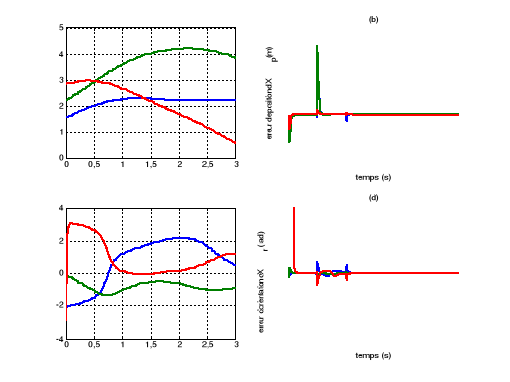
Figure
V.15. La position de l'effecteur et les erreurs de position
dans l'espace opérationnelle.
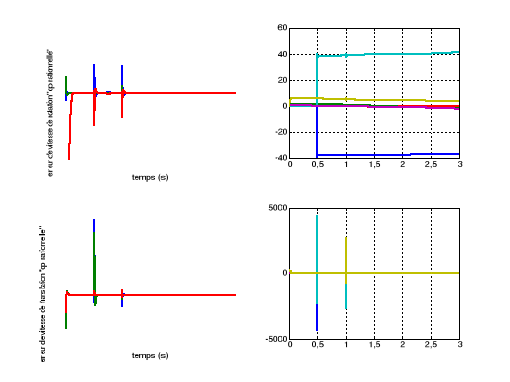
Figure V.16.
« à gauche » l'erreur de vitesse
opérationnelle
« à
droite » les positions et les vitesses articulaires
calculées.
On a fait le calcul de la matrice inverse
généralisée , avec , avec , les résultats de simulation obtenus dans ce cas sont
montrés par les figures (V.17), (V.18). , les résultats de simulation obtenus dans ce cas sont
montrés par les figures (V.17), (V.18).
On voit clairement que la commande au voisinage des positions
singulières, est très bien traitée par cette
solution.
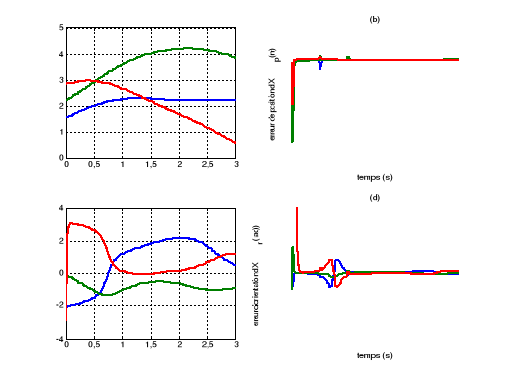
Figure V.17.
Le cas d'utilisation de l'inverse
généralisée.
La position de l'effecteur et les erreurs de
position dans l'espace opérationnelle
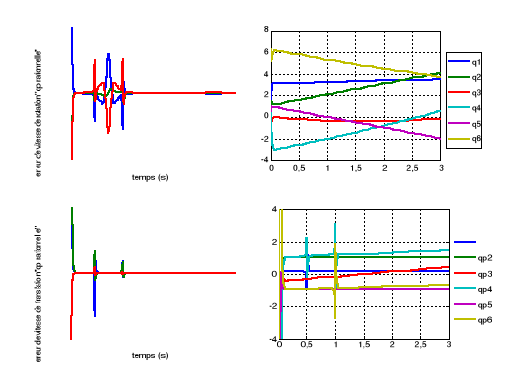
Figure
V.18. Le cas d'utilisation de l'inverse
généralisée.
« à
gauche » l'erreur de vitesse opérationnelle
« à
droite »les positions et les vitesses articulaires
calculées.
V.4. Conclusion
Dans ce chapitre, nous avons présenté la
synthèse de la commande dynamique d'un bras manipulateur rigide dans les
espaces articulaire et opérationnel.
C'est dans l'étape de validation des différents
schémas de commande que nous avons constaté l'importance des
modèles géométrique, cinématique et dynamique pour
le calcule des consignes de commande.
Nous obtenons un haut niveau de performance de la boucle
d'asservissement dans l'espace opérationnel, même en
présence de configurations singulières. L'utilisation de
l'inverse généralisée a permis de traverser les
configurations singulières sans problèmes.
Finalement, après toutes ces simulations, nous
obtenons un schéma de commande qui satisfait les contraintes du robot
choisi ; le repère référence est celui de l'atelier,
une vitesse grande , un effort extérieur statique et la connaissance
parfaite des paramètres inertiels et géométriques.
Conclusion générale
La commande des robots manipulateurs est l'une des
préoccupations majeures des recherches en robotique. En effet, un robot
manipulateur est caractérisé par un comportement purement non
linéaire, de plus, la majorité des tâches qui lui sont
confiées sont délicates et exigent une très grande
précision sous des trajectoires rapides, excluant ainsi toute
utilisation des méthodes classiques de synthèse des
régulateurs standard.
Dans le but d'améliorer les performances des
manipulateurs, nous avons présenté dans ce travail une loi de
commande très connue en robotique et nécessitant la connaissance
précise du modèle dynamique du robot, à savoir la commande
dynamique.
L'objectif de ce travail est la modélisation et la
commande dynamique d'un robot manipulateur industriel à 6ddl, dont une
de ses liaisons est prismatique.
Le mémoire présenté comporte cinq
parties :
La première partie de ce travail est
dédiée à la modélisation géométrique
direct des robots à structure ouverte simple, où on a choisi de
représenter les coordonnées opérationnelles de position
par les coordonnées cartésiennes et celles de la rotation par les
angles de Roulis Tangage Lacet. L'utilisation des paramètres de Denavit
Hartenberg et le bon choix des repères, nous a permet de calculer le
modèle géométrique direct du robot et son espace de
travail en dehors de ses positions singulières.
La deuxième partie est relative au problème
géométrique inverse, des solutions analytiques du modèle
géométrique inverse ont été trouvées par
l'utilisation de la méthode de Paul accompagnée par la
méthode de découplage cinématique.
La troisième partie est consacrée à
l'étude cinématique du robot, on a fait le calcul de ses matrices
jacobienne, géométrique et analytique, ainsi que la
détermination de son modèle cinématique inverse du premier
et de deuxième ordre, ensuite on a appliqué ces principes sur le
robot choisi.
Nous avons détaillé dans le chapitre quatre les
deux formalismes de calcul du modèle dynamique d'un robot manipulateur,
à travers l'application des deux formalismes on a calculé le
modèle dynamique direct et inverse, bien sure ils nous ont
données les mêmes résultats.
La dernière partie de ce travail est
dédiée à la commande des bras manipulateurs. On a
commencé par l'application de la commande dans l'espace articulaire puis
dans l'espace opérationnel, dont la correction pour ce dernier est faite
soit dans l'espace articulaire ou bien dans l'espace opérationnel lui
même en utilisant, dans ce cas, les angles de Roulis Tangage Lacet,
comme signal de retour pour l'orientation, les positions singulières
sont traitées par l'introduction de l'inverse
généralisée de la matrice jacobienne.
À partir des schémas de commande nous pouvons
formuler trois remarques ; Tout d'abord la commande dans l'espace
articulaire est très facile à mettre en ouvre mais ,puisqu'on ne
peut pas imaginer la trajectoire suivi par l'outil, cette méthode reste
valable que lorsqu'on veut faire commander un axe après axe. Ensuite la
commande dans l'espace opérationnel avec correction dans l'espace
articulaire, malgré, qu'elle a résolue le problème de la
précédente et qu'elle nous a donnée des bons
résultats, elle a aussi le problème de la non unicité des
solutions de MGI. Finalement, la commande dans l'espace opérationnel
avec correction dans cet espace donne une bonne précision, elle est
robuste au passage des configurations singulières pendant le suivi d'un
chemin réalisé en respectant les contraintes cinématiques,
ce qui permet la réalisation des tâches « en aveugle
».
Des résultats de simulation sous Maple et
Matlab/Simulink sont présentés pour valider les
différentes approches.
A cause de suppositions tenues au cours de notre travail, on
peut dire que ce travail ne réalise pas une recherche exhaustive pour
satisfaire toutes les contraintes, mais essaie de proposer un schéma de
commande qui permet la réalisation de différentes tâches en
respectant des contraintes cinématiques lorsque l'information provient
de capteurs proprioceptifs, dans le cas particulier de ce travail seules la
position et la vitesse ont été utilisées.
Les perspectives ouvertes par ce travail peuvent
concerner :
· Développer des techniques d'identification des
paramètres inertiels et les paramètres de frottements du
robot.
· Simplifier au maximum, les éléments de
tous les modèles entrant dans la boucle de commande afin de
réduire le temps d'exécution de la commande et de l'implanter
sur calculateur.
· La loi de commande développée ici, peut
être utilisée pour la commande de deux robots coopératifs,
en supposant que ces deux derniers sont de même type. Les seuls
paramètres qui seront changés, pour notre loi, sont les
paramètres de la représentation des deux robots par rapport au
repère atelier. Mais dans la pratique, il faut aussi étudier la
loi de distribution des forces entre les deux robots.
· Les déformations des corps constituant les
mécanismes ont été toutefois négligées ici
et des modèles plus compliqués seraient nécessaires pour
la modélisation. Les lois de commande de robots
« souples » seraient également plus
compliquées car elles devraient contrôler les déformations
qui constituent autant de degrés de liberté
supplémentaires. Pour l'instant, de tels manipulateurs ne sont pas
utilisés dans l'industrie, mais comme bras
téléopérés dans les navettes spatiales par exemple.
Références
bibliographiques
|
[AGU 07] I.H. Aguilar. « Commande des bras
manipulateurs et retour visuel pour des applications à la robotique de
service ». Thèse de doctorat, Université Toulouse III,
2007.
|
|
[AIS 06] A. Aissaoui, « Conception et
commande neuronal d'une patte d'un robot marcheur », mémoire
de magister, Université de Oum EL Bouaghi, Algérie, mars
2006
|
|
[BEJ 85] Bejczy A.K, Tarn T.J, Yun X, Hans S « Non linear
feedback control of Puma 560 robot arm by computer », Proc 24
th IEEE conf on Decision and control, Fort Lauderdale , déc
1985, p 1680-1688.
|
|
[BEN 06] A. Benmisra « Programmation des robots
industriel et application sur le robot manipulateur Algérie machines
outil 1 », mémoire de magister, Université de Saad
Dahleb de Blida, Algérie, 2006
|
|
[BIL 05] B. Goodwine « Inverse Kinematics »,
"Robotics and Automation Handbook", CRC Press LLC publication 2005
|
|
[BOI 88] J. Boissonat, B. Faverjon « Technique de la
robotique, Architecture et commande », Hermes sciences, paris, 1988
|
|
[BOR 90] J.J. Borrelly, D. Simon «Proposition
d'architecture de contrôleur ouvert pou le robotique », rapport
de recherche, INRIA université de Rennes1, France, octobre 1990
|
|
[CHE 03] C.CHEN, «A Lagrangian Formulation in Terms of
Quasi-Coordinates for the Inverse Dynamics of the General 6-6 Stewart Platform
Manipulator», JSME International Journal Series C, Vol. 46,
No. 3 (2003), pp.1084-1090
|
|
[CHE 08] S. Chemami, C. Mahfoudi, K.
Djouani «Comparaison entre les deux formalismes dynamiques (Newton
Euler et Lagrange) pour la commande d'un robot manipulateur à
6ddl »,2ème Conférence Internationale sur
les Sciences de la Mécanique, Université d'Oum EL Bouaghi,
Algérie 16, 17 et 18 Novembre 2008.
|
|
[CRA 89] John J .Craig, « Introduction to Robotics
and control», Second Edition, Addison Wesley, Publication, 1989
|
|
[DOM 01] E. Dombre, «Analyse ET Modélisation des
Robots Manipulateurs », Hermes Science, Publications, 2001.
|
|
[ESP 08] B. Espiau «Commander les
robots » publier le 26/05/08 sur le site interstices @
http://interstices.info/commande-robot.
|
|
[FEA 07] R. Featherstone «Robot dynamics
» publier le 9 /10/ 2007 sur le site Scholarpedia, @
www.scholarpedia.org/article/Robot_dynamics
|
|
[FIS 04] P. Fisette, H. Buyse, J.C. Samin «Introduction
à la robotique» France, 10 novembre 2004
|
|
[FLÜ 98] L. Flückiger « Interface pour le
pilotage et l'analyse des robots basée sur un générateur
de cinématique »Thèse de doctorat, Ecole polytechnique
Fédérale de Lausanne 1998.
|
|
[GRE 05] G. S. Chirikjian «Rigid-Body
Kinematics»,"Robotics and Automation Handbook", CRC Press LLC publication
2005
|
|
[KHA 78] W. Khalil « Contribution à la commande
automatique des manipulateurs avec l'aide d'un modèle
mathématique des mécanismes», Thèse d'état.
USTL. Montpellier, oct. 1978.
|
|
[KHA 99] W. Khalil, E. Dombre, « Modélisation,
Identification et Commande des Robots », 2ième
édition, Hermes Science Publication, 1999.
|
|
[KUR 05] Thomas R. Kurfess, « Robotics and
Automation Handbook», CRC Press LLC, publication 2005
|
|
[LUH 80] LUH J.Y.S. Walker M.W. Paul RCP, « Resolved
acceleration control of mechanical manipulators », IEEE trans on Automatic
control. Vol AC-25(3), juin 1980, p 467-474
|
|
[MAH 06] C. Mahfoudi « Contribution à la
modélisation des robots à pattes, Application aux
Hexapodes», mémoire de doctorat, Ecole National Polytechnique,
Algérie, octobre 2006
|
|
[NAG 05] M.L. Nagurka «Newton-Euler Dynamics of
Robots», "Robotics and Automation Handbook ", CRC Press LLC publication
2005
|
|
[NAK 91] Y. Nakamura « Advanced Robotics. Robotics
and Optimization ». Addison Wesley Publishing Company, 1991.
|
|
[SAM 83] C. Samson «Commande non linéaire robuste
des robots manipulateurs », rapport de recherche, INRIA université
de Rennes1, France, 1983
|
|
[SIL 82] W.M. Silver «On the
Equivalence of Lagrangian and Newton-Euler Dynamics for Manipulators», The
International Journal of Robotics Research, Vol. 1, No. 2, 60-70 (1982)
|
|
[SPO 04] Mark W. Spong, S. Hutchinson, M. Vidyasagar
«Robot Dynamics and Control», Second Edition, January 28, 2004
|
|
[SPO 05] Mark W. Spong «Robust and Adaptive Motion
Control of Manipulators», "Robotics and Automation Handbook", CRC Press
LLC publication 2005
|
|
[TEC 07] ANDRÉ (G.). « Modélisation et
commande des robots manipulateurs», Techniques de l'Ingénieur,
traité Informatique Industrielle, Doc S 7730, octobre 2007
|
|
[VEN 02] G. Venture, M. Gautier, W. Khalil
«Identification des paramètres physiques par modèle inverse
appliquée à la dynamique véhicule », 2002
|
|
[VIV 04] O.A.VIVAS Albán « Contribution
à l'identification et à la commande des robots
parallèles » Thèse de doctorat, Montpellier II, le 10
novembre 2004
|
|
[XIE 03] M.Xie « Fundamentals of robotics: linking
perception to action »
p. cm. -- (Series in machine perception and artificial
intelligence; v. 54), World Scientific Publishing 2003.
|
|
[éEF 05] M. éefran, F. Bullo « Lagrangian
Dynamics », "Robotics and Automation Handbook", CRC Press LLC publication
2005
|
Résumé : Le travail
développé dans ce mémoire concerne la commande des robots
manipulateurs par retour d'état estimé. Nous nous sommes
intéressés à la classe des robots manipulateurs rigides
à chaîne ouverte simple. Nous présentons en premier lieu
une étude détaillée sur les modèles
utilisés pour le contrôle et la commande du robot, à
savoir le modèle géométrique, cinématique et
dynamique : directs et inverses. En supposant mesurables les variables de
positions et de vitesses articulaires, nous avons proposé un
schéma de commande basé sur un observateur à grands gains
et une commande non linéaire. La commande utilisée
linéarise exactement l'observateur ce qui rend son implantation
très facile. Nous avons également traité la commande au
voisinage des positions singulières. Les résultats de simulation
confirment la validité du schéma de commande proposé.
Mots-clés : Robot rigide, Robot
manipulateur, Commande non linéaire, Modélisation, 6ddl
Abstract: The work developed in this memory
concern the control of the manipulators robots by return of estimated state. We
were interested in the class of the rigid manipulators robots with simple open
chain. We initially present a study detailed on the models used for the
control of the robot, namely the geometrical, kinematics and dynamic model:
direct and reverse. By supposing measurable the joints variables of positions
and speeds, we proposed a diagram of control based on an observer with great
gains and a nonlinear control. The control used linearise the observer exactly
what makes its establishment very easy. We also treated the control in the
vicinity of the singular positions. The results of simulation confirm the
validity of the diagram of control proposed.
Key words: Rigid robot, Manipulator robot,
nonlinear control, Modeling, 6ddl
ãáÎÕ:
ÇáÚãá
ÇáãÞÏã í åÐå
ÇáãÐßÑÉ íÎÕ
ÇáÊÍßã í
ÇáÑæÈæÊ
ÈÚæÏÉ
ÇáÍÇáÉ
ÇáãÞíãÉ,
æáÞÏ ßÇä
ÅåÊãÇãäÇ
ÈÇáÞÓã
ÇáÎÇÕ
ÈÇáÑæÈæÊÇÊ
ÇáÕáÈÉ ÐÇÊ
ÇáÓáÓáÉ
ÇáãÊæÍÉ
ÇáÈÓíØÉ.
ÈÏÇíÉ, ÞãäÇ
ÈÏÑÇÓÉ ãÕáÉ
áßá ÇáäãÇÐÌ
ÇáÊí
äÍÊÇÌåÇ
ááãÑÇÞÈÉ æ
ÇáÊÍßã í
ÇáÑæÈæÊ: æ åí
ÇáäãæÐÌ
ÇáåäÏÓí,
ÇáÓíäíãÇÊíßí,
æ
ÇáÏíäÇãíßí,
ÇáãÈÇÔÑ æ
ÇáÚßÓí.
ÈÇÊÑÇÖ ä
ãæÖÚ æ ÓÑÚÉ
ÇáãÕá
ÕÇáÍíä
ááÞíÇÓ,
äÞÊÑÍ ØÑíÞÉ
ááÊÍßã
ÊÚÊãÏ ÓÇÓÇ
Úáì ãáÇÍÙ Ðæ
ßÓÈ ÚÇáí æ
ÊÍßã áÇ ÎØí
ÏíäÇãíßí.
ÞãäÇ ßÐÇáß
ÈãÚÇáÌÉ
ÇáÊÍßã
ÈÇáÞÑÈ ãä
ÇáãæÇÖÚ
ÇáÍÑÌÉ
ÇáÊí íãÑ
ÈåÇ ÇáÑæÈæÊ
ËäÇÁ ÍÑßÊå.
ßáãÇÊ
ãÊÇÍíå:
ÇáÑæÈæÊ
ÇáÕáÈ,
ÇáÑæÈæÊ
ÇáÚÇãá,
ÇáÊÍßã
ÇááÇÎØí,
ÇáäãÐÌÉ, 6
ÏÑÌÇÊ ÍÑíÉ
.
| 
