Praogrammation des charrois automobiles pour la distribution de la boisson dans la ville de Bukavu: Cas de la Bralima/Bukavu(2005-2006)

CHAPITRE 1

CONSIDERATIONS THEORIQUES

Ce chapitre est constitué des considérations d'ordre théorique qui comprend les points suivants :

· Définition des concepts ;

· Présentation de la BRALIMA/Bukavu.

1 .1. Définition des concepts

Il s'agit de définir les mots clés utilisés pour permettre aux lecteurs de bien comprendre le contenu sémantique de nos propos.

1.1.1 La programmation

D'après le petit Robert (2001, p122), la programmation est l'établissement, l'organisation des programmes. Elle est l'élaboration et la codification de la suite d'opérations formant un programme.

Par exemple, la programmation d'une machine.

Le même auteur ajoute en disant qu'elle est une action de prévoir et d'organiser, et c'est ici le noeud de l'utilisation de ce terme par les entreprises.

Quant au programme, le petit Robert (2001, p122), le définit comme un écrit annonçant et décrivant les diverses parties d'une cérémonie d'un spectacle .C'est l'annonce des matières d'un cours, du sujet d'un concours etc.

Il s'ajoute en outre, que c'est la suite d'actions que l'on se propose d'accomplir pour arriver à un résultat. C'est l'ensemble ordonné d'opérations effectuées par un système automatique. L'ensemble des instructions, rédigées dans un langage de programmation, permettant à un système informatique d'exécuter une tâche donnée. Par exemple : logiciel, progiciel, c'est-à-dire le programme enregistré dans le mémoire d'un ordinateur, programme stocké sur une mémoire de masse, sur une disquette, etc.

Un programme décrit une procédure de calcul qui, à partir d'information en entrée (données), produit des informations en sortie (résultat). Enfin, c'est l'ensemble des tâches que nous devons réaliser. Parmi les programmations, nous pouvons retenir :

1.1.2  La programmation linéaire

Le dictionnaire d'analyse économique de BERNARD G., (2001, p201) définit la programmation linéaire comme étant la méthode de recherche des extremums d'une fonction linéaire dont les variables sont soumises à des contraintes qui prennent la forme d'inégalité linéaire. Cette méthode peut être appliquée à des nombreux problèmes.

Par exemple la gestion de stocks ou le transport des marchandises entre divers points et plus généralement à la planification. Elle s'appuie sur le théorème de la dualité qui permet d'associer à chaque contrainte un nombre (positif) qui peut être interprété comme un prix ou comme un coût.

J. M'VIBUDULU KALUYIT. (2007, p72), écrit que programmation linéaire a pour but de déterminer la valeur à affecter à un certain nombre de variables :

- en vue d'optimiser (minimiser ou maximiser) une fonction linéaire de ces variables ;

- en vue de tenir compte de certaines contraintes (équation ou inéquation linéaire) aux quelles sont soumises les valeurs de ces variables.

Ainsi du point de vue mathématique, on appelle problème linéaire tout problème dans lequel il s'agit d'optimiser selon le cas la fonction de plusieurs variables, celles-ci devant satisfaire à un ensemble de contraintes linéaires, par exemple y= ax + b.

Cette fonction est linéaire avec x comme variable indépendante et y variable que nous voulons étudier qui est la production de la bière à la BRALIMA, en tenant compte de la variable x qui est la quantité des matières premières utilisées, a étant une charge fixe et b étant une valeur résiduelle, c'est-à-dire difficile à maîtriser car elle tient compte des circonstances dans lesquelles la gestion des matières premières et l'activité de production se déroulent ; ainsi si a= 3 et b=25, f(x) devient y=3x+25.

Pour K. MAGENDO (ISP, 2006), la Programmation linéaire est définie comme étant d un modèle d'optimalisation d'une solution qui permet de guider le décideur dans le sens d'allouer des ressources limitées par des contraintes, à une série d'activités, en fonction de l'objectif que l'on s'est fixer.

Dans toute étude linéaire optimale, l'analyse doit arriver à transformer un problème économique sous la forme ci- haut donnée.

· Formulation mathématique d'une fonction économique

La fonction économique associe linéairement les quantités des facteurs, les unités et les profils unitaires correspondants (les couts unitaires dans le cas de minimisation).

Max (C₁X₁+A₂X₂+............+.A_nX_n)

Min (C₁X₁₊A₂X₂+.................+A_nX_n)

1.1.2.1 La programmation duale

Le problème consiste à déterminer le prix minimum à fixer pour qu'afin que :

- la restriction soit avantageuse pour le pays dans la mise en valeur directe des terres.

- Le coût global de location soit minimal pour la société.

Le programme dual est définit toujours :

1°) par des contraintes :

- dont les coefficients correspondent aux colonnes de A ;

- dont les seconds membres sont les élément de C ;

- dont le sens est opposé à celle du primal ;

2°) par une fonction économique :

-dont les coefficients sont les éléments de B ;

-à maximiser si celle du primal est à minimiser et inversement.

Par exemple : soient A=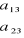

B = C =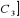

PROGRAMMATION PRIMALE

a₁₁x₁ + a₁₂x₂ + a₁₃x₃ = b₁

a₂₁x₁ + a₂₂x₂ + a₂₃x₃ = b₂

x_1, x_2, x₃ = 0

Zmax: C₁x₁ + C₂x₂ + C₃x₃

PROGRAMMATION DUALE

a₁₁u₁ + a₂₁u₂ = C₁

a₁₂u₁ + a₂₂u₂ = C₂

a₁₃u₁ + a₂₃u₂ = C₃

Zmax: (b₁u₁ + b₂u₂)

Sous forme matricielle, les deux programmes peuvent s'écrire comme suit :

PRIMAL DUAL

- X étant un vecteur colonne, c'est un vecteur ligne U₁, U₂

- Chercher x tel que : C_x soit : A_x = B

- Chercher U tel que U_B soit : minimum sous les contraintes U_A = C

La méthode de résolution du primal est aussi valable pour le Dual, si l'un des deux programmes admet une solution optimale,l'autre en admet également une, le maximum de l'un est égal au minimum de l'autre.

1.1.2.2 La programmation linéaire par méthode simplexe (méthode de DANTZIG)

La méthode du simplexe prend pour point de départ une solution de base pour laquelle la fonction économique a pour valeur zéro ;

A chaque étape on cherche à améliorer la solution de départ de façon créative afin d'atteindre un meilleur membre de la contrainte.

(J. M'VIBUDULU KALUYIT J., 2007, p73).

La programmation par méthode simplexe est une solution permettant d'aboutir à cet objectif et pour y arriver il faut d'abord transformer le problème économique posé sous une forme linéaire. En programmation, par méthode simplexe, deux méthodes s'imposent à savoir la méthode graphique et la méthode algorithmique simplexe.

1) La méthode graphique

Partons d'un exemple pour expliquer cette méthode graphique. Soient XP matières première et XF les produits finis fabriqués à la BRALIMA/BUKAVU, dont X_p matières premières et X_F produits finis.

Max Z = 3 x p + 5 x F

S/C X_P = 4

2X_F = 12

3X_P + 2X_F = 18

X_P, X_F = 0

Pour résoudre notre problème nous devons d'abord déterminer les coordonnées du graphique. Ainsi nous pouvons le procéder de la manière suivante :

a) Les contraintes

1) X_P = 4, X_P = 4

2) 2X_P = 12, 2X_P = 12, X_P = 6

3) 3X_P + 2X_F = 18

3X_P + 2X_F = 18

Pour X_P = 0, 3.O+2X_F

2X_F = 18

X_F = 18/2 =9

X_F = 0,3Xp+2.0=18

3Xp=18

Xp=18/3=6

b) la représentation graphique

b) Interprétation du graphique

Zmax=3Xp + 5XF

-Pour Xp=4 et Xf=0 , on a :

Zmax= 3.4 +5.0=12

- Pour Xp=0 et Xf=6 , on a :

Zmax=3.0+ 5.6= 30

- Pour Xp=4 et Xf=3, on a :

Zmax=3.4+5.3=27

- Pour Xp=2 et Xf=6,on a :

Zmax=3.2+5.6=36

On observe que l'entreprise pourra maximiser coût de production dans la contrainte 3Xp+2Xf =18

2) L'argorithme simplexe

L'algorithme complexe est une suite d'observation bien définie qui amène progressivement à la solution optimale du problème en respectant certains principes mathématiques.

1.1.2.3 Les contraintes linéaires

Elles représentent la manière dont les facteurs peuvent être constitués pour utiliser les ressources et générer un résultat au travers de la fonction économique.

Elles s'écrivent comme suit :

a₁x₁ + a₂x₂ + ....................... + a₁x₁ = b₁

a₁x₁ + a₂x₂ + ....................... + a₁x₁ = b₂

.

.

.

A_n1x₁ + a_n2x₂ + ....................... + a_n1x_n = b_n

Notons que les contraintes sont souvent représentées par les inégalités.