Praogrammation des charrois automobiles pour la distribution de la boisson dans la ville de Bukavu: Cas de la Bralima/Bukavu(2005-2006)

IN MEMORIAM

A vous feu notre Père Florentin Lindjandja que le trépas nous a précocement ravi. Vous avez semé mais vous n'avez plus récolté. Votre absence crée en nous un vide que nul ne saurait combler.

Je vous resterai reconnaissant.

Que la terre de nos ancêtres vous soit douce !

Papy HAMULI Lindjandja

EPIGRAPHE

La crainte de l'éternel est le commencement de la science ;

Les insensés méprisent la sagesse et l'instruction. Proverbes 1 :7

« Or, la science souveraine, la science supérieure à toute science subordonnée, est celle qui connaît pourquoi il faut faire chaque chose.

Et ce pourquoi c'est le bien de chaque être, pris au général, c'est le mieux dans tout l'ensemble des êtres »

(Aristote, Métaphysique Livre 1^er, 2ème

Un fils sage fait la joie d'un Père, et un fils insensé le chagrin de sa mère.

Proverbe 10 :1

Dans toute circonstance apprenez à garder le silence, car le silence instruit.

Papy HAMULI Lindjandja

DEDICACE

A l'éternel Dieu tout puissant pour nous avoir donné la force, le courage et la santé afin de bien mener à bon port ce travail ;

A notre regretté Père Florentin BAHATI LINDJANDA pour nous avoir quitté tôt sans manger sur les fruits de ta sueur ;

A notre mère Bernadett RIZIKI M'POTOLE, Grand Frère Pierrot BULIMWENGU LINDJANDJA, oncles KALEGAMIRE LINDJANDJA, Guillaume LINDJANJDA et Beaux pères MUSEMA MURHIMBO et Emmanuel SHAMAVU de qui nous avons eu la vie et sans vous la réalisation de cette oeuvre scientifique serait vaine ;

A notre épouse Gulaine MURHIMBO, pour un accompagnement sans cesse pour l'accomplissement de ce travail ;

A nos fils BAHATI et IRAGI, que ce travail soit un exemple à suivre pour votre détermination ;

Papy HAMULI LINDJANDJA

REMERCIEMENTS

Il nous est pratiquement impossible de terminer ce travail sans pour autant remercier toutes les personnes qui de loin ou de près ont contribués à sa réalisation.

Pour ce faire nous remercions le Professeur MUKE ZIHISIRE et l'Assistant Bernard HALIMANA HANGI respectivement Directeur et co-directeur qui , malgré leurs multiples occupations, ont accepté de diriger ce travail avec patience et bonté.

Et à travers eux nous remercions tout le corps enseignant de l'ISP/BUKAVU et particulièrement ceux de sciences commerciales et administratives qui ont assuré notre formation.

Que nos oncles, tantes, cousins et cousines, amis et connaissances trouvent en ce travail le fruit de leur dévouement, de leur engagement et leur soutien dans la mission qu'ils se sont assignés.

Que tous ceux qui ne sont pas cités ici acceptent ce travail comme une marque de remerciement que nous leur prêtons pour leur noble sentiment envers nous.

Papy HAMULI LINDJANDJA

SIGLES ET ABREVIATIONS

$ : Dollars

Adm : Administration

AV : Avenue

BG : Boissons Gazeuses

BRALIMA : Brasserie Limonaderie et Malteserie

CAE  : Comptabilité analytique d'exploitation

DG : Direction Générale

Dpt : Département

GEFIN : Gestion Financière

ISP : Institut Supérieur Pédagogique

Max : Maximum

Min : Minimum

RDC : République Démocratique du Congo

TFC : Travail de fin de Cycle

UCB : Université Catholique de Bukavu

UEA : Université Evangélique en Afrique

0. INTRODUCTION

0.1. Problématique

Gérer est autre chose que du pilotage automatique ou simple une question de bon sens. La gestion, par intuition, par proverbe, n'a aujourd'hui plus de place. Le gestionnaire doit savoir décider efficacement. Par ailleurs, les facteurs qui affectent la qualité de décision sont de plus en plus nombreux et font que l'utilisation des méthodes quantitatives de décision telles que la programmation à laquelle nous faisons allusion dans ce travail soit l'objet d'une étude approfondie voire prioritaire. L'économie dite moderne ne peut prétendre avoir un quelconque niveau de croissance que dans la mesure où elle réussit à maintenir son unité de production, à accroître ses investissements et surtout à assurer convenablement les circuits de distribution permettant de mettre des produits finis à la disposition des acheteurs. Ce qui implique, certes, une bonne organisation du travail.

Or, la plupart des entreprises tant publiques, para-étatiques que privées connaissent des difficultés énormes dues à une mauvaise organisation du travail.

La programmation des charrois automobiles pour la distribution des boissons sucrées ou alcooliques dans la ville de Bukavu par la BRALIMA est l'une des exigences du genre auxquelles elle doit faire face pour maximiser les recettes et rendre plus rentables et plus efficace les entreprises. C'est dans ce cadre que la BRALIMA/Bukavu doit se doter d'un système de distribution des boissons bien structuré et planifié pour atteindre les objectifs qu'elle s'est assignée.

Néanmoins, la BRALIMA/Bukavu, confrontée aujourd'hui à des difficultés d'ordre financier, économique et social (transport) ne parvient plus à satisfaire les attentes des clients en matière de distribution des boissons.

Dans ce cas, les problèmes essentiels qui ont attiré notre attention peuvent être regroupés en trois catégories :

- La déception des clients due souvent au dysfonctionnement de la distribution ;

- La rareté des certains produits préférés par les clients ;

- La multiplication des dépôts relais sans tenir comptes de paramètres tels que la variété des boissons, la croissance démographique ; etc.

Et pourtant qu'une entreprise qui veut atteindre son succès commercial dispose de méthodes et de techniques appropriées pendant la programmation des activités.

La non programmation bien réfléchie peut se répercuter sur la vie de toute l'entreprise au moment où les responsables n'effectuent pas des études approfondies de l'influence de celle-ci sur la situation microéconomique de la firme.

Cette observation nous amène à formuler les questions suivantes :

- Quelle est la politique relative à l'affectation des charrois automobiles utilisés par la BRALIMA /Bukavu pour la distribution de ses produits ?

- L'itinéraire pratiquée par ces charrois automobiles pour atteindre les dépôt - relais ne sont - elles pas longues ?

- Est-il possible de mettre sur pieds une politique optimale permettant à cette entreprise de minimiser les coûts alloués à ce service ?

Telles sont les préoccupations auxquelles nous allons tenter de répondre tout au long de cette étude et qui constitue le noeud de notre problématique.

0.2. Hypothèses

Pour donner réponse à notre problématique, nous avons formulé des hypothèses selon lesquelles :

- La politique d'affectation des charrois automobiles de la BRALIMA/Bukavu posséderait des canaux de distribution par lesquels elle fait écouler ses produits.

- L'itinéraire emprunté pour la distribution semblerait long et en mauvais état.

- La programmation efficiente des charrois automobiles pourrait contribuer, entre autre, à minimiser le coût alloué à ce service.

0.3. Objectifs

Au cours de cette étude, nous nous sommes fixé trois objectifs, à savoir :

- Mener une analyse approfondie relative à la programmation de la distribution des boissons par la BRALIMA/Bukavu ;

- Appréhender la politique utilisée par la BRALIMA/Bukavu pour l'affectation des charrois automobiles ;

- Interpréter le résultat trouvé par la méthode de la programmation dynamique afin de faire l'analyse et d'envisager d'autres mécanismes pour faciliter la distribution à moindre frais.

0.4 Choix et intérêt du sujet

Le choix de notre sujet n'a pas été un fait du hasard. Il a été motivé par deux raisons principales :

A) Raison d'ordre personnel,

Après avoir passé en revue les différentes activités réalisées par la BRALIMA/Bukavu en tant qu'entreprise industrielle, seule l'affectation des charrois automobiles pour la distribution des boissons à ses multiples dépôt relais a attiré notre attention par le fait qu'elle est figurée par parmi les activités essentielles que doit effectuer une entreprise industrielle pour le bon fonctionnement du département commercial

B) Raisons d'ordre scientifique ;

Il est bien évident que tant des personnes se posent des questions sur la distribution des boissons produites par la BRALIMA/Bukavu à travers ses multiples dépôts - relais.

Nous sommes convaincu qu'à partir de notre travail d'aucuns pourront avoir les informations modestes soient- elles, sur l'ambiguïté qui se manifeste en matière de la programmation des charrois automobiles utilisé pour la distribution des boissons sucrées et alcooliques de la BRALIMA/Bukavu.

0.5. Délimitation du sujet

L'analyse de ce thème impose une délimitation tant spatiale que temporelle. Notre étude couvre une période allant de 2005 à 2006 qui est une période pouvant nous donner une idée claire sur la distribution de la boisson par la BUKAVU/Bukavu.

Notre étude porte sur la BRALIMA/Bukavu dont le siège social se trouve à KINSHASA. Le choix de la BRALIMA/Bukavu a été dicté par le fait que celle-ci dispose pour le moment, de plusieurs dépôts - relais. Nous avions considéré que la distribution pourrait être un problème majeur pour cette firme. C'est la raison pour laquelle nous avons choisi le sujet relatif à la Programmation de charrois automobiles pour la distribution de la boisson dans la ville de Bukavu.

0.6. Approche méthodologique

6.1. Méthodes

La méthode, c'est l'ensemble d'opérations intellectuelles sciemment coordonnées par lesquelles une discipline cherche à atteindre les vérités qu'elle poursuit, les démontre, les vérifie Grawitz M. et Pinto R., 1993, p.208)

Pour réaliser notre étude, nous avons fait recours aux méthodes ci-après :

a) La méthode comparative : cette méthode tend à systématiser une tendance naturelle de l'esprit humain : le mouvement spontané qui nous pousse à comparer ce que nous voyons. Elle laisse la latitude et la liberté à comparer les aspects sociaux des sociétés choisies comme centre d'investigation. C'est dans ce cadre que cette méthode nous a permis de comparer les différentes distances reliant les points de ventes (dépôts - relais) qui ont été effectifs au cours des années 2005 et 2006.

b) La méthode descriptive : elle nous a permis de décrire les réalités découvertes, mieux les analyser et de les interpréter pour afin formuler des recommandations concrètes.

C) La méthode structuro-fonctionnelle : celle-ci nous a permis de comprendre la structure et le fonctionnement de la Bralima/BUKAVU pour la période retenue à cette fin.

7. Techniques

Selon Rohmer R. (1983, p.990), le mot technique signifie l'ensemble des procédés d'un art, d'un métier, d'une industrie. C'est un ensemble d'outils de travail pour appuyer les méthodes.

En ce qui nous concerne, nous avons fait recours aux techniques ci-dessous :

a) La technique documentaire : qui est une principale technique de la recherche scientifique. Elle consiste à consulter les documents pour obtenir les informations nécessaires à la recherche. C'est grâce à cette technique que nous avons pu exploiter les bibliothèques de la place et certains documents de la BRALIMA en vue de réunir les données relatives à ce sujet.

b) L'interview : c'est une forme de communication établie entre deux personnes qui se connaissent ou pas, ayant pour but de recueillir des informations concernant un objet précis (M.Grawitz, cité par F. Dépelteau, 2000, p.315).

Cette technique nous a aidé à trouver certaines données auprès des agents du département commercial et cela d'une façon directe.

0.7. Etat de la question.

Pour poser le problème à examiner, il nous a semblé utile de le situer par rapport aux études antérieures ayant trait à notre recherche. Cela nous a poussé à fouiller les documents se trouvant dans les différentes bibliothèques de la place.

Les travaux de recherche qui nous ont intéressé sont ceux que nous présentons ci-dessous :

KILAULI BITUBI Jean, L2 SCA, ISP, (2003-2004), dont le titre de mémoire est : « Impact des actions marketing sur la vente des produits BRALIMA dans une période de basse conjoncture » il a été question dans ce travail de faire connaître au monde scientifique l'accélération de la vente durant la période de la basse conjoncture par rapport à la haute conjoncture.

MURHULA BISIMWA Fidèro, G3IGE, ISP, (2003-2004) dans :  « Essai d'automatisation du circuit dans une entreprise de production : cas de la BRALIMA/Bukavu » il a été question de mettre sur pied un logiciel propre permettant de connaître le mouvement de vente de la BRALIMA/ Bukavu.

BARWANI BWASHI Jean, G3SCA, ISP, (2005-2006), dans :  « Gestion des activités de formation du personnel et leur rendement dans le milieu Professionnel : cas de la BRALIMA/Bukavu », il a été question dans ce travail de connaître quels intérêts les employés et les salariés ont pour leur formation et que, c'est que les entreprises font pour leurs résultats réalisés lors de celle-ci.

KANKOLONGO MBOWA Justine, G3SCA, ISP, (2004-2005), a traité de la «  Pratique de l'audit et l'application des mesures de contrôle interne, atouts majeurs du succès de la BRALIMA/BUKAVU », Il a été question dans ce travail de savoir si le contrôle interne de la BRALIMA est efficace pour lui permettre d'être performante.

LWESSO WEMA Patron, G3SCA, ISP, (2005-2006), a traité de « la comptabilité analytique d'exploitation de la fixation du prix de vente au sein d'une entreprise industrielle au Congo : cas de la BRALIMA/BUKAVU »

Il a été question dans ce travail de connaître comment la CAE intervient dans la fixation de prix de vente et contribue à la variation de ce même prix par la BRALIMA.

NZIGIRE RUCHOGEZA, UCB, (1996-1997), dont le titre de mémoire est «  Modèle de gestion de production des bières et boissons gazeuses à la BRALIMA SARL siège de BUKAVU », il a été question dans ce travail de voir si le modèle de gestion de production de bières et boissons gazeuses avait une influence sur le bénéfice.

KINDU MUNDEKE, UCB, L2GEFIN, (1998-1999) dans « Analyse systématique de la possibilité de proposer une technique d'ordonnancement des travaux de la BRALIMA Bukavu » Il a été question dans ce travail de déterminer le modèle d'ordonnancement qui offre les possibilités respectives de réduction de temps d'exécution de taches.

De son coté, Dorah MBAHE MBAMBU, UCB, L2 GEFIN, (1998-199), a traité de «  la rationalisation du circuit de distribution interne à la Bralima Bukavu ». Il a été question, pour lui, d'analyser l'efficacité du circuit de distribution de la BRALIMA et de formuler des mesures correctives à adopter compte tenu de l'environnement conjoncturel étant donné que

les recettes réalisées par certains dépôts n'arrivent plus à couvrir tous les frais de leurs exploitations.

Pour BONANE MUSHAWA, UCB, L2GEFIN,(2001-2002), dans «  la corrélation entre la productivité du travail et les facteurs motivationnels : cas de la BRALIMA Bukavu » Il s'est agi dans ce travail de déterminer s'il existait une corrélation entre la production et la masse salariale.

MBUMBA KALONGO, UEA, TFC, (2001-2002), le sujet était «  la contribution au volume de vente d'un produit à faible rotation par la recherche de nouvelles pistes commerciales : cas de Fanta tropical de 1996 à 2000 à la BRALIMA /Bukavu ». Il a été question dans ce travail de cibler les causes d'une faible rotation de ce produit « Fanta tropical à la BRALIMA.

Dans le mémoire de même auteur, UEA, (2003-2004), dont le titre de mémoire est : « Analyse de la structure financière d'une entreprise : cas de la BRALIMA Congo de 2000 à 2003 » il a été question dans ce travail de faire connaître aux dirigeants de la BRALIMA et le monde scientifique la santé financière de cette firme.

Il sied de faire remarquer qu'aucun de ces travaux mentionnés ci-haut, n'a traité de la programmation des charrois automobiles pour la distribution de la boisson.

Notre contribution dans ce domaine se situe au niveau de la programmation des charrois automobile pour la distribution de la Boisson : cas de la BRALIMA/ Bukavu de 2005 à 2006.

Il sera donc question d'étudier la politique relative à l'affectation des charrois automobiles, les distances parcourues par ces charrois pour atteindre les dépôts -relais et de mettre sur pied une politique optimale capable de minimiser les coûts alloués par ce service en usant de la programmation dynamique.

0.8. Difficultés rencontrées.

Au cours de nos recherches et pendant la rédaction du présent travail, nous nous sommes heurtés à des difficultés telles que l'absence de certaines données statiques, la réticence de certains agents de l'entreprise à pouvoir fournir de données dont nous avions besoins et autres difficultés de diverses natures.

0.9. SUBDIVISION DU TRAVAIL

Outre l'introduction et la conclusion, nous avons subdivisé cette étude en trois chapitres :

- Le premier chapitre comprend les éclaircissements notionnels et l'organisation structurelle de la BRALIMA/Bukavu ;

- Le deuxième chapitre présente la politique générale de la distribution de la boisson par la BRALIMA/ Bukavu ; et

- Le troisième chapitre, décrit la programmation dynamique pour la minimisation des coûts alloués pour la distribution de la boisson par les charrois automobiles de la BRALIMA/Bukavu

CHAPITRE 1

CONSIDERATIONS THEORIQUES

Ce chapitre est constitué des considérations d'ordre théorique qui comprend les points suivants :

· Définition des concepts ;

· Présentation de la BRALIMA/Bukavu.

1 .1. Définition des concepts

Il s'agit de définir les mots clés utilisés pour permettre aux lecteurs de bien comprendre le contenu sémantique de nos propos.

1.1.1 La programmation

D'après le petit Robert (2001, p122), la programmation est l'établissement, l'organisation des programmes. Elle est l'élaboration et la codification de la suite d'opérations formant un programme.

Par exemple, la programmation d'une machine.

Le même auteur ajoute en disant qu'elle est une action de prévoir et d'organiser, et c'est ici le noeud de l'utilisation de ce terme par les entreprises.

Quant au programme, le petit Robert (2001, p122), le définit comme un écrit annonçant et décrivant les diverses parties d'une cérémonie d'un spectacle .C'est l'annonce des matières d'un cours, du sujet d'un concours etc.

Il s'ajoute en outre, que c'est la suite d'actions que l'on se propose d'accomplir pour arriver à un résultat. C'est l'ensemble ordonné d'opérations effectuées par un système automatique. L'ensemble des instructions, rédigées dans un langage de programmation, permettant à un système informatique d'exécuter une tâche donnée. Par exemple : logiciel, progiciel, c'est-à-dire le programme enregistré dans le mémoire d'un ordinateur, programme stocké sur une mémoire de masse, sur une disquette, etc.

Un programme décrit une procédure de calcul qui, à partir d'information en entrée (données), produit des informations en sortie (résultat). Enfin, c'est l'ensemble des tâches que nous devons réaliser. Parmi les programmations, nous pouvons retenir :

1.1.2  La programmation linéaire

Le dictionnaire d'analyse économique de BERNARD G., (2001, p201) définit la programmation linéaire comme étant la méthode de recherche des extremums d'une fonction linéaire dont les variables sont soumises à des contraintes qui prennent la forme d'inégalité linéaire. Cette méthode peut être appliquée à des nombreux problèmes.

Par exemple la gestion de stocks ou le transport des marchandises entre divers points et plus généralement à la planification. Elle s'appuie sur le théorème de la dualité qui permet d'associer à chaque contrainte un nombre (positif) qui peut être interprété comme un prix ou comme un coût.

J. M'VIBUDULU KALUYIT. (2007, p72), écrit que programmation linéaire a pour but de déterminer la valeur à affecter à un certain nombre de variables :

- en vue d'optimiser (minimiser ou maximiser) une fonction linéaire de ces variables ;

- en vue de tenir compte de certaines contraintes (équation ou inéquation linéaire) aux quelles sont soumises les valeurs de ces variables.

Ainsi du point de vue mathématique, on appelle problème linéaire tout problème dans lequel il s'agit d'optimiser selon le cas la fonction de plusieurs variables, celles-ci devant satisfaire à un ensemble de contraintes linéaires, par exemple y= ax + b.

Cette fonction est linéaire avec x comme variable indépendante et y variable que nous voulons étudier qui est la production de la bière à la BRALIMA, en tenant compte de la variable x qui est la quantité des matières premières utilisées, a étant une charge fixe et b étant une valeur résiduelle, c'est-à-dire difficile à maîtriser car elle tient compte des circonstances dans lesquelles la gestion des matières premières et l'activité de production se déroulent ; ainsi si a= 3 et b=25, f(x) devient y=3x+25.

Pour K. MAGENDO (ISP, 2006), la Programmation linéaire est définie comme étant d un modèle d'optimalisation d'une solution qui permet de guider le décideur dans le sens d'allouer des ressources limitées par des contraintes, à une série d'activités, en fonction de l'objectif que l'on s'est fixer.

Dans toute étude linéaire optimale, l'analyse doit arriver à transformer un problème économique sous la forme ci- haut donnée.

· Formulation mathématique d'une fonction économique

La fonction économique associe linéairement les quantités des facteurs, les unités et les profils unitaires correspondants (les couts unitaires dans le cas de minimisation).

Max (C₁X₁+A₂X₂+............+.A_nX_n)

Min (C₁X₁₊A₂X₂+.................+A_nX_n)

1.1.2.1 La programmation duale

Le problème consiste à déterminer le prix minimum à fixer pour qu'afin que :

- la restriction soit avantageuse pour le pays dans la mise en valeur directe des terres.

- Le coût global de location soit minimal pour la société.

Le programme dual est définit toujours :

1°) par des contraintes :

- dont les coefficients correspondent aux colonnes de A ;

- dont les seconds membres sont les élément de C ;

- dont le sens est opposé à celle du primal ;

2°) par une fonction économique :

-dont les coefficients sont les éléments de B ;

-à maximiser si celle du primal est à minimiser et inversement.

Par exemple : soient A=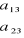

B = C =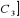

PROGRAMMATION PRIMALE

a₁₁x₁ + a₁₂x₂ + a₁₃x₃ = b₁

a₂₁x₁ + a₂₂x₂ + a₂₃x₃ = b₂

x_1, x_2, x₃ = 0

Zmax: C₁x₁ + C₂x₂ + C₃x₃

PROGRAMMATION DUALE

a₁₁u₁ + a₂₁u₂ = C₁

a₁₂u₁ + a₂₂u₂ = C₂

a₁₃u₁ + a₂₃u₂ = C₃

Zmax: (b₁u₁ + b₂u₂)

Sous forme matricielle, les deux programmes peuvent s'écrire comme suit :

PRIMAL DUAL

- X étant un vecteur colonne, c'est un vecteur ligne U₁, U₂

- Chercher x tel que : C_x soit : A_x = B

- Chercher U tel que U_B soit : minimum sous les contraintes U_A = C

La méthode de résolution du primal est aussi valable pour le Dual, si l'un des deux programmes admet une solution optimale,l'autre en admet également une, le maximum de l'un est égal au minimum de l'autre.

1.1.2.2 La programmation linéaire par méthode simplexe (méthode de DANTZIG)

La méthode du simplexe prend pour point de départ une solution de base pour laquelle la fonction économique a pour valeur zéro ;

A chaque étape on cherche à améliorer la solution de départ de façon créative afin d'atteindre un meilleur membre de la contrainte.

(J. M'VIBUDULU KALUYIT J., 2007, p73).

La programmation par méthode simplexe est une solution permettant d'aboutir à cet objectif et pour y arriver il faut d'abord transformer le problème économique posé sous une forme linéaire. En programmation, par méthode simplexe, deux méthodes s'imposent à savoir la méthode graphique et la méthode algorithmique simplexe.

1) La méthode graphique

Partons d'un exemple pour expliquer cette méthode graphique. Soient XP matières première et XF les produits finis fabriqués à la BRALIMA/BUKAVU, dont X_p matières premières et X_F produits finis.

Max Z = 3 x p + 5 x F

S/C X_P = 4

2X_F = 12

3X_P + 2X_F = 18

X_P, X_F = 0

Pour résoudre notre problème nous devons d'abord déterminer les coordonnées du graphique. Ainsi nous pouvons le procéder de la manière suivante :

a) Les contraintes

1) X_P = 4, X_P = 4

2) 2X_P = 12, 2X_P = 12, X_P = 6

3) 3X_P + 2X_F = 18

3X_P + 2X_F = 18

Pour X_P = 0, 3.O+2X_F

2X_F = 18

X_F = 18/2 =9

X_F = 0,3Xp+2.0=18

3Xp=18

Xp=18/3=6

b) la représentation graphique

b) Interprétation du graphique

Zmax=3Xp + 5XF

-Pour Xp=4 et Xf=0 , on a :

Zmax= 3.4 +5.0=12

- Pour Xp=0 et Xf=6 , on a :

Zmax=3.0+ 5.6= 30

- Pour Xp=4 et Xf=3, on a :

Zmax=3.4+5.3=27

- Pour Xp=2 et Xf=6,on a :

Zmax=3.2+5.6=36

On observe que l'entreprise pourra maximiser coût de production dans la contrainte 3Xp+2Xf =18

2) L'argorithme simplexe

L'algorithme complexe est une suite d'observation bien définie qui amène progressivement à la solution optimale du problème en respectant certains principes mathématiques.

1.1.2.3 Les contraintes linéaires

Elles représentent la manière dont les facteurs peuvent être constitués pour utiliser les ressources et générer un résultat au travers de la fonction économique.

Elles s'écrivent comme suit :

a₁x₁ + a₂x₂ + ....................... + a₁x₁ = b₁

a₁x₁ + a₂x₂ + ....................... + a₁x₁ = b₂

.

.

.

A_n1x₁ + a_n2x₂ + ....................... + a_n1x_n = b_n

Notons que les contraintes sont souvent représentées par les inégalités.

1.1.3 La programmation dynamique

J. M'VIBUDULU KALUYIT, (2OO6-2007) définit la programmation dynamique comme étant une procédure de résolution des problèmes qui se posent dans différents domaines de gestion telle que la gestion de stock, la gestion de production, la gestion des équipements et de remplacement des matériels et les décisions commerciales ; elle est encore plus utile dans les problèmes de décisions sécuritaires.

La différence entre la programmation dynamique et la programmation statique est que dans le modèle statique, on considère le problème posé comme un tout isolé tandis que dans le modèle dynamique on tient compte de répercussions dans le temps de décisions prises.

Par exemple, dans la gestion de stock, le stock en fin de période pour une période t se répercute à la période t+1 et devient stock initial de début de la période.

Quant à la programmation linéaire, elle concerne la maximisation et la minimisation d'un système qu'on évalue en plusieurs périodes consécutives et distinctes.

Le Petit Larousse illustré (1983, 101) définit la programmation d'une part et la dynamique d'autre part.

Selon lui, la programmation est l'établissement d'un programme alors que la dynamique consiste à faire la preuve d'efficacité d'une entreprise.

1.1.4. La distribution

E. Cohen, (2001, p.112) définit la distribution comme étant un ensemble d'activités qui permettent d'assurer la circulation physique de marchandises entre l'entreprise qui les produits et leurs utilisateurs finaux.

Le Petit Larousse illustré (1983,57), la définit comme étant un ensemble d'activités et opérations mettant les produits à la disposition des consommateurs (final ou intermédiaire).

Les distributeurs jouent un rôle d'intermédiaire et d'ajustement entre les offreurs et les demandeurs du commerce de gros, par la constitution de stocks qui régularise le flux en garantissant des débouchés importants aux producteurs et des approvisionnements réguliers aux détaillants. Ceux-ci, tout en conseillant la clientèle, orientent la production vers les goûts des consommateurs. 

Dans cette mesure, la distribution joue un rôle économique qui justifie une prise de marge.

Mais la concurrence doit jouer entre les distributeurs et les différentes formes de commerce (commerce isolé, commerce associé ou groupement d'achat, grand commerce intégré tel que les grands magasins hyper et supermarchés, etc.

Cela est nécessaire pour que les gains de productivité à la production soient répercutés dans le prix de vente  au consommateur final et ne soient pas absorbés par la distribution.

1.1.5. La production

Selon H.QUINTTON et VITRAY (1986, p.480), la production est une activité économique sociale organisée, consistant à créer des biens et /ou des services s'échangeant habituellement sur le marché et/ou obtenus à partir des facteurs de production.

Ces auteurs ajoutent qu'on peut appeler « produit » tout ce qui peut être offert sur le marché de façon à y être vendu ou consommé.

D'une manière générale la production générale la production est la transformation des matières premières (in put) aux produit finis (out put) .

1.1.6. Le charroi

Le petit Robert (2001, p72) le définit comme étant le transport par charrette, par chariot (voiture à quatre roues pour le transport de fardeau).

1.1.7. La boisson

Le Petit Robert (2001,45) la définit comme étant un liquide qui se boit, contenant de l'alcool. (Bière, liqueur, vin, sucré,...)

1.1.8. Le coût

Le plan comptable générale français de 1979 définit le coût comme étant l'ensemble des charges incorporables correspondant soit à un calcul relatif à une fonction, soit à un objet, une prestation de services, un groupe d'objet à un stade autre que le stade final.

Rapin et KINZONZI, tous du conseil permanent de la comptabilité en RDC ont défini le coût comme étant un total de dépenses rapportées à un moment donné, soit à une fonction de l'entreprise, soit à un ou des objets pour de prestations des services pris à un stade autre que le stade final de la livraison au client.

Selon les besoins de chaque entreprise on pourrait calculer les calculer les coût ci-après :

Le coût élémentaire

Le dictionnaire d'analyse économique le définit comme étant une fonction qui associée à toute quantité offerte par une entreprise, les coûts minimaux en outputs nécessaire pour produire cette quantité. Nous distinguons :

- Le coût marginal : dérivé de la fonction de coût si l'on note celle-ci C (q), le coût marginal pour la quantité produite q est donc égal à C'(q), expression qui donne approximativement l'augmentation de coût qu'entraîne la production d'une unité supplémentaire de bien lorsque la production est q.

- Le coût moyen : c'est le coût unitaire de production qui est obtenu en divisant le coût total tel qu'il est donné par la fonction de coût par la quantité.

- Le coût de transaction : coûts poqués par toutes les procédures ou opération qui rendent possibles des échanges mutuellement avantageux, entre deux ou plusieurs individus.

- Les fixes : coût d'une entreprise qui ne dépendent pas de la quantité qu'elle produit. Si celle-ci est faible, alors le coût unitaire de production est élevé, le bien n'est produit que si son prix est suffisamment élevé.

D'une manière générale, le coût de production est la somme des dépenses que chaque entreprise supporte pour se procurer des ressources facteurs, pour se procurer le processus ou facteurs et mettre en oeuvre le processus productif.

L'analyse marginaliste de la firme suppose que le seul critère de décision de l'entrepreneur rationnel est la recherche du profit maximum immédiat.

1.1.9. Optimisation

En économie, tout comme en gestion ce terme est utilisé conformément à son exception commune : « Principe, norme qui permet de distinguer le vrai du faux, de porter un jugement sur quelqu'un ou quelque chose » (l'univers documentaire axis, t.1, p.734, Hachette, 1993)

Lorsqu'il est question de critère d'optimisation ou d'analyse multicritère comme c'est le cas en recherche opérationnelle, plus généralement, on aide à la décision, ce critère acquiert un sens plus restreint. Le jugement qu'il s'agit de porter est essentiellement comparatif.

D'une manière générale optimiser une fonction linéaire c'est minimiser ou maximiser cette fonction linéaire à ces variables.

1.1.1O Modèle de transport d'une programmation linéaire

Le modèle de transport n'est rien de moins qu'une illusion adéquate d'un groupe de problème dont le mobile principal est de trouver le coût minimum de transport pour acheminer un certain nombre d'éléments à partir de (m) ressources avec leurs disponibilités (offres) vers (n) destinataires en tenant compte de leurs besoins (M'VIBUDULU KALUYIT J. p.124)

Par différence avec la programmation dynamique, celle-ci sert à résoudre les problèmes aux variables non stochastiques (non affecté d'une probabilité quelconque) c'est-à-dire que la nature est parfaitement connue et l'on se trouve dans une situation de certitude tandis que le modèle de transport sert à résoudre les problèmes aux variables stochastiques (affectés d'une probabilité quelconque) c'est-à-dire que la nature n'est connue et l'on se trouve dans une situation d'incertitude.

1.1.11. Les dépôts relais

Il s'agit des coins de vente de la Bralima/BUKAVU dissimulés à travers toute la ville et placé sous la responsabilité d'un meilleur client sélectionné à partir de son pouvoir d'achat.

Ces dépôts relais vendent au prix de la Bralima.

Avec, cette stratégie de vente, on retrouve que même les petits consommateurs sont obligés d'acheter au prix de la Bralima. Qu'il s'agisse d'une ou deux caisses achetées au dépôt relais, cette vente est enregistrée par la Bralima/BUKAVU à partir de son, coin de vente.

Nous constatons que ce système de maximisation de la clientèle à gagner du terrain et place la commercialisation des produits Bralima à un rang élevé. Dès lors, les responsables de ces dépôts relais bénéficient lors de la mise en jour d'un nouveau produit ou lors de la vente promotionnelle les crédits emballages uniquement.

Les responsables de ces dépôts relais sont rémunérés en fonction de la quantité des marchandises écoulées et mensuellement. Cette rémunération est selon nos enquêtes de 6% du total des marchandises écoulées, soit 6% du chiffre d'affaire réalisé.

1.2. Présentation de la Bralima / Bukavu

1.2.1 Situation géographique

La Bralima /Bukavu anciennement située dans la commune de Bagira est située actuellement dans la commune urbano-rurale de KASHA, à 4 Km de la ville de Bukavu, en face de la rivière  WESHA.

1.2.2. Historique

Etant une société par action à responsabilité limitée (SPRL) .Elle est la première firme industrielle du type Brassicole installée au CONGO-BELGE et également l'une de 151 Brasseries du groupe HEINEKEN HOLLANDE à travers 53 pays du monde.

Elle a vu le jours à Léopold Ville, actuellement Kinshasa, le 23/10/1923 où elle installa son siège social au n°912 sur l'avenu de Flambeau.

Jusqu'aux années 1920, les boissons alcoolisées étaient les seules connues et consommées en Afrique centrale et particulièrement au Congo Belge.

Il y a eu quelques hésitations dans l'établissement du siège central de la BRALIMA au Congo. En effet, son choix impliquait une bonne situation géographique par rapport à l'ensemble du pays, alors Léopold Ville fut finalement choisi.

Au départ, sous la direction de M. DUMOULIN, la société regroupait Cinq expatriés (deux Belges, un Français, un Suisse, et un Russe) et une trentaine d'employés nationaux. Le 27/12/1926, la première bière fut produite mais sa libre circulation va susciter beaucoup de problèmes :

- le marché de la bière présentait un produit non pasteurisé : la Bière ne pouvait être commercialisée qu'à l'intérieur de Léopoldville, ce qui réduisait le nombre des consommateurs ;

- ce marché était dominé par les fournisseurs Allemands et Hollandais qui importaient la bière en quantité et en qualité supérieur à celle de la PRIMUS, malgré son prix bas par rapport aux marques importées ;

- la Primus, dont on doutait encore de la qualité ne pouvait s'imposer sur le marché parce qu'inconnue des consommateurs.

Avec l'arrivée de Monsieur VISER,deuxième directeur après DUMOULIN, la brasserie quitte lentement sa position initiale. Durant ses 23ans de règne (1933 à 1956), il améliore la qualité de la bière, après avoir renouvelé l'équipement. Il augmenta aussi les salaires des ouvriers.

Le nouvel équipement a permis l'augmentation de la production, ainsi la qualité produite de la bière qui n'était que de trente cinq mille (35000) hectolitres par mois en 1936 est passé à cent et huit milles (1O8000) hectolitres par mois en 1945,soit le triple .

Après la deuxième guerre mondiale, la brasserie connaîtra une croissance sans précèdent dans la production de la bière. Ainsi, de nouveaux sièges d'exploitation s'ouvriront à travers le pays :

· A BUKAVU, en 1951

· A KISANGANI, en 1957

· A BOMA, en 1958

· A MBANDAKA, en 1972

1.2.3. Champ d'action

1°) Sur le plan national

La Bralima/BUKAVU oeuvre sur toute l'étendue de la province du sud Kivu et la province du nord Kivu. Elle est composée de deux district : le district de BUKAVU, le dépôt d'UVIRA, de KALEMIE, de GOMA, de BUTEMBO, et de BUNIA.

2°) Sur le plan international

La Bralima /BUKAVU n'expedie pas ses produits à l'étranger et reste locale

1.2.4 Produits fabriqués

Il s'agit de deux grandes subdivisions de produits fabriqués par la Bralima/BUKAVU aux quelles nous pouvons ajouter la fabrication des glaces. Il s'agit de :

1°) Les boissons alcoolisées : dans cette catégorie, on retrouve essentiellement la PRIMUS généralement appelé PRIMUS BUKAVU, MEETZING BUKAVU, TURBO KING.

2°) Les boissons sucrées ( BG) : cette catégorie est la plus diversifiée et se compose des produits suivantes : Coca-cola, Fanta orange, Soda, eau gazeuse.

1.2.5. Objet de la Bralima Bukavu

La Bralima Bukavu a pour objet la production et la commercialisation des bières et boissons gazeuses. Son action vise à relever le niveau de vente de ses produits en vue de la réhabilitation de sa part du marché. Pour y arriver, elle a choisi la qualité comme son cheval de batail.

1.2.6. Organisation structurelle et Fonctionnelle

Commentaire sur l'organigramme

La succursale BRALIMA /BUKAVU (SPRL) « société des personne à responsabilité limitée » est composée de 6 principaux département assistés par la direction centrale. Celle-ci a 3 fonctions principales comme toute entreprise industrielle. Il s'agit de la fonction approvisionnement (achat), fonction production et la fonction distribution.

· La Direction Centrale : est dirigée par un directeur du siège actuellement une directrice ainsi qu'un secrétaire de la direction. Elle doit superviser toutes les activités de l'entreprise ainsi que les rapports avec la société mère de Kinshasa et doit veiller à la réalisation des objectifs que l'entreprise s'est assignée.

· Département médical : comme dans toute entreprise bien organisée, le département médical a pour rôle de soigner les agents de l'entreprise, le département médical a pour rôle de soigner les agents de l'entreprise en question ainsi que les membres de leurs familles respectives.

· Département des ressources humaines : c'est vrai que la réalisation des objectifs d'une entreprise doit dépendre de certains facteurs importants, et il est donc inconcevable de s'en passer outre la nature, le capital, il y a donc du travail assuré par les humains.

· Département de Finances : son rôle est de contrôler les caisses, les relations avec les bailleurs, les prévisions de trésorerie, la tenue de la comptabilité générale, les déclarations des taxes et impôts et comporte une cédule chargée de calculer et d'effectuer la paie des agents et gère aussi la caisse de l'entreprise.

· Département de technique : il s'occupe de la gestion des machines et de tous les détails techniques relatifs à la production. Il doit aussi assumer l'entretien et les maintenances de l'outillage de la production. Il organise en son sein un ensemble de services techniques.

· Département de la production : il s'occupe de la transformation des matières précieuses en produits finis, il s'agit donc de la production de la bière, des boissons sucrées et doit veiller aussi à l'embouteillage de ces boissons.

· Département commercial : comme il est inconcevable de produire sans pour autant penser à la commercialisation ; le département commercial assure la distribution de différents produits fabriqués ainsi que les rapports entre les différents dépôts et points de vente, les secteurs de vente ainsi que le service client. Il gère donc en définitive les relations entre entreprise et la clientèle.

Nous pouvons toutefois noter qu'outre ces départements, la BRALIMA dispose de différents services attachés à ces derniers. C'est entre autre :

- le service informatique : chargé du traitement automatique et rationnel des données.

- Le service du contrôle qualité : pour le contrôle de la qualité des produits à lancer au marché.

1.2.7. Conclusion partielle

Par ce premier chapitre, nous avions à décortiquer sur les quelques de noter sujet, en donnant des définitions sur quelques concepts et en différencient, les programmations existantes les unes par rapport à d'autres.

En plus, nous avions essayé de présenter d'une manière générale les Bralima Bukavu en la situant géographiquement, en donnant son historique, son champ d'action, son objet, ses produits fabriqués et son organisation structurelle.

CHAPITRE II

GENERALITES ET POLITIQUES DE LA DISTRIBUTION DE LA BRALIMA/BUKAVU

2.1. Généralités sur la Distribution

2.1.1. Définition de la distribution

Par Elie Cohen dans son dictionnaire de gestion p. 112, la distribution constitue un ensemble d'activités qui permettent d'assurer la circulation physique des marchandises entre l'entreprise qui les produits et leur utilisateur final.

Elle englobe des tâches relatives au transport à l'entreposage, au conditionnement, à la présentation, à la vente des produits et parfois au financement de sa production.

Mais elle constitue également un métier né d'une accentuation de la division du travail au sein des filières de production et de commercialisation ; on est alors conduit à analyser les structures et les canaux qui permettent la circulation des marchandises grâce à l'intervention d'utilités de professionnels spécialisés.

2.1.2. Les fonctions de la distribution

Dans les économies fondées sur la division du travail et sur une large ouverture spatiale des échanges, une médiation s'impose entre des entreprises assurant une production concentrée en terme économique et utilisateurs largement dispensés, aussi bien sur le territoire national qu'à l'étranger. C'est précisément cette médiation qui est assurée par la distribution.

L'activité de la distribution doit être distinguée du commerce, même si de nombreux commerçants assument essentiellement un rôle de distributeur. Notons qu'ici celle la firme BRALIMA/Bukavu qui assume le rôle de distributeur.

En effet, l'activité commerciale se définit en général par l'achat de marchandises destinées à être revendues soit en général par état, soit après transformation.^1(*)

Elle présente un caractère générique dans une économie d'échange et prend place à tous les stades des filières de production et de commercialisation. Ainsi, une entreprise industrielle comme la BRALIMA/Bukavu se livre à des opérations commerciales lorsqu'elle acquiert des approvisionnements nécessaire pour sa consommation intermédiaire, des équipements nécessaires par sa production, ou encore lorsqu'elle cède sa production à un client.

Dans notre cas, la BRALIMA/Bukavu étant une entreprise industrielle et commerciale, elle acquiert des approvisionnements nécessaires pour sa production, parce qu'elle est située parmi les entreprises poumon de la province du Sud Kivu en particulier et de la RDC en général, donc c'est une entreprise acceptable pour le plan structurel.

Par rapport au commerce, l'activité de distribution présente deux caractéristiques distinctives :

D'une part elle intervient qu'au terme de processus de production et met en cause le passage des marchandises de la sphère. De l'utilisation finale ; elle concerne donc par les opérations commerciales qui se déroulent entre entreprise, aux différents stades de la transformation pour des produits complexe.

D'autre part, les opérations ne correspondent pas necésserement à des transactions successives entre les vendeurs et les acheteurs, alors que l'activité commerciale se définit justement par la réalisation d'une suite d'opération d'activité. Ainsi, des professionnels de la distribution tels que les transporteurs prennent matériellement en charge des produits pour en assurer le déplacement ; mais ils ne se réalisent pas une opération commerciale puisqu'ils n'achètent pour le compte d'autrui.

A la limite, une chaîne de distribution intégrée dans laquelle la même entreprise contrôle la production et la commercialisation peut faire circuler un produit entre le site de production et le lieu de vente sans qu'aucune transaction n'intervienne, jusqu'à l'acquisition par l'utilisateur final.

La Bralima Bukavu a des professionnels de la distribution tels que nombreux transporteurs prennent eux même en charge des produits pour en assurer le déplacement moyennant une rémunération selon qu'il ont vendues. Par exemple pour le transport de la bière et le BG nous avons rencontré que 17 transporteurs prennent en charge des produits et ils se fixent les modalités de payement à la fin du mois. (voir le 17^e annexe).

Xxxxxxxxxxxx

2.1.3. Les canaux de distribution

Les quatre canaux classiques du circuit de distribution : production, grossistes, détaillants et consommateur sont analysés quant à leurs caractéristiques proposes, leur historique, leur valeur (centres d'appréciation) et leurs évolutions et perspectives

La Bralima produit de la bière et le BG qui à son tour les met à la disposition d grossistes par les dépôts relais et les dépôts relais à leur tour le vend aux détaillants quant à eux de les mettre à la disposition des consommateurs considérés comme par exemple les hôtels, Nganda, restaurant, etc.

Chacun de ces canaux a subi au cours de l'histoire des changements professionnels sur l'effet de facteurs contradictoires les uns renforçant parfois leur position, les autres l'atténuant au point de les faire parfois disparaître. A la Bralima/Bukavu, ces facteurs ont contribué à imposer à ces canaux une évolution marquante sur l'influence des nouvelles techniques de distribution celles de mettre en place les dépôts relais.

« Le canal de distribution est l'ensemble des intermédiaires qui définis la production jusqu'à la consommation ont pour rôle de base de transformer les ressources hétérogènes trouvées dans la matière en un ensemble des biens désirables pour l'home » (Kotler).

2.1.4. Canaux de distribution

Dans le but de faire parvenir les bières et les boissons gazeuses à ses clients, la Bralima/Bukavu dispose de plusieurs moyens de distribution :

- le personnel affecté à la distribution

- les points de vente (dépôts relais)

- les véhicules affectés à la distribution.

La Bralima/Bukavu dispose de 5 camions à son propre compte et 17 autres camions pour les transporteurs privés mais se fixe les modalités de paiement (en fonction de consommation de chaque véhicule) suivant l'écoulement des produits retirés à la source.

2.2. La politique de la distribution à la BRALIMA/BUKAVU

2.2.1. Notion générale sur la politique de la distribution

Du point de vue de l'entreprise productrice, la distribution des produits soulève quatre ensembles de problèmes d'ampleur inégale^2(*) : une première série de décision d'importance majeure, concerne le choix des canaux de distribution par lesquels la production sera écoulée.

Dans certains cas, le choix est fortement contraint, soit parce qu'un seul circuit de distribution est envisageable à moyen terme pour un type de produit ou pour une zone géographique, soit parce que l'entreprise concernée n'a pas vraiment le choix de ses distributeurs, compte tenu de sa dimension restreinte ou de son faible pouvoir de négociation. Mais une certaine latitude de choix demeure souvent ouverte, au moins à propos du choix des partenaires, de la gamme offerte, de la cible géographique visée, si non à propos du choix des circuits.

Un deuxième ensemble de décision concerne la gestion de relations stratégiques entre l'entreprise et les distributeurs. Ajoutons que, la maîtrise des rapports de force avec l'aval constitue un enjeu qui échappe à de nombreux producteurs, même lorsqu'il s'agit d'entreprises moyennes ou grandes.

De ce fait, l'acceptation d'une relation d'intégration ou de quasi-intégration par la distribution traduit une solution de survie pour des entités qui préfèrent sacrifier une part de leur autonomie. Cette situation est par exemple fréquente dans les branches encore faiblement concentrées de l'industrie alimentaire telles que les activités de charcuterie assure elle-même l'acheminement grâce à une flotte de camions acquis ou loués ? Doit-elle plutôt sous-traiter. Cette tâche à un transporteur spécialisé ? De même, certaines opérations de conditionnement, d'entreposage, voire de mise en magasin peuvent être confiées à des tiers et vient donc une possibilité d'externalisation.

2.2.2.1. Circuit de distribution de la BRALIMA/Bukavu

Quelle que soit la distribution avec laquelle l'entreprise productrice aborde la gestion de ses problèmes de distribution, elle est de toute façon contrainte par l'existence de circuits de distribution, qui à la BRALIMA, sont puissamment structurés.

En effet, la BRALIMA, pour satisfaire la majorité de ses clients de la ville de Bukavu, et leur faire parvenir la boisson dans les bonnes conditions, suite aux multiplicités des clients, celle-ci ne disposant pas des véhicules assez nombreux, et par sa politique monopolaire, elle utilise les véhicules des certains partenaires des dépôts relis qui sont rémunérés en fonction de leur vente, plus il vend une grande quantité de la boisson plus il est bien rémunéré à fin du mois.

La BRALIMA Bukavu dispose de 5 véhicules facilitant certaines distributions et 17 véhicules de particuliers utilisés pour cette distribution. Son circuit de distribution est divisé en deux grands axes dont l'axe 1 est appelée la VILLE 1 et l'axe 2, LA VILLE 2, chacune d'elle regroupe des sous axes. Les différents intervenants dans les deux axes, ainsi que leur localisation sont décrits de la manière suivante :

I. AXE 1 « VILLE 1 »

I1. LA LIGNE BIERE ET BG

Les chauffeurs programmés pour cette catégorie de la boisson pour cet axe, prend la direction. BRALIMA - LABOTTE jusqu'à PANZI. Elle est subdivisée en 5 sous axes dont :

1. SOUS AXES 1, celui-ci prend les directions de La Place de l'indépendance jusqu'à l'Athénée d'Ibanda, elle regroupe 7 dépôts relais dont :

· BAMANYIRWE TEM'S 1, Place de l'independance

· MUSHAGALUSA GANY, AV. de la Poste à IBANDA

· FAIDA SIMWERAGI, AV. P.E LUMUMBA/LABOTTE

· NABINTU 4, AV.P.E LUMIMBA/LABOTTE

· JEANNE MAPENDO, AV. P.E LUMUMBA

· NOTRE SOURCE 2, AV. P.E LUMUMBA/ IBANDA

2. SOUS AXE 2

Il prend la direction VRAI SIEGE jusqu'au CAMP SAIO, ici nous comprendrons que vers cette direction on trouve les dépôts relais et lieu de vente de la BRALIMA. Ce point de vente possède 9 dépôts relais dont :

· KITAMBALA ALWATA 2, au bon prix npNyawera

· MAMAN JENIFER, Athénée d'Ibanda

· NOTRE VRAI SIEGE, AV. P.E LUMUMBA/IBANDA

· MAMAN MUDERWA, Cercle HYPPIQUE/IBANDA

· MAMAN BAGALWA, CAMP SAIO/IBANDA

· BEKAO, AV. SAIO/ IBANDA

· SUPER COPAINS, NYAWERA MARCHE/IBANDA

· ALEXIS BAGUMA CHIRIZA 2, NYAWERA MARCHE/IBANDA

3. SOUS AXE 3

Il prend la direction de NYAWERA MARCHE vers RUZIZI I^er

Il présente 6 dépôts relais, dont :

· BITIJULA, NYAWERA MARCHE

· KITAMBALA 1, AU BON PRIX NYAWERA

· BIGIRIMANA, NGANDA BELVEDERE

· KONDA BAGALWA 2, PLACE MULAMBA

· MUSHAMALIRWA, AV. CIMETIERE/NGUBA

· NABINTU3, AV. LUMUMBA/NGUBA

4. SOUS AXE 4

De la direction vers la 10^ème Région militaire (Avenue Maniema/IBANDA jusqu'au Camp PROFESSEURS/ISP, elle présente 5 dépôts relais dont :

· MUGENGE NTAHIZA, AV.MUHUNGU

· MUKULU ODESIRE, AV. MANIEMA/IBANDA.

· CHIRINGWI CIKIZA, avenue Kasongo Rond point ISP/Bukavu

· MASUMBUKO ZAGABE, maison Rafiki rond point ISP/Bukavu

· NTAKOBAJIRA BIREMB., en face de la direction provinciale des impôts.

5. SOUS AXE 5

De rond point Major Vangu jusqu'à Panzi, cet axe présente 7 dépôts relais à savoir :

· WASSO AKILI, Rond Point Major Vangu ; Ibanda

· MUFUNGIZI MUHAHANO à L'Essence chez Ishega

· Jean MADO, à Panzi

· NCHANGU BUHENDWA, à l'Essence chez Ishega

· CHOKOLA, chez Frangambele/MAJOR VANGU ESSENCE

· MUNGANGA CIGOHO, AV. MANIEMA/IBANDA

· MUSAFIRI JOSEPH, MAISON SOLIDARITE à PANZI/IBANDA

II. AXE 2  «  VILLE2 »

Cette Ville comprend les dépôts relais de la commune de Kadutu et la commune de BAGIRA. Il prend la direction de BEACH MUHANZI, KADUTU, et BAGIRA.

1. SOUS AXE 1

De Beach MUHANZI Jusqu'à l'Essence chez KIBONGE,11 dépôts relais constituent cet axe à savoir :

· AYAYS SAMVURA à Nyamugo Marché de Kadutu

· MAMAN TANTINE à l'avenue Industriel

· JOMBA MONGANE à l'essence chez KIBONGE

· BAMANYIRWE TEN'S, Marché Beach Muhanzi, commune de KADUTU

· BANYWESIZE MATATA, Beach MUHANZI/Commune de Kadutu

· ALAIN, Nyamugo marché/Commune de KADUTU

· TAIFA, Nyamugo marché/commune de kadutu

· BAGALWA KANDA1, Nyamugo marché/Commune de Kadutu

· LUMAMBO LWITA, Auberge trois canards/ Kadutu

· MUSHAGALUSA CARITAS, Essence/Kibonge

· Da LETHY, en face de la 3^ème République/AV. KIBOMBO

2. SOUS AXE 2

De Kadurhu à la commune de Kadutu jusqu'à CIRIRI à Kadutu, 13 dépôts relais à savoir :

· PLACE DU DIALOGUE, avenue Kasali ancienne coopérative de Kadutu

· N'SHANGALUME RUNIGA, Nyamugo stade de Kadutu

· KABI à l'ISDR/Bukavu

· MAMAN MIKA, AV. KADURHU/ Commune de KADUTU

· MAKERA à CIRIRI/ Commune de kadutu

· JANVIER MBASWA à CIRIRI/Commune de Kadutu

· BABA TANTINE, Camp TV/Commune de kadutu

· Kwinja claire à CIRIRI/Commune de kadutu

· MAMAN NVOMERWA au LYCEE WIMA/KADUTU

· MAMAN JOLIE à L'ISDR/BUKAVU

· VITAL à l'ITFM/BUKAVU

· MARTIN à L'UCB

· MAMAN ROMAIN, CAMP TV/KADUTU

8. Sous axe 3

De BUHOLO 5 Jusqu'à CIMPUNDA, il comprend 10 dépots relais.

· M' BISIMWA, Buholo 5 à Kadutu

· MAMAN NGOMO, Buholo 4 à kadutu

· INTERNET, BUHOLO 5 à kadutu

· MWABO KIZO'S à Buholo 5 à Kadutu

· BAHUGUKE CISHUSI, Pas à pas commune de Kadutu

· MUSHAGALUSA CARITAS 1, pas à pas commune de Kadutu

· PERE FLAVIEN, Chimpunda ONL à Kadutu

· Alexis BAGUMA CHIRUZA 1, Nganda ABC au pas à pas

· MAMA ANNY, pas à pas Kadutu

· MAMAN AURELIE, chimpunda à Kadutu

4. SOUS AXE 4

Il prend la direction du marché de LA BRASSERIE jusqu'à Bagira. 9 dépôts relais constituent cet axe.

· SIKUZANI M'MUNGOMBE, marché NKAFU/BAGIRA

· MAFUALA, marché NKAFU/ BAGIRA

· VERONIQUE KAJURU, marché NKAFU/BAGIRA

· M'NYAMUKONDE, AV. ROUTE DE GOMA/BAGIRA

· MAMAN SILLY, Quartier A/ BAGIRA

· NABINTU 1, aux 7 fontaine/ BAGIRA

· NOTRE SOURCE 1, Quartier B/BAGIRA

· MUHIGIRWA BISHIKWABO, marché NKAFU/BAGIRA

SOUS AXE 3

Du marché de la Brasserie jusqu'à Bagira. Il regroupe 9 dépôts relais dont :

· SIKUZANI M'MUNGOMBE, marché Nkafu/Kasha/Bagira

· MAFUALA, marché Nkafu/Kasha/Bagira

· VERONIQUE KAJURU, marché Nkafu/Kasha/Bagira

· M'NYAMUKONDE, avenue Route de Goma à Bagira

· MAMA SILLY au quartier A à Bagira

· NABINTU 1 aux 7 fontaines/Place commune de Bagira

· WENGA CLEMENTINE Quartier A à Bagira

· NOTRE SOURCE 1 Quartier B à Bagira

· MUHIGIRWA BISHIKWABO chez Maman WANNY, marché Nkafu/Kasha/Bagira.

Schématiquement, le circuit de distribution de la Ligne bière se présente comme suit :

POINT DE VENTE DEPART AXES SOUS AXE DESTINATION CHAUFFEURSAPPROPRIES/N° COMPTE

1 Place de l'ind-Athénée BULAMBO MWILIKW 111860

2 Notre vrai siege-camp MIHIGO PATIENT 1200

3 MAISON BLEUE-chez Da Lethy ANYAWA GBALANGA 1180

4 Chez NTAKOBAJIRA-Chez MAMA DEBSI MAISHA KYALONDAWA 11110

5 Rond point Major vangu-Panzi SINGA KASELE DOUGLAS

VILLE 1 6 Place de l'indép.-Marché Kadutu PALIPALI FIKIRI 11210

7 Beach MUHANZI-BUHOLO 5 KAVANGA Daniel 10990

8 KADURU-BUHOLO 5 Bahay Kapitula 11030

BRALIMA

VILLE 2 1 Pas à pas-cimpunda KULIMUSHI MUHARABU 11080

2 Beach Muhanzi-Ciriri CHIRIBAGULA Gratien 11000

3 Marché Brasserir-Baagira TASILE MAKIMA 11790

Source : Département commercial à la BRALIMA

Commentaire

Il se remarque que la Bralima Bukavu présente son circuit en le substituant en deux axes, l'axe 1 est appelé VILLE 1 tandis que l'axe 2 est appelé VILLE 2. Chaque axe est subdivisé en sous axe, l'axe 1 comporte 8 sous axes et l'axe 2, 3 sous axes. Chaque sous axe a une destination précise et son chauffeur approprié.

2.3 Le coût de distribution de la Bralima Bukavu

Ce coût de représente seulement tout ce qu'ont coûté les opération relatives à la vente.

Il est constitué exclusivement et uniquement par les charges de la fonction de distribution. La fonction de distribution concerne les charges liées à la distribution autres que les charges d'exploitation supportées par l'entreprise durant l'exercice. Il s'agit essentiellement des frais de transport vers les dépôts relais et l'ensemble des frais accessoires payés pour la distribution.

Les charges de distribution sont affectées directement aux produits distribués par la Bralima (Bières et BG) tandis que les autres sont repartis entre les différents secteurs de l'entreprise selon les critères d'imputation.

Les Frais de distribution en dollars sont de :

Mois Rubrique frais de distribution	Janv.	Fév.	Mars	Avril	mai	Juin	Juil.	Août	Sept.	Oct.	Nov	Déc.
Frais de transport	2550	3000	4000	2750	2500	2000	2115	2100	3100	3550	3100	320
Accessoires	400	350	375	477	415	380	400	400	550	300	300	320
Total	2950	3350	4375	3227	2915	2380	2515	2500	3600

Source : Bralima Bukavu comptabilité

Au courant de l'année 2005 la Bralima/Bukavu a affecté 38.502$

Tableau n° 2 : Coût de distribution 2006 en dollars

Mois Rubrique frais de distribution	Janv.	Fév.	Mars	Avril	mai	Juin	Juil .	Août	Sept.	Oct.	Nov	Déc.
Transport	3120	3150	2050	2750	4000	3000	3000	2850	2500	3550	3750	4500
Accessoires	320	270	300	370	410	300	300	250	315	375	375	450
Total	3440	3420	2350	3120	4410	3300	3300	3130	2815	3925	4125	4950

Source : Département comptabilité Bralima/Bukavu

Au courant de l'année 2006 la Bralima/Bukavu a affecté 42.285$ pour la distribution de ces produits.

Le montant de transport et accessoires est représenté par la somme des dépenses allouées par les charrois automobiles de la Bralima et des particuliers. Les particuliers sont rémunérés par mois selon les nombres de caisses de BG ou bières écoulées durant cette période.

Selon nos recherches, une caisse de BG écoulée revient à 0,14$/caisse bière 0,22$/caisse. Paiement une fois écoulé 100 caisses de BG cela revient à être rémunéré à un montant équivalent à 0,14 x 100 = 14$ et vice versa.

2.4. Conclusion partielle

Le second chapitre porte sur les généralités et la pratique de la distribution de la Bralima/Bukavu. Ce chapitre est réparti en trois points : dans son premier point partout sur les généralités nous avions défini la distribution d'une manière générale, donné les moyens et fonctions de la distribution. Dans son point partout sur la politique de la distribution à la Bralima nous avions essayé de donner une notion générale et la politique proprement dite de la distribution de la Bralima/Bukavu. Enfin, dans le 3^e point nous avions relevé les différents coûts liés à la distribution à la Bralima/Bukavu.

Sur base de quoi nous avions trouvé que le coût que doit parcourir les charrois automobiles, faute de quoi, avions décidé d'aider cette firme pour programmer d'une façon dynamique les distances parcourues par les charrois automobiles pour atteindre les dépôts relais afin de minimiser les coûts et le temps à effectuer au courant de la journée.

Pour ce faire, la nécessité d'introduire le 3^e chapitre portant sur la programmation dynamique. Nous avions évité de l'introduire par le modèle de transport parce que la Bralima utilise les véhicules des particuliers, elle ne tient pas compte des contraintes liées à cette distribution.

CHAPITRE 3

LA PROGRAMMATION DYNAMIQUE DE CHARROIS AUTOMOBILES DE LA BRALIMA/BUKAVU

3.1. Introduction sur la programmation dynamique

La programmation dynamique est une technique quantitative utilisée pour résoudre les problèmes relatifs aux décisions interdépendances et séquentielles. Comme le programmation linéaire, elle concerne la maximisation et la minimisation d'un système qu'on évalue en plusieurs périodes consécutives et distinctes.

A titre d'exemple, une direction de marketing d'une société peut chercher à connaître la décision qui lui procure une vente optimale parmi tant de décisions à prendre. Une autre organisation peut s'intéresser à trouver une décision optimale qui lui permet de minimiser le coût afin d'atteindre la production attendue.

Ce type de problèmes peut comprendre des stratégies affectées de probabilités ou encore des stratégies non affectées des probabilités. Dans le premier cas, ils seraient résolus par les méthodes d'arbre de décision (chaînes MARKOV) et dans le deuxième cas par les méthodes de la programmation dynamique dont l'objet de notre chapitre.

La programmation dynamique sert à résoudre les problèmes variables non stochastiques (non affectés d'une probabilité quelconque). Cela sous tend que la nature est parfaitement commune, et l'on se trouve dans une situation de certitude. L'approche de la programmation dynamique s'effectue par la décomposition en sous-problème, du problème concerné, et l'analyse commence par traiter d'abord les sous-problèmes qui sont situés chronologiquement les derniers en terminant par les sous-problèmes situés en première position. L'opération s'effectue d'une façon recursive ou encore selon les principes LIFO (Last in First out).

Ainsi, lorsqu'un problème est divisé en sous-problèmes 1, 2, 3, les impôts de 3^e sous-problème sont considérés comme étant les outputs du 2^e problème. Et des inputs du deuxième sous problème sont les outputs du 1^er sous-problème. Les données des problèmes traités par la programmation dynamique peuvent être exprimées en variables discrètes ou continues. Ainsi nous pouvons distinguer l'algorithme de résolution.

Remarque : Dans le domaine de gestion, dans le problème d'ordonnancement c'est-à-dire de conduire, planification, réalisation des projets, de production, d'élaboration de projet et dans le domaine de transport les concepts sur la théorie de graphes sont utilisés. Ainsi donc, il est nécessaire que pour avoir une bonne canalisation des routes pratiquées par la Bralima d'introduire la notion de théorie de graphe.

3.2. Introduction à la théorie de graphe

3.2.1. Définition de graphe

Soit x un ensemble de sommets fini et dénombrable

X = (x₁, x₂, x₃, ...x₄), soit m, une application multivoque et ex une appliation de x dans lui-même noté x de x, dans ce cas, le couple (x, m) défini un graphe noté G. (MVIBUDULU KALUYIT Jacques, cours de la recherche opérationnelle).

Ex. : Soit l'ensemble de sommets de x = (x₁, x₂, x₃, x₄, x₅, x₆) l'application multivoque correspondant à chaque sommet et peut se présenter comme suit :

X m (x)

X₁ x₂, x₃

X₂ x₄

X₃ x₂, x₄

X₄ x₅, x₆

X₅ x₆

X₆

Représentation d'un graphe

Le graphe est représenté par un ensemble de points reliés entre eux par des flèches. La flèche relie un sommet X_i X_j appartenant à un sommet X_i X_j si X_j m (X_i). Partant de notre exemple, on peut avoir la représentation de graphe ci-après :

X₂

X₁

X₃ X₄

X₅ X₆

3.2.2. Sommet suivant et sommet précédent

Un sommet X_j est dit « suivant » de X_i s'il y a une flèche de X_i vers X_j m (X_i). Dans ce cas, X_i est dit « précédent » de X_j. L'ensemble de suivants de x est symbolisé par S (x). L'ensemble de précédents de x est symbolisé par P (x).

Ainsi pour notre exemple on aura le tableau de suivant.

Tableau de suivant (Dictionnaire de suivant)

S S (x)

X₁ -

X₂ x₁, x₃

X₃ x₁

X₄ x₂, x₃

X₅ x₄

X₆ x₄, x₅

Le tableau de précédent est ainsi appelé dictionnaire de précédent. Il s'obtient du dictionnaire de suivant. Pour cela, la procédure est la suivante :

On note sur la ligne x_i les numéros des lignes dans lesquelles x_i apparaît comme suivant. Ainsi, si on applique cette procédure on aura le tableau de précédent ci-après :

P P (x)

X₁ -

x₂ x₁, x₃

x₃ x₁

x₄ x₂, x₃

x₅ x₄

x₆ x₅, x₄

3.2.3. Les points de vente de la BRALIMA

A partir de cette théorie nous pouvons l'applliquer à la réalité rencontrée à la Bralima/Bukavu. Ainsi donc, par son circuit de distribution, la ville de Bukavu a 2 axes, dont le 1^er axe appelé VILLE 1 et le 2^e axe VILLE 2. Et chacun d'axes a ses points de ventes bien identifiés.

I) Les principaux points de vente de l'axe 1 peuvent se présenter comme suit :

X₁ : Bralima (point de départ)

x₂ : Place de l'indépendance (ces points de vente a comme dépôts relais :

TEM'S 1)

X₃ : Av. P.E LUMUMBA/Labotte (FAIDA, NABINTU 4, JEANNE)

X₄ : Athénée d'Ibanda (KITAMBALA 2, MAMAN JENIFER)

X₅ : AV. P.E LUMUMBA (La source 2, NOTRE VRAI SIEGE)

X₆ : NYAWERA Marché (super Copin, NABINTU 2, Alexis BAGUMA 2,

BITIJULA)

X₇ : Cercle Hippique (Maman MUDERHWA)

X₈ : Camp Saïo (Maman MUDERWHA)

X₉ : Nganda Belvédère (KONDA, BIGIRIMANA, KITAMBALA 1)

X₁₀ : AV. Cimetière (MUSHAMALIRWA, NABINTU 3)

X₁₁ : DGI (MUKULU, BIREM, CIGOHO)

X₁₂ : Rond point ISP (CIKIZA, BOUTIQUE RAFIKI, MAMAN DEPS,

MUGENGE)

X₁₃ : Rond point Major Vangu (WASSO AKILI, BUHENDWA, MUHANANO,

CHOKOLA)

X₁₄ : Panzi (MUSAFIRI, Jean MADO).

Pour l'axe 2 les principaux points des ventes sont :

X₁ : Bralima (Point de départ)

x₂ : Beach MUHANZI (MATATA, TEM'S 2)

x₃ : AV. KIBOMBO (Trois canards, DA LETHY)

x₄ : Av. Industriel (Maman Tantine)

x₅ : Nyamugo deux poteaux (TAIFA)

x₆ : Nyamugo Marché (Alain, KONDA 1, AYAYS)

x₇ : Essence KIBONGE (JOMBA MONGANE, CARITAS)

x₈ : BUHOLO V (INTERNET, M'BISIMWA, KIZO'S)

x₉ : Pas à pas (Maman Anny, BAHUGUKE, MUSHAGA, CIRUZA 1)

x₁₀ : BUHOLO IV (NGOMO)

x₁₁ : CHIMPUDA (Flavien, urelie)

x₁₂ : Avenue KADURU (MAMAN MUOMERWA)

x₁₃ : Avenue KASALI (Place du Dialogue)

x₁₄ : Nyamugo Stade (N'SHANGALUME RUNINGA)

x₁₅ : CIRIRI (MAKERA, MBASWA, CLAIRE)

x₁₆ : CAMP TV (BABA TANTINE, ROMAIN)

x₁₇ : Marché Nkafu (SIKUZANI, MAFUALA, VERONIQUE)

x₁₈ : AV. Route de Goma (M'NYAMUKONDE) « BAGIRA »

x₁₉ : QUARTIER A (WENGA, MAMA SILLY)

x₂₀ : AUX 7 FONTAINES/Place communale Bagira (NABINTU 1)

x₂₁ : Quartier B (NOTRE SOURCE 1)

D'une manière générale, nous pouvons représenter ces deux axes en utilisation la méthode de graphe évoquée précédemment.

I. L'AXE 1 (VILLE 1)

a) Le graphe de l'axe 1

P P (x)

X₁ -

X₂ X₂, X₃, X₄

X₃ X₃, X₄, X₅

X₄ X₄, X₅, X₆

X₅ X₅, X₆, X₇

X₆ X₆, X₇, X₈

X₇ X₇, X₈, X₉

X₈ X₈, X₉, X₁₀

X₉ X₉, X₁₀, X₁₁

X₁₀ X₁₀, X₁₁, X₁₂

X₁₁ X₁₁, X₁₂, X₁₃

X₁₂ X₁₂, X1₃, X₁₄

X₁₃ X₃, X₁₄

X₁₄ X₄

b) Construction graphe ordonné

La procédure de détermination de niveau :

1. On commence toujours par la détermination de niveau zéro (NO), on le détermine comme suit : les sommets de NO correspondent aux sommets n'ayant pas de précèdent

NO = {x₁}

2. Niveau 1 (N₁)

Les sommets de N₁ s'obtiennent à partir des sommets de niveau zéro.

Pour cela, on barre sur toutes les lignes partout où se trouve les sommets de NO. Si la ligne est complètement barrée, les sommets correspondant sont de N_1.

N₁= {x₂, x3, x4}

3. Niveau 2 (N₂)

Les sommets de N₂ s'obtiennent de niveau un, pour cela, on barre sur trouves lignes partout où se trouve les sommets de NO. Si la ligne est complètement barrée, les sommets correspondant sont de N₁

N₂= {x₅, x₆}

4. niveau 3 (N₃)

Le processus continue comme précédemment en portant du niveau 2.

N₃= {x₆, x₇}

5. Niveau 4 (N₄)

N₄={x₇, x₈}

6. Niveau 5 (N₅)

N₅= {x₈,x₉}

7. Niveau 6 (N₆)

N₆={x₉,x₁₀}

8. Niveau 7 (N₇)

N₇={x₁₀,x₁₁}

9. Niveau 8 (N₈)

N₈={x₁₁,x₁₂}

10. Niveau 9 (N₉)

N₉={x₁₂,x₁₃}

5. Niveau 10 (N₁₀)

N₁₀={x₁₃,x₁₄}

6. Niveau 11 (N₁₁)

N₁₁={x₁₄}

c) Construction de graphe ordonné pour l'axe1 (N° 1)

7h30' N 6h°° 4h30' 3h°° 1h30é de la journée

8h°° de la journée

X₂ x₅ x₉ x₁₃

400m

X₁ x₃ x₇ x₁₁

X₈

X₁₄

X₄ x₆ x₁₀ x₁₂

SOURCE : nos constructions

Comme nous l'avons évoqué précédemment, l'approche de la programmation dynamique s'effectue par la décomposition en sous-problème, du problème concerné et l'analyse commence par traiter d'abord les sous problèmes qui sont situés chronologiquement les derniers en terminant par les sous problèmes situé ou encore selon les principes LIFO (last in first out) « première sortie, dernière entrée »

Ainsi, lorsqu'un problème est divisé en sous-problème :1, 2,3 les inputs des 3è sous-problèmes sont considérés comme étant les out put du 2è problème. Et des inputs du deuxième sous-problème sont les outputs du 1è sous-problème.

d) Résolution de problème

· Procédure

Imaginons un poste de vente quelconque Pi où le vendeur veut minimiser les coùts (c) pendant une allée de m heures vers la déstination J.

Ainsi, ces coûts C est fonction du point de départ (Poste Pi) et du nombre de jour de W requises (n) pour effectuer le travail au point J. on peut alors dire :

C (i, r) au coût minimal de kilomètres à parcourir par les charrois automobile de la Bralima au moment où il ne reste que n heures pour atteindre la destination.

Ces coûts peuvent être exprimés mathématiquement par une option fonctionnelle. Ainsi, l'équation fonctionnelle à maximiser ou à minimiser au niveau de chaque sous-problème sera :

C (i,n) = max [C_ij + C(j, n-1)].

Pour le problème de minimisation, l'équation sera alors:

C(i, n) = min [C_ij + C(j, n-1]

C_ij = les kilomètres à parcourir en allant du poste X_i vers le poste X_j.

C_j, n-1 = les kilomètres à parcourir pendant l e reste de temps du travail soit n-1 heures vers X_j.

· Analyse

Soit le 1^er sous-problème, en effet, le vendeur de la Bralima se trouvant à une 1h30' du point d'arrivée.

PANZI (X₁₄), il sera alors à l'un des points de vente ci-après

(Points de départ) : X₁₂, X₁₁, X₁₃.

L'équation fonctionnelle de minimisation sera appliquée à chacun de ces points de vente : C(14, 1), C(11, 1), C(13, 1).

C(13, 1) = min (C_nj + C(j, 1-1) tel que j = 14

= min (C(nj) + C(j, 0) tel que j = 14

= min [(C_nj + C(14,0)]

N.B : c(14, 0) = 0

C'est-à-dire que C (13, 1) = 500+0 = 500m 5 km

· Point de vente X₁₁

C₁₁, ₁ = min (C_11j + C_j, 1-1) tel que j = 14

= min (C_11j = Cj, 0 tel que j = 14

= 915 + 0 = 915m 9,15km

· Point de vente X₁₂

C₁₂, ₁ = min (C_12j + C_j, 1-1) tel que j = 14

= min (C_{12, 1} + C₁₄, ₀)

= min (800 + 0)

= 800m 8km

9. Deuxième sous-problème

A ce niveau les vendeurs de la Bralima sera à 3h°° de vente (journée) pendant la journée. Le vendeur peut atteindre les points de vente suivant : X₉, X₈, X₁₀.

· Point de vente X₉

C (₉, ₂) = min (C_9, 2 + C_j, 2-1) tel que j = 13, 12

= min (C_{9, 2} = C_j, ₁) tel que j = 13, 12

= min (600 + 500, 200 + 800)

= min (1100, 1000)

= 1000m 10km.

· Point de vente X₈

· C (₈, ₂) = min (C_8, 2 + C_j, 1) tel que j = 11, 12

= min (790 + 914, 600 + 800)

= min (1705, 1400)

= 1400m 14km.

· Point de vente X₁₀

C (₁₀, ₂) = min (C_{10, 2} + C_j, 1) tel que j = 13, 14

= min (940 + 500, 1560 + 0)

= min (1440, 1560)

= 1440m 14,4km.

10. Troisième sous-problème

Le vendeur de la Bralima est à 4h30' de la distribution et peut se trouver à l'un des points de ventes X₅, X_7, X₆ et doit passer par l'un des postes suivants : X_8, X_9, X₁₀ avant d'arriver à la destination. A partir du poste X₅ = C(5,3), C(7, 3), C(6, 3).

C (₅, ₂) = min (C_{5, 3} + C_j, 3-1) tel que j = 9, 8

= min (C_{5, 3} + C_j, 2) tel que j = 9, 8

= min (280 + 1000, 730 + 1400)

= min (1280, 2130)

= 1280m 12,8km.

· Point de vente X₇

C(7,3) = min [C(_7,3) + C(_j,2)] tel que j =11, 10

= min (214 + 915, 375 + 1440)

= min (1229, 1815)

= 1229m 12,29km

· Point de vente X₆

C(6,3) = min [C(_6,3) + C(_j,2)] tel que j =9, 10

= min (170 + 1000, 413 + 1440)

= min (1170, 1815)

= 1170m 11,70km

11. Quatrième sous-problème

Le vendeur de la Bralima est à 6h°° de la journée vers la destination finale. Aussi à 6h°° vers Panzi, le vendeur peut arriver à l'un des ces 3 points de ventes : X₅, x₆, x₇. a partir de ces points de vente

X₂ = C(_2,4), C(_3,4), C(_4,4)

· Point de vente X₂

C(_2,4)) = min [C(_2,4) + C(_j,3)] tel que j = 5,6

= min (320 + 1280, 435 + 1170)

= min (1600, 1605)

= 1600m 16km

· Point de vente X₃

C(_3,4)) = min [C(_3,4) + C(_j,3)] tel que j = 7,6

= min (7000 + 1229, 310 + 1170)

= min (1929, 1480)

= 1480m 14,8km

· Point de vente X₄

C(_4,4)) = min [C(_4,4) + C(_j,3)] tel que j = 7,8

= min (320 + 1280, 435 + 1170)

= min (1441, 2070)

= 1441m 14,41km

12. Cinquième sous-problème

Le vendeur est à 7h30 ou à 8h°° avant d'atteindre le point final. Le vendeur peut arriver à l'un de ces 3 points de vente : x₁, x₂, x₃.

De la Bralima X₁

C(_1,5) = min [C(_1,5) + C(_j,4)] tel que j = 2,3,4

= min (400 + 600, 615 + 1480, 775 + 1441)

= min (2000, 2095, 2216)

= 2000m 20km

Au courant de la journée le vendeur de la Bralima pourra effectuer 20km. Après avoir évalué les distances à parcourir, on peut alors indiquer le tableau de l'itinéraire relatif à ces différents points de vente :

- C(14,0) = 0 - C(7,3) = 12,9km

- C(13,1) = 5km - C(6,3) = 11,7km

- C(12,1) = 8km - C(2,4) = 16km

- C(11,1) = 10km - C(3,4) = 14,8km

- C(9,2) = 14km - C(4,4) = 14,41km

- C(10,2) = 14,4 - C(1,5) = 20km

- C(5,3) = 12,8

Le tableau de l'itinéraire peut se présenter comme suit:

C(₁₃,₁) = 5km

C(₁₂,₁) = 8km

C(₁₁,₁) = 9,15km

C(₁₄,₀) = 0

On place à gauche les distances à parcourir ci-dessous, d'autres distances au niveau du 5^e sous problème.

C₁₃,₁ = 5km

C₁₂,₁ = 8km

C₁₁,₁ = 9,15km

C₁₄,₀ = 0

C₉,₂ = 10km

C₈,₂ = 14km

C₁₀,₂ = 14,4km

C₁₀,₂ = 14,4km

C₈,₂ = 14km

Au niveau du 4^e sous-problème, on placera les 3 points de vente au coût optimale à gauche de 3 points de ventes situés à droite.

C₉,₁ = 10km

C₈,₂ = 14km

C₁₀,₂ = 14,4km

C₁₄,₀ = 0

C₅,₃ = 12,8km

C₆,₃ = 11,7km

C₁₃,₁ = 5km

C₁₂,₁ = 8km

C₁₁,₁ = 9,15km

C₇,₃ = 12,8km

Au 4^e sous-problème, on place toujours les distances minimales à parcourir par le vendeur de la Bralima à gauche de ces 3 points de vente situés à droite.

C₆,₂ = 11,7km

C₁₄,₀ = 0

C₂,₄ = 16km

C₄,₄ = 14,41km

C₁₃,₁ = 5km

C₁₂,₁ = 8km

C₁₁,₁ = 9,15km

C₃,₄ = 14,8km

C₉,₂ = 10km

C₈,₂ = 14km

C₁₀,₂ = 14,4km

C₇,₃ = 12,29km

C₅,₃ = 12,8km

Quant au 5^e sous-problème, on aura un seul poste (le point de départ) la flèche sera de la case C (^1,4) vers la case C (_4,4) car il a obtenu son niveau minimum de j = 4.

C₆,₃ = 11,7km

C₁₄,₀ = 0

C₂,₄ = 16km

C₄,₄ = 14,41km

C₁₃,₁ = 5km

C₁₂,₁ = 8km

C₁₁,₁ = 9,15km

C₃,₄ = 14,8km

C₉,₂ = 10km

C₈,₂ = 14km

C₁₀,₂ = 14,4km

C₇,₃ = 12,29km

C₅,₃ = 12,8km

C₄,₁=20km

Le chemin qui désigne le point de vente au coût minimal se fait ressortir facilement.

C(₄,₁) C(₄,₄) C(₇,₃) C(₉,₂) C(₁₃,₁) C(₄,₀)

Ou X₁ X₄ X₇ X₉ X₁₃ X₁₄

Pour l'axe qui est la VILLE 1, le vendeur peut adopter le programme de vente minimum en commençant par la Bralima successivement aux points de ventes de l'athénée, cercle hippique, Belvédère, Rond point Major Vangu jusqu'à Panzi.

Ainsi, il aura évité le risque de gaspillage inutile enfin pour la bonne marche de l'entreprise.

II. L'axe 2 (VILLE 2)

a) Le graphe de l'axe 2 b) Construction de graphe ordonné

1) sommet 0 (N₀)

N₀ = {y₁}

2) sommet 1 (N₁)

N₁ = {y_2, y₃, y₄}

3) sommet 2 (N₂)

N₂ = {y_5, y₆}

4) sommet 3 (N₃)

N₃ = {y_6, y₇}

5) sommet 4 (N₄)

N₄ = {y_7, y₈}

6) sommet 4 (N₄)

N₄ = {y_7, y₈}

7) sommet 6 (N₆)

N₆ = {y_9, y₁₀}

8) sommet 7 (N₇)

N₇ = {y_10, y₁₁}

9) sommet 8 (N₈)

N₈ = {y_11, y₁₂}

10) sommet 9 (N₉)

N₉ = {y_11, y₁₂}

11) sommet 10 (N₁₀)

N₁₀ = {y_13, y₁₄}

12) sommet 11 (N₁₁)

N₁₁ = {y_14, y₁₅}

13) sommet 12 (N₁₂)

N₁₂ = {y_15, y₁₆}

14) sommet 13 (N₁₃)

N₁₃ = {y_16, y₁₇}

15) sommet 14 (N₁₄)

N₁₄ = {y_17, y₁₈}

16) sommet 15 (N₁₅)

N₁₅ = {y_18, y₁₉}

17) sommet 16 (N₁₆)

N₁₆ = {y_19, y₂₀}

18) sommet 17 (N₁₇)

N₁₇ = {y_20, y₂₁}

19) sommet 18 (N₁₈)

N₁₈ = {y₂₁}

P P(y) Procédure

Y₁

Y₂ Y₂, Y₃, Y₄

Y₃ Y₃, Y₄, Y₅

Y₄ Y₄, Y₅, Y₆

Y₅ Y₅, Y₆, Y₇

Y₆ Y₆, Y₇, Y₈

Y₇ Y₇, Y₈, Y₉

Y₈ Y₈, Y₉, Y₁₀

Y₉ Y₉, Y₁₀, Y₁₁

Y₁₀ Y₁₀, Y₁₁, Y₁₂

Y₁₁ Y₁₁, Y₁₂, Y₁₃

Y₁₂ Y₁₂, Y₁₃, Y₁₄

Y₁₃ Y₁₃, Y₁₄, Y₁₅

Y₁₄ Y₁₄, Y₁₅, Y₁₆

Y₁₅ Y₁₅, Y₁₆, Y₁₇

Y₁₆ Y₁₆, Y₁₇, Y₁₈

Y₁₇ Y₁₇, Y₁₈, Y₁₉

Y₁₈ Y₁₈, Y₁₉, Y₂₀

Y₁₉ Y₁₉, Y₂₀, Y₂₁

Y₂₀ Y₂₀, Y₂₁

Y₂₁ Y₂₁

Le graphe ordonné peut se schématiser comme suit :

Y₂ Y₅ Y₉ Y₁₃ Y₁₆ Y₁₉

Y₁ Y₃ Y₇ Y₁₁ Y₁₅ Y₁₇ Y₂₀

Y₄ Y₈ Y₁₄

Y₆ Y₁₀ Y₁₂ Y₁₈ Y₂₁ source : nos constructions

c) Résolution de problème

- Analyse

Soit le 14er sous-problème, le vendeur se trouve à 1h30' à la zone de Bagira et au Quartier B. de quartier B et de la zone de Bagira, il sera alors à l'un des points de vente ci-après : y₁₉, y₁₇, y₁₈. L'équation fonctionnelle de minimisation sera appliquée à chacun de ces points de vente : C₁₉,₁ , C₁₇,₁ , C₁₇,₁.

C(_19,1) = min [C(_nj + C(_{j, 1-1})] tel que j = 20,

= min [(C_nj + C(_{j, 0})] tel que j = 20

= min (60 + 0)

= 60m 0,6km

· Point de vente Y₁₇

C_17,1 = min (C_17,1 + C_{j, 0}) tel que j = 20, 21

= min (600 + 0, 620 + 0)

= min (600, 620)

= 600m 6km

· Point de vente Y₁₈

C_18,1 = min (C_18,1 + C_{j, 0}) tel que j = 21

= min (150+0)

= 150m 1,5km

2. Deuxième sous-problème

A ce niveau le vendeur de la Bralima sera à 3h°° de vente pendant la journée. Le vendeur peut attendre l'un des points suivants : y₁₆, y₁₇, y₁₄.

· Point de vente Y₁₆

C_16,2 = min (C_16,2 + C_{j, 2-1}) tel que j = 19, 20

= min (3500+600, 3508+0)

= min (3560,3508)

= 3508m 35,08km

· Point de vente Y₁₅

C_15,2 = min (C_15,2 + C_j,1) tel que j = 19, 18

= min (3900+60, 3890+150)

= min (39600, 4040)

= 3960m 39,6km

· Point de vente Y₁₄

C_14,2 = min (C_14,2 + C_j,1) tel que j = 17, 18

= min (800+600, 1300+150)

= min (1400, 1450)

= 1400m 14km

3. Troisième sous-problème

Le vendeur étant à 4h30', il peut atteindre l'un de ces points de vente : y₁₃, y₁₁, y₁₂.

· Point de vente Y₁₃

C_13,3 = min (C_13,3 + C_{j, 3-1}) tel que j = 16, 17

= min (C_13,3 + C_j,2) tel que j = 16, 17

= min (2200+3508, 1350+600)

= min (5708, 1950)

= 1950m 19,50km

· Point de vente Y₁₁

C_11,3 = min (C_13,2 + C_j,2) tel que j = 15, 14

= min (310 + 3960, 770+1400)

= min (4270, 2170)

= 2170m 21,7km

· Point de vente Y₁₂

C_12,3 = min (C_12,2 + C_j,2) tel que j = 16, 15

= min (1000+3508, 990+3960)

= min (4508, 4950)

= 4508m 45,08km

4. Quartier sous-problème

Il se trouve maintenant à 6h, il peut atteindre l'un de ces points de vente : y₉, y₈, y₁₀.

· Point de vente Y₉

C_9,4 = min (C_9,4 + C_{j, 4-1}) tel que j = 13, 12

= min (C_9,4 + C_j,3) tel que j = 13, 12

= min (400+1950, 300+4508)

= min (2350, 4808)

= 2350m 23,50km

· Point de vente Y₈

C_8,4 = min (C_8,4 + C_j,3) tel que j = 11, 12

= min (500+2170, 350+4508)

= min (2670, 4858)

= 2670m 26,7km

· Point de vente Y₁₀

C_10,4 = min (C_10,4 + C_j,3) tel que j = 13, 14

= min (350+1950, 275+1400)

= min (2300, 1675)

= 1675m 16,75km

5. Cinquième sous-problème

Il se trouve alors à 7h30', il pourra atteindre l'un de ces points suivants : y₅, y₇, y₆.

· Point de vente Y₅

C_5,5 = min (C_5,5 + C_{j, 5-1}) tel que j = 9, 8

= min (415+2350, 900+26700)

= min (2765, 3570)

= 2765m 27,65km

· Point de vente Y₇

C_7,5 = min (C_7,5 + C_j,4) tel que j = 11, 10

= min (2220+2170, 1440+1675)

= min (4390, 3115)

= 3115m 31,15km

· Point de vente Y₆

C_6,5 = min (C_6,5 + C_j,4) tel que j = 9, 10

= min (450+2350, 1512+1675)

= min (2800, 3187)

= 2800m 28km

13. Sixième sous-problème

A 9h°°, ilpourra atteindre l'un de ces points suivants : y₂, y₃, y₄.

· Point de vente Y₂

C_2,6 = min (C_2,6 + C_{j, 6-1}) tel que j = 5, 7

= min (200+275, 400+2800)

= min (2969, 3200)

= 2969m 29,69km

· Point de vente Y₃

C_3,6 = min (C_3,6 + C_j,5) tel que j = 7, 6

= min (365+3115, 200+2800)

= min (3480, 3000)

= 3000m 30km

· Point de vente Y₄

C_4,6 = min (C_4,6 + C_j,5) tel que j = 7, 8

= min (380+3115, 995+2670)

= min (3495, 3665)

= 3495m 34,95km

14. Septième sous-problème

A 10h°° et 30', il a un seul point, qui est le point de départ Y₁ (La Bralima), il peut atteindre l'un de ces points suivants :

y₂, y₃, y₄.

De la Bralima Y₁ :

C(_1,7) = min (C_1,7 + C_{j, 7-1}) tel que j = 2, 3, 4

= min (C_1,7 + C_j,6) tel que j = 2, 3, 4

= min (300+2969, 500+3000, 550+3495)

= min (3269, 3500, 4045)

= 3269m 32,69km

Au cours de cette allé, le vendeur de la Bralima pourra parcourir une distance minimum de 32, 69km. Le tableau de l'itinéraire relatif à ces différentes points de vente peut se présenter comme suit :

C₁₉, ₁= 0,6km C₁₁, ₃= 21,70km C₇, ₅= 31,15km

C₁₇, ₁= 6km C₁₂, ₃= 45,08km C₆, ₅= 28km

C₁₈, ₁= 1,5km C₉, ₄= 23,5km C₂, ₆= 29,69km

C₁₆, ₂= 35,08km C₈, ₄= 26,7km C₃, ₆= 30km

C₁₅, ₂= 39,6km C₁₀, ₄= 16,75km C₄, ₆= 34,95km

C₁₄, ₂= 14km C₅, ₅= 27,65km C₁= 32,69km

C₁₃, ₃= 19,50km

Le tableau de l'itinéraire est le suivant:

C₁₉, ₁= 0,6km

C₁₇, ₁= 6km

C₁₈, ₁= 1,5km

C₂₀, ₀= 0

C₂₁, ₀= 0

On place à gauche les distances à parcourir ci-dessous, d'autres distances au niveau du 6^e sous-problème.

C₂₀, ₀= 0

C₁₉, ₁= 0,6km

C₁₆, ₂= 35,08km

C₁₇, ₁= 6km

C₁₅, ₂= 39,6km

C₂₁, ₀= 0

C₁₈, ₁= 1,5km

C₁₄, ₂= 14km

Au niveau du 5^e sous-problème, on placera les 3 points de vente au coût optimale à gauche de 3 points de ventes situés à droite.

C₁₃, ₃= 19,50km

C₁₁, ₃= 21,70km

C₁₂, ₃= 45,08km

C₁₆, ₂= 35,08km

C₁₅, ₂= 39,6km

C₁₄, ₂= 14km

C₁₉, ₁= 0,6km

C₁₇, ₁= 6km

C₁₈, ₁= 1,5km

C₂₀, ₀= 0

C₂₁, ₀= 0

C₁₃, ₃= 19,50km

C₁₃, ₃= 19,50km

C₁₃, ₃= 19,50km

C₁₃, ₃= 19,50km

Le processus continue de la manière suivante :

C₉, ₄= 23,5km

C₈, ₄= 26,7km

C₁₀, ₄= 16,75km

C₁₃, ₃= 19,50km

C₁₁, ₃= 21,70km

C₁₂, ₃= 45,08km

C₁₆, ₂= 35,08km

C₁₅, ₂= 39,6km

C₁₄, ₂= 14km

C₁₉, ₁= 0,6km

C₁₇, ₁= 6km

C₁₈, ₁= 1,5km

C₂₁, ₀= 0

C₂₀, ₀= 0

Au niveau du 4^e sous-problème, on place toujours les 3 points de vente au coût optimal à gauche de 3 points de vente situés à droite.

C₅, ₅= 27,65km

C₇, ₅= 31,15km

C₆, ₅= 28km

C₉, ₄= 23,5km

C₈, ₄= 26,7km

C₁₀, ₄= 16,75km

C₁₃, ₃= 19,50km

C₁₁, ₃= 21,70km

C₁₂, ₃= 45,08km

C₁₆, ₂= 35,08km

C₁₅, ₂= 39,6km

C₁₄, ₂= 14km

C₁₇, ₁= 6km

C₁₉, ₁= 0,6km

C₁₈, ₁= 1,5km

C₂₀, ₀= 0

C₂₁, ₀= 0

On continue le processus :

C₂, ₆= 29,69km

C₃, ₆= 30km

C₄, ₆= 34,95km

C₅, ₅= 27,65km

C₇, ₅= 31,15km

C₆, ₅= 28km

C₉, ₄= 23,5km

C₈, ₄= 26,7km

C₁₀, ₄= 16,75km

C₁₂, ₃= 45,08km

C₁₁, ₃= 21,70km

C₁₃, ₃= 19,50km

C₁₆, ₂= 35,08km

C₁₅, ₂= 39,6km

C₁₄, ₂= 14km

C₁₈, ₁= 1,5km

C₁₇, ₁= 6km

C₁₉, ₁= 0,6km

C₂₀, ₀= 0

C₂₁, ₀= 0

On pourra compléter le coût minimal précédent :

C₂₁, ₀= 0

C₁₈, ₁= 1,5km

C₁₄, ₂= 14km

C₁₂, ₃= 45,08km

C₁₀, ₄= 16,75km

C₁₇, = 32,69km

C₄, ₆= 34,95km

C₆, ₅= 28km

C₁₇, ₁= 6km

C₁₅, ₂= 39,6km

C₁₁, ₃= 21,70km

C₈, ₄= 26,7km

C₇, ₅= 31,15km

C₃, ₆= 30km

C₁₉, ₁= 0,6km

C₁₆, ₂= 35,08km

C₂, ₆= 29,69km

C₅, ₅= 27,65km

C₉, ₄= 23,5km

C₁₃, ₃= 19,50km

C₂₁, ₀= 0

La route qui désigne les points de vente au coût minimal se fait ressortir facilement :

C_1,7 C_2,6 C_5,5 C_9,4 C_13,3 C₁₆,₂ C_19,2 C₂₀

Y₁ Y₂ Y₅ Y₉ Y₁₃ Y₁₆ Y₁₉ Y₂₀

Le programme de vente minimum à ce niveau commence à partir de point de départ en commençant par le Beach Muhanzi, Nyamugo deux poteaux, pas à pas, avenue Kasali, camp TV, quartier A et puis à la commune de Bagira.

A partir de cette analyse, nous pouvons conclure en disant que le manager de les Bralima n'ayant pas introduit les notions de programmation en subdivisant le circuit de distribution, cela nous a amené aux résultats biaisés. Par exemple, du au camp TV au quartier A à Bagira il n'y a aucune route qui relie ce tronçon, et puis si la route existait on n'aurait pas minimisé les coûts liés à cette affectation, car quitter Camp TV jusqu'à Bagira au Q/A il y a une longue distance. Cela va nous amener à aider la Bralima à faire une subdivision ordonnée de son circuit de distribution en tenant compte des notions de programmation dynamique.

Pour faciliter la distribution à la Bralima, il a été préférable de faire une étude approfondie sur la politique optimale capable de minimiser les coûts. C'est le point qui fera la troisième partie de notre chapitre.

3.3. La Politique optimale de la distribution à la Bralima/Bukavu

Beaucoup de problèmes de décisions consistent à rendre maximum ou minimum un résultat tout en respectant des contraintes des moyens disponibles. Ce type des problèmes peut être résolus par la programmation dynamique.

La programmation dynamique sert à résoudre les problèmes aux variables non stochastiques (non affectés d'une probabilité quelconque).

3.3.1. Subdivision de circuit de distribution de la Bralima

Pour l'atteinte de l'objectif de la Bralim, celui de maximiser des recettes et minimiser des coûts, celle-ci pourrait subdiviser son circuit en 3 axes afin de faire un programme analytique convenable. Ainsi donc on peut le subdiviser comme suit :

- L'axe 1 (VILLE 1) peut regrouper tous les dépôts relais de la commune de Bagira ;

- L'axe 2 (VILLE 2) peut aussi regrouper tous les dépôts relais de la commune de Kadutu et

- L'axe 3 (VILLE 3) les dépôts relais de la commune d'Ibanda.

a) Les dépôts relais de la ville 1 (Commune de Bagira)

Ø X₁ : Bralima

Ø X₂ : Marché Nkafu (M'MUN GOMBE)

Ø X₃ : Marché Nkafu (MAFUALA)

Ø X₄ : Marché Nkafu (KAJURU)

Ø X₅ : Marché Nkafu (BISHIKWABO)

Ø X₆ : Av. Route de Goma (M'NYAMUKONDE)

Ø X₇ : Quartier A/Bagira (WENGA)

Ø X₈ : Quartier A (MAMA SILLY)

Ø X₉ : Aux 7 fontaines/Bagira (NABINTU 1)

Ø X₁₀ : Quartier B (NOTRE SOURCE)

b) Les dépôts relais de la ville 2 (Commune de Kadutu)

y₁ : Bralima (Point de départ)

y₂ : Beach MUHANZI (MATATA, TEM'S 2)

y₃ : AV. KIBOMBO (Trois canards, DA LETHY)

y₄ : Av. Industriel (Maman Tantine)

y₅ : Nyamugo deux poteaux (TAIFA)

y₆ : Nyamugo Marché (Alain, KONDA 1, AYAYS)

y₇ : Essence KIBONGE (JOMBA MONGANE, CARITAS)

y₈ : BUHOLO V (INTERNET, M'BISIMWA, KIZO'S)

y₉ : Pas à pas (Maman Anny, BAHUGUKE, MUSHAGA, CIRUZA 1)

y₁₀ : BUHOLO IV (NGOMO)

y₁₁ : CHIMPUDA (Flavien, urelie)

y₁₂ : Avenue KADURU (MAMAN MUOMERWA)

y₁₃ : Avenue KASALI (Place du Dialogue)

y₁₄ : Nyamugo Stade (N'SHANGALUME RUNINGA)

y₁₅ : CIRIRI (MAKERA, MBASWA, CLAIRE)

y₁₆ : CAMP TV (BABA TANTINE, ROMAIN)

c) Les dépôts relais de la ville 3 (Commune d'Ibanda)

z₁ : Bralima (point de départ)

z₂ : Place de l'indépendance (ces points de vente a comme dépôts relais :

TEM'S 1)

z₃ : Av. P.E LUMUMBA/Labotte (FAIDA, NABINTU 4, JEANNE)

z₄ : Athénée d'Ibanda (KITAMBALA 2, MAMAN JENIFER)

z₅ : AV. P.E LUMUMBA (La source 2, NOTRE VRAI SIEGE)

z₆ : NYAWERA Marché (super Copin, NABINTU 2, Alexis BAGUMA 2,

BITIJULA)

z₇ : Cercle Hippique (Maman MUDERHWA)

z₈ : Camp Saïo (Maman MUDERWHA)

z₉ : Nganda Belvédère (KONDA, BIGIRIMANA, KITAMBALA 1)

z₁₀ : AV. Cimetière (MUSHAMALIRWA, NABINTU 3)

z₁₁ : DGI (MUKULU, BIREM, CIGOHO)

z₁₂ : Rond point ISP (CIKIZA, BOUTIQUE RAFIKI, MAMAN DEPS,

MUGENGE)

z₁₃ : Rond point Major Vangu (WASSO AKILI, BUHENDWA, MUHANANO,

CHOKOLA)

z₁₄ : Panzi (MUSAFIRI, Jean MADO).

3.3.2. Analyse proprement dite de chaque axe

A. AXE 1 (VILLE 1)

a. Construction de graphe ordonné

X₁ -

X₂ X₂, X₃, X₄

X₃ X₆, X₄, X₅

X₄ X₄, X₅, X₆

X₅ X₅, X₆, X₇

X₆ X₆, X₇, X₈

X₇ X₇, X₈, X₉

X₈ X₈, X₉, X₁₀

X₉ X₉, X₁₀

X₁₀ X₁₀

b. Procédure de détermination de niveau

· Niveau 0(N₀)

N₀ = {X₁}

· Niveau 1 (N₁)

N₁ = {X_2, X₃, X₄}

· Niveau 2 (N₂)

N₂ = {X_5, X₆}

· Niveau 3 (N₃)

N₃ = {X_6, X₇}

· Niveau 4 (N₄)

N₄ = {X_7, X₈}

· Niveau 5 (N₅)

N₅ = {X_8, X₉}

· Niveau 6 (N₆)

N₆ = {X_9, X₁₀}

· Niveau 7 (N₇)

N₇ = {X₁₀}

c. Construction de graphe ordonné n° 3

2H 2H 2H 2H

X₂ X₅ X₉

X₁ X₃ X₇ X₁₀

X₆

X₄ X₈

d. Analyse

Soit le 1^er sous-problème, en effet, le distributeur se trouvant à 2h de la journée, il pourra alors atteindre l'un de ces points des ventes :

X₉, X₈

Au point de vente X₉ : C_9,1 C_10,1

· Point de vente

C_9,1 = min (C_9,1 + C_j, _1-1) tel que j = 10

= min (C_9,1 + C_j, ₀) tel que j = 10

= min (20+0)

= 20m 0,6k

2. 2^e sous-problème

Le vendeur se trouve à 4h au courant de la journée, il peut atteindre l'un de ces points : X₅, X₇, X₆

· Point de vente X₅

C_5,2 = min (C_5,2 + C_j, _2-1) tel que j = 9, 8

= min (800+20, 728+60)

= 788m 7,88km

· Point de vente X₇

C_7,2 = min (C_7,2 + C_j,₁) tel que j = 10

= min (50+0)

= 50m 0,5km

· Point de vente X₈

C_6,2 = min (C_6,2 + C_j,₁) tel que j = 9, 8

= min (50+20, 30+0)

= min (70, 30)

= 30m 0,3km

3. 3^e sous-problème

Le vendeur se trouve à 6h au courant de la journée, il peut atteindre l'un de ces points X₂, X₃, X₄

· Point de vente X₂

C_2,3 = min (C_2,3 + C_j, _3-1) tel que j = 5, 6

= min (78+788, 746+30)

= min (866, 776)

= 776m 7,66km

· Point de vente X₃

C_3,3 = min (C_3,3 + C_j, ₂) tel que j = 7, 8

= min (775+50, 728+30)

= min (825, 758)

= 758m 7,58km

· Point de vente X₄

C_4,3 = min (C_4,3 + C_j,₂) tel que j = 7, 8

= min (728+50, 728+60)

= min (778, 788)

= 778m 7,78km

4. 4^e sous-problème

Le vendeur est à 8h au courant de la journée, il peut atteindre l'un de ces points X₂, X₃, X₄

De la Bralima X₁

C(_1,4) = min (C_1,4 + C_j,_3-1) tel que j = 2, 3, 4

= min (60+776,65+758,72+778)

= min (836, 823, 850)

= 823m 8,23km

Le tableau de l'itinéraire peut se présenter comme suit :

C_10,0 = 0 C_6,2 = 0,3km

C_9,1 = 0,2km C_2,3 = 7,76km

C_8,1 = 0,6km C_3,3 = 7,58km

C_5,2 = 7,88km C_4,3 = 7,78km

C_7,2 = 0,5km C_1,4 = 8,23km

On peut schématiser l'itinéraire minimum comme suit:

C_1,4 = 8,23km

C_3,3 = 7,58km

C_7,2 = 0,5km

C_10,0 = 0

C_2,3 = 7,76km

C_5,2 = 7,88km

C_6,2 = 0,3km

C_4,3 = 7,78km

C_8,1 = 0,6km

C_9,1 = 0,2km

La route qui désigne les points de vente au coût minimal se fait ressortir facilement.

C_1,4 C_3,3 C_6,2 C_9,1 C_10,0

X₁ X₃ X₆ X₉ X₁

La Bralima/Bukavu pourra adopter le programme de distribution au coût minimum en commerçant par la Bralima (point de départ) successivement aux points de vente :

Marché Nkafu, Avenue route de Goma, Aux 7 fontaines (commune de Bagira) jusqu'au quartier B.

B. AXE 2 (VILLE 2) « COMMUNE DE KADUTU »

a) Construction de graphe ordonné

P P(y)

Y₁

Y₂ Y₂, Y₃,Y ₄

Y₃ Y₃, Y₄,Y ₅

Y₄ Y₄, Y₅,Y₆

Y₅ Y₅, Y₆,Y₇

Y₆ Y₆, Y₇,Y₈

Y₇ Y₇, Y₈,Y₉

Y₈ Y₈, Y₉,Y₁₀

Y₉ Y₉, Y₁₀,Y₁₁

Y₁₀ Y₁₀, Y₁₁,Y₁₂

Y₁₁ Y₁₁, Y₁₂,Y₁₃

Y₁₂ Y₁₂, Y₁₃,Y₁₄

Y₁₃ Y₁₃, Y₁₄,Y₁₅

Y₁₄ Y₁₄, Y₁₅,Y₁₆

Y₁₅ Y₁₅, Y₁₆

Y₁₆ Y₁₆

Y₁₇

b) Le graphe n° 4

Y₂ Y₅ Y₉ Y₁₃

Y₁ Y₃ Y₇ Y₁₁ Y₁₅ Y₁₆

Y₄ Y₈ Y₁₄

Y₆

Y₁₀ Y₁₂

c) Analyse

Soit le 19 sous-problème, en effet, le vendeur se trouve à 1h30' du point de vente d'arrivée. De CIRIRI (Y₁₆), il sera alors à l'un de point de vente ci-après point de départ Y_12, Y_11, Y₁₇. L'équation fonction de minimisation sera appliquée à chacun de ces points de vente : C_14,1, C_15,1.

C_15,1 = min (C_15,1 + (C C_{j, 1-1}) tel que j = y₁₆

= min (500+0)

= 500m 5km

· Point de vente Y₁₄

C_15,1 = min (C_15,1 + (C_j, _1-1) tel que j = y₁₆

= min (500+0)

= 500m 5km

· Point de vente Y₁₄

C_14,1 = min (C_14,1 + (C_j, ₀) tel que j = y₁₆

= min (1000+0)

= 1000m 10km

2. Deuxième sous-problème

Le vendeur pourra passer à l'un des points suivants : Y_3, Y₁₆ Y₁₂

· Point de vente Y₁₃

C_13,2 = min (C_13,2 + (C_j,₁) tel que j = y_{16, 15}

= min (2200+0, 950+500

= min (2200, 1450)

= 1450m 14,5km

· Point de vente y₁₁

C_11,2 = min (C_11,2 + (C_j,₁) tel que j = y_{15, 14}

= min (310+500, 770+650)

= min (810, 1420)

= 810m 8,1km

· Point de vente y₁₂

C_12,2 = min (C_12,2 + (C_j, ₁) tel que j = y_{15, 16}

= min (990+500, 1000+0)

= min (1490, 1000)

= 1000m 10km

3. Troisième sous-problème

Le vendeur se trouve à l'un des points suivants : Y_9, Y_8, Y₁₀

· Point de vente Y₉

C_9,3 = min (400+1450, 300+1000)

= min (1850, 1300)

= 1300m 13km

· Pointe de vente Y₈

C_8,3 = min (C_8,3 + (C_j,₂) tel que j = 11, 12

= min (500+810, 350+1000)

= min (1310, 1350))

= 1310m 13,1km

· Point de vente Y₁₀

C_10,3 = min (C_10,3 + (C_j, ₂) tel que j = 13, 14

= min (350+2200, 275+650)

= min (2500, 925)

= 925m 9,25km

4. Quatrième sous-problème

Le vendeur à l'un des points suivants : Y₅, Y₇ Y₆

· Pointe de vente Y₅

C_5,4 = min (C_5,4 + (C_j,_4-1) tel que j = 9, 8

= min (415+1300, 900+1310)

= min (1715, 2210)

= 1715m 17,15km

· Point de vente Y₇

C_7,4 = min (C_7,4 + (C_j, ₃) tel que j = 11, 10

= min (2220+810, 1440+915)

= min (3030, 2355)

= 2355m 23,55km

· Point de vente Y₆

C_6,4 = min (C_6,5 + (C_j, ₃) tel que j = 9, 10

= min (450+1300, 1512+925)

= min (1750, 2437)

= 1750m 17,50km

5. Cinquième sous-problème

Le vendeur de la Bralima se trouve à l'un des points suivants :

Y₂, Y₃ Y₄

· Pointe de vente Y₂

C_2,5 = min (C_2,5 + (C_j,_5-1) tel que j = 5, 6

= min (C_2,5 + (C_j,₄) tel que j = 5, 6

= min (200+1715, 400+1750)

= min (1915, 2150)

= 1915m 19,15km

· Point de vente Y₃

C_3,5 = min (C_3,5 + (C_j, ₄) tel que j = 7, 6

= min (365+2355, 400+1750)

= min (2720, 2150)

= 2150m 21,50km

· Point de vente Y₄

C_4,5 = min (C_4,5 + (C_j, ₄) tel que j = 7, 8

= min (380+2355, 995+1310)

= min (2735, 2305)

= 2305m 23,05km

6. Sixième sous-problème

Ici le vendeur se trouve au point de départ c'est-à-dire à la Bralima/Bukavu ; il ne peut atteindre l'un de ces points Y₂, Y₃ Y₄.

De la Bralima Y₁ nous pouvons avoir :

C_1,6 = min (C_1,6 + (C_j, _6-1) tel que j = 2, 3, 4

= min (300+1915, 500+2150, 550+2305)

= min (2215, 2650, 2855)

= 2215m 22,15km

Ainsi, le tableau de l'itinéraire peut se présenter comme suit :

C₁₆, ₁= 0km C₈, ₃= 13,1km C₂, ₅ = 19,5km

C₁₅, ₁= 5km C₉, ₃= 13km C₆, ₄ = 17,50km

C₁₄, ₁= 10km C₁₀, ₃ = 9,25km C₃, ₅ = 21,50km

C₁₃, ₂= 14,58km C₅, ₄= 17,15km C₄, ₆= 30km

C₁₁, ₂= 8,1km C₇, ₄= 23,55km C₄, ₅ = 23,05km

C₁₂, ₂= 10km C₆, ₄ = 17,50km C_1,6 = 22,15km

Nous pouvons schématiser l'itinéraire minimum comme suit:

C_1,6 = 22,15km

C₃, ₅ = 21,50km

C₇, ₄ = 23,55km

C₉,₃ = 13km

C₁₁, ₂ = 8,1km

C_16,0 = 0

C₂, ₅ = 19,5km

C₅, ₄ = 17,15km

C₈, ₃ = 13,1km

C₁₃, ₂ = 14,58km

C₁₅, ₁ = 5km

C₄, ₅ = 23,05km

C₆, ₄ = 17,50km

C₁₀, ₃ = 9,25km

C₁₂, ₂ = 10km

C₁₄, ₁ = 10km

La route qui désigne les points au coût minimal se fait ressortir facilement :

C_1,6 C_2,5 C_5,4 C_9,3 C_12,2 C_15,1 C_16,0

Y₁ Y₂ Y₅ Y₉ Y₁₂ Y₁₅ Y₁₆

La Bralima/Bukavu poura adopter le programme de destination au coût minimum en commençant par la Bralima (point de départ) successivement aux points de vente :

Beach MUHANZI, Nyamugo deux poteaux, pas à pas, avenue Kadurhu, Ciriri jusqu'au Camp TV.

C. AXE 3 (VILLE 3) : « COMMUNE D'IBANDA »

Ici nous fait ressortir sur le graphe n° 1 vu précédemment à la page 39. Par analyse la route qui désigne la route au coût minimum était ressorti comme suit :

C_4,1 C_4,4 C_7,3 C_9,2 C_13,1 C_14,0 ou encore

Z₁ Z₄ Z₇ Z₉ Z₁₃ Z₁₄

Pour cet axe, le vendeur pourra adopter le programme de vente minimum en commençant par la Bralima successivement aux points de vente de l'athénée, cercle hippique, Belvédère, rond point Major Vangu jusqu'à Panzi.

Ainsi, il aura évité le risque de gaspillage inutile pour la bonne marche de cette entreprise.

3.4. Conclusion partielle

Le troisième chapitre porte sur la programmation dynamique de charrois automobiles. Il est subdivisé en trois grandes parties. La première porte sur l'introduction sur la programmation dynamique en différencient la programmation dynamique ave la programmation linéaire. La 2^ème parti porte sur la théorie du graphe, on essaye de voir sur base de son circuit de distribution, comment on peut tracer un schéma permettant de déterminer la distance qui relie chaque dépôt relais suivant leurs sommets.

Enfin, le 3^e point traite sur la politique optimale de la distribution, c'est le point important de notre travail parce qu'il est même la solution à notre problématique. Il donne à la Bralima les pistes de solution pour la bonne minimisation de son coût de distribution, il donne une nouvelle stratégie de la subdivision de son circuit.

Si la Bralima pourrait suivre cette stratégie ; elle s'épargnerait des transporteurs extérieurs parce que ces derniers profitent beaucoup plus que si la Bralima disposerait eux-mêmes le moyen pour le transport de ses produits.

Ajoutons qu'à part le coût de transport, les transporteurs paquent d'autres subsides qui pourraient même aller plus loin du taux d'amortissement que la Bralima pourrait assurer à ses véhicules.

CONCLUGION GENERALE

Nous voici au terme de notre travail intitulé « Programmation de charrois automobiles pour la distribution de la Boisson : cas de la Bralima/Bukavu de 2005 à 2006 » dont l'objectif était de mener une analyse, d'appréhender une politique et d'interpréter les résultats trouvés par cette analyse afin de faciliter la distribution à moindre frais à la Bralima/Bukavu.

A la lumière de cet objectif, il a été question de vérifier la politique utilisée par la Bralima/Bukavu pour la distribution de la boisson à travers son circuit de distribution par la méthode de programmation dynamique.

Eu égard aux difficultés d'ordre financier, économique et social que connaît cette entreprise, il a été utile d'étudier sa situation sociale enfin pour la gestion rationnelle de son circuit de distribution.

C'est ainsi que les questions suivantes ont mérité d'être posées :

- Quelle est la politique relative à l'affection des charrois automobiles utilisés par la Bralima/Bukavu pour la distribution de ses produits ?

- Les routes pratiquées par ces charrois pour atteindre les dépôts relais ne sont-elles pas longues ?

- Est-il possible de mettre sur pieds une politique optimale capable de minimiser les coûts alloués à ce service ?

Pour répondre à ces questions, les informations recueillies au cours de nos investigations ont été analysées et présentées dans trois chapitres : le premier chapitre a présenté le cadre théorique qui est la toile de fond sur laquelle s'est inscrit notre étude. Il a compris 2 points, à savoir : la définition des concepts et la présentation de la Bralima. Le deuxième chapitre a porté sur les généralités et politiques de la distribution de la Bralima/Bukavu. Ce chapitre a permis de connaître le circuit de distribution de cette entreprise. Il nous a permis de connaître les généralités d'abord de la distribution et ensuite la politique et le coût de la distribution de la Bralima/Bukavu.

Le troisième chapitre a traité de la programmation dynamique de charrois automobiles de la Bralima/Bukavu, a introduit d'une manière générale la programmation dynamique, la théorie de graphe qui nous a permis de tracer le schéma lié au circuit de distribution et nous avons mis à la porté de la Bralima une politique optimale de la distribution pouvant permettre à cette firme de minimiser son coût de distribution, en analysant ses points de ventes.

Toutes nos hypothèses ont été vérifiées et nous avons constaté ce qui suit :

- La Bralima/Bukavu possède des canaux de distribution par lesquels elle fait écouler ses produits mais son circuit de distribution était male subdivisé compte tenu qu'elle n'utilise aucune méthode quantitative pour la prise de décision.

- L'itinéraire emprunté pour la distribution est longue pour la même cause de la non praticabilité des méthodes quantitative et sur ce, il ce compte aucune contrainte parce que les charrois utilisés pour la plus part seraient des particuliers d'où la condition de route ne lui dit rien.

- Par analyse nous avions trouvé que la programmation efficiente des charrois automobiles pourrait contribuer entre autres à minimiser le coût alloué à la distribution de la boisson à la Bralima.

Partant de ceci, nous suggérons aux responsables de ladite maison et à toute personne intéressée pour l'amélioration des activités de la Bralima ce qui suit :

- De renouveler le système de transport en adoptant l'entreprise par des charrois automobiles propre à elle. L'utilisation de charrois automobiles de particulier cause un coût élevé dans sa fonction de distribution.

- De recruter les experts en recherche opérationnelle pouvant lui aider de faire les analyses par les méthodes quantitative pour l'optimisation de coûts liés à cette firme

- De pratiquer les méthodes quantitatives pouvant lui permettre de minimiser son coût de distribution

Nous n'avons pas la prétention d'avoir épuisé tous les éléments relatifs à ce sujet, d'autres chercheurs pourront nous compléter dans les pistes suivantes :

- Sur la programmation de charrois automobiles en utilisant la méthode de transport, ici tenant compte des circonstances liées à ce service.

- Soit l'optimisation de circuit de distribution en tenant compte de la maximisation et minimisation de ce service.

BIBLIOGRAPHIE

A. OUVRAGES

1. BAMWISHO, M., Initiation à la méthodologie de la recherche en

éducation, éd. PUZ, Kinshasa, 1975.

2. BEITONE, A. et al., Dictionnaire des sciences économiques, éd. Colin,

Paris, 2001.

3. COHEN, E., Dictionnaire de gestion, éd. La découverte, Paris, 2001.

4. M'VIBUDULU KALUYIT, J., Initiation aux méthodes et pratiques de

recherche opérationnel, T.1, Kin., 2007.

5. KAUFMAN, A., Méthodes et modèles de la recherche opérationnelle,

T.1, éd. Dunod, Paris, 1962.

6. KAUFMAN, A. et DESBASEILLE, Méthodes du chemin critique,

applications aux programmations et d'étude de la

méthode PERT et ses variables, éd. Dunod, Paris, 1968.

7. QUINTTON, H. et VITRY A., économie politique, éd. Dalloz, Pars, 1986.

8. PAGGOLI P., Pratique de la méthode PERT, éd. Organisation, Paris,

1984.

9. ROHMER, B., Petit Larousse illustré, éd. CEDEX, Paris, 1983.

10. ECHUDE MAISON, C.D., Dictionnaire d'analyse économique, 6^e éd.,

Nathan, 2001.

11. BREMOND J. et Cie., Dictionnaire des sciences économiques e

sociales, éd. Hatier, Paris, 1983.

12. BERNARD GUERRIEU, Dictionnaire d'analyse économique, éd.

Dalloz, Paris, 2001.

B. MEMOIRES ET TFC

1. KILAURI BITUBI J., Impact des actions marketing sur la vente des produits Bralima dans une période de basse conjonctureImpact des actions marketing sur la vente des produits Bralima dans une période de basse conjoncture, inédit, ISP, 2003-2004

2. MURHULA BISIMWA F., Essai d'automatisation du circuit en vente dans une entreprise de production « cas de la Bralima/Bukavu, ISP/TFC, 2003-2004.

3. BARWANI BWASHI J., Gestion des activités de formation du personnel et leur rendement dans le milieu professionnel : cas de la Bralima/Bukavu, inédit, ISP, TFC, 2005-2006.

4. KANKOLONGO MBOWA J., Pratique de l'audit et l'application des mesures de contrôle interne, atouts majeurs du succès de la Bralima/Bukavu, ISP, inédit, TFC, 2004-2005.

5. BALIBUNO MURHULA I., Gestion des créances commerciales dans une entreprise industrielle : cas de la Bralima/Bukavu 2001-2004, inédit, TFC, ISP, 2004-2005.

6. 7. LWESSO WEMA P., Comptabilité analytique d'exploitation de la fixation du prix de vente au sein d'une entreprise industrielle au Congo : cas de la Bralima/Bukavu, inédit, TFC, ISP, 2005-2006.

8. NZIGIRE RUCHOGEZA, Modèle de gestion de production des bières et boissons gazeuses à la Bralima SARL siège de Bukavu, UCB, Mémoire, inédit, 1996-1997.

9. KINDU MUNDEKE, Analyse systématique de la possibilité de proposer une technique d'ordonnancement des canaux de la Bralima/Bukavu, UCB, Mémoire, inédit, 1998-1999.

10. MBAHE MBAMBU, D., Rationalisation du circuit de distribution interne à la Bralima/Bukavu, UCB, Mémoire, 1998-1999.

11. BUNANE MUSHAMUKA, Correction entre la productivité du travail et les facteurs motivationnels : cas de la Bralima/Bukavu, YCB, Mémoire, inédit, 2001-2002.

12. MBUMBA KALONGO F., Construction au volume de vente d'un produit à faible rotation par la recherche de nouvelles pistes commerciales : cas de Fanta tropical de 1996 à 2000 à la Bralima/Bukavu, UEA, TFC, inédit, 2001-2002.

13. MBUMBA KALOLNGO F., Analyse de la structure Financière d'une entreprise : cas de la Bralima Condo de 2000 à 2003, UEA, Mémoire, inédit, 2003-2004.

C. COURS

- M'VIBUDULU KALUYIT J., Recherche opérionnelle, ISP/Bukavu,

L₁SCAI, inédit, 2006-2007.

- MAGENDO NAKACIGA, Recherche opérationnelle, ISP/Bukavu, inédit,

L₁ SCAI, 2005-2006.

TABLE DES MATIERES

IN MEMORIAM I

EPIGRAPHE II

DEDICACE III

REMERCIEMENTS IV

SIGLES ET ABREVIATIONS V

0. INTRODUCTION 1

0.1. Problématique 1

0.2. Hypothèses 2

0.3. Objectifs 3

0.4 Choix et intérêt du sujet 3

0.5. Délimitation du sujet 4

0.6. Approche méthodologique 4

6.1. Méthodes 4

0.7. Etat de la question. 6

0.8. Difficultés rencontrées. 8

0.9. SUBDIVISION DU TRAVAIL 9

CHAPITRE 1 10

CONSIDERATIONS THEORIQUES 10

1 .1. Définitions des concepts 10

1.1.1 La programmation 10

1.1.2  La programmation linéaire 11

1.1.3 La programmation dynamique 16

1.1.4. La distribution 17

1.1.5. La production 17

1.1.6. Le charroi 18

1.1.7. La boisson 18

1.1.8. Le coût 18

1.1.9. Optimisation 19

1.1.1O Modèle de transport d'une programmation linéaire 19

1.1.11. Les dépôts relais 20

1.2. Présentation de la Bralima / Bukavu 21

1.2.1 Situation géographique 21

1.2.2. Historique 21

1.2.3. Champ d'action 22

1.2.4 Produits fabriqués 23

1.2.5. Objet de la Bralima Bukavu 23

1.2.6. Organisation structurelle et Fonctionnelle 24

1.2.7. Conclusion partielle 26

CHAPITRE II 27

GENERALITES ET POLITIQUES DE LA DISTRIBUTION DE LA BRALIMA/BUKAVU 27

2.1. Généralités sur la Distribution 27

2.1.1. Définition de la distribution 27

2.1.2. Les fonctions de la distribution 27

2.1.3. Les canaux de distribution 29

2.1.4. Canaux de distribution 30

2.2. La politique de la distribution à la BRALIMA/BUKAVU 30

2.2.1. Notion générale sur la politique de la distribution 30

2.3 Le coût de distribution de la Bralima Bukavu 26

2.4. Conclusion partielle 28

CHAPITRE 3 29

LA PROGRAMMATION DYNAMIQUE DE CHARROIS AUTOMOBILES DE LA BRALIMA/BUKAVU 29

3.1. Introduction sur la programmation dynamique 29

3.2. Introduction à la théorie de graphe 30

3.2.1. Définition de graphe 30

3.2.2. Sommet suivant et sommet précédent 31

3.2.3. Les points de vente de la BRALIMA 32

3.3. La Politique optimale de la distribution à la Bralima/Bukavu 51

3.3.1. Subdivision de circuit de distribution de la Bralima 52

3.3.2. Analyse proprement dite de chaque axe 54

3.4. Conclusion partielle 63

CONCLUGION GENERALE 64

BIBLIOGRAPHIE 67

TABLE DES MATIERES 69

* ¹

* ²