Etude ab-initio de la stabilité ou de la métastabilité d'un anion tétratomique. Cas du système N2O2-/N2O2

CHAPITRE 2

RESOLUTION DE L'EQUATION DE

SCHRÖDINGER NUCLEAIRE.

UNIVERSITE DE DOUALA /ECOLE DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.

2.1. INTRODUCTION.

Après avoir déterminé les puits de potentiel sur lesquels se meuvent les

électrons, il est tout aussi très intéressant de maîtriser les mouvements des noyaux. Dans cette section, la théorie des groupes nous sera d'une très grande utilité.

2.2. RESOLUTION DE L'EQUATION DE SCHRÖDINGER NUCLEAIRE PAR

LA METHODE DES PERTUBATIONS.

L'étude de la dynamique des noyaux revient à la résolution l'équation de Schrödinger nucléaire (1.21) :

? T _N + V _j ( ) ? Ø _Nj ( ) = E _T Ø _Nj ( ) .

R R R

? ?

Pour résoudre cette équation, on fait en plus de l'approximation de Born-Oppenheimer, une deuxième approximation d'ordre zéro qui suppose que le mouvement de rotation de la molécule est indépendant de ses mouvements de vibration ; de sorte que l'on peut étudier la vibration de la molécule en ne tenant pas compte de sa rotation, puis la rotation globale de la molécule supposée indéformable.

2.2.1. Vibrations moléculaires.

2.2.1.1. Cas simple d'une molécule diatomique.

2 2

? ?

h ?

? - ₂ U(R) n E

+ ? Ø = n

Ø . (2.1)

? ì ?

2 R ?

Considérons le cas d'une molécule diatomique qu'on assimilera à un système constitué de deux atomes de masses ponctuelles M1 et M2 séparées par une distance R et interagissant par l'intermédiaire d'un potentiel U(R). Le système ainsi formé a une énergie totale E et vérifie l'équation de Schrödinger suivante :

Le premier terme dans (2.1) est l'énergie cinétique de vibration ; est la masse réduite

ì

du système.

Un développement en série de Taylor de U au voisinage de son minimum ( R = R _e)

donne :

UNIVERSITE DE DOUALA /ECOLE DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.

(2.2)

? ?

dU 1 d U

? ?

2 2 1 d U

? ?

3

3

U(R R )

- = ? ? - + ? ? -

( )

R R ( )

R R + ? ? -

( )

R R + ...

e e 2 e 3 e

? ?

dR 2! dR

R ? ? 3! dR

? ?

e R R

e e

2! ?dR

1 d ² U (R -R _e)² + 1 d3U1 ( R -R _e)³ +...
2 R 3! ? dR3 _R

e e

Les mouvements moléculaires étant de faible amplitude, on peut, dans l'approximation harmonique, négliger les termes de degré supérieur à deux. Ainsi, on a :

.

(2.3)

U(R - R _e ) = ₂¹k ( R -R_e)²

Où k = C1.2U

dR2 est la constante de force harmonique. Ainsi, la résolution de

Re

l'équation (2.1) conduit aux solutions suivantes :

[ Ø n p) C _p e 2 á ( R -Re) 2H p ( á ( R - R_e ))

(2.4)

E ( p) = ( p+ ¹² )hù

1

L_ì 1 dRd 2 U2 ?2

03 = Avec p ? 0 , =pulsation de l'oscillateur. ; H _p=polynôme

R_e

d'Hermite ;

( 2 ^p p! á ð) ²

ìù

= Constante de normalisation et .

á =

h

C_p =

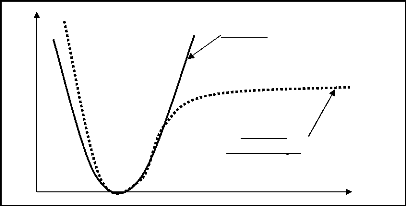
Potentiel

Potentiel
anharmonique

Figure 2.1 : Potentiel harmonique et anharmonique.

UNIVERSITE DE DOUALA /ECOLE DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.

Physiquement, le potentiel harmonique ne parvient pas à expliquer la dissociation des molécules et certaines transitions vibroniques. En effet, l'approximation harmonique devient très vite insuffisante dès que l'on s'éloigne de la position d'équilibre. D'où l'idée de l'approximation anharmonique.

2.2.1.2. Potentiel anharmonique.

Pour un tel potentiel, on ne néglige plus les termes de degré supérieur à 2 dans l'équation (2.2). Toute fois, comme ils sont très inférieures au terme quadratique, on peut considérer la correction qu'ils apportent à l'hamiltonien total du système comme une perturbation stationnaire. Ainsi, en première approximation, on peut écrire :

1 2 1 d U ? ? 3 3 U(R R ) k R R - ( ) - + ? ? - ( ) R R e e 3 e 2 6 dR ? ? R e Par suite, au second ordre de perturbation, on a :

. (2.5)

( )

p ? ? ?

1 1

E = ? + ? ù - ? +

p h p

? ? ?

2 2

? ? ù x

h . (2.6)

e

?

2

Où x_e est une constante positive appelée constante d'anharmonicité. L'écart entre deux niveaux consécutifs d'énergie n'est plus constant et vaut :

E E

( p ) ( p 1 )

1 ?? ? ? . 2 ? ?

(2.7)

- ? ?

- = ù ? - ? +

h 1 x p

e

? ?

Ainsi, les niveaux se resserrent lorsqu'on monte en énergie.

Une des formes analytiques de potentiel anharmoniques la plus couramment utilisée est le potentiel de Morse^[21] (fig. 2.2) :

U R D _e 1 _e-â -

( e ) 2

R R

( ) = ? - ? ? . (2.8)

?

.

hù_e

=

x e

(2.11)

4D

e

UNIVERSITE DE DOUALA /ECOLE DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.

.
.

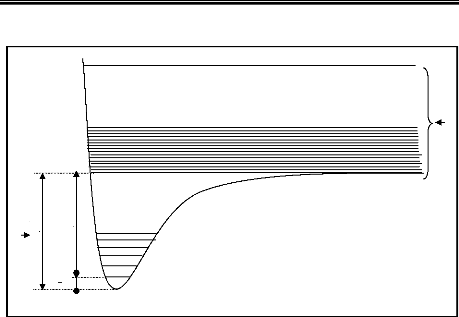
(a)

.

.
.

D_e

D0

.

⁽b⁾

₂ hù

1

Figure 2.2 : Potentiel de Morse. (a) Continuum, (b) Limite de dissociation

Où D_e est l'énergie de dissociation et â une constante caractéristique de la molécule considérée.

En faisant un développement limité à l'ordre 3 au voisinage de la position d'équilibre _Re, on trouve :

( ) ( ) ( ) ( ( ) )

â ³

2 2 3 3

U R D e R R e

= â - - R R e

- + Ï -

R R . (2.9)

e

2

En identifiant cette relation à la relation (2.5), on arrive à :

1

? ì ? 2

â = ? ? ù . (2.10)

e

? ?

2D_e

Et l'énergie du système est donnée par la relation (2.6) avec

UNIVERSITE DE DOUALA /ECOLE DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.

2.2.1.3. Vibrations moléculaires en mécanique quantique^[22].

Dans une molécule polyatomique, les atomes constitutifs subissent des oscillations autour de leur position d'équilibre. Au cours de ces oscillations, les longueurs des liaisons et les angles intramoléculaires changent de façon périodique.

En posant

q i = Miri,

n

M M

% = +? m

i i i

. (2.12)

i 1

=

L'énergie totale de vibration s'écrit :

^N 1 ^N

= ? % r & = ? & q_i . (2.13)

1 2 2

E M

V i i

2 = 2 =

i 1 i 1

L'énergie potentiel de vibration V(q), où q désigne l'ensemble des coordonnées qi, peut
être développée en série de Taylor au voisinage de la position d'équilibre de chaque

qi0

atome ; soit :

N ? ? ? V 1 N N ? ? ? ^2 V V q V q ( ) ( ) = + ? ? + ? q ?? ? ? + q q ... 0 i i j i 1 = q ? ? ? 2 i i 1 j 1 ? ? ? ? ? ? q q = = q i j i0 q i0

(2.14)

En prenant l'origine de l'énergie potentiel à l'équilibre, on a ; la courbe

V ( q 0 ) = 0

d'énergie potentiel passe par un minimum pourq_i = q ₀ . Ainsi, le second terme du

i

membre de droite de (2.14) est nul. En se limitant à l'approximation harmonique, on a :

N N ? ? ? 2 1 V V q ( ) = ?? á q q , á = ? ? ij i j ij 2 i 1 j 1 = = ? ? ? ? ? ? q q i j q i0

. (2.15)

Pour étudier complètement le mouvement vibratoire d'un système, nous devons préciser ses coordonnées normales, ses coordonnées internes et ses coordonnées de symétrie.

2.2.1.3.1 Coordonnées normales

Les coordonnées normales sont les nouvelles coordonnées qui conservent la forme

Q_i

de l'énergie cinétique, tout en permettant d'exprimer l'énergie potentiel sous une forme quadratique. En effet,

UNIVERSITE DE DOUALA /ECOLE DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.

1 1

2 2

E = ? ?

q & = Q&

V i i

2 2

i i

1 1 2 2

V q

( ) = ? á q q = ? ù Q

ij i j k k

2 2

i, j k

(2.16)

?

Où est une fréquence propre du système. Dans ce cas, une énergie propre du

ù_k

système est donnée par

3N 6

-? ?

1

E = ? + ? ù +

? h ? ? xij

n

k k

k 1 ? ?

2

= j j i

<

L'intérêt des coordonnées normales réside dans le fait qu'elles permettent de réaliser une représentation irréductible du groupe de symétrie du système étudié. En effet, à chaque fréquence propre du système, on peut toujours associer une coordonnée normale. Ce qui caractérise un mode propre de vibration précis, qu'on peut aisément associer à une représentation irréductible du groupe de symétrie du système global. On comprend donc que les coordonnées normales d'un système permettent de classifier ses vibrations. Mais, la détermination explicite de ces coordonnées normales est assez épineuse. Pour s'affranchir de cette difficulté, on utilisera la théorie des groupes.

2.2.1.3.2. Classification des vibrations moléculaires.

Pour classifier les vibrations moléculaires, on procède comme suit :

· On détermine la représentation totale engendrée par les 3N coordonnées de déplacement des atomes de la molécule.

· On détermine la représentation vibratoire totale _v en éliminant dans les

représentations associées aux translations et rotations d'ensemble.

· On décompose ensuite _v en représentations irréductibles.

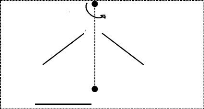
ó_v

C2

O

H H

Figure 2.3 La molécule d'eau

Etudions par exemple le cas de la molécule d'eau (H2O) dont la structure géométrique est représentée par la figure 2.3.

UNIVERSITE DE DOUALA /ECOLE DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.

Compte tenu de ses éléments de symétrie, cette molécule appartient au groupe _C2v. Sa représentation vibratoire totale est donc :

Ainsi, T = 3A 1 ? A 2 ? 2B 1 ? 3B₂ (2.17)

La représentation engendrée par les
translations et les rotations d'ensemble

C 2v

E	C 2	óv	' ó v	T
9	-1	3	-1

est :

T + R = A 1 ? A 2 ? 2B 1 ? 2B₂ (2.18)

Par suite, la représentation vibratoire totale est : V = 2A₁ ? B₂ (2.19)

On conclut donc que la molécule d'eau a :

9 2 modes de vibrations complètement symétriques (A1).

9 1 mode de vibration complètement antisymétrique (B1).

Parlant des modes de vibrations, on distingue :

9 Stretching mode (allongement)

9 Bending mode (courbure)

9 Twisting mode (torsion)

9 Wagging mode (hochement)

9 Scissoring mode (cisaillement)

9 Rocking mode (rotation plane)

De part cet exemple, on constate que la détermination du nombre de fréquences fondamentales d'une molécule ainsi que leur classement selon le type de symétrie correspondant aux représentations irréductibles contenues dans la représentation vibratoire totale, ne nous apprend rien sur le mouvement réel des atomes. Il faut donc penser à introduire les coordonnées internes et les coordonnées de symétrie.

2.2.1.3.3. Coordonnées internes.

Les déplacements des atomes dans une molécule peuvent en effet être repérés en
considérant les allongements des liaisons, ainsi que les variations des angles entre

q_i â i

les axes de liaison des atomes. Ces variations de longueur et d'angle sont appelées coordonnées internes de la molécule.

Pour illustration, reprenons l'exemple du H2O.

UNIVERSITE DE DOUALA /ECOLE DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.

H H

Figure 2.4. coordonnées internes de la molécule d'eau.

O

â

q₁ q₂

Ainsi, on a : v = q ? _â , (2.20)

avec q = A ₁ + B ₂ et â = A₁. (2.21)

2.2.1.3.4. Coordonnées de symétrie.

Les coordonnées de symétrie sont des fonctions de base des représentations figurant dans une décomposition canonique. Elles sont des combinaisons linéaires d'un seul type de coordonnées internes. Elles ont l'avantage de livrer le secret des mouvements réel des atomes dans une symétrie donnée.

Pour déterminer ces coordonnées de symétrie, on applique sur tous les coordonnées internes, l'opérateur projecteur P_á défini par :

n á = ? ÷ á P g G

* ( ) ( ) ^á G

.

(2.22)

Où ÷ est le caractère associé à la représentation irréductible du groupe de

( á )

á

symétrie G ; ( G) est le caractère de la représentation totale de ce groupe ; n_á est la dimension de _á et g est l'ordre du groupe G.

Ainsi, les coordonnées de symétrie de la molécule de H2O sont :

( )

q q

1 + 2

2

? ? S A

2 ( ) = â

1

1

( ) ( )

= q q

-

1 2

²

1

S A

1 ( ) =

1

?
?
?

?

S A

3 1

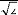
(2.23)

Maintenant, on sait comment les atomes bougent dans un mode de vibration donnée.

UNIVERSITE DE DOUALA /ECOLE DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.

2.2.2. Rotations moléculaires (rotateur rigide)

2.2.2.1. Molécules linéaires.

Si on assimile la molécule à un rotateur rigide, l'Hamiltonien H_r relatif à la rotation s'écrit :

Hr

L2 2I

.

(2.24)

I est le moment d'inertie du système par rapport à son centre d'inertie G. L étant

l'opérateur moment cinétique dont les composantes , , dans un repère mobile

L _x L _y L z

(Gxyz) et , , dans un repère fixe (OXYZ) vérifient la relation :

L_X L_Y L_Z

L L L L L L L

2 = + + = + + Z

2 2 2 2 2 ² . (2.25)

x y z X Y

{ }

L , L z

² Constitue un E.C.O.C. Donc les fonctions J,M , sont les bonnes fonctions

propres associées à H_r ; et on a :

H _r J,M = E _r J,M . (2.26)

En remplaçant H_r par son expression en (2.24), on obtient :

E J = hcB _eJ(J + 1). (2.27)

h

Où =

B est la constante de rotation.

^e 8 cI

ð ²

Pour une valeur de J, il existe (2J+1) harmoniques sphériques è ?

Y , =-

^M ( ) . Donc

J M J,...,J

chaque valeur propre EJ est (2J+1) fois dégénérée.

2.2.2.2. Molécules non linéaires.

Si on assimile la molécule à un rotateur rigide, l'Hamiltonien H_r relatif à la rotation s'écrit :

H r

2 2 2

1? L ^L L ? x y

= + + ^z . (2.28)

2 I I I

? ?

? xx yy zz ?

Par ailleurs, { }

L , L _z , L Z

² est un E.C.O.C. D'où la base J,K,M est une base propre

associée à H_r telle que :

UNIVERSITE DE DOUALA /ECOLE DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.

J 0,1,...

=

2

? J,K,M J J 1 J,K,M

2

L = +

( ) h

? L J,K,M K J,K,M

?

?

??

(2.29)

K J,...J

=-

= h

z

M J,...J

=-

LJ,K,M M J,K,M

= h

Z

L_Z

Les fonctions propres correspondant aux vecteurs propres simultanés de , et

L ² Lz

sont de la forme [23] :

Ö ( ) È è J iK J,K,M , , è ? ÷ = N J,K,M K,M e ÷ eiM ? ( )

.

(2.30)

Où est la constante de normation, et est un polynôme de Legendre. ,

J

N J,K,M È K , M Ixx

Iyy

et sont les moments principaux d'inertie dans les directions (Gx), (Gy) et (Gz) Izz

respectivement. Ils permettent de caractériser la molécule :

· Si les trois moments principaux d'inertie sont égaux, la molécule est une toupie sphérique.

· Si I xx = I yy ? I _zz , la molécule est une toupie symétrique.

· Si I xx ? I yy ? I _zz, la molécule est dite toupie asymétrique.

Par ailleurs, l'énergie de rotation du système est donnée par l'équation :

H _r J,K,M = E _J J,K,M . (2.31)

Ainsi,

V' Dans le cas d'une toupie sphérique, on a :

E J = hcB _e J ( J + 1). (2.32)

Et, pour chaque valeur de J ; K et M prennent chacun (2J+1) valeurs. Par suite, à
chaque niveau d'énergie EJ correspond (2J+1)² valeurs de J,K,M différentes. EJ

est alors (2J+1)² fois dégénérée.

V' Dans le cas d'une toupie symétrique, on a :

E J, K hc ? B _e J J 1 A _e B _e K

= ( ) ( ) ²

+ + - ? . (2.33)

? ?

B		h			h et sont les constantes rotationnelles à l'équilibre. A = ^e 8 cI ð ^2 zz
	xx

Pour une valeur donnée de J, le nombre quantique M peut prendre (2J+1)
valeurs différentes ; et comme EJ, K dépend de la valeur absolue de K, il lui

UNIVERSITE DE DOUALA /ECOLE DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.

correspond 2(2J+1) valeurs de J,K,M différentes. E J, K est donc 2(2J+1)

fois dégénérée.

v' Dans le cas d'une toupie asymétrique, plusieurs calculs ont été faits pour obtenir une formule donnant les énergies EJ. Nous donnons l'expression proposée par Wang^[24] :

? 1 1

E hc B C J J 1 A

J ( e

= ? + e ) ( ) e ( e

? ? ?

+ + - B C W

+ e ) ? ? , (2.34)

? ô

? 2 ? 2 ? ?

h

avec C = .

yy

^e 8 cI

ð ²

Pour J donnée, prend (2J+1) valeurs différentes ; et par conséquent, on a (2J+1)

W_ô

états différents ^[23].

2.2.3. Solution du problème nucléaire.

Le mouvement nucléaire peut se décomposer en vibrations, rotations et translations. Dans un premier temps, on se place dans le référentiel du centre de masse de la molécule. Ce qui revient à ne plus percevoir le mouvement de translation. Par ailleurs, les vibrations et les rotations sont faiblement couplées. On néglige donc ce couplage. Ce qui revient à exprimer la fonction d'onde nucléaire comme un produit de fonctions d'onde vibrationnelle et rotationnelle.

La fonction d'onde vibrationnelle est le produit d'une vibration d'élongation et d'une vibration angulaire.

Ainsi, la fonction d'onde vibrationnelle peut s'exprimer :

2

( ( ) ) ( ) ( )

1 R R

á - e l

Ö = 2

vib A H n á -

R R _e e P _n cos ã . (2.35)

Par suite, la fonction d'onde nucléaire pourra être écrite comme suit :

2

( ( ) ) ( ) ( ) ( )

2 1 R R

á - e l J iK

N A H n R R _e e ã È è

P _n cos K,M e e

÷ iM ?

Ö = á - . (2.36)

UNIVERSITE DE DOUALA /ECOLE DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.