Evaluation des options à barrière dans le modèle GARCH

Bibliographie

[1] Ben-Ameur, H., M. Breton, J.-M. Martinez, "A Dynamic Programming Approach for Valuing Options in the GARCH model", Avril 2008.

[2] Black, F.et M. Scholes, "The Pricing of Options and Corporate Liabilities", The Journal of Political Economy, Vol 81(1973), 637-659.

[3] Bollerslev, T., "Generalized Autoregressive Conditional Heteroscedasticity", Journal of Econometrics, Vol 31(1986), 307-327.

[4] Boyle, P. et Hoon Lau, S., "Bumping Up Against the Barrier with the Binomial Method", The Journal of Derivatives, 1994.

[5] Boyle, P., M. Broadie et P. Glasserman, "Monte Carlo Methods for Security Pricing", Journal of Economic Dynamins and Control, Vol 21(1997), 1263-1321.

[6] Cheuk, T. et T. Vorst, "Complex Barrier Options", The Journal of Derivatives, 1996, 8-3 2.

[7] Cox, J., Ross, S. et Rubinstein, M., "Option Pricing: A Simplified Approach", Journal of Financial Economics, Vol 7 (1979), 229-264.

[8] Duan, J.-C., "The GARCH Option Pricing Model", Mathematical Finance, Vol 5 (1995), 13-32.

[9] Duan, J.-C., J.-G. Simonato, "American Option Pricing under GARCH by a Markov Chain Approximation", Journal of Economic Dynamics and Control, Vol 25 (2001), 1689-1718.

[10] Duan, J.-C., E. Dudley, G. Gauthier, J.-G. Simonato, "Pricing Discretely Monitored Barrier Options by a Markov Chain", The Journal of Derivatives, 2003.

[11] Engle, R. F., "Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation", Econometrica, Vol 50 (1982, 987-1008.

[12] Harrison, J.-M., D.-M. Kreps, "Martingales and Arbitrage in Multiperiod Securities Markets", Journal of Economic Theory, Vol 20 (1979), 381-408.

[13] Heston, S.-L., S. Nandi, "A Closed-Form GARCH Option Valuation Model", The review of Financial Studies, Vol 13 (2000), 585-625.

[14] Merton, R., "Theory of Rational Option Pricing", Bell Journal of Economics and Management Science, Vol 4 (1973), 141-183.

[15] Reiner, E. et Rubinstein, M., "Breaking Down the Barriers", Risk, 1991, 28-35.

[16] Ritchken, P., "On Pricing Barrier Options", The Journal of Derivatives, 1995, 19-28.

Annexe A : Matrices de transition

dans le modèle NGARCH

Le modèle NGARCH pour l'évaluation des options s'écrit comme suit:

St+1 ^lnSt

= r-

1 2

\/ Ht+1 + Ht+1Et+1 (3.1)

Ht+1 = /30 + /31Ht + /32Ht(Et - À - O)² (3.2)

Q

Et+1 j Ft~ N (0, 1),(3.3) On pose 'y = O + À, s = St,o = St-1, y = Ht+1 et h = Ht. A partir des équations (3.1) et (3.2), nous allons déterminer le terme d'erreur Et en fonction des variables du modèle.

Ainsi, l'équation (3.1) donne :

ln(8 _o ) - r + h 2

a(o, s, h) = _p

h

L'équation (3.2) donne deux formes de Et données par les fonctions f1 et f2 comme suit:

_s

y - /30 - h/31

f1(y,h) = 'y + , y ~ /3₀ + h/3₁

h/32

_s

y - /30 - h/31

f2(y, h) = 'y - , y ~ /3₀ + h/3₁

h/32

Maintenant, en appliquant ces équations aux points de la grille MN, ces formules deviennent:

aikl =	ln(ai) -- r + dl ak 2
	bl

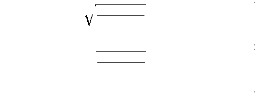
1jl 2jl

= =

8 < : 8 'Y < :

+ --

qd3^-00^-dl01

si d e0+ do1

dl02

00 sinon

si dj > _!B0+ dl/1

d3-00-dl01
dl02

+oc sinon

}

}

On note ainsi que l'événement ak exp(r -- bl ₂+ NdlE) 2 [ai, ai+1) correspond à l'événement E 2 [aikl, ai+1,kl)
· De même, on note que l'événement y 2 [dj, dj+1) correspond à E 2 [ 1 jl, 1j+1,l)u [ 2j+1,l, 2

jl)
· Afin de tenir compte de ces deux contraintes, on pose les nouvelles

bornes suivantes :

c1_;ijkl= maxfaikl, 1 jlg

c2,ijkl = minfai+1,kl, 1 j+1;lg

c3,ijkl = maxfaikl, 2 j+1;lg

c4_;ijkl= ^minf ai+1,kl , 2jl1

Ainsi, on a :

{ [aikl, ai+1,kl) n [ ¹jl, ¹j+1,l) = [c1,ijkl, c2,ijkl) ^si c1,ijkl ^Ç c2,ijkl

0 sinon

[aikl, ai+1,kl) n [..1+1,l, ..72.l) = [c3,ijkl, c4,ijkl)

{

25 si c3,ijkl c4,ijkl

sinon

On rappelle que les matrices de transition pour l'approximation quadratique-linéaire sont :

avec

Aklij = Eakdl[1[(Rij)] Cklij = Eakdl[Ht+21[(Rij)] Eklij = Eakdl[S^2t+11[(Rij)]

, , ,

Bklij = Eakdl[St+11[(Rij)] , Dklij = Eakdl[St+1Ht+21[(Rij)] , Fklij = Eakdl[S^2t+1Ht+21[(Rij)].

Rij = {St + 1 E [ai, ai+2) et Ht+2 E [dj, dj+1)}

Afin d'alléger l'écriture des formules de ces matrices, on pose Cp,ijkl = c_p pour p E {1, 2, 3, 4} et on pose :

1[1= 1[(C2 > c1)
1[2 = 1[(C4 > C3)

Si on pose 4) la fonction de répartition de la loi normale centrée réduite, les matrices de transition s'écrivent alors :

Aklij = Eakdl[1[(Rij)]

= 1[1(4)(C2) -- 4)(C1)) +1[2(4)(C4) -- 4)(C3))

Bklij = Eakdl[St+11[(Rij)]

= ake^r (1[1(4)(C2--'Vdl) -- 4)(c1 --_/'Vdl)) +(1[2(4)(C4 -- 'Vdl) -- 4)4 -- \Ml)))

Cklij = Eakdl[Ht+21[(Rij)]

= Aklij(~0 + ~1dl + e2dl(1+-²))

1[1^e2dl (c2e-- _e--¹c²_-- 2,₇ (e--12c22-- e--1c21)

N/2R-

(e2dl1c2 1 _c

1[2 a4e--2 4 -- c3e-- 2 c2 3 -- 2-y (e-- 1 _{2 c}2 2 4-- e--2 ³⁾⁾

N/27r

Dklij = Eak dl [St+1Ht+2I(Rij )1

= Bklij (⁸0 + Q1dl + ₂ dl (1 + -y -- N/dl)²)

akere2dl2 2

(c2 -- N/dl) (c2-,/dl) -- (c1 -- N/dl) e-2(c1- \Ml)

N/27r

2 (-y -- N/dl) (e-12(c2-,/dl)2--e-12.(c1-,/dl)2)

T

ake _e2dl ( (

I2c4-- _N/ ) dl e-12. (c4-,/dl)2 -- (c3 -- _N/ ) dl e-12. (c3- \Ml)2

27r

2 (-y -- N/dl) (e-12(c4-,/dl)2 -- e-2(c3-,/dl)2))

Eklij = Eakdl[S²t+1I(Rij)1

(= a?,e^2r+dl I1 ((D (c2 -- Wdl) -- 4e (c2 -- Wdl)) +I2 (l) (c4 -- Wdl) -- 4) (c3 -- Wdl)))

)2) )

Fklij = Eak dl [S²t+ 1Ht+2I(Rij )1

= Eklij (8 0 + !B1dl + e2dl (1 + (-y -- 2N/dl

_a2 e2r+dl /32d? (C2 I1

C2 -- Wdl) e-2(c2-2,/dl) ²

- -- Wdl) _e^-12(c1 -2,/dl )2

N/27r

2 (-y-- 2N/dl) (e-12(c2-2,/dl)2 -- e-12-(c1-2,/dl)2) k Na

2 _e2r#177;di e _2d?

I2 a (c4 -- 2 N/dl) e-2(c4-2,/dl)2

(c3 -- Wdl) e-2(c3-2\Ml)2

(c4^-2,/dl)^{2 1--} e-12(c3-2,/dl)2)

7r

2 (-y -- Wdl) (e-