IV.6.1 AG en îlots (ou avec demes)
Au lieu d'utiliser une seule population, on peut
trouver des AG qui utilisent des ensembles de petites sous-populations
(appelées des demes) qui évoluent
séparément. Ce modèle est appelé modèle en
îlots. Grâce à cette isolation, chaque îlot peut
évoluer avec ses propres paramètres, dans des directions
différentes, c'est-à-dire vers des solutions différentes.
Dans ce type d'AG, on peut faire migrer un certain nombre d'individus d'une
sous-population ( j ) à une sous population
voisine ( j +1). L'îlot qui évolue vers
un optimum local ou qui a convergé prématurément peut
être aidé par l'arrivée d'un ou de plusieurs individus
migrants.
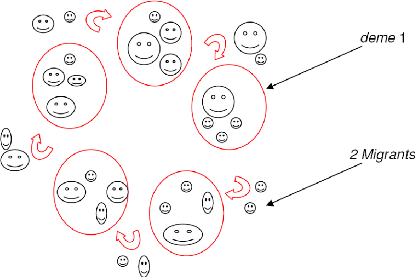
La Figure 27 présente un exemple d'une
population avec cinq demes, dans laquelle deux
individus sont choisis aléatoirement pour migrer du deme (
j ) au deme ( j +1). Les
individus sélectionnés pour la migration peuvent rester dans leur
îlot et seulement une copie est envoyée dans l'îlot voisin,
ou bien ces individus sont envoyés directement dans l'îlot
voisin.
D'après Ryan (1995), la sélection des
individus migrants peut se faire de deux façons. La première est
aléatoire, l'avantage de cette méthode est la plus grande
variété des individus qui peut en résulter. La seconde
méthode consiste à sélectionner les individus en fonction
de leurs fonctions d'adaptation et choisir les plus performants de chaque
îlot pour les copier dans les autres îlots, ce qui peut engendrer
une évolution plus directe que la première
méthode.
[ Cantù-Paz ,00] a testé plusieurs
autres configurations, par exemple : les meilleurs migrants remplacent les
moins bons, les migrants sélectionnés aléatoirement
remplacent les moins bons, les meilleurs migrants remplacent des migrants
sélectionnés aléatoirement. Le choix des individus
migrants d'un deme à l'autre et des individus remplacés dans
chaque deme peut influencer la pression de sélection. Les configurations
qui sélectionnent les individus migrants ou remplacés en fonction
de leur fonction d'adaptation ont tendance à accélérer la
convergence.
94
Figure 27 Représentation d'un AG en
îlots
L'avantage du modèle en îlots est que la
recherche de la meilleure solution se fait en parallèle, dans
différents espaces de recherche, ce qui permet d'avoir plusieurs
solutions qui peuvent être très utiles surtout dans le cas des
fonctions multimodales. Le second avantage est que, lorsque l'on envoie des
individus d'un îlot à l'autre, on peut éviter une
convergence prématurée de l'AG dans chaque îlot et le fait
de copier des individus d'un îlot à l'autre plutôt que de
les envoyer à l'îlot voisin ne cause aucune perte dans la
qualité des individus, même lorsque ces individus devront
s'apparier avec d'autres individus moins bons.
L'AG en îlots nécessite de
préciser, en plus des paramètres de l'AG standard cités
précédemment , les paramètres suivants : la taille des
sous-populations (ou nombre de demes), la fréquence de migration des
individus (exprimée en nombre de générations) et le nombre
d'individus qui migrent à chaque fois (peut être exprimé en
% de la taille du deme).
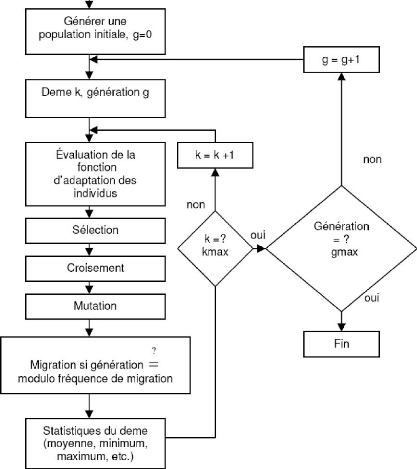
L'algorithme pour le modèle en îlots est
schématisé à la Figure 28. Dans chaque deme
(sous-population), un AG est exécuté séquentiellement. Les
demes peuvent s'échanger de l'information de temps à autre en
permettant à certains individus de migrer d'une sous-population à
l'autre selon certaines topologies.
95
Figure 28 Processus d'évolution dans un
modèle d'AG en îlots, générationnel
96
| 


