|
UNIVERSITÉ PARIS 8 - VINCENNES SAINT-DENIS
LICENSE ÉCONOMIE ET GESTION - PARCOURS
ÉCONOMIE-FINANCE
DÉPARTEMENT D'ÉCONOMIE ET GESTION
Francisco Pitthan
ECONOMÉTRIE FINANCIÈRE
Une comparaison entre les données
boursières et le chiffre d'affaires
2014
Paris
Francisco Pitthan
ECONOMÉTRIE FINANCIÈRE
Une comparaison entre les données boursières et le
chiffre d'affaires
Mémoire de License 3 présenté au
département
d'économie et gestion de l'Université Paris
8 -
Vincennes Saint-Denis comme une exigence
partielle pour obtenir le
grade de License
Directeur de Mémoire: Prof. David Guerreiro
2014
Paris
REMERCIEMENTS
Tout d'abord, je voudrais remercier mon Directeur de
Mémoire énormément pour son aide, attention et patience.
Monsieur David Guerreiro, sans vous mon travail n'aurait pas été
possible, je vous remercie infiniment.
Je voudrais également remercier tous mes enseignants qui
ont beaucoup m'aidé, même à distance, avec du support
bibliographique et des conseils très importants. Sabino da Silva Porto
Jr., Nelson Seixas dos Santos, Hudson da Silva Torrent et Fernando Boeira
Sabino, merci beaucoup pour votre aide extraordinaire.
Je souhaite remercier mon professeur de ma bourse d'initiation
scientifique à l'UFRGS au Brésil, Pedro Cezar Dutra Fonseca, pour
ouvrir mon esprit à la recherche. Cela n'est pas un travail facile,
quand même, avec une bonne guidance on peut arriver à des grands
résultats, merci beaucoup.
Je tiens à remercier vivement l'enseignant Stefano
Florissi pour ces livres d'économie de la culture, mais surtout pour
avoir cru en moi. Vous m'avez beaucoup motivé à
poursuivre mes études en économie, ce qui m'a
permis d'être en mesure de rêver plus grand, merci beaucoup.
Ma chère famille, je vous remercie pour tout le soutien
affectif et financier, sans vous je ne serais pas ici, j'ai passé
quelques moments difficiles et vous m'avez énormément aidé
à les surmonter. Mon bien-aimé père, tu étais ma
plus grande source d'inspiration pour continuer à travailler tous les
jours, je te remercie chaque jour pour m'avoir aidé à
conquérir ce rêve.
Je voudrais remercier ma cousine Leticia Pitthan, son compagnon
Edouard Rogé et la petite Clara pour m'avoir accueillie quand je suis
arrivé à Paris et pour me laisser faire partie de leur famille.
Je vous souhaite un grand succès et beaucoup de bonheur, un bisou
à Clara !
Je tiens également à remercier mes amis qui ont
écoutés mes réclamations et qui m'ont fait
découvrir que l'amitié existe même à distance,
particulièrement Bruno de Oliveira, Lucas Beppler, Bruno Birkheur et
Gustavo Jung (qui a beaucoup m'aider avec quelques idées pour mon
mémoire). Je voudrais remercier mon colocataire et ami Yan Huapaya pour
tous les verres, les conversations et les idées d'affaires qu'on a
partagés, tu as beaucoup m'aidé à devenir plus
ambitieux.
"Je dédie ce travail à mon père,
aujourd'hui
je peux voir plus loin parce que je suis sur
tes
épaules, merci beaucoup."
RÉSUMÉ
Ce présent travail a comme objectif principal l'analyse de
l'influence des données comptables sur le marché boursier. Cet
objectif a été établi par une inquiétude
personnelle sur le fonctionnement des marchés financiers, plus
précisément, sur la façon dont les cours des actions
varient. Pour le réaliser, une étude économétrique
a été réalisée en faisant des tests de
stationnarité et de cointégration afin de savoir si les
séries ont une relation de long terme entre elles. D'après les
résultats on constate que les séries ne sont pas
cointégrées et que les relations à court terme qui ont
été estimés n'ont pas un grand pouvoir d'explication.
Mots-clés : Économétrie Financière
; Cours Boursier ; Chiffre d'Affaires ; Modèle à Correction
d'Erreur ; Test ADF ; Test d'Engle-Granger ; Cointégration
ABSTRACT
The present work has as main objective the analysis of the
influence of accounting data on the stock market. This target was set by a
personal concern about the functioning of financial markets, more precisely,
how stock prices vary. To achieve this, an econometric study was performed by
testing for stationarity and cointegration to determine whether the series have
a long-term relationship between them. From the results we see that the series
are not cointegrated and that short-term relationships that have been found not
to have a great explanatory power.
Keywords: Financial Econometrics; Stock Prices; Revenue; Error
Correction Model; ADF test; Engle-Granger test; Cointegration
Liste des Graphiques
Graphique 1 : Exemple d'un bruit blanc (stationnaire)
Graphique 2 : Inflation aux États-Unis entre 1959 et 1995
(processus de différence stationnaire)
Graphique 3 : Consommation per capita réel aux
États-Unis entre 1959 et 1995 (processus de tendance stationnaire)
Graphique 4 : Log du CA de l'entreprise TOTAL SA
Graphique 5 : Log du CA différencié de l'entreprise
TOTAL SA Graphique 6 : Log du CA différencié deux fois de
l'entreprise LVMH Graphique 7 : Log du CA différencié deux fois
de l'entreprise Sanofi Graphique 8 : Log des cours boursiers de l'entreprise
TOTAL SA Graphique 9 : Log des cours boursiers différenciés de
l'entreprise TOTAL SA
Liste des Tableaux
Tableau 1 : Valeurs critiques de Dickey-Fuller pour
l'hypothèse de racine unitaire
Tableau 2 : Valeurs critiques de Dickey-Fuller pour la
constante et tendance temporelle
Tableau 3 : Valeurs critiques d'Engle et Yoo
Tableau 4: Modèle (3) du test ADF pour le log du CA de
l'entreprise TOTAL SA
Tableau 5: Modèle (2) du test ADF pour le log du CA de
l'entreprise TOTAL SA
Tableau 6: Modèle (1) du test ADF pour le log du CA de
l'entreprise TOTAL SA
Tableau 7: Modèle (3) du test ADF pour le log du CA
différencié de TOTAL SA
Tableau 8: Modèle (2) du test ADF pour le log du CA
différencié de TOTAL SA
Tableau 9: Modèle (3) du test ADF pour le log du CA
différencié de TOTAL SA
Tableau 10: Modèle (3) du test ADF pour le log du CA
différencié deux fois de LVMH
Tableau 11: Modèle (3) du test ADF pour le log du CA
différencié deux fois de Sanofi
Tableau 12: Modèle (2) du test ADF pour le log du CA
différencié deux fois de LVMH
Tableau 13: Modèle (2) du test ADF pour le log du CA
différencié deux fois de Sanofi
Tableau 14: Modèle (1) du test ADF pour le log du CA
différencié deux fois de LVMH
Tableau 15: Modèle (1) du test ADF pour le log du CA
différencié deux fois de Sanofi
Tableau 16: Modèle (3) du test ADF pour le log des
cours boursiers de TOTAL SA
Tableau 17: Modèle (2) du test ADF pour le log des
cours boursiers de TOTAL SA
Tableau 18: Modèle (1) du test ADF pour le log des
cours boursiers de TOTAL SA
Tableau 19: Modèle (3) du test ADF pour le log des
cours boursiers différenciés de TOTAL SA
Tableau 20: Modèle (2) du test ADF pour le log des
cours boursiers différenciés de TOTAL SA
Tableau 21: Modèle (1) du test ADF pour le log des
cours boursiers différenciés de TOTAL SA
Tableau 22: Modèle de MCO avec 3 variables dummies pour
TOTAL SA
Tableau 23: Test d'Engle-Granger pour l'entreprise TOTAL SA
Tableau 24: Relation de court terme estimé par MCO pour
TOTAL SA
Tableau 25: Relation de court terme estimé par MCO pour
BNP Paribas
Tableau 26: Relation de court terme estimé par MCO pour
L'Oréal
Tableau 27: Relation de court terme estimé par MCO pour
LVMH
Tableau 28: Relation de court terme estimé par MCO pour
Sanofi
Liste des Annexes
Annexe 1 : Chiffre d'Affaires de TOTAL SA
Annexe 2: Chiffre d'Affaires de BNP Paribas
Annexe 3: Chiffre d'Affaires de L'Oréal
Annexe 4: Chiffre d'Affaires de LVMH
Annexe 5: Chiffre d'Affaires de Sanofi
Annexe 6: Graphique de série temporelle pour le log du
CA de BNP Paribas
Annexe 7: Graphique de série temporelle pour le
CA de L'Oréal
Annexe 8 : Graphique de série temporelle pour le CA de
LVMH
Annexe 9 : Graphique de série temporelle pour le
CA de Sanofi
Annexe 10 : Test ADF pour le log du CA de BNP Paribas -
Modèle (3)
Annexe 11 : Test ADF pour le log du CA de BNP Paribas -
Modèle (2)
Annexe 12 : Test ADF pour le log du CA de BNP Paribas -
Modèle (1)
Annexe 13 : Test ADF pour le log du CA de L'Oréal -
Modèle (3)
Annexe 14 : Test ADF pour le log du CA de L'Oréal -
Modèle (2)
Annexe 15 : Test ADF pour le log du CA de L'Oréal -
Modèle (1)
Annexe 16 : Test ADF pour le log du CA de LVMH - Modèle
(3)
Annexe 17 : Test ADF pour le log du CA de LVMH - Modèle
(2)
Annexe 18 : Test ADF pour le log du CA de LVMH - Modèle
(1)
Annexe 19 : Test ADF pour le log du CA de Sanofi -
Modèle (3)
Annexe 20 : Test ADF pour le log du CA de Sanofi -
Modèle (2)
Annexe 21 : Test ADF pour le log du CA de Sanofi -
Modèle (3)
Annexe 22 : Graphique de série temporelle pour le log
du CA différencié de BNP Paribas
Annexe 23 : Graphique de série temporelle pour le log
du CA différencié de L'Oréal
Annexe 24 : Graphique de série temporelle pour le log
du CA différencié de LVMH
Annexe 25 : Graphique de série temporelle pour le log
du CA différencié de Sanofi
Annexe 26 : Test ADF pour le log du CA
différencié de BNP Paribas - Modèle (3)
Annexe 27 : Test ADF pour le log du CA
différencié de BNP Paribas - Modèle (2)
Annexe 28 : Test ADF pour le log du CA
différencié de BNP Paribas - Modèle (1)
Annexe 29 : Test ADF pour le log du CA
différencié de L'Oréal - Modèle (3)
Annexe 30 : Test ADF pour le log du CA
différencié de L'Oréal - Modèle (2)
Annexe 31 : Test ADF pour le log du CA
différencié de L'Oréal - Modèle (1)
Annexe 32 : Test ADF pour le log du CA
différencié de LVMH - Modèle (3)
Annexe 33 : Test ADF pour le log du CA
différencié de LVMH - Modèle (2)
Annexe 34 : Test ADF pour le log du CA
différencié de LVMH - Modèle (1)
Annexe 35 : Test ADF pour le log du CA
différencié de Sanofi - Modèle (3)
Annexe 36 : Test ADF pour le log du CA
différencié de Sanofi - Modèle (2)
Annexe 37 : Test ADF pour le log du CA
différencié de Sanofi - Modèle (1)
Annexe 38 : Cours Boursiers de TOTAL SA
Annexe 39 : Cours Boursiers de BNP Paribas
Annexe 40 : Cours Boursiers de L'Oréal
Annexe 41 : Cours Boursiers de LVMH
Annexe 42 : Cours Boursiers de Sanofi
Annexe 43 : Graphique de série temporelle pour le log
des Cours Boursiers de BNP Paribas
Annexe 44 : Graphique de série temporelle pour le log
des Cours Boursiers de L'Oréal
Annexe 45 : Graphique de série temporelle pour le log
des Cours Boursiers de LVMH
Annexe 46 : Graphique de série temporelle pour le log
des Cours Boursiers de Sanofi
Annexe 47 : Test ADF pour le log des Cours Boursiers de BNP
Paribas - Modèle (3)
Annexe 48 : Test ADF pour le log des Cours Boursiers de BNP
Paribas - Modèle (2)
Annexe 49 : Test ADF pour le log des Cours Boursiers de BNP
Paribas - Modèle (1)
Annexe 50 : Test ADF pour le log des Cours Boursiers de
L'Oréal - Modèle (3)
Annexe 51 : Test ADF pour le log des Cours Boursiers de
L'Oréal - Modèle (2)
Annexe 52 : Test ADF pour le log des Cours Boursiers de
L'Oréal - Modèle (3)
Annexe 53 : Test ADF pour le log des Cours Boursiers de LVMH -
Modèle (3)
Annexe 54 : Test ADF pour le log des Cours Boursiers de LVMH -
Modèle (2)
Annexe 55 : Test ADF pour le log des Cours Boursiers de LVMH -
Modèle (1)
Annexe 56 : Test ADF pour le log des Cours Boursiers de Sanofi
- Modèle (3)
Annexe 57 : Graphique de série temporelle pour le log
des Cours Boursiers Différenciés de
BNP Paribas
Annexe 58 : Graphique de série temporelle pour le log des
s Cours Boursiers Différenciés de L'Oréal
Annexe 59 : Graphique de série temporelle pour le log des
Cours Boursiers Différenciés de LVMH
Annexe 60 : Graphique de série temporelle pour le log des
Cours Boursiers Différenciés de Sanofi
Annexe 61 : Test ADF pour le log des Cours Boursiers
différenciés de BNP Paribas - Modèle (3)
Annexe 62 : Test ADF pour le log des Cours Boursiers
différenciés de BNP Paribas - Modèle (2)
Annexe 63 : Test ADF pour le log des Cours Boursiers
différenciés de BNP Paribas - Modèle (1)
Annexe 64 : Test ADF pour le log des Cours Boursiers
différenciés de L'Oréal - Modèle (3) Annexe 65 :
Test ADF pour le log des Cours Boursiers différenciés de
L'Oréal - Modèle (2) Annexe 66 : Test ADF pour le log des Cours
Boursiers différenciés de L'Oréal - Modèle (1)
Annexe 67 : Test ADF pour le log des Cours Boursiers différenciés
de LVMH - Modèle (3) Annexe 68 : Test ADF pour le log des Cours
Boursiers différenciés de LVMH - Modèle (2) Annexe 69 :
Test ADF pour le log des Cours Boursiers différenciés de LVMH -
Modèle (1) Annexe 70 : Test ADF pour le log des Cours Boursiers
différenciés de Sanofi - Modèle (3) Annexe 71 : Test ADF
pour le log des Cours Boursiers différenciés de Sanofi -
Modèle (2) Annexe 72 : Test ADF pour le log des Cours Boursiers
différenciés de Sanofi - Modèle (1) Annexe 73 : Test
d'Engle-Granger pour l'entreprise BNP Paribas
Annexe 74 : Test d'Engle-Granger pour l'entreprise
L'Oréal
Annexe 75 : Test d'Engle-Granger pour l'entreprise LVMH
Annexe 76 : Test d'Engle-Granger pour l'entreprise Sanofi
Annexe 77: Modèle de MCO avec 3 variables dummies pour BNP
Paribas
Annexe 78: Modèle de MCO avec 3 variables
dummies pour L'Oréal
Annexe 79: Modèle de MCO avec 3 variables dummies pour
LVMH
Annexe 80: Modèle de MCO avec 3 variables
dummies pour Sanofi
SOMMAIRE
1. AVANT-PROPOS 12
2. MÉTHODOLOGIE 14
3. MODÉLISATION 23
4. CONSIDÉRATIONS FINALES 38
5. RÉFÉRENCES 39
ANNEXES 41
12
1. AVANT-PROPOS
Ce présent travail a comme objectif principal l'analyse de
l'influence des données comptables sur le marché boursier. Cet
objectif a été établi par une inquiétude
personnelle sur le fonctionnement des marchés financiers, plus
précisément, sur la façon dont les cours des actions
varient. Pour le réaliser, une étude économétrique
a été réalisée.
Tout d'abord, il faut qu'on définisse la thématique
de notre travail, l'économétrie et la finance.
L'économétrie, d'après Frisch (1933) : "n'est pas du
tout la même chose que la statistique économique. Elle ne doit pas
non plus être identifiée avec ce que l'on appelle la
théorie économique générale, bien qu'une partie
considérable de cette théorie ait un caractère
résolument quantitatif. L'économétrie ne doit pas non plus
être considérée comme synonyme de l'application des
mathématiques à l'économie. L'expérience a
montré que chacun de ces trois points de vue, celui des statistiques,
celui de la théorie économique et celui des mathématiques,
est une condition nécessaire, mais non suffisante en elle-même,
à une compréhension réelle des relations quantitatives
dans la vie économique. C'est l'unification des trois qui est puissante.
Et c'est cette unification qui constitue l'économétrie."
La finance, d'autre part, apparaît, d'après Robert
Shiller (2010), comme la
« technologie » ou l'ensemble des activités qui
rendent possible la subvention l'économie, ce qui l'amène
à être essentielle à la moderne accumulation de capital.
Pour sa complexité, ses nouvelles technologies et produits, la finance
est en constante mouvement, ce qui la rend un grand sujet de recherche et
discussion. Les cours boursiers sont qualifiés comme l'une des plusieurs
technologies financières.
D'après SCHWERT (1989), sur la variabilité et
volatilité des cours boursiers: "if investors have heterogeneous
beliefs, new information will cause both price changes and trading". Comme
nouvelle information sur le marché, la divulgation du chiffre d'affaires
peut, possiblement, être une des causes de la variation des cours des
actions (en acceptant que les agents aient des croyances
hétérogènes), ce que le travail de recherche essaie de
répondre.
En ce qui concerne l'analyse, l'entreprise
pétrolière française composante du CAC 40, TOTAL SA (code
:
FP.PA), a été choisie pour
faire la comparaison entre les données boursières et comptables.
Elle a été choisie parce qu'elle est l'entreprise avec la
capitalisation (produit du nombre des actions en circulation par la valeur de
marché de chaque action) plus importante sur l'EURONEXT avec une
capitalisation de 118,75 milliard d'euros (d'après
boursier.com). Quatre autres
entreprises, BNP Paribas (code :
BNP.PA), L'Oréal (code :
OR.PA), LVMH (code :
MC.PA) et Sanofi (code :
SAN.PA), par ordre alphabétique, ont
été choisi pour faire une étude complémentaire.
Conjointement, elles forment les cinq plus grandes capitalisations sur
l'EURONEXT.
Puisque notre analyse s'appuie une étude
économétrique, les données financières et
comptables ont besoin d'être testées afin de savoir si une
relation de dépendance entre elles existe. Pour une question
d'accessibilité des données, le travail a pris en compte les
résultats trimestriels des cours boursiers et des chiffres d'affaires
comme variables testées.
13
Les cours boursiers ont été choisis parce qu'ils
sont les variables financières les plus significatives pour comprendre
les résultats sur les marchés financiers des entreprises
côtés en bourse et parce que les résultats sont publiques.
Les chiffres d'affaires ont été élus parce qu'ils sont
représentatives pour observer la variation des résultats
comptables d'une entreprise et parce qu'ils sont l'un des seuls données
comptables trimestriels qui sont publics.
Le travail ne prend pas en compte des variables de contrôle
ni des mouvements de saisonnalité spécifiques (comme le "sell
in may and go away", d'après Andrade (2012)). Il est évident
qu'il existe plusieurs variables indépendantes qui peuvent expliquer les
résultats boursiers, mais pour des motifs de simplification, seulement
le chiffre d'affaire a été retenu. L'article de Fama et French
(1988) explique très bien les components temporaires et permanents des
cours boursiers, il peut être utilisé pour une étude plus
approfondie sur ce sujet.
D'après les sites des entreprises, on peut apercevoir que
les résultats trimestriels sont habituellement divulgués un mois
après le trimestre écoulé (à la fin d'avril, de
juillet, d'octobre et de janvier). Vu que le travail cherche à tester si
les cours boursiers sont expliqués par les chiffres d'affaires, les prix
des cours trimestriels des mois suivants à la divulgation ont
été pris en compte (début de mai, début d'aout,
début de novembre et début de février).
Pour le présent travail, les données du premier
trimestre de 2006 jusqu'au dernier trimestre de 2013 ont été pris
en compte, ce qui représente un échantillon de 32 observations.
Les données des chiffres d'affaires n'ont pas été
trouvées pour les années précèdent 2006.
Les données des cours boursiers ont été
recueillies dans le site Yahoo Finance France. En revanche, les données
comptables ont été obtenues d'après les informations
financières trimestrielles divulguées dans les sites des
entreprises et dans le site Daily Bourse. Les chiffres d'affaires des
entreprises sélectionnées sont présentés en annexe
(Annexes 1, 2, 3, 4 et 5) et les cours boursiers sont présentés
dans les annexes 38, 39, 40, 41 et 42.
14
2. MÉTHODOLOGIE
Comme but du travail, la modélisation
économétrique apparaît comme un moyen de résoudre le
problème en question. La méthodologie ici présente donne
les étapes nécessaires pour élaborer des modèles
qui puissent expliquer la relation existante (ou non) entre le cours boursier
et le chiffre d'affaires des entreprises concernées.
Pour des raisons de simplification, on accepte
l'homoscedasticité et le non autocorrélation des résidus.
Cette hypothèse nous permet d'estimer les paramètres par le
modèle des moindres carrés ordinaires si les séries sont
stationnaires.
Pour rendre plus facile les estimations et computations des
données le software libre de statistique gretl a
été utilisé. Il a été utilisé parce
que son usage est libre et parce qu'il possède la plupart des
computations des tests et modèles nécessaires pour la
modélisation économétrique du présent travail.
Avant d'élaborer le modèle
économétrique, deux tests de stationnarité ont
été réalisés, un pour chaque variable, afin
d'observer les comportements de ces séries temporelles en ce qui
concerne la stationnarité. D'après LARDIC et MIGNON (2002), la
définition de stationnarité est la suivante:
"Le processus Xt est stationnaire au sens strict si pour tout
(t1, t2,...,tn) avec ti € T, i= 1,..., n, et si pour tout ô € T
avec ti+ ô € T (Xt, ... Xn) a la même distribution de
probabilité jointe que (Xt1+ ô, ..., Xtn+ ô) ".
Comme la définition de stationnarité au sens strict
est trop restrictive, nous préférons utiliser celle de Brooks
(2008), la définition de stationnarité faible: "(...) can be
defined as one with a constant mean, constant variance, and constant
autocovariance for each given lag ". Un exemple de série
stationnaire et le processus de bruit blanc (BB), qui suit la loi normale avec
moyenne et variances constantes. D'après la console du software libre
gretl, il' est possible de générer un processus
stationnaire, comme celui du tableau, de moyenne et variance égales
à 0 et 1 respectivement :
15
Graphique 1 : Exemple d'un bruit blanc
(stationnaire)

Brooks (2008) nous présente deux types des séries
non-stationnaires, les séries de marche aléatoire avec
dérive ou sans dérive (elles sont aussi appelées des
processus de différence stationnaire - DS), et les séries de
tendance stationnaire (TS). Les séries les plus courants en finance sont
les séries de marche aléatoire, par exemple une marche
aléatoire avec dérive (processus AR(1)) :
yt = ì + yt-1 + ut
(1)
Elles sont décrites comme, d'après Lardic et Mignon
(2002) : "Un processus DS est un processus que l'on peut rendre
stationnaire par l'utilisation d'un filtre aux différences" i.e.
qu'après une différentiation elles seront I(0). Dans son ouvrage
de 2008, Wooldridge a un ensemble des données qui sont disponibles sur
le site de gretl, comme exemple, d'après son étude sur
la consommation américaine entre les années 1959 et 1995, on a
l'inflation du période qui ressemble à un processus de marche
aléatoire :
16
Graphique 2 : Inflation aux
États-Unis entre 1959 et 1995 (processus de différence
stationnaire)

D'autre part on a les processus de tendance stationnaire, un
processus divisé en une partie déterministe et en une autre
partie stochastique, donnée par :
yt = á + 8t + ut
(2)
où 8t est une fonction déterministe du
temps et où ut suit un BB de moyenne 0 et variance constante.
Comme exemple, dans la même étude de Wooldridge, on constate la
série de consommation per capita réel qui ressemble à un
processus TS :
17
Graphique 3 : Consommation per capita
réel aux États-Unis entre 1959 et 1995 (processus de tendance
stationnaire)

Comme, d'après Brooks (2008), les séries
financières ont un comportement des séries DS dans la
majorité des cas, nous nous concentrons sur ce processus. Il est
important, avant de tester la stationnarité des variables,
présenter la notion de racine unitaire. Si on prend une série DS
et on la généralise pour n'importe quel coefficient de retard
(q,), on a :
yt = p + q,yt-1 + ut (3)
Ayant cela, on pourrait déduire plusieurs variations sur
ce système. Si q, >1, ce qu'on appelle de processus
explosif, les chocs au système n'ont pas seulement des effets permanents
sur la série, mais des effets croissants (comme les processus explosifs
ne sont pas courants en finance, on ne va pas les utiliser description
plausible des données). Par contre, si q, est inférieur
à l'unité, les chocs vont avoir des effets temporaires, traduit
par un cas de stationnarité. Mais si q, est égal
à l'unité, les chocs ont des effets permanents, le cas de non
stationnarité, c'est ce qu'on appelle aussi de cas de la racine
unitaire. Cette notion est utilisée pour les tests de racine unitaire
qui cherchent à expliquer si une série est stationnaire ou
non.
Le test de racine unitaire utilisé a été le
test développé par David Dickey et Wayne Fuller en 1976 (par
Fuller) et 1979 (par les deux), le test de Dickey-Fuller dans sa version
augmenté (ADF).
Selon Brooks (2008), on constate trois types des modèles
de base : (1) le modèle sans tendance ni constante, (2) le modèle
sans tendance avec constante et (3) le modèle avec tendance et
constante. La tendance présente dans les modèles n'est pas une
tendance stochastique, mais déterministe. Pour travailler avec ces
modèles, on suppose que les résidus suivent un bruit blanc de
moyenne égale à zéro et variance constante et égale
à ó2å.
18
On a comme hypothèse nulle l'existence de racine unitaire
dans la série (donc non stationnarité) et comme
l'hypothèse alternative la stationnarité, où la racine est
inférieure à l'unité. Par exemple, dans le modèle
(3) :
yt = öyt-1 + ì + ët + ut (4)
On teste si ö est égale à
l'unité ou non. Comme attesté par Brooks (2008), pour rendre plus
facile la compréhension et l'interprétation, on soustrait
yt-1 dans chaque côté de l'équation :
Äyt = øyt-1 + ì + ët + ut (5)
D'où ø est égale à
(ö-1). Donc le test est défini par :
Test statistique = ( àø)/
àó ( àø) (6)
Le test n'utilise pas les valeurs critiques du test t-student,
mais les valeurs critiques tabulées par Fuller (1976). Ces valeurs sont
plus importantes que les valeurs du test t. D'après Lardic et Mignon
(2002), on constate les valeurs critiques pour la racine unitaire :
Tableau 1 : Valeurs critiques de
Dickey-Fuller pour l'hypothèse de racine unitaire
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Taille 1% 5% 10%
|
|
|
|
Modèle (1)
|
|
100
|
-2.60
|
-1.95
|
-1.61
|
|
250
|
-2.58
|
-1.95
|
-1.62
|
|
500
|
-2.58
|
-1.95
|
-1.62
|
|
-2.58
|
-1.95
|
|
|
8
|
|
100
|
-3.51
|
-2.89
|
|
|
250
|
-3.46
|
-2.88
|
|
|
500
|
-3.44
|
-2.87
|
|
|
8
|
-3.43
|
-2.86
|
|
-1.62
Modèle (2)
-2.58
-2.57
-2.57
-2.57
Modèle (3)
-4.04
-3.45
-3.15
-3.99
-3.43
-3.13
-3.98
-3.42
-3.13
-3.96
-3.41
-3.12
et les valeurs critiques pour la constante et tendance temporelle
:
19
Tableau 2 : Valeurs critiques de
Dickey-Fuller pour la constante et la tendance temporelle
Taille
Modèle (2)
Modèle (3)
Constante
Constante
Trend
1%
5%
10%
1%
5%
10%
1%
5%
10%
100
3.22
2.54
2.17
3.78
3.11
2.73
3.53
2.79
2.38
250
3.19
2.53
2.16
3.74
3.09
2.73
3.49
2.79
2.38
500
3.18
2.52
2.38
8
3.18
2.52
2.16
3.71
3.08
2.72
3.46
2.78
2.38
Selon Brooks (2008), pour le test normal, on suppose que les
résidus ne sont pas
autocorrélés, par contre, si on utilise n
décalages de la variable dépendante on peut
supprimer le besoin de cette supposition. Cette «
augmentation » du test s'appelle test de
Dickey Fuller augmenté (ADF), d'où I
áiÄyt représente la somme des décalages :
2.16
3.72
3.08
2.72
3.48
2.78
Äyt = øyt-1 + I áiÄyt-i + ut
(7)
Il n'y a pas de consensus pour la définition du nombre
optimal des décalages du test ADF. Brooks (2008) présente
quelques règles empiriques, dont on va utiliser la définition du
nombre optimal de décalages d'après la fréquence des
données. Comme on travaille avec des données trimestrielles, on
va utiliser quatre décalages pour notre test.
D'après Lardic et Mignon (2002), on peut apercevoir qu'on
ne réalise pas le test sur les trois modèles, par contre on
utilise une méthode séquentielle divisée en trois
étapes. Premièrement, on prendre le modèle (3) et on teste
la significativité de la tendance temporelle, si elle n'est pas
significative on passe à l'étape suivante, en revanche, si elle
est significative, on teste H0 pour savoir si la racine unitaire existe. En
acceptant H0, la série va être non stationnaire (donc il faut la
différencier et élaborer un nouveau test), mais si l'on n'accepte
pas, la variable concerné est stationnaire et le travail avec la
série va être possible.
La deuxième étape de la procédure,
appliquée si la tendance n'a pas été significative,
consiste en travailler avec le modèle (2) en testant la
significativité de la constante. Si elle n'est pas significative on
passe à la prochaine étape, mais si la constante est en fait
significative on teste si l'hypothèse nulle sur l'existence de la racine
unitaire est vraie, si l'on constate sa véracité, la série
est non stationnaire, nous forçant à la différencier pour
recommencer la méthode. En revanche, si H0 est rejetée, on peut
commencer à travailler avec la série, parce qu'elle est
stationnaire.
Dans la dernière étape, employée si la
constante de la deuxième étape n'a pas été
significative, on utilise le modèle (1) pour savoir si la racine
unitaire est significative, d'après les valeurs critiques de Fuller.
Avec l'acceptation de l'hypothèse nulle, la série va être
non stationnaire, donc on a besoin de la différencier pour faire la
procédure une autre fois, mais si l'on rejette l'hypothèse de
l'existence de la racine unitaire on observe la stationnarité et on peut
travailler sans aucune modification dans la série.
En résumé, on continue avec la procédure
jusqu'au moment où on obtient une série stationnaire, même
s'il faut qu'on la différencie une ou plusieurs fois. Il y a d'autres
méthodes et tests pour observer la stationnarité des
séries temporelles comme les méthodes d'analyse graphique,
d'analyse de la fonction d'autocorrélation et d'autres tests de racine
unitaire (comme le test de Phillips-Perron). On ne va pas utiliser la
méthode d'analyse de la fonction d'autocorrélation (acf) ni
d'autocorrélation partiel (pacf) parce que,
20
d'après Brooks (2008) : »(...) although shocks to
a unit root process will remain in the system indefinitely, the acf for a unit
root process (a random walk) will often be seen to decay away very slowly to
zero. Thus, such a process may be mistaken for a highly persistent but
stationary process. Hence it is not possible to use the acf or pacf to
determine whether a series is characterised by a unit root or not.»
La méthode d'analyse graphique peut être utilisée en
analysant si la série fluctue sur sa moyenne et si elle a une variance
constante. Pour commodité on ne va pas réaliser d'autres tests de
racine unitaire que le test de Dickey-Fuller.
Après le test de racine unitaire, si l'on atteste que les
deux séries sont stationnaires on va utiliser la modélisation de
MCO (moindres carrés ordinaire), où on va observer si les cours
boursiers sont expliqués par le chiffre d'affaires de TOTAL SA en
estimant les paramètres du modèle et en testant leur
significations. Par contre, si les séries ne sont pas stationnaires, on
ne peut pas estimer les paramètres du modèle par MCO parce que
cela impliquerait à une régression fallacieuse (spurious
regressions), d'après Brooks (2008), les suppositions standard pour
l'analyse asymptotique ne seront pas valide, les séries non
stationnaires ont des comportements et propriétés
différents des séries stationnaires.
Dans le cas où les séries ne sont pas
stationnaires, il faut qu'on teste si les séries ont une relation de
long terme entre eux, autrement dit, si les séries sont
cointégrées. Pour savoir si les séries sont
cointégrées on va tester la cointégration à partir
du test d'Engle-Granger.
La définition de cointégration viens d'Engle et
Granger (1987), d'après Brooks (2008): "a set of variables is defined as
cointegrated if a linear combination of them is stationary". Selon Lardic et
Mignon (2002), avec deux séries intégrées d'ordre (d), si
la combinaison linéaire entre elles gt :
gt = Xt - aYt (8)
est d'ordre (d-v), où v est un nombre entier positif, donc
les séries vont être cointégrées. Dans les
séries financières, le cas le plus fréquent est quand d =
v = 1.
Avant de tester la cointégration, nous tenons d'abord
à expliciter les modèles à correction d'erreur, ou
Error Correction Model (ECM) introduits par Hendry (1978) qui cherchent
à estimer un équilibre de long terme. Comme des modèles de
première différence pures n'ont pas de solution de long terme, on
peut utiliser des modèles avec une combinaison entre les séries
différenciées de premier ordre et les niveaux
décalés des variables cointégrées qui peuvent
résoudre ce problème, cela est l'intuition des modèles
à correction d'erreur.
D'après Brooks (2008), on a le modèle à
correction d'erreur :
Äyt = â1Äxt + â2(yt?1 ? ã xt?1)
+ ut (9)
où yt-1 - ã xt?1 est connu comme le terme à
correction d'erreur. À condition que yt et xt sont
cointégrées avec le coefficient de cointégration ã,
le terme à correction d'erreur va être stationnaire, même si
ses composants sont intégrées à ordre un. Autrement dit,
il faut que les résidus du modèle de MCO entre yt et xt soient
stationnaires (yt?1 ? ã xt?1 est équivalent aux
résidus décalés en un période).
Le modèle à correction d'erreur rendre possible
l'estimation par MCO par inférence statistique. Une
interprétation intuitive du modèle, donnée par Brooks
(2008), est la
21
suivante : la variable y est censé à changer entre
t -1 et t en raison des changements dans les valeurs de la variable
explicative, x, entre t - 1 et t, et aussi en partie à corriger tout
déséquilibre qui existait pendant la période
précédente ; ã décrirait la relation de
long terme entre x et y, 81 la relation de court terme et 82
la vitesse d'ajustement jusqu'au équilibre.
Comme le terme à correction d'erreur est équivalent
aux résidus décalés du modèle de MCO, pour savoir
si les variables sont cointégrées entre eux ont va utiliser le
test de Engle-Granger. Si la vraie valeur de 8 est connue,
d'après Wooldridge (2008), pour tester la cointégration:
"(...) we simply define a new variable, st yt xt, and apply either the
usual DF or augmented DF test to {st}. If we reject a unit root in {st} in
favor of the I(0) alternative, then we find that yt and xt are cointegrated."
Comme intuition, on peut interpréter st comme s'il
représentait les résidus d'une régression simple sans
constante.
Par contre, si on ne connait pas la vraie valeur de 8,
on va l'estimer avec un modèle de MCO avec constante. Après
l'estimation, les résidus du modèle vont être pris en
compte à fin de faire un test de stationnarité. On peut utiliser
le test de Dickey-Fuller augmenté comme test de racine unitaire, par
contre, comme ici on travaille avec des résidus, on va utiliser les
valeurs critiques d'Engle et Yoo (1987), qui est connu comme le test
d'Engle-Granger :
Tableau 3 : Valeurs critiques d'Engle et
Yoo
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Taille
|
1%
|
5%
|
10%
|
|
N=2
|
50
|
-4.12
|
-3.29
|
-2.90
|
|
100
|
-3.73
|
-3.17
|
|
|
200
|
-3.78
|
-3.25
|
|
|
N=3
|
50
|
-4.45
|
-3.75
|
|
|
100
|
-4.22
|
-3.62
|
|
|
200
|
-4.34
|
-3.78
|
|
-2.91 -2.98 -3.36
-3.32 -3.51
N=4
50
-4.61
-3.98
-3.67
100
-4.61
-4.02
-3.71
200
-4.72
-4.13
-3.83
N=5
50
-4.80
-4.15
-3.85
100
-4.98
-4.36
-4.06
200
-4.97
-4.43
-4.14
Afin d'éliminer des problèmes éventuelles
de saisonnalité et rendre possible la
modélisation du ECM (même si les séries n'ont
pas de racine unitaire), on va ajouter des
variables dummies. Comme on travaille avec des
données trimestriels, on va utiliser trois
variables dummies, une pour chaque trimestre, la
dernière sera liée à la constante et pour
cela n'entre pas comme dummy.
Si après le test d'Engle-Granger les résidus sont
stationnaires, alors les variables sont
cointégrées entre elles et on peut estimer le
modèle à correction d'erreur. En revanche, si
les résidus ne sont pas stationnaires, les variables ne
sont pas cointégrées entre elles (on ne
peut pas estimer une relation de long terme par l'ECM), dans ce
cas, on peut chercher une
relation de court terme entre les variables dépendantes et
indépendantes en estimant un
modèle de MCO avec les variables
stationnarisées.
La dernière étape consiste en regarder la
signification des variables et le pouvoir
explicatif du modèle. Pour la signification, on
réalise un test de student pour chaque variable
22
indépendante de l'ECM ou de la relation à court
terme. Ensuite, pour le pouvoir explicatif du modèle, on prend les
valeurs R2 et R2 ajusté (la valeur ajustée
est préférable si on compare plusieurs modèles).
23
3. MODÉLISATION
Cette section présente la partie empirique de nos travaux
: la modélisation. Pour cette partie on va seulement suivre les
étapes décrites précédemment dans la
méthodologie. Les corrélogrammes des variables, pour des raisons
explicités dans la méthodologie, ne seront pas être ici
discutés.
Afin de stationnariser les séries temporelles en variance,
on va plutôt travailler avec des séries en logarithme,
d'après Mignon (2008), on peut constater que la transformation d'une
série en logarithme diminue le phénomène de
l'hetétéroscédasticité. Hendry et Juselius (2000)
constatent que si un ensemble de séries est cointégré en
niveau, il sera également cointégré en niveau
logarithmique.
Premièrement, cinq groupes d'études ont
été créé dans le software gretl, un pour
chaque entreprise, en ajoutant ses variables financières et comptables.
Ensuite, on teste la stationnarité avec le test de Dickey-Fuller
augmenté (ADF). Pour le log du chiffre d'affaire de l'entreprise TOTAL
SA, si on regarde le graphique de la série temporelle (les
résultats sont en puissance de dix écrites avec la notation
computationnelle e):
Graphique 4 : Log du CA de l'entreprise
TOTAL SA

On peut apercevoir que la série n'a pas de tendance
stationnaire ni de variance constante, ce qui ressemble à un processus
de marche aléatoire. D'après les annexes 6, 7 et 9, on peut
remarquer que les autres entreprises ont un comportement similaire à ce
qui concerne ces graphiques, à l'exception du graphique de l'entreprise
LVMH (annexe 8), d'où on peut constater qui le phénomène
de la saisonnalité est très évident (des sommets toujours
dans le quatrième trimestre).
24
Pour être sûr à propos de la
stationnarité de la série on va passer le test ADF à
partir du software gretl (les valeurs p. critiques sont liées aux
valeurs critiques de student). On va comparer les statistiques t avec
les valeurs critiques du test ADF, qui sont présentes dans les tableaux
1 et 2, afin de savoir si l'hypothèse nulle est vraie. En regardant le
test en trois étapes pour l'entreprise TOTAL SA, la première
étape avec le modèle (3) :
Tableau 4: Modèle (3) du test
ADF pour le log du CA de l'entreprise TOTAL SA
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
const
|
5,87805
|
2,47770
|
2,372
|
0,0260
|
|
|
l_CA_1
|
-0,337847
|
0,142570
|
-2,370
|
0,3956
|
|
|
d_l_CA_1
|
0,483413
|
0,176323
|
2,742
|
0,0114
|
|
|
d_l_CA_2
|
-0,0474088
|
0,197423
|
-0,2401
|
0,8123
|
|
|
time
|
0,00322662
|
erreur std.
0,00211218
|
1,528
|
0,1397
|
|
p. critique
**
**
Comme la tendance temporelle (time) n'a pas été
significative (d'après la valeur critique du tableau 2, de 2.79 à
5% ou de 2.38% à 10%). Si on regarde les statistiques t des annexes 10,
13, 16 et 19, on peut constater que la tendance temporelle n'est pas
significative pour les autres entreprises non plus. On passe à
l'étape suivante, pour le deuxième modèle :
Tableau 5: Modèle (2) du test
ADF pour le log du CA de l'entreprise TOTAL SA
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
const
|
3,50014
|
erreur std.
1,97843
|
1,769
|
p. critique
0,0891
|
|
|
l_CA_1
|
-0,199027
|
0,112747
|
-1,765
|
0,3983
|
|
|
d_l_CA_1
|
0,457754
|
0,180142
|
2,541
|
0,0176
|
|
|
d_l_CA_2
|
-0,144040
|
0,191938
|
-0,7505
|
0,4600
|
|
*
**
On observe que la constante (const) n'a pas été
significative au seuil de 10% (valeur critique de 2.17 pour la constante du
modèle (2)). D'après les annexes (11, 14, 17 et 20), on peut
apercevoir que les statistiques t pour les constantes des autres entreprises
ont une valeur absolue trop faible, et pour cela on peut conclure qu'elles ne
sont pas significatives. Donc on passe à la dernière étape
du test :
Tableau 6: Modèle (1) du test
ADF pour le log du CA de l'entreprise TOTAL SA
erreur std.
p. critique
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
l_CA_1
|
0,000172064
|
0,000841220
|
0,2045
|
0,7457
|
|
d_l_CA_1
|
0,281719
|
0,179449
|
1,570
|
0,1277
|
Comme la valeur t de la variable (l_CA_1) est trop faible et
inférieur à la valeur absolue critique au seuil de 10% de
significance (valeur critique de -1.61), d'après le tableau 1, on ne
rejette pas l'hypothèse nulle de racine unitaire (ou non
stationnarité). D'après les
25
annexes 12, 15, 18 et 21, on n'a pas rejeté
l'hypothèse nulle pour les autres entreprises non plus, ce qui nous
oblige à différencier les séries à fin de trouver
des séries stationnaires.
On peut regarder le graphique de la série
différencié : Graphique 5 : Log du CA
différencié de l'entreprise TOTAL SA

Maintenant, on peut apercevoir que le graphique passe souvent sur
la valeur nulle et que sa variance est constante presque tous les temps
(à l'exception des périodes de crise). Cela suit les
caractéristiques d'une série stationnaire. Si on regarde les
annexes 22 et 23, on peut vérifier que les entreprises BNP Paribas et
L'Oréal ont un comportement similaire à celui de TOTAL SA. Par
contre, d'après l'annexe 25, on constate que le graphique pour
l'entreprise Sanofi a une variance très expressive et que ne semble pas
constante ce qui semble à une série non stationnaire. Comme le
test ne prend pas en compte des caractéristiques d'une série avec
saisonnalité, la série différenciée du log du CA de
LVMH ne va pas être stationnaire, d'après son graphique (annexe
24), on peut apercevoir que la série différencié a encore
un comportement de saisonnalité, qui ne correspond pas à une
série stationnaire.
On recommence le test ADF pour le log du CA
différencié de l'entreprise TOTAL SA. Pour le troisième
modèle:
26
Tableau 7: Modèle (3) du test
ADF pour le log du CA différencié de TOTAL SA
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
const
|
0,00716634
|
0,0351270
|
0,2040
|
0,8400
|
|
|
d_l_CA_1
|
-0,891631
|
0,222727
|
-4,003
|
0,0086
|
|
|
d_d_l_CA_1
|
0,284764
|
0,185167
|
1,538
|
0,1366
|
|
|
time
|
3,62948e-05
|
erreur std.
0,00177139
|
0,02049
|
0,9838
|
|
p. critique
***
La tendance temporelle (time) n'est pas significative au seuil de
10% si on compare avec la valeur critique présente au tableau 2.
D'après les annexes 26, 29, 32 et 35, on peut constater que la tendance
temporelle n'est pas significative pour les autres entreprises non plus. Donc
il faut qu'on passe à la prochaine étape. Pour le modèle
(2) :
Tableau 8: Modèle (2) du test ADF
pour le log du CA différencié de TOTAL SA
|
coefficient
|
|
t de Student
|
|
|
|
|
erreur std.
|
|
p. critique
|
|
|
const
|
0,00781853
|
0,0145678
|
0,5367
|
0,5960
|
|
|
d_l_CA_1
|
-0,891397
|
0,218117
|
-4,087
|
0,0010
|
|
|
d_d_l_CA_1
|
0,284747
|
0,181571
|
1,568
|
0,1289
|
|
***
Comme la statistique t de la constante est inférieur
à la valeur critique au seuil de 10% (valeur critique de 2.17), on
trouve qu'elle n'est pas significative, si on regarde les annexes 27, 33 et 36,
on peut apercevoir que les résultats sont similaires pour les
entreprises BNP Paribas, LVMH et Sanofi. Par contre, d'après l'annexe
30, on observe que la constate à été significative au
seuil de 10% (d'après le tableau 2) et on rejette l'hypothèse
nulle au seuil de 1% (valeur critique de -3.51), d'après le tableau 1,
avec cela on peut arrêter le test de stationnarité pour
l'entreprise L'Oréal, parce que son chiffre d'affaire est devenu
stationnaire après une différentiation. Par contre, il faut qu'on
continue le test ADF pour les autres quatre entreprises. Pour la
dernière étape du test :
Tableau 9: Modèle (1) du test ADF
pour le log du CA différencié de TOTAL SA
erreur std.
p. critique
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
***
|
|
d_l_CA_1
|
-0,881115
|
0,214390
|
-4,110
|
4,11e-05
|
|
|
d_d_l_CA_1
|
0,277580
|
0,178675
|
1,554
|
0,1319
|
|
On peut apercevoir que la statistique t de la variable en
question est inférieur à la valeur critique de 1% (-2.60), ce qui
nous permet de rejeter l'hypothèse nulle. Après cela, on peut
constater que la série différencié est stationnaire. On
peut apercevoir, en regardant l'annexe 28, que le log du CA de BNP Paribas est
aussi stationnaire quand on prend sa différence première. En
contrepartie, si on analyse les annexes 34 et 37, on peut apercevoir que le log
du CA différencié des entreprises LVMH, à cause de sa
saisonnalité, et Sanofi, à cause de sa variance, n'est pas
stationnaire, donc on a besoin de les différencier une autre fois afin
de les rendre stationnaires.
27
On peut apercevoir que le phénomène de la
saisonnalité est moins évident maintenant pour le CA de
l'entreprise LVMH. Dans les deux graphiques la variance n'est pas
Si on différencie une autre fois le CA pour les
entreprises LVMH et Sanofi, on peut observer le nouveau graphique pour
l'entreprise LVMH :
Graphique 6 : Log du CA
différencié deux fois de l'entreprise LVMH
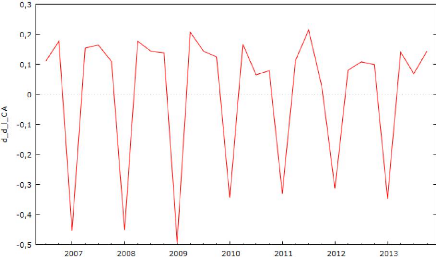
Et le graphique pour l'entreprise Sanofi :
Graphique 7 : Log du CA
différencié deux fois de l'entreprise Sanofi

28
assez significative et plus ou moins constante, ce qui est une
caractéristique des séries stationnaires.
On passe maintenant au test ADF. On commence par le
modèle (3) de l'entreprise
LVMH :
Tableau 10: Modèle (3) du test
ADF pour le log du CA différencié deux fois de LVMH
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
const
|
-0,0533037
|
0,0945157
|
-0,5640
|
0,5780
|
|
|
d_d_l_CA_1
|
-2,00873
|
0,283099
|
-7,095
|
1,31e-09
|
|
|
d_d_d_l_CA_1
|
0,499192
|
erreur std.
0,173176
|
2,883
|
0,0082
|
|
|
time
|
0,00274186
|
0,00468233
|
0,5856
|
0,5636
|
|
Et de l'entreprise Sanofi :
p. critique
***
***
Tableau 11: Modèle (3) du test
ADF pour le log du CA différencié deux fois de Sanofi
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
const
|
0,0276510
|
0,0571589
|
0,4838
|
0,6329
|
|
|
d_d_l_COURS_1
|
-2,28104
|
erreur std.
0,345310
|
-6,606
|
3,18e-08
|
|
|
d_d_d_l_COURS_1
|
0,396165
|
0,193878
|
2,043
|
0,0521
|
|
|
time
|
-0,00138574
|
0,00283375
|
-0,4890
|
0,6293
|
|
p. critique
*** *
En comparant les statistiques t des tendances temporelles avec
les valeurs critiques présentes dans le tableau 2, on peut apercevoir
qu'au seuil de 10%, aucune des tendances n'est significative. À cause de
cela, on passe à l'étape suivante, pour l'entreprise LVMH :
Tableau 12: Modèle (2) du test ADF
pour le log du CA différencié deux fois de LVMH
|
|
|
t de Student
|
|
|
|
coefficient
|
|
erreur std.
|
|
p. critique
|
|
|
const
|
-0,00257749
|
0,0373034
|
-0,06910
|
0,9455
|
|
|
d_d_l_CA_1
|
-2,01090
|
0,279330
|
-7,199
|
9,49e-011
|
|
|
d_d_d_l_CA_1
|
0,501999
|
0,170820
|
2,939
|
0,0070
|
***
|
Et pour l'entreprise Sanofi :
***
Tableau 13: Modèle (2) du test
ADF pour le log du CA différencié deux fois de Sanofi
|
coefficient
|
erreur std.
|
t de Student
|
p. critique
|
|
|
|
|
|
|
|
|
const
|
0,00201869
|
0,0224465
|
0,08993
|
0,9291
|
|
|
d_d_l_COURS_1
|
-2,26587
|
0,338638
|
-6,691
|
2,19e-09
|
***
|
|
d_d_d_l_COURS_1
|
0,387136
|
0,190037
|
2,037
|
0,0524
|
*
|
On peut apercevoir que les valeurs des statistiques t des
constantes pour les deux entreprises ne sont pas assez fortes, par
conséquent les constantes ne sont pas significatives au seuil de 10%.
Donc on passe à la dernière étape du test, pour
l'entreprise LVMH :
29
Tableau 14: Modèle (1) du test
ADF pour le log du CA différencié deux fois de LVMH
|
|
|
|
|
|
|
|
|
|
|
|
|
d_d_l_CA_1
|
-2,01085
|
0,273931
|
-7,341
|
2,43e-012
|
|
|
d_d_d_l_CA_1
|
0,502002
|
0,167519
|
2,997
|
0,0059
|
|
Et pour l'entreprise Sanofi :
***
***
Tableau 15: Modèle (1) du test
ADF pour le log du CA différencié deux fois de Sanofi
erreur std.
p. critique
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
d_d_l_COURS_1
|
-2,26565
|
0,332108
|
-6,822
|
4,91e-011
|
|
|
d_d_d_l_COURS_1
|
0,387244
|
0,186373
|
2,078
|
0,0477
|
|
***
**
On peut comparer les valeurs des statistiques t avec les valeurs
critiques de racine unitaire (d'après le tableau 1), ce qui nous
amène à conclure qu'elles sont significatives au seuil de 1%
(valeur critique de -2.60). Avec cela, on déduit que les séries
deviennent stationnaires après deux différentiations et on peut
terminer les tests ADF pour les chiffres d'affaires.
Maintenant, on passe à tester la stationnarité pour
la variable dépendante du travail, le cours boursier (COURS). On va
travailler avec les logarithmes des cours boursiers pour le même motif
explicité au début de la modélisation. Si on regarde le
graphique du Log des cours boursiers de l'entreprise TOTAL SA :
Graphique 8 : Log des cours boursiers de
l'entreprise TOTAL SA
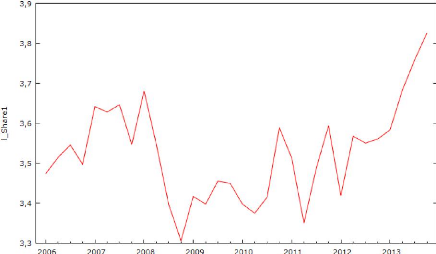
30
On peut observer que la série temporelle a un comportement
similaire à une série de marche aléatoire, ce qui semble
à une série non stationnaire. D'après les annexes 43, 44,
45 et 46, on constate un mouvement aléatoire dans toutes les graphiques.
Afin de savoir à coup sûr, on va tester la stationnarité
avec le test ADF. La première étape pour l'entreprise TOTAL SA
:
Tableau 16: Modèle (3) du test ADF
pour le log des cours boursiers de TOTAL SA
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
const
|
0,280682
|
0,913986
|
0,3071
|
0,7617
|
|
l_Share1_1
|
-0,0928986
|
0,259057
|
-0,3586
|
0,9890
|
|
d_l_Share1_1
|
-0,277037
|
0,306231
|
-0,9047
|
0,3754
|
|
d_l_Share1_2
|
-0,283570
|
0,268913
|
-1,055
|
0,3031
|
|
d_l_Share1_3
|
-0,0704265
|
0,237068
|
-0,2971
|
0,7692
|
|
time
|
0,00333827
|
erreur std.
0,00249514
|
1,338
|
0,1946
|
p. critique
Comme la statiques t de la tendance temporelle est trop faible,
on conclue, en comparant avec le tableau 2, qu'elle n'est pas significative. Si
on regarde les annexes 47, 50 et 53, on peut apercevoir que la tendance
temporelle n'est pas significative pour les entreprises BNP Paribas,
L'Oréal et LVMH non plus. Par contre, d'après l'annexe 56, on
conclue au seuil de 5% (valeur critique de 2.79, d'après le tableau 2),
que la tendance est significative pour l'entreprise Sanofi, donc on a besoin de
tester la racine unitaire, comme la statistique t de la variable en question
est trop faible, on ne peut rejeter l'hypothèse nulle (la série
est non stationnaire), donc il faut qu'on la différencie. On passe au
modèle (2) du test :
Tableau 17: Modèle (2) du test ADF
pour le log des cours boursiers de TOTAL SA
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
const
|
0,469339
|
0,918421
|
0,5110
|
0,6142
|
|
l_Share1_1
|
-0,129399
|
erreur std.
0,262003
|
-0,4939
|
p. critique
0,8901
|
|
d_l_Share1_1
|
-0,178522
|
0,302308
|
-0,5905
|
0,5606
|
|
d_l_Share1_2
|
-0,204275
|
0,266767
|
-0,7657
|
0,4516
|
|
d_l_Share1_3
|
-0,0165149
|
0,237596
|
-0,06951
|
0,9452
|
Après comparer la statistique t de la constante avec les
valeurs critiques (tableau 2), on constate qu'elle n'est pas significative au
seuil de 10%. Si on consulte les annexes 48, 51 et 54 on peut remarquer que les
résultats sont similaires, les constantes pour les entreprises BNP
Paribas, L'Oréal et LVMH n'ont pas été significatives. Il
faut qu'on continue le test ADF pour le modèle (1) :
31
Tableau 18: Modèle (1) du test
ADF pour le log des cours boursiers de TOTAL SA
|
|
|
|
|
|
|
|
|
|
|
l_Share1_1
|
0,00334959
|
0,00516501
|
0,6485
|
0,8563
|
|
d_l_Share1_1
|
-0,209726
|
0,186111
|
-1,127
|
0,2694
|
La statistique t est trop faible ce qui nous amène
à conclure que la variable n'est pas significative au seuil de 10%, on
ne peut pas rejeter l'hypothèse nulle (la série est
non-stationnaire), il faut qu'on la différencie pour la rendre
stationnaire. D'après les annexes 49, 52 et 55, on peut apercevoir que
les séries sont non-stationnaires, parce qu'on n'a pas rejette
l'hypothèse d'existence de racine unitaire d'après la comparaison
entre les statistiques t et les valeurs critiques du tableau 1.
Comme les cours boursiers en logarithme ne sont pas
stationnaires, il faut qu'on différencie les séries afin de les
rendre stationnaires. On peut analyser le graphique du log des cours boursiers
différenciés de l'entreprise TOTAL SA :
Graphique 9 : Log des cours boursiers
différenciés de l'entreprise TOTAL SA

On peut constater que la série a sa moyenne centrée
en zéro et que sa variance est relativement constante, ce qui correspond
à un comportement d'une série stationnaire. D'après les
annexes 57, 58, 59 et 60, on peut observer que les autres entreprises ont un
comportement similaire à ceux de TOTAL SA. Maintenant on passe au test
ADF pour la série différencie. On commence par le modèle
(3) pour l'entreprise TOTAL SA :
32
Tableau 19: Modèle (3) du test ADF
pour le log des cours boursiers différenciés de TOTAL SA
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
const
|
-0,0434535
|
0,0428877
|
-1,013
|
0,3207
|
|
|
d_l_Share1_1
|
-1,62475
|
0,298300
|
-5,447
|
2,18e-05
|
|
|
d_d_l_Share1_1
|
0,304577
|
0,189227
|
1,610
|
0,1200
|
|
|
time
|
0,00322198
|
erreur std.
0,00218567
|
1,474
|
0,1529
|
|
p. critique
***
On constate que la statistique t pour la tendance temporelle est
trop faible, donc elle n'est pas significative quand on compare sa valeur avec
les valeurs critiques du tableau 2. D'après les annexes 61, 64, 67 et
70, on peut avoir la même conclusion pour les autres entreprises. On
continue le test par la prochaine étape :
Tableau 20: Modèle (2) du test ADF
pour le log des cours boursiers différenciés de TOTAL SA
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
const
|
0,00963056
|
0,0196630
|
0,4898
|
0,6291
|
|
d_l_Share1_1
|
-1,25533
|
0,601752
|
-2,086
|
0,2505
|
|
d_d_l_Share1_1
|
0,00956670
|
0,503242
|
0,01901
|
0,9850
|
|
d_d_l_Share1_2
|
-0,210895
|
erreur std.
0,362796
|
-0,5813
|
0,5669
|
|
d_d_l_Share1_3
|
-0,211704
|
0,214153
|
-0,9886
|
0,3336
|
p. critique
Si on compare la statistique t de la constance avec les valeurs
critiques de Dickey-Fuller, on conclue qu'elle n'est pas significative au seuil
de 10% (valeur critique de 2.17, d'après le tableau 2). Pour les autres
entreprises, selon les annexes 62, 65, 68 et 71, on trouve que les constantes
ne sont pas significatives. À cause de cela, il faut qu'on passe
à la dernière étape du modèle :
Tableau 21: Modèle (1) du test ADF
pour le log des cours boursiers différenciés de TOTAL SA
|
coefficient
|
|
t de Student
|
|
|
|
|
erreur std.
|
|
p. critique
|
|
|
d_l_Share1_1
|
-1,21125
|
0,585070
|
-2,070
|
0,0369
|
|
|
d_d_l_Share1_1
|
-0,0211718
|
0,490994
|
-0,04312
|
0,9660
|
**
|
|
d_d_l_Share1_2
|
-0,229447
|
0,354801
|
-0,6467
|
0,5242
|
|
|
d_d_l_Share1_3
|
-0,219534
|
0,209997
|
-1,045
|
0,3067
|
|
En comparant la statistique t avec les valeurs critiques de
racine unitaire du tableau 1, on conclue qu'elle est significative au seuil de
5% (valeur critique de -1.95), donc on rejette l'hypothèse nulle, la
série est maintenant stationnaire et on peut arrêter le test ADF.
D'après les annexes 63, 66, 69 et 72, on peut rejeter l'hypothèse
de racine unitaire pour les autres entreprises aussi.
33
Comme on a bien trouvé les séries stationnaires
après la différentiation, on peut maintenant commencer les tests
de cointégration. On estime les paramètres par MCO en
introduisant des variables dummies de correction de
saisonnalité, ce qui nous permet de travailler même avec les
séries qui n'ont pas de racine unitaire dans les variables
indépendantes (LVMH et Sanofi). La modélisation par MCO pour
l'entreprise TOTAL SA est comme suit :
Tableau 22: Modèle de MCO avec 3
variables dummies pour TOTAL SA
Modèle 2: MCO, utilisant les observations 2006:1-2013:4
(T = 32)
Variable dépendante: l_Share1
|
Coefficient
|
Erreur Std
|
t de Student
|
p. critique
|
|
|
const
|
-1,6625
|
2,7005
|
-0,6156
|
0,54330
|
|
|
l_CA
|
0,295532
|
0,153838
|
1,9211
|
0,06534
|
*
|
|
T1
|
-0,0220082
|
0,0603018
|
-0,3650
|
0,71798
|
|
|
T2
|
-0,0397488
|
0,0601486
|
-0,6608
|
0,51431
|
|
|
T3
|
-0,0167468
|
0,0601588
|
-0,2784
|
0,78284
|
|
|
Moy. var. dép.
|
3,525173
|
Éc. type var. dép.
|
0,120628
|
|
Somme carrés résidus
|
0,390673
|
Éc. type de régression
|
0,120289
|
|
R2
|
0,133924
|
R2 ajusté
|
0,005616
|
|
F(4, 27)
|
1,043771
|
p. critique (F)
|
0,403088
|
|
Log de vraisemblance
|
25,08388
|
Critère d'Akaike
|
-40,16776
|
|
Critère de Schwarz
|
-32,83908
|
Hannan-Quinn
|
-37,73851
|
|
rho
|
0,583789
|
Durbin-Watson
|
0,856695
|
Les annexes 77, 78, 79 et 80 présentent la même
modélisation pour les autres entreprises. D'après ces
modèles de MCO, on va prendre les résidus afin de tester la
cointégration (ou la relation de long terme) entre les variables
dépendantes (les cours boursiers) et indépendantes (les chiffres
d'affaires). Le test d'Engle-Granger pour l'entreprise TOTAL SA :
Tableau 23: Test d'Engle-Granger pour
l'entreprise TOTAL SA
|
coefficient
|
|
erreur std.
|
t de Student
|
p. critique
|
|
|
|
|
|
|
l_resid_sais_1
|
-0,349350
|
0,253701
|
-1,377
|
0,1569
|
|
d_l_resid_sais_1
|
-0,0500037
|
0,247398
|
-0,2021
|
0,8414
|
|
d_l_resid_sais_2
|
-0,126447
|
0,215999
|
-0,5854
|
0,5633
|
On va comparer la statistique t avec les valeurs critiques
d'Engle et Yoo (d'après le tableau 3), comme elle n'est pas assez forte
on conclue qu'au seuil de 10% (valeur critique de -2.90) elle n'est pas
significative. Cela indique que les variables ne sont pas
cointégrées entre elles, donc il n'existe pas une relation de
long terme. D'après les annexes 73, 74, 75 et 76, on peut constater que
les valeurs absolues des statistiques t sont inférieurs à les
valeurs critiques absolues au seuil de 10%, donc on a la même conclusion
pour les autres entreprises, il n'y a pas de relation de long terme entre les
variables.
34
Comme on n'a pas trouvé une relation de long terme entre
les variables, on ne peut pas estimer un modèle à correction
d'erreur. Quand même, on peut essayer d'estimer une relation de court
terme avec les séries stationnarisées. On va continuer à
utiliser des variables dummies afin de résoudre des
problèmes éventuels de saisonnalité.
On commence par la modélisation de court terme par MCO
pour l'entreprise TOTAL SA. On prendre le log des cours boursiers
différenciés une fois comme variable dépendante et le log
des chiffres d'affaires différenciés comme variable
indépendante en ajoutant les variables dummies de
saisonnalité :
Tableau 24: Relation de court terme
estimé par MCO pour TOTAL SA
Modèle 6: MCO, utilisant les observations 2006:2-2013:4
(T = 31)
Variable dépendante: d_l_Share1
|
Coefficient
|
Erreur Std
|
t de Student
|
p. critique
|
|
const
|
0,0130686
|
0,0184859
|
0,7069
|
0,48589
|
|
d_l_CA
|
-0,223961
|
0,23223
|
-0,9644
|
0,34373
|
|
T1
|
0,00326834
|
0,0530074
|
0,0617
|
0,95131
|
|
T2
|
-0,0129109
|
0,0520758
|
-0,2479
|
0,80614
|
|
T3
|
0,0127453
|
0,0512569
|
0,2487
|
0,80558
|
|
Moy. var. dép.
|
0,011357
|
Éc. type var. dép.
|
0,097742
|
|
Somme carrés résidus
|
0,272360
|
Éc. type de régression
|
0,102349
|
|
R2
|
0,049692
|
R2 ajusté
|
-0,096509
|
|
F(4, 26)
|
0,339890
|
p. critique (F)
|
0,848525
|
|
Log de vraisemblance
|
29,39946
|
Critère d'Akaike
|
-48,79891
|
|
Critère de Schwarz
|
-41,62898
|
Hannan-Quinn
|
-46,46169
|
|
rho
|
-0,152319
|
Durbin-Watson
|
2,275254
|
On peut apercevoir, d'après la valeur du R2
ajusté, que le pouvoir explicatif du modèle est trop faible, en
outre, la variable indépendante n'a pas été significative
au seuil de 10% d'après la valeur p. critique, donc la relation
statistique n'est pas trop forte. On passe à l'estimation de la relation
de court terme pour l'entreprise BNP Paribas :
35
Tableau 25: Relation de court terme
estimé par MCO pour BNP Paribas
Modèle 3: MCO, utilisant les observations 2006:2-2013:4
(T = 31)
Variable dépendante: d_l_COURS
|
Coefficient
|
Erreur Std
|
t de Student
|
p. critique
|
|
|
const
|
-0,0131812
|
0,03198
|
-0,4122
|
0,68359
|
|
|
d_l_CA
|
1,19091
|
0,250651
|
4,7513
|
0,00006
|
***
|
|
T1
|
-0,178337
|
0,112236
|
-1,5889
|
0,12416
|
|
|
T2
|
-0,0556102
|
0,0909686
|
-0,6113
|
0,54630
|
|
|
T3
|
-0,0561573
|
0,0890435
|
-0,6307
|
0,53376
|
|
|
Moy. var. dép.
|
0,003235
|
Éc. type var. dép.
|
0,230508
|
|
Somme carrés résidus
|
0,808473
|
Éc. type de régression
|
0,176338
|
|
R2
|
0,492810
|
R2 ajusté
|
0,414781
|
|
F(4, 26)
|
6,315705
|
p. critique (F)
|
0,001089
|
|
Log de vraisemblance
|
12,53512
|
Critère d'Akaike
|
-15,07025
|
|
Critère de Schwarz
|
-7,900310
|
Hannan-Quinn
|
-12,73303
|
|
rho
|
-0,122873
|
Durbin-Watson
|
2,234871
|
Pour le cas de BNP Paribas, on vérifie que le pouvoir
explicatif du modèle est assez significatif (d'après la valeur du
R2 ajusté) et que la variable indépendante est
significative au seuil de 1%, on peut conclure que la relation statistique de
court terme est expressive. Maintenant on va estimer la relation de court terme
pour l'entreprise L'Oréal :
Tableau 26: Relation de court terme
estimé par MCO pour L'Oréal :
Modèle 4: MCO, utilisant les observations 2006:2-2013:4
(T = 31)
Variable dépendante: d_l_Cours
|
Coefficient
|
Erreur Std
|
t de Student
|
p. critique
|
|
|
const
|
0,0257661
|
0,0181012
|
1,4234
|
0,16650
|
|
|
d_l_CA
|
-0,104435
|
0,273181
|
-0,3823
|
0,70535
|
|
|
T1
|
0,0935905
|
0,0515365
|
1,8160
|
0,08092
|
*
|
|
T2
|
0,0243706
|
0,0529019
|
0,4607
|
0,64886
|
|
|
T3
|
0,0324862
|
0,0501883
|
0,6473
|
0,52312
|
|
|
Moy. var. dép.
|
0,022678
|
Éc. type var. dép.
|
0,098435
|
|
Somme carrés résidus
|
0,253792
|
Éc. type de régression
|
0,098799
|
|
R2
|
0,126917
|
R2 ajusté
|
-0,007404
|
|
F(4, 26)
|
0,944880
|
p. critique (F)
|
0,453896
|
|
Log de vraisemblance
|
30,49395
|
Critère d'Akaike
|
-50,98791
|
|
Critère de Schwarz
|
-43,81797
|
Hannan-Quinn
|
-48,65069
|
|
rho
|
0,152381
|
Durbin-Watson
|
1,615571
|
Comme le R2 ajusté du modèle est trop
faible, le pouvoir explicatif du modèle est insignifiant. La variable
indépendante n'est pas significative au seuil de 10% d'après la
valeur p. critique. On ne peut pas inférer significativement sur ce
modèle parce que son pouvoir explicatif est trop faible. On passe
à estimer la relation de court terme pour la prochaine
36
étape, LVMH (comme le log du chiffre d'affaire
différencié n'est pas stationnaire, on va travailler avec la
série différencié deux fois) :
Modèle 3: MCO, utilisant les observations 2006:3-2013:4
(T = 30)
Variable dépendante: d_l_COURS
|
Coefficient
|
Erreur Std
|
t de Student
|
p. critique
|
|
const
|
0,0241802
|
0,0235336
|
1,0275
|
0,31404
|
|
d_d_l_CA
|
-0,726442
|
0,470918
|
-1,5426
|
0,13549
|
|
T1
|
-0,2815
|
0,246057
|
-1,1440
|
0,26344
|
|
T2
|
0,0386927
|
0,0686993
|
0,5632
|
0,57830
|
|
T3
|
-0,00598602
|
0,0646872
|
-0,0925
|
0,92701
|
|
Moy. var. dép.
|
0,022697
|
Éc. type var. dép.
|
0,130751
|
|
Somme carrés résidus
|
0,413475
|
Éc. type de régression
|
0,128604
|
|
R2
|
0,166009
|
R2 ajusté
|
0,032571
|
|
F(4, 25)
|
1,244089
|
p. critique (F)
|
0,317963
|
|
Log de vraisemblance
|
21,69717
|
Critère d'Akaike
|
-33,39434
|
|
Critère de Schwarz
|
-26,38835
|
Hannan-Quinn
|
-31,15306
|
|
rho
|
0,055241
|
Durbin-Watson
|
1,887621
|
Tableau 27: Relation de court terme
estimé par MCO pour LVMH :
Le R2 ajusté a une valeur trop faible, donc le
pouvoir d'explication du modèle n'est suffisant pour avoir une bonne
relation statistique. La valeur p. critique pour la variable
indépendante est supérieure à 10%, ainsi on peut conclure
qu'elle n'est pas significative. On passe à la dernière
estimation d'une relation de court terme, l'estimation pour l'entreprise Sanofi
(on va travailler avec le log du chiffre d'affaires différencié
deux fois pour la même raison de l'entreprise LVMH) :
Modèle 2: MCO, utilisant les observations 2006:3-2013:4
(T = 30)
Variable dépendante: d_l_COURS
|
Coefficient
|
Erreur Std
|
t de Student
|
p. critique
|
|
|
const
|
0,0136852
|
0,0125237
|
1,0927
|
0,28492
|
|
|
d_d_l_COURS
|
0,500418
|
0,0960236
|
5,2114
|
0,00002
|
***
|
|
T1
|
0,0362847
|
0,0378377
|
0,9590
|
0,34676
|
|
|
T2
|
0,0316733
|
0,0361709
|
0,8757
|
0,38955
|
|
|
T3
|
-0,00283213
|
0,0350154
|
-0,0809
|
0,93618
|
|
|
Moy. var. dép.
|
0,012155
|
Éc. type var. dép.
|
0,101867
|
|
Somme carrés résidus
|
0,117103
|
Éc. type de régression
|
0,068440
|
|
R2
|
0,610866
|
R2 ajusté
|
0,548605
|
|
F(4, 25)
|
9,811304
|
p. critique (F)
|
0,000065
|
|
Log de vraisemblance
|
40,62039
|
Critère d'Akaike
|
-71,24077
|
|
Critère de Schwarz
|
-64,23479
|
Hannan-Quinn
|
-68,99950
|
|
rho
|
0,533101
|
Durbin-Watson
|
0,923259
|
Tableau 28: Relation de court terme
estimé par MCO pour Sanofi:
37
On peut constater que le R2 ajusté a une valeur
considérable, ce qui rend le pouvoir d'explication à un niveau
assez significatif. La variable indépendante est significative au seuil
de 1% d'après la valeur p. critique, donc on peut apercevoir une
relation statistique expressive au court terme.
38
4. CONSIDÉRATIONS FINALES
D'après tous les tests explicités dans la
modélisation du travail, on constate qu'il n'y a pas une relation de
long terme existante entre le cours boursier et le chiffre d'affaire. On peut
expliquer ces résultats par les limitations de notre modèle.
Un des motifs pour l'inexistence d'une relation de long terme
dans notre modèle est dû à l'échantillon
utilisé qui n'a pas été assez grand. C'est qu'on appelle
d'une limite purement statistique. Le travail de recherche a eu des
problèmes pour trouver des données comptables
précèdent 2006 à cause des valeurs privées ou
d'accès payante. Comme une relation de cointégration de long
terme exige un échantillon assez significatif, on peut observer que la
taille insuffisante des observations aurait pu être la cause de
l'échec de cette relation.
Un autre motif statistique est l'absence des variables de
contrôle dans le modèle. Les variables de contrôle sont des
variables instrumentales qui ont une relation significative avec la variable
dépendante. Comme explicité dans l'introduction, il existe
plusieurs variables qui peuvent avoir une relation significative avec
l'évolution des cours boursiers, par contre, pour simplification on ne
les a pas pris en compte, l'absence des variables de contrôle peut causer
une spurious regression (régression fallacieuse).
On a des motifs d'ordre économique également. Le
chiffre d'affaire est un résultat purement comptable, sans une
implication économique directe, il n'est prend pas en compte les
coûts et les dettes d'une entreprise. D'autres données de
l'analyse financière, ou même d'ordre comptable, ont une
implication plus directe, comme les bénéfices ou les
résultats liquides d'une entreprise. Par contre, ces autres
données ne sont pas assez accessibles comme le CA et parfois ne sont pas
trimestriels.
Une autre limite du modèle est le comportement des
marchés boursiers. Ils ont des mouvements qui parfois n'ont pas
d'explication, ce qui semble à une vraie marche aléatoire. Robert
Shiller (2010) et d'autres experts en finance comportementale essayent de
répondre les mouvements de la finance et de l'économie dans son
ensemble par la psychologie humaine. Shiller nous démontre que parfois
les agents n'ont pas des comportements rationnels surtout en périodes
des crises, cela contribue aux mouvements aléatoires des cours
boursiers.
D'après les estimations des relations à court
terme, on peut apercevoir que seulement les modèles de l'entreprise BNP
Paribas et de l'entreprise Sanofi ont eu un pouvoir explicatif assez
significatif. Cela peut indiquer que même au court terme, la relation
entre les cours boursiers et les chiffres d'affaires n'est pas assez
significative. C'est évident que les différentiations des
variables compliquent le travail d'intuition économique. Quand on parle
des deux séries différenciées une fois on a une relation
entre l'évolution d'une variable en fonction de l'évolution de
l'autre variable. Par contre, quand on différencie deux ou plusieurs
fois une série temporelle, on perd l'intuition économique, on a
qu'un résultat statistique, la relation entre l'évolution de
l'évolution d'une variable en fonction d'une autre variable n'a pas un
grand pouvoir d'inférence économique.
39
5. RÉFÉRENCES
ANDRADE, Sandro C. et CHHAOCHHARIA, Vidhi etFUERST, Michael E.,
'Sell in May and Go Away' Just Won't Go Away (July 1). Financial Analysts
Journal, Forthcoming, 2012.
BROOKS, Chris. Introductory Econometrics for Finance. Cambridge
University Press. Cambridge, 2008.
DICKEY, D. A. et FULLER, W. A. Distribution of the Estimators for
Autoregressive Time Series With a Unit Root. Journal of the American
Statistical Association, 74, 427-431, 1979.
ENGLE, R. F. et GRANGER, C. W. J. Co-Integration and Error
Correction: Representation, Estimation and Testing. Econometrica
55, 251--76, 1987.
ENGLE, R. F. and YOO, B. S. Forecasting and Testing in
Cointegrated Systems. Journal of Econometrics 35, 143--59, 1987.
FABOZZI, F. J. et MODIGLIANI, F. et JONES, F. J. Foundations of
Financial Markets and Institutions. PEARSON. Boston, 2010.
FAMA, Eugene et FRENCH, Kenneth. Permanent and Temporary
Components of Stock Prices. The Journal of Political Economy, Vol. 96, No. 2.
(Apr 1988), pp. 246-273, 1988.
FRISCH, R.A.K. Editorial, Econometrica, 1, pp. 1-4, 1933.
FULLER, W. A. Introduction to Statistical Time Series, New York,
Wiley, 1976. HENDRY, D. F. Econometrics -- Alchemy or Science?, Economica 47,
387--406, 1980.
HENDRY, D. F. et JUSELIUS, K. Explaining Cointegration Analysis:
Part I, Energy Journal 21, 1--42, 2000.
HENDRY, D. F. et MIZON, G. E. Serial Correlation as a Convenient
Simplification, not a Nuisance: a Comment on a Study of the Demand for Money by
The Bank of England, Economic Journal 88, 549--63, 1978.
LARDIC, S. et MIGNON, V. Econométrie des Séries
Temporelles Macroéconomiques et Financières. ECONOMICA. Paris,
2002.
MIGNON, V. Econométrie - Théorie et applications.
ECONOMICA, Paris 2008.
SCHWERT, G. W. Why Does Stock Market Volatility Change Over
Time? The Journal of Finance, Volume 44, Issue 5, pages 1115-1153, December
1989.
SHILLER, R. J. et AKERLOF, G. A. (2010) Animal Spirits: How Human
Psychology Drives the Economy, and Why It Matters for Global Capitalism,
Princeton University Press. Princeton, 2010.
WOOLDRIDGE, J. M. Introductory Econometrics - A Modern Approach.
SOUTHWESTERN. Mason, 2009.
http://www.boursier.com/indices/composition/cac-40-FR0003500008,FR.html?tri=dcapi
Accès le 20avril
40
http://www.societe.com/bilan/total-sa/542051180201212311.html
Accès le 20 avril de 2014
http://www.fortuneo.fr/fr/bourse/fiche-valeur/FTN000023FR0000120271/informations-total.jsp
Accès le 20 avril de 2014
http://bourse.lesechos.fr/bourse/profil/comptes
societe.jsp?place=XPAR&code=FR0000120 271&codif=ISIN Accès
le 20 avril de 2014
https://fr.finance.yahoo.com/q/hp?s=FP.PA
Accès le 26 avril de 2014
http://www.daily-bourse.fr/resultats-TOTAL-chiffre-affaire-FR0000120271.php
Accès le 26 avril de 2014
http://total.com/fr/actionnaires/informations-reglementees/informations-financieres-trimestrielles/
http://www.loreal-finance.com/fr/resultats-annuels
Accès le 10 mai de 2014
http://www.sanofi.com/investisseurs/actualites
publications/publications financieres/publi cations financieres.aspx#para
11 Accès le 10 mai de 2014
http://www.lvmh.fr/communication-financiere/documentation/resultats
Accès le 10 mai de
2014
http://invest.bnpparibas.com/fr/pid5813/resultats.html
Accès le 10 mai de 2014
41
ANNEXES
42
Annexe 1 : Chiffre d'Affaires de TOTAL
SA
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TRIMESTRE CA
|
|
|
1° Trim 2006
|
38,103,000.00
|
|
2° Trim 2006
|
40,909,000.00
|
|
3° Trim 2006
|
38,357,000.00
|
|
4° Trim 2006
|
36,433,000.00
|
|
1° Trim 2007
|
37,043,000.00
|
|
2° Trim 2007
|
39,094,000.00
|
|
3° Trim 2007
|
39,430,000.00
|
|
4° Trim 2007
|
43,185,000.00
|
|
1° Trim 2008
|
44,213,000.00
|
|
2° Trim 2008
|
48,200,000.00
|
|
3° Trim 2008
|
48,849,000.00
|
|
4° Trim 2008
|
38,714,000.00
|
|
1° Trim 2009
|
30,041,000.00
|
|
2° Trim 2009
|
31,430,000.00
|
|
3° Trim 2009
|
33,628,000.00
|
|
4° Trim 2009
|
36,228,000.00
|
|
1° Trim 2010
|
37,603,000.00
|
|
2° Trim 2010
|
41,329,000.00
|
|
3° Trim 2010
|
40,180,000.00
|
|
4° Trim 2010
|
40,157,000.00
|
|
1° Trim 2011
|
46,029,000.00
|
|
2° Trim 2011
|
45,009,000.00
|
|
3° Trim 2011
|
46,163,000.00
|
|
4° Trim 2011
|
47,492,000.00
|
|
1° Trim 2012
|
51,168,000.00
|
43
Annexe 2: Chiffre d'Affaires de BNP
Paribas
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TRIMESTRE CA
|
|
|
1° Trim 2006
|
6,817,000.00
|
|
2° Trim 2006
|
7,245,000.00
|
|
3° Trim 2006
|
6,829,000.00
|
|
4° Trim 2006
|
7,052,000.00
|
|
1° Trim 2007
|
8,213,000.00
|
|
2° Trim 2007
|
8,214,000.00
|
|
3° Trim 2007
|
7,690,000.00
|
|
4° Trim 2007
|
6,920,000.00
|
|
1° Trim 2008
|
7,395,000.00
|
|
2° Trim 2008
|
7,517,000.00
|
|
3° Trim 2008
|
7,614,000.00
|
|
4° Trim 2008
|
4,850,000.00
|
|
1° Trim 2009
|
9,477,000.00
|
|
2° Trim 2009
|
9,993,000.00
|
|
3° Trim 2009
|
10,663,000.00
|
|
4° Trim 2009
|
10,058,000.00
|
|
1° Trim 2010
|
11,530,000.00
|
|
2° Trim 2010
|
11,174,000.00
|
|
3° Trim 2010
|
10,856,000.00
|
|
4° Trim 2010
|
10,320,000.00
|
|
1° Trim 2011
|
11,685,000.00
|
|
2° Trim 2011
|
10,981,000.00
|
|
3° Trim 2011
|
10,032,000.00
|
|
4° Trim 2011
|
9,686,000.00
|
|
1° Trim 2012
|
9,886,000.00
|
44
Annexe 3: Chiffre d'Affaires de L'Oréal
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TRIMESTRE CA
|
|
|
1° Trim 2006
|
3,938,400.00
|
|
2° Trim 2006
|
3,847,100.00
|
|
3° Trim 2006
|
3,814,500.00
|
|
4° Trim 2006
|
4,190,000.00
|
|
1° Trim 2007
|
4,268,000.00
|
|
2° Trim 2007
|
4,246,000.00
|
|
3° Trim 2007
|
4,125,000.00
|
|
4° Trim 2007
|
4,424,000.00
|
|
1° Trim 2008
|
4,359,000.00
|
|
2° Trim 2008
|
4,287,000.00
|
|
3° Trim 2008
|
4,266,000.00
|
|
4° Trim 2008
|
4,630,000.00
|
|
1° Trim 2009
|
4,370,000.00
|
|
2° Trim 2009
|
4,399,000.00
|
|
3° Trim 2009
|
4,234,800.00
|
|
4° Trim 2009
|
4,468,800.00
|
|
1° Trim 2010
|
4,721,700.00
|
|
2° Trim 2010
|
4,945,100.00
|
|
3° Trim 2010
|
4,851,700.00
|
|
4° Trim 2010
|
4,977,500.00
|
|
1° Trim 2011
|
5,160,000.00
|
|
2° Trim 2011
|
4,989,300.00
|
|
3° Trim 2011
|
4,938,100.00
|
|
4° Trim 2011
|
5,255,700.00
|
|
1° Trim 2012
|
5,643,000.00
|
45
Annexe 4: Chiffre d'Affaires de LVMH
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TRIMESTRE CA
|
|
|
1° Trim 2006
|
3,555,000.00
|
|
2° Trim 2006
|
3,413,000.00
|
|
3° Trim 2006
|
3,658,000.00
|
|
4° Trim 2006
|
4,680,000.00
|
|
1° Trim 2007
|
3,804,000.00
|
|
2° Trim 2007
|
3,608,000.00
|
|
3° Trim 2007
|
4,034,000.00
|
|
4° Trim 2007
|
5,035,000.00
|
|
1° Trim 2008
|
4,002,000.00
|
|
2° Trim 2008
|
3,797,000.00
|
|
3° Trim 2008
|
4,160,000.00
|
|
4° Trim 2008
|
5,234,000.00
|
|
1° Trim 2009
|
4,018,000.00
|
|
2° Trim 2009
|
3,793,000.00
|
|
3° Trim 2009
|
4,135,000.00
|
|
4° Trim 2009
|
5,107,000.00
|
|
1° Trim 2010
|
4,472,000.00
|
|
2° Trim 2010
|
4,627,000.00
|
|
3° Trim 2010
|
5,111,000.00
|
|
4° Trim 2010
|
6,110,000.00
|
|
1° Trim 2011
|
5,247,000.00
|
|
2° Trim 2011
|
5,045,000.00
|
|
3° Trim 2011
|
6,011,000.00
|
|
4° Trim 2011
|
7,356,000.00
|
|
1° Trim 2012
|
6,582,000.00
|
46
Annexe 5: Chiffre d'Affaires de Sanofi
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TRIMESTRE CA
|
|
|
1° Trim 2006
|
7,035,000.00
|
|
2° Trim 2006
|
7,081,000.00
|
|
3° Trim 2006
|
6,901,000.00
|
|
4° Trim 2006
|
7,356,000.00
|
|
1° Trim 2007
|
7,177,000.00
|
|
2° Trim 2007
|
6,939,000.00
|
|
3° Trim 2007
|
7,025,000.00
|
|
4° Trim 2007
|
6,911,000.00
|
|
1° Trim 2008
|
6,937,000.00
|
|
2° Trim 2008
|
6,689,000.00
|
|
3° Trim 2008
|
6,853,000.00
|
|
4° Trim 2008
|
7,089,000.00
|
|
1° Trim 2009
|
7,107,000.00
|
|
2° Trim 2009
|
7,438,000.00
|
|
3° Trim 2009
|
7,400,000.00
|
|
4° Trim 2009
|
7,361,000.00
|
|
1° Trim 2010
|
7,385,000.00
|
|
2° Trim 2010
|
7,783,000.00
|
|
3° Trim 2010
|
7,821,000.00
|
|
4° Trim 2010
|
7,395,000.00
|
|
1° Trim 2011
|
7,779,000.00
|
|
2° Trim 2011
|
8,349,000.00
|
|
3° Trim 2011
|
8,753,000.00
|
|
4° Trim 2011
|
8,508,000.00
|
|
1° Trim 2012
|
8,511,000.00
|
47
Annexe 6: Graphique de série temporelle pour le
log du CA de BNP Paribasp

Annexe 7: Graphique de série temporelle pour le
CA de L'Oréal

48
Annexe 8 : Graphique de série temporelle pour le
CA de LVMH

Annexe 9 : Graphique de série temporelle pour le
CA de Sanofi
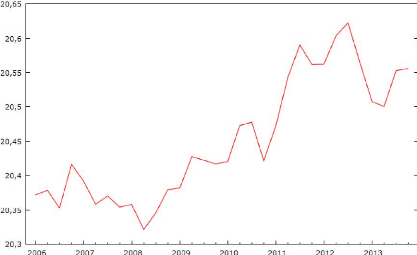
49
Annexe 10 : Test ADF pour le log du CA de
BNP Paribas - Modèle (3)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
const
|
7,01102
|
5,50990
|
1,272
|
0,2165
|
|
l_CA_1
|
-0,340769
|
0,271173
|
-1,257
|
0,8977
|
|
d_l_CA_1
|
-0,280888
|
0,280017
|
-1,003
|
0,3267
|
|
d_l_CA_2
|
-0,165196
|
0,257202
|
-0,6423
|
0,5273
|
|
d_l_CA_3
|
-0,177871
|
0,214773
|
-0,8282
|
0,4165
|
|
time
|
0,00207409
|
0,00570832
|
0,3633
|
0,7198
|
erreur std.
p. critique
Annexe 11 : Test ADF pour le log du CA de
BNP Paribas - Modèle (2)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
const
|
5,49686
|
3,53590
|
1,555
|
0,1337
|
|
l_CA_1
|
-0,265447
|
0,171486
|
-1,548
|
0,5093
|
|
d_l_CA_1
|
-0,342741
|
0,218097
|
-1,572
|
0,1297
|
|
d_l_CA_2
|
-0,211447
|
erreur std.
0,219237
|
-0,9645
|
0,3448
|
|
d_l_CA_3
|
-0,206632
|
0,195850
|
-1,055
|
0,3024
|
p. critique
Annexe 12 : Test ADF pour le log du CA de
BNP Paribas - Modèle (1)
erreur std.
p. critique
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
l_CA_1
|
0,000616749
|
0,00136499
|
0,4518
|
0,8119
|
|
|
d_l_CA_1
|
-0,379206
|
0,174668
|
-2,171
|
0,0386
|
|
Annexe 13 : Test ADF pour le log du CA de
L'Oréal - Modèle (3)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
const
|
17,7583
|
6,98116
|
2,544
|
0,0178
|
|
|
l_CA_1
|
-0,898437
|
erreur std.
0,353976
|
-2,538
|
p. critique
0,3095
|
|
|
d_l_CA_1
|
-0,144747
|
0,297780
|
-0,4861
|
0,6313
|
|
|
d_l_CA_2
|
-0,0262941
|
0,205921
|
-0,1277
|
0,8995
|
|
|
time
|
0,0118152
|
0,00505157
|
2,339
|
0,0280
|
|
Annexe 14 : Test ADF pour le log du CA de
L'Oréal - Modèle (2)
|
coefficient
|
|
t de Student
|
|
|
|
|
erreur std.
|
|
p. critique
|
|
|
const
|
0,608011
|
2,17641
|
0,2794
|
0,7827
|
|
|
l_CA_1
|
-0,0288494
|
0,109022
|
-0,2646
|
0,9277
|
|
|
d_l_CA_1
|
-0,823224
|
0,231020
|
-3,563
|
0,0018
|
|
|
d_l_CA_2
|
-0,451158
|
0,291428
|
-1,548
|
0,1365
|
***
|
|
d_l_CA_3
|
-0,223022
|
0,296637
|
-0,7518
|
0,4605
|
|
|
d_l_CA_4
|
-0,0875169
|
0,224030
|
-0,3906
|
0,7000
|
|
50
Annexe 15 : Test ADF pour le log du CA de
L'Oréal - Modèle (1)
|
|
|
|
|
|
|
l_CA_1 0,000987355 0,000553175 1,785
|
0,9826
|
|
|
d_l_CA_1 -0,575260 0,154916 -3,713
|
0,0009
|
|
Annexe 16 : Test ADF pour le log du CA de LVMH -
Modèle (3)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
const
|
6,04030
|
4,23717
|
1,426
|
0,1680
|
|
|
l_CA_1
|
-0,307554
|
0,216732
|
-1,419
|
0,8558
|
|
|
d_l_CA_1
|
-0,555150
|
0,196685
|
-2,823
|
0,0099
|
|
|
d_l_CA_2
|
-0,683299
|
0,144605
|
-4,725
|
0,0001
|
|
|
d_l_CA_3
|
-0,691653
|
0,127136
|
-5,440
|
1,83e-05
|
|
|
time
|
0,0105907
|
erreur std.
0,00578157
|
1,832
|
0,0806
|
|
p. critique
Annexe 17 : Test ADF pour le log du CA de
LVMH - Modèle (2)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
const
|
0,771171
|
2,08026
|
0,3707
|
0,7140
|
|
|
l_CA_1
|
-0,0360142
|
erreur std.
0,103882
|
-0,3467
|
0,9156
|
|
|
d_l_CA_1
|
-0,270181
|
0,168908
|
-1,600
|
0,1223
|
|
|
d_l_CA_2
|
-0,618912
|
0,164374
|
-3,765
|
0,0009
|
|
p. critique
Annexe 18 : Test ADF pour le log du CA de
LVMH - Modèle (1)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
l_CA_1
|
0,000831786
|
0,000757937
|
1,097
|
0,9297
|
|
|
d_l_CA_1
|
-0,154957
|
erreur std.
0,135750
|
-1,141
|
p. critique
0,2659
|
|
|
d_l_CA_2
|
-0,179212
|
0,134755
|
-1,330
|
0,1972
|
|
|
d_l_CA_3
|
-0,162594
|
0,133238
|
-1,220
|
0,2353
|
|
|
d_l_CA_4
|
0,751997
|
0,135411
|
5,553
|
1,39e-05
|
|
Annexe 19 : Test ADF pour le log du CA de Sanofi -
Modèle (3)
|
coefficient
|
|
t de Student
|
|
|
|
erreur std.
|
|
p. critique
|
|
const
|
6,08811
|
3,61293
|
1,685
|
0,1049
|
|
l_CA_1
|
-0,299602
|
0,178102
|
-1,682
|
0,7594
|
|
d_l_CA_1
|
0,190870
|
0,192201
|
0,9931
|
0,3306
|
|
d_l_CA_2
|
-0,233409
|
0,206097
|
-1,133
|
0,2686
|
|
time
|
0,00260121
|
0,00178871
|
1,454
|
0,1588
|
51

Annexe 20 : Test ADF pour le log du CA de
Sanofi - Modèle (2)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
const
|
1,35176
|
1,59834
|
0,8457
|
0,4057
|
|
|
l_CA_1
|
-0,0656923
|
0,0781634
|
-0,8404
|
0,8071
|
|
|
d_l_CA_1
|
0,0925412
|
0,183883
|
0,5033
|
0,6192
|
|
|
d_l_CA_2
|
-0,368385
|
erreur std.
0,188072
|
-1,959
|
0,0614
|
|
p. critique
Annexe 21 : Test ADF pour le log du CA de
Sanofi - Modèle (3)
|
coefficient
|
|
t de Student
|
|
|
|
|
erreur std.
|
|
p. critique
|
|
|
l_CA_1
|
0,000412032
|
0,000325314
|
1,267
|
0,9484
|
|
|
d_l_CA_1
|
0,0566824
|
0,177945
|
0,3185
|
0,7526
|
|
|
d_l_CA_2
|
-0,400500
|
0,183187
|
-2,186
|
0,0380
|
|
*
**
Annexe 22 : Graphique de série
temporelle pour le log du CA différencié de BNP Paribas
52
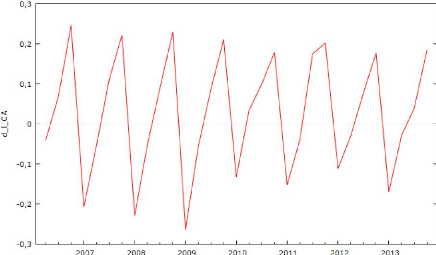
Annexe 23 : Graphique de série
temporelle pour le log du CA différencié de L'Oréal
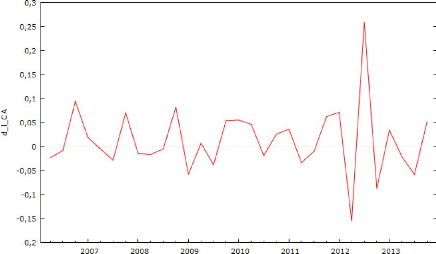
Annexe 24 : Graphique de série
temporelle pour le log du CA différencié de LVMH
53
Annexe 25 : Graphique de série
temporelle pour le log du CA différencié de Sanofi

Annexe 26 : Test ADF pour le log du CA
différencié de BNP Paribas - Modèle (3)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
const
|
0,0644236
|
0,0702046
|
0,9177
|
0,3676
|
|
|
d_l_CA_1
|
-1,67758
|
erreur std.
0,323991
|
-5,178
|
p. critique
8,01e-05
|
|
|
d_d_l_CA_1
|
0,212437
|
0,194832
|
1,090
|
0,2860
|
|
|
time
|
-0,00256022
|
0,00351847
|
-0,7277
|
0,4736
|
|
***
Annexe 27 : Test ADF pour le log du CA
différencié de BNP Paribas - Modèle (2)
|
coefficient
|
erreur std.
|
t de Student
|
p. critique
|
|
|
|
|
|
|
|
|
const
|
0,0180515
|
0,0291836
|
0,6186
|
0,5416
|
|
|
d_l_CA_1
|
-1,65059
|
0,318936
|
-5,175
|
8,82e-06
|
|
|
d_d_l_CA_1
|
0,199381
|
0,192240
|
1,037
|
0,3092
|
***
|
Annexe 28 : Test ADF pour le log du CA
différencié de BNP Paribas - Modèle (1)
erreur std.
p. critique
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
***
|
|
d_l_CA_1
|
-1,62742
|
0,313086
|
-5,198
|
2,86e-07
|
|
|
d_d_l_CA_1
|
0,186719
|
0,188949
|
0,9882
|
0,3318
|
|
54
Annexe 29 : Test ADF pour le log du CA
différencié de L'Oréal - Modèle (3)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
const
|
0,0393255
|
0,0265694
|
1,480
|
0,1513
|
|
|
d_l_CA_1
|
-2,07909
|
0,334091
|
-6,223
|
3,23e-07
|
|
|
d_d_l_CA_1
|
0,313717
|
0,189786
|
1,653
|
0,1108
|
|
|
time
|
-0,000643292
|
erreur std.
0,00131710
|
-0,4884
|
0,6295
|
|
p. critique
***
Annexe 30 : Test ADF pour le log du CA
différencié de L'Oréal - Modèle (2)
|
coefficient
|
|
t de Student
|
|
|
|
|
erreur std.
|
|
p. critique
|
|
|
const
|
0,0276991
|
0,0116277
|
2,382
|
0,0248
|
|
|
d_l_CA_1
|
-2,07519
|
0,329069
|
-6,306
|
2,12e-08
|
**
|
|
d_d_l_CA_1
|
0,313943
|
0,186986
|
1,679
|
0,1051
|
|
***
Annexe 31 : Test ADF pour le log du CA
différencié de L'Oréal - Modèle (1)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
d_l_CA_1
|
-1,40159
|
0,711525
|
-1,970
|
0,0468
|
|
|
d_d_l_CA_1
|
-0,306349
|
0,640239
|
-0,4785
|
0,6372
|
|
|
d_d_l_CA_2
|
-0,485962
|
erreur std.
0,533783
|
-0,9104
|
0,3729
|
|
|
d_d_l_CA_3
|
-0,361673
|
0,395216
|
-0,9151
|
0,3705
|
|
|
d_d_l_CA_4
|
-0,152139
|
0,210842
|
-0,7216
|
0,4785
|
|
p. critique
**
Annexe 32 : Test ADF pour le log du CA
différencié de LVMH - Modèle (3)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
const
|
0,0177180
|
0,0255988
|
0,6921
|
0,4964
|
|
|
d_l_CA_1
|
-0,735042
|
erreur std.
0,549561
|
-1,338
|
p. critique
0,8784
|
|
|
d_d_l_CA_1
|
-0,417054
|
0,414407
|
-1,006
|
0,3257
|
|
|
d_d_l_CA_2
|
-0,593870
|
0,279019
|
-2,128
|
0,0453
|
|
|
d_d_l_CA_3
|
-0,754300
|
0,148305
|
-5,086
|
4,89e-05
|
|
|
time
|
-6,24383e-05
|
0,00133323
|
-0,04683
|
0,9631
|
|
**
***
Annexe 33 : Test ADF pour le log du CA
différencié de LVMH - Modèle (2)
|
coefficient
|
|
t de Student
|
|
|
|
|
erreur std.
|
|
p. critique
|
|
|
const
|
0,0167622
|
0,0151004
|
1,110
|
0,2790
|
|
|
d_l_CA_1
|
-0,744742
|
0,497359
|
-1,497
|
0,5352
|
|
|
d_d_l_CA_1
|
-0,409878
|
0,376204
|
-1,090
|
0,2877
|
|
|
d_d_l_CA_2
|
-0,589017
|
0,253118
|
-2,327
|
0,0296
|
|
|
d_d_l_CA_3
|
-0,751740
|
0,134699
|
-5,581
|
1,31e-05
|
|
55
Annexe 34 : Test ADF pour le log du CA
différencié de LVMH - Modèle (1)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
d_l_CA_1
|
-0,312311
|
0,310763
|
-1,005
|
0,2833
|
|
|
d_d_l_CA_1
|
-0,736275
|
0,235853
|
-3,122
|
0,0048
|
|
|
d_d_l_CA_2
|
-0,806629
|
0,160925
|
-5,012
|
4,52e-05
|
|
|
d_d_l_CA_3
|
-0,862341
|
erreur std.
0,0911018
|
-9,466
|
2,13e-09
|
|
p. critique
***
***
***
Annexe 35 : Test ADF pour le log du CA
différencié de Sanofi - Modèle (3)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
const
|
0,0144725
|
0,0192364
|
0,7523
|
0,4611
|
|
d_l_CA_1
|
-0,690104
|
0,549955
|
-1,255
|
0,8981
|
|
d_d_l_CA_1
|
-0,171425
|
0,502791
|
-0,3409
|
0,7369
|
|
d_d_l_CA_2
|
-0,500891
|
0,428683
|
-1,168
|
0,2571
|
|
d_d_l_CA_3
|
-0,494044
|
0,332967
|
-1,484
|
0,1543
|
|
d_d_l_CA_4
|
-0,240438
|
0,237206
|
-1,014
|
0,3235
|
|
time
|
-0,000555109
|
erreur std.
0,000947374
|
-0,5859
|
0,5648
|
p. critique
Annexe 36 : Test ADF pour le log du CA
différencié de Sanofi - Modèle (2)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
const
|
0,00414962
|
0,00759639
|
0,5463
|
0,5909
|
|
d_l_CA_1
|
-0,753293
|
0,530352
|
-1,420
|
0,5739
|
|
d_d_l_CA_1
|
-0,104414
|
0,481507
|
-0,2168
|
0,8305
|
|
d_d_l_CA_2
|
-0,444703
|
erreur std.
0,410903
|
-1,082
|
0,2920
|
|
d_d_l_CA_3
|
-0,439185
|
0,314244
|
-1,398
|
0,1775
|
|
d_d_l_CA_4
|
-0,204243
|
0,225230
|
-0,9068
|
0,3753
|
p. critique
Annexe 37 : Test ADF pour le log du CA
différencié de Sanofi - Modèle (1)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
d_l_CA_1
|
-0,619053
|
erreur std.
0,462064
|
-1,340
|
p. critique
0,1674
|
|
|
d_d_l_CA_1
|
-0,217387
|
0,427506
|
-0,5085
|
0,6164
|
|
|
d_d_l_CA_2
|
-0,545695
|
0,360780
|
-1,513
|
0,1453
|
|
|
d_d_l_CA_3
|
-0,505474
|
0,284984
|
-1,774
|
0,0906
|
|
|
d_d_l_CA_4
|
-0,243484
|
0,209872
|
-1,160
|
0,2590
|
|
56
Annexe 38 : Cours Boursiers de TOTAL
SA
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TRIMESTRE COURS
|
|
|
1° Trim 2006
|
32.25
|
|
2° Trim 2006
|
33.59
|
|
3° Trim 2006
|
34.66
|
|
4° Trim 2006
|
33.02
|
|
1° Trim 2007
|
38.15
|
|
2° Trim 2007
|
37.64
|
|
3° Trim 2007
|
38.33
|
|
4° Trim 2007
|
34.69
|
|
1° Trim 2008
|
39.66
|
|
2° Trim 2008
|
34.68
|
|
3° Trim 2008
|
29.86
|
|
4° Trim 2008
|
27.27
|
|
1° Trim 2009
|
30.47
|
|
2° Trim 2009
|
29.89
|
|
3° Trim 2009
|
31.66
|
|
4° Trim 2009
|
31.48
|
|
1° Trim 2010
|
29.89
|
|
2° Trim 2010
|
29.21
|
|
3° Trim 2010
|
|
|
4° Trim 2010
|
|
|
1° Trim 2011
|
|
|
2° Trim 2011
|
|
|
3° Trim 2011
|
|
|
4° Trim 2011
|
|
|
1° Trim 2012
|
|
57
Annexe 39 : Cours Boursiers de BNP
Paribas
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TRIMESTRE COURS
|
|
|
1° Trim 2006
|
52.23
|
|
2° Trim 2006
|
61.73
|
|
3° Trim 2006
|
60.54
|
|
4° Trim 2006
|
58.74
|
|
1° Trim 2007
|
69.39
|
|
2° Trim 2007
|
60.24
|
|
3° Trim 2007
|
60.03
|
|
4° Trim 2007
|
46.35
|
|
1° Trim 2008
|
54.29
|
|
2° Trim 2008
|
50.32
|
|
3° Trim 2008
|
35.46
|
|
4° Trim 2008
|
21.27
|
|
1° Trim 2009
|
40.76
|
|
2° Trim 2009
|
46.96
|
|
3° Trim 2009
|
45.98
|
|
4° Trim 2009
|
44.42
|
|
1° Trim 2010
|
39.92
|
|
2° Trim 2010
|
42.57
|
|
3° Trim 2010
|
|
|
4° Trim 2010
|
|
|
1° Trim 2011
|
|
|
2° Trim 2011
|
|
|
3° Trim 2011
|
|
|
4° Trim 2011
|
|
|
1° Trim 2012
|
|
58
Annexe 40 : Cours Boursiers de
L'Oréal
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TRIMESTRE COURS
|
|
|
1° Trim 2006
|
59.54
|
|
2° Trim 2006
|
69.64
|
|
3° Trim 2006
|
64.87
|
|
4° Trim 2006
|
67.45
|
|
1° Trim 2007
|
76.29
|
|
2° Trim 2007
|
74.29
|
|
3° Trim 2007
|
82.02
|
|
4° Trim 2007
|
68.01
|
|
1° Trim 2008
|
68.87
|
|
2° Trim 2008
|
59.79
|
|
3° Trim 2008
|
56.05
|
|
4° Trim 2008
|
45.18
|
|
1° Trim 2009
|
50.53
|
|
2° Trim 2009
|
62.2
|
|
3° Trim 2009
|
65.44
|
|
4° Trim 2009
|
68.85
|
|
1° Trim 2010
|
70.49
|
|
2° Trim 2010
|
72.45
|
|
3° Trim 2010
|
|
|
4° Trim 2010
|
|
|
1° Trim 2011
|
|
|
2° Trim 2011
|
|
|
3° Trim 2011
|
|
|
4° Trim 2011
|
|
|
1° Trim 2012
|
|
59
Annexe 41 : Cours Boursiers de LVMH
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TRIMESTRE COURS
|
|
|
1° Trim 2006
|
64.28
|
|
2° Trim 2006
|
67.34
|
|
3° Trim 2006
|
65.62
|
|
4° Trim 2006
|
70.44
|
|
1° Trim 2007
|
74.76
|
|
2° Trim 2007
|
69.88
|
|
3° Trim 2007
|
71.00
|
|
4° Trim 2007
|
58.41
|
|
1° Trim 2008
|
65.44
|
|
2° Trim 2008
|
63.28
|
|
3° Trim 2008
|
39.33
|
|
4° Trim 2008
|
40.04
|
|
1° Trim 2009
|
52.72
|
|
2° Trim 2009
|
60.06
|
|
3° Trim 2009
|
62.78
|
|
4° Trim 2009
|
72.05
|
|
1° Trim 2010
|
79.24
|
|
2° Trim 2010
|
84.34
|
|
3° Trim 2010
|
|
|
4° Trim 2010
|
|
|
1° Trim 2011
|
|
|
2° Trim 2011
|
|
|
3° Trim 2011
|
|
|
4° Trim 2011
|
|
|
1° Trim 2012
|
|
60
Annexe 42 : Cours Boursiers de Sanofi
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TRIMESTRE COURS
|
|
|
1° Trim 2006
|
51,40
|
|
2° Trim 2006
|
50,00
|
|
3° Trim 2006
|
47,55
|
|
4° Trim 2006
|
46,09
|
|
1° Trim 2007
|
51,39
|
|
2° Trim 2007
|
44,08
|
|
3° Trim 2007
|
47,83
|
|
4° Trim 2007
|
35,89
|
|
1° Trim 2008
|
36,82
|
|
2° Trim 2008
|
37,36
|
|
3° Trim 2008
|
33,39
|
|
4° Trim 2008
|
31,44
|
|
1° Trim 2009
|
36,43
|
|
2° Trim 2009
|
38,35
|
|
3° Trim 2009
|
40,78
|
|
4° Trim 2009
|
43,53
|
|
1° Trim 2010
|
42,08
|
|
2° Trim 2010
|
38,52
|
|
3° Trim 2010
|
|
|
4° Trim 2010
|
|
|
1° Trim 2011
|
|
|
2° Trim 2011
|
|
|
3° Trim 2011
|
|
|
4° Trim 2011
|
|
|
1° Trim 2012
|
|
61
Annexe 43 : Graphique de série
temporelle pour le log des Cours Boursiers de BNP Paribas

Annexe 44 : Graphique de série
temporelle pour le log des Cours Boursiers de L'Oréal

62
Annexe 45 : Graphique de série
temporelle pour le log des Cours Boursiers de LVMH
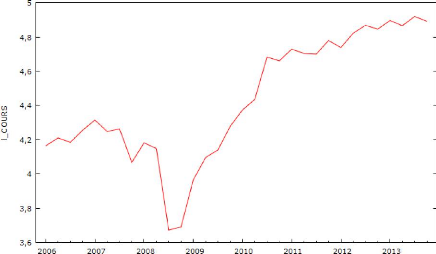
Annexe 46 : Graphique de série
temporelle pour le log des Cours Boursiers de Sanofi

63
Annexe 47 : Test ADF pour le log des
Cours Boursiers de BNP Paribas - Modèle (3)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
const
|
1,47121
|
0,999515
|
1,472
|
0,1540
|
|
l_COURS_1
|
-0,385587
|
0,242690
|
-1,589
|
0,7978
|
|
d_l_COURS_1
|
0,0706560
|
0,242343
|
0,2916
|
0,7731
|
|
d_l_COURS_2
|
-0,0675983
|
0,220063
|
-0,3072
|
0,7614
|
|
time
|
-0,00134781
|
0,00685907
|
-0,1965
|
0,8459
|
erreur std.
p. critique
Annexe 48 : Test ADF pour le log des
Cours Boursiers de BNP Paribas - Modèle (2)
|
coefficient
|
|
t de Student
|
|
|
|
|
erreur std.
|
|
p. critique
|
|
|
const
|
1,32881
|
0,675033
|
1,969
|
0,0602
|
|
|
l_COURS_1
|
-0,354192
|
0,179133
|
-1,977
|
0,2971
|
*
|
|
d_l_COURS_1
|
0,0462931
|
0,204183
|
0,2267
|
0,8225
|
|
Annexe 49 : Test ADF pour le log des
Cours Boursiers de BNP Paribas - Modèle (1)
erreur std.
p. critique
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
l_COURS_1
|
-0,00223476
|
0,0113537
|
-0,1968
|
0,6155
|
|
d_l_COURS_1
|
-0,109791
|
0,186443
|
-0,5889
|
0,5607
|
Annexe 50 : Test ADF pour le log des Cours Boursiers de
L'Oréal - Modèle (3)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
const
|
0,706083
|
erreur std.
0,425883
|
1,658
|
p. critique
0,1094
|
|
|
l_Cours_1
|
-0,182843
|
0,106358
|
-1,719
|
0,7431
|
|
|
d_l_Cours_1
|
0,105690
|
0,187299
|
0,5643
|
0,5774
|
|
|
time
|
0,00580155
|
0,00284686
|
2,038
|
0,0519
|
|
*
Annexe 51 : Test ADF pour le log des Cours Boursiers de
L'Oréal - Modèle (2)
|
coefficient
|
erreur std.
|
t de Student
|
p. critique
|
|
|
|
|
|
|
const
|
0,146584
|
0,344059
|
0,4260
|
0,6735
|
|
l_Cours_1
|
-0,0299492
|
0,0796670
|
-0,3759
|
0,9109
|
|
d_l_Cours_1
|
0,0567145
|
0,196297
|
0,2889
|
0,7748
|
Annexe 52 : Test ADF pour le log des
Cours Boursiers de L'Oréal - Modèle (3)
erreur std.
p. critique
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
l_Cours_1
|
0,00394175
|
0,00428614
|
0,9197
|
0,9050
|
|
d_l_Cours_1
|
0,0308230
|
0,183904
|
0,1676
|
0,8681
|
64
Annexe 53 : Test ADF pour le log des
Cours Boursiers de LVMH - Modèle (3)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
const
|
0,844568
|
0,487657
|
1,732
|
0,0961
|
|
|
l_COURS_1
|
-0,221617
|
0,126995
|
-1,745
|
0,7312
|
|
|
d_l_COURS_1
|
0,140096
|
0,196189
|
0,7141
|
0,4821
|
|
|
d_l_COURS_2
|
-0,0942339
|
0,198232
|
-0,4754
|
0,6388
|
|
|
time
|
0,00892818
|
0,00515534
|
1,732
|
0,0961
|
|
erreur std.
p. critique
*
*
Annexe 54 : Test ADF pour le log des Cours Boursiers de
LVMH - Modèle (2)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
const
|
0,210999
|
0,335092
|
0,6297
|
0,5346
|
|
l_COURS_1
|
-0,0417564
|
0,0759538
|
-0,5498
|
0,8790
|
|
d_l_COURS_1
|
0,0924657
|
erreur std.
0,201869
|
0,4580
|
0,6509
|
|
d_l_COURS_2
|
-0,159297
|
0,202272
|
-0,7875
|
0,4384
|
p. critique
Annexe 55 : Test ADF pour le log des
Cours Boursiers de LVMH - Modèle (1)
erreur std.
p. critique
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
l_COURS_1
|
0,00449166
|
0,00560410
|
0,8015
|
0,8855
|
|
d_l_COURS_1
|
0,0510853
|
0,190275
|
0,2685
|
0,7903
|
Annexe 56 : Test ADF pour le log des Cours Boursiers de
Sanofi - Modèle (3)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
const
|
0,838288
|
0,424605
|
1,974
|
0,0623
|
|
|
l_COURS_1
|
-0,275893
|
0,119420
|
-2,310
|
0,4277
|
|
|
d_l_COURS_1
|
-0,180194
|
erreur std.
0,201654
|
-0,8936
|
p. critique
0,3822
|
|
|
d_l_COURS_2
|
0,0562646
|
0,209449
|
0,2686
|
0,7910
|
|
|
d_l_COURS_3
|
-0,0382880
|
0,230357
|
-0,1662
|
0,8697
|
|
|
d_l_COURS_4
|
-0,104304
|
0,215591
|
-0,4838
|
0,6338
|
|
|
time
|
0,0123877
|
0,00385449
|
3,214
|
0,0044
|
|
65
Annexe 57 : Graphique de série
temporelle pour le log des Cours Boursiers Différenciés de BNP
Paribas
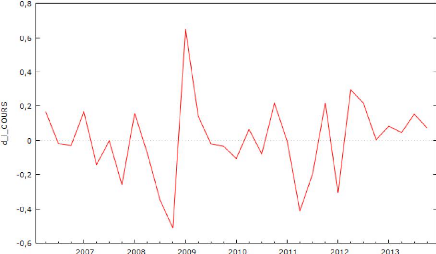
Annexe 58 : Graphique de série
temporelle pour le log des s Cours Boursiers Différenciés de
L'Oréal
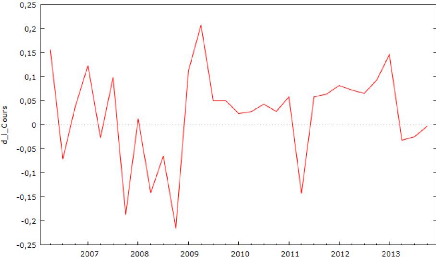
66
Annexe 59 : Graphique de série
temporelle pour le log des Cours Boursiers Différenciés de
LVMH
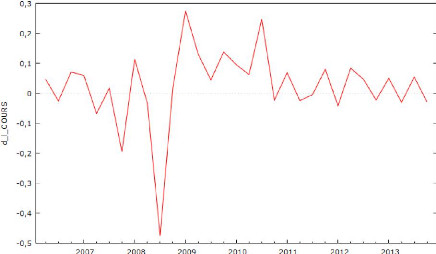
Annexe 60 : Graphique de série
temporelle pour le log des Cours Boursiers Différenciés de
Sanofi

67
Annexe 61 : Test ADF pour le log des
Cours Boursiers différenciés de BNP Paribas - Modèle
(3)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
const
|
-0,108467
|
0,105488
|
-1,028
|
0,3137
|
|
|
d_l_COURS_1
|
-1,43045
|
0,288584
|
-4,957
|
0,0001
|
|
|
d_d_l_COURS_1
|
0,256550
|
0,190721
|
1,345
|
0,1907
|
|
|
time
|
0,00582648
|
erreur std.
0,00531810
|
1,096
|
0,2837
|
|
p. critique
***
Annexe 62 : Test ADF pour le log des
Cours Boursiers différenciés de BNP Paribas - Modèle
(2)
|
coefficient
|
|
t de Student
|
|
|
|
|
erreur std.
|
|
p. critique
|
|
|
const
|
-0,00334756
|
0,0440072
|
-0,07607
|
0,9399
|
|
|
d_l_COURS_1
|
-1,37850
|
0,285756
|
-4,824
|
4,61e-05
|
|
|
d_d_l_COURS_1
|
0,238550
|
0,190743
|
1,251
|
0,2222
|
|
***
Annexe 63 : Test ADF pour le log des
Cours Boursiers différenciés de BNP Paribas - Modèle
(1)
erreur std.
p. critique
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
d_l_COURS_1
|
-1,37785
|
0,280320
|
-4,915
|
1,12e-06
|
|
|
d_d_l_COURS_1
|
0,238239
|
0,187155
|
1,273
|
0,2139
|
|
***
Annexe 64 : Test ADF pour le log des Cours Boursiers
différenciés de L'Oréal - Modèle (3)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
const
|
-0,0108544
|
erreur std.
0,0447152
|
-0,2427
|
p. critique
0,8102
|
|
d_l_Cours_1
|
-0,837670
|
0,276672
|
-3,028
|
0,1245
|
|
d_d_l_Cours_1
|
-0,118162
|
0,190284
|
-0,6210
|
0,5402
|
|
time
|
0,00157353
|
0,00233134
|
|
|
0,6749
0,5059
Annexe 65 : Test ADF pour le log des
Cours Boursiers différenciés de L'Oréal - Modèle
(2)
|
coefficient
|
|
erreur std.
|
t de Student
|
p. critique
|
|
|
|
|
|
|
|
|
const
|
0,0162908
|
0,0193377
|
0,8424
|
0,4072
|
|
|
d_l_Cours_1
|
-0,783028
|
0,261777
|
-2,991
|
0,0357
|
**
|
|
d_d_l_Cours_1
|
-0,140993
|
0,185283
|
-0,7610
|
0,4535
|
|
68
Annexe 66 : Test ADF pour le log des
Cours Boursiers différenciés de L'Oréal - Modèle
(1)
|
|
|
|
|
|
|
|
|
|
|
|
|
d_l_Cours_1
|
-0,717383
|
0,248564
|
-2,886
|
0,0038
|
|
|
d_d_l_Cours_1
|
-0,177813
|
0,179083
|
-0,9929
|
0,3296
|
|
***
Annexe 67 : Test ADF pour le log des Cours Boursiers
différenciés de LVMH - Modèle (3)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
const
|
-0,00682850
|
0,0841535
|
-0,08114
|
0,9362
|
|
d_l_COURS_1
|
-0,875524
|
0,518210
|
-1,690
|
0,7562
|
|
d_d_l_COURS_1
|
-0,00570760
|
0,457961
|
-0,01246
|
0,9902
|
|
d_d_l_COURS_2
|
-0,248706
|
0,406844
|
-0,6113
|
0,5482
|
|
d_d_l_COURS_3
|
-0,0262982
|
0,308413
|
-0,08527
|
0,9329
|
|
d_d_l_COURS_4
|
-0,103428
|
0,232149
|
-0,4455
|
0,6610
|
|
time
|
0,00141174
|
erreur std.
0,00422574
|
0,3341
|
0,7420
|
p. critique
Annexe 68 : Test ADF pour le log des
Cours Boursiers différenciés de LVMH - Modèle (2)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
const
|
0,0191567
|
0,0314028
|
0,6100
|
0,5487
|
|
d_l_COURS_1
|
-0,814739
|
0,474319
|
-1,718
|
0,4223
|
|
d_d_l_COURS_1
|
-0,0526640
|
0,426069
|
-0,1236
|
0,9029
|
|
d_d_l_COURS_2
|
-0,287523
|
erreur std.
0,381143
|
-0,7544
|
0,4594
|
|
d_d_l_COURS_3
|
-0,0496497
|
0,293641
|
-0,1691
|
0,8674
|
|
d_d_l_COURS_4
|
-0,117422
|
0,223210
|
-0,5261
|
0,6046
|
p. critique
Annexe 69 : Test ADF pour le log des
Cours Boursiers différenciés de LVMH - Modèle (1)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
d_l_COURS_1
|
-0,703958
|
erreur std.
0,431579
|
-1,631
|
p. critique
0,0972
|
|
|
d_d_l_COURS_1
|
-0,141605
|
0,394317
|
-0,3591
|
0,7231
|
|
|
d_d_l_COURS_2
|
-0,360832
|
0,356254
|
-1,013
|
0,3227
|
|
|
d_d_l_COURS_3
|
-0,0919038
|
0,281057
|
-0,3270
|
0,7469
|
|
|
d_d_l_COURS_4
|
|
0,215951
|
|
|
|
*
-0,142945
-0,6619
0,5152
Annexe 70 : Test ADF pour le log des
Cours Boursiers différenciés de Sanofi - Modèle (3)
|
coefficient
|
|
t de Student
|
|
|
|
|
erreur std.
|
|
p. critique
|
|
|
const
|
-0,0615520
|
0,0485452
|
-1,268
|
0,2165
|
|
|
d_l_COURS_1
|
-1,30205
|
0,329263
|
-3,954
|
0,0101
|
|
|
d_d_l_COURS_1
|
0,00853164
|
0,204540
|
0,04171
|
0,9671
|
**
|
|
time
|
0,00446981
|
0,00259993
|
1,719
|
0,0979
|
|
69
Annexe 71 : Test ADF pour le log des
Cours Boursiers différenciés de Sanofi - Modèle (2)
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
const
|
0,0156966
|
0,0210252
|
0,7466
|
0,4626
|
|
d_l_COURS_1
|
-0,936980
|
0,367966
|
-2,546
|
0,1045
|
|
d_d_l_COURS_1
|
-0,232453
|
0,304217
|
-0,7641
|
0,4523
|
|
d_d_l_COURS_2
|
-0,0938105
|
erreur std.
0,207091
|
-0,4530
|
0,6546
|
p. critique
Annexe 72 : Test ADF pour le log des
Cours Boursiers différenciés de Sanofi - Modèle (1)
|
coefficient
|
|
t de Student
|
|
|
|
|
erreur std.
|
|
p. critique
|
|
|
d_l_COURS_1
|
-0,866798
|
0,352591
|
-2,458
|
0,0135
|
|
|
d_d_l_COURS_1
|
-0,278520
|
0,295244
|
-0,9434
|
0,3545
|
**
|
|
d_d_l_COURS_2
|
-0,116569
|
0,203014
|
-0,5742
|
0,5710
|
|
Annexe 73 : Test d'Engle-Granger pour
l'entreprise BNP Paribas
erreur std.
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
l_resid_sais_1
|
-0,418990
|
0,169514
|
-2,472
|
0,0130
|
|
|
d_l_resid_sais_1
|
0,0921506
|
0,190314
|
0,4842
|
0,6320
|
|
Annexe 74 : Test d'Engle-Granger pour
l'entreprise L'Oréal
erreur std.
|
coefficient
|
|
t de Student
|
|
|
|
|
|
|
|
|
|
l_resid_sais_1
|
-0,276370
|
0,163017
|
-1,695
|
0,0853
|
|
|
d_l_resid_sais_1
|
-0,211900
|
0,186400
|
-1,137
|
0,2653
|
|
Annexe 75 : Test d'Engle-Granger pour l'entreprise
LVMH
|
|
|
t de Student
|
|
|
|
coefficient
|
erreur std.
|
|
p. critique
|
|
|
l_resid_1
|
-0,326232
|
0,160815
|
-2,029
|
0,0408
|
|
|
d_l_resid_1
|
0,167686
|
0,191154
|
0,8772
|
0,3884
|
**
|
|
d_l_resid_2
|
-0,119084
|
0,195277
|
-0,6098
|
0,5473
|
|
Annexe 76 : Test d'Engle-Granger pour l'entreprise
Sanofi
|
coefficient
|
erreur std.
|
t de Student
|
p. critique
|
|
|
|
|
|
|
l_resid_sais_1
|
-0,174669
|
0,135711
|
-1,287
|
0,1832
|
|
d_l_resid_sais_1
|
0,121275
|
0,198570
|
0,6107
|
0,5467
|
|
d_l_resid_sais_2
|
-0,161007
|
0,200786
|
-0,8019
|
0,4299
|
70
Annexe 77: Modèle de MCO avec 3
variables dummies pour BNP Paribas
Modèle 2: MCO, utilisant les observations
2006:1-2013:4 (T = 32)
Variable dépendante: l_COURS
|
Coefficient
|
Erreur Std
|
t de Student
|
p. critique
|
|
const
|
8,18482
|
5,63018
|
1,4537
|
0,15754
|
|
l_CA
|
-0,213553
|
0,273179
|
-0,7817
|
0,44117
|
|
T1
|
0,0916186
|
0,151237
|
0,6058
|
0,54971
|
|
T2
|
0,103129
|
0,151551
|
0,6805
|
0,50199
|
|
T3
|
0,0583606
|
0,149845
|
0,3895
|
0,69998
|
|
Moy. var. dép.
|
3,783705
|
Éc. type var. dép.
|
0,281186
|
|
Somme carrés résidus
|
2,368372
|
Éc. type de régression
|
0,296171
|
|
R2
|
0,033727
|
R2 ajusté
|
-0,109424
|
|
F(4, 27)
|
0,235607
|
p. critique (F)
|
0,915807
|
|
Log de vraisemblance
|
-3,749504
|
Critère d'Akaike
|
17,49901
|
|
Critère de Schwarz
|
24,82769
|
Hannan-Quinn
|
19,92826
|
|
rho
|
0,626073
|
Durbin-Watson
|
0,757788
|
Modèle 2: MCO, utilisant les observations
2006:1-2013:4 (T = 32)
Variable dépendante: l_Cours
|
Coefficient
|
Erreur Std
|
t de Student
|
p. critique
|
|
|
const
|
-25,2465
|
4,66345
|
-5,4137
|
0,00001
|
'K'K'K
|
|
l_CA
|
1,48088
|
0,233432
|
6,3440
|
<0,00001
|
'K'K'K
|
|
T1
|
0,0259694
|
0,0870319
|
0,2984
|
0,76769
|
|
|
T2
|
0,0788175
|
0,0877068
|
0,8986
|
0,37679
|
|
|
T3
|
0,0813698
|
0,0873548
|
0,9315
|
0,35986
|
|
|
Moy. var. dép.
|
4,337658
|
Éc. type var. dép.
|
0,255849
|
|
Somme carrés résidus
|
0,812815
|
Éc. type de régression
|
0,173506
|
|
R2
|
0,599445
|
R2 ajusté
|
0,540104
|
|
F(4, 27)
|
10,10163
|
p. critique (F)
|
0,000039
|
|
Log de vraisemblance
|
13,36178
|
Critère d'Akaike
|
-16,72355
|
|
Critère de Schwarz
|
-9,394873
|
Hannan-Quinn
|
-14,29430
|
|
rho
|
0,645951
|
Durbin-Watson
|
0,721459
|
Annexe 78: Modèle de MCO avec 3 variables
dummies pour L'Oréal
71
Annexe 79: Modèle de MCO avec 3 variables
dummies pour LVMH
Modèle 1: MCO, utilisant les observations 2006:1-2013:4
(T = 32)
Variable dépendante: l_COURS
Coefficient Erreur Std t de Student p. critique
const -21,7729 2,86447 -7,6010 <0,00001 ***
l_CA 1,30761 0,142935 9,1483 <0,00001 ***
T1 0,335057 0,103071 3,2507 0,00308 ***
T2 0,399793 0,10494 3,8097 0,00073 ***
T3 0,264972 0,10021 2,6442 0,01347 **
Moy. var. dép. 4,430347 Éc. type var.
dép. 0,362043
Somme carrés résidus 0,990687 Éc. type de
régression 0,191552
R2 0,756188 R2 ajusté 0,720068
F(4, 27) 20,93530 p. critique (F) 5,95e-08
Log de vraisemblance 10,19545 Critère d'Akaike
-10,39090
Critère de Schwarz -3,062217 Hannan-Quinn -7,961647
rho 0,703355 Durbin-Watson 0,582678
Annexe 80: Modèle de MCO avec 3
variables dummies pour Sanofi
Modèle 1: MCO, utilisant les observations 2006:1-2013:4
(T = 32)
Variable dépendante: l_COURS
|
Coefficient
|
Erreur Std
|
t de Student
|
p. critique
|
|
|
const
|
-34,2078
|
8,2387
|
-4,1521
|
0,00030
|
***
|
|
l_CA
|
1,86085
|
0,402824
|
4,6195
|
0,00008
|
***
|
|
T1
|
0,0789282
|
0,0998311
|
0,7906
|
0,43606
|
|
|
T2
|
0,020361
|
0,0993525
|
0,2049
|
0,83916
|
|
|
T3
|
0,0056622
|
0,0993506
|
0,0570
|
0,95497
|
|
|
Moy. var. dép.
|
3,850529
|
Éc. type var. dép.
|
0,248316
|
|
Somme carrés résidus
|
1,064899
|
Éc. type de régression
|
0,198597
|
|
R2
|
0,442895
|
R2 ajusté
|
0,360360
|
|
F(4, 27)
|
5,366199
|
p. critique (F)
|
0,002594
|
|
Log de vraisemblance
|
9,039662
|
Critère d'Akaike
|
-8,079325
|
|
Critère de Schwarz
|
-0,750645
|
Hannan-Quinn
|
-5,650075
|
|
rho
|
0,832313
|
Durbin-Watson
|
0,347544
|
|
|



