|
UNIVERSITE DE NGAOUNDERE

Faculté des Sciences
Département de Mathématiques et
Informatique
MEMOIRE DE MASTER
Spécialité:
SYSTEMES ET LOGICIELS EN
ENVIRONNEMENTS
DISTRIBUES
Présenté par:
Franklin TCHAKOUNTE
Sur le sujet :
ENVIRONNEMENTS DE GRAPPES DE CALCUL INTENSIF
SUR
RESEAUX D'ENTREPRISE: DEPLOIEMENT,
EXPLOITATION ET PERFORMANCES
Directeur du mémoire : Pr
TAYOU
Encadreur: Dr Jean Michel NLONG II
DEDIDACES
Je dédie ce travail en premier lieu au Dieu tout
Puissant qui jusqu'aujourd'hui m'a donné le souffle
de vie.
En second lieu :
AMon père TCHAKOUNTE Elie. Ma
mère NGOUNDJIO Elisabeth. Mes frères
et soeur.
REMERCIEMENTS
CEtte uvre a vu le jour grace au concours de plusieurs
personnes.
Je saisi cette occasion pour exprimer mes sincères
remerciements à tous ceux qui, de près comme
de loin, ont contribué à la mise en uvre de ce
mémoire.
J'adresse ma profonde reconnaissance au Docteur Jean Michel
NLONG II , qui m'a donné un sens de travail plus sérieux et qui,
une fois de plus a bien voulu sacrifier ses préoccupations importantes
en ne ménageant aucun effort pour suivre inlassablement ce travail. Il a
été pour moi comme un parent qui sanctionne son enfant quand il
faut pour le remettre sur le droit chemin.
Je remercie les membres du jury qui ont bien voulu accepter
d'évaluer ce travail.
J'adresse mes remerciements aux enseignants du
département d'Informatique et Mathématiques de
l'Université de Ngaoundéré. dont la volonté et la
moralité infaillibles témoignent du chemin exemplaire à
suivre par toute la communauté scientifique.
Je n'oublie pas mes camarades de promotion, ensemble, nous avons
constitué une véritable famille dans laquelle la volonté
de travailler en équipe m'a permis de surmonter les obstacles
rencontrés.
Je saisi cette occasion pour dire particulièrement
merci à une très chère amie DASSI TCHOMTE Naomi, à
ma soeur SAYOU NYASSI Flavienne, à mon frère SIME NYASSI Virgile,
à l'AEE-NDE , à la congrégation des Témoins de
JEHOVAH de DANG, à la famille DASSI de Yaoundé-Ekounou et
à mes très chers potes Urbain et Patrick qui m'ont toujours et de
très près soutenu dans les moments bons comme mauvais.
Je dis merci à toute ma famille, mes amis et ceux dont les
noms ne figurent pas dans ce mémoire, mais qui ont tous constitué
pour moi un soutien certain.
RESUME
Le calcul à haute performance(HPC) est de plus en plus
utilisé dans les laboratoires de recherche. Le but est d'exécuter
les applications le plus rapidement possible. De nos jours, les ordinateurs
offrent de bonnes performances à des coûts raisonnables et les
réseaux informatiques croissent rapidement. Une méthode
consistant à fédérer plusieurs ressources de calcul
ensemble pourrait fournir une puissance de calcul considérable pour
exécuter l'application : on parle de calcul parallèle. Il
faudrait donc trouver un moyen de subdiviser l'application en tâches, de
trouver les processeurs surlesquels les exécuter et de trouver leur date
de début d'exécution : on parle d'ordonnancement. Le
problème d'ordonnancement des tâches d'un graphe est connu et de
nombreux travaux ont déja été effectués sur ce
sujet. La plupart des algorithmes d'ordonnancement de graphe de tâches
visent des grappes homogènes constituées de ressources de calcul
identiques reliées à travers un réseau homogène.
Les noeuds et liens réseau d'une grappe peuvent avoir des
caractéristiques différentes facilitant ainsi le fait qu'on
puisse disposer facilement de plusieurs ressources. Dans ce cas on parle de
grappe hétérogène. L'utilisation de ce type d'architecture
rend l'ordonnancement des tâches difficile du fait de la synchronisation
entre les différentes tâches d'une même application et des
caractéristiques variables des composantes de calcul. Par exemple, deux
noeuds de calcul peuvent disposer des processeurs de puissances
différentes ainsi que leurs mémoires locales. Ainsi, le temps de
gestion d'une reception d'un message par l'un est différent de celui de
l'autre. Ils peuvent entraîner une baisse des performances de l'ensemble
du système si les tâches sont ordonnançées d'une
manière quelconque. Le problème d'ordonnancement sous ces
conditions est un problème NP-Complet. Il est donc très difficile
de trouver un algorithme qui le résoud en temps polynomial. Notre
travail consiste à proposer une heuristique d'ordonnancement sur ce type
d'architecture d'une part et de l'évaluer sur un exemple d'application
parallèle d'autre part.
Mots clés : Application, graphe, tâche,
ordonnancement, grappes, hétérogènes, homogène,
calcul parallèle.
ABSTRACT
High performance computing are more needed in research and
industry. It is objective is to execute an application in the fastest manner.
Nowadays, it is easy for us to buy a personnal computer that have high
performance more cheaper. A method by putting computing nodes together could
provide considerable performance to compute a parallel application.This is the
parallelism. It is therefore important to subdivide the application into tasks,
to find the processors on which we will execute them and the date of their
execution this is the problem of scheduling. This problem is well known and
many works have been done on that subject. Most of them have been done on
homogeonous clusters consisting of identical nodes of computing interconnected
with an homogeonous network. On the other hands, the nodes and links can have
no identical caracteristics. In this case, we speaking about heterogeonous
clusters. Although they facilitate to have many resources of computing,
heteregeonous clusters get tasks scheduling difficult in the sense that tasks
have to communicate each others. For instance, two adjacents nodes with
different performance will deal differently the reception of a message. So if
tasks are scheduled randomly, the system can be affected in performance. The
problem of scheduling in these conditions is NP-Complete. It is therefore too
difficult to find a polynomial algorithm as a solution. Our work is to propose
a heuristic of scheduling in heterogeonous clusters and evaluate it on an
application.
Keywords Application, graph, task, scheduling, clusters,
heterogeneous, homogeonous, parallelism.
Table des matières
Table des figures xi
Introduction générale 1
I CALCUL PARALLELE ET ARCHITECTURE DES GRAPPES
4
1 Calcul parallèle 4
1.1 Motivations et principes 4
1.2 Programmation parallèle 5
1.2.1 Objectifs de la programmation parallèle 5
1.2.2 Classes d'applications parallèles 6
1.2.3 Modèle de la programmation parallèle 6
2 Taxonomie des machines parallèles 8
2.1 Architecture SISD 8
2.2 Architecture MISD 9
2.3 Architecture SIMD 10
2.4 Architecture MIMD 11
2.4.1 Exemple d'application des quatre classes principales
14
3 Grappes d'ordinateurs 15
3.1 Origine et évolution de grappes 15
3.1.1 Les supercalculateurs 15
3.1.2 les réseaux de station de travail 15
3.1.3 Les grappes de PC 16
3.1.4 Les architectures actuelles 17
3.2 Caractéristiques des grappes 19
3.2.1 Accès aux ressources 19
3.2.2 Sécurité 20
3.2.3 Tolérances aux fautes 20
3.3 Infrastructures matérielles des grappes 20
3.3.1 Architectures matérielles des grappes 20
3.4 Infrastructures logicielles des grappes 21
4 Analyse des performances d'une architecture multiprocesseurs
22
4.1 Modèles de Calcul 22
4.1.1 Modèle à durée égale 22
4.1.2 Modèle de calcul parallèle avec des parties
séquentielles 23
4.2 Un argument pour les architectures parallèles 25
4.2.1 Loi d'Amdahl 25
4.2.2 Loi de gustafson 26
II CONCEPTS D'ORDONNANCEMENT 28
1 Modélisation d'une application 28
1.1 Graphe de précédence 28
1.2 Graphe de flots de données 29
1.3 Graphe de tâches 32
2 Les Modèles classiques d'ordonnancement 33
2.1 Modèles à coût de communications nul
33
2.2 Modèle délai 34
2.3 Les modèles LogP et BSP 35
3 Modèles d'exécution et ordonnancement 36
3.1 Le modèle PRAM 36
3.2 Les modèles avec délai de communications
37
3.2.1 Modèle UET 38
3.2.2 Modèle UET-UCT 39
3.2.3 Modèle UET-LCT 39
3.2.4 Modèle SCT 41
3.3 Le modèle LogP 41
3.4 Le modèle BSP 42
III GRAPPES HETEROGENES et ORDONNANCEMENT 46
1 Eléments de coût 46
1.1 Les stations de travail 46
1.2 Les équipements réseau 46
1.2.1 Les commutateurs 47
1.2.2 Les concentrateurs 49
1.2.3 Les routeurs 49
1.3 Technologie réseau 49
1.4 Système d'exploitation et pile réseau 49
2 Proposition d'un modèle d'ordonnancement sur les grappes
hétérogènes 51
2.1 Modélisation de l'architecture
hétérogène 51
2.2 Graphe de tâches. 52
2.3 L'ordonnancement 52
2.4 Modéle des communications 52
2.5 Idée Générale 53
IV EVALUATION DU MODELE SUR UNE APPLICATION
54
1 Présentation de l'architecture de notre grappe 54
2 Calcul des caractéristiques des noeuds du graphe de
grappe 55
2.1 Les surcoûts engendrés par la pile réseau
relatifs à chaque station de travail . 55
2.2 Tableau récapitulatif et discussion 58
3 Calcul des caractéristiques des arcs du graphe de grappe
58
3.1 Evaluation des latences 58
3.2 Evaluation des débits des liens 61
3.2.1 Discussion 61
4 Programmation de l'application 61
4.1 Algorithme 61
4.2 Code 61
5 Ordonnancement sur la grappe 63
5.1 Résultats et discussion 64
Conclusion générale et perspectives
68
A Annexe 71
1 CONFIGURATION DE NOTRE GRAPPE 71
1.1 Configuration logicielle 71
1.1.1 OAR: gestionnaire de tâches 71
1.1.2 MPICH2 : bibliothèque de communications 73
1.1.3 Serveur NFS : Network file system 74
1.1.4 Serveur NIS : Network information service 75
2 Code séquentiel du produit d'une matrice par un vecteur
76
Bibliographie 77
LISTE DES ABBREVIATIONS
API : Application Program Interface
ARP : Address Resolution Protocol BSP : Bulk
Synchronous Parallel
CESDIS : Center of Excellence in Space Data and
Information Sciences
CM : Connection Machine
CONDOR: Open Grid Computing
COTS: Commodity Off The Shelf
CRAY: Supercomputer Company ( Name of the father
of Supercomuting : Seymour Cray)
CRC : Cyclic Redondancy Control
CRCW : Concurrent Read Concurrent Write
CREW: Concurrent Read Exclusive Write
EREW : Exclusive Read Exclusive Write FTP :
File Transfer Protocol
GNU: GNU is Not Unix
HPC : High Personal Computing HTC
: High Throughput Computing HTTP : Hypertext Transfer
Protocol IBM: International Business Machine
IBM SP : International Business Machine Scalable
Power
ICL DAP : International Computer LTds
Distributed Array Processor
IPC : InterProcess Communication LAN
: Local Area Network
LCT : Large Communication Time MAC
: Media Access Control
MFLOPS : Mega Floatting Operations Per Second
MIMD : Multiple Instruction Multiple Data
MISD : Multiple Instruction Single Data MPI :
Message Passing Interface
MPICH : Message Passing Interface Chameleon
MPMD : Mutiple Programs Multiple Data MVP :
Model View Presenter
NEC : Network Enterprise Center
NFS : Network File System
NIS : Network Information System NOW
: Network Of Workstations
NP : Non Polynomial
NUMA : Non Uniform Access
OAR: Resource Manager
OSI : Open Systems International
PC : Personal Computer
PRAM : Parallel Random Access Machine
PVM : Parallel Virtual Machine
SAN: System Area Network
SCT : Small Communication Time SGI
: Silicon Graphics Image
SISD : Single Instruction Single Data
SIMD : Single Instruction Multiple Data SMP :
Symmetric Multiprocessing SMTP : Simple Mail Transfer Protocol
SPMD : Single Program Multiple data SSH :
Secure Socket Shell
SSI : Single System Image
TFLOPS : Tera Floatting Operations Per Second
UET : Unit Execution Time
UCT : Unit Communication Time
Table des figures
I.1 Architecture SISD 8
I.2 Architecture SIMD 9
I.3 Architecture MIMD 9
I.4 Modèle d'architecture SIMD 10
I.5 Les deux schémas SIMD 11
I.6 Architecture à mémoire partagée et
Architecture de passage de messages 12
I.7 Un réseau de stations de travail 16
I.8 Une grappe de PC 16
I.9 Une grappe de grappes faiblement couplées 17
I.10 Une grappe multiplement câblée (avec des
partitions) 18
I.11 Segments de programme 23
I.12 Modèle Amdahl 26
II.1 Exemple de Programme 29
II.2 Un graphe de précédence pour le programme. Les
tâches sont représentées par des cercles et les arcs
représentent les précédences. 30
II.3 Un graphe de flots de données pour le programme. Les
tâches sont représentées par des
cercles. Les données à transférer dans un
rectangle 31
II.4 Graphe de précédence G 31
II.5 Exemple de graphe de tâche du programme. Les chiffres
en bleu représentent les coûts de chaque tâches. Ceux en
noir représentent le volume des données à
transférer d'une
tâche à l'autre par unité de temps. 32
II.6 Le modèle LogP 35
II.7 A gauche nous avons une représentation de
l'ensemble des processeurs : P=8, L=6, g=4,
o=2 et à droite l'activité de chaque processeur dans le
temps. Le nombre montré pour chaque noeud est le temps auquel chaque
processeur a reçu les données et peut
commencer à envoyer. 36
II.8 Le modèle PRAM pour le calcul parallèle
37
II.9 Exécution dans le modèle UET 39
II.10 Exécution dans le modèle UET-UCT sans et avec
duplication 40
II.11 Exécution dans le modèle UET-LCT sans et avec
duplication 40
II.12 Exécutions dans le modèle SCT sans et avec
duplication 41
II.13 Exemple des paramètres LogP 42
II.14 Ordonnancement sous le modèle LogP 43
II.15 Schéma d'exécution dans le modèle BSP
44
III.1 Trame ethernet 47
III.2 Un message classique tel qu'il transite sur le
réseau 51
IV.1 Notre grappe 55
IV.2 Courbe représentant l'accélération de
l'algorithme parallèle 66
IV.3 Courbe représentant l'efficacité de
l'algorithme parallèle 67
Introduction générale
D
E nos jours, aussi bien dans l'industrie que dans les
laboratoires de recherche, la puissance de calcul est de plus en plus
recherchée pour l'exécution d'applications de plus en plus
gourmandes en ressources. Par exemple dans l'industrie cinématographique
la puissance de calcul est employée
pour du calcul d'image. Dans des laboratoires de biologie,
elle peut être employée pour des calculs d'affinité
génétique entre différentes familles d'animaux. Dans tous
les cas, l'objectif est d'exécuter les applications le plus rapidement
possible, c'est-à-dire réduire le temps entre la soumission de
l'application et l'obtention des résultats. C'est cela qu'on appelle le
calcul à haute performance (HPC - High Performance Computing). Dans les
années quatre-vingt à quatre-vingt dix, ce dernier s'appuyait sur
des solutions coûteuses, basées sur des processeurs et des
logiciels spécialisés, et destinés à un nombre
limité de domaines tels que la météorologie, les
phénomènes physiques, le nucléaire etc.. Cela exigeait que
les centres de recherche disposent d'une puissance de calcul sans cesse
croissante, qui n'était pas accessible financièrement à
des organisations moyennes. L'évolution technologique permet aujourd'hui
de disposer d'ordinateurs de bureau standard très performants à
tel point qu'il est envisageable de construire à partir de ces machines
des systèmes parallèles aussi rapides que les supercalculateurs
dédiés type CRAY, IBM SP, NEC, Fujitsi. Chaque progression
technologique ouvre l'horizon à de nouveaux besoins; et de nouvelles
exigences. En effet, les applications deviennent de plus en plus gourmandes en
temps de calcul et en espace mémoire.
Le calcul parallèle a toujours été une
possibilité de répondre à cette demande de performances.
Il consiste en l'exécution d'un traitement pouvant être
partitionné en tâches élémentaires adaptées
afin de pouvoir être réparties entre plusieurs processeurs
opérant simultanément. L'objectif est de traiter des
problèmes de grandes tailles plus rapidement que dans une
exécution séquentielle. Les avantages du calcul parallèle
sont nombreux. Du fait de contraintes physiques et technologiques, la puissance
d'un ordinateur monoprocesseur reste limitée. En effet, il est difficile
pour les fabricants de processeurs de produire des processeurs dont la
puissance atteigne les centaines de MégaFlops1. La
quantité de mémoire présente dans les ordinateurs
monoprocesseurs est également limitée et il est par
conséquent impossible d'exécuter certaines applications de grande
taille sur de telles machines. Le calcul parallèle peut en revanche
permettre de résoudre ce genre de problème. Ainsi, les machines
parallèles actuelles utilisent des techniques originales de calcul
parallèle pour maintenir l'activité des unités de
calcul.
Les machines peuvent, par exemple disposer d'une
mémoire partagée physique pour permettre aux différentes
unités de calcul de coopérer. Dans d'autres cas, les machines
parallèles sont construites
'million d'opérations ou calcul par seconde en
virgule flottante
autour d'unités de calcul dotées de leur propre
mémoire. Ces unités communiquent par échange de messages;
on parle ici de machine à mémoire distribuée. Aujourd'hui,
on assiste au développement rapide des machines parallèles de ce
type: les grappes. Elles sont construites à partir de l'interconnexion
de composants standards donc bon marché, comme les stations de travail
ou les ordinateurs (PC). Ces architectures pouvant être
constituées de plusieurs centaines de processeurs, offrent des
performances potentiellement exceptionnelles pour un prix modeste. Avec
l'avènement du logiciel libre et le coût assez bas des ordinateurs
de bureau, la très forte demande en calcul haute performance
(scientifique et technique) peut être satisfaite à un coût
raisonnable. Les grappes de PC apparaissent donc comme une très bonne
alternative aux moyens de calculs traditionnels. Cependant, leur exploitation
reste très délicate et pose encore de très nombreux
problèmes.
La programmation sur ce type de machines demande beaucoup plus
d'efforts que l'écriture d'un programme séquentiel pour plusieurs
raisons:
- Peu d'équipes sont capables de développer et de
maîtriser l'environnement de grappe.
- l'hétérogénéité de la grappe
au niveau des ressources de calcul (processeur) et au niveau des
capacités de communication (réseau) contraint
l'utilisateur de monter lui même son système
afin d'adapter l'exécution des applications sur ce
système.
- La programmation dépend fortement de la machine cible
et de son support au parallélisme. Par exemple, les processeurs d'une
machine parallèle peuvent avoir des propriétés distinctes,
telles que le mode d'échange des données (mémoire
partagée ou distribuée via un réseau d'interconnexion), de
même que la cadence de son mode de fonctionnement.
L'environnement de grappes hétérogènes
admet donc une complexité liée à l'application que l'on
veut exécuter en termes de graphe de tâches (dépendances),
à la topologie du système (communications entre les noeuds via le
réseau), aux ressources disponibles dans le système (processeurs,
mémoire). Il est donc capital de tenir en compte ces différents
paramètres pour pouvoir exécuter efficacement une application sur
une plate-forme hétérogène.
Il est question pour nous de proposer un algorithme
d'ordonnancement efficace de tâches d'une application en tenant compte de
ces éléments.
L'élaboration des applications
parallèles
Dans l'informatique séquentielle, l'écriture
d'une application consiste à choisir un algorithme qui
résout un problème et de faire son analyse. Pour concevoir une
application parallèle, nous devons d'abord choisir un algorithme qui
résout le problème envisagé. Cet algorithme est alors
partitionné en tâches lesquelles correspondent à
des portions du code qui seront exécutées en séquentiel.
Ensuite, le programme parallèle est conçu en attribuant à
chaque tâche un processeur et une date d'exécution. La performance
de l'application est mesurée alors par le temps d'exécution
parallèle. Si une tâche a besoin des données produites par
une autre tâche, il existe une relation de dépendance. Les
tâches et leurs relations de dépendance sont
représentées sous la forme d'un graphe, où les sommets
correspondent aux tâches et les arcs aux relations de
précédence entre elles. Ce graphe exprime le degré de
parallélisme de l'algorithme et est nommé graphe de
précédence ou de tâches. L'opération qui
attribue aux tâches des dates d'exécution et des processeurs est
dénommée ordonnancement, elle sera présentée en
détail au chapitre 3.
Il est clair qu'il faut distinguer la phase d'extraction du
parallélisme d'un algorithme de la phase d'exploitation de ce
parallélisme. Dans un premier temps un graphe de
précédence est construit, et ensuite un schéma
d'ordonnancement est appliqué en fonction de l'architecture du
modèle de machine. Or, pour certains problèmes, le graphe de
précédence est construit au cours de l'exécution. Dans ce
cas, les deux étapes ne peuvent pas être dissociées dans le
temps.
Nous nous intéressons aux problèmes où le
graphe de précédence est fourni de façon explicite avant
le début de l'exécution (ordonnancement statique). Dans ces
problèmes d'ordonnancement notre objectif est de minimiser le temps
d'exécution total encore appelé makespan.
Problématique
La répartition des calculs et des données est
l'un des problèmes majeurs à résoudre pour réaliser
une application parallèle efficace. Il faut décider de la date et
du lieu d'exécution des calculs du programme parallèle sur
l'ensemble des ressources (processeur, mémoire..) de la machine.
L'efficacité de l'exécution va dépendre de ces
décisions. Dans ce mémoire, nous nous attachons à
décrire le modèle de coût de notre grappe et de proposer
une solution au problème d'ordonnancement de tâches d'une
application sur une grappe hétérogène.
Organisation du travail
Ce document est divisé en quatre chapitres : le premier
nous introduit à l'architecture des grappes et au calcul
parallèle en présentant de manière concise les
différents types d'architectures parallèles d'après la
classification de Flynn et de l'évolution des grappes de PCs. Ce
chapitre est l'occasion pour nous d'insister sur l'architecture de grappes
hétérogènes notamment sur leurs caractéristiques
matérielles, logicielles et sur
l'hétérogénéité qui les rend plus complexes.
Il parle également de la notion de programmation sur ces types
d'architecture et de certains standards de programmation d'applications
parallèles dont MPI qui nous intéresse. Ce standard est la cible
d'un nombre impressionnant dans le monde et est doté des
caractéristiques favorables aux grappes
hétérogènes. Comment analyser les performances d'une
application parallèle a été la question répondue
après avoir présenté des postulats existants. La
représentation d'une application parallèle en graphe de
tâches, l'ordonnancement de ces dernières suivant les
modèles de communication font l'objet du deuxième chapitre.
L'étude des éléments définis aux chapitres
précédents nous permet de formuler au chapitre 3 un modèle
d'ordonnancement sur grappes hétérogènes en tenant compte
de ses caractéristiques. Le chapitre 4 est la partie pratique de notre
contribution car il expose l'implémentation de notre modèle en
effectuant des évaluations sur un exemple. Nous concluons ensuite ce
travail et apportons des perspectives pour la suite de nos recherches.
Chapitre I
CALCUL PARALLELE ET ARCHITECTURE
DES GRAPPES
D
Epuis les débuts de l'informatique s'est posée
la question de résoudre rapidement des problèmes (le plus souvent
numériques) coûteux en temps de calcul : simulations
numériques, cryptographie, imagerie, S.G.B.D., etc. Pour résoudre
plus rapidement un problème donné, une idée naturelle
consiste à faire coopérer simultanément
plusieurs agents à sa résolution, qui travailleront donc en
parallèle.
1 Calcul parallèle
1.1 Motivations et principes
La puissance des ordinateurs séquentiels augmentant de
manière régulière (en gros, elle est multipliée par
deux tous les dix-huit mois1), on pourrait croire qu'elles sera
toujours suffisante, et que les machines parallèles (ordinateurs
multiprocesseurs) sont inutiles. Plusieurs raisons contredisent cette
tendance.
1. A mesure que la puissance des machines augmente, on
introduit l'outil informatique dans des disciplines où il ne pouvait
jusqu'alors pénétrer, et on cherche à intégrer de
plus en plus de paramètres dans les modèles numériques :
météorologie, synthèse et reconstruction d'images,
simulations numériques, etc. Un certain nombre d'applications
<sensibles> ont été classées <Grand
Challenge> , et font l'objet de recherches intensives, tant au niveau du
matériel que du logiciel. Elles sont également appelées
< applications 3T >, parcequ'elles nécessitent pour leur
exécution: - 1 Téra flops2 (floating operation per
second);
- 1 Téra octets de mémoire centrale;
- 1 Téra octets par seconde de bande passante pour
produire les résultats.
2. La vitesse de la lumière est (actuellement) une
limitation intrinsèque à la vitesse des processeurs. Supposons en
effet que l'on veuille construire une machine entièrement
séquentielle disposant d'une puissance de 1 Tflops et de 1 To de
mémoire. Soit d la distance maximale entre la mémoire
1Loi de Moore
21 Téra = 103Giga =
106Méga = 109Kilo =
1012.
et le micro-processeur. Cette distance doit pouvoir être
parcourue 1012 fois par seconde à la vitesse de la
lumière, c
3.108m.s-1,d'où
L'ordinateur devrait donc tenir dans une sphère de 0,3
mm de rayon. Avec cette contrainte de distance, si l'on considère la
mémoire comme une grille carrée de 106 x
106 octets, alors chaque octet doit occuper une cellule de 3Å
de côté, c'est à dire la surface occupée par un
petit atome. On ne tient ici pas compte de l'espace nécessaire à
l'acheminement de l'information et de l'énergie, ainsi qu'à
l'extraction de la chaleur.
Bien que la puissance et la capacité mémoire des
ordinateurs ne cessent de croître, certains utilisateurs désirent
toujours obtenir leurs résultats plus rapidement. D'autres souhaitent
aussi faire tourner des simulations de plus grande précision en
conservant un temps de calcul raisonnable. Le coût de fabrication d'un
processeur toujours plus puissant croît exponentiellement avec la vitesse
avec laquelle il peut faire les calculs. Par contre obtenir N
processeurs ne représente qu'un coût N fois plus
grand que celui d'un seul processeur. Le coût total de la machine
parallèle (incluant le réseau d'interconnexion...) reste donc du
même ordre. Le parallélisme consiste à utiliser plusieurs
ressources disponibles (processeurs, mémoires, disques, etc.) pour
qu'elles participent ensemble au calcul d'une application. En multipliant les
ressources par N , un utilisateur peut espérer :
- calculer N fois plus vite,
- calculer des problèmes occupant N fois plus
d'espace mémoire.
Le calcul parallèle est donc un moyen pour fournir de
la haute puissance de calcul à un prix raisonnable en utilisant des
ordinateurs personnels. Pourtant, cela ne suffit pas; il faudrait trouver une
bonne méthode pour soumettre l'application aux différentes
ressources présentes en vue de son exécution. Pour cela, il faut
appliquer une bonne programmation de l'application en vue de bien
répartir les données pour résoudre un problème de
grande taille qui satureraient la mémoire d'un seul ordinateur ou
même d'un supercalculateur.
Les applications parallèles sont une classe très
importante d'applications concurrentes pour le calcul scientifique : elles
visent à diminuer les temps d'exécution des calculs
numériques intensifs, ou bien à répartir les
données pour résoudre des problèmes de grande taille qui
satureraient la mémoire d'un seul ordinateur ou même d'un seul
supercalculateur. Cette section présente la classe des applications
parallèles, puis elle se focalise sur deux technologies de programmation
parallèle, à savoir les bibliothèques MPI et les
systèmes de MVP.
1.2 Programmation parallèle
1.2.1 Objectifs de la programmation
parallèle
La programmation parallèle s'est imposée dans le
domaine du calcul scientifique, car son objectif est essentiellement la haute
performance. La programmation parallèle vise :
- à répartir les tâches de calcul dans
plusieurs processus sur plusieurs processeurs;
- à répartir les données des
problèmes de grande taille qui satureraient la mémoire d'un seul
ordinateur ou même d'un superordinateur;
- à recouvrir les calculs et les opérations
d'entrées-sorties, afin de masquer leur latence.
Dans tous les cas, l'objectif de la programmation
parallèle est de diminuer les temps d'exécution des calculs
numériques intensifs. Cette propriété permet alors
d'augmenter la précision des calculs (et donc la taille des
données) tout en conservant des temps de calcul acceptables.
1.2.2 Classes d'applications
parallèles
Programmation multi-threads ou multiprocessus.
La programmation < multi-threads > est une méthode de
programmation parallèle qui consiste à faire coopérer
plusieurs threads au sein d'un même processus pour exécuter
l'application : elle permet en particulier de recouvrir les calculs et les
opérations d'entrées-sorties. Une autre approche est la
programmation < multi-processus »3 : soit tous les processus
de l'application sont issus du même code source (SPMD4), soit
l'application est faite de plusieurs programmes (ou codes sources)
différents (MPMD5). Dans le cas de la programmation
multi-processus, les tâches de calcul sont le plus souvent
réparties sur des ordinateurs qui ne partagent pas de mémoire
commune. Or les processus doivent coopérer, donc s'échanger des
données ou se synchroniser. Les communications entre les processus sont
susceptibles de ralentir l'exécution d'une application parallèle
multi-processus. Le ratio calcul/communications est le rapport entre le temps
passé par les processus à faire des opérations de calcul
et le temps qu'ils passent à communiquer. Plus ce ratio est faible et
moins l'intérêt de la parallélisation est évident.
C'est pourquoi on peut rarement augmenter indéfiniment le nombre de
processus qui se répartissent les tâches de calcul car ils passent
alors plus de temps à communiquer qu'à calculer et le temps
global d'exécution de l'application augmente.
Applications statiques et applications dynamiques.
Parmi les applications parallèles, on peut distinguer les
applications statiques et les applications dynamiques.
Applications statiques. Dans une application
statique, tous les processus sont lancés au moment du déploiement
de l'application : l'utilisateur sait combien de processus composent
l'application au début de son exécution et le nombre de processus
reste le même tout au long de l'exécution. Applications
dynamiques. Dans une application dynamique, il se peut qu'un ou
plusieurs processus soient créés en cours d'exécution, ou
bien soient terminés avant la fin de l'exécution de
l'application. Cette création ou terminaison de processus en cours
d'exécution se fait à l'initiative de l'application et les
processus ajoutés doivent faire partie intégrante de
l'application, au même titre que les processus lancés au moment du
déploiement initial de l'application. Par exemple, un utilisateur qui
lance par ailleurs un programme de visualisation ou d'analyse des traces de
l'application en cours d'exécution ne permet pas de qualifier
l'application de dynamique.
Actuellement, la plupart des applications de calcul scientifique
sont statiques, car elles sont plus simples à programmer, et il existe
peu de support pour les applications parallèles dynamiques.
1.2.3 Modèle de la programmation
parallèle
Nous distinguons deux grandes classes de modèles de
programmation parallèle :
- avec le parallélisme explicite, le
programmeur fait l'effort de parallélisation de l'application :
décomposition en sous-tâches, placement des tâches sur les
processeurs, répartition et redistribution des données,
communications (échange de données et synchronisation) entre les
tâches, etc.;
- avec le parallélisme implicite, le travail
de parallélisation de l'application est effectué par un
compilateur (pour les langages parallèles), par un outil de
parallélisation automatique, ou bien par une bibliothèque de
fonctions déjà parallélisées.
3Les approches multi-threads et multi-processus ne
sont pas incompatibles. 4Single Program, Multiple Data
5Multiple Program, Multiple Data.
Comme le programmeur est souvent le plus à même
de décider comment le parallélisme peut être
exploité pour un problème particulier, le parallélisme
explicite donne en général de meilleures performances que la
parallélisme implicite.
La programmation par passage de messages, celle par
mémoire partagée et certains langages parallèles font
partie de la classe du parallélisme explicite; les bibliothèques
parallèles de haut niveau d'abstraction relèvent du
parallélisme implicite, même si la frontière entre ces deux
types de parallélisme n'est pas toujours très nette.
Passage de messages. La programmation par
passage de messages consiste à faire coopérer les
différentes tâches qui constituent l'application par l'envoi
et la réception explicites de données,
typées ou non. Le plus souvent, les environnements de programmation par
passage de messages ( MPI (Message-Passing Interface) et PVM
(Parallel Virtual Machine) ) offrent également des
opérations de synchronisation simples (la < barrière >,
qu'un processus ne peut franchir que lorsque tous les autres processus de
l'application l'ont aussi atteinte), ainsi que des opérations <
collectives >, telles que :
- envoyer une donnée à tout un groupe de processus
en une seule opération (diffusion, ou Broad-
cast);
- effectuer une opération arithmétique simple
(produit, somme, etc.) ou logique ( < et > , < ou > ,
etc.) sur des données détenues par tous les processus d'un groupe
(opération de < réduction >, Reduce);
- regrouper dans un seul processus des données qui sont
dispersées dans chaque processus d'un groupe (Gather);
- disperser des données situées dans un vecteur sur
un processus vers les autres processus d'un groupe (Scatter).
Deux grands standards sont disponibles pour le passage de
messages: Message Passing Interface (MPI) et Parallel Virtual Machine (PVM).
MPI est une API6 pour écrire des programmes
parallèles portables. C'est une bibliothèque portable de
programmation parallèle sur des ordinateurs distribués,
hétérogènes (systèmes d'exploitation, architectures
matérielles) et reliés en réseau. PVM est plus ancien,
mais nous avons choisi de travailler avec MPI qui présente de nombreux
avantages :
- MPI est une norme définie par le ' MPI Forum
[29], soutenu par les milieux académiques et industriels;
- il existe un très grand nombre
d'implémentations de MPI, tant académiques (gratuites ou non)
qu'industrielles (IBM, Sun Microsystems, SGI, etc.), et qui sont portées
sur de nombreuses plates-formes;
- MPI est toujours un sujet de recherche actif et fait l'objet de
nombreux développements;
- MPI est très massivement utilisé dans les milieux
scientifiques (physiciens, chimistes, etc.) pour le calcul numérique
parallèle.
Ainsi, la programmation par passage de messages est un
modèle d'assez bas niveau : le travail de parallélisation revient
intégralement au programmeur.
Mémoire Partagée. Dans le
modèle de programmation parallèle par mémoire
partagée, les tâches qui constituent l'application
coopèrent par l'écriture et la lecture dans une mémoire
commune : ces opérations permettent d'échanger des données
et de se synchroniser. Si les tâches sont les threads d'un même
processus, alors ils peuvent lire et écrire dans l'espace d'adressage du
processus. Si les tâches sont des processus au sein d'un même
système d'exploitation, alors ils peuvent partager des segments
6Application Programming Interface.
de mémoire c'est le cas par exemple avec les
IPC7, ou bien encore avec les systèmes à image unique
(SSI8). Enfin, le mécanisme de < mémoire
virtuellement partagée > (MVP) permet de programmer des
systèmes à mémoire distribuée en utilisant le
modèle de programmation parallèle par mémoire
partagée un environnement de MVP donne l'illusion à des processus
localisés sur des machines distribuées (avec des systèmes
d'exploitation distincts) de partager un espace mémoire commun.
Dans ce modèle, la distribution des données est
transparente et les communications entre les tâches de l'application
parallèle sont implicites ce modèle est d'un peu plus haut niveau
que celui de la programmation par passage de messages. Cependant, la
programmation par mémoire partagée laisse encore le soin au
programmeur de gérer lui-même la décomposition du
problème en tâches de calcul, le placement de ces tâches, et
la gestion de la localité des accès.
2 Taxonomie des machines parallèles
Pour ordonnancer finement une application parallèle, il
est également nécessaire de bien identifier les paramètres
clés qui reflètent les architectures de la machine
parallèle surlesquelles on envisage d'exécuter des applications.
Historiquement, l'une des premières classifications est celle
proposée par Flynn [12] en 1966. Le système de classification de
Flynn [12] est basé sur la notion de flots d'information. Il existe deux
types de flots d'informations dans un processeur les instructions et les
données [14]. Le flot d'instructions est défini comme la
séquence d'instructions exécutée par l'unité de
calcul. Le flot de données est défini comme le trafic de
données échangé entre la mémoire et l'unité
de calcul. Selon la classification de Flynn, les flots d'instructions ou de
données peuvent être uniques ou multiples. L'architecture de
l'ordinateur peut être classifiée en quatre catégories
distinctes [14].
- Single-instruction single-data streams (SISD);
- Single-instruction multiple-data streams (SIMD);
- Multiple-instruction single-data streams (MISD);
- Multiple-instruction multiple-data streams (MIMD).
2.1 Architecture SISD
Les machines Von Neumann monoprocesseur conventionnelles sont
classifiés comme les systèmes SISD. Les algorithmes pour les
calculateurs SISD ne contiennent aucun parallélisme. La figure I.1
représente cette machine.
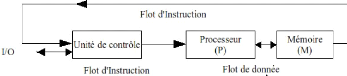
Figure I.1 - Architecture SISD
7InterProcess communication
8Single System Image, où un système
d'exploitation unique couvre un ensemble d'ordinateurs distribués, tel
que Kerrighed : http ://
www.kerrighed.org/.
2.2 Architecture MISD
Dans la catégorie MISD, le même flot de
données circule dans un vecteur linéaire de processeurs qui
exécutent des flots d'instructions différentes. En pratique, il
n'existe aucune machine construite sur ce modèle. Certains auteurs ont
considérés les machines pipelines comme des exemples de machines
MISD.
Les ordinateurs parallèles sont soit SIMD ou MIMD.
Lorsqu'il ya seulement une unité de contrôle et lorsque tous les
processeurs exécutent la même instruction de manière
synchrone, la machine parallèle est classifiée comme SIMD. Dans
la machine MIMD, chaque processeur a sa propre unité de contrôle
et peut exécuter des instructions différentes sur des
données différentes.
Les figures I.2 et I.3 représentent les machines SIMD et
MIMD respectivement.

Figure I.2 - Architecture SIMD

Figure I.3 - Architecture MIMD
2.3 Architecture SIMD
Le modèle SIMD du calcul parallèle comprend deux
parties : l'ordinateur frontal de style Von Neumann et un ensemble de
processeurs comme montre la figure I.4. Le vecteur de processeurs est un
ensemble d'éléments de calcul identiques synchronisés
capables d'exécuter simultanément la même opération
sur des données différentes. Chaque processeur dans le vecteur a
une petite mémoire locale où résident les données
distribuées lors du calcul parallèle. Le vecteur de processeurs
est connecté au bus mémoire du frontal ainsi donc le frontal peut
accéder aléatoirement aux mémoires locales des processeurs
comme si c'était une autre mémoire.
Figure I.4 - Modèle d'architecture
SIMD
Les processeurs opèrent de façon synchrone et
une horloge globale est utilisée pour effectuer les opérations en
mode <lockstep> c'est à dire qu'à chaque étape (top
de l'horloge globale) tous les processeurs exécutent la même
instruction, chacun sur une donnée différente. Dans ce
système, soit les processeurs ne font rien, soit ils effectuent la
même opération au même moment. Les processeurs <array>
comme le ICL DAP (Distributed Array Processor) et les processeurs
vectoriels pipelinés comme les CRAY 1, le CRAY 2 et le CYBER 205 font
partie de la classe des calculateurs SIMD. Aussi, plus récemment, Maspar
et CM (Connection Machine). Les machines SIMD sont
particulièrement utiles pour traiter les problèmes à
structure régulière où la même instruction
s'applique à des sous-ensembles de données. Il y a deux
schémas majeurs qui sont utilisés dans les machines SIMD (voir
figure I.5).
Dans la première configuration, chaque processeur a sa
mémoire locale. Les processeurs peuvent communiquer entre eux via le
réseau d'interconnexion. Si le réseau d'interconnexion ne fournit
pas une connexion directe entre une paire de processeurs donnée, alors
cette paire pourra échanger les données via un processeur
intermédiaire.
Dans la seconde configuration SIMD, les processeurs
communiquent entre eux via un réseau d'interconnexion. Deux processeurs
peuvent s'échanger les données par l'intermédiaire des
modules de mémoire ou par un processeur intermédiaire.
Exemple : Addition de deux matrices
A + B = C Soient deux matrices A et B d'ordre 2, et 4 processeurs. A11 +
B11 = C11 ... A12 + B12 = C12
A21 + B21 = 1 ... A22 + B22 = 2
La même instruction est envoyée aux 4 processeurs
(ajouter les 2 nombres) et tous les processeurs exécutent cette
instruction simultanément. Un pas de temps suffit contre quatre sur une
machine séquentielle.

Figure I.5 - Les deux schémas SIMD
Une instruction peut être simple (addition de 2 nombres)
ou complexe (fusion de 2 listes). De la même façon les
données peuvent être simples (un nombre) ou complexes (plusieurs
nombres). Il peut parfois être nécessaire de limiter
l'exécution de l'instruction a un sous ensemble des processeurs c'est
à dire seulement certaines données ont besoin d'être
traitées par cette instruction. Cette information peut être
codée par un 11drapeau 11sur chaque processeur qui
indique si :
1. le processeur est actif (exécute
l'instruction)
2. le processeur est inactif (attend la
prochaine instruction) 2.4 Architecture MIMD
C'est la classe la plus générale et la plus
puissante de toute cette classification. Les architectures parallèles
MIMD sont faites de plusieurs processeurs et de plusieurs modules de
mémoires connectées via un moyen de communication. Elles sont
subdivisées en deux catégories : La mémoire
partagée et le passage de messages. La figure I.6 illustre
l'architecture générale de ces deux catégories.




Figure I.6 - Architecture à
mémoire partagée et Architecture de passage de messages
Dans les systèmes à mémoire
partagée, les processeurs s'échangent les informations à
travers leur mémoire centrale partagée tandis qu'ils
s'échangent les informations à travers le réseau
d'interconnexion dans le système d'échange de messages.
Un système à mémoire partagée
typique accomplit la coordination interprocesseur par une mémoire
globale partagée par tous les processeurs. Ils représentent
généralement les systèmes serveurs qui communiquent par un
bus et le contrôleur de la mémoire cache. Les architectures
à mémoire partagée multiprocesseurs SMP (symmetric
multiprocessor) sont des architectures très courantes et
très populaires. Parce que l'accès à la mémoire
partagée est stable, ces systèmes sont nommés SMP
(symmetric multiprocessor). Chaque processeur a la même
opportunité de lire/écrire dans la mémoire, avec la
même vitesse. Comme exemple de machines à mémoire
partagée on a : les serveurs multiprocesseurs Sun Microsystems, les
serveurs multiprocesseurs Silicon Graphics Inc.
Le système par passage de messages (ou a
mémoire distribuée) typiquement combine la mémoire locale
et le processeur sur chaque noeud du réseau d'interconnexion. Il n y a
pas de mémoire globale, ainsi il est nécessaire de
déplacer les données d'une mémoire locale a une autre par
le moyen d'envoi de messages. Ceci est réalisé typiquement en
utilisant les commandes Send/Receive, qui doivent être écrits dans
le logiciel d'application par le programmeur. Ainsi, les programmeurs doivent
apprendre le paradigme du passage de messages qui implique des mouvements de
données. Les exemples commerciaux de telles architectures sont nCUBE,
iPSC/2 etc.
Il était aussi apparent que la mémoire
distribuée est le seul moyen efficace pour augmenter le nombre de
processeurs administrés par un système parallèle et
distribué. Les techniques a mémoires distribuées sont les
plus appropriées pour le passage a l'échelle. Un conflit a donc
existé entre ces deux architectures : programmer dans le modèle
de mémoire partagée était facile et concevoir des
systèmes dans le modèle de passage de messages fournissait le
passage a l'échelle.
Les calculateurs MIMD a mémoire commune sont
appelés multiprocesseurs ou machines fortement
couplées. Dans cette classe, l'accès a la mémoire
est uniforme(UMA)9 ; c'est a dire tous les processeurs
accèdent a toutes les zones de la mémoire commune avec la
même vitesse. Le point fort de ces machines est la rapidité du
partage de données entre des processeurs qui exécutent une
même application parallèle. Cela est dû au fait que la
mémoire commune est relativement proche des différents
processeurs mis en jeu. Par exemple ENCORE, MULTIMAX, SEQUENT et BALANCE. Sur
ce type d'architecture, tout le trafic entre les processeurs et la
mémoire commune passe par un bus. Le trafic augmentant avec le nombre de
processeurs, ce bus devient rapidement un goulot d'étranglement. C'est
vraisemblablement pourquoi ce type de calculateur n'est pas massivement
"scalable". Souvent, pour résoudre partiellement ce problème, une
mémoire cache est associée a chaque processeur. L'objectif est de
diminuer le trafic sur le bus et de rendre les données accessibles plus
rapidement au processeur puisqu'il est plus rapide pour lui de les lire dans un
cache rapide que dans une grande mémoire globale. Typiquement, le nombre
de processeurs ne dépasse pas quelques dizaines.
Les calculateurs MIMD avec un réseau d'interconnexion
sont appelés multiordinateurs ou machines
faiblement couplées. Par exemple INTEL iPSC, NCUBE/7, IBM SP1
et SP2 et réseaux de Transputers. Dans cette classe de calculateurs, les
processeurs sont souvent appelés "noeuds" et ne partagent rien
d'autre que le réseau. L'accès a la mémoire est non
uniforme(NUMA)10 ;c'est a dire tous les processeurs
n'accèdent pas a toutes les zones de la mémoire commune avec la
même vitesse. Ce réseau peut avoir des performances très
différentes : réseau local a crossbar ou switch Omega. Ce
réseau est comparativement peu utilisé par rapport au trafic sur
le bus d'une mémoire commune. Il sert uniquement a échanger des
données entre les processeurs en utilisant un protocole de communication
de type "passage de messages". Ce type d'architecture est fortement
"scalable" et le nombre de noeuds peut atteindre plusieurs centaines.
Les types de plates-formes multi-ordinateurs couramment cités dans la
littérature sont :
1. Les grappes homogènes : Elles sont
constituées de noeuds identiques reliés entre eux a travers un
réseau homogène. Beaucoup de travaux ont été
réalisés dans le cadre de l'ordonnancement d'applications
parallèles sur les grappes homogènes de stations de travail
[25-27]. L'avantage de ces plates-formes est qu'elles permettent d'exploiter au
mieux l'exécution des tâches parallèles qui
nécessitent une synchronisation entre les noeuds impliqués. L'un
des inconvénients des grappes homogènes est qu'il est difficile
de les étendre car les offres de matériels informatiques sont en
constante évolution. De plus, ces grappes sont en général
constituées d'un nombre relativement limité de noeuds.
2. Les grappes hétérogènes
: Elles sont également constituées de noeuds
reliés au sein d'un
9uniform memory access 10Non uniform memory
access
réseau local. Mais les différents noeuds et
liens peuvent avoir des caractéristiques différentes. L'avantage
qu'il y a à utiliser les grappes hétérogènes est de
pouvoir disposer facilement de plusieurs ressources au sein d'un réseau
local. Par contre, il est très difficile d'approcher les performances
optimales pour les tâches parallèles du fait de la
nécessité de synchronisation entre divers processus d'une
même tâche.
3. Les grappes hétérogènes de
grappes homogènes : Ces plates-formes qu'on qualifie souvent de
»grilles légères» sont composées de
plusieurs grappes distantes reliées entre elles par un réseau
hétérogène. Il s'agit en général d'un
réseau relativement rapide. Chaque grappe est homogène mais les
caractéristiques entre deux grappes peuvent être
différentes (comme exemple Grid'5000). L'avantage des grappes
hétérogènes de grappes homogènes est qu'elles
servent à agréger un nombre important de ressources tout en
conservant un minimum d'homogénéité. On peut donc
facilement adapter des travaux d'ordonnancement sur grappes homogènes
à ces plates-formes extensibles qui sont de plus en plus
répandues [4]. Toutefois, on ne doit pas négliger la latence
entre les différents sites d'une telle plate-forme si on y
déploie une application parallèle.
4. La grille: Il s'agit d'une notion de
plates-formes beaucoup plus hétérogènes et plus
générales. La grille est constituée [13] par
l'agrégation d'unités centrales, de réseaux et de
ressources de stockage distincts. Elle permet entre autre de disposer de
nombreuses ressources via Internet. Aujourd'hui, quelques difficultés
pratiques font qu'il n'existe quasiment pas de travaux dédiés
à l'ordonnancement sur la grille. Il s'agit notamment du coût trop
important des communications entre réseaux distants ou encore des
problèmes de la gestion et de la disponibilité des ressources.
2.4.1 Exemple d'application des quatre classes
principales
A, B, C et D sont les données. + et * sont les
instructions ou les opérations.

Une des tendances claires dans le calcul est la substitution des
machines parallèles coûteuses et spécialisées par
les grappes de postes de travail plus rentables.
3 Grappes d'ordinateurs
3.1 Origine et évolution de grappes
Cette section donne un tour d'horizon sur les origines et
l'évolution des grappes de machines. Nous avons décomposé
en quatre phases l'évolution des architectures parallèles qui
n'est bien entendu pas achevée, mais il nous semble que les phases
décrites ci-dessous reflètent correctement la situation.
3.1.1 Les supercalculateurs
Les premières plate-formes possédant une
architecture parallèle sont les machines désignées
fréquemment par le terme de supercalculateurs. Il s'agit
là d'un matériel très conséquent, aussi bien au
niveau de la taille que des moyens nécessaires à leur
exploitation. En effet, l'implantation et l'entretien d'une machine de ce type
posent des problèmes logistiques concrets qui induisent un coût
non négligeable en plus de la machine proprement dite, dispendieuse.
Ces machines ont un succès cyclique et il est si
courant de lire dans la presse les difficultés rencontrées par
tel ou tel constructeur, que l'on peut se poser la question du maintien d'une
niche de ce type tant le marché paraît moribond. Cependant, les
sorties de plusieurs modèles de supercalculateurs semblent indiquer un
regain d'intérêt pour ces architectures citons par exemple les
Cray X-1 et RedStorm, l'Earth Simulator ou encore l'IBM BlueGene/L. Ce
dernier est même premier du dernier classement du top 50011
montrant bien l'enracinement des supercalculateurs (au moins de type vectoriel)
dans le paysage du calcul haute-performance.
Du point de vue de l'utilisation, ces machines sont en
général conçues pour des besoins applicatifs
spécifiques et surtout gourmands en puissance de calcul. L'approche est
de type High Performance Computing (HPC) on cherche à obtenir
une importante puissance de calcul sur une durée de temps
limitée. Ces architectures ne sont pas aisément extensibles et
lorsque les performances deviennent insuffisantes, le changement de
matériel s'impose.
3.1.2 les réseaux de station de
travail
Le coût et la logistique nécessaires pour
l'implantation d'un supercalculateur étant prohibitifs pour une
majorité de laboratoires et d'universités, des solutions de repli
(ou de rechange) ont été adoptées afin de disposer d'un
accès à une machine parallèle. Or, les laboratoires
possèdent des moyens de calcul souvent inutilisés qui sont les
stations de travail. L'idée de base est la suivante les temps de cycles
inutilisés sont exploités en fédérant un ensemble
de stations avec un réseau d'interconnexion (Figure I.7). Ce
matériel étant plus standard, il est moins onéreux qu'un
supercalculateur et surtout plus facilement implantable.
L'approche est quelque peu différente du cas
précédent, car il s'agit d'une vision de type High-Throughput
Computing (HTC) où la puissance de calcul désirée
doit être maintenue sur une longue période de temps (plusieurs
mois, voire années). Nous avons moins affaire au parallélisme
qu'aux systèmes répartis, et le projet Condor ( [8]) est typique
de cette approche. C'est à partir de l'exploitation des configurations
de cette nature que se sont posés les enjeux du support de la gestion
dynamique des processus et des applications ainsi que de la tolérance
aux pannes. Ces aspects étaient le plus souvent ignorés dans la
programmation des supercalculateurs, entités fiables et offrant un
modèle d'exécution statique.
11Novembre 2004

Figure I.7 - Un réseau de stations de
travail
3.1.3 Les grappes de PC
Les réseaux de stations de travail ont
été massivement adoptés par les laboratoires, mais les
réseaux d'interconnexion étaient souvent peu rapides et
constituaient un goulot d'étranglement pour les performances.
L'arrivée des réseaux rapides, avec une amélioration
substantielle du débit (plusieurs ordres de grandeur) a bousculé
cette situation et permis l'émergence d'un nouveau type d'architecture
les grappes, dont le projet NOW est un représentant [32].
Architecturalement, il s'agit d'une interconnexion de PC
standards (encore moins chers que les stations de travail) avec un
réseau haut-débit. Cet ensemble de machines est localisé
dans un même lieu physique (exemple la même pièce), à
la différence des réseaux de stations qui pouvaient
s'étendre sur une échelle plus grande, comme un bâtiment
par exemple. La figure I.8 schématise une telle grappe de PC.

Figure I.8 - Une grappe de PC
Cette approche est un mélange des deux
précédentes les grappes sont dédiées au calcul
haute-performance (HPC), mais avec des composants standards.
L'extensibilité est très bonne, puisqu'il suffit
de rajouter des noeuds pour augmenter la puissance de calcul.
Cependant, la difficulté d'exploitation et de programmation est plus
importante qu'avec les supercalculateurs car ces derniers sont
équipés d'outils spécifiques. Dans le cas des grappes, les
outils d'exploitation sont souvent calqués sur ceux des
supercalculateurs et la gestion dynamique des processus ou la tolérance
aux pannes sont souvent reléguées au second plan. Malgré
ces quelques désagréments, l'excellent ratio performances/prix
favorise les grappes qui tendent à s'imposer plus de la moitié
des machines classées au top 500 sont des grappes.
3.1.4 Les architectures actuelles
Ce sont ces architectures de type <grappes> qui connaissent
des évolutions multiples. Nous trouvons donc les catégories
décrites dans les paragraphes suivants.
les grappes de grappes
Cette évolution est naturelle et découle des
excellentes capacités d'extensibilité des grappes. Le principe
consiste en une interconnexion de plusieurs grappes potentiellement
séparées par une forte distance géographique. En quelque
sorte, il s'agit d'une méta-grappe avec une approche
plutôt de type HTC, en remplaçant les stations de travail par des
unités plus importantes (les grappes). Une telle évolution doit
être replacée dans le contexte du [19] Grid computing et
du metacomputing, dont le but est l'exploitation de ressources
réparties. Cette agrégation pose de nouveaux problèmes car
les composants sont hétérogènes processeurs,
systèmes d'exploitation et réseaux d'interconnexion varient
potentiellement d'une grappe à l'autre. La nature du réseau
d'interconnexion est importante car cela permet de créer des
sous-classes de grappes de grappes. L'une de ces classes de grappes de grappes
est très présente les grappes faiblement couplées
où les différentes grappes sont reliées par un nombre de
liens tel que l'ensemble des noeuds ne forme pas un graphe complet (mais les
grappes de départ continuent à l'être cependant). Les liens
peuvent être à haut-débit et potentiellement distincts de
ceux utilisés à l'intérieur de ces sous-grappes (Figure
I.9).

Figure I.9 - Une grappe de grappes faiblement
couplées
Les grappes multiplement câblées
Une autre tendance consiste à équiper une grappe
avec plusieurs réseaux haut-débit. La multiplicité des
technologies disponibles favorise cette situation. La grappe sera soit
totalement câblée avec les multiples réseaux, soit
organisée en partitions, avec un réseau haut-débit
dédié à une partition particulière (Figure 1.10).
La difficulté réside alors dans la capacité du logiciel
à prendre en compte ou non cette multiplicité des
réseaux.
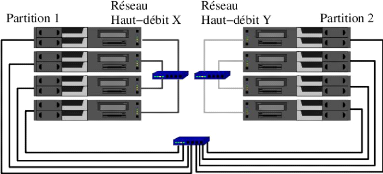

Figure I.10 - Une grappe multiplement
câblée (avec des partitions)
Les grappes de grande taille
Comme les grappes sont facilement extensibles, il devient
possible de construire des machines avec de nombreux noeuds. Si les
premières générations de grappes étaient
constituées par quelques dizaines de noeuds, les
générations actuelles peuvent aller jusqu'à plusieurs
centaines, voire milliers d'unités (par exemple, le projet Colombus
de Fujitsu avec 16384 noeuds). Dans ce cas, le problème
réside dans la capacité des logiciels à exploiter de
telles configurations. Les mécanismes mis en place sont-ils aussi
extensibles pour suivre l'évolution du matériel?
Les grappes de type beowulf
En 1994, Thomas Sterling et Don Becker du CESDIS (Center of
Excellence in Space Data and Information Sciences) construisirent une grappe de
16 processeurs DX4 reliés par un réseau Ethernet 10BaseT. Ils
appelèrent cette grappe Beowulf. Une grappe Beowulf est le type
de grappe le plus simple que l'on puisse rencontrer. La seule
différence majeure avec un réseau de stations de travail
(NOW12) est que les noeuds sont complètement
dédiés aux activités de la grappe. Le concept d'une grappe
Beowulf repose sur l'utilisation de matériel issu de l'industrie du COTS
(Commodity Off The Shelf) et des logiciels du domaine public. Les
noeuds sont généralement des PC, ils ne sont pas forcément
homogènes et sont interconnectés par un réseau classique
de type Ethernet ou FastEthernet. Les logiciels sont généralement
du domaine public; on retrouve donc principalement le système
d'exploitation
12Network of workstations
Linux13, les compilateurs GNU et des librairies de
passage de messages comme MPI (Message Passing Interface) et PVM
(Parallel Virtual Machine). Ce type d'architecture permet de faire
tourner des applications qui ne nécessitent pas ou très peu de
communications. Les applications parallèles à très gros
grain14 ou à indépendance de données peuvent en
bénéficier. Ce sont des architectures non
génériques. Elles sont montées manuellement en utilisant
des logiciels libres selon les besoins et les capacités de
l'utilisateur. Ces logiciels y sont installés dépendamment de
l'utilisateur et des traitements qu'il veut effectuer. Les ressources
informatiques constituants ce type d'architecture peuvent être
hétérogènes en termes d'unités de traitement,
d'architecture, de logiciels, des réseaux d'interconnexion.
Moyens de calcul. En termes de puissance de
calcul, on peut aussi bien trouver des supercalculateurs que des ordinateurs de
bureau (PC), des serveurs d'exécution, des stations de travail, etc. Ce
point distingue le calcul sur grille du metacomputing, qui ne fait intervenir
que des supercalculateurs.
Architectures. En termes d'architecture
matérielle, les ordinateurs peuvent être équipés de
différents types de processeurs PowerPC, compatibles i386, des Alphas,
des Mips, etc.
Logiciels. En termes d'installation
logicielle, les ordinateurs peuvent avoir différents systèmes d'-
exploitation avec une version précise (AIX 5.3, IRIX 6.5, Solaris 9,
Linux 2.6.10, Windows XP, Ubuntu, Debian, Windows Vista etc.). Les logiciels
disponibles ainsi que leurs versions peuvent également être
différents et installés à des endroits variés
(compilateurs, bibliothèques de calcul, etc.).
Réseaux. En termes de réseaux
d'interconnexion entre les ordinateurs, les liens de communication peuvent
avoir des débits, latences, gigues, taux de pertes différents.
Les avantages clés pour les grappes de type Beowulf sont
la haute performance pour un prix bas, le passage à l'échelle et
l'ajustement rapide aux avancées technologiques.
C'est ce genre d'architecture que nous avons adopté dans
le cadre de notre travail.
3.2 Caractéristiques des grappes
Cette section présente quelques caractéristiques
importantes des grappes de calcul que nous devrons prendre en
considération pour l'ordonnancement des tâches de notre
application parallèle le partage des ressources,
l'hétérogénéité des ressources et des
politiques d'administration, la sécurité et la tolérance
aux fautes.
3.2.1 Accès aux ressources
Dans une grappe le partage et l'accès aux informations
du système se font de manière transparente à
l'utilisateur. Une information présente sur un noeud A peut
être accessible sur un noeud B (Comme exemples, un utilisateur
enregistré sur le noeud A peut se logger sur le noeud B
sans toute fois être enregistré sur ce dernier. Egalement une
donnée enregistrée sur le noeud A peut être
utilisée par un utilisateur du noeud B. Toutes ces
opérations se font de façon transparente aux utilisateurs de la
grappe).
'3il est parfaitement adapté aux calculs
parallèles, stable, efficace et libre (gratuité et code source
disponible). Les mises à jour ne posent aucun problème technique
ou financier.
'4Applications nécessitant de gros calculs mais
peu de communications
3.2.2 Sécurité
Une grappe est constituée d'utilisateurs qui se font
une confiance limitée. De plus, la mise en place d'une grappe doit
respecter (et non infléchir) les politiques d'accès aux
ressources de chaque ressource. Ainsi, la sécurité et ses
mécanismes de mise en oeuvre sont des problématiques cruciales
des grappes. La sécurité concerne l'authentification mutuelle des
utilisateurs et des ressources : ces mécanismes consistent à
prouver qu'un utilisateur est bien qui il prétend être, et qu'une
ressource est effectivement ce qu'elle prétend être (service
d'information, serveur d'exécution, etc.). La sécurité
concerne également les questions d'autorisation définies au
paragraphe précédent, et le chiffrement des données. Le
chiffrement sert non seulement pour les informations en transit sur les liens
de communication, mais aussi pour celles qui sont stockées dans les
mémoires et les disques. Il évite la lecture des données
secrètes et protège leur intégrité en
empêchant leur modification sans autorisation. Enfin, la
sécurité peut impliquer la nécessité de
comptabiliser les accès (en nombre et en durée) des utilisateurs
aux ressources (accounting).
3.2.3 Tolérances aux fautes
Les défaillances matérielles et logicielles font
partie intégrante des grappes : lien réseau coupé,
ordinateur qui tombe en panne, programme non conforme aux
spécifications, etc. Pour pallier à cela, les méthodes
comme le checkpointing, la migration des processus sont
implémentées.
Les politiques d'accès aux ressources.
Chaque grappe décide de façon autonome et
indépendante des politiques :
- d'authentification, en sélectionnant une ou plusieurs
méthodes de connexion (NIS, telnet, SSH, etc.) et éventuellement
des algorithmes de chiffrement des communications;
- d'autorisation d'accès aux ressources, afin de
déterminer quels utilisateurs possèdent quels droits (lecture,
écriture, effacement) sur chaque ensemble de données;
- d'attribution des noms d'utilisateurs.
3.3 Infrastructures matérielles des
grappes
Dans la section précédente, nous avons
défini les grappes de façon générale, et
relativement abstraite. Cette section présente quelques infrastructures
matérielles typiques des grappes.
3.3.1 Architectures matérielles des
grappes
De quoi une grappe est-elle constituée? Une grappe se
compose d'un ensemble de noeuds reliés par des liens réseau comme
l'illustrent les deux paragraphes suivants.
Noeud de calcul et stockage
Les noeuds d'une grille de calcul sont ses moyens de stockage
de données informatiques, ses moyens de calcul, des dispositifs de
visualisation (écrans de réalité virtuelle immersive). Les
noeuds peuvent aussi désigner des instruments de mesure ou des capteurs,
tels que des télescopes, des senseurs météorologiques,
mais on rencontre plus rarement ce type de ressource dans les grappes de calcul
génériques qui sont déployées de nos jours. Parmi
les moyens de calcul, on trouve le plus souvent des ordinateurs de bureau
(PCs), des stations de travail, des serveurs d'exécution, des
supercalculateurs (calculateurs parallèles à mémoire
partagée tels que des SGI Origin 3000 [1] ou des SMP, calculateurs
vectoriels tels que des Cray XT3 [31]), ainsi que dans une
moindre mesure, des PDA et des ordinateurs portables.
Réseau de communication
Les noeuds d'une grappe de calcul, quelle que soit leur
nature, doivent être interconnectés par un réseau de
communication pour coopérer en échangeant des données. Les
liens réseau font partie à part entière des ressources
informatiques d'une grappe de calcul.
Les noeuds peuvent être reliés par des
réseaux locaux (Local Area Network, LAN), de type FastEthernet
(débit 100 Mb/s, latence de l'ordre de 90 s) ou Gigabit Ethernet
(débit 1 Gb/s), ou bien encore par des réseaux sans fil
(débit 54 Mb/s par exemple). Les noeuds d'un cluster peuvent être
interconnectés par un réseau haute performance (System Area
Network, SAN) tel que Myrinet [20, 21] (débit 2 Gb/s, latence de l'ordre
de la microseconde), Quadrics [24](débit plus de 6 Gb/s, latence de
l'ordre de la microseconde), ou InfiniBand [16].
3.4 Infrastructures logicielles des grappes
Comme nous venons de le voir dans la section
précédente, les ressources d'une grappe sont
hétérogènes (du point de vue du matériel, comme des
politiques d'administration), très nombreuses, et elles
nécessitent des garanties en matière de sécurité.
Les grappes sont donc des environnements particulièrement complexes.
L'intergiciel. Une des clés du
succès des grappes est la suite logicielle qui facilite l'accès
à leurs diverses ressources de manière sécurisée.
Cette section définit les rôles d'une telle suite logicielle. Pour
approcher l'objectif de transparence d'utilisation des grappes, on ne peut pas
laisser un utilisateur qui voudrait lancer son application seul face aux
ressources matérielles brutes de la grappe. Entre
- l'application qui fait un calcul utile ,
- et les multiples systèmes d'exploitation et politiques
d'accès des ressources des grappes, se trouve un < intergiciel
d'accès aux ressources de la grappe >.
Le rôle de cet intergiciel est de faciliter
l'utilisation de la grappe, en donnant une vision plus uniforme et
intégrée de ses ressources hétérogènes, et
en assurant la sécurité des données et des
communications.
Les langages de programmation. Les langages
de programmation nécessaire pour les traitements à faire devront
être installés. Typiquement, on peut avoir des langages
mathématiques pour le calcul scientifique etc..
Les serveurs. Les grappes sont dotées
des services d'information sur les utilisateurs du système et de
sécurité. Les serveurs de partage de fichiers est
également présent pour distribuer des fichiers de manière
transparente à l'utilisateur.
Les grappes de PCs constituent une architecture en plein essor
et qu'il faut considérer par conséquent. Elles sont dotées
de caractéristiques qui rend son fonctionnement et son utilisation
simple vis à vis de l'utilisateur. Pourtant le comportement
hétérogène les rend très difficile à
manipuler lorsqu'on y fait de la programmation parallèle tant sur le
plan du choix du bon placement que de l'analyse de leur performances. Certains
postulats révèlent que les performances d'une architecture
parallèle sont indépendantes du nombre de processeurs existants
tandis que d'autres révèlent le contraire.
4 Analyse des performances d'une architecture
multiprocesseurs
Dans les sections précédentes , nous avons
introduit les concepts fondamentaux liés aux systèmes
multiprocesseurs. Dans cette section, nous allons aborder les notions sur
l'analyse des mesures des performances des architectures parallèles.
Nous allons commencer par introduire le concept des modèles de calcul
liés aux multiprocesseurs. Deux modèles seront
étudiés : Le modèle de calcul parallèle avec des
parties séquentielles et le modèle de processus à
durée égale. En étudiant ces modèles, on discutera
de deux mesures qui sont : l'accélération et
l'efficacité. Par la suite, des lois seront
présentées pour mesurer les performances d'une architecture
multiprocesseur.
4.1 Modèles de Calcul
On supposera qu'une application est divisée en
tâches concurrentes15 pour l'exécution sur les
différents processeurs. Partant de là, deux modèles de
calcul seront décrits.
4.1.1 Modèle à durée
égale
Dans ce modèle [14], on suppose qu'une application peut
être divisée en n tâches égales, chacune
pouvant être exécutée par un processeur. Si
ts est le temps d'exécution de l'application en
utilisant un seul processeur, alors le temps pris par chaque processeur pour
exécuter sa tâche est tm = ts n .
comme dans ce modèle, tous les processeurs
exécutent leurs tâches simultanément, alors le temps pris
pour exécuter l'application est tm = ts n
.
Le facteur accélération du système
parallèle peut être défini comme le rapport entre le temps
pris par un seul processeur pour résoudre le problème et le temps
pris par le système constitué de n processeurs pour
résoudre le même problème.
ts ts
S(n) = facteur
d'accélération = = =
n
ts
tm n
L'équation indique que, selon le modèle à
durée égale, le facteur accélération
résultant de l'utilisation de n processeurs est égal au
nombre de processeurs utilisé, n. Un facteur important a
été omis dans les relations ci-haut. Ce facteur est le
surcoût des communications qui résulte du temps nécessaire
aux processeurs pour communiquer et échanger les données en
exécutant leurs tâches respectives. Considérons que le
temps induit par le surcoût des communications est
tc, alors le temps pris par chaque processeur pour
exécuter sa tâche est donné par tm =
ts n + tc.
|
S(n) =
|
ts ts n
= =
tm ts n + tc 1 + ntc
ts
|
L'équation ci-dessus indique que les valeurs relatives
de ts et tc affectent
l'accélération. Si on essaie d'étudier certains cas : (1)
si tc << ts alors le facteur
accélération est approximativement égal à n; (2) si
tc >> ts alors le potentiel
accélération est ts
tc << 1; (3)sitc =
ts alors le potentiel accélération est
n
n+1
1, pour n >> 1.
Dans l'optique de faire varier le facteur
accélération entre 0 et 1, on le divise par le nombre de
processeurs, n. La mesure résultante est appelée
efficacité, . L'efficacité est une mesure de
l'accélération par processeur. Selon ce modèle,
l'efficacité est égale à 1 si le surcoût dû
aux communications est
15tâches qui se communiquent les
données
ignoré. Cependant si le surcoût dû aux
communications est pris en compte, l'expression de l'efficacité est la
suivante : î= 1
1+ tc
ts
Bien que simple, le modèle de durée égale
n'est pas réaliste. Cela parcequ'il est basé sur le fait qu'une
application peut être divisée en tâches égales qui
peuvent être exécutées par des processeurs. Cependant, il
est important ici d'indiquer que les algorithmes réels contiennent des
parties séquentielles qui ne peuvent pas être divisées
entre les processeurs. Ces parties séquentielles doivent être
exécutées sur un seul processeur.
Considérons, par exemple, les segments de programme
donnés dans la figure I.11. Dans ces segments de programme, on suppose
qu'on commence avec une valeur de l'un des deux vecteurs a et b
stockés dans un des n processeurs disponibles. Le premier
bloc de programme (encadré dans un carré) peut être
résolu en parallèle; C'est à dire que chaque processeur
peut calculer un élément du tableau c. Les
éléments du tableau c sont distribués entre les
processeurs et chaque processeur a un élément. Le prochain
segment de programme ne peut pas être exécuté en
parallèle. Ce bloc aura besoin que les éléments du tableau
c soient envoyés à un processeur et additionnés
sur ce processeur.
Le dernier segment de programme peut être résolu
en parallèle. Chaque processeur peut mettre à jour ses
éléments de a et b. Cet exemple illustratif
montre qu'un modèle de calcul réaliste devrait





Figure I.11 - Segments de programme
assumer l'existence de parties séquentielles dans un
programme qui ne peuvent être divisées. Cela est la base du
modèle suivant.
4.1.2 Modèle de calcul parallèle avec des
parties séquentielles
Dans ce modèle de calcul[14], une fraction f d'un
programme donné est séquentielle. La partie restante (1-f
) elle est parallélisable.
Les dérivations similaires effectuées dans le
modèle à durée égale vont résulter comme
suit.
Le temps nécessaire pour exécuter le programme sur
n processeurs est
tm = fts + (1 -
f)(ts n )
.
Le facteur accélération est par conséquent
donné par:
|
S(n) =
|
ts n
fts + (1 -- f)(ts
n ) = 1 + (n - 1)f
|
Selon cette équation, l'accélération due
à l'accélération des n processeurs est
déterminée primairement par la fraction de code non
parallélisable. Si le programme est complètement
séquentiel, c'est à dire, f =1, alors aucune
accélération ne sera atteinte peu importe le nombre de
processeurs utilisés. Ce principe est la loi d'Amdahl.C'est
intéressant de noter que selon cette loi le facteur
accélération maximal est donné par:
lim
n-400
1
S(n) = f
Par conséquent, selon la loi d'Amdahl
l'amélioration de la performance(vitesse) de l'algorithme
parallèle par rapport à l'algorithme séquentielle n'est
pas limitée par le nombre de processeurs mais plutôt par la partie
de l'algorithme qui ne peut pas être paralléliser. A
première vue, la loi d'Amdahl indiques que peu importe le
nombre de processeurs utilisé, il existe une limite intrinsèque
sur l'utilité des architectures parallèles
utilisées. Souvent et selon la loi d'Amdahl, les
chercheurs étaient amenés à penser qu'une substantielle
croissante du facteur d'accélération ne serait pas possible en
utilisant les architectures parallèles. On discutera de la
validité de cela et d'un postulat similaire dans la section suivante.
Cependant, montrons l'effet du surcoût dû aux communications sur le
facteur d'accélération sachant qu'une fraction f du
programme n'est pas parallélisable. Comme on l'a mentionné depuis
le début, le surcoût dû aux communications devrait
être inclus dans le temps de traitement.
Considérons le temps induit par le surcoût des
communications, l'accélération est donnée par:
|
S(n) =
|
ts n
=
fts + (1 -- f)(ts
n ) + tc 1 + (n - 1)f +
ntc
ts
|
Le facteur d'accélération maximum dans ces
conditions est donné par:
|
lim
n-400
|
S(n) = lim
n-400
|
n =
1 + (n - 1)f + ntc
ts
|
1
|
|
f + tc
ts
|
La formule ci-dessous indique que le facteur
d'accélération n'est pas déterminé par le nombre de
processeurs parallèles utilisés mais par la fraction du programme
qui n'est pas parallélisable et par le surcoût des
communications.
Ayant considéré le facteur
d'accélération, calculons maintenant la mesure
d'efficacité. On sait que l'efficacité est le ratio entre le
facteur d'accélération et le nombre de processeurs n.
L'efficacité peut être calculée ainsi :
î(sans surcoût de
communications) = 1
1+(n-1)f
1
î(avec surcoût de
communications) =
1+(n-1)f+n tc
ts
Comme dernière observation, il est a noté que
dans une architecture parallèle, les processeurs maintiennent un certain
niveau d'efficacité. Cependant, comme le nombre de processeurs augmente,
il devient difficile de les utiliser efficacement. En vue de maintenir un
certain niveau d'efficacité de processeur, il devrait exister une
relation entre la fraction séquentielle du programme, f, et le
nombre de processeurs employés. Après avoir introduit les deux
modèles de calcul ci-haut, nous présenterons des lois de
performance qui ont des hypothèses sur le gain potentiel des
architectures parallèles. Parmi ces lois on a celle d'Amdahl, de
Gustafson-Brasis.
4.2 Un argument pour les architectures
parallèles
Dans cette section, on introduit un nombre de lois
nécessaires pour exprimer l'utilité des architectures
parallèles.
4.2.1 Loi d'Amdahl
Nous avons défini précédemment
l'accélération d'un système parallèle comme le
ratio entre le temps pris par un seul processeur pour résoudre le
problème divisé par le temps pris par le système
parallèle constitué de n processeurs pour
résoudre le même problème.
ts
S(n) = fts + (1 -
f)(ts n )
Une observation intéressante à faire ici est que
selon la loi d'Amdahl[3], f est fixé et n'augmente pas avec la
taille du problème, n. Cependant, il a été
pratiquement observé que certains algorithmes parallèles
réels ont une fraction f qui est une fonction de n.
Supposons que f est une fonction de n telle que
lim f(n)=0. Alors
|
S(n) = lim
n-400
|
n
1 + (n - 1)f(n) ~ n
|
Ceci est une contradiction à la loi d'Amdahl.
Cette loi stipule donc qu'une application parallèle
peut se décomposer en une partie parallélisable et une partie non
parallélisable. Le temps d'exécution de la partie
parallélisable est inversement proportionnel aux nombre de processeurs
tandis que le temps d'exécution de la partie non parallélisable
ne varie pas quelque soit le nombre de processeurs disponibles (elle ne
s'exécute que sur un processeur). On peut remarquer que ce modèle
ne tient pas explicitement compte d'éventuels coûts de
communications entre les processeurs. Ce modèle est donc plutôt
adapté aux tâches pour lesquelles les communications internes sont
négligeables ou celles dont les calculs recouvrent totalement les
communications.
Ce modèle est illustré à la figure I-12. On
voit effectivement qu'avec plusieurs noeuds pour le calcul, le temps
parallèle peut tendre vers zéro mais le temps séquentiel
ne change pas.

Figure I.12 - Modèle Amdahl
4.2.2 Loi de gustafson
En 1988, Gustafson and Barsis dans les laboratoires Sandia ont
étudié le paradoxe crée par la loi d'Amdahl et le fait que
les architectures parallèles constituées de centaines de
processeurs étaient construites avec amélioration de
performances. En introduisant leur loi, Gustafson a reconnu que la fraction non
parallélisable d'un algorithme peut ne pas être connue à
priori. Ils affirment qu'en pratique, la taille du problème augmente
avec le nombre de processeurs, n. Ceci contredit la base de la loi
d'Amdahl qui stipule que le temps d'exécution de la partie
parallélisable d'un programme, (1-f ), est indépendant
du nombre de processeurs, n. Gustafson et Brasis ont postulé
que lorsqu'on utilise un processeur plus puissant, le problème tend
à utiliser plus de ressources. Ils ont trouvé que la partie
parallèle du programme croît avec la taille du problème.
Ils ont postulé que si s et p représentent
respectivement le temps d'exécution de la partie séquentielle et
de la partie parallèle, alors s + p * n
représente le temps requis par un processeur séquentiel pour
exécuter le programme. Ils ont ainsi introduit un nouvel facteur,
appelé scaled sppedup factor, SS(n), qui peut
être calculé ainsi :
s + pn
SS(n) = = s + p * n
= s + (1 - s) * n = n + (1 --
n) * s
s + p
Cette équation montre qu'on peut atteindre une
performance parallèle efficace contrairement à
l'accélération d'Amdahl. L'accélération devrait
être mesurée en augmentant le nombre de processeurs pas en fixant
la taille du problème L'accélération et
l'efficacité sont deux facteurs pour mesurer les performances sur une
architecture parallèle. Mais ils ne tiennent pas compte de
l'architecture du réseau d'interconnexion pourtant un facteur important
à prendre en compte pour pouvoir effectuer un bon ordonnancement des
tâches composantes d'une application parallèle.
Conclusion
Dans ce chapitre, après avoir donné les
motivations et les objectifs du calcul parallèle, nous avons
présenté un certain nombre de concepts importants pour le calcul
haute performance (HPC) via le parallélisme. En particulier, on a fourni
des concepts généraux et terminologies utilisés dans le
contexte des multiprocesseurs. La populaire classification de Flynn a
été fournie. Nous avons donné les caractéristiques
explicites des architectures SISD, MISD, SPMD, SIMD et MIMD. Cette
classification est aujourd'hui obselète. La plupart des machines
parallèles sont MIMD à savoir l'architecture à
mémoire partagée qui regroupe les calculateurs multiprocesseurs
qui ne permet pas le passage à l'échelle contrairement à
l'architecture à mémoire distribuée qui regroupe les
calculateurs multiordinateurs. Nous avons présenté un cas
particulier des multiordinateurs à savoir l'architecture des grappes de
calcul, plus particulièrement celles hétérogènes.
Ces dernières constituera notre architecture cible dans le cadre de
notre travail. On a vu que deux grands modèles de programmation sont
utilisés sur les architectures distribuées de type grappe de
machines le passage de messages et la mémoire partagée. Dans
notre travail on utilisera le premier modèle et plus
précisément le standard MPI qui est doté de
caractéristiques favorables à notre machine cible. Nous avons
étudier comment analyser les performances d'une application
parallèle avec des postulats de Flynn et Gustafson en utilisant les
paramètres d'accélération et d'efficacité. Une fois
qu'on connaît parfaitement les spécificités de notre
architecture cible tant matérielle que logicielle, il nous revient de
bien représenter notre application parallèle pour pouvoir
l'exécuter sur les ressources de calcul. Dans le chapitre suivant nous
verrons comment représenter une application parallèle de
manière plus formelle en graphe et quels sont les différents
modèles qu'on peut utiliser pour ordonnancer les tâches.
Chapitre II
CONCEPTS D'ORDONNANCEMENT
A
Près que notre application soit conçue et
réalisée en ensemble de tâches, une assignation de ces
tâches aux processeurs de notre architecture doit être
déterminée. Ce problème est appelé problème
d'ordonnancement et est connu comme étant le plus grand défi dans
le domaine du calcul distribué
et parallèle. Le but de l'ordonnancement est de
déterminer une bonne allocation des tâches aux processeurs de
l'architecture. Un algorithme d'ordonnancement prend en compte une
représentation de l'application sous forme de graphe de
précédence, de flots de données ou de tâches et
consiste à répartir ces tâches sur les différents
processeurs du système en fonction d'un critère de performance
donné. Certains modèles d'ordonnancement ont des supports de
communication entre les processeurs de la machine cible tandis que d'autres
négligent l'influence des communications entre les processeurs de la
machine cible. Nous les présenterons et illustrerons après avoir
décrit les différentes représentations d'une application
en tâches par un graphe.
1 Modélisation d'une application
L'algorithme est faite principalement de deux façons,
chacune utilisant un graphe orienté comme structure de base. Nous
pouvons représenter un programme par un graphe de flots de
données (data-flow graph), par un graphe de
précédence(precedence task graph) [5]. En dehors de ces
deux types, nous avons un autre type plus général : le graphe de
tâches(task graph). Dans la suite, nous caractérisons ces
représentations sous la forme d'un graphe orienté sans cycle
(C, V ) où G est l'ensemble des sommets et V est l'ensemble des
arcs. Un graphe de tâches est composé des noeuds
représentant les tâches et les arcs représentant les
dépendances entre les tâches. Nous utilisons le programme
ci-dessous (figure II-1) pour donner un exemple de ces types de graphe.
1.1 Graphe de précédence
Dans la représentation d'un programme par un graphe de
précédence, l'algorithme est divisé en unités de
base dénommées tâches (qui sont des instructions ou groupes
d'instructions). Les tâches sont représentées par des
sommets du graphe. Les dépendances entre les tâches sont
explicitées par des arcs. L'existence d'un arc (u, v) d'une
tâche u à une tâche v dans le graphe
signifie que la tâche v ne peut pas être
exécutée sans les données produites par la tâche
u. Nous associons à chaque arc un poids proportionnel à
la quantité de données à transmettre, et à chaque
sommet un poids correspondant au

Figure II.1 - Exemple de Programme
temps de calcul de la tâche. Dorénavant, nous
ferons référence à cas valeurs comme poids de l'arc ou du
sommet. Lorsque les arcs ne sont pas associés à des poids, c'est
à dire seules les dépendances entre les tâches sont
données, nous avons la représentation par graphe de
dépendance.
Un graphe de précédence est donné en
exemple dans la figure II.2 où les tâches sont
représentées par des cercles et les relations de
précédence par des arcs. Les dépendances étant
introduites pour régler des conflits d'accès à des
données, elles peuvent être interprétées comme des
communications entre les tâches. Dans ce type de graphe, une tâche
est considérée comme prête dès que toutes les
tâches qui la précèdent dans le graphe sont
terminées.
1.2 Graphe de flots de données
Si les dépendances entre tâches sont
considérées comme des communications d'échange de
données, le graphe de flots de données est construit à
partir de l'évolution des données. Les relations de
précédence sont induites par la circulation des données.
Typiquement, les sommets correspondent à l'évaluation d'une
instruction et les précédences aux accès en lecture ou
écriture des opérandes [10]. Un graphe de flots de données
est un graphe biparti, où sont représentées les
tâches et les données. La figure II.3 représente le graphe
de flots de données pour une exécution du programme du calcul de
fibonacci. Connaissant une représentation d'un programme par un graphe
de flots de données, sa transformation en graphe de
précédence est immédiate car le premier fournit plus
d'informations que le dernier. La différence entre les graphes de
précédence et de flots de données se situe au niveau des
synchronisations. Dans le graphe de flot de données, une tâche est
considérée comme prête dès que les données
qu'elle a en entrée sont disponibles. Notons néanmoins qu'un
graphe de flots de données contient les informations d'un graphe de
précédence.
A priori, les tâches peuvent être quelconques et le
graphe de précédence inconnu au moment de

Figure II.2 - Un graphe de
précédence pour le programme. Les tâches sont
représentées par des cercles et les arcs représentent les
précédences.
l'exécution d'un programme. Pour un graphe de
précédence G donné, nous adoptons la terminologie suivante
:
Successeurs : l'ensemble des successeurs d'un
sommet v est constitué de tous les noeuds u tels qu'il
existe un chemin orienté de v à u dans G.
Successeurs directs : l'ensemble des successeurs
directs d'un sommet v est constitué de tous les noeuds u
tels qu'il existe un arc de v à u dans G.
Prédécesseurs : l'ensemble des
prédécesseurs d'un sommet v est constitué de tous les
noeuds u tels qu'il existe un chemin orienté de u
à v dans G.
Prédécesseurs directs : l'ensemble
des prédécesseurs directs d'un sommet v est
constitué de tous les noeuds u tels qu'il existe un arc de
u à v dans G.
Largeur : le cardinal du plus grand ensemble de
sommets du graphe tel qu'il n'existe pas deux sommets appartenant au même
chemin orienté.
Chemin critique: le plus long chemin
orienté du graphe, prenant en compte les temps de calcul.
Granularité : rapport entre le poids des sommets et des
arcs. La granularité p d'un graphe orienté G est le
rapport entre le plus petit poids d'un sommet et le plus grand poids d'un arc
de G. Si p < 1 alors le graphe est dit à grain fin, sinon il
est dit à gros grain. Intuitivement, les tâches d'un graphe
à gros grain calculent plus qu'elles ne communiquent.
Pour illustrer ces terminologies, dans le graphe
orienté G de la figure II.4, nous avons (v8, v9,
v10, v11) pour successeurs du sommet v5. Les
successeurs de v2 sont (v6 , v11). Les
prédécesseurs directs de v9 sont (v5,
v7). La largeur du graphe G est de 4. Si toutes les tâches du
graphe G ont le même poids, le graphe a trois chemins critiques :
(v1, v3, v7, v9), (v1,
v4, v7, v9) et (v1, v5,
v8, v10).

Figure II.3 - Un graphe de flots de
données pour le programme. Les tâches sont
représentées par des cercles. Les données à
transférer dans un rectangle.

Figure II.4 - Graphe de
précédence G
1.3 Graphe de tâches
Dans ce type de graphe (figure II-5), un sommet du graphe
représente un calcul local à un processeur. Ces calculs locaux
sont nommés tâches. Les arcs du graphe
représentent les contraintes de précédence entre calculs.
Par exemple un arc peut modéliser le fait qu'une tâche attend un
résultat produit par une autre tâche.
Le graphe peut être pondéré. La
pondération d'un noeud représente le coût (nombre
d'instructions, temps, etc.) du calcul associé à ce noeud. La
pondération d'un arc représente le volume de données
à transmettre d'un noeud à un de ses successeurs.1
Une tâche est prête si tous ses
prédécesseurs ont déjà été
exécutés et que les données utiles, calculées par
les prédécesseurs de la tâche ont été
acheminées dans la mémoire locale du processeur où vont
avoir lieu les calculs.
Si les données sont déjà présentes
localement, elles n'ont pas besoin d'être communiquées. Le
coût de transfert de données entre deux tâches
exécutées par le même processeur est donc
considéré comme nul.
Si les données ne sont pas présentes localement,
il va falloir les communiquer. Une tâche ne devient prête que
lorsque toutes les données en provenance de tous ses
prédécesseurs sont finalement arrivées. La date à
laquelle elle devient prête dépend donc du nombre de
prédécesseurs, du volume des données à
transférer et du temps que va mettre le réseau pour effectuer
chacun de ces transferts.
Les différences entre les modèles
d'exécution correspondent à des différences dans
l'évaluation du coût de telles communications. Ces
différences ont un impact sur les stratégies d'ordonnancement. Un
exemple de graphe de tâches correspondant au programme du Fibonacci
ci-haut est illustré ci-dessous.

Figure II.5 - Exemple de graphe de
tâche du programme. Les chiffres en bleu représentent les
coûts de chaque tâches. Ceux en noir représentent le volume
des données à transférer d'une tâche à
l'autre par unité de temps.
'Contrairement, au graphe de flots de
données, les données ne seront pas représentées
mais plutôt le volume des données à transmettre. Egalement,
en plus des tâches représentées dans le graphe de
précédence, leur coût de calcul seront
représentés.
L'ordonnancement des calculs et le placement des
données sont deux facteurs importants pour concevoir une application
parallèle efficace; nous présentons par la suite les
modèles typiques d'ordonnancement que l'on rencontre dans la
littérature .
2 Les Modèles classiques
d'ordonnancement
Le comportement réel d'une application est relativement
facile à prévoir en séquentiel. On peut aisément
approcher le temps d'exécution d'un programme, en étudiant par
exemple sa complexité. En parallèle, d'infimes variations dans
l'environnement d'exécution, que ce soit sur un noeud de calcul ou sur
la rapidité du réseau, peuvent changer complètement le
temps d'exécution d'un algorithme non déterministe sensible aux
synchronisations. Quelques outils de réexécution
déterministes. existent et peuvent faciliter le débogage des
applications. Le comportement réel d'une application est donc
très souvent difficile à prévoir, et plus encore à
optimiser. Dans une exécution séquentielle, les portions de code
où le programme passe le plus de temps, sont facilement identifiables.
En parallèle, l'optimisation du code n'est pas suffisante, il faut aussi
que l'ordre des opérations et leurs lieux d'exécution soient
judicieusement choisis. Dans le cas contraire, même si chaque
opération se déroule rapidement, les processeurs de la machine
peuvent rester inactifs en attendant des données calculées sur
d'autres processeurs. Le problème de ce choix est nommé autrement
problème d'ordonnancement. Le temps d'exécution va donc
dépendre de toutes les charges de calculs de tous les processeurs et de
la charge du réseau. En pratique, pour pouvoir concevoir et
évaluer des algorithmes, les machines parallèles sont
modélisées plus ou moins finement. Les différences entre
les modèles concernent principalement la modélisation des
communications. Pour qu'un ordonnancement soit valide, Une
tâche ne débutera son exécution que lorsque ses
prédécesseurs directs ont terminé leurs exécutions
et lorsque les données nécessaires pour leurs exécutions
sont présentes sur les machines sur lesquelles elles
s'exécuteront respectivement.
En d'autres termes, il faut qu'il respecte les contraintes de
précédence et du volume des données à communiquer
entre les tâches. Ces contraintes dépendent du modèle de
coût des communications.
2.1 Modèles à coût de communications
nul
Beaucoup de travaux ont été menés en
négligeant l'influence des communications. Cette hypothèse est
plus ou moins réaliste. Elle est justifiée pour les applications
dont les coûts de calcul sont très grands devant les coûts
de communication et pour des exécutions se déroulant sur des
machines parallèles à mémoire partagée.
Ordonnancer un graphe sans tenir compte des coûts de
communication est relativement facile. De très bonnes garanties de
performance peuvent être obtenues avec des heuristiques simples, par
exemple, en commençant à exécuter une des tâches
prêtes sur le premier processeur qui devient disponible. Quel que soit
l'ordre dans lequel les tâches sont placées, l'exécution
dure moins de 2 fois plus longtemps que le meilleur ordonnancement. Pour
être précis, la garantie est au pire de 2- m,
où m est le nombre de processeurs de la machine.
En fonction du graphe de précédences, de bien
meilleures approximations peuvent être trouvées. Par exemple, si
toutes les tâches sont indépendantes, en plaçant la plus
grosse tâche d'abord, on obtient un rapport de performance avec le
meilleur ordonnancement de 4/3. L'exemple des tâches indépendantes
est en fait pleinement approximable. Pour tout €, un
ordonnancement s'exécutant en moins de 1+ fois le temps du meilleur
ordonnancement peut être construit en temps polynômial (
polynôme en n, le nombre de tâches, et ~ ). En
pratique, ce modèle est réaliste dans deux cas :
- la mémoire de la machine parallèle est
physiquement partagée. Il n'y a pas de communications car les
données sont toujours «locales»;
- le coût de calcul de chaque tâche est très
grand devant le coût d'une communication. Les com-
munications n'influencent pas réellement le temps
d'exécution si l'algorithme est déterministe.
Un premier modèle plus général consiste
à prendre comme modèle du temps d'acheminement des données
de la mémoire d'un processeur à un autre, une fonction de la
taille des données.
2.2 Modèle délai
La première extension possible est de considérer
un délai d constant, lors de la transmission d'un message dans
le réseau entre deux tâches situées sur des processeurs
différents. Ce délai est une fonction de la taille des
données à acheminer. Les processeurs peuvent calculer librement
sans être «gênés» par les communications. Il n'y a
pas, dans ce modèle, de contention (embouteillage) sur le
réseau.
L'ordonnancement dans ce modèle est
généralement plus difficile que l'ordonnancement avec coût
de communication nul. La difficulté d'ordonnancer un graphe de
tâches dans ce modèle dépend du rapport entre le plus petit
coût de calcul d'une tâche et le plus grand coût de
communications entre deux tâches.
1. Dans les problèmes dits à petit temps de
communications, le coût de communication est plus petit que le coût
de calcul. Ce sont des problèmes relativement simples car ils sont
proches des algorithmes sans communication..
2. Dans les problèmes dits à grand temps de
communication, le coût de communication est plus grand que le coût
de calcul. Trouver une solution proche de la solution optimale devient plus
difficile dans le cas général. Il est possible de limiter le
nombre de communications en dupliquant des tâches.
Lorsqu'une application parallèle est
considérée à son grain le plus fin, le coût des
communications est souvent bien supérieur à celui des quelques
calculs locaux. En pratique, des algorithmes de regroupement linéaire
sont utilisés pour ordonnancer ces graphes. Ils consistent à
diviser le graphe en chaînes critiques. Une chaîne critique est un
chemin dans le graphe avec des communications de coût important. Une
chaîne est exécutée par le même processeur. Le
problème revient alors à distribuer ces chaînes sur les
processeurs en essayant de minimiser le coût des communications entre
chaînes. Ceci peut être fait par un algorithme de partitionnement
de graphe non-orienté. Malheureusement, ces algorithmes ont des
garanties de performance qui dépendent du coût de la plus grande
chaîne de communication.
Approximations faites dans le modèle
délai
En fait, le modèle délai néglige deux
aspects importants de la modélisation des communications d'une
application parallèle :
- le surcoût d'exécution dû à la
gestion des communications : Pile de protocole à l'envoi et à la
réception, interruptions, etc. A cela, on peut encore ajouter les
éventuelles copies de mémoires lors des communications. Dans le
modèle délai, un grand nombre de communications peut être
fait sans surcoût, tant que ces dernières sont recouvertes par du
calcul.
- la contention due aux goulots d'étranglements du
réseau. Dans les algorithmes par phases, tous les processeurs ont
tendance à envoyer et recevoir leurs messages en même temps.
Suivant l'architecture et la performance du réseau, cela peut
entraîner un ralentissement important dans la vitesse d'acheminement d'un
message.
Ces deux aspects sont partiellement pris en compte par deux
autres modèles, logP et BSP.
2.3 Les modèles LogP et
BSP
Ces deux modèles sont un raffinement du modèle
délai pour être plus proche du comportement matériel :
LogP modélise plus finement le coût d'une communication
tandis que BSP est en fait un modèle de machine et
d'exécution.
LogP
Le modèle LogP est une extension du
modèle délai plus proche du véritable comportement d'une
machine parallèle. C'est un modèle multiprocesseurs à
mémoire distribuée dans lequel les processeurs font des
communications point à point. Le modèle spécifie les
caractéristiques de performance du réseau d'interconnexion mais
ne décrit pas la structure du réseau. Les paramètres
principaux du modèle sont :
L(Latency) : le temps de transmission d'un
court message d'un processeur source à l'autre.
o(Overhead) : le surcoût en temps
nécessaire au processeur pour recevoir (or) et
transmettre un message (os), durant lequel le processeur ne
peut effectuer d'autres opérations.
g(Gap) : L'intervalle de temps minimum entre
deux transmissions consécutives ou deux réceptions
consécutives sur un processeur. 1/g est le débit de communication
par processeur.
P(Processor) : le nombre de processeurs (les
éléments processeur et mémoire ) dans le réseau.
Le modèle LogGP est une extension du
modèle LogP et il ajoute un paramètre pour prendre en
compte le débit pour les longs messages. Ce paramètre est :
C : Gap par octets pour les longs messages.
On suppose que le réseau a une capacité finie,
telle que au plus [L/g messages peuvent être en transit d'un processeur
à un autre chaque fois. Si un processeur essaie de transmettre un
message qui dépassera cette limite, jusqu'à ce que le message
soit envoyé en respectant la capacité limite.
La figure II.6 schématise ce modèle et la figure
II.7 donne un exemple illustratif.
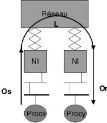
Figure II.6 - Le modèle LogP
BSP
Le modèle BSP (Bulk-synchronous Parallel) sert
à rendre les algorithmes parallèles et leur analyse assez
détaillé pour qu'on puisse en tirer des prévisions assez
réalistes sur le temps de calcul. Son principe de base est de concevoir
toute architecture parallèle comme réseau d'ordinateurs
séquentiels complets et de la quantifier par un petit nombre de
paramètres numériques. Dans le modèle BSP, une machine
parallèle à mémoire distribuée est décrite
en termes de trois éléments :
- Les modules processeur/mémoire,

Figure II.7 - A gauche nous avons une
représentation de l'ensemble des processeurs P=8, L=6,
g=4, o=2 et à droite l'activité de chaque
processeur dans le temps. Le nombre montré pour chaque noeud est le
temps auquel chaque processeur a reçu les données et peut
commencer à envoyer.
- Le réseau d'interconnexion,
- Un synchroniseur qui effectue une barrière de
synchronisation.
Un calcul est une séquence de super-étapes.
Pendant une super-étape, chaque processeur effectue un calcul local,
reçoit et envoie des messages et est sujet aux contraintes suivantes le
calcul local ne doit dépendre que des données présentes
dans la mémoire locale du processeur au début de la
superétape et un processeur doit envoyer au plus h et recevoir
au plus h messages dans une super-étapes. Une telle
communication est appelée une h-relation.
Les modèles d'exécution servent de base à
la programmation d'une machine parallèle. Il donne la sémantique
d'exécution. Un des principaux buts des modèles
d'exécution est de servir à la prédiction du temps
d'exécution d'un programme parallèle. Nous nous
intéresserons aux machines MIMD. Les processeurs sont identiques c'est
à dire qu'ils ont la même vitesse de traitement. Les
modèles de machines que nous avons décrit au chapitre 1 servent
à classer les machines existantes mais ils ne sont pas suffisants lors
du développement d'une application. Si nous voulons connaître le
traitement des conflits lors de l'accès à une donnée
partagée, ou les formes de communication entre les processeurs, nous
avons besoin des modèles d'exécution.
3 Modèles d'exécution et
ordonnancement
Il est clair que le modèle d'exécution doit
être adapté au modèle de machine. Un modèle
d'exécution qui ne prend pas en compte le temps d'accès à
une donnée distante s'avère peu pratique pour une machine MIMD de
type NUMA. Nous allons diviser la présentation des modèles selon
leur origine. Nous présenterons des modèles théoriques,
c'est-à-dire ceux qui n'ont pas été inspirés de
machines existantes d'une part et des modèles basés sur les
caractéristiques de machines réelles d'autre part.
3.1 Le modèle PRAM
Le modèle PRAM (Parallel Random Access
Machine) est un modèle théorique utilisé en calcul
parallèle et qui a servi de raffinement pour obtenir d'autres
modèles. Il est le premier modèle à avoir
été proposé pour l'informatique parallèle
[? ]. Encore aujourd'hui il sert de référence.
Il est très populaire pour l'évaluation et la comparaison
d'algorithmes parallèles [17]. Ce modèle comprend une
unité de contrôle, des processeurs identiques fonctionnent en
cadence par cycle d'une instruction, et qui ont accès à une
mémoire globale commune. En dehors de la mémoire globale, chaque
processeur a
sa mémoire locale. Le nombre de processeurs ainsi que
la taille de la mémoire sont illimités. Ce modèle se
révèle irréaliste en pratique, car le coût de
maintien d'une mémoire globale dépend du nombre de processeurs.
Dans le but de définir les règles d'accès à la
mémoire dans le modèle PRAM, plusieurs versions ont
été proposées. Les types sont :
- le EREW (Exclusive Read Exclusive Write), où chaque
cellule est accédée par au plus un processeur à chaque
cycle,
- le CREW (Concurrent Read Exclusive Write),
- le CRCW (Concurrent Read Concurrent Write), où
l'accès aux cellules peut se faire par plusieurs processeurs pour la
lecture, et pour la lecture et écriture, respectivement.
Dans le dernier cas, des règles de résolution de
conflits sont définies. Les plus courantes, en ordre croissant de
complexité sont : arbitraire, prioritaire et
combinaison de valeurs (par un maximum, une somme, etc). Dans les
modèles du type PRAM les problèmes de communication sont
masqués. La communication est incluse implicitement dans le
modèle. Pourtant en pratique c'est un point important dont il faut tenir
en compte. La figure II.8 illustre les composants du modèle PRAM.

Figure II.8 - Le modèle PRAM pour le
calcul parallèle
3.2 Les modèles avec délai de
communications
Dans les modèles avec délai de communication, il
existe un support pour la communication entre les processeurs. Ce support
consiste en l'envoi et la réception de messages. Dorénavant nous
dénotons par modèles délai, les modèles que
considèrent uniquement la taille des tâches et le délai de
communication entre tâches successives allouées à des
processeurs différents, lequel peut être aussi
considéré comme étant zéro.
Les modèles délai et des techniques
d'ordonnancement associés ont été proposés
simultanément. Pour ne pas anticiper la présentation de
l'ordonnancement, nous allons donner une description informelle. Un
ordonnancement d'un graphe sur une machine consiste à attribuer à
chaque tâche du graphe un processeur et une date de début
d'exécution.
Lors de la transmission ou de la réception d'un message
dans une machine réelle, le processeur est occupé pendant une
période de temps (avec des copies mémoire, allocation de tampons,
etc.). Les modèles de cette section ne prennent pas en compte cette
période sur le temps d'exécution des processeurs. Le recouvrement
total des communications par du calcul est autorisé, c'est-à-dire
que les processeurs peuvent calculer pendant les communications. Les
modèles délai ne prennent également pas en compte la
congestion du réseau. Le surcoût de communication sur le temps de
calcul et la congestion ont été considéré dans le
modèle LogP. Nous présentons d'abord le modèle avec bande
passante illimitée, c'est-à-dire, sans surcoût de
communication. Ensuite nous présentons les modèles avec bande
passante limitée, ce qui introduit des délais de communication.
Une des façons d'alléger ce surcoût peut se faire à
travers la duplication de tâches. Dans ce cas, nous pouvons au lieu de
communiquer à partir des prédécesseurs, dupliquer
quelques-uns d'entre eux. Les paramètres que nous utiliserons pour les
modèles suivants sont le nombre de processeurs et la possibilité
de dupliquer des tâches.
Nous présentons des exemples d'exécution du
graphe G de la figure II.4 sous les différents modèles
d'exécution. La représentation utilisée est le diagramme
de Gantt (diagramme espace temps classique où l'espace correspond
à l'occupation des processeurs) où les tâches, les
communications et les temps d'attente sont placés selon leurs dates,
processeurs et durées d'exécution. Le poids des sommets du graphe
G sont identiques, le poids de ses arcs sera explicité pour chaque
modèle.
3.2.1 Modèle UET Le modèle
L'approche théorique de base est simplement d'ignorer
le temps de communication entre processeurs. La bande passante est
considérée illimitée. Le modèle UET (unit
execution time) a été proposé par Papadimitriou et
Ullman [22]. Le temps d'exécution des tâches est unitaire, les
attentes dues aux communications ne sont pas considérées. Il est
clair que dans ce cas la duplication de tâches s'avère inutile. Ce
modèle est similaire au modèle PRAM.
Ordonnancement avec UET
Dans le diagramme de la figure II.9, nous présentons un
schéma d'exécution optimal. Les zones rayées correspondent
au temps d'inactivité, cette notion sera utilisée
dorénavant. L'ordonnancement est valide si la contrainte de
précédence est vérifiée. Au temps t = 0,
on place les tâches sans prédécesseurs directs v1
et v2 sur des processeurs libres p1 et p2. A ce
moment, un processeur sera inactif. Au temps t = 1, étant
donné qu'il n y a que 3 processeurs disponibles , on va donc choisir et
placer les tâches v3, v5, v4 sur les
processeurs. L'ordre importe peu car ils ont le même temps
d'exécution et le temps de communication est nul. Au temps t =
2, on choisit v6 qui n'était pas encore allouée et aussi
les tâches v5 et v7 sur les 3 processeurs. Au temps
t = 3, on place les trois dernières tâches
v11, v9, v10. On
remarque bel et bien que cet ordonnancement est valide et optimal car le temps
d'exécution est de 4 qui est presque égal au nombre de
tâches divisé par le nombre de processeurs = 11/3.
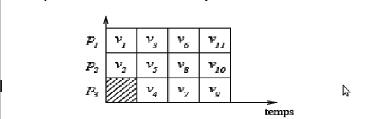
Figure II.9 - Exécution dans le
modèle UET
3.2.2 Modèle UET-UCT
Le modèle
L'extension naturelle du modèle UET considère de
manière simplifiée les communications. Lorsque les temps
d'exécution des tâches ainsi que les temps de communication sont
unitaires, nous avons le modèle UET-UCT (unit execution time -
unit communication time). Ce modèle a été
proposé par Rayward-Smith [28]. Les schémas d'exécution
avec et sans duplication sont représentés dans la Figure
II.10.
Dans l'exemple de la figure II.10, en permettant la
duplication, le temps d'exécution a été diminué
d'une unité. Dans la figure II.10 et dorénavant, lorsqu'une
tâche est exécutée plusieurs fois, une de ses allocations
est dénommée par l'index de la tâche. Les autres
exécutions d'une tâche v sont désignées par
v0 .
Ordonnancement avec UET-UCT
Ici l'idée est de chercher à placer les
tâches qui communiquent sur le même processeur pour annuler le
temps de communication.
Sans duplication : Au temps t
= 1, on place les tâches sans prédécesseurs
v1 et v2 sur p1 et p2 respectivement.
p3 est à ce moment inutilisé. Au temps t = 2,
on place les tâches v5 et v6 sur p1 et
p2 respectivement car v5 communique avec v1 et
v6 avec v2. p3 est toujours inutilisé. Au
temps t = 3, on place v4 sur p3 ( v1 a
terminé son exécution plus le temps de communication entre
p1 et p3.) Avec le même principe, on parcourt toutes
les tâches avec un temps de 6. On remarque que p3 passe beaucoup
de temps inactif.
Avec duplication : La tâche
v1 a été dupliquée sur p2 et p3
pour pouvoir placer v4, v5, v3 au même
moment.
3.2.3 Modèle UET-LCT Le modèle
Le modèle proposé par Papadimitriou et
Yannakakis [23] considère toujours des tâches de durée
unitaire, mais le coût de communication est donné par 'y >
1. Ce modèle est dénommé UET-LCT (unit
execution time - large communication time). Ce modèle convient
aux réseaux d'ordinateurs où les processeurs sont rapides et le
réseau représente le point d'étranglement du
système.

Figure II.10 - Exécution dans le
modèle UET-UCT sans et avec duplication
Ordonnancement avec UET-LCT
Dans la figure II-10, le temps de communication entre
tâches exécutées sur processeurs distincts est de 2,
5, c'est-à-dire deux fois et demi le temps d'exécution d'une
tâche.
Sans duplication : Au temps t
= 0, v1 et v2 sont allouées aux processeurs
p1 et p2.
Au temps t = 1, on choisit d'allouer v3,
v6 et v5 aux processeurs p1, p2 et
p3 ainsi les temps de communication entre v1 et v3 ,
v2 et v6 sont annulés. Tandis que v5
débutera son exécution au temps t = 1 + 1 + 2,
5 = 4, 5 puisqu'il s'exécute sur un processeur
différent de son prédécesseur direct.
Au temps t = 2, on choisit d'allouer v4
à p1.
Au temps t = 3, on alloue v7 sur le même
processeur que v3 et v4 annulant ainsi les temps de
communication.
Au temps t = 4.5, étant donné que
les tâches v7 et v5 ont déjà
terminées leur exécution, on choisit de lancer v9 sur
p1. Il débutera au temps t = 4,5 +
2,5 = 7.
On applique le même principe aux autres tâches.On
remarque que p2 est inactif longtemps.
Avec duplication : La tâche
v1 uniquement est dupliquée sur p2 pour pouvoir lancer
les tâches v3, v5 et v6 au temps 1. Egalement,
on a dupliqué v1 et v5 sur p3 pour pouvoir
lancer v11 tôt. v9 débute son
exécution au temps t = 4, 5 sur p1 puisque la
tâche v5 a terminé au temps 2 et v7 a
été exécuté sur p1.
On obtient un temps de t = 5,5 au lieu de t
= 8 sans duplication.

Figure II.11 - Exécution dans le
modèle UET-LCT sans et avec duplication
Jusqu'ici, les coûts des tâches ainsi que les
coûts des communications ont été constants. Il existe aussi
la possibilité d'avoir des coûts variables.
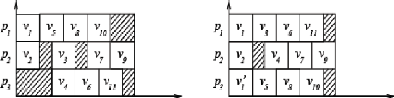
3.2.4 Modèle SCT Le modèle
Il existe d'autres approches telles que le modèle SCT
(small communication time) proposé par Colin et Chrétienne [7].
Dans ce cas, les temps d'exécution sont plus grands que les temps de
communication.
Ordonnancement avec SCT
La figure II-12 montre des schémas d'exécution du
graphe G avec et sans duplication. Le temps de communication est la
moitié de la durée d'une tâche.
Sans duplication : Avec un raisonnement
similaire à celui appliqué au modèle
précédent, on obtient un temps égal à 5 sans
duplication de tâches.
Avec duplication : On choisit de
dupliquer la tâche v1 sur p3 pour pouvoir
débuter v3 plutôt et réduire les temps
d'inactivité de p3. On obtient un temps de t = 4,
5.


Figure II.12 - Exécutions dans le
modèle SCT sans et avec duplication
L'intérêt de l'introduction de plusieurs
restrictions sur les modèles délai réside dans la
possibilité de pouvoir donner des garanties de performances plus fines
pour les problèmes d'ordonnancement.
3.3 Le modèle LogP Le modèle
Le modèle LogP [9] a le mérite d'avoir
été conçu conjointement par des spécialistes en
architectures, en environnements d'exécution et en algorithmique. Ce
modèle suppose un nombre fini P de processeurs à mémoire
locale. La topologie du réseau n'est pas prise en compte. Les
synchronisations sont faites par échange de messages. Le temps de
communication considère le coût d'échanges de message pour
chaque processeur. Dans le modèle LogP, les coûts de communication
sont déterminés à travers les paramètres L, o
et g.
Lors de l'envoi d'un message le processeur expéditeur
ne peut pas calculer pendant un période de temps, ce surcoût est
dénoté par o (overhead). La réception d'un
message coûte aussi un temps de calcul o du processeur
récepteur.
Il existe aussi un intervalle de temps minimal entre l'envoi
de deux messages par le même processeur, cet intervalle est
dénoté par g (gap). Cet intervalle de temps doit aussi
être respecté lors de la réception des messages.

Figure II.13 - Exemple des paramètres
LogP
La latence L(latency) est le maximum entre le temps
d'envoi d'un message (achèvement de l'opération d'envoi) et le
temps de réception de ce message (début de l'opération de
réception), sur des conditions de communication normales.
Pour éviter la congestion du réseau, au plus
partie supérieure de L/g messages peuvent transiter
simultanément. Dans la Figure II.13 nous illustrons les
paramètres du modèle LogP, "les tâches noires" sont dues
aux surcoûts de transmission et de réception. Un carré gris
représente la latence. Entre deux communications consécutives il
existe un intervalle de taille au moins g. La définition première
de LogP a été donnée pour de petits messages.
Avec de gros messages, la latence peut devenir
négative, le premier mot du message peut arriver avant le départ
de son dernier mot. Quelques variations plus générales du
modèle LogP ont été proposées par Hwang et al. [2,
11].
Ordonnancement avec LogP
La figure II-14 exhibe deux ordonnancements sous le
modèle LogP sans duplication. Dans le premier (à gauche) o
= 0, 125 et L = 0, 25 du temps
d'exécution d'une tâche, le paramètre g est au
plus 1. Dans le deuxième exemple (à droite) nous utilisons les
mêmes valeurs pour o et L cependant g =
1.5.
Dans le premier cas, on choisit d'ordonnancer v1 et
v2 sur les processeurs p1 et p2 respectivement.
v5 débute son exécution au temps t = 1 + 0,
125 puisqu'il utilise un surcoût de 0, 125 pour l'envoi du
message à v3.
La tâche v6 débute au temps 1. La
tâche v11 débutera au temps t = 1 +
0, 125 + 1 + 0, 125 + 0, 25 + 0, 125 =
2, 625 tenant en compte le temps de transmission du message venant de
v5, le temps de traitement de l'envoi par v5 et le temps
traitement de la réception par v11. v3
débute à son tour sur p3 au temps t = 1 +0,
125 +0, 25 +0, 125 = 2 tenant en compte le temps de
transmission du message, le temps de traitement de l'envoi par v1 et
le temps de traitement de réception du message par v3. Les
tâches v4, v7 et v9 sont allouées au
processeur p3 mais la dernière devra traiter la
réception du message de v5 au coût 0, 125.
v8 et v10 sont allouées à
p1.
La figure de droite s'explique pareillement à la seule
différence qu'il faut considérer g = 1, 5.
3.4 Le modèle BSP Le modèle
Plus qu'un modèle d'exécution, BSP [15, 18, 30]
(Bulk Synchronous Parallel) est un modèle de programmation. Son
objectif est de fournir un cadre permettant de concevoir facilement des
algorithmes portables et efficaces. Le modèle BSP n'est pas basé
sur des modèles de machines existantes,

Figure II.14 - Ordonnancement sous le
modèle LogP
mais il convient aux machines MIMD. L'idée principale
du modèle BSP est la séparation du calcul de la communication.
Ses concepts de base sont la super-étape (de l'anglais super-step) et la
synchronisation.
L'application est divisée en super-étapes. Tous
les processeurs commencent une super-étape au même instant. Entre
deux super-étapes, il existe une étape de synchronisation. Les
données communiquées lors d'une super-étape seront
disponibles aux processeurs destinataires au début de la
super-étape suivante.
Les trois paramètres utilisés afin de
décrire le modèle sont p, l et g. Nous
utilisons les mêmes notations que celles utilisées dans [18],
malgré l'utilisation de g auparavant pour la description du
modèle LogP. Ce choix est motivé par la standardisation de ces
notations pour les deux modèles. p le nombre de processeurs de
la machine; l le coût d'une synchronisation globale; g
le temps de transport d'un mot par le réseau. Autrement dit, 1/g
est la bande passante. Le modèle original proposé par Valiant
[30] introduit un paramètre qui représente la
périodicité d'une synchronisation. Dans son modèle, une
vérification globale est effectuée après chaque
période de L unités de temps. Elle sert à
déterminer si la super-étape a été achevée
sur tous les processeurs. Dans la version du modèle
présentée par McColl [28] il n'y a pas de référence
à la périodicité. Cette approche a été
probablement choisie parce que dans les machines courantes la
périodicité peut être aussi petite que le coût de
synchronisation. C'est cette approche que nous avons adoptée dans ce
document. Pour pouvoir estimer le temps d'une application BSP nous introduisons
les terminologies suivantes :
- pi processeurs de la machine (0 i < p);
- Wis coût des calculs
exécutés par le processeur pi au cours de la
super-étape s;
- hs i - désigne le maximum du nombre de mots
reçus (ou envoyés) par le processeur pi au cours de la
super-étape s.
Une h-relation est une opération
d'échanges de données point à point entre les processeurs,
où chaque processeur peut envoyer et recevoir au plus h mots.
L'estimation du temps total d'un programme BSP est obtenue en sommant les temps
de ses super-étapes. Les démarches pour obtenir une application
efficace dans le modèle BSP sont donc : équilibrer la charge de
calcul entre les processeurs au cours de chaque super-étape,
équilibrer les communications au cours d'une super-étape
(éviter les congestions) et finalement minimiser le nombre de
super-étapes.
Pour les schémas d'exécution dans le
modèle BSP nous avons choisi une représentation explicite des
communications entre les processeurs (figure II-15 à gauche)2
et représentation implicite des communications entre les processeurs
entre les super-étapes. Les communications entre les processeurs sont
représentés comme une barrière grise ( correspondant
à la h-relation ) qui se trouve juste avant la synchronisation (
barrière noire dans la figure II-15 à droite ). De cette
façon les communications
2Les flèches représentent les
données envoyées d'un processeur à l'autre
restent implicites3. Ordonnancement avec
BSP
Dans l'exemple, le temps pour achever une h-relation est 0,5 du
temps d'exécution d'une tâche. Le temps de synchronisation est
0,25.
On alloue les tâches v1 et v2 aux
processeurs p1 et p2. On choisit d'exécuter les
tâches v3, v5, v6 sur les processeurs
p1, p2, p3 respectivement.
Dès que les tâches v1 et v2 ont
terminées leur exécution, une h-relation est effectuée
puisque les données doivent être transmises de p1
à p2, de p2 à p3.
Tous les processeurs vont donc débuter cette
super-étape. Elle sera suivie par une étape de synchronisation
pour s'assurer que les processeurs ont terminés les communications au
même instant. Egalement, il y aura une h-relation après
l'exécution des tâches v7 et v10 pour
pouvoir transférer les données entre les processeurs.
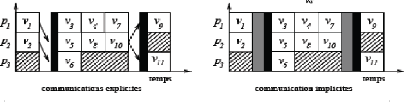
Figure II.15 - Schéma
d'exécution dans le modèle BSP
Conclusion
Dans ce chapitre on a vu comment représenter des
applications parallèles en utilisant des graphes de
précédence et de flots de données. Un autre plus
général que nous adopterons par la suite a été
présenté : le graphe de tâches. Il contient les
caractéristiques des deux graphes précédemment
cités mais de manière plus fine. Après avoir
présenté de manière succinte les modèles
d'ordonnancement avec délai et sans délai de communications sur
des graphes, nous avons décrit les modèles d'exécution les
plus souvent employés qui donnent une prédiction sur le temps
d'exécution parallèle. Les modèles sans délais de
communication sont très loin de la réalité concernant les
machines à mémoire distribuée alors que les modèles
avec délai sont raisonnablement plus proches de la réalité
bien qu'ils ne tiennent pas compte des paramètres comme le débit
du processeur, la latence de communication entre des processeurs distants. Les
modèles LogP et BSP par contre tiennent compte de ces paramètres
en plus du nombre d'unités de calcul. Le second utilise également
un synchroniseur général après les super-étapes de
calcul.
Il ressort des modèles d'exécution qu'on obtient
un temps optimal lorsque l'on néglige les temps de communication, mais
on s'éloigne du temps optimal lorsque l'on tient compte des
délais de communication. Le principe de la duplication de tâches
est souvent employée pour réduire les temps d'inactivité
des processeurs. Jusqu'ici, les modèles utilisés négligent
des éléments importants comme la congestion du réseau
pourtant présents dans une architecture MIMD à mémoire
distribuée telle que les grappes
3Les communications sont cachées
hétérogènes dans la cadre de
l'ordonnancement. Dans le chapitre suivant, nous proposons un modèle
d'ordonnancement sous ces architectures.
Chapitre III
GRAPPES HETEROGENES et
ORDONNANCEMENT
N
otre travail a pour objectif de proposer un ordonnancement des
tâches issues d'une application parallèle sur une grappe
hétérogène en tenant compte de toutes les ressources
informatiques présentes. En d'autres termes, étant donnés,
l'application parallèle traduite en graphe de tâches et la
grappe
hétérogène, il s'agira pour nous de trouver
un bon placement des tâches.
Il convient donc de bien maîtriser d'une part notre
architecture MIMD donc de cerner ses caractéristiques en termes de
ressources logicielles( les bibliothèques de communication ) et
matérielles ( le réseau d'interconnexion, les noeuds, les
équipements réseaux etc.) et d'autre part le graphe de
tâches (les précédences, les volumes de données
etc..) pour répartir efficacement les tâches de notre application
entre les différentes unités de traitement et de traiter chacune
en parallèle.
1 Eléments de coût
Les grappes hétérogènes impliquent de
prendre en compte plusieurs facteurs de coût pour une bonne exploitation.
Parmi ces facteurs, on peut citer les stations de travail, les
éléments d'interconnexion entre eux, la technologie du
réseau utilisé et le système d'exploitation et la pile
réseau.
1.1 Les stations de travail
Les machines constituants la grappe peuvent être des
machines constituées de plusieurs processeurs ou des monoprocesseurs.
Ces machines peuvent avoir des mémoires de capacités de stockage
différentes(256 Mo, 128 Mo etc..).
1.2 Les équipements réseau
Les équipements permettant de faire transiter les
données entre les stations de travail peuvent être :
- Les commutateurs
- Les routeurs
- Les concentrateurs
1.2.1 Les commutateurs
Ce sont des équipements de couche 2 du modèle OSI
qui filtrent, acheminent et font circuler les trames ( figure III-1 ) en
fonction de l'adresse de destination de chaque trame.
Les commutateurs utilisent des adresses MAC pour orienter les
communications réseau via leur matrice de commutation vers le port
approprié et en direction du noeudde destination. La matrice de
commutation désigne les circuits intégrés et les
éléments de programmation associés qui permettent de
contrôler les chemins de données par le biais du commutateur. Pour
qu'un commutateur puisse connaître les ports à utiliser en vue de
la transmission d'une trame de monodiffusion, il doit avant tout savoir quels
noeuds existent sur chacun de ses ports.
Un commutateur détermine le mode de gestion des trames
de données entrantes à l'aide d'une table d'adresses MAC. Il
crée sa table d'adresses MAC en enregistrant les adresses MAC des noeuds
connectés à chacun de ses ports.
Dès que l'adresse MAC d'un noeudspécifique sur
un port spécifique est enregistrée dans la table d'adresses, le
commutateur peut alors envoyer le trafic destiné au noeudvers le port
mappé à ce dernier pour les transmissions suivantes.
Lorsqu'un commutateur reçoit une trame de
données entrantes et que l'adresse MAC de destination ne se trouve pas
dans la table, il transmet la trame à l'ensemble des ports, à
l'exception du port sur lequel elle a été reçue.
Dès que le noeudde destination répond, le commutateur enregistre
l'adresse MAC de ce dernier dans la table d'adresses à partir du champ
d'adresse source de la trame. Dans le cadre de réseaux dotés de
plusieurs commutateurs interconnectés, les tables d'adresses MAC
enregistrent plusieurs adresses MAC pour les ports chargés de relier les
commutateurs qui permettent de voir au-delà du noeud. En règle
générale, les ports de commutateur utilisés pour connecter
entre eux deux commutateurs disposent de plusieurs adresses MAC
enregistrées dans la table d'adresses MAC.

Figure III.1 - Trame ethernet
Ils transmettent des trames Ethernet sur un réseau selon
différents modes : commutation Store and Forward (stockage et
retransmission) ou cut-through (direct).
Commutation store and forward. Lorsque le
commutateur reçoit la trame, il stocke les données dans des
mémoires tampons jusqu'à ce qu'il reçu
l'intégralité de la trame. Au cours de ce processus de stockage,
le commutateur recherche dans la trame des informations concernant sa
destination. Dans le cadre de ce même processus, le commutateur
procède à un contrôle d'erreur à l'aide du
contrôle par redondance cyclique (CRC) de l'en-queue de la trame
Ethernet. Le contrôle par redondance cyclique (CRC) a recours à
une formule mathématique fondée sur le nombre de bits (de uns)
dans la trame afin de déterminer si la trame reçue possède
une erreur. Une fois l'intégrité de la trame confirmée,
celle-ci est transférée via le port approprié vers la
destination. En cas d'erreur détectée au sein de la trame, le
commutateur ignore la trame. L'abandon des trames avec erreurs réduit le
volume de bande passante
consommé par les données altérées.
Commutation cut-through. Dans le cas de la
commutation cut-through, le commutateur agit sur les données à
mesure qu'il les reçoit, même si la transmission n'est pas
terminée. Le commutateur met une quantité juste suffisante de la
trame en tampon afin de lire l'adresse MAC de destination et déterminer
ainsi le port auquel les données sont à transmettre. L'adresse
MAC de destination est située dans les six premiers octets de la trame
à la suite du préambule. Le commutateur recherche l'adresse MAC
de destination dans sa table de commutation, détermine le port
d'interface de sortie et transmet la trame vers sa destination via le port de
commutateur désigné. Le commutateur ne procède à
aucun contrôle d'erreur dans la trame.
Il existe deux variantes de la commutation cut-through:
- Commutation fast-forward : ce mode de commutation offre le
niveau de latence le plus faible. La commutation fast-forward transmet un
paquet immédiatement après la lecture de l'adresse de
destination. Du fait que le mode de commutation fast-forward entame la
transmission avant la réception du paquet tout entier, il peut arriver
que des paquets relayés comportent des erreurs. Cette situation est
occasionnelle et la carte réseau de destination ignore le paquet
défectueux lors de sa réception. En mode fast-forward, la latence
est mesurée à partir du premier bit reçu jusqu'au premier
bit transmis. La commutation fast-forward est la méthode de commutation
cut-through classique.
- Commutation fragment-free : en mode de commutation
fragment-free, le commutateur stocke les 64 premiers octets de la trame avant
la transmission. La commutation fragment-free peut être
considérée comme un compromis entre la commutation store
andforward et la commutation cut-through. La raison pour laquelle la
commutation fragment-free stocke uniquement les 64 premiers octets de la trame
est que la plupart des erreurs et des collisions sur le réseau
surviennent pendant ces 64 premiers octets. La commutation fragment-free tente
d'améliorer la commutation cut-through en procédant à un
petit contrôle d'erreur sur les 64 premiers octets de la trame afin de
s'assurer qu'aucune collision ne s'est produite lors de la transmission de la
trame. La commutation fragment-free offre un compromis entre la latence
élevée et la forte intégrité de la commutation
store and forward; et la latence faible et l'intégrité
réduite de la commutation cut-through.
La commutation cut-through est bien plus rapide que la
commutation store and forward, puisque le commutateur n'a ni à attendre
que la trame soit entièrement mise en mémoire tampon, ni besoin
de réaliser un contrôle d'erreur. En revanche, du fait de
l'absence d'un contrôle d'erreur, elle transmet les trames
endommagées sur le réseau. Les trames qui ont été
altérées consomment de la bande passante au cours de leur
transmission. La carte de réseau de destination ignore ces trames au
bout du compte.
De plus, les commutateurs peuvent être
symétriques ou asymétriques. La commutation
symétrique offre des connexions commutées entre les ports
dotés de la même bande passante, notamment tous les ports
100Mbits/s ou 1000Mbits/s. Un commutateur de réseau local
asymétrique assure des connexions commutées entre des ports
associés à des bandes passantes différentes, par exemple
entre une combinaison de ports de 10Mbits/s, 100Mbits/s et 1000Mbits/s.
Un commutateur asymétrique dispose donc de débit
différents sur chacun de ses ports.
1.2.2 Les concentrateurs
Ce sont des équipements réseau d'interconnexion
de couche 1 du protocole OSI qui contrairement aux switchs sont moins
intelligents. Ils n'ont aucune fonction de commutation, de traitement
de données. Lorsqu'ils reçoivent un signal (0 ou 1), ils ne
savent à qui transmettre l'information; ils propagent l'information sur
tous les ports y compris le port de réception.
1.2.3 Les routeurs
Cet équipement de couche 3 du protocole OSI
maintient une table de routage contenant des routes de sortie vers
d'autres réseaux. Lorsqu'il recoit message, son rôle est choisir
le meilleur chemin pour parvenir au destinataire. Ce choix s'éffectue
à l'aide des algorithmes de routage très complexes : la route la
plus courte n'est pas forcément la meilleure. Ce qui importe en
réalité, c'est la somme des temps de transit pour une destination
donnée qui, elle même, est proportionnelle à l'importance
du traffic et au nombre de messages qui attendent d'être transmis sur les
différentes lignes.
1.3 Technologie réseau
Les communications dans un réseau local commuté
surviennent sous trois formes : monodiffusion, diffusion et multidiffusion :
- Monodiffusion : communication dans laquelle une trame est
transmise depuis un hôte vers une destination spécifique. Ce mode
de transmission nécessite simplement un expéditeur et un
récepteur. La transmission monodiffusion est la forme de transmission
prédominante adoptée sur les réseaux locaux et sur
Internet. HTTP, SMTP, FTP et Telnet sont des exemples de transmission
monodiffusion.
- Diffusion : communication dans laquelle une trame est
transmise d'une adresse vers toutes les autres adresses existantes. Un seul
expéditeur intervient dans ce cas, mais les informations sont transmises
à tous les récepteurs connectés. La transmission par
diffusion est un incontournable si vous envoyez le même message à
tous les périphériques sur le réseau local. Un exemple de
diffusion est la requête de résolution d'adresse que le protocole
ARP (Address Resolution Protocol) transmet à tous les ordinateurs sur un
réseau local.
- Multidiffusion : communication dans laquelle une trame est
transmise à un groupe spécifique de périphériques
ou de clients. Les clients de transmission multidiffusion doivent être
membres d'un groupe de multidiffusion logique pour recevoir les informations.
Les transmissions vidéo et vocales employées lors de
réunions professionnelles collaboratives en réseau sont des
exemples de transmission multidiffusion.
Selon chacune des formes, les liens peuvent être de
latence et débit différents. Typiquement, si on a trois machines
M1 , M2 , M3 reliées via un commutateur
S1, le temps de transmission de M1 à M2 peut
être différent du temps de M1 à M3 par
exemple. Cela peut être dû aux congestions intervenues sur chaque
liaison ou même aux performances des machines.
1.4 Système d'exploitation et pile
réseau
Les ordinateurs constituants la grappe peuvent avoir des
systèmes d'exploitation différents avec une version
précise.Comme exemple, Ubuntu 9.04, Windows Vista, Solaris 9 etc.. Ces
systèmes sont constitués de module de gestion des communications.
Dans la suite nous donnons une description générale de la pile
réseau utilisée pour les communications entre deux
hôtes.
Dans un système monoprocesseur, la plupart des
communications inter-processus supposent l'existence d'une mémoire
partagée. Dans le cas d'une grappe, le mémoire est
distribuée et les communications se font par échange de messages.
Quand le processus A veut communiquer avec le processus B, il commence
par élaborer un message dans son propre espace d'adressage. Il
exécute ensuite un appel système qui va prendre le message et
l'envoyer à B via le réseau. L'émetteur et le
récepteur doivent être en accord sur de nombreuses choses; depuis
les détails de bas niveau de la transmission des bits jusqu'à
ceux de plus haut niveau de la représentation des données. Pour
résoudre plus facilement ces problèmes, l'ISO (organisation
internationale de Normalisation) a défini un modèle de
référence qui identifie clairement les différents niveaux
d'une communication. Ce modèle est le modèle OSI (Open
Systems Interconnection) qui comporte sept couches:
1. la couche physique : c'est la couche la plus basse. Elle est
concernée par la normalisation des interfaces électriques et
mécaniques et des signaux.
2. la couche liaison : Son rôle primordial est de
détecter et traiter les erreurs dans les réseaux de
communication.
3. la couche réseau : Son rôle est de choisir le
meilleur chemin pour faire transiter un message.
4. la couche transport : Son rôle est de gérer le
service de connexion fiable entre l'expéditeur et le destinataire.
5. la couche session: C'est une version enrichie de la couche
transport. Elle fournit des dialogues de contrôle pour mémoriser
les connexions en cours ainsi que des mécanismes de synchronisation.
6. la couche présentation : Elle s'occupe de la
signification des bits.
7. la couche application: c'est la couche la plus haute. Elle
comporte un ensemble de protocoles divers pour gérer des applications
utilisateurs comme le transfert de fichiers.
Dans ce modèle, la communication est partagée en
ces sept couches. L'ensemble des protocoles utilisés est appelé
suite de protocoles ou pile de protocoles. Quand le processus
A de la machine 1 veut communiquer avec le processus B de la
machine 2, il élabore un message et passe ce message à la couche
application de la machine 1. Le logiciel de la couche application ajoute une
en-tête au début du message et passe le message qui en
résulte à la couche présentation au travers de l'interface
des couches 6/7. La couche présentation rajoute son en-tête et
passe le résultat à la couche session et ainsi de suite.
Certaines couches ne se contentent pas d'ajouter des informations en
début du message, elles en ajoutent également à la fin.
Quand le message arrive en bas de la pile, la couche physique transmet le
message qui ressemble alors à ce qui est décrit à la
figure III.2.
Quand le message arrive sur la machine 2, il remonte les
couches et chacune de celles-ci prend et examine l'en-tête qui lui
correspond. Le message finit par arriver au récepteur, c'est à
dire que la machine 2 peut alors répondre en suivant le chemin
inverse.
Si on examine encore notre cas de tout à l'heure entre
la machine 1 et la machine 2, l'existence des en-têtes implique une perte
d'éfficacité considérable. Chaque fois qu'un message est
envoyé, il doit être traité par une demi douzaines de
couches. Chacune d'entre elles génère et ajoute un en-tête
dans le chemin descendant ou bien retire et traite dans le chemin ascendant.
Tout ce travail prend du temps. La perte d'éfficacité due
à la gestion de la pile de protocoles n'est pas négligeable pour
un système qui utilise un réseau local. On perd réellement
de temps UC1 pour cette gestion que le débit effectif est
souvent une fraction de la capacité nominale du réseau.
Cette description est variable selon des systèmes
d'exploitation.
'Unité centrale
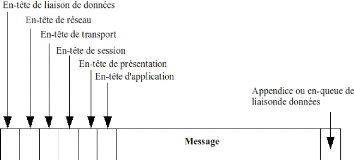

Figure III.2 - Un message classique tel qu'il
transite sur le réseau
Nous voyons donc que chacun des éléments de
coût ci-haut sont non uniformes et complexes dans leur fonctionnement.
Chacun d'eux induit des surcoûts considérables.
Les modèles d'ordonnancement traditionnels
présentés au chapitre précédent ne sont pas
réellement adaptés aux grappes hétérogènes
puisqu'ils ne tiennent pas compte d'un grand nombre de paramètres
cités ci-haut. Notamment, le coût de gestion de la pile de
protocoles est toujours considéré comme négligeable, la
congestion du réseau est négligée (ces modèles
supposent généralement que le réseau est parfait). Ils
nécessitent par conséquent d'être plus affinés. Nous
développons dans la suite un modèle plus fin de placement des
tâches sur les ressources de calcul sur notre architecture. Nous donnons
également une modélisation de cette dernière.
2 Proposition d'un modèle d'ordonnancement sur
les grappes hétérogènes
Notre système d'ordonnancement comprend : le graphe de
tâches, la grappe hétérogène et l'ordonnancement
proprement dit dans lequel des critères de performance et de
validité seront détaillés. Ces composantes sont
présentées plus formellement.
2.1 Modélisation de l'architecture
hétérogène
Notre environnement hétérogène peut donc
être modélisé par un graphe Gr =
(Vr, Er) que nous appellons graphe de la
grappe. Vr = {P1, P2, ...,
Pm} est l'ensemble des unités de calcul.
Er est l'ensemble des liens de communication entre les
noeuds.
1. m noeuds Pi, 1 < i < m
caractérisés par: - Leur puissance Si,
- Leur capacité mémoire Mi,
- L'impact du protocole réseau Ri.
2. Chaque arc (i, j) de Er
connectant deux noeuds Pi et Pj de Vr est
caractérisé par: - Sa latence lij,
- Son débit dij.
2.2 Graphe de tâches.
Les caractéristiques de notre application parallèle
sont définis comme les 4-uplets (T,<,D,A) ainsi qu'il suit :
- T=t1,...,tn qui est
l'ensemble des tâches à exécuter.
- < est l'ordre partiel défini sur T qui
spécifie les contraintes sur l'ordre de précédence entre
les tâches. C'est à dire ti < tj veut dire que ti
doit être complètement exécutée avant que
tj ne débute son exécution.
- D est une matrice n x n de
données communiquées entre les tâches, où dataij
~ 0 est le volume des données réquis à transmettre de
la tâche ti à la tâche tj, 1 < ti,
tj < n.
- A un vecteur de taille n qui représente
l'ensemble des coûts des chaque tâche. C'est à dire, cij
> 0 est le coût en calcul de la tâche ti sur le
processeur Pj, 1 ti, tj n.
Le graphe de tâche (T,E) est acyclique
où E est l'ensemble des arcs.
Un arc (ti,tj) entre deux tâches
ti et tj spécifie la relation de
précédence entre ti et tj. A chaque sommet
ti est associé son temps de calcul qui représente le
nombre d'instructions ou d'opérations présentes dans la dite
tâche. A Chaque arc (ti,tj) connectant les tâches
ti et tj est associé la taille des données
dataij, c'est à dire la taille du message de ti
à tj.
Ordonnancer les tâches revient donc à
répartir les tâches sur la grappe en respectant les contraintes de
précédence entre elles.
2.3 L'ordonnancement.
Un ordonnancement f prend en entrée: - Le graphe
de grappe Gr =
(Vr,Er),
- Le graphe de tâches G = (V, E) Plus
formellement,
- f : V -? Vr X
[0,00) Ti -? (Pj,s)
f(Ti) = (Pj, t) signifie que la
tâche Ti sera traitée par le processeur Pj au
temps t.
- F inTim est le temps de fin
d'exécution de la tâche Ti sur le processeur
Pm.F inTim = sim + cim où
sim est son temps de début d'exécution sur le
processeur Pm.
2.4 Modéle des communications
Une tâche est considérée comme
prête si tous ses prédécesseurs ont terminé
leur éxécution et que toutes les données utiles
calculées par ses prédécesseurs ont été
acheminées dans la mémoire locale du processeur où vont
avoir lieu les calculs.
Deux tâches d'un arc du graphe peuvent être
allouées au même processeur ou non. Lorsque nous sommes dans le
premier cas, cela veut dire que le coût de communication de
données est identique à celui d'un accès à la
mémoire locale puisque les données nécéssaires
à l'exécution des tâches sont présentes. Ce
coût est négligeable et est considéré égal
à zéro. Lorsque nous sommes dans le deuxième cas, le
coût de communication de données est le temps de transfert des
données nécessaires à la tâche seconde pour
débuter son exécution.
Plus formellement, Si une tâche Ti (
ordonnançée sur Pm ) doit communiquer les
données à l'un de ses successeurs Tj (
ordonnançée sur Pn ), le coût est
modéliser par :
1
0 si Pm = Pn
C(Tim, Tjn) = lmn +
dataij × 1
dmn sinon.
La date de début d'exécution de Tj est
donc sjn = F inTim +
C(Tim, Tjn).
Les problèmes NP-complet sont des problèmes qui
sont très difficilement solubles en temps polynomial. Il ya un bon
nombre de problèmes qui sont équivalents en complexité et
forment la classe des problèmes NP-complets. Cette classe inclut
plusieurs problèmes classiques de combinatoire, de théorie de
graphe, et d'informatique comme le problème du voyageur de commerce, le
problème du circuit hamiltonien, le problème d'affectation etc.
Les meilleurs algorithmes connus pour ces problèmes peuvent avoir une
complexité exponentielle avec certaines entrées. La
complexité exacte de ces problèmes NP-complets reste un
problème ouvert en informatique théorique. Soit tous ces
problèmes ont des solutions en temps polynomial ou aucun d'entre eux n'a
une telle solution.
Il a été prouvé que le problème
d'ordonnancement[6] d'un ensemble de m tâches sur n
processeurs identiques est NP-Complet en tenant compte des communications
entre les processeurs. Nous avons choisi d'aller vers une solution heuristique
permettant d'avoir un bon ordonnancement.
2.5 Idée Générale
Les points suivants constituent l'idée
générale à appliquer lorsque l'on doit effectuer une
instance d'ordonnancement f comme décrit
précédemment.
1. Exécuter les tâches les plus longues sur les
processeurs les plus rapides.
2. Exécuter les tâches qui communiquent beaucoup
sur les processeurs disponibles les plus proches.2
3. Exécuter les tâches qui communiquent un gros
volume de données sur des processeurs connectés sur des gros
réseaux.
4. On exécute Ti sur Pj si :
- le temps de transfert des données de Ti sur
Pj est minimal
- Pj est libre à cet instant
- cij est «acceptable »
La décision d'exécuter une tâche ti
sur un processeur Pj à un instant donné est donc
motivée par: - L'ensemble des tâches prêtes
- Le coût des tâches cij
- Le surcoût des communications
- L'état des processeurs
Le chapitre suivant illustrera sur un exemple cette
heuristique.
2Les processeurs interconnectés par des liens
de latence faible
Chapitre IV
EVALUATION DU MODELE SUR UNE
APPLICATION
Ce chapitre est la phase la plus pratique de notre travail. Il
est constitué du déploiement de la grappe, de
l'implémentation de l'ordonnancement d'un exemple sur cette grappe et du
calcul des performances d'une réseau (latence, débit) d'une part
et d'autre part de l'analyse des performances de l'application sur la grappe.
Nous commencerons par présenter notre grappe, ensuite nous calculerons
ses caractéristiques comme décrit dans le modèle, et par
la fin nous analyserons les performances d'une application parallèle sur
la grappe.
1 Présentation de l'architecture de notre
grappe
Notre grappe est constituée de cinq stations de travail,
reliées par un switch de 12 ports. La figure IV.1 l'illustre clairement.
Pour le déploiement de notre grappe, des outils ont été
installés à la base. - Nous avons installé un gestionnaire
de tâches : OAR.
- le service NIS1 : qui a pour rôle de
distribuer les informations sur les utilisateurs et même sur les postes
à travers toute la grappe. Ainsi, tout utilisateur ayant un compte sur
le serveur NIS pourra se logger sur n'importe quelle machine de la grappe.
- Le service NFS2 : On l'utilise en
corrélation avec le serveur NIS pour distribuer le répertoire
utilisateur sur les autres machines. Ainsi, tous les répertoires
utilisateurs sur le serveur NFS seront accessibles sur n'importe quelle machine
de la grappe.
- Le service SSH nécessaire pour se logger à
distance.
- La bibliothèque de communications MPICH2 qui nous
permettra de paralléliser les applications. L'installation de toutes ces
composantes est précisée en annexe. Les caractéristiques
des stations de travail sont récapitulées dans le tableau
ci-dessous :
1network information service 2network file
system

Figure IV.1 - Notre grappe
|
Processeur
|
Mémoire
|
Nom/adresse IP
|
SE
|
|
Machine1
|
Pentium 4, 3GHZ
|
512Mo
|
host1.labomaster/192.168.12.1
|
Debian 4.0
|
|
Machine2
|
Intel Celeron, 2GHZ
|
256Mo
|
host2.labomaster/192.168.12.2
|
Debian 4.0
|
|
Machine3
|
Pentium Dual @2GHZ
|
2Go
|
server.labomaster/192.168.12.3
|
Ubuntu 9.4
|
|
Machine4
|
Pentium 4,3.40GHZ
|
1Go
|
host3.labomaster/192.168.12.4
|
Debian 5.0
|
|
Machine5
|
Pentium 4,3GHZ
|
1Go
|
host4.labomaster/192.168.12.5
|
Debian 5.0
|
La machine 3 représente à la fois le serveur
OAR, le serveur NIS, le serveur NFS et le serveur DNS. MPICH2 a
été installé sur ce poste et est dupliqué via NFS
sur les autres postes. Chacune de ces machines sont interconnectées par
un réseau fast Ethernet 100Mbits/s. D'après notre modèle,
une grappe hétérogène est modélisée par un
graphe où les sommets sont les stations de travail
caractérisées par la puissance du processeur, la mémoire
et l'impact de la pile réseau. Dans le suite, nous décrirons
comment nous avons estimé la troisième caractéristique.
2 Calcul des caractéristiques des noeuds du graphe
de grappe
Lorsqu'une trame sort ou entre dans un hôte, elle traverse
toutes les couches de la pile réseau et cela engendre un coût non
négligeable.
2.1 Les surcoûts engendrés par la pile
réseau relatifs à chaque station de travail
Il a été difficile de trouver un outil pour
évaluer l'impact du protocole réseau; nous avons écrit un
algorithme basé sur les sockets pouvoir évaluer les coûts
engendrés par chaque ordinateur. Cet algorithme est basé sur le
modèle client/serveur avec pour protocole UDP3 où le
client envoie un message de 8 octets au serveur qui est déjà
lançé. Ici le client et le serveur sont sur un même poste.
Le code que nous avons écrit est le suivant.
CODE DU CLIENT
3User Datagram Protocol
#include <sys/types.h> #include <sys/socket.h>
#include <netinet/in.h> #include <arpa/inet.h> #include
<unistd.h> #include <stdio.h> #include <stdlib.h> #include
<sys/un.h> #include<time.h>
int main (int argc, char* argv[]) {
struct timeval start,m;
struct sockaddr_in id; char s[3];
int id_socket,tempo,envoi,i=1,argument;
int erreur;
id_socket=socket(AF_INET,SOCK_DGRAM,0);
if (id_socket<0)
{perror("\nErreur dans la création du socket");
exit(1);
}
else
printf("\n socket : OK"); id.sin_family=AF_INET;
id.sin_addr.s_addr=htonl(INADDR_ANY);
id.sin_port=htons(333); tempo=sizeof(id);
argument=atoi(argv[1]); while(i<=argument)
{
gettimeofday(&start,NULL);
envoi=sendto(id_socket,&start,sizeof(start),0,(struct
sockaddr*)&id,tempo);
i++;
sleep(1);
}
erreur=close(id_socket); exit(0);
return 0;
}
CODE DU SERVEUR
....
....
#define minim(a,b) ((a)<(b)?a:b)
#define maxim(a,b)
((a)>(b)?a:b)
int main (int argc, char* argv[]) {
id_de_la_socket=socket(AF_INET,SOCK_DGRAM,0);
if (id_de_la_socket<0)
{perror("\nErreur dans la création du socket");
exit(1);
}
else
printf("\n socket : OK"); is.sin_family=AF_INET;
is.sin_addr.s_addr=htonl(INADDR_ANY);
is.sin_port=htons(333); tempo=sizeof(is);
erreur=bind(id_de_la_socket,(struct
sockaddr*)&is,sizeof(is));
if (erreur<0)
{
perror("\nserver: bind\n"); exit(1);
}
else
printf("\nbind : OK\n");
printf("\n==NbrEnvoi=====MinRTT==================MaxRTT================MoyenneRTT\n");
max=0;
min=1000000;
argument=atoi(argv[1]); while(i<=argument)
{//printf("%d",i);
reception=recvfrom(id_de_la_socket,&start,sizeof(start),0,(struct
sockaddr*)&is,&tempo); gettimeofday(&end,NULL);
res=(end.tv_sec-start.tv_sec)*1000000 +
(end.tv_usec-start.tv_usec);
min=minim(min,res);
max=maxim(max,res);
moy=moy+res;
printf("Temps mis=%ld microsecondes \n",res);
i++;
}
printf("\n==%d===%d====%d===%1.f\n",(atoi(argv[1])),min,max,(moy/(atoi(argv[1]))));
erreur=close(id_de_la_socket);
....
}
Le surcoût de la pile est considéré comme
le temps mis par le message en local. Nous avons effectué l'envoi de
1.521.110 messages de 8 octets par machine à des
moments différents. Après ces envois, nous avons recueilli les
temps mis par le transfert en utilisant la fonction gettimeofdate et
nous avons effectué la moyenne pour avoir une estimation fine.
2.2 Tableau récapitulatif et
discussion
Nous obtenons donc la tableau ci-dessous qui regroupe tous les
impacts correspondants aux différentes machines.
|
Processeur
|
Mémoire
|
Coût induit par la pile(microsecondes)
|
|
Machine1
|
Pentium 4, 3GHZ
|
512Mo
|
23
|
|
Machine2
|
Intel Celeron, 2GHZ
|
256Mo
|
32
|
|
Machine3
|
Pentium Dual @2GHZ
|
2Go
|
5
|
|
Machine4
|
Pentium 4,3.40GHZ
|
1Go
|
31
|
|
Machine5
|
Pentium 4,3GHZ
|
1Go
|
12
|
On pourrait croire que l'impact du protocole réseau est
proportionnel à la vitesse de traitement des processeurs mais la tableau
nous présente le contraire. En effet, nous remarquons que les machines 1
et 5 ayant les mêmes vitesses de traitement induisent des coûts
tout à fait différents. Celui de la machine 1 est à peu
près le double de celui de la machine 5. D'autre part, la machine 4
ayant une vitesse d'exécution supérieure à celles des
machines 1 et 5 induit un coût qui est presque la somme des coûts
relatifs aux machines 1 et 2. Ceci nous amène à penser que les
raisons plausibles sont liées aux activités du processeur au
moment du calcul et à la gestion du protocole réseau par le
système d'exploitation puisqu'on note que les systèmes
d'exploitation sont différents. Le système d'exploitation aurait
passer la main à un autre processus différent du notre pour un
temps.
3 Calcul des caractéristiques des arcs du graphe
de grappe
Pour évaluer les latences des liens, nous avons
également écrit un programme basé sur les sockets tandis
que pour évaluer les débits des liens nous avons utilisé
des outils existants.
3.1 Evaluation des latences
Comme nous l'avons dit précédemment, nous avons
écrit un programme sur le principe client/serveur basé sur les
sockets en utilisant le protocole UDP mais cette fois on calcule le temps d'une
requête réponse par le client c'est à dire que le client
fait émet un message de 8 octets au serveur et attend la réponse
de ce dernier. Il faut noter ici que le client et le serveur sont sur des
postes différents. La latence est donc le temps
requête/réponse UDP ou le RTT(Round trip time). Le code
que nous avons fait est fourni ci-dessous :
Code du client
.... .... #define minim(a,b) ((a)<(b)?a:b)
#define maxim(a,b) ((a)>(b)?a:b)
....
int erreur;
int main (int argc, char* argv[])
{
....
4celui lancé pour exécuter le
programme
....
int id_socket,tempo,envoi,i=1,reception;
id_socket=socket(AF_INET,SOCK_DGRAM,0);
if (id_socket<0)
{perror("\nErreur dans la création du socket\n");
exit(1);
}
else printf("\n socket : OK\n");
id.sin_family=AF_INET;
id.sin_addr.s_addr=inet_addr("adresse_du_serveur");
id.sin_port=htons(3333); tempo=sizeof(id);
printf("\n==NbrEnvoi=====MinRTT======MaxRTT=====MoyenneRTT\n");
max=0;
min=100000;
argument=argv[1];
while(i<=argument)
{gettimeofday(&start,NULL);
envoi=sendto(id_socket,&start,sizeof(start),0,(struct
sockaddr*)&id,tempo);
reception=recvfrom(id_socket,&end,sizeof(end),0,(struct
sockaddr*)&id,&tempo); gettimeofday(&endl,NULL);
res=(endl.tv_sec-start.tv_sec)*1000000 +
(endl.tv_usec-start.tv_usec); min=minim(min,res);
max=maxim(max,res);
moy=moy+res;
i++;
//sleep(3);
}
printf("\n=====%d======%d====%d====%1.f\n",atoi(argv[1]),min,max,(moy/(atoi(argv[1]))));
erreur=close(id_socket);
exit(0);
return 0;
Code du serveur
int main (int argc, char* argv[])
{
struct timeval end,start;
long int res;
int erreur,tempo,id_de_la_socket,reception,n,i=1,envoi; struct
sockaddr_in is;
id_de_la_socket=socket(AF_INET,SOCK_DGRAM,0); if
(id_de_la_socket<0)
{perror("\nErreur dans la création du socket\n");
exit(1);
}
else
printf("\n socket : OK\n");
is.sin_family=AF_INET;
is.sin_addr.s_addr=htonl(INADDR_ANY); is.sin_port=htons(3333);
tempo=sizeof(is);
erreur=bind(id_de_la_socket,(struct
sockaddr*)&is,sizeof(is)); if (erreur<0)
{
perror("\nserver: bind\n");
exit(1);
}
else
printf("\nbind : OK\n");
//gettimeofday(&end,NULL);
argument = atoi(argv[1]);
while(i<=argument)
{
reception=recvfrom(id_de_la_socket,&start,sizeof(start),0,(struct
sockaddr*)&is,&tempo); gettimeofday(&end,NULL);
envoi=sendto(id_de_la_socket,&end,sizeof(end),0,(struct
sockaddr*)&is,tempo);
i++;
}
erreur=close(id_de_la_socket);
Nous avons effectué l'envoi de 1.521.110
messages de 8 octets par lien à des moments différents.
Après chaque envoi, nous avons recueilli les temps mis par le transfert
requête/réponse en utilisant la fonction gettimeofdate.
Après tous les envois, nous avons effectué la moyenne de tous les
résultats trouvés pour avoir une estimation fine. Nous avons
obtenu les latences regroupées dans la tableau ci-dessous
correspondantes aux liens entre les hôtes. Elles sont exprimées en
microsecondes.
|
Machine1
|
Machine2
|
Machine3
|
Machine4
|
Machine5
|
|
Machine1
|
x
|
272
|
107
|
127
|
125
|
|
Machine2
|
223
|
x
|
266
|
187
|
184
|
|
Machine3
|
123
|
255
|
x
|
260
|
91
|
|
Machine4
|
29
|
398
|
127
|
x
|
148
|
|
Machine5
|
126
|
355
|
100
|
132
|
x
|
La latence d'une machine M1 à une machine
M2 n'est pas forcément la même de M2 à
M1. Ceci est dû aux performances des processeurs qui sont
différentes et au fait que les systèmes d'exploitation
gèrent la pile réseau différemment. Il faut noter que le
paquet arrive au niveau du commutateur qui étant donné son
fonctionnement mettra un temps pour faire transiter le message.
3.2 Evaluation des débits des liens
Pour évaluer les débits des liens nous avons
utilisé les outils netperf et iperf. Nous avons
utilisé iperf pour confirmer les débits trouvés
avec netperf. La syntaxe de la commande avec netperf est :
#netperf -H <adresse de la machine destinatrice> Le
resultat est de la forme
Recv Send Send
Socket Socket Message Elapsed
Size Size Size Time Throughput
bytes bytes bytes secs. 10^6bits/sec
On a obtenu les résultats suivants en Mbits/s :
|
Machine1
|
Machine2
|
Machine3
|
Machine4
|
Machine5
|
|
Machine1
|
x
|
94
|
87
|
94
|
83
|
|
Machine2
|
94
|
x
|
73
|
94
|
77
|
|
Machine3
|
65
|
81
|
x
|
90
|
94
|
|
Machine4
|
87
|
90
|
82
|
x
|
88
|
|
Machine5
|
86
|
82
|
94
|
82
|
x
|
3.2.1 Discussion
Le débit d'une machine M1 à une machine
M2 n'est pas forcément le même de M2 à
M1. Ceci peut être dû aux différences entre les
vitesses de traitement des processeurs et aux charges des processeurs à
un moment donné. Si un processeur est trop surchargé par rapport
à l'autre, alors il y aura influence sur le débit. Par ailleurs,
on voit que les 100 Mbits/s constituant le débit du réseau
Fast-Ethernet n'est jamais atteint. On a en moyenne 85.85 Mbits/s. Cela peut
être dû au fait qu'il y a des collisions sur le réseau
entrainant ainsi des pertes de messages.
4 Programmation de l'application
Nous avons choisi de paralléliser la multiplication d'une
matrice A par un vecteur V . 4.1
Algorithme
Le principe est le suivant : Le processus 0 est le processeur
maître et détient la matrice et le vecteur. Les autres processus
n'ont que le vecteur. Initialement le maître découpe la matrice et
envoie une ligne de la matrice aux autres processeurs. Dès que le
processeur termine d'exécuter la tâche qui est le produit d'une
ligne reçue par le vecteur, il renvoie le résultat au
maître. Le maître chaque va tester s'il y a encore une ligne non
envoyée et si tel est le cas, il envoie à un processeur libre. Le
code est le suivant :
4.2 Code
#define min(a,b) ((a)<(b)?a:b)
void initialiser(double m[SIZE][SIZE])
{
int i,j;
for(i=0;i<SIZE;i++) for(j=0;j<SIZE;j++) m[i][j]=1.0;
}
void maitre(int numprocs)
{
int i,j, sender,row,numsent=0; double a[SIZE][SIZE],c[SIZE];
double r;
MPI_Status status;
initialiser(a);
for(i=1;i<min(numprocs,SIZE);i++)
{
MPI_Send(a[i-1],SIZE,MPI_DOUBLE,i,i,MPI_COMM_WORLD);
numsent++;
}
for(i=0;i<SIZE;i++)
{
MPI_Recv(&r,1,MPI_DOUBLE,MPI_ANY_SOURCE,MPI_ANY_TAG,MPI_COMM_WORLD,&status);
sender=status.MPI_SOURCE;
row= status.MPI_TAG-1;
c[row]=r;
if(numsent<SIZE){
MPI_Send(a[numsent],SIZE,MPI_DOUBLE,sender,numsent+1,MPI_COMM_WORLD);
numsent++;
} else
MPI_Send(MPI_BOTTOM,0,MPI_DOUBLE,sender,0,MPI_COMM_WORLD);
}
}
void esclave()
{
double b[SIZE], c[SIZE];
int i, row, myrank;
double r;
MPI_Status status;
for(i=0;i<SIZE;i++) b[i]=2.0;
MPI_Comm_rank(MPI_COMM_WORLD,&myrank);
if(myrank<=SIZE)
{
MPI_Recv(c,SIZE,MPI_DOUBLE,0,MPI_ANY_TAG,MPI_COMM_WORLD,&status);
while(status.MPI_TAG>0)
{
row=status.MPI_TAG-1;
r=0.0;
for(i=0;i<SIZE;i++)
r+=c[i]*b[i];
MPI_Send(&r,1,MPI_DOUBLE,0,row+1,MPI_COMM_WORLD);
MPI_Recv(c,SIZE,MPI_DOUBLE,0,MPI_ANY_TAG,MPI_COMM_WORLD,&status);
}
} } int main (int argc, char **argv){
int myrank,p;
MPI_Init (&argc, &argv);
MPI_Comm_rank (MPI_COMM_WORLD, &myrank);
MPI_Comm_size (MPI_COMM_WORLD, &p);
double startwtime = 0.0, endwtime;
char processor_name[MPI_MAX_PROCESSOR_NAME];
int namelen;
MPI_Get_processor_name(processor_name,&namelen);
fprintf(stdout,"Le Processus %d parmi %d est sur %s\n",myrank,p,
processor_name); MPI_Barrier(MPI_COMM_WORLD);
if(myrank==0) {startwtime = MPI_Wtime();parent(p);}
else enfant();
MPI_Barrier(MPI_COMM_WORLD);
if(myrank==0)
{endwtime = MPI_Wtime();
printf("TEMPS DE CALCUL = %f\n", endwtime-startwtime);
}
...
Le code séquentiel du même problème est
fournit en annexe. Pour calculer son temps d'exécution, il suffit de
faire
#time ./executable
Nous avons utilisé MPICH2 pour réaliser cette
application. Cependant l'ordonnancement que nous fait est fixée au
départ et ne change pas tout au long de l'exécution.
5 Ordonnancement sur la grappe
L'ordonnancement est statique c'est à dire qu'il ne
change pas tout au long de l'exécution de l'algorithme. Toutes les
machines sont utilisées pour l'ordonnancement. La machine server
est la machine sur laquelle s'exécute le premier processus. L'ordre
d'ordonnancement est server - host2 - host3 -
host4 - host1 : le premier processus s'exécute sur la
machine server, le second sur la machine host2, le
troisième sur la machine host3, le quatrième sur la
host4 et le dernier sur la machine host1. S'il y
a encore des processus, alors on reprend avec la machine
server et ainsi de suite. Exemple d'exécution avec 8 processus
:
user@labofs:~/Desktop/codes$ mpdtrace // Pour avoir l'ordre
d'ordonnancement
server
host2
host3
host4
host1
user@labofs:~/Desktop/codes$mpiexec -n 8 av Le Processus 0 parmi
8 est sur server
Le Processus 2 parmi 8 est sur host3 Le Processus 5 parmi 8
est sur server Le Processus 3 parmi 8 est sur host4 Le Processus 4 parmi 8 est
sur host1 Le Processus 7 parmi 8 est sur host3 Le Processus 1 parmi 8 est sur
host2 Le Processus 6 parmi 8 est sur host2 TEMPS DE CALCUL = 0.054822
5.1 Résultats et discussion
Nous avons obtenu les résultats suivants avec 5, 6, 8, 10,
12, 15, 20, 25, 30, 32, 40, 50, 100 processus.
Nous avons travaillé sur une matrice de tailles n=100,
1000, 3000, 5000 et 8000. Nous dénotons par T _par le
temps parallèle, T_seq le temps séquentiel,
Acc l'accélération et Eff
l'efficacité.
Le temps de calcul séquentiel pour n=100, 1000,
3000, 5000 et 8000 sont respectivement 0.016 secondes, 0.042 secondes, 0.083
secondes, 0.092 secondes et 0.11 secondes sur la machine 3.
pour n=100 -*
Processus
|
T_par(s)
|
Acc(T_seq/T_par)
|
Eff
|
|
5
|
0.69
|
0.02
|
0.004
|
|
6
|
0.06
|
0.26
|
0.04
|
|
8
|
0.05
|
0.32
|
0.04
|
|
10
|
0.07
|
0.22
|
0.02
|
|
12
|
0.08
|
0.20
|
0.01
|
|
15
|
0.09
|
0.17
|
0.01
|
|
20
|
0.14
|
0.11
|
0.005
|
|
25
|
0.19
|
0.08
|
0.003
|
|
30
|
0.3
|
0.05
|
0.001
|
|
32
|
0.36
|
0.04
|
0.001
|
|
40
|
0.55
|
0.029
|
0.0007
|
|
50
|
1.06
|
0.01
|
0.0003
|
|
100
|
6.1
|
0.02
|
0.00002
|
pour n=1000 -*
Processus
|
T_par(s)
|
Acc(T_seq/T_par)
|
Eff
|
|
5
|
0.006
|
7
|
1.14
|
|
6
|
0.007
|
6
|
1
|
|
8
|
0.008
|
5.25
|
0.65
|
|
10
|
0.009
|
4.66
|
0.46
|
|
12
|
0.0095
|
4.42
|
0.36
|
|
15
|
0.0072
|
5.83
|
0.38
|
|
20
|
0.0075
|
5.6
|
0.28
|
|
25
|
0.3
|
0.14
|
0.0056
|
|
30
|
0.42
|
0.1
|
0.0033
|
|
32
|
0.5
|
0.084
|
0.0026
|
|
40
|
1.1
|
0.038
|
0.0009
|
|
50
|
2.4
|
0.017
|
0.00035
|
|
100
|
6.29
|
0.0066
|
0.00006
|
pour n=3000 -*
Processus
|
T_par(s)
|
Acc(T_seq/T_par)
|
Eff
|
|
5
|
0.004
|
20.75
|
4.15
|
|
6
|
0.003
|
27.66
|
4.61
|
|
8
|
0.0032
|
25.93
|
3.24
|
|
10
|
0.002
|
41.5
|
4.15
|
|
12
|
0.0021
|
39.52
|
3.29
|
|
15
|
0.0023
|
36.08
|
2.40
|
|
20
|
0.0025
|
33.2
|
1.66
|
|
25
|
0.003
|
27.06
|
1.10
|
|
30
|
0.3
|
0.27
|
0.009
|
|
32
|
0.47
|
0.17
|
0.005
|
|
40
|
0.7
|
0.11
|
0.002
|
|
50
|
2.04
|
0.040
|
0.0008
|
|
100
|
3.5
|
0.023
|
0.0002
|
pour n=5000 -*
Processus
|
T_par(s)
|
Acc(T_seq/T_par)
|
Eff
|
|
5
|
0.0033
|
27.8
|
5.57
|
|
6
|
0.0034
|
27.05
|
4.50
|
|
8
|
0.0036
|
25.5
|
3.19
|
|
10
|
0.0038
|
24.21
|
2.42
|
|
12
|
0.0027
|
34.07
|
2.83
|
|
15
|
0.002
|
46
|
3.06
|
|
20
|
0.0024
|
38.33
|
1.91
|
|
25
|
0.0038
|
24.21
|
0.96
|
|
30
|
0.47
|
0.195
|
0.006
|
|
32
|
0.473
|
0.194
|
0.006
|
|
40
|
0.5
|
0.184
|
0.0046
|
|
50
|
3.04
|
0.030
|
0.0006
|
|
100
|
5.5
|
0.016
|
0.0001
|
n=8000 -?
Processus
|
T_par(s)
|
Acc(T_seq/T_par)
|
Eff
|
|
5
|
0.0036
|
30.55
|
6.11
|
|
6
|
0.0037
|
29.41
|
4.90
|
|
8
|
0.0038
|
28.94
|
3.61
|
|
10
|
0.004
|
27.5
|
2.75
|
|
12
|
0.0017
|
64.70
|
5.39
|
|
15
|
0.0022
|
50
|
3.33
|
|
20
|
0.0024
|
45.83
|
2.29
|
|
25
|
0.0038
|
28.94
|
1.15
|
|
30
|
0.47
|
0.23
|
0.007
|
|
32
|
0.77
|
0.14
|
0.004
|
|
40
|
0.6
|
0.18
|
0.004
|
|
50
|
4.02
|
0.027
|
0.0005
|
|
100
|
7.9
|
0.013
|
0.0001
|
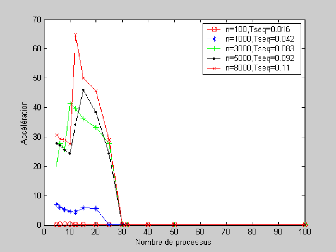
Figure IV.2 - Courbe représentant
l'accélération de l'algorithme parallèle
Nous remarquons qu'avec une matrice de taille 100,
l'accélération est presque nulle; cela veut dire que l'algorithme
parallèle est inutile puisque le temps d'exécution en
parallèle est plus grand que le temps séquentiel. Avec une
matrice de taille 1000, on constate une amélioration des performances
avec des processus allant de 5 à 20 processus. Et on trouve que
l'algorithme est efficace avec 5 et 6 processus. Lorsqu'on passe aux tailles
2000, 3000, 8000, on remarque que l'algorithme est plus efficace lorsqu'on
parallélise avec 20 ou 25 processus. Aussi, l'algorithme
accélère avec 5, 6, 8, 10, 12, 15, 20, 25 processus bien qu'elle
ne fournit pas une bonne efficacité dans ces cas. Lorsqu'on
excède 25 processus, l'accélération et l'efficacité
se dégradent rapidement jusqu'à zéro. En effet, le temps
de calcul parallèle est alors considérablement réduit
lorsque le nombre de processus augmente ceci les processus passent plus de
temps à communiquer qu'à calculer.
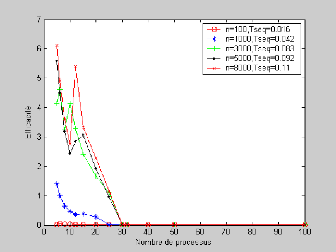
Figure IV.3 - Courbe représentant
l'efficacité de l'algorithme parallèle
Conclusion
Il n'est pas toujours utile de paralléliser une
application car elle peut fournir un temps inférieur au temps
séquentiel. C'est le cas dans notre exemple avec la matrice de taille
100. La parallélisation de notre exemple pour les tailles 1000, 3000,
5000 et 8000 améliore le temps séquentiel selon que le nombre de
processus ne dépasse pas 25 sinon l'algorithme séquentielle est
préférable. Ceci nous amène à dire que dans une
grappe hétérogène, augmenter le nombre de processeurs
n'améliore pas nécessairement le temps de calcul. En plus,
l'hétérogénéité ne permet pas d'avoir des
performances stables, elles varient beaucoup. En effet,
l'accélération n'implique pas forcément une bonne
efficacité. Pour avoir une bonne efficacité sur une telle grappe,
il faudrait ordonnancer convenablement en tenant compte de toutes ses
caractéristiques et de toutes les caractéristiques de
l'application.
Conclusion générale et perspectives
Rappel des objectifs
Le problème d'ordonnancement est un problème
complexe. Il est encore plus difficile lorsque l'on veut l'appliquer sur une
grappe de ressources non uniformes. Il a été question pour nous
dans ce travail de proposer un modèle d'ordonnancement de tâches
issues d'une application parallèle sur une grappe de calcul
hétérogène. Car il a été constaté que
la majorité des travaux sur l'ordonnancement s'applique sur les grappes
homogènes c'est à dire des grappes constitués de machines
identiques interconnectées par réseau uniforme. Dans certains,
des éléments indispensables comme la pile réseau pour
évaluer le coût sont négligés. Or les grappes
homogènes limitent le passage à l'échelle ce qui n'est pas
le cas pour les clusters hétérogènes qui nous permettent
d'avoir n'importe quel type de ressources de calcul mis ensemble pour fournir
une certaine puissance de calcul. Cependant beaucoup de contraintes
liées à l'hétérogénéité
existent dans ce type d'architecture puisque les différents modules
processeurs/mémoires sont différents, les liens d'interconnexion
aussi pour ne citer que ceux-là. Pour parvenir à nos objectifs,
nous avons d'abord fait une revue de la littérature; une revue qui
devait nous permettre d'une part d'étudier les différents types
d'architectures parallèles existantes et leur fonctionnement, d'autre
part comprendre les principes et concepts du calcul parallèle ainsi que
de l'ordonnancement des tâches. Ensuite, il a été question
pour nous d'extraire de la littérature des éléments
nécessaires sur ce qui a déjà été fait
jusqu'aujourd'hui pour constituer notre modèle de base pour allouer les
processeurs aux tâches et leur date de début d'exécution
bien sûr sur une grappe quelconque non homogène. Enfin,
après avoir installé une grappe de manière
matérielle et logicielle nous avons évalué ses
performances telles que décrite dans le modèle sur un exemple
d'application.
Bilan et évaluation du travail
réalisé
Pour une bonne compréhension de ce qui a été
fait, il importe que nous présentons d'une part le bilan du travail qui
a été réalisé et d'autre part que nous essayons de
l'évaluer.
Bilan
Ici, il est question pour nous de revenir sur tout ce qui a
été fait tout au long de notre travail. En effet nous avons
divisé notre travail en cinq principaux chapitres.
Le premier chapitre traite du calcul parallèle et de
l'architecture des grappes de calcul. Il a été question pour nous
de décrire les raisons qui incitent à faire du calcul en
parallèle et quels sont ses fondements. En effet le calcul
parallèle est un moyen pour fournir de la haute puissance de calcul
à un prix raisonnable en utilisant des ordinateurs standards. Son
efficacité dépend fortement de la programmation sou jacente qui
consiste à répartir les tâches sur plusieurs processeurs,
à repartir les données des problèmes de grande taille qui
satureraient la mémoire d'un seul ordinateur et de recouvrir les calculs
et les opérations d'entrées-sorties. Nous avons fait ressortir
deux types d'applications : statiques et dynamiques ainsi que
deux types de parallélisme explicites et implicites
qui sont des notions qui nous ont été utiles dans la suite.
Egalement, nous avons distingué les différentes architectures
parallèles décrites selon la classification de Flynn et
expliqué leurs modes de fonctionnement. De cette taxonomie, nous avons
extrait notre architecture qui est la grappe de calcul. Calculer les
critères de performances d'une application parallèle qui sont
l'accélération et l'efficacité ont fait
l'objet de la dernière section de ce chapitre.
Le second chapitre a traité essentiellement des
concepts de l'ordonnancement. L'ordonnancement est le fait d'allouer aux
processeurs des tâches et la date de début de l'exécution
de ces dernières. Il a été question pour nous de
présenter comment représenter une application parallèle
sous forme de graphe de tâches : les sommets sont les tâches, les
arêtes sont les synchronisations entre les tâches. Après
avoir défini la notion d'ordonnancement, nous avons
présenté les modèles classiques d'ordonnancement et les
modèles d'exécution pour ces ordonnancements. Il en est ressorti
que pour avoir des performances optimales, les éléments de
coût comme le surcoût induit par la pile réseau
nécessaire pour une grappe devait être négligée
ainsi que la congestion du réseau.
L'objet du troisième chapitre a été de
modéliser formellement un ordonnancement sur une grappe
hétérogène en tenant compte des éléments de
coût tels que les stations de travail qui peuvent avoir des
caractéristiques différentes, les éléments
d'interconnexion ( concentrateurs, commutateurs, routeurs ) utilisés
pour interconnecter les stations de travail qui ont des modes de fonctionnement
distincts l'un de l'autre, la pile réseau qui induit un surcoût
non négligeable puisqu'une trame doit parcourir toutes les couches avant
de quitter la machine source ainsi qu'à l'arrivée à la
machine de destination. A l'issue de cela, nous avons caractérisé
une grappe hétérogène en utilisant un modèle de
graphe où les sommets sont les stations de travail
caractérisées par leur puissance, leur capacité
mémoire, l'impact du protocole réseau et les arcs sont les liens
réseau caractérisés par leurs latences et leurs
débits.
L'ordonnancement sera donc constitué du graphe
représentant l'architecture et du graphe représentant
l'application parallèle. Nous avons aussi modéliser les
communications entre les tâches de l'application en tenant compte des
éléments de coût. Ce modèle permettra d'estimer le
temps de traitement d'un message transitant entre deux tâches.
Etant conscient du fait que notre problème est
NP-Complet, nous nous sommes limités à donner une solution
heuristique à notre problème. Elle a pour idée
générale de choisir à un instant t, la
tâche de coût minimal qui s'exécutera sur le processeur le
plus rapide et libre de telle sorte que le temps de transfert des
données nécessaires pour son exécution soit minimal.
Le dernier chapitre a constitué la partie pratique de
notre travail. C'est la partie d'implémentation de notre modèle.
Pour cela, nous avons dans un premier temps installer la grappe sur le plan
matériel et logiciel en y intégrant tous les outils logiciels
nécessaire à l'évaluation des performances du
réseau et à la programmation de l'application exemple sur
laquelle nous avons travaillé. Nous avons dans le même cadre
dévéloppé certains programmes pour estimer les temps de
latence et de surcoût induits par la pile réseau. Nous avons
choisi le problème de multiplication d'une matrice par un vecteur et
nous y avons appliqué un ordonnancement statique par nous-même et
avons recueilli des performances.
Une fois que nous avons fait le bilan du travail qui a
été fait, nous sommes passé à l'évaluation
pour faire une sorte de mesure par rapport aux objectifs du départ.
Evaluation
Comme nous l'avons dit dans l'introduction
générale, notre travail était de pouvoir modéliser
un ordonnancement sur une grappe de calcul hétérogène
après avoir décrit son modèle de coût.
Nous pensons avoir réalisé une revue de
littérature consistante pour la bonne compréhension de notre
problème. Cette bonne compréhension nous a permis de ressortir et
illustrer correctement et essentiellement les éléments qui
devaient nous être utiles tout au long de notre travail. En effet, les
concepts de parallélisme et d'ordonnancement ont été bien
compris ainsi que leurs constituants.
Nous avons pu élaborer un modèle d'ordonnancement
qui correspond effectivement à un environnement de grappe
hétérogène.
Concernant l'implémentation de notre modèle,
nous nous sommes confrontés à un problème : celui de la
non-existence d'un support d'exécution qui puisse permettre
d'ordonnancer en tenant compte des éléments de coût tels
que présentés dans notre modèle. Néanmoins, nous
avons utilisé la bibliothèque de communication MPICH2 qui nous
permet de faire une gestion dynamique des tâches tout au long de
l'exécution de l'application. Elle nous a aussi permis de programmer une
application parallèle test notamment la multiplication d'une matrice par
un vecteur. Elle ne permet que de faire un ordonnancement est statique, c'est
à dire le choix des processeurs est fixé au début de
l'exécution du programme et reste inchangée jusqu'à la fin
de l'exécution du dit programme. Ceci le rend indépendant
après la première étape ( qui est celle
réalisée par le programmeur ) des paramètres du
modèle comme par exemple quelle tâche est minimale en terme de
coût et qui nécessite ses données en temps minimal et quel
processeur choisir?
Malgré ces manquements, nous avons pu mesurer les
performances du réseau tels que les latences des liens, leurs
débits respectifs et les surcoûts relatifs à chaque station
de travail et paralléliser l'application test. Bien que l'ordonnancement
a été statique nous avons pu tirer des analyses
intéressantes sur les performances obtenues.
Perspectives
Afin d'atteindre nos objectifs, nous devons
développé un gestionnaire de tâches qui tiendra en compte
toutes les spécifications de notre modèle et de lui associer
MPICH25 pour permettre la gestion dynamique des
processeurs. Ensuite, il faudra le rendre générique pour
certaines applications sur toutes les plateformes
hétérogènes.
5ou éventuellement un autre outil
Annexe A
Annexe
1 CONFIGURATION DE NOTRE GRAPPE
1.1 Configuration logicielle
1.1.1 OAR : gestionnaire de tâches
La première chose à savoir est l'architecture OAR.
L'installation du gestionnaire OAR est composé: - du server OAR qui
détient <l'intelligence> de OAR.
- du serveur de base de données.
- du frontal de soumission des tâches sur lequel on va se
logger pour réserver certains noeuds de calcul.
- des noeuds de calcul sur lesquels les calculs
s'exécuteront.
Etant donné qu'on fait une installation sur les
distributions Debian, on installera le paquet oar-server sur le serveur OAR, le
paquet oar-user sur le frontal de soumission et le paquet oar-node sur les
machines de calcul. On installe également mysql-server. Ajouter
environment="OAR_KEY=1" au début de la clé publique dans le
fichier oar/.ssh/authorized_keys.
Préréquis
Sur chaque noeud (serveur, frontal , calcul), les paquets
suivants doivent être installés : sudo Perl
Perl-base
openssh (serveur et client)
Sur le serveur OAR et sur le frontal, les paquets suivants
doivent être installés : Perl-Mysql Perl-DBI
MySQL
MySQL-shared
libmysql
Vers l'installation
- Ajouter un utilisateur nommé <oar> dans le groupe
< <oar> sur chaque noeud.
- Créer un ensemble de clés ssh pour l'utilisateur
<oar> en utilisant ssh-keygen. Pour notre cas, id_dsa.pub et id_dsa.
- Copier ces clés dans le dossier .ssh de l'utilisateur
<oar>
- Ajouter le contenu de 'id_dsa.pub' au fichier
oar/.ssh/authorized_keys
- Dans /.ssh/config ( créer le fichier s'il n'existe pas
), ajouter les lignes :
Host *
ForwardX11 no
StrictHostKeyChecking no
PasswordAuthentication no
AddressFamily inet
- Ajouter dans le fichier de configuration du serveur ssh
AcceptEnv OAR_CPUSET OAR_JOB_USER
PermitUserEnvironment yes
UseLogin no
AllowUsers oar
Ajouter dans le fichier ~oar/.bashrc export
PATH=/usr/local/oar/oardodo:\$PATH
On n'a plus qu'à installer les paquets OAR.
Lancer le serveur OAR en utilisant l'utilisateur <oar>.
Utiliser le script "/etc/init.d/oar-server" pour lancer le démon. Editer
le fichier /etc/oar.conf pour faire correspondre la configuration de la
grappe.
DB_TYPE=mysql
DB_HOSTNAME=localhost
DB_BASE_NAME=oar
DB_BASE_LOGIN=oar
DB_BASE_PASSWD=oar
DB_BASE_LOGIN_RO=oar_ro
SERVER_HOSTNAME=localhost
DEPLOY_HOSTNAME="127.0.0.1"
... ... ALLOWED_NETWORKS="127.0.0.1/32 0.0.0.0/0"
S'assurer que la variable d'environnement PATH contient
$PREFIX/$BINDIR de notre installation. Pour notre cas, le chemin est le chemin
par défaut /usr/local/bin.
Initialisation de la base de données
L'initialisation de la base de données (MySQL) est
effectuée en utilisant le script oar_mysql_db_init fournit avec le
paquet d'installation du serveur et stocké par défaut dans
/usr/local/sbin. Etant en root, lancer ce script .
Quelques commandes
oarnodesetting
Cette commande permet de changer l'état ou la
propriété d'un noeud ou de plusieurs ressources. -a : ajouter une
nouvelle ressource
-s : l'état à assigner au noeud :
* "Alive" : une tâche peut être lancée sur ce
noeud.
* "Absent" : L'administrateur veut enlever le noeud de la liste
un moment. * "Dead" : Le noeud ne sera pas utilisé et sera
supprimé.
-h : spécifier le nom du noeud.
-r : spécifier le numéro de la ressource.
Oarsub
Cette commande permet à l'utilisateur de soumettre une
tâche.
Oarnodes
Cette commande affiche les informations sur les ressources de la
grappe.
1.1.2 MPICH2 : bibliothèque de
communications
Pré-réquis.
Pour une installation par défaut, les
éléments suivants doivent être installés :
- Une distribution de la copie mpich2.tar.gz
- Le compilateur C
- Les compilateurs Fortran-77 , Fortran-90 et/ou C++ si on veut
écrire nos programmes dans ces langages.
- Python 2.2 ou la dernière version pour construire le
système de gestion par défaut des processus. Les
étapes d'installation.
Les étapes suivantes sont celles à appliquer pour
pouvoir installer MPICH2 en vue d'exécuter un programme parallèle
sur plusieurs machines.
1. # tar xvzf mpich2.tar.gz
2. On choisit de créer notre répertoire
d'installation avec la commande mkdir /home/user/mpich2- install. On le partage
en utilisant NFS sur toutes les machines qu'on utilisera pour lancer le
programme parallèle.
3. Choisir le répertoire de construction1 :
mkdir /tmp/user/mpich2-1.0.8p1
4. Configurer MPICH2 en spécifiant le répertoire
d'installation et exécuter le script configure dans le répertoire
source :
# cd /tmp/you/mpich2-1.0.8p1
#./configure -prefix=/home/user/mpich2-install| tee
configure.log
5. On construit MPICH2 # make | tee make.log
6. Installer les commandes MPICH2 # make install | tee
install.log
7. Ajouter le sous répertoire bin du
répertoire d'installation dans le PATH # export
PATH=/home/user/mpich2-install/bin :$PATH
Tester que tout marche bien à ce niveau en faisant
# which mpd
# which mpicc
'build directory
# which mpiexec
# which mpirun
Le résultat devrait être le sous répertoire
/home/user/mpich2-install/bin
8. MPICH2 contrairement à MPICH utilise un
gestionnaire externe de processus pour lancer un grand nombre de tâches
MPI. Il est appelé MPD qui est un anneau de daemons sur les machines
où on va exécuter nos programmes MPI. Pour des raisons de
sécurité, MPD cherche dans le répertoire de l'utilisateur
un fichier nommé .mpd.conf contenant la ligne :
# secretword=<secretword> où secretword
est une chaine de caractère qui uniquement connue par nous.
Ensuite, on rend ce fichier lisible et modifiable uniquement par nous :
# cd
# touch .mpd.conf
# chmod 600 .mpd.conf
Ensuite on utilise, un éditeur pour placer une ligne
comme :
secretword=chaine de caractères
Le premier contrôle consiste à faire à
exécuter un programme non-MPI avec le demon MPD : # mpd&
# mpiexec -n 1 /bin/hostname
# mpdallexit
Ceci doit afficher le nom de la machine locale.
9. Etant donné que l'on veuille exécuter le
programme parallèle sur plusieurs machines, on devrait lancer le daemon
MPD sur chacune de ces machines. Nous devons créer un fichier
nommé mpd.hosts qui contient la liste des noms complets des
machines, un par ligne. Ces machines seront des cibles ssh ou rsh
donc il faudrait préciser le nom complet de domaine si
nécessaire. Vérifier si on peut atteindre ces machines par
ssh : # ssh remotemachine date
qui doit afficher l'heure système de la machine
distante
Lancer les démons sur chaque certaines (ou toutes les)
machines du fichier mpd.hosts. # mpdboot -n <number to start >
-f mpd.hosts
ou
# mpdboot -n <number to start>
# mpdtrace -l
<number to start > peut être inférieur
à 1+ le nombre d'hôtes dans le fichier mpd.hosts mais ne
peut pas être plus grand.
10. Compilation d'un programme parallèle # mpicc -o
<executable> <programme.c>
11. exécution d'un programme parallèle
Après avoir lancer les daemons sur les autres machines, #
mpiexec -n <nombre de processus> <executable>
1.1.3 Serveur NFS : Network file system Installation du
serveur NFS
Pour installer le serveur NFS sous débian, il suffit de
taper la commande :
# apt-get install nfs-kernel-server Configuration du
serveur NFS.
La configuration du serveur NFS est stockée dans le
fichier /etc/exports. Ce fichier de configuration
dispose d'une page de manuel :
# man exports
Ouvrir le fichier /etc/exports et ajouter la ligne pour pouvoir
partager le repertoire d'installation de MPICH2 à toutes les machines
/home/user/mpich2 - install * (ro)
A chaque modification du fichier /etc/exports, il faut relancer
le serveur NFS pour que les modifications soient prises en compte :
# /etc/init.d/nfs-kernel-server restart
Utilisation de NFS depuis un poste client.
Si on veut que ce répertoire soit accessible à
chaque boot, il suffit de rajouter la ligne suivante dans le fichier /etc/fstab
:
serveur : /home/user/mpich2 - install
/home/user/mpich2 - install nfs defaults 0 0
1.1.4 Serveur NIS : Network information
service
Pour installer NIS sous Débian, utiliser la commande
suivante :
# apt-get install nis Configuration du
serveur.
Il faut tout d'abord vérifier que le fichier /etc/hosts
contient l'adresse IP et le nom complet du serveur : Il faut ensuite ajouter
dans le fichier /etc/defaultdomain le nom du domaine NIS : labonis
Dans le fichier /etc/ypserv.securenets, on restreint
l'utilisation du domaine NIS au domaine du réseau local.
On remplace la ligne 0.0.0.0 0.0.0.0 par : 255.255.255.0
192.168.12.0.
On modifie ensuite /etc/default/nis pour indiquer qu'il s'agit du
serveur NIS :
NISSERVER=master
On relance le serveur NIS :
# /etc/init.d/nis restart
On lance ensuite la création des bases de données
NIS avec la commande suivante :
# /usr/lib/yp/ypinit -m
Ceci va créer les fichiers partagés dans le
répertoire /var/yp/DOMAINENIS.
Configuration du client
Il faut préciser le nom du domaine NIS fichier
/etc/defaultdomain contienne le domaine NIS : labonis #vi
/etc/defauldomain labonis Dans le fichier /etc/yp.conf, on indique
l'adresse IP du serveur NIS : # vi /etc/yp.conf
ypserver 192.168.12.3
On démarre le client NIS :
# /etc/init.d/nis start
On vérifie que le fichier /etc/nsswitch.conf contient bien
les lignes suivantes :
# cat /etc/nsswitch.conf
...
passwd : compat
group : compat
shadow : compat
...
netgroup: nis
2 Code séquentiel du produit d'une matrice par un
vecteur
A la fin du fichier /etc/passwd, on rajoute la ligne suivante
:
# echo 11+ : : : : : :11 >
/etc/passwd
A la fin du fichier /etc/shadow, on rajoute la ligne suivante
:
# echo 11+ : : : : : : : :11 >
/etc/shadow
A la fin du fichier /etc/group, on rajoute la ligne suivante : #
echo 11+ : : :11 > /etc/shadow
Test
Sur le serveur NIS, on rajoute un utilisateur : # adduser
franklin
On met à jour la base de données NIS : #
/usr/lib/yp/ypinit -m
Si tout fonctionne, on doit pouvoir se logger sur un des
clients NIS avec l'utilisateur franklin.
2 Code séquentiel du produit d'une matrice par un
vecteur
... ... int main()
{
double a[SIZE][SIZE],b[SIZE],c[SIZE];
struct timeval start,end;
int i,j;
initialiser(a);
for(i=0;i<SIZE;i++) b[i]=2.0;
for(i=0;i<SIZE;i++)
{c[i]=0.0;
for(j=0;j<SIZE;j++)
c[i]=c[i]+a[i][j]*b[j];
}
....
...
Bibliographie
[1] SGI Origin 3000. URL : http ://
www.SGI.com/products/servers/origin/3000/.
20
[2] A. Alexandrov, M.F. Ionescu, K.E. Schauser et C.
Scheiman. LogGP : incorporating long messages into the logP model for
parallel computation. Journal of parallel and distributed computing. July
1997. 42
[3] Gene M. Amdahl. Validity of the single processor
approach to achieving large scale computing capabilities.afips 1967 spring
joint computer conference. volume 30, page 483-485, Apr 1967. 25
[4] Henri Casanova, Frédéric Desprez et
Frédéric Suter. From heterogeneous task scheduling to
heterogeneous mixed parallel scheduling. In Marco Danelutto, Domenico
Laforenza, et Marco Vanneschi, editors, Proceedings of the 10th International
Euro-Par Conference (Euro-Par'04), volume 3149 of LNCS, page 230-237,
Pisa, Italy, August/September 2004. Springer. 14
[5] Gerson G.H Cavalheiro. Thèse : ATHAPASCAN-1 :
Interface générique pour l'ordonnancement dans un environnement
d'exécution parallèle. 22 Novembre 1999. 28
[6] Philippe Chretienne. Task Scheduling Over Distributed
Memory Machines In Michel Cosnard Patrice Quinton Michel Raynal et Yves Robert,
editors, Parallel and distributed Algorithms. 1988. 53
[7] Y. Colin et P. Chretienne. CPM scheduling with small
interprocessor communication delays. operations research. 1991. 41
[8] Condor. URL : http ://
www.cs.wisc.edu/condor/.
15
[9] D.E. Culler, R.M. Karp, D. Patterson, A. Sahay, E.E.
Santos, K.E. Schauser, R. Subramonian et T. von Eicken. LogP : A practical
model of parallel computation. Communications of the ACM. November 1996.
41
[10] V.-D. Cung, P. Fraigniaud, T. Gautier et D. Trystram.
De l'algorithme au support. In D. Barth, J. Chassin de Kergommeaux, J.-L.
Roch, and J. Roman, editors, ICaRE'97 : Conception et mise en xuvre
d'applications parallèles irrégulières de grande
taille. Aussois, France, December 1997. CNRS. 29
[11] J. Eisenbiegler, W. Lowe et A. Wehrenpfennig. On the
optimization by redundancy using an extended logP model. In international
conference advances in parallel and distributed computing. 1997. 42
[12] M.J Flynn. Reaction of the absorber as the mechanism of
radiative damping. volume 54, pages 1901-1909, Decembre 1966. 8
[13] Ian Foster et Carl Kesselman. The grid : Blueprint for
a new computing infrastructure. Morgan Kaufmann, San Francisco, 1999.
14
[14] hesham el rewimi et mostafa abd-el barr. Advanced
Computer Architecture and Parallel Processing. A John Wiley and Sons, INC
PUBLICATION, 2005. 8, 22, 23
[15] J.M.D. Hill, W.F. McColl et D.B. Skillircon. Questions
and answers about BSP. Technical report PRG-TR-15-96, Oxford University
Computing Laboratory. November 1996. 42
[16] InfiniBand. URL : http ://www.OpenPBS.org/. 21
[17] R. M. Karp et V. Ramachandran. Parallel algorithms
for sharedmemory machines. in j. van leeuwen, editor, handbook of theoretical
computer science. A : Algorithms and Complexity : 870-941, 1990. 36
[18] W.F. McColl. Scalable computing.In J. van Leeuwen,
editor, Computer Science Today : Recent Trends and Developments
Springer-Verlag, 1995. 42, 43
[19] Guillaume MERCIER. Communications à hautes
performances portables en environnements hiérarchiques,
hétérogènes et dynamiques. decembre 2004. 17
[20] technologie réseau Myrinet Myricom. URL : http
://www.myri.com/. 21
[21] Nanette J. B ODEN Danny C OHEN, Robert E. F ELDERMAN,
Alan E. K ULAWIK, Charles L.S EITZ, Jakov N. S EIZOVIC et Wen-King S U.
Myrinet : A Gigabit-per-Second Local Area Network. IEEE Micro, volume
15., février 1995. 21
[22] C.H. Papadimitriou et J. Ullman. A communication time
tradeoff. SIAM journal on computing. pages 16(4) :639-646, 1987. 38
[23] C.H. Papadimitriou et M. Yannakakis. Towards an
architectureindependent analysis of parallel algorithms. siam journal on
computing. pages 19(2) : 322-328, April 1990. 39
[24] Quadrics. URL : http ://www.Quadrics.com/. 21
[25] Andrei Radulescu, Cristina Nicolescu, Arjan J. C. van
Gemund et Pieter Jonker. CPR. Mixed task and data parallel scheduling for
distributed systems. In Proceedings of the 15th International Parallel and
Distributed Processing Symposium (IPDPS'01). IEEE Computer Society, 2001.
13
[26] Andrei Radulescu et Arjan J. C. van Gemund. A
low-cost approach towards mixed task and data parallel scheduling. In
Proceedings of the 15th International Conference on Parallel Processing
(ICPP'01), page 69-76. IEEE Computer Society, 2001. 13
[27] Shankar Ramaswamy, Sachin Sapatnekar et Prithviraj
Banerjee. A Framework for Exploiting Task and Data Parallelism on
Distributed Memory Multicomputers. IEEE Transactions on Parallel and
Distributed Systems. IEEE Computer Society, Nov 1997. 13
[28] V.J. Rayward-Smith. UET scheduling with unit
interprocessor communication delays. Discrete Applied Mathematics. 1987.
39
[29] MPI Forum ( Standards; archives; etc.). URL : http
://www.MPI-Forum.org/. 7
[30] L.G. Valiant. A bridging model for parallel
computation. communications of the ACM. pages 33(8) :103-111 August 1990.
42, 43
[31] Cray XT3. URL : http ://
www.Cray.com/products/xt3/index.html.
21
[32] YAMPII. URL : http ://now.cs.berkeley.edu/. 16
| 


